Prediction of Heat Transfer During Condensation in Annuli

Abstract

Many applications involve condensation in annuli; therefore, accurate prediction of heat transfer is important. While there have been a large number of experimental studies on condensation in tubes and several well-verified correlations are available for them, there have been very few experimental studies on annuli, and no well-verified correlation is available for prediction of heat transfer during condensation in annuli. This research was done to identify reliable correlations for this purpose and to develop a new one if needed. Literature was surveyed to identify experimental studies, test data, and predictive methods. Test data was compared to general correlations which have had considerable verification with data for condensation in channels. None of them was found fully satisfactory. A new correlation was developed by modifying the present author’s published correlation for condensation in tubes. It gives a MAD of 19.2% with available data from eight sources. Deviations of other correlations were much higher. The occurrence of surface tension effects and mini/macro channel boundary are investigated. The results of this research are presented and discussed.

1. Introduction

Many applications involve condensation in annuli; therefore, accurate prediction of heat transfer during condensation in annuli is needed. However, no well-verified correlation for this purpose is available. On the other hand, there have been a large number of experimental studies on condensation in tubes, and several well-verified correlations are available for them. It is well known that heat transfer during single-phase flow in annuli is satisfactorily predicted by correlations for tubes by using an equivalent diameter. Data for heat transfer during boiling in annuli have been satisfactorily predicted by correlations for tube by using them with an equivalent diameter, for example in Shah [1]. It may therefore be expected that heat transfer in condensation in annuli may be correctly predicted by correlations for tubes with a suitable equivalent diameter. Some authors have shown encouraging results with this approach through analysis of a limited amount of data, for example Cavallini et al. [2]. Whether this approach is generally valid and, if so, which equivalent diameter to use is not known. The present research was undertaken to answer these questions, to identify reliable correlations, and to develop a new one if needed. Literature was surveyed to identify experimental studies, test data, and predictive methods. Test data was compared to general correlations which have had considerable verification with data for condensation in channels. None of them was found fully satisfactory. Among these, the Shah [3] correlation gave the best agreement. A new correlation was developed by modifying it. It gave a MAD of 19.2% with available data from eight sources. Deviations of other correlations were much higher.

A related question is the effect of surface tension and the threshold for its occurrence in annuli. During condensation inside tubes, Shah [4] determined that surface tension effects can become dominant at We_GT < 100 and thus it is the boundary between macro and minichannels for condensation in tubes. Whether it is also the boundary for condensation in annuli is investigated.

The results of these researches are presented and discussed in the following. Before doing that, previous work is briefly reviewed.

2. Previous Work

Previous work on condensation in channels has most recently been reviewed by Shah [5].

2.1. Experimental Studies

The experimental studies that were found in literature are listed in Table 1 together with the range of parameters covered in them. There are a total of ten studies. Among these, Hashizume [6] and Cavallini et al. [2] do not provide data in analyzable form. Hence only eight of them give data which can be analyzed. In all of these studies, condensation occurred on the outer surface of the inner tube. Two of the studies were for vertical downflow, while the others were for horizontal flow. Fluids were water, ammonia, and halocarbon refrigerants. All fluids were single-component except for R-410A, which is a zeotropic mixture. However, its condensation involves negligible mass transfer effect, as its glide is only about 0.1 K. All fluids were free of contaminants such as compressor oil.

Among these studies, the most recent is that of Ruzaikin et al. [7]. They performed tests with two different annuli, one with annular gap of 2.5 mm and the other with annular gap of 1 mm, the latter being the smallest annular gap in the entire database. The tests were done using ammonia. Data for condensation of ammonia are scarce even for tubes. Hence these data are of special interest. Cooling fluid flowed through the inner tube while ammonia flowed in the annular gap. Condensation occurred on the outer surface of the inner tube. The outer tube was insulated. Wall surface temperatures were measured with thermocouples, and the condensing heat transfer coefficient was calculated using these measured wall temperatures. This method usually gives more accurate results than obtained by the method in which the overall heat transfer coefficient is measured and the condensing heat transfer coefficient calculated from it. All the other data analyzed in this paper were obtained by the latter method except those of Miropoloskiy et al., for which the methodology is not stated.

Table 1. Published experimental studies on condensation in annuli and their range of parameters. Condensation occurred on the inner tube in all studies.

Source	Dout/Din mm/mm (Flow Direction)	Dhyd (DHP) mm	Fluid	pr	G kg·m−2 s−1	x	ReLT	WeGT	FrLT	Are Analyzable Data Provided?
Li et al. [8]	17/12.7 (H)	4.3 (10.5)	R-410A	0.4347 0.5542	75 225	0.2 0.8	8830 26482	76 693	0.15 1.3	Yes
Borchmann [9]	38/ 31.2 (H)	6.8 (15.0)	R-11	0.0373	29 286	0.55 1.0	1245 12278	39 3747	0.006 0.59	Yes
He et al. [10]	22.0/16.0 (H)	6.0 (14.2)	R-410A	0.5542	54 96	0.12 0.76	8628 15333	55 176	0.055 0.175	Yes
Tang et al. [11]	26.0/19.05 (H)	6.95 (16.4)	R-134A	0.2846	50 100	0.50 0.60	5436 10844	55 221	0.029 0.116	Yes
	25.0/19.05 (H)	5.9 (13.7)	R-134A	0.2846	52 108	0.5	4746 9781	51 218	0.038 0.160	Yes
Wang et al. [12])	26.0/15.8 (H)	10.2 (27.0)	R-11	0.059	13 103	0.5	1151 9198	8 538	0.00084 538	Yes
Chen et al. [13]	17.0/12.7 (H)	4.3 (10.1)	R-410	0.5542	38 227	0.45	4255 25588	19 706	0.038 1.36	Yes
			R-22	0.3453	52 247	0.45	4004 18985	29 649	0.053 1.2	Yes
	25.0/12.7 (H)	12.3 (38.1)	R-410	0.5542	9 56	0.45 0.65	3692 24110	3 129	0.00067 0.029	Yes
			R-22	0.3453	18 41	0.45	3896 11811	6 52	0.0012 0.011	Yes
Miropoloskiy et al. [14]	21.7/18.0 (VD)	3.7 (8.16)	Water	0.0361 0.4523	100 600	0.02 0.99	5115 42884	56 805	0.34 14.7	Yes
Ruzaikin et al. [7]	8.0/6.0 (H)	2.0 (4.7)	NH3	0.1609 0.2593	80 200	0.13 0.78	1613 3707	52 359	1.1 6.3	Yes
	11.0/6.0 (H)	5.0 (14.2)		0.1221 0.2032	41 122	0.09 0.80	1728 6151	44 300	0.100 0.987	Yes
Cavallini et al. [2]	38.5/24.0 (VD)	14.5 (37.8)	R-11	0.0236 0.0329	58 187	0.47 1.0				No
			R-113	0.0295 0.0410	63 223	0.11 1.0				No
Hashizume [6]	25.0/15.88 (H)	9.12. (23.4)	R-22	0.2710 0.3458						No

Table 1. Published experimental studies on condensation in annuli and their range of parameters. Condensation occurred on the inner tube in all studies.

Source	Dout/Din mm/mm (Flow Direction)	Dhyd (DHP) mm	Fluid	pr	G kg·m−2 s−1	x	ReLT	WeGT	FrLT	Are Analyzable Data Provided?
Li et al. [8]	17/12.7 (H)	4.3 (10.5)	R-410A	0.4347 0.5542	75 225	0.2 0.8	8830 26482	76 693	0.15 1.3	Yes
Borchmann [9]	38/ 31.2 (H)	6.8 (15.0)	R-11	0.0373	29 286	0.55 1.0	1245 12278	39 3747	0.006 0.59	Yes
He et al. [10]	22.0/16.0 (H)	6.0 (14.2)	R-410A	0.5542	54 96	0.12 0.76	8628 15333	55 176	0.055 0.175	Yes
Tang et al. [11]	26.0/19.05 (H)	6.95 (16.4)	R-134A	0.2846	50 100	0.50 0.60	5436 10844	55 221	0.029 0.116	Yes
	25.0/19.05 (H)	5.9 (13.7)	R-134A	0.2846	52 108	0.5	4746 9781	51 218	0.038 0.160	Yes
Wang et al. [12])	26.0/15.8 (H)	10.2 (27.0)	R-11	0.059	13 103	0.5	1151 9198	8 538	0.00084 538	Yes
Chen et al. [13]	17.0/12.7 (H)	4.3 (10.1)	R-410	0.5542	38 227	0.45	4255 25588	19 706	0.038 1.36	Yes
			R-22	0.3453	52 247	0.45	4004 18985	29 649	0.053 1.2	Yes
	25.0/12.7 (H)	12.3 (38.1)	R-410	0.5542	9 56	0.45 0.65	3692 24110	3 129	0.00067 0.029	Yes
			R-22	0.3453	18 41	0.45	3896 11811	6 52	0.0012 0.011	Yes
Miropoloskiy et al. [14]	21.7/18.0 (VD)	3.7 (8.16)	Water	0.0361 0.4523	100 600	0.02 0.99	5115 42884	56 805	0.34 14.7	Yes
Ruzaikin et al. [7]	8.0/6.0 (H)	2.0 (4.7)	NH3	0.1609 0.2593	80 200	0.13 0.78	1613 3707	52 359	1.1 6.3	Yes
	11.0/6.0 (H)	5.0 (14.2)		0.1221 0.2032	41 122	0.09 0.80	1728 6151	44 300	0.100 0.987	Yes
Cavallini et al. [2]	38.5/24.0 (VD)	14.5 (37.8)	R-11	0.0236 0.0329	58 187	0.47 1.0				No
			R-113	0.0295 0.0410	63 223	0.11 1.0				No
Hashizume [6]	25.0/15.88 (H)	9.12. (23.4)	R-22	0.2710 0.3458						No

2.2. Correlations

No correlations have been proposed specifically for annuli. A few authors compared a limited amount of data with correlations for tubes as described below.

Cavallini et al. [2] condensed R-11 and R-113 in a vertical annulus. The data were compared to the correlation of Shah [15] using D_HYD as the equivalent diameter. Data were over-predicted by 20% to 25%. The Shah [15] correlation is given by the following equation.

$$h_{TP}=h_{LS}\left(1+3.8/Z^{0.95}\right)$$

(1)

where h_LS is the superficial heat transfer coefficient of the liquid phase given by

$$h_{LS}=0.023{Re}_{LS}^{0.8}{Pr}_L^{0.4}{k}_L/D$$

(2)

Z is the correlating parameter introduced by Shah [15] defined as

$$Z=(1/x-1{)}^{0.8}{p_r}^{0.4}$$

(3)

Miropoloskiy et al. [14] compared their data for water with the correlation of Ananiev et al. [16]; satisfactory agreement was reported. For equivalent diameter, they used (D_HYD. ε) where ε is the void fraction. The Ananiev et al. correlation for tubes is given by the following equation.

$$h_{TP}=h_{LT}{\left({\displaystyle \frac{{\rho }_L}{{\rho }_{TP}}}\right)}^{0.5}$$

(4)

where h_LT is the heat transfer coefficient assuming that all mass is flowing as liquid. ρ_TP is the density of vapor-liquid mixture calculated by the homogeneous model as below.

$${\rho }_{TP}={\displaystyle \frac{{{\rho }_G\rho }_L}{{\rho }_G+x\left({\rho }_L-{\rho }_G\right)}}$$

(5)

Shah [3] gave a correlation which was verified with a vast amount of data for condensation in channels. Included in the data were those of Borchman [9] and Li et al. [8] for annuli; both were in satisfactory agreement with the correlation. The Shah [3] correlation uses the following two equations.

$$h_I=h_{LS}\left(1+{\displaystyle \frac{3.8}{Z^{0.95}}}\right){\left({\displaystyle \frac{{\mu }_L}{14{\mu }_G}}\right)}^{(0.0058+0.557p_r)}$$

(6)

$$h_{\mathit{Nu}}=1.32{Re}_{LS}^{-1/3}{\left[{\displaystyle \frac{{\rho }_L({\rho }_L-{\rho }_G)g{k_L}^3}{{{\mu }_L}^2}}\right]}^{1/3}$$

(7)

Equation (7) is the Nusselt equation for laminar condensation in vertical tubes, with the constant increased by 20% as recommended by McAdams [17].

There are three regimes of heat transfer in this correlation.

In Regime I,

$$h_{TP}=h_I$$

(8)

In Regime II,

$$h_{TP}=h_I+h_{Nu}$$

(9)

In Regime III:

$$h_{TP}=h_{Nu}$$

(10)

Separate criteria are given for determining the heat transfer regimes in horizontal and vertical downflow. These depend mainly on the dimensionless vapor velocity J_g which is defined below.

$$J_g={\displaystyle \frac{xG}{{\left(gD{\rho }_G\left({\rho }_L-{\rho }_G\right)\right)}^{0.5}}}$$

(11)

An important factor determining heat transfer in horizontal channels is Weber number We_GT,

$${We}_{GT}={\displaystyle \frac{G^{2}D}{{\rho }_G\sigma }}$$

(12)

when We_GT < 100, surface tension effects become significant if at the same time Fr_LT < 0.026 and heat transfer Regime is I. Fr_LT is defined as

$${Fr}_{LT}={\displaystyle \frac{G^2}{{gD\rho }_L^2}}$$

(13)

In the Shah correlation, D_HP is used as the equivalent diameter in calculating h_LS; D_HYD is used as equivalent diameter in all other parameters. Definitions of these equivalent diameters are

$$D_{HP}={\displaystyle \frac{4\times Flowarea}{Perimeterwithheattransfer}}$$

(14)

$$D_{HYD}={\displaystyle \frac{4\times Flowarea}{WettedPerimeter}}$$

(15)

Many other correlations have been proposed for condensation in tubes. Among these, those which were reported to be in agreement with a wide range of data from many sources are Kim and Mudawar [18], Dorao and Fernandino [19], Hosseini et al. [20], Moradkhani et al. [21], Nie et al. [22], Marinheiro et al. [23], and Moser et al. [24]. Correlation of Traviss et al. [25] was derived from a theoretical analysis with many simplifying assumptions.

3. Data Analysis

The available analyzable test data are listed in Table 1. They were analyzed in two stages. In the first stage, the test data were compared to the correlations for tubes mentioned in Section 2.2. As none of those correlations gave satisfactory agreement with data, further analyses were done in which attempts were made to develop an accurate method for predicting heat transfer in annuli.

3.1. Comparison with Correlations for Tubes

3.1.1. Calculation Methodology

In calculations with the Shah [3] correlation, D_HP was used in calculating single-phase heat transfer coefficient and Reynolds number as required by it. D_HYD was used throughout with all other correlations. Kim and Mudawar [18], Dorao and Fernandino [19], Hosseini et al. [20], Moradkhani et al. [21], and Marinheiro et al. [23] had specified use of D_HYD throughout. Others had not specified the equivalent diameter to be used.

Where the authors reported mean heat transfer coefficients, data were analyzed using the arithmetic mean quality. All the data were for mean heat transfer coefficients except those of Miropoloskiy et al. and Borchmann.

Miropoloskiy et al. [14] have reported their data in terms of (h_TP/h_LT). To get h_TP from their data, h_LT was calculated with Equation (2) by substituting Re_LT in place of Re_LS. D_HYD was used as equivalent diameter in these calculations. Only data for Re_LT > 2300 were analyzed, as the formula used by them to calculate h_LT in this range was not clear.

All properties were obtained from REFPROP 9.1, Lemmon et al. [26]. All properties used were at saturation temperature. Deviations of correlations were calculated as below.

Mean absolute deviation (MAD) is defined as

$$MAD={\displaystyle \frac{1}{N}}{\sum }_1^{N}ABS\left\{\left(h_{predicted}-h_{measured}\right)/h_{measured}\right\}$$

(16)

Average deviation (AD) is defined as

$$AD={\displaystyle \frac{1}{N}}{\sum }_1^N\left\{\left({\mathrm{h}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}-{\mathrm{h}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}}\right)/{\mathrm{h}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}}\right\}$$

(17)

3.1.2. Results of Data Analysis

The results of data analysis are given in

Table 2. Results of comparison of test data for annuli with various correlations.

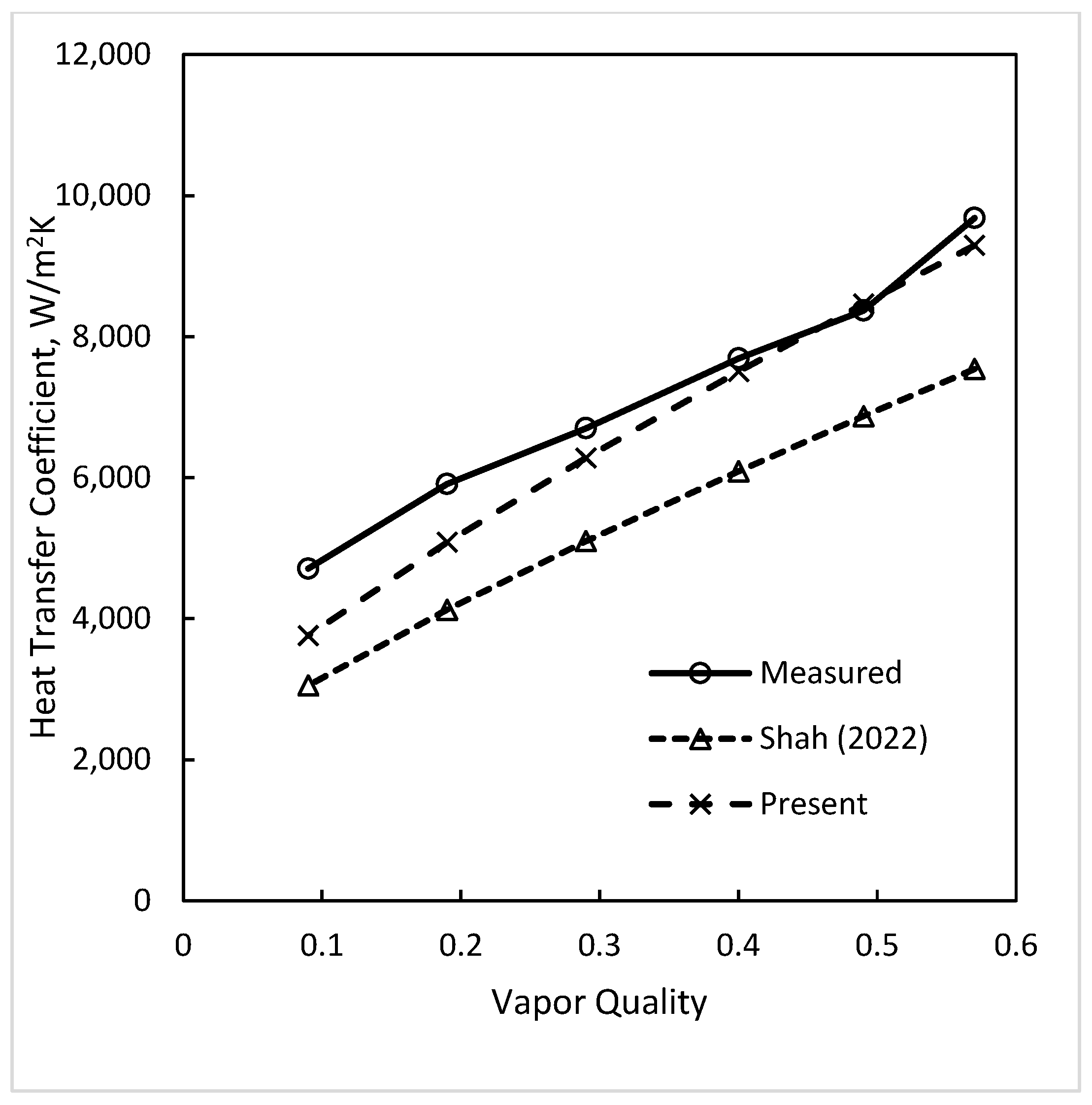
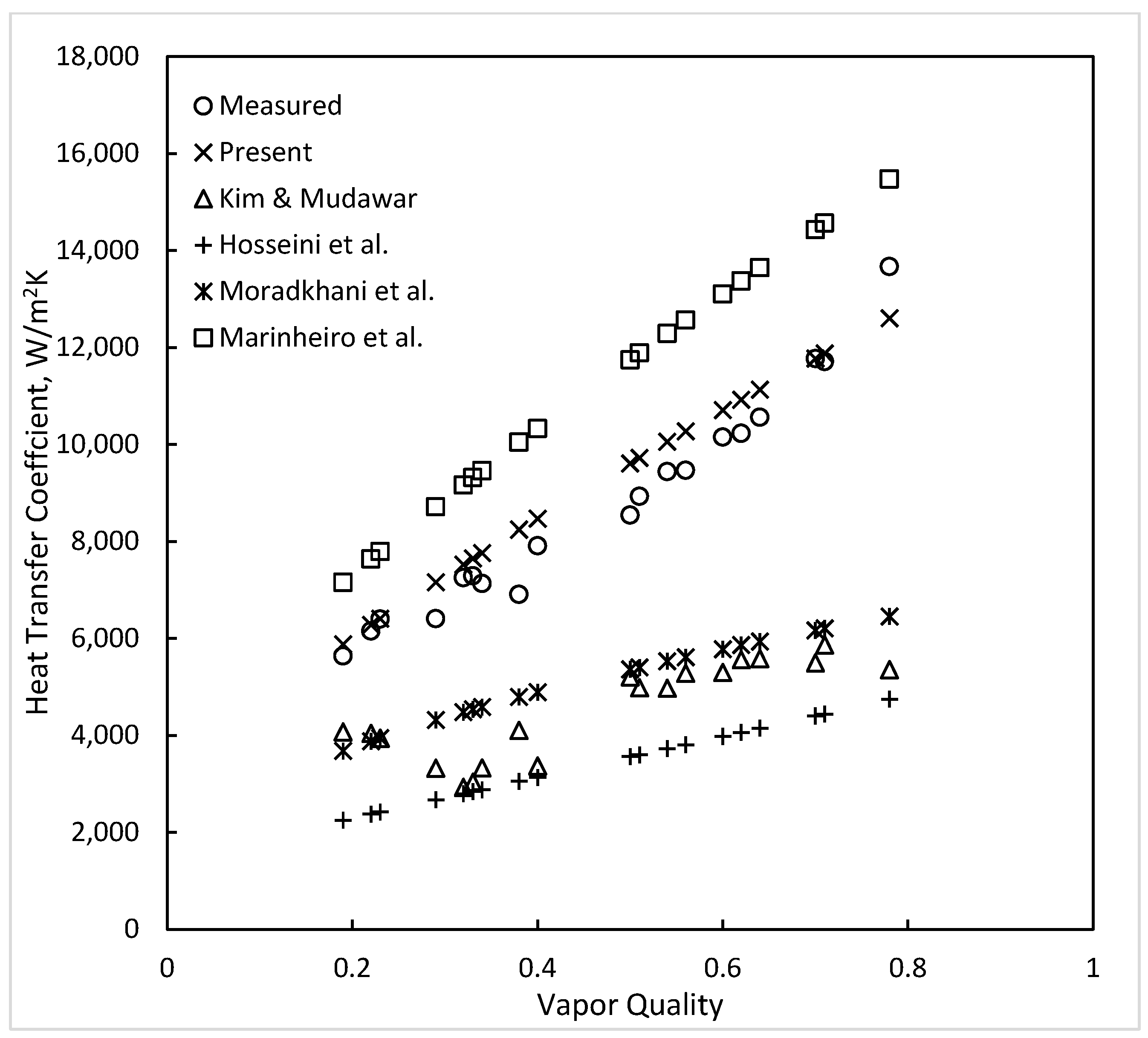
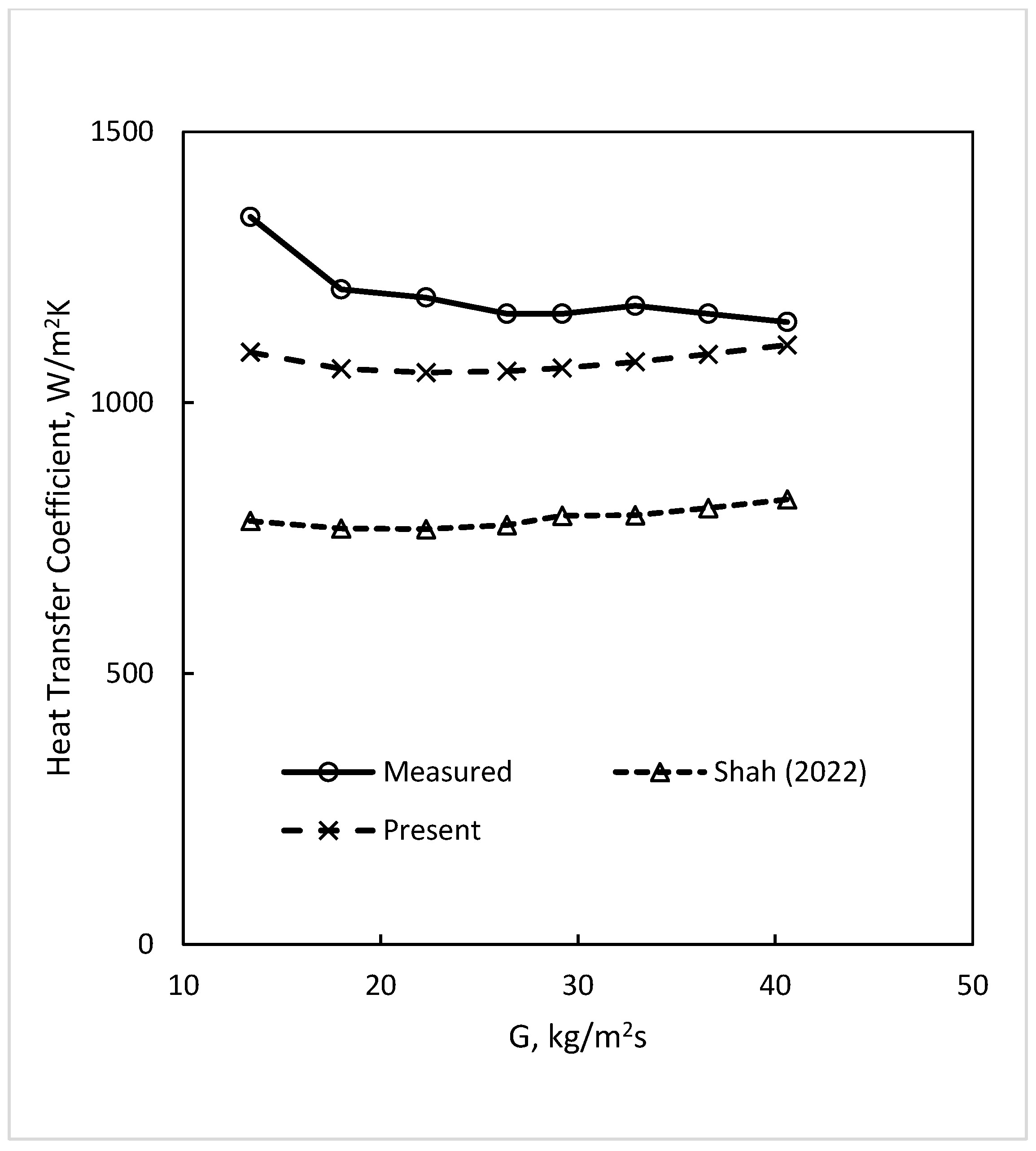
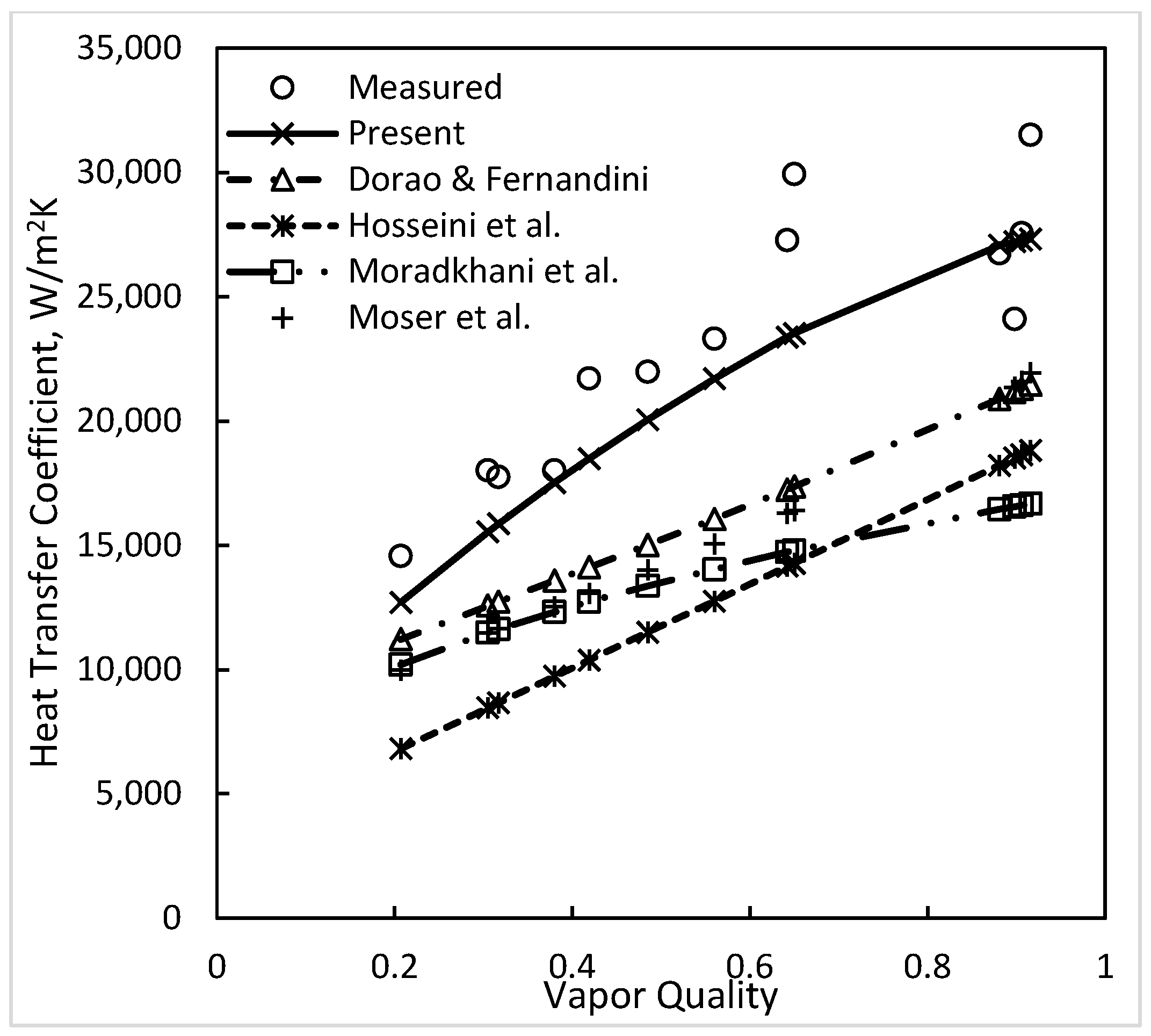
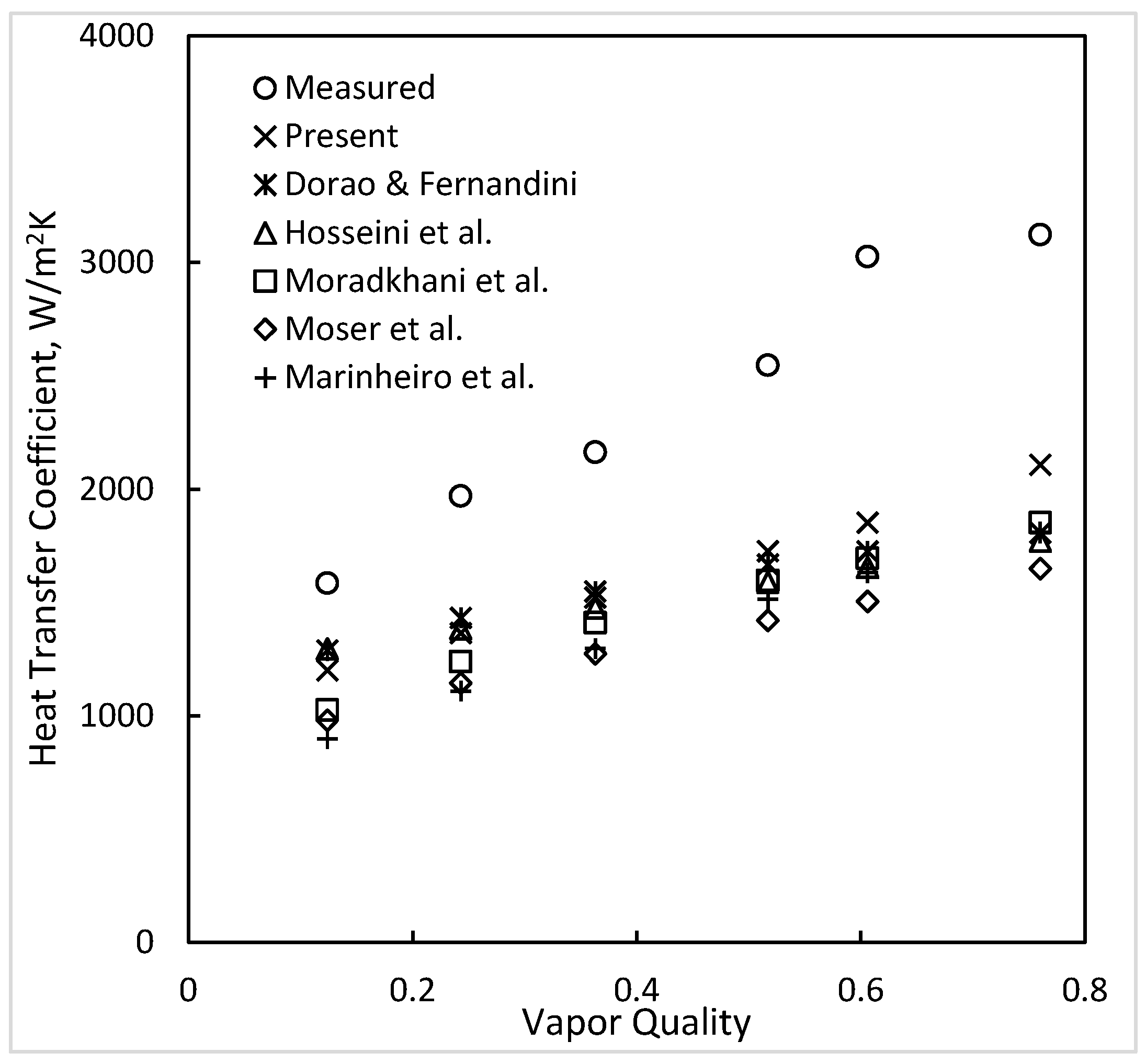
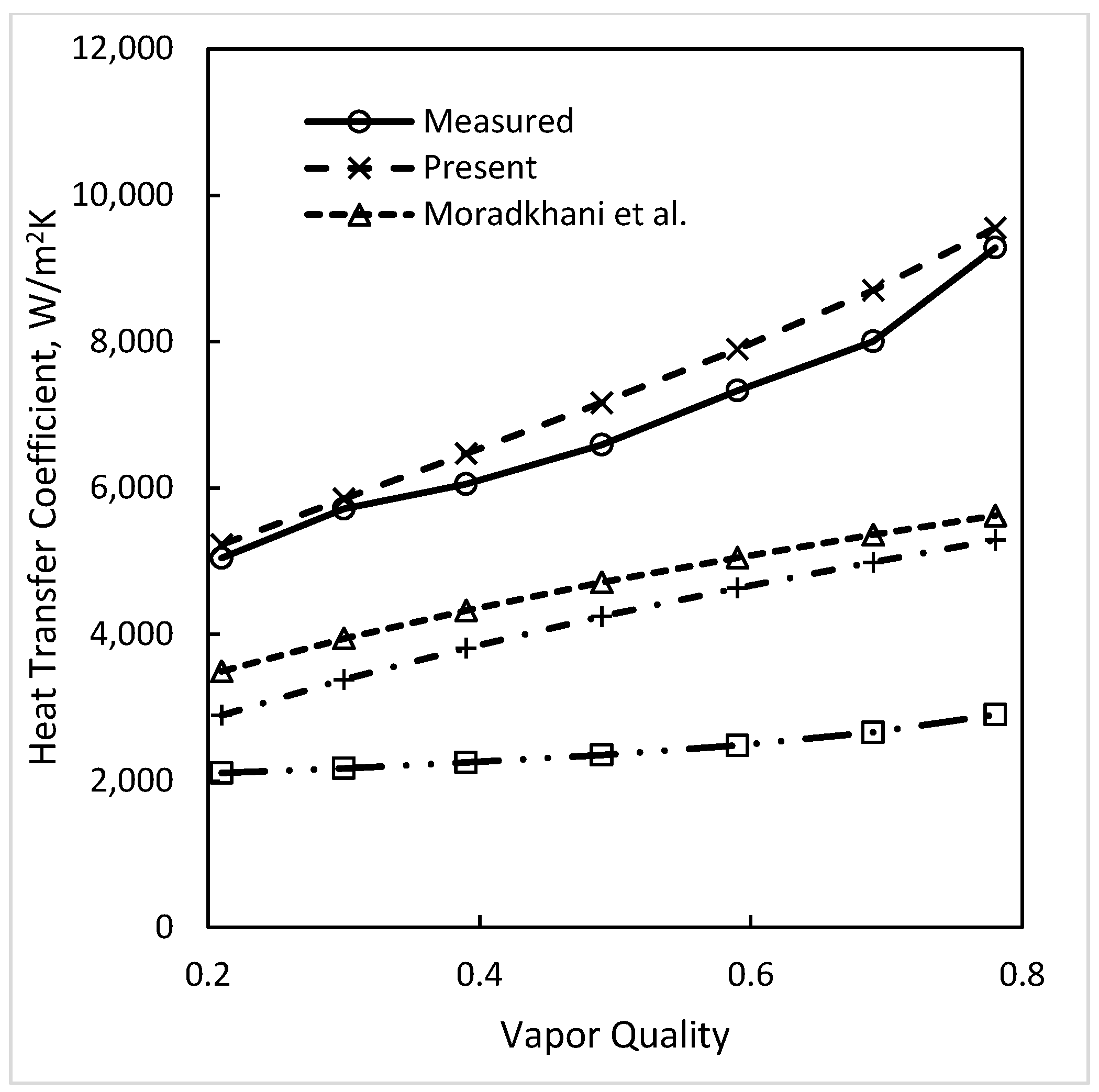
Source	Dout/Din mm/mm (Orient.)	Dhyd (DHP) mm	Fluid	N	Deviation, % Mean Absolute Average
					Kim & Mudawar [18]	Ananiev et al. [16]	Dorao & Fernandino [19]	Hosseini et al. [20]	Moradkhani et al. [21]	Moser et al. [24]	Marinheiro et al. [23]	Shah [3]	New Correlation
Li et al. [8] *	17/12.7 (H)	4.3 (10.5)	R-410A	13	10.1 −6.2	12.5 −9.0	24.9 24.9	17.7 17.7	29.3 29.3	22.9 22.1	21.3 21.3	10.5 5.2	17.8 15.6
Borchmann [9]	38/ 31.2 (H)	6.8 (15.0)	R-11	5	13.1 −6.5	28.1 −28.1	33.5 −33.5	16.6 −16.3	5.6 −2.0	20.9 −20.9	24.3 −24.3	30.3 −30.3	24.1 −17.1
He et al. [10]	22.0/16.0 (H)	6.0 (14.2)	R-410A	18	53.2 −53.3	66.8 −66.1	36.4 −36.4	30.1 −30.1	44.6 −44.6	50.9 −50.9	47.6 −47.6	46.5 −46.5	33.0 −33.0
Tang et al. [11]	26.0/19.05 (H)	6.95 (16.4)	R-134a	6	18.1 −18.1	29.3 −29.3	29.4 29.4	61.1 61.1	16.3 16.3	7.6 5.3	16.5 16.5	14.5 14.5	41.7 41.7
	25.0/19.05 (H)	5.9 (13.7)	R-134a	7	20.7 20.7	10.4 10.1	77.2 77.2	129.2 129.2	62.2 62.2	52.1 52.1	65.4 65.4	52.0 52.0	87.7 87.7
Wang et al. [12]	26.0/15.8 (H)	10.2 (27.0)	R-11	10	62.2 −25.4	64.0 −64.0	34.6 −34.6	40.0 −40.0	38.9 −38.9	55.9 −55.9	44.6 −44.6	46.8 −46.8	31.5 −31.5
Chen et al. [13]	17.0/12.7 (H)	4.3 (10.1)	R-410A	9	12.3 0.9	23.6 −15.6	23.2 22.6	22.2 22.2	28.1 20.9	29.7 18.4	22.6 16.3	11.7 −6.6	19.9 13.7
			R-22	8	25.9 17.4	21.6 −16.7	18.0 17.8	9.0 8.7	24.7 19.1	23.7 10.2	21/8 18.0	7.8 −6.8	16.3 12.6
	25.0/12.7 (H)	12.3 (38.1)	R-410	22	49.8 −32.9	76.5 −76.5	33.3 −31.2	42.9 −42.9	49.1 −49.1	4.3 −64.3	53.1 −53.1	45.7 −45.7	27.6 −25.7
			R-22	8	130.1 122.5	76.3 −76.3	22.5 −22.5	53.7 −53.7	45.7 −45.7	64.9 −64.9	48.2 −48.2	34.1 −34.1	9.9 −9.9
Miropoloskiy et al. [14]	21.7/18.0 (VD)	3.7 (8.16)	Water	96	20.7 18.9	12.2 0.3	27.9 −17.4	29.0 −23.0	28,1 −19.7	26.8 −26.8	27.6 −21.7	23.7 −23.7	12.7 −10.6
Ruzaikin et al. [7]	8.0/6.0	2.0 (4.7).	NH3	60	62.0 62.0	32.4 32.3	29.2 29.2	13.4 −2.7	55.3 55.3	18.3 17.3	31.1 31.1	34.9 34.7	15.0 13.1
	11.0/6.0	5.0 (14.2)		50	32.3 20.5	24.8 −24.4	11.9 4.0	22.8 −1.7	20.6 −20.5	31.4 −31.4	15.5 −12.8	15.0 −3.6	15.0 −3.6
All sources				312	38.1 18.2	30.2 −13.1	27.2 −1.2	28.5 −9.9	35.5 −3.2	31.8 −18.2	30.4 −8.7	25.3 −26.5	19.2 −2.4

. It is seen that for all data, the Shah [3] correlation has the least MAD at 25.3%. The next best are Dorao & Fernadino and Hosseini et al. with MAD of 27.2% and 28.5%, respectively.

Table 2 does not include the results for the correlation of Traviss et al. and Nie et al., as they had large deviations with most data.

While the overall accuracy of all correlations is fair to poor, many of the data sets give good agreement with some correlations. On the other hand, some of the data sets show poor agreement with all correlations.

While the Shah correlation has the least MAD, better accuracy is needed. Attempts were therefore made to develop a more accurate correlation as described below.

3.2. Development of Improved/New Correlation

As the Shah [3] correlation had given the best results, efforts were directed to improve its accuracy. Several approaches were tried.

3.2.1. First Approach

The first approach tried was to use D_HYD throughout the calculations instead of using D_HP in some places and D_HYD in some places as required. The results with this approach are seen in

Table 3. Comparison of deviations from data of the published Shah [25] correlation and its modification.

Source	Dout/Din Mm/mm (Orient.)	Dhyd (DHP) mm	Fluid (Glide, K) **		N	Deviation, % Mean Absolute (Upper Line) Average (Lower Line)
						Shah [3] Published	Shah [3] DHYD Used Throughout	Shah [3] with Alferov-Rybin Cor.	New Correlation
Li et al. [8]	17.0/12.7 (H)	4.3 (10.5)	R-410A (0.1)		13	10.5 5.2	17.8 15.6	12.6 6.1	17.8 15.6
Borchmann [9]	38/ 31.2 (H)	6.8 (15.0)	R-11		5	30.3 −30.3	24.1 −17.1	31.4 −31.1	24.1 −17.1
He et al. [10]	22.0/16.0 (H)	6.0 (14.2)	R-410A (0.1)		18	46.5 −46.5	33.0 −33.0	40.2 −40.2	33.0 −33.0
Tang et al. [11]	26.0/19.05 (H)	6.95 (16.4)	R-134a		6	14.5 14.5	41.7 41.7	25.3 25.3	41.7 41.7
	25.0/19.05 (H)	5.9 (13.7)	R-134a		7	52.0 52.0	87.7 87.7	63.8 63.8	87.7 87.7
Wang et al. [12]	26.0/15.8 (H)	10.2 (27.0)	R-11		10	46.8 −46.8	31.5 −31.5	35.0 −35.0	31.5 −31.5
Chen et al. [13]	17.0/12.7 (H)	4.3 (10.1)	R-410		9	11.7 −6.6	19.9 13.7	13.7 0.3	19.9 13.7
			R-22		8	7.8 −6.8	16.3 12.6	7.7 −1.1	16.3 12.6
	25.0/12.7 (H)	12.3 (38.1)	R-410		22	45.7 −45.7	27.6 −25.7	27.1 −24.8	27.6 −25.7
			R-22		8	34.1 −34.1	9.9 −9.9	9.9 −9.9	9.9 −9.9
Miropoloskiy et al. [14]	21.7/18.0 (VD)	3.7 (8.16)	Water		96	23.7 −23.7	12.7 −12.6	26.0 −26.0	12.7 −12.6
Ruzaikin et al. [7]	8.0/6.0 (H)	2.0 (4.7)	Ammonia		60	15.0 13.1	34.9 34.7	14.8 −5.7	15.0 13.1
	11.0/6.0 (H)	5.0 (14.2)			50	24.7 −24.3	15.0 −3.6	19.1 18.0	15.0 −3.6
All sources	MAD %, giving equal weight to each data point			312		25.3 −26.5	23.0 1.7	23.2 −9.2	19.2 −2.4

** Glide give only for mixtures.

. Deviations of some data sets improved while those of others increased. For all data, the MAD with this approach improved to 23.0% compared to 25.3% with the published correlation.

3.2.2. Second Approach

The next approach tried was to use a single-phase heat transfer correlation developed by Alferov and Rybin [27] in place of the Dittus–Boelter equation, Equation (2). They performed tests with water flowing in vertical annuli in which the inner tube had OD of 15 mm while annular gaps were 1, 1.5, 3, and 5 mm. In some tests, only the inner tube was heated; in some, only the outer tube was heated; and in some tests, both tubes were heated. They developed the following correlation for single-phase heat transfer.

$$h_{LT}=0.023E{\left({\displaystyle \frac{G{D}_{HYD}}{{\mu }_L}}\right)}^{0.8}{{Pr}_L}^{0.4}{k}_L/D_{HYD}$$

(18)

If only the inner tube is heated,

$$E={\left({\displaystyle \frac{D_{OUT}}{D_{IN}}}-1\right)}^{0.12}$$

(19)

This relation was shown to be also in good agreement with data from three other sources in which (D_OUT/D_IN) varied from 1.24 to 1.375. Thus, for all data for heating on inner tube only, (D_OUT/D_IN) ranged 1.13–1.67. With heating on outer tube only and with heating on both tubes, E = 1.

Calculations were done with the Shah [3] correlation using the Alferov & Rybin correlation to calculate the single-phase heat transfer coefficient. As seen in Table 3, this approach resulted in MAD of 23.2% with all data. This is an improvement over the result with the published Shah correlation.

3.2.3. Third Approach

While developing correlations for saturated and subcooled boiling heat transfer, the present author had obtained good agreement with data for annuli by calculating single-phase heat transfer using D_HYD for larger annular gaps and D_HP for smaller annular gaps. For example, the Shah [28] correlation for subcooled boiling in channels calculates single-phase heat transfer coefficient of liquid as below.

Use D_HYD when annular gap > 3 mm.

Use D_HP when annular gap < 3 mm.

It was decided to try out this approach. Study of the results in Table 3 shows that for most data sets, use of D_HYD throughout gives comparable or lower deviations than while using D_HP. A notable exception is the data of Ruzaikin et al. for the annulus with 1 mm gap, for which use of D_HP for calculating the single-phase heat transfer coefficient gives much lower deviations. The data set with the next smallest annular gap (1.85 mm) is that of Miropoloskiy et al., which has much lower deviation when using D_HYD throughout. Using D_HP for the 1 mm gap annulus and D_HYD for all other data, the resulting MAD for all data is 19.2%. This is much lower than the MAD of 25.2% of the Shah [3] correlation. It is also well below the MAD of 23.0 and 23.2 percent of the other two approaches that were tried.

3.2.4. Selected New Correlation

As seen in Section 3.2.3, the third approach gives significantly lower MAD for the database compared to the other three approaches. Therefore, the new correlation should be based on it.

The data of Miropoloskiy et al. for 1.85 mm annular gap give good result using D_HYD, while the data of Ruzaikin et al. for 1 mm annular gap give good agreement using D_HP. Hence the transition point is somewhere between 1 mm and 1.85 mm annular gap. Until more data are available within this range, the transition point may tentatively be taken midway between them at 1.5 mm annular gap. Thus, the new correlation is as follows:

For annuli with annular gap > 1.5 mm, use D_HYD throughout in the Shah [3] correlation.

For annuli with annular gap < 1.5 mm, use the Shah [3] correlation without any change, i.e., use D_HP in calculating single-phase heat transfer coefficient; use D_HYD in all other calculations.

The results using this modified/new correlation are listed in Table 3. It is seen that the MAD of the new correlation is 19.2%, well below that of the published correlation as well as those of the other two approaches that were tried.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 illustrate the greater accuracy of the new correlation compared to Shah [3] correlation as well as other correlations.

4. Discussion

4.1. Accuracy of Test Data

Some of the data analyzed seem to be inaccurate as discussed below.

Figure 7 shows the comparison of the data of He et al. [9] with a number of correlations. It is seen that all correlations considerably underpredict the data. Further, all correlations underpredict the data by 30 to 40 percent. The fact that all correlations underpredict and agree among themselves suggests that these data may be inaccurate.

He et al. had reported good agreement with the correlation of Cavallini et al. [29]. This correlation has two regimes, ΔT-independent and ΔT-dependent. Present calculations showed that all their data fall in the latter regime. The formula for the ΔT-dependent regime requires the insertion of ΔT. He et al. also reported good agreement with three other correlations; all of them require insertion of ΔT. As ΔT is unknown, proper evaluation requires iterative calculations with assumed ΔT. He et al. have not stated that they did iterative calculations. It appears that they substituted the measured ΔT in the formulas during their evaluation. This will naturally give good agreement with data.

The data of Wang et al. [12] are also grossly underpredicted by almost all correlations. Therefore, these data are also suspected to be inaccurate.

Tang et al. [11] performed tests with two annuli. The diameter of the inner tube was 19 mm for both annuli. The diameter of the external tube was 26 mm in the first annulus and 25 mm in the second annulus; D_HYD of the two were 6.95 mm and 5.95 mm, respectively. The fluid and operating conditions in the two annuli were the same. Experience with both single-phase and condensing flow indicates that the heat transfer coefficient increases with decreasing diameter. Yet the reported heat transfer coefficients for the 5.95 mm hydraulic diameter annulus are 25–45 percent lower than those in the annulus with 6.95 mm hydraulic diameter. As seen in Table 2, the data for the 25 mm diameter outer tube are greatly overpredicted by most of the correlations. It therefore appears that the data for the annulus with the 25 mm diameter outer tube are very inaccurate.

If the data mentioned above as probably inaccurate are not considered, the MAD of the present correlation becomes 16.1%. The deviations of most other correlations also become lower.

4.2. Effect of Surface Tension, Mini/Macro Channel Boundary

The Shah [3] correlation provides a criterion for determining the mini/macro channel boundary during condensation in tubes and includes a method to calculate heat transfer in the minichannel regime. These are incorporated into the present correlation for application to annuli. It is therefore necessary to know whether the methodology for tubes also works for annuli. This investigation was done and reported in the following. First, some background is provided.

Channels with hydraulic diameter ≤3 mm are generally considered to be minichannels. This boundary was suggested by Kandlikar [30] without any consideration of surface tension effects. Many authors regard minichannels to be those in which heat transfer is affected by surface tension and as a result the correlations based on macro channel data fail. A number of criteria have been proposed for the mini/macro boundary based on the Bond number and its equivalent confinement number and Eotvos number. Bond number Bd is the ratio of gravity forces to surface tension forces defined as below.

$$Bd={\displaystyle \frac{g{D}^2\left({\rho }_L-{\rho }_G\right)}{\sigma }}$$

(20)

The relation between Bond number Bd, confinement number Co, and Eotvos number Eo is expressed by the following equation.

$$Eo={\displaystyle \frac{Bd}{8}}={\displaystyle \frac{1}{8{Co}^2}}$$

(21)

Several definitions of Eo have been given by different authors. The definition used above is that given by Brauner and Ullman [31], who gave a criterion for mini/macro channel boundary based on this definition. Similarly, there are several definitions of Co in the literature. The definition used here is that given by Kew and Cornwell [32] who gave a criterion for the mini/macro channel boundary based on this definition. Ong and Thome [33] have also used the same definitions of Eo and Co as in this paper.

Some criteria have been based on the capillary number, also known as the Laplace constant. Shah [5,34] reviewed the evaluation of these criteria against experimental data by various authors. None of them was found satisfactory.

For condensation in tubes, Shah [4] determined that surface tension effects can become important when the ratio of inertia force to surface tension force becomes low. Weber number We_GT is that ratio. This factor is included in the Shah [3] correlation. According to it, surface tension effects enhance heat transfer in horizontal tubes when all these three conditions are met: Shah correlation’s heat transfer regime is I, Fr_LT < 0.026, and We_GT < 100. Surface tension has no effect in vertical flow. This criterion was verified in Shah [3] with data for 51 fluids from 130 sources. It was shown that all other correlations underpredict data when this criterion is met.

It is important to know whether this criterion for tubes is applicable to annuli and whether the Shah correlation gives satisfactory results for annuli under this condition. To find that, the data analyzed during the present research were carefully examined. The range of Fr_LT and We_GT in the data are listed in Table 1 and

Table 4. Complete range of data for which the present correlation has been verified. All annuli were cooled only on the inner tube.

Parameter	Range
DHYD, mm	2.0–12.3
DHP, mm	8.2–27.0
Annular gap, mm	1.0–6.15
DOUT/DIN	1.2–1.97
Fluids	Water, ammonia, R-11, R-22, R-113, R-134a, R-410A
Flow direction	Horizontal, vertical downwards
pr	0.0236–0.5542
G, kg/m2 s	9–600
x	0.02–1.0
ReLT	1245–42,884
WeGT	8–805
FrLT	0.00084–338

. Several data sets included We_GT < 100, but for all such data the heat transfer regime was II. There were no data for which Shah’s heat transfer regime is I together with Fr_LT < 0.026 and We_GT < 100. Hence, according to this criterion, none of the annuli data analyzed fall into minichannel category. Nevertheless, the data for We_GT < 100 were reviewed to see whether any enhancement due to surface tension may have occurred.

Figure 8 shows data of Ruzaikin et al. at We_GT = 50. The Shah correlation heat transfer regime is II. Hence, according to the present correlation, these data are in the macro channel regime and there is no enhancement due to surface tension. The present correlation is seen to be in close agreement with the data, thus showing that the mini/macro boundary according to this correlation is correct.

Figure 9 and Figure 10 show the data of Chen et al. for R-410A and R-22 as a function of Weber number. For all these data, We_GT < 100 and the heat transfer regime is II. Hence, according to the present correlation, these data are in the macro channel regime and therefore surface tension has no effect. It is seen that the present correlation is in good agreement with these data. This indicates that the mini/macro channel demarcation according to the present correlation is valid.

As there are no data in the minichannel regime, the applicability of the present correlation to annuli in the minichannel regime remains to be confirmed. This can be done only when such data become available.

4.3. Design Recommendation

The present correlation is recommended for condensation in annuli in which only the inner tube is cooled. Caution should be exercised in the minichannel regime of the present correlation, as none of the data analyzed were in that regime. The complete range of data analyzed is given in Table 4.

All data analyzed are for horizontal and vertical downflow. It should be used for only those orientations. Use for other orientations is not recommended.

As no data for annuli in which condensation occurred on the outer tube or both tubes have been analyzed, use of this correlation for such annuli is not recommended.

5. Conclusions

• The literature on heat transfer during condensation in annuli was surveyed. It was found that there is no well-verified method for the prediction of heat transfer in annuli.
• Analyzable data were found from eight sources, all for condensation on the inner tube. Those were compared to general correlations which had been verified with a wide range of data for condensation in tubes, using the equivalent diameter recommended by them for partially cooled channels. Considering all data, none of them gave good agreement, the best being the Shah [3] correlation with MAD of 25.3%.
• A new correlation was developed by modifying the Shah (3) correlation. It gave a MAD of 19.2%. The MAD of other correlations were much higher. The data correlated included water, ammonia, and halocarbon refrigerants in vertical and horizontal annuli over a considerable range of flow rate and reduced pressure.
• There is need for more test data to cover a wider range of conditions, especially very small annular gaps, to further verify and improve the new correlation. Data are also needed for annuli in which condensation occurs on the outer tube or on both tubes, and on flow directions other than horizontal and vertically downwards.