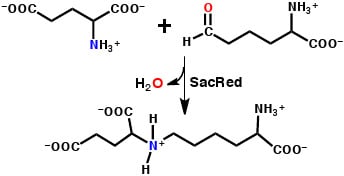
A QM/MM–Based Computational Investigation on the Catalytic Mechanism of Saccharopine Reductase
Abstract
:1. Introduction


2. Computational Methods

3. Results and Discussion
3.1. The pKa of the Substrate Glutamate’s α-Amine

3.2. Mechanism for Formation of Saccharopine
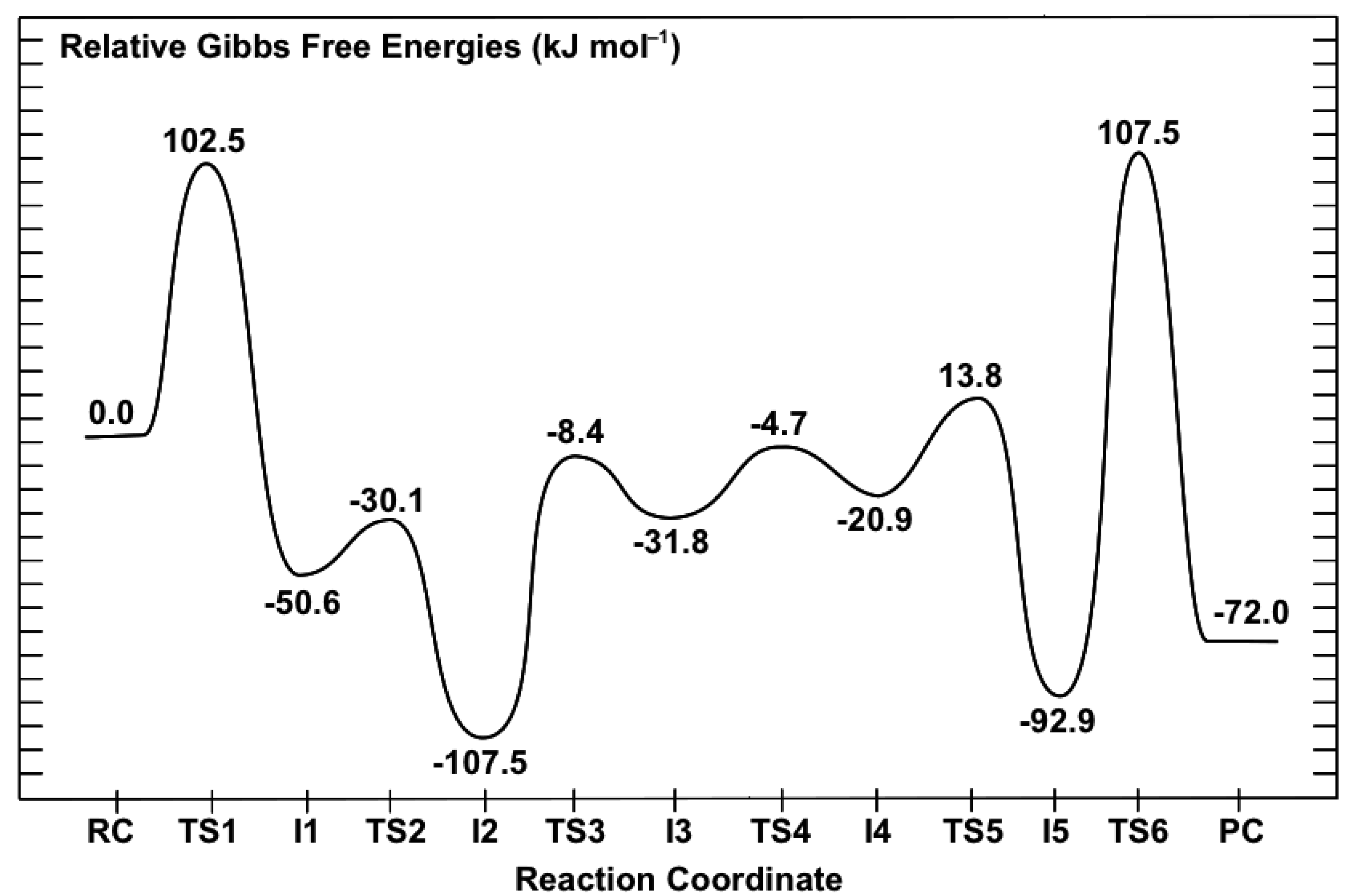
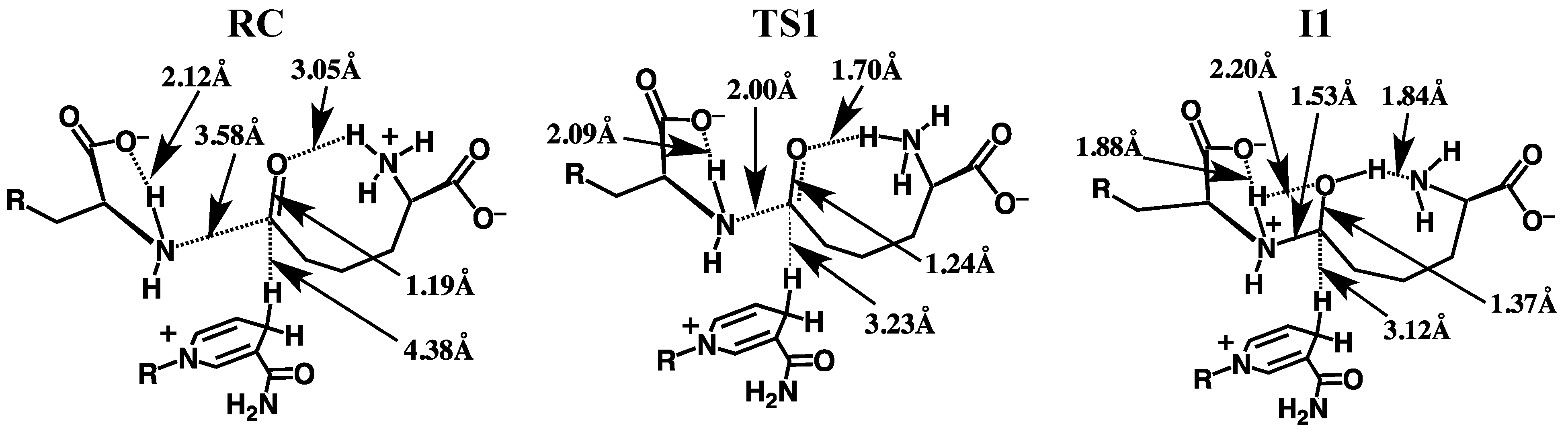


3.2.1. Formation of a Carbinolamine Intermediate
3.2.2. Rearrangement of the Carbinolamine Intermediate I1
3.2.3. Formation of the Schiff Base and its Reduction
3.3. Obtaining More Accurate and Reliable Energies for the Mechanism of Saccharopine Reductase
3.3.1. The Inclusion of Electron Correlation Effects

3.3.2. The Effects of the Protein’s Anisotropic Polar Environment
3.3.3. The Effects of Increasing the Basis Set Size
4. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
References
- Vashishtha, A.K.; West, A.H.; Cook, P.F. Chemical mechanism of saccharopine reductase from saccharomyces cerevisiae. Biochemistry 2009, 48, 5899–5907. [Google Scholar] [CrossRef]
- Zabriskie, T.M.; Jackson, M.D. Lysine biosynthesis and metabolism in fungi. Nat. Prod. Rep. 2000, 17, 85–97. [Google Scholar] [CrossRef]
- Xu, H.Y.; Andi, B.; Qian, J.H.; West, A.H.; Cook, P.F. The alpha-aminoadipate pathway for lysine biosynthesis in fungi. Cell Biochem. Biophys. 2006, 46, 43–64. [Google Scholar] [CrossRef]
- Johansson, E.; Steffens, J.J.; Lindqvist, Y.; Schneider, G. Crystal structure of saccharopine reductase from magnaporthe grisea, an enzyme of the alpha-aminoadipate pathway of lysine biosynthesis. Structure 2000, 8, 1037–1047. [Google Scholar] [CrossRef]
- Talbot, N.J. Having a blast: Exploring the pathogenicity of magnaporthe grisea. Trends Microbiol. 1995, 3, 9–16. [Google Scholar] [CrossRef]
- Ribot, C.; Hirsch, J.; Batzergue, S.; Tharreau, D.; Notteghem, J.L.; Lebrun, M.H.; Morel, J.B. Susceptibility of rice to the blast fungus, magnaporthe grisea. J. Plant Physiol. 2008, 165, 114–124. [Google Scholar] [CrossRef]
- Erdtman, E.; Bushnell, E.A.C.; Gauld, J.W.; Eriksson, L.A. Computational studies on Schiff-base formation: Implications for the catalytic mechanism of porphobilinogen synthase. Comput. Theory Chem. 2011, 963, 479–489. [Google Scholar] [CrossRef]
- Kaya, I.; Dogan, F.; Bilici, A. Schiff base-substituted polyphenol: Synthesis, characterisation and non-isothermal degradation kinetics. Polym. Int. 2009, 58, 570–578. [Google Scholar] [CrossRef]
- Lochee, Y.; Jhurry, D.; Bhaw-Luximon, A.; Kalangos, A. Biodegradable poly(ester-ether)s: Ring-opening polymerization of d,l-3-methyl-1,4-dioxan-2-one using various initiator systems. Polym. Int. 2010, 59, 1310–1318. [Google Scholar] [CrossRef]
- Godoy-Alcantar, C.; Yatsimirsky, A.K.; Lehn, J.M. Structure-stability correlations for imine formation in aqueous solution. J. Phys. Org. Chem. 2005, 18, 979–985. [Google Scholar] [CrossRef]
- Ilieva, S.; Cheshmedzhieva, D.; Tasheva, D. The origin of diastereoselectivity in the michael addition reaction: A computational study of the interaction between ch-acidic Schiff base and alpha, beta-unsaturated ketones. Tetrahedron 2010, 66, 5168–5172. [Google Scholar] [CrossRef]
- Lo Presti, L.; Soave, R.; Longhi, M.; Ortoleva, E. Conformational polymorphism in a Schiff-base macrocyclic organic ligand: An experimental and theoretical study. Acta Crystallogr. Sect. B Struct. Sci. 2010, 66, 527–543. [Google Scholar] [CrossRef]
- Platas-Iglesias, C.; Esteban, D.; Ojea, V.; Avecilla, F.; de Blas, A.; Rodriguez-Blas, T. Templating Schiff-base lateral macrobicycles: An experimental and theoretical structural study of the intermediates. Inorg. Chem. 2003, 42, 4299–4307. [Google Scholar] [CrossRef]
- Praveen, P.L.; Ajeetha, N.; Ojha, D.P. Ordering in smectogenic Schiff base compound: A computational analysis based in intermolecular interactions. Russ. J. Gen. Chem. 2009, 79, 2267–2271. [Google Scholar] [CrossRef]
- Sato, Y.; Hata, M.; Neya, S.; Hoshino, T. Computational analysis of the proton translocation from asp96 to Schiff base in bacteriorhodopsin. J. Phys. Chem. B 2006, 110, 22804–22812. [Google Scholar] [CrossRef]
- Bearpark, M.J.; Ogliaro, F.; Vreven, T.; Boggio-Pasqua, M.; Frisch, M.J.; Larkin, S.M.; Robb, M.A. Casscf Calculations for Excited States of Large Molecules: Choosing When to Use the RASSCF, ONIOM and MMVB Approximations. In Computation in Modern Science and Engineering; Simos, T.E., Maroulis, G., Eds.; Amer Inst Physics: Melville, Canada, 2007; Volume 2 (parts a and b), pp. 583–585. [Google Scholar]
- Dapprich, S.; Komaromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part i. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. Theochem. J. Mol. Struct. 1999, 461, 1–21. [Google Scholar]
- Humbel, S.; Sieber, S.; Morokuma, K. The IMOMO method: Integration of different levels of molecular orbital approximations for geometry optimization of large systems: Test for n-butane conformation and s(n)2 reaction: RCl+Cl. J. Chem. Phys. 1996, 105, 1959–1967. [Google Scholar] [CrossRef]
- Maseras, F.; Morokuma, K. IMOMM – A new integrated ab-initio plus molecular mechanics geometry optimization scheme of equilibrium structures and transition-states. J. Comput. Chem. 1995, 16, 1170–1179. [Google Scholar] [CrossRef]
- Morokuma, K.; Musaev, D.G.; Vreven, T.; Basch, H.; Torrent, M.; Khoroshun, D.V. Model studies of the structures, reactivities, and reaction mechanisms of metalloenzymes. IBM J. Res. Dev. 2001, 45, 367–395. [Google Scholar] [CrossRef]
- Svensson, M.; Humbel, S.; Froese, R.D.J.; Matsubara, T.; Sieber, S.; Morokuma, K. ONIOM: A multilayered integrated MO+MM method for geometry optimizations and single point energy predictions. A test for diels-alder reactions and pt(p(t-bu)(3))(2)+h-2 oxidative addition. J. Phys. Chem. 1996, 100, 19357–19363. [Google Scholar] [CrossRef]
- Vreven, T.; Byun, K.S.; Komaromi, I.; Dapprich, S.; Montgomery, J.A.; Morokuma, K.; Frisch, M.J. Combining quantum mechanics methods with molecular mechanics methods in oniom. J. Chem. Theory Comput. 2006, 2, 815–826. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K. On the application of the imomo (integrated molecular orbital plus molecular orbital) method. J. Comput. Chem. 2000, 21, 1419–1432. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K.; Farkas, O.; Schlegel, H.B.; Frisch, M.J. Geometry optimization with qm/mm, oniom, and other combined methods. I. Microiterations and constraints. J. Comput. Chem. 2003, 24, 760–769. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09,Revision b.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Himo, F. Quantum chemical modeling of enzyme active sites and reaction mechanisms. Theor. Chem. Acc. 2006, 116, 232–240. [Google Scholar] [CrossRef]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory, 2nd ed; Wiley-VCH: New York, NY, USA, 2001. [Google Scholar]
- Williams, I.H. Theoretical modeling of specific solvation effects upon carbonyl addition. J. Am. Chem. Soc. 1987, 109, 6299–6307. [Google Scholar] [CrossRef]
- Hall, N.E.; Smith, B.J. High-level ab initio molecular orbital calculations of imine formation. J. Phys. Chem. A 1998, 102, 4930–4938. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Brault, M.; Pollack, R.M.; Bevins, C.L. Kinetics and mechanism of hydrolysis of 2,2,2-trifluoro-n-(3-methyl-2-cyclohexenylidene)ethylamine. α, β-unsaturated Schiff-base. J. Org. Chem. 1976, 41, 346–350. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M.; Borowski, T. Modeling enzymatic reactions involving transition metals. Acc. Chem. Res. 2006, 39, 729–738. [Google Scholar] [CrossRef]
- Rosenberg, S.; Silver, S.M.; Sayer, J.M.; Jencks, W.P. Evidence for 2 concurrent mechanisms and a kinetically significant proton-transfer process in acid-catalyzed o-methyloxime formation. J. Am. Chem. Soc. 1974, 96, 7986–7998. [Google Scholar] [CrossRef]
- Llano, J.; Eriksson, L.A. First principles electrochemistry: Electrons and protons reacting as independent ions. J. Chem. Phys. 2002, 117, 10193–10206. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Almasi, J.N.; Bushnell, E.A.C.; Gauld, J.W. A QM/MM–Based Computational Investigation on the Catalytic Mechanism of Saccharopine Reductase. Molecules 2011, 16, 8569-8589. https://doi.org/10.3390/molecules16108569
Almasi JN, Bushnell EAC, Gauld JW. A QM/MM–Based Computational Investigation on the Catalytic Mechanism of Saccharopine Reductase. Molecules. 2011; 16(10):8569-8589. https://doi.org/10.3390/molecules16108569
Chicago/Turabian StyleAlmasi, Joel N., Eric A.C. Bushnell, and James W. Gauld. 2011. "A QM/MM–Based Computational Investigation on the Catalytic Mechanism of Saccharopine Reductase" Molecules 16, no. 10: 8569-8589. https://doi.org/10.3390/molecules16108569
APA StyleAlmasi, J. N., Bushnell, E. A. C., & Gauld, J. W. (2011). A QM/MM–Based Computational Investigation on the Catalytic Mechanism of Saccharopine Reductase. Molecules, 16(10), 8569-8589. https://doi.org/10.3390/molecules16108569