Mechanical Characterization of Compact Basalt by Using SHPB Device †
Abstract
:1. Introduction
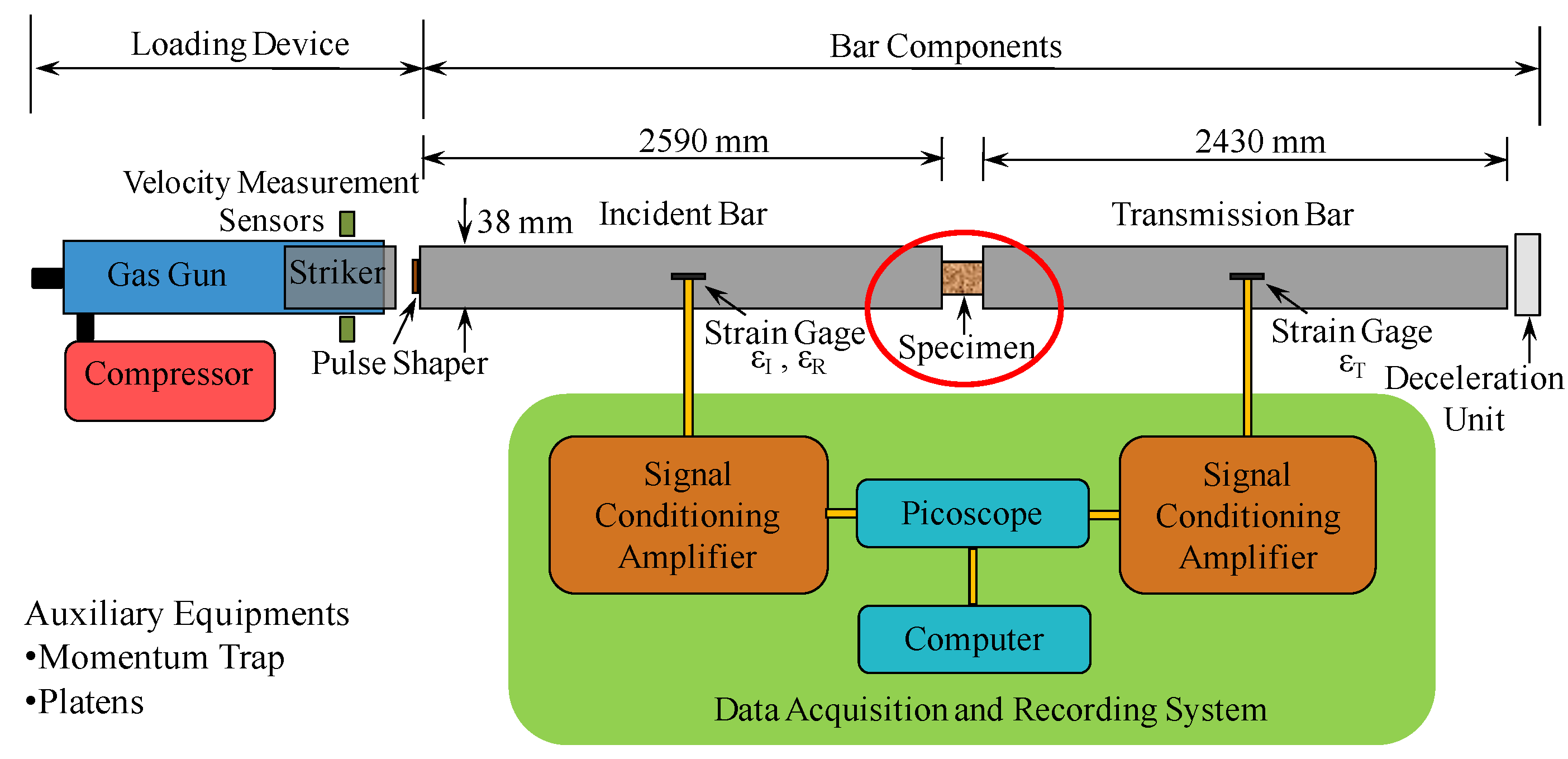
2. SHPB Test Setup
3. Results and Discussion
3.1. Physical Properties
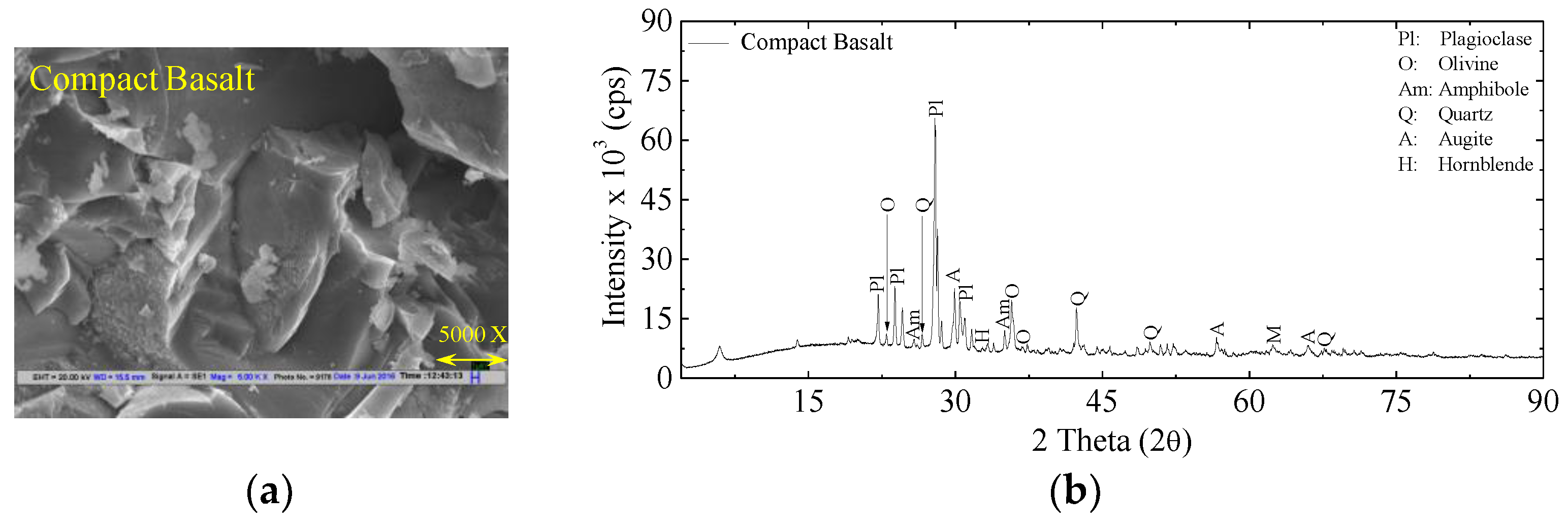
3.2. Results of Petrological Studies
3.3. Static Uniaxial Compressive Strength
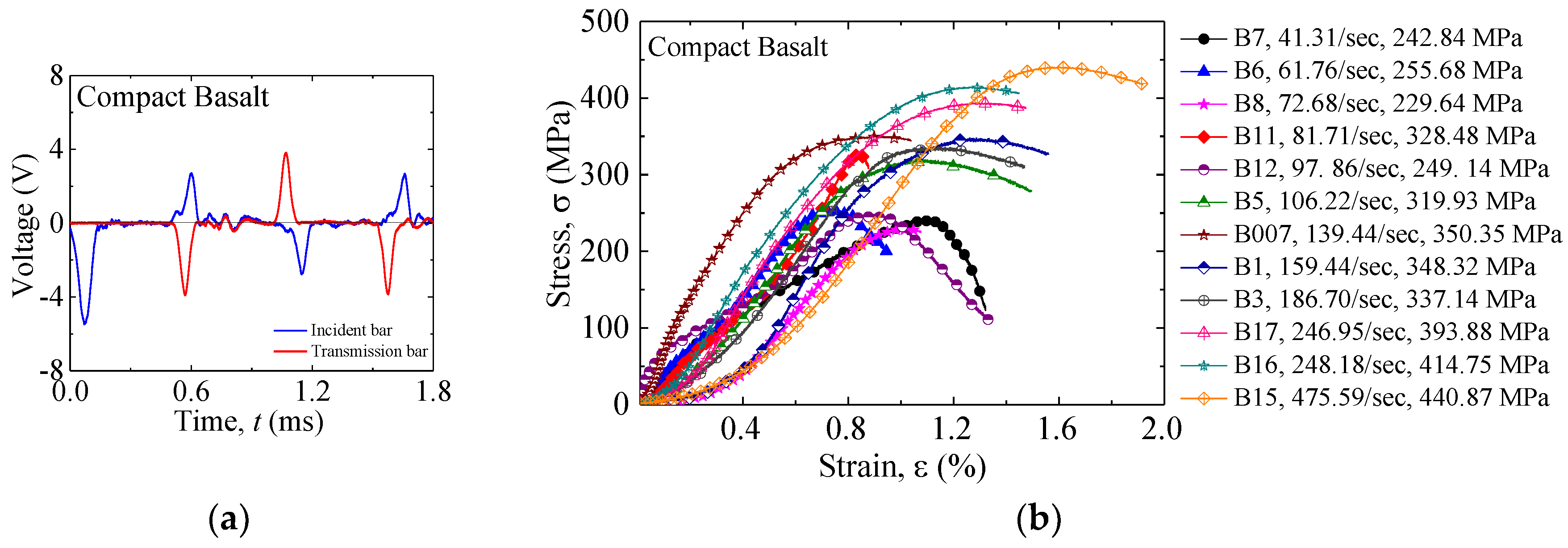
3.4. Stress-Strain Response for Compact Basalt
3.5. Dynamic Increase Factor and Proposed Correlation Equation
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Ngo, T.; Mendis, P.; Gupta, A.; Ramsay, J. Blast Loading and Blast Effects on Structures—An Overview. Electr. J. Struct. Eng. 2007, 7, 76–91. [Google Scholar] [CrossRef]
- Dusenberry, D.O. Handbook for Blast Resistant Design of Buildings, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 2010; p. 512. [Google Scholar]
- Perkins, R.D.; Green, S.J. Macroscopic Description Low and Medium Strain Rates. Int. J. Rock Mech. Min. Sci. 1970, 7, 527–535. [Google Scholar] [CrossRef]
- Christensen, R.J.; Swanson, S.R.; Brown, W.S. Split Hopkinson Bar Tests on Rock under Confining Pressure. Exp. Mech. 1972, 12, 508–541. [Google Scholar] [CrossRef]
- Lindholm, U.S.; Yeakley, L.M.; Nagy, A. The Dynamic Strength and Fracture Properties of Dresser Basalt. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 181–191. [Google Scholar] [CrossRef]
- Lundberg, B. A Split Hopkinson Bar Study of Energy Absorption in Dynamic. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 187–197. [Google Scholar] [CrossRef]
- Blanton, T.L. Effect of Strain Rates from 10−2 to 10 s−1 in Triaxial Compression Tests on Three Rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 47–62. [Google Scholar] [CrossRef]
- Klepaczko, J.R. Behavior of Rock-like Materials at High Strain Rates in Compression. Int. J. Plast. 1990, 6, 415–432. [Google Scholar] [CrossRef]
- Olsson, W.A. The Compressive Strength of Tuff as a Function of Strain Rate from 10−6 to 103/s. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 115–118. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.B.; Wu, M.B.; Li, T.J. Dynamic Uniaxial Compression Tests on a Granite. Int. J. Rock Mech. Min. Sci. 1999, 36, 273–277. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. A Split Hopkinson Pressure Bar Technique to Determine Compressive Stress-strain Data for Rock Materials. Exp. Mech. 2000, 41, 40–46. [Google Scholar] [CrossRef]
- Fukui, K.; Okubo, S.; Ogawa, A. Some Aspects of Loading-Rate Dependency of Sanjome Andesite Strengths. Int. J. Rock Mech. Min. Sci. 2004, 41, 1215–1219. [Google Scholar] [CrossRef]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic Characteristics of Granite Subjected to Intermediate Loading Rate. Rock Mech. Rock Eng. 2005, 138, 21–39. [Google Scholar] [CrossRef]
- Qi, C.Z.; Wang, M.Y.; Qihu, Q. Strain-Rate Effects on the Strength and Fragmentation Size of Rocks. Int. J. Imp. Eng. 2009, 36, 1355–1364. [Google Scholar] [CrossRef]
- Lu, Y.B.; Li, Q.M.; Ma, G.W. Numerical Investigation of the Dynamic Compressive Strength of Rocks based on Split Hopkinson Pressure Bar Tests. Int. J. Rock Mech. Min. Sci. 2010, 47, 829–838. [Google Scholar] [CrossRef]
- Chakraborty, T.; Mishra, S.; Loukus, J.; Halonen, B.; Bekkala, B. Characterization of three Himalayan Rocks using a Split Hopkinson Pressure Bar. Int. J. Rock Mech. Min. Sci. 2016, 85, 112–118. [Google Scholar] [CrossRef]
- Chen, W.; Song, B. Split Hopkinson (Kolsky) Bar—Design, Testing and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jhanwar, J.C.; Goel, R.K.; Chakraborty, A.K.; Bandopadhyay, C. Development of Tunnel Support Guidelines for Tunneling in Basaltic Rocks—A Case Study. In Proceedings Geomechanics and Ground Control; Allied Publishers Pvt. Ltd.: Gandhinagar, India, 2003; pp. 29–35. [Google Scholar]
- Brandes, H.G.; Robertson, I.N.; Johnson, G.P. Soil and Rock Properties in a Young Volcanic Deposit on the Island of Hawaii. J. Geotech. Geoenviron. Eng. ASCE 2011, 137, 597–610. [Google Scholar] [CrossRef]
- Gupta, A.S.; Rao, K.S. Weathering Effects on the Strength and Deformational Behaviour of Crystalline Rocks under Uniaxial Compression State. Eng. Geol. 2000, 56, 257–274. [Google Scholar] [CrossRef]
- ASTM International. Standard Practices for Preparing Rock Core as Cylindrical Test Specimens and Verifying Conformance to Dimensional and Shape Tolerances; ASTM D4543-08; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ISRM. Suggested Methods for Determining the Uniaxial Compressive Strength and Deformability of Rock Materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 138–140. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Elastic Moduli of Intact Rock Core Specimens in Uniaxial Compression; ASTM D3148-02; ASTM: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Zhou, Y.X.; Xia, K.; Li, X.B.; Li, H.B.; Ma, G.W.; Zhao, J.; Zhou, Z.L.; Dai, F. Suggested Methods for Determining the Dynamic Strength Parameters and Mode-I Fracture Toughness of Rock Materials. Int. J. Rock Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar] [CrossRef]

| Rocks | Dry Density, ρd (kg/m3) | Specific Gravity, G | Uniaxial Compressive Strength, σc (MPa) | Modulus of Elasticity, Et (GPa) |
|---|---|---|---|---|
| Compact Basalt | 2927 | 2.89 | 58.58 | 24.00 |
| S.R.R. | S.N. | l (mm) | d (mm) | Ls (mm) | Ps (psi) | Vst (m/s) | σdc (MPa) | ε | Ed (GPa) | DIF | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Low | B7 | 18.08 | 37.16 | 558.8 | 32 | 13.16 | 41.31 | 242.84 | 0.011 | 31.19 | 4.14 |
| B6 | 17.34 | 37.26 | 228.6 | 25 | 15.72 | 61.76 | 255.68 | 0.007 | 33.88 | 4.36 | |
| B8 | 18.79 | 37.26 | 35 | 16.72 | 72.68 | 229.64 | 0.009 | 19.79 | 3.92 | ||
| Medium | B11 | 16.71 | 37.23 | 228.6 | 74 | 33.95 | 81.71 | 328.48 | 0.008 | 31.77 | 5.60 |
| B12 | 16.12 | 37.31 | 304.8 | 30 | 17.58 | 97.86 | 249.14 | 0.008 | 31.94 | 4.25 | |
| B5 | 16.51 | 37.77 | 139.7 | 45 | 25.78 | 106.22 | 319.93 | 0.011 | 31.94 | 5.46 | |
| B007 | 18.67 | 37.26 | 304.8 | 50 | 22.98 | 139.44 | 350.35 | 0.009 | 67.43 | 5.98 | |
| B1 | 15.36 | 37.33 | 139.7 | 45 | 30.01 | 159.44 | 348.32 | 0.012 | 26.65 | 5.94 | |
| High | B3 | 17.67 | 37.77 | 139.7 | 45 | 32.06 | 186.70 | 337.13 | 0.011 | 30.16 | 5.75 |
| B17 | 18.67 | 37.26 | 228.6 | 60 | 28.31 | 246.95 | 393.88 | 0.012 | 39.11 | 6.72 | |
| B16 | 18.92 | 37.26 | 228.6 | 60 | 28.11 | 248.18 | 414.75 | 0.012 | 43.77 | 7.08 | |
| B15 | 17.62 | 37.26 | 60 | 28.93 | 475.59 | 440.87 | 0.016 | 25.32 | 7.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, S.; Chakraborty, T.; Matsagar, V. Mechanical Characterization of Compact Basalt by Using SHPB Device. Proceedings 2018, 2, 383. https://doi.org/10.3390/ICEM18-05202
Mishra S, Chakraborty T, Matsagar V. Mechanical Characterization of Compact Basalt by Using SHPB Device. Proceedings. 2018; 2(8):383. https://doi.org/10.3390/ICEM18-05202
Chicago/Turabian StyleMishra, Sunita, Tanusree Chakraborty, and Vasant Matsagar. 2018. "Mechanical Characterization of Compact Basalt by Using SHPB Device" Proceedings 2, no. 8: 383. https://doi.org/10.3390/ICEM18-05202
APA StyleMishra, S., Chakraborty, T., & Matsagar, V. (2018). Mechanical Characterization of Compact Basalt by Using SHPB Device. Proceedings, 2(8), 383. https://doi.org/10.3390/ICEM18-05202






