Spatio-Temporal Variations of Soil Active Layer Thickness in Chinese Boreal Forests from 2000 to 2015
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Remote Sensing Data
2.3. Modeling the Active Layer
2.4. Parameter Estimation and ALT Prediction
2.5. Model Evaluation and Output Analyses
3. Results
3.1. Model Evaluation and Parameter Sensitivity
3.2. Active Layer Thickness
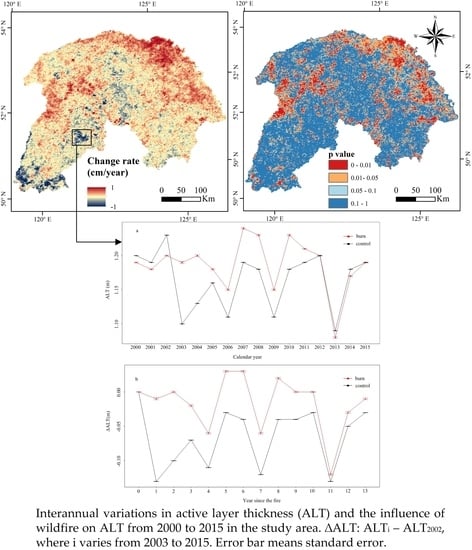
3.3. Effects of Wildfire and Climatic Warming on the Active Layer
4. Discussion
4.1. Estimation of Active Layer Thickness
4.2. Spatio-Temporal Variations in Active Layer Thickness
4.3. Uncertainty Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonnaventure, P.P.; Lamoureux, S.F. The active layer: A conceptual review of monitoring, modelling techniques and changes in a warming climate. Prog. Phys. Geogr. 2013, 37, 352–376. [Google Scholar] [CrossRef]
- Anisimov, O.A.; Shiklomanov, N.I.; Nelson, F.E. Global warming and active-layer thickness: Results from transient general circulation models. Glob. Planet Chang. 1997, 15, 61–77. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Paetzold, F.; Nelson, F.E.; Bockheim, J.G. Patterns of soil temperature and moisture in the active layer and upper permafrost at Barrow, Alaska 1993–1999. Glob. Planet Chang. 2001, 29, 293–309. [Google Scholar] [CrossRef]
- Shiklomanov, N.I.; Nelson, F.E. Analytic representation of the active layer thickness field, Kuparuk River Basin, Alaska. Ecol. Model. 1999, 123, 105–125. [Google Scholar] [CrossRef]
- Liu, L.; Schaefer, K.; Zhang, T.; Wahr, J. Estimating 1992–2000 average active layer thickness on the Alaskan North Slope from remotely sensed surface subsidence. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Romanovsky, V.E.; Osterkamp, T.E. Thawing of the active layer on the coastal plain of the Alaskan Arctic. Permafr. Periglac. Process. 1997, 8, 1–22. [Google Scholar] [CrossRef]
- Shiklomanov, N.I.; Nelson, F.E. Active-layer mapping at regional scales: A 13-year spatial time series for the Kuparuk region, north-central Alaska. Permafr. Periglac. Process. 2002, 13, 219–230. [Google Scholar] [CrossRef]
- Heggem, E.S.F.; Etzelmüller, B.; Anarmaa, S.; Sharkhuu, N.; Goulden, C.E.; Nandinsetseg, B. Spatial distribution of ground surface temperatures and active layer depths in the Hövsgöl area, northern Mongolia. Permafr. Periglac. Process. 2006, 17, 357–369. [Google Scholar] [CrossRef]
- Schuur, E.A.; Vogel, J.G.; Crummer, K.G.; Lee, H.; Sickman, J.O.; Osterkamp, T.E. The effect of permafrost thaw on old carbon release and net carbon exchange from tundra. Nature 2009, 459, 556–559. [Google Scholar] [CrossRef] [PubMed]
- Schuur, E.A.; Abbott, B. Climate change: High risk of permafrost thaw. Nature 2011, 480, 32–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cannone, N.; Guglielmin, M.; Hauck, C.; Muhll, D.V. The impact of recent glacier fluctuation and human activities on permafrost distribution, Stelvio Pass (Italian Central-Eastern Alps). In Proceedings of the 8th International Conference on Permafrost, Zürich, Switzerland, 21–25 July 2003. [Google Scholar]
- Jin, H.; Yu, Q.; Wang, S.; Lü, L. Changes in permafrost environments along the Qinghai–Tibet engineering corridor induced by anthropogenic activities and climate warming. Cold Reg. Sci. Technol. 2008, 53, 317–333. [Google Scholar] [CrossRef]
- Péwé, T.L. Permafrost—And its effects on human activities in arctic and subarctic regions. GeoJournal 1979, 3, 333–344. [Google Scholar] [CrossRef]
- Brown, J.; Hinkel, K.M.; Nelson, F.E. The circumpolar active layer monitoring (calm) program: Research designs and initial results. Polar Geogr. 2000, 24, 166–258. [Google Scholar] [CrossRef]
- Hoelzle, M.; Gruber, S. Borehole and ground surface temperatures and their relationship to meteorological conditions in the Swiss Alps. In Proceedings of the Ninth International Conference on Permafrost, Fairbanks, Alaska, 25–29 June 2008. [Google Scholar]
- Beck, I.; Ludwig, R.; Bernier, M.; Lévesque, E.; Boike, J. Assessing Permafrost Degradation and Land Cover Changes (1986–2009) using Remote Sensing Data over Umiujaq, Sub-Arctic Québec. Permafr. Periglac. Process. 2015, 26, 129–141. [Google Scholar] [CrossRef] [Green Version]
- Farbrot, H.; Isaksen, K.; Etzelmüller, B.; Gisnås, K. Ground Thermal Regime and Permafrost Distribution under a Changing Climate in Northern Norway. Permafr. Periglac. Process. 2013, 24, 20–38. [Google Scholar] [CrossRef]
- Peng, X.; Frauenfeld, O.W.; Cao, B.; Wang, K.; Wang, H.; Su, H.; Huang, Z.; Yue, D.; Zhang, T. Response of changes in seasonal soil freeze/thaw state to climate change from 1950 to 2010 across china. J. Geophys. Res. Earth Surf. 2016, 121, 1984–2000. [Google Scholar] [CrossRef]
- Sazonova, T.S.; Romanovsky, V.E. A model for regional-scale estimation of temporal and spatial variability of active layer thickness and mean annual ground temperatures. Permafr. Periglac. Process. 2003, 14, 125–139. [Google Scholar] [CrossRef]
- Zhang, Y.; Olthof, I.; Fraser, R.; Wolfe, S.A. A new approach to mapping permafrost and change incorporating uncertainties in ground conditions and climate projections. Cryosphere 2014, 8, 2177–2194. [Google Scholar] [CrossRef] [Green Version]
- Leverington, D.W.; Duguay, C.R. A neural network method to determine the presence or absence of Permafrost near Mayo, Yukon Territory, Canada. Permafr. Periglac. Process. 1997, 8, 205–215. [Google Scholar] [CrossRef]
- Bartsch, A.; Kidd, R.A.; Wagner, W.; Bartalis, Z. Temporal and spatial variability of the beginning and end of daily spring freeze/thaw cycles derived from scatterometer data. Remote Sens. Environ. 2007, 106, 360–374. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Burn, C.R.; King, D.J.; Smith, S.L. Estimating the extent of near-surface permafrost using remote sensing, Mackenzie Delta, Northwest Territories. Permafr. Periglac. Process. 2009, 20, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Panda, S.K.; Prakash, A.; Solie, D.N.; Romanovsky, V.E.; Jorgenson, M.T. Remote sensing and field-based mapping of permafrost distribution along the Alaska Highway corridor, interior Alaska. Permafr. Periglac. Process. 2010, 21, 271–281. [Google Scholar] [CrossRef]
- Jin, H.; Yu, Q.; Lü, L.; Guo, D.; He, R.; Yu, S.; Sun, G.; Li, Y. Degradation of permafrost in the Xing’anling Mountains, northeastern China. Permafr. Periglac. Process. 2007, 18, 245–258. [Google Scholar] [CrossRef]
- Guo, D.; Li, Z. Geological evolution and age of formation of permafrost in northeastern China since the late Pleistocene. J. Glaciol. Geocryol. 1981, 3, 1–6. [Google Scholar]
- Cahoon, D.R.; Stocks, B.J.; Levine, J.S.; Cofer, W.R.; Pierson, J.M. Satellite analysis of the severe 1987 forest fires in northern China and southeastern Siberia. J. Geophys. Res. Atmos. 1994, 99, 18627–18638. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Chang, Y.; Weisberg, P.J.; He, H. Spatial patterns and drivers of fire occurrence and its future trend under climate change in a boreal forest of Northeast China. Glob. Chang. Biol. 2012, 18, 2041–2056. [Google Scholar] [CrossRef]
- Cui, X.; Gao, F.; Song, J.; Sang, Y.; Sun, J.; Di, X. Changes in soil total organic carbon after an experimental fire in a cold temperate coniferous forest: A sequenced monitoring approach. Geoderma 2014, 226–227, 260–269. [Google Scholar] [CrossRef]
- Jorgenson, M.T.; Romanovsky, V.; Harden, J.; Shur, Y.; O’Donnell, J.; Schuur, E.A.G.; Kanevskiy, M.; Marchenko, S. Resilience and vulnerability of permafrost to climate change. Can. J. Earth Sci. 2010, 40, 1219–1236. [Google Scholar]
- Li, X.; Cheng, G.; Jin, H.; Kang, E.; Che, T.; Jin, R.; Wu, L.; Nan, Z.; Wang, J.; Shen, Y. Cryospheric change in China. Glob. Planet Chang. 2008, 62, 210–218. [Google Scholar] [CrossRef]
- Cai, W.; Yang, J.; Liu, Z.; Hu, Y.; Weisberg, P.J. Post-fire tree recruitment of a boreal larch forest in Northeast China. For. Ecol. Manag. 2013, 307, 20–29. [Google Scholar] [CrossRef]
- Hachem, S.; Duguay, C.R.; Allard, M. Comparison of MODIS-derived land surface temperatures with ground surface and air temperature measurements in continuous permafrost terrain. Cryosphere 2012, 6, 51–69. [Google Scholar] [CrossRef] [Green Version]
- Ran, Y.; Li, X.; Jin, R.; Guo, J. Remote Sensing of the Mean Annual Surface Temperature and Surface Frost Number for Mapping Permafrost in China. Arct. Antarct. Alp. Res. 2015, 47, 255–265. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.Z.; Cai, W.H.; Yang, J. Evaluation of MODIS Land Surface Temperature Data to Estimate Near-Surface Air Temperature in Northeast China. Remote Sens. 2017, 9, 410. [Google Scholar] [CrossRef]
- Choi, T.; Helder, D.L. Generic sensor modeling for modulation transfer function (MTF) estimation. In Proceedings of the Pecora 16 Global Priorities in Land Remote Sensing, Sioux Falls, South Dakota, 23–27 October 2005. [Google Scholar]
- Anisimov, O.A.; Shiklomanov, N.I.; Nelson, F.E. Variability of seasonal thaw depth in permafrost regions: A stochastic modeling approach. Ecol. Model. 2002, 153, 217–227. [Google Scholar] [CrossRef]
- Matyshak, G.V.; Goncharova, O.Y.; Moskalenko, N.G.; Walker, D.A.; Epstein, H.E.; Shur, Y. Contrasting Soil Thermal Regimes in the Forest-Tundra Transition Near Nadym, West Siberia, Russia. Permafr. Periglac. Process. 2015, 28, 108–118. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.W.; Riseborough, D.W. Permafrost monitoring and detection of climate change. Permafr. Periglac. Process. 1996, 7, 301–309. [Google Scholar] [CrossRef]
- Smith, S.L.; Riseborough, D.W.; Bonnaventure, P.P. Eighteen Year Record of Forest Fire Effects on Ground Thermal Regimes and Permafrost in the Central Mackenzie Valley, NWT, Canada. Permafr. Periglac. Process. 2015, 26, 289–303. [Google Scholar] [CrossRef]
- Kersten, M.S. Laboratory Research for the Determination of Thermal Properties of Soils; ACFEL Tech Rep 23; University of Minnesota: Minneapolis, MN, USA, 1949. [Google Scholar]
- Zhang, Y.; Sun, M.; Liu, T. Effect of Forest Fire on Soil Physical and Chemical Properties of typical Forests in Daxing’an Mountains. J. Northeast For. Univ. 2012, 40, 41–43. (In Chinese) [Google Scholar]
- Wilhelm, K.R.; Bockheim, J.G.; Kung, S. Active Layer Thickness Prediction on the Western Antarctic Peninsula. Permafr. Periglac. Process. 2015, 26, 188–199. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dilts, T.E.; Yang, J.; Weisberg, P.J. The landscape similarity toolbox: New tools for optimizing the location of control sites in experimental studies. Ecography 2010, 33, 1097–1101. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.; Yi, X.; Wu, Y.; Ma, Y. Application of ground penetration radar to permafrost survey in Mohe County, Heilongjiang Province. J. Glaciol. Geocryol. 2015, 37, 723–730. [Google Scholar]
- Lv, J.; Li, X.; Hu, Y.; Wang, X.; Liu, H.; Bing, L. Factors affecting the thickness of permafrost’s active layer in Huzhong National Nature Reserve. Chin. J. Ecol. 2007, 26, 1369–1374. [Google Scholar]
- Li, Z.; Tang, B.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Dickinson, R.E.; Tian, Y.; Vose, R.S.; Dai, Y. Impact of vegetation removal and soil aridation on diurnal temperature range in a semiarid region: Application to the Sahel. Proc. Natl. Acad. Sci. USA 2007, 104, 17937–17942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aguirre, A.; del Río, M.; Condés, S. Intra-and inter-specific variation of the maximum size-density relationship along an aridity gradient in Iberian pinewoods. For. Ecol. Manag. 2018, 411, 90–100. [Google Scholar] [CrossRef]
- Wu, Q.; Shi, B.; Fang, H. Engineering geological characteristics and processes of permafrost along the Qinghai–Xizang (Tibet) Highway. Eng. Geol. 2003, 68, 387–396. [Google Scholar] [CrossRef]
- Brown, J.; Rickard, W.; Vietor, D. The effect of disturbance on permafrost terrain. Cold Reg. Res. Eng. Lab. Spec. Rep. 1969, 138, 1–13. [Google Scholar]
- Zhang, T.; Osterkamp, T.E.; Stamnes, K. Effects of Climate on the Active Layer and Permafrost on the North Slope of Alaska, U.S.A. Permafr. Periglac. Process. 1997, 8, 45–67. [Google Scholar] [CrossRef]
- Serreze, M.C.; Walsh, J.E.; Iii, F.S.C.; Osterkamp, T.; Dyurgerov, M.; Romanovsky, V.; Oechel, W.C.; Morison, J.; Zhang, T.; Barry, R.G. Observational Evidence of Recent Change in the Northern High-Latitude Environment. Clim. Chang. 2000, 46, 159–207. [Google Scholar] [CrossRef]
- Ling, F.; Zhang, T. Impact of the timing and duration of seasonal snow cover on the active layer and permafrost in the Alaskan Arctic. Permafr. Periglaci. Process. 2003, 14, 141–150. [Google Scholar] [CrossRef]
- Zhang, T.J.; Frauenfeld, O.W.; Serreze, M.C.; Etringer, A.; Oelke, C.; McCreight, J.; Barry, R.G.; Gilichinsky, D.; Yang, D.Q.; Ye, H.C.; et al. Spatial and temporal variability in active layer thickness over the Russian Arctic drainage basin. J. Geophys. Res. 2005, 110, 110. [Google Scholar] [CrossRef]
- Chang, X.; Jin, H.; Zhang, Y.; He, R.; Luo, D.; Wang, Y.; Lü, L.; Zhang, Q. Thermal Impacts of Boreal Forest Vegetation on Active Layer and Permafrost Soils in Northern da Xing’Anling (Hinggan) Mountains, Northeast China. Arct. Antarc. Alp. Res. 2015, 47, 267–279. [Google Scholar] [CrossRef]
- Woo, M.; Mollinga, M.; Smith, S.L. Climate warming and active layer thaw in the boreal and tundra environments of the Mackenzie Valley. Can. J. Earth Sci. 2007, 44, 733–743. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.; Yang, J.; Tao, B.; Ren, W. Spatio-Temporal Variations of Soil Active Layer Thickness in Chinese Boreal Forests from 2000 to 2015. Remote Sens. 2018, 10, 1225. https://doi.org/10.3390/rs10081225
Bai X, Yang J, Tao B, Ren W. Spatio-Temporal Variations of Soil Active Layer Thickness in Chinese Boreal Forests from 2000 to 2015. Remote Sensing. 2018; 10(8):1225. https://doi.org/10.3390/rs10081225
Chicago/Turabian StyleBai, Xiongxiong, Jian Yang, Bo Tao, and Wei Ren. 2018. "Spatio-Temporal Variations of Soil Active Layer Thickness in Chinese Boreal Forests from 2000 to 2015" Remote Sensing 10, no. 8: 1225. https://doi.org/10.3390/rs10081225
APA StyleBai, X., Yang, J., Tao, B., & Ren, W. (2018). Spatio-Temporal Variations of Soil Active Layer Thickness in Chinese Boreal Forests from 2000 to 2015. Remote Sensing, 10(8), 1225. https://doi.org/10.3390/rs10081225