Efficient Deployment of Multi-UAVs in Massively Crowded Events †
Abstract
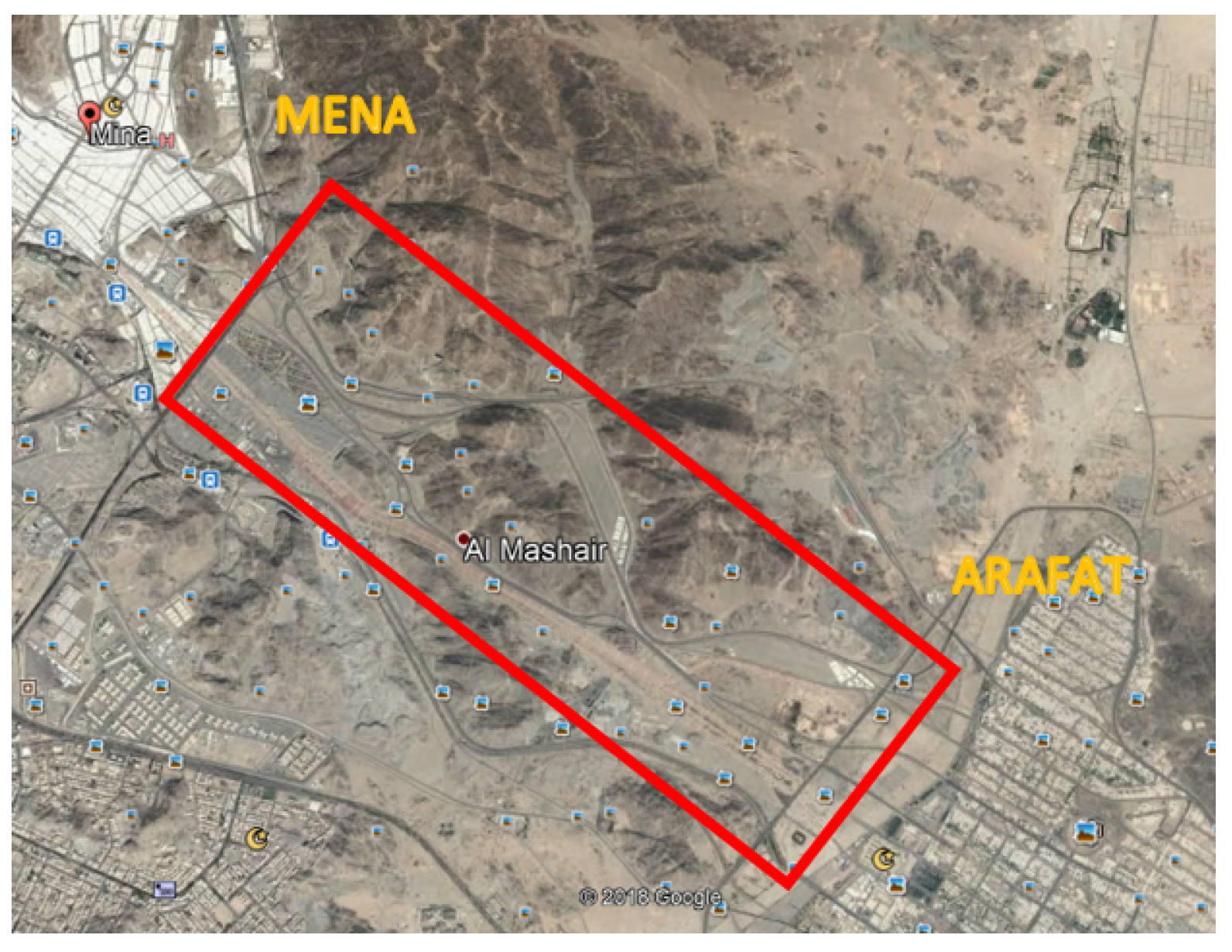
:1. Introduction
1.1. Related Works
1.2. Paper Contributions
- The existing ATG path loss model [9] and outdoor to indoor path loss model [21] are used to study the problem of a single UAV placement to provide coverage in crowded events for both outdoor and indoor receivers simultaneously, with the objective to minimize the required UAV transmit power. Due to the intractability of the formulated problem, two algorithms are developed to find an efficient 3D UAV placement using two optimization techniques, namely the PSO and KTS algorithms. The proposed algorithms consider the problem in providing wireless coverage for indoor and outdoor users, in a small area using a single UAV.
- The efficient 3D placements of multiple UAVs that provide maximum wireless coverage and minimize the transmission power are found for each UAV.
- The CPT is utilized to find the number of UAVs needed for providing wireless coverage for outdoor users in a large coverage area having three different shapes of coverage area, namely square, rectangle and circular. The problem is formulated with the objective to maximize the wireless coverage area using multiple UAVs. In each subarea, the UAV altitude is optimized using the algorithm to provide wireless coverage using a single UAV above.
2. Providing Wireless Coverage Using a Single UAV
2.1. System Model
2.1.1. ATG Path Loss Model
2.1.2. Outdoor-to-Indoor Path Loss Model
2.2. Problem Formulation
2.3. Efficient UAV 3D Placement Algorithms
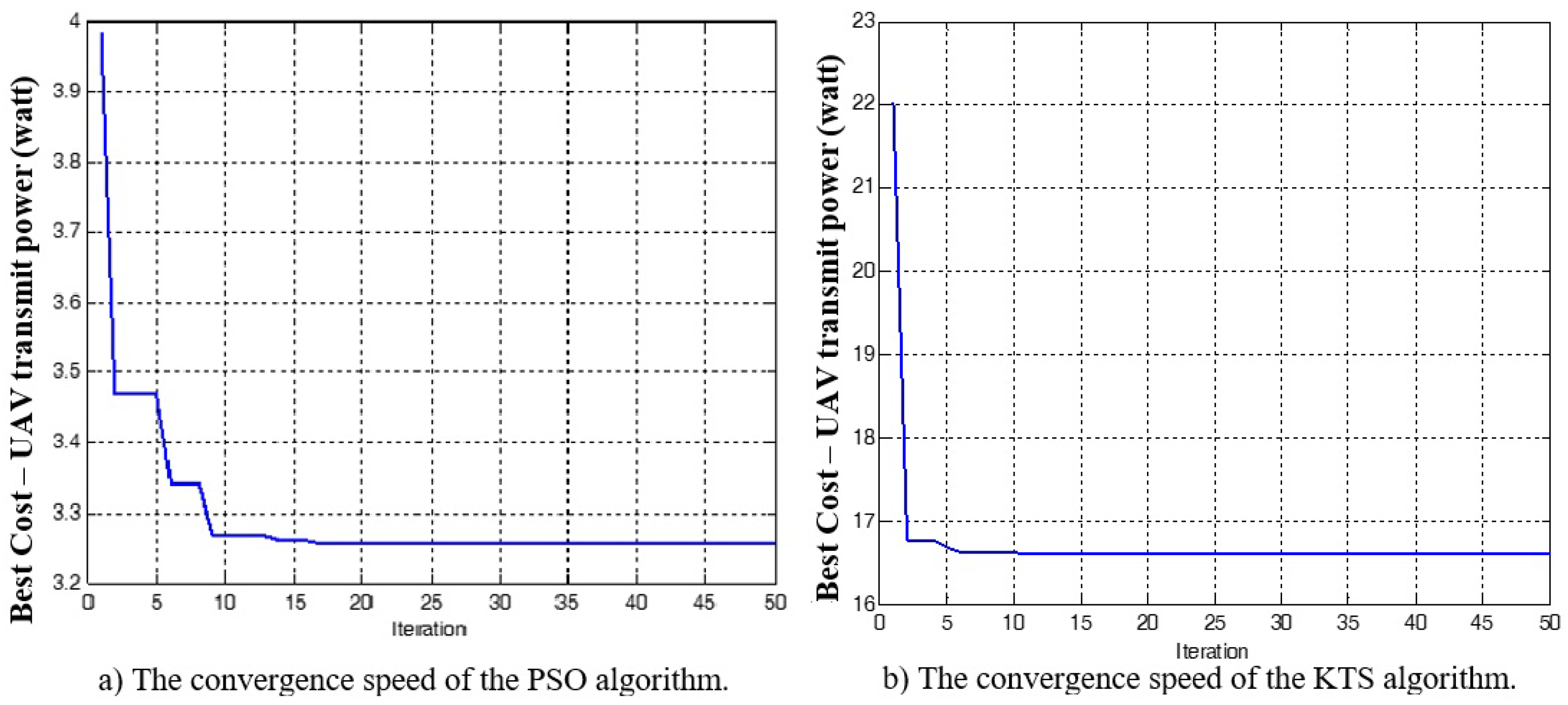
2.3.1. Particle Swarm Optimization Algorithm (PSO)
2.3.2. K-Means with Ternary Search Algorithms
- Initially, random guesses for cluster centroids are made, as shown in Step 3 of Algorithm 2.
- The nearest centroid is determined for each data point, by calculating the Euclidean distance between each point and the centroid of the cluster, as shown in Step 5 of Algorithm 2.
- In each cluster, the centroid is replaced by a new value. This new value is the means of the points belonging to the cluster, as in Step 6 of Algorithm 2.
- Repeat the process in Items 2 and 3 above, until the solution converges. The convergence happens when the centroids and their locations are no longer changed; more specifically, when the cluster mean is not changed as in Steps 4 to 6 of Algorithm 2.
| Algorithm 1 Particle swarm optimization algorithm. |
|
| Algorithm 2 K-means with ternary search algorithm. |
|
3. Providing Wireless Coverage Using Multiple UAVs Equipped with Directional Antennas
3.1. Case of a Square Region
3.1.1. Problem Formulation
- : Place n identical non-overlapping circles in a unit square, with the objective function to maximize the radius of the circles r, such that the coverage area and coverage density are maximized.
3.2. Case of a Rectangle Region
3.2.1. Problem Formulation
- : Place n identical non-overlapping circles in a rectangle region , with the Cartesian origin as the rectangle center. The objective function is to maximize the radius of the circles r such that the coverage area and density are maximized.
3.2.2. Algorithms for Packing Circles in a Rectangle Region
| Algorithm 3 CPA-MinOSA algorithm. |
|
| Algorithm 4 Formulation space search pseudocode. |
|
3.3. Case of a Circular Region
3.3.1. Problem Formulation
- : Place n identical non-overlapping circles into a unit circle with radius of . The objective function is to maximize the radius of the packed circles, such that the coverage area and density are maximized.
3.3.2. Algorithms for Packing Circles into a Circular Region
4. Simulation Results and Analysis
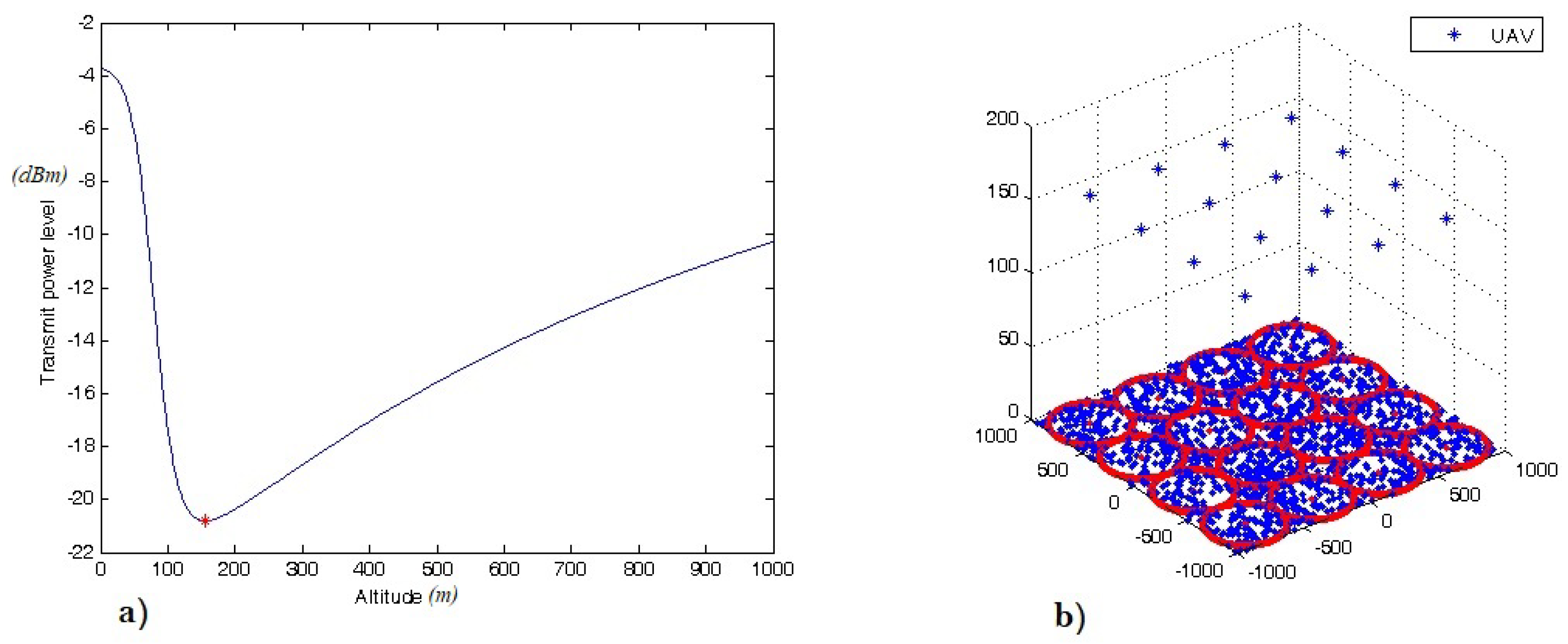
4.1. Providing Wireless Coverage Using a Single UAV
4.2. Providing Wireless Coverage Using Multiple UAVs
4.2.1. Case of a Square Region
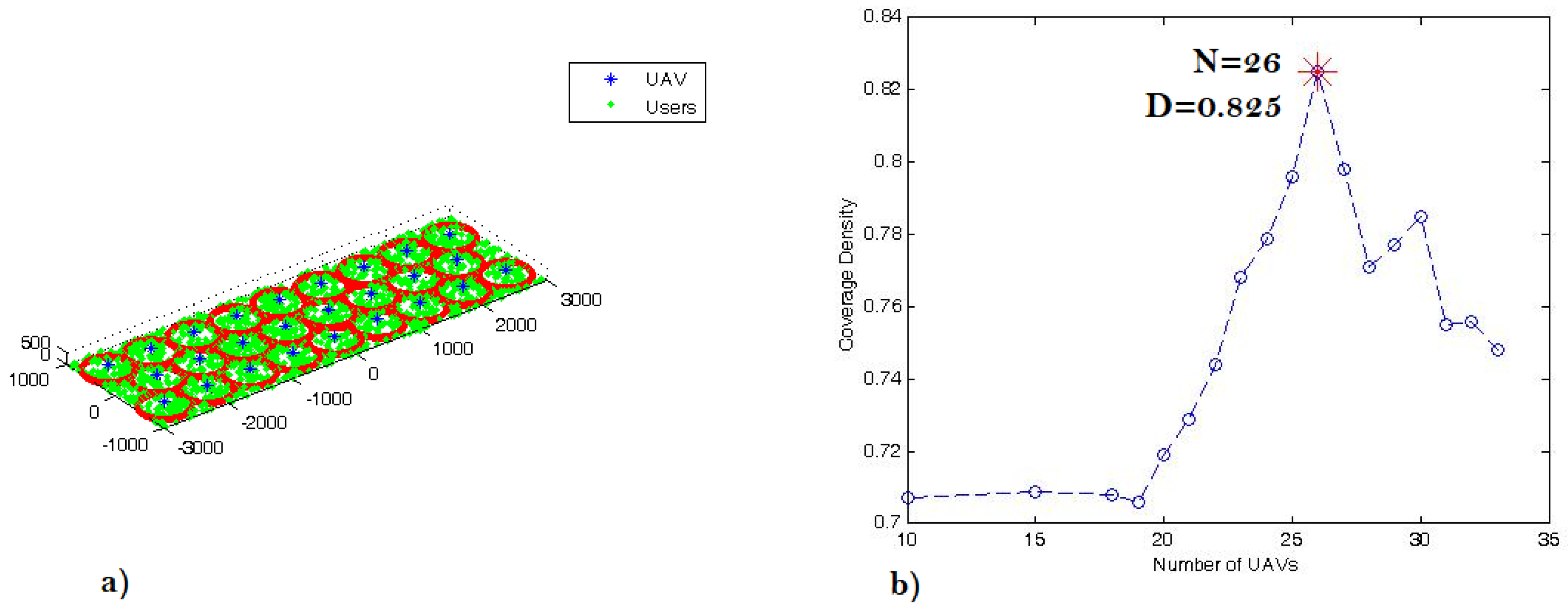
4.2.2. Case of a Rectangle Region
4.2.3. Case of a Circular Region
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shakhatreh, H.; Sawalmeh, A.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles: A Survey on Civil Applications and Key Research Challenges. arXiv, 2018; arXiv:1805.00881. [Google Scholar]
- Orfanus, D.; de Freitas, E.P.; Eliassen, F. Self-organization as a supporting paradigm for military UAV relay networks. IEEE Commun. Lett. 2016, 20, 804–807. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Khreishah, A.; Alsarhan, A.; Khalil, I.; Sawalmeh, A.; Othman, N.S. Efficient 3D placement of a uav using particle swarm optimization. In Proceedings of the 8th IEEE International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 4–6 April 2017; pp. 258–263. [Google Scholar]
- Hayat, S.; Yanmaz, E.; Muzaffar, R. Survey on unmanned aerial vehicle networks for civil applications: A communications viewpoint. IEEE Commun. Surv. Tutor. 2016, 18, 2624–2661. [Google Scholar] [CrossRef]
- Chandrasekharan, S.; Gomez, K.; Al-Hourani, A.; Kandeepan, S.; Rasheed, T.; Goratti, L.; Reynaud, L.; Grace, D.; Bucaille, I.; Wirth, T.; et al. Designing and implementing future aerial communication networks. IEEE Commun. Mag. 2016, 54, 26–34. [Google Scholar] [CrossRef] [Green Version]
- Henderson, J.C. Religious tourism and its management: The Hajj in Saudi Arabia. Int. J. Tour. Res. 2011, 13, 541–552. [Google Scholar] [CrossRef]
- General Authority for Statistics. Hajj Statistics Report 2016. 2016. Available online: https://www.stats.gov.sa/en (accessed on 20 May 2018).
- Kumbhar, A.; Koohifar, F.; Güvenç, I.; Mueller, B. A survey on legacy and emerging technologies for public safety communications. IEEE Commun. Surv. Tutor. 2017, 19, 97–124. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling air-to-ground path loss for low altitude platforms in urban environments. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Austin, TX, USA, 8–12 December 2014; pp. 2898–2904. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Drone small cells in the clouds: Design, deployment and performance analysis. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Optimal transport theory for power-efficient deployment of unmanned aerial vehicles. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Bor-Yaliniz, R.I.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an aerial base station in next generation cellular networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Kalantari, E.; Yanikomeroglu, H.; Yongacoglu, A. On the Number and 3D Placement of Drone Base Stations in Wireless Cellular Networks. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Efficient deployment of multiple unmanned aerial vehicles for optimal wireless coverage. IEEE Commun. Lett. 2016, 20, 1647–1650. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Khreishah, A.; Othman, N.S.; Sawalmeh, A. Maximizing indoor wireless coverage using uavs equipped with directional antennas. In Proceedings of the 2017 IEEE 13th Malaysia International Conference on Communications (MICC), Johor Bahru, Malaysia, 28–30 November 2017; pp. 175–180. [Google Scholar]
- Shakhatreh, H.; Khreishah, A.; Khalil, I. Indoor Mobile Coverage Problem Using UAVs. IEEE Syst. J. 2018. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Khreishah, A.; Ji, B. Providing wireless coverage to high-rise buildings using UAVs. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Feng, Q.; McGeehan, J.; Tameh, E.K.; Nix, A.R. Path loss models for air-to-ground radio channels in urban environments. In Proceedings of the IEEE 63rd Vehicular Technology Conference, Melbourne, Australia, 7–10 May 2006; Volume 6, pp. 2901–2905. [Google Scholar]
- Holis, J.; Pechac, P. Elevation dependent shadowing model for mobile communications via high altitude platforms in built-up areas. IEEE Trans. Antennas Propag. 2008, 56, 1078–1084. [Google Scholar] [CrossRef]
- Feng, Q.; Tameh, E.K.; Nix, A.R.; McGeehan, J. WLCp2-06: Modelling the likelihood of line-of-sight for air-to-ground radio propagation in urban environments. In Proceedings of the IEEE Global Telecommunications Conference, GLOBECOM’06, San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–5. [Google Scholar]
- Series, M. Guidelines for evaluation of radio interface technologies for IMT-Advanced. Report ITU 2009. [Google Scholar]
- Sawalmeh, A.; Othman, N.S.; Shakhatreh, H.; Khreishah, A. Providing Wireless Coverage in Massively Crowded Events Using UAVs. In Proceedings of the IEEE 13th Malaysia International Conference on Communications (MICC), Johor Bahru, Malaysia, 28–30 November 2017; pp. 158–163. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP altitude for maximum coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Hifi, M.; Paschos, V.T.; Zissimopoulos, V. A simulated annealing approach for the circular cutting problem. Eur. J. Oper. Res. 2004, 159, 430–448. [Google Scholar] [CrossRef]
- DeGroot, C.; Peikert, R.; Würtz, D. The Optimal Packing of Ten Equal Circles in a Square; Eidgenössische Technische Hochschule Zürich, Interdisziplinäres Projektzentrum für Supercomputing: Zurich, August 1990. [Google Scholar]
- Nurmela, K.J.; Östergård, P.R. Packing up to 50 equal circles in a square. Discret. Comput. Geom. 1997, 18, 111–120. [Google Scholar] [CrossRef]
- Nurmela, K.J.; Östergård, P.R. More optimal packings of equal circles in a square. Discret. Comput. Geom. 1999, 22, 439–457. [Google Scholar] [CrossRef]
- Horst, R.; Tuy, H. Global Optimization: Deterministic Approaches; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Musin, O.R.; Nikitenko, A.V. Optimal packings of congruent circles on a square flat torus. Discret. Comput. Geom. 2016, 55, 1–20. [Google Scholar] [CrossRef]
- Szabó, P.G.; Markót, M.C.; Csendes, T. Global optimization in geometry—Circle packing into the square. In Essays and Surveys in Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 233–265. [Google Scholar]
- Schaer, J.; Meir, A. On a geometric extremum problem. Canad. Math. Bull. 1965, 8, 21–27. [Google Scholar] [CrossRef]
- Schaer, J. The densest packing of nine circles in a square. Canad. Math. Bull. 1965, 8, 273–277. [Google Scholar] [CrossRef]
- Demaine, E.D.; Fekete, S.P.; Lang, R. Circle packing for origami design is hard. arXiv, 2010; arXiv:1008.1224. [Google Scholar]
- Correia, M.H.; Oliveira, J.F.; Ferreira, J.S. Cylinder packing by simulated annealing. Pesqui. Oper. 2000, 20, 269–286. [Google Scholar] [CrossRef]
- López, C.O.; Beasley, J.E. A heuristic for the circle packing problem with a variety of containers. Eur. J. Oper. Res. 2011, 214, 512–525. [Google Scholar] [CrossRef]
- Birgin, E.G.; Martınez, J.; Ronconi, D.P. Optimizing the packing of cylinders into a rectangular container: A nonlinear approach. Eur. J. Oper. Res. 2005, 160, 19–33. [Google Scholar] [CrossRef] [Green Version]
- Isermann, H. Heuristiken zur Lösung des zweidimensionalen Packproblems für Rundgefäße. Oper.-Res.-Spektrum 1991, 13, 213–223. [Google Scholar] [CrossRef]
- Specht, E. Packomania. 2009. Available online: http://packomania.com (accessed on April 2018).
- Mladenović, N.; Plastria, F.; Urošević, D. Reformulation descent applied to circle packing problems. Comput. Oper. Res. 2005, 32, 2419–2434. [Google Scholar] [CrossRef]
- Hifi, M.; M’hallah, R. A literature review on circle and sphere packing problems: Models and methodologies. Adv. Oper. Res. 2009, 2009. [Google Scholar] [CrossRef]
- Graham, R.L.; Lubachevsky, B.D. Dense packings of equal disks in an equilateral triangle: From 22 to 34 and beyond. Electron. J. Combin 1995, 2, 39. [Google Scholar]
- Bose, P.; Czyzowicz, J.; Kranakis, E.; Maheshwari, A. Algorithms for packing two circles in a convex polygon. In Proceedings of the Japanese Conference on Discrete and Computational Geometry, Tokyo, Japan, 9–12 December 1998; pp. 93–103. [Google Scholar]
- Machchhar, J.; Elber, G. Dense packing of congruent circles in free-form non-convex containers. Comput. Aided Geom. Des. 2017, 52, 13–27. [Google Scholar] [CrossRef]






| n | Ref. | n | Ref. | ||||
|---|---|---|---|---|---|---|---|
| 2 | 0.292893 | 0.539 | [32] | 13 | 0.133994 | 0.733 | [27] |
| 3 | 0.254333 | 0.6096 | [32] | 14 | 0.128556 | 0.727 | [27] |
| 4 | 0.250000 | 0.785 | [32] | 15 | 0.126478 | 0.754 | [27] |
| 5 | 0.207107 | 0.674 | [32] | 16 | 0.125000 | 0.785 | [27] |
| 6 | 0.187681 | 0.664 | [32] | 17 | 0.117186 | 0.733 | [27] |
| 7 | 0.174458 | 0.669 | [33] | 18 | 0.115522 | 0.755 | [27] |
| 8 | 0.170541 | 0.731 | [33] | 19 | 0.112265 | 0.752 | [27] |
| 9 | 0.166666 | 0.785 | [34] | 20 | 0.111382 | 0.779 | [27] |
| 10 | 0.148204 | 0.690 | [27] | 21 | 0.106839 | 0.753 | [27] |
| 11 | 0.142399 | 0.701 | [27] | 22 | 0.105665 | 0.772 | [27] |
| 12 | 0.139959 | 0.738 | [27] |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 2 GHz | (Vmin, Vmax, Vsize) | (0, 1000, 3) |
| Noise power | −120 dBm | Population size () | 50 |
| Total available | 50 MHz | Max number of iterations | 50 |
| bandwidth | () | ||
| UAV transmit power | = 5 watt | (, , ) | (1, 2.05, 2.05) |
| Data rate | 0.5 Mbps | Tolerance () | 0.1 |
| Environment Parameter | Value | Environment Parameter | Value |
| a | 9.6 | 1 | |
| b | 0.28 | 20 |
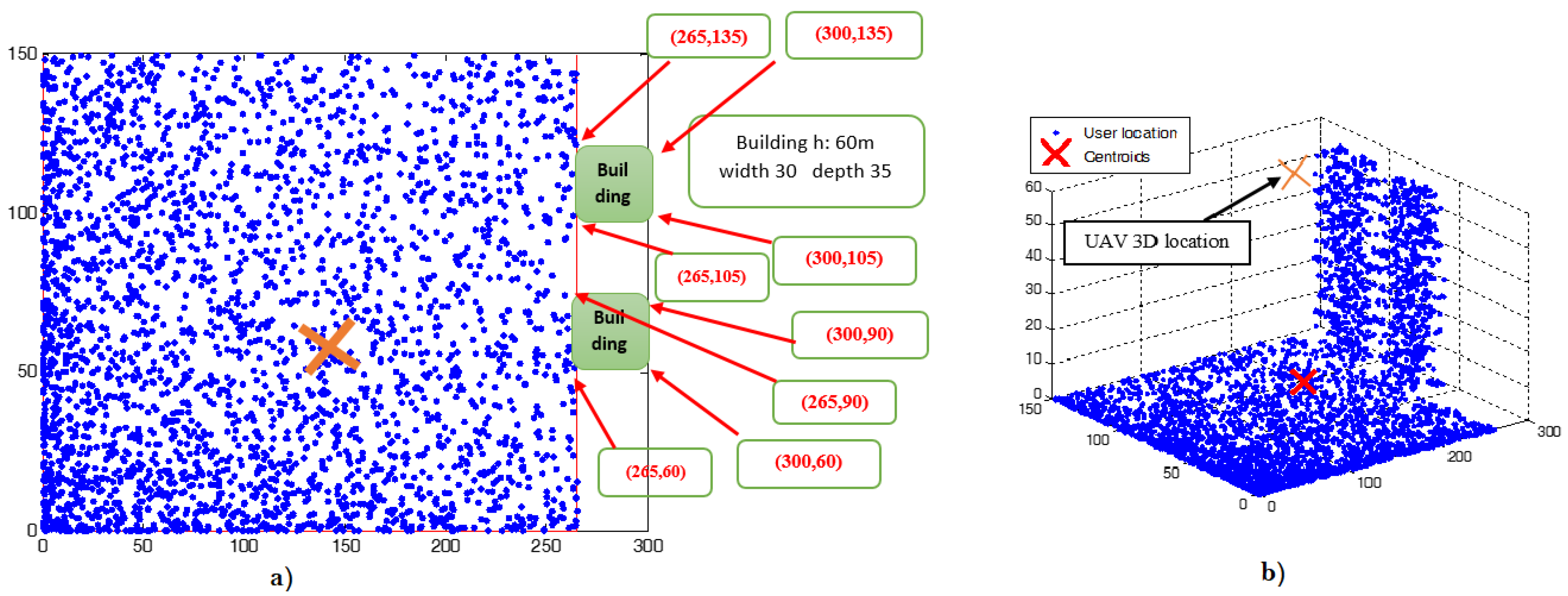
| Algorithm | (Outdoor) Subarea Dimensions | (Indoor) Building Dimensions | Number of Outdoor Users | Number of Active Indoor Users | Efficient UAV Placement (, , ) | UAV Transmit Power (watt) | Enhanced PSO than KTS |
|---|---|---|---|---|---|---|---|
| PSO | 300 m × 150 m | 2750 | One Building, 12 floors → 600 | (117.49, 58.78, 60.89) | 0.42 | 5.7× | |
| KTS | (129.53, 60.26, 49.1) | 2.39 | |||||
| PSO | 300 m × 150 m | 2750 | One Building, 12 floors → 750 | (151.95, 58.3, 61.5) | 0.86 | 5.4× | |
| KTS | (158, 60.76, 46.5) | 4.639 | |||||
| PSO | 300 m × 150 m | 2750 | Two Buildings, 12 floors →960 | (161.66, 62.79, 62.12) | 3.255 | 5.1× | |
| KTS | (162.64, 63.23, 41.11) | 16.594 |
| n | Circle Radius r | Number of Active Receivers 35% | Optimal 3D UAV Placement | UAV Transmit (Power) watt | Density | Antenna Half Beamwidth θ/2 |
|---|---|---|---|---|---|---|
| 8 | 341.1 m | 5076 | (, , 213) | 5095 Very High | 0.731 | 58.01 |
| 9 | 333.3 m | 4925 | (, , 208) | 2068 Very High | 0.785 | 58.03 |
| 10 | 296.4 m | 3819 | (, , 185) | 16.5 | 0.690 | 58.03 |
| 11 | 284.8 m | 3565 | (, , 178) | 3.39 | 0.701 | 58.0 |
| 12 | 279.9 m | 3445 | (, , 175) | 1.61 | 0.738 | 57.9 |
| 13 | 267.9 m | 3200 | (, , 167) | 0.373 | 0.733 | 58.06 |
| 14 | 257.1 m | 2973 | (, , 160) | 0.091 | 0.727 | 58.1 |
| 15 | 252.9 m | 2860 | (, , 158) | 0.043 | 0.754 | 58.0 |
| 16 | 250.0 m | 2745 | (, , 156) | 0.020 | 0.785 | 58.03 |
| 17 | 234.4 m | 2422 | (, , 147) | 2.60 | 0.733 | 57.91 |
| 18 | 231.0 m | 2328 | (, , 144) | 1.40 | 0.755 | 58.06 |
| 19 | 224.5 m | 2226 | (, , 140) | 7.34 | 0.752 | 58.05 |
| 20 | 222.8 m | 2136 | (, , 139) | 3.87 | 0.779 | 58.04 |
| 21 | 213.7 m | 2025 | (, , 133) | 2.03 | 0.753 | 58.10 |
| 22 | 211.3 m | 1953 | (, , 132) | 1.24 | 0.772 | 58.0 |
| n | Circle Radius r | Number of Active Receivers 35% | Optimal 3D UAV Placement | UAV Transmit (Power) watt | Density | Antenna Half Beamwidth θ/2 |
|---|---|---|---|---|---|---|
| 10 | 493 m | 7634 | (, , 307) | Very High | 0.707 | 58.089 |
| 15 | 402 m | 5020 | (, , 251) | Very High | 0.709 | 58.02 |
| 18 | 368 m | 4181 | (, , 229) | 53.9 High | 0.708 | 58.107 |
| 19 | 357 m | 3953 | (, , 223) | 11.95 | 0.706 | 58.009 |
| 20 | 351 m | 3843 | (, , 219) | 6.088 | 0.719 | 58.039 |
| 21 | 345 m | 3736 | (, , 215) | 3.306 | 0.729 | 58.069 |
| 22 | 341 m | 3626 | (, , 213) | 1.59 | 0.744 | 58.010 |
| 23 | 339 m | 3559 | (, , 211) | 1.013 | 0.768 | 58.101 |
| 24 | 334 m | 3518 | (, , 208) | 0.847 | 0.779 | 58.087 |
| 25 | 331 m | 3418 | (, , 206) | 0.435 | 0.796 | 58.104 |
| 26 | 330 m | 3384 | (, , 20 6) | 0.246 | 0.825 | 58.026 |
| 27 | 319 m | 3213 | (, , 199) | 0.125 | 0.798 | 58.043 |
| 28 | 308 m | 3006 | (, , 192) | 0.036 | 0.771 | 58.062 |
| 29 | 303 m | 2890 | (, , 189) | 0.018 | 0.777 | 58.046 |
| 30 | 300 m | 2821 | (, , 187) | 0.011 | 0.785 | 58.063 |
| 31 | 289 m | 2636 | (, , 180) | 0.0037 | 0.755 | 58.084 |
| 32 | 285 m | 2543 | (, , 178) | 0.0020 | 0.756 | 58.013 |
| 33 | 279 m | 2459 | (, , 174) | 0.0012 | 0.748 | 58.050 |
| n | Radius (r) (Unit Circle) | Circle Radius (r) (R = 1125 m) | Number of Active Receivers 35% | Optimal 3D UAV Placement | UAV Transmit (Power) watt | Density | Antenna Half Beamwidth θ/2 |
|---|---|---|---|---|---|---|---|
| 8 | 340 | 5077 | (, , 212) | 53,564 Very High | |||
| 9 | 0.27676865 | 311 | 4252 | (, , 194) | 267.1 Very high | 0.68940799 | |
| 10 | 0.26225892 | 295 | 3820 | (, , 184) | 17.43 | 0.68779743 | |
| 11 | 0.2548547 | 287 | 3600 | (, , 179) | 4.29 | 0.71446011 | |
| 12 | 0.24816347 | 279 | 3445 | (, , 174) | 1.63 | 0.7390213 | |
| 13 | 0.23606798 | 266 | 3082 | (, , 166) | 0.166 | 0.72446517 | |
| 14 | 0.23103073 | 260 | 2973 | (, , 162) | 0.0874 | 0.74725276 | |
| 15 | 0.22117254 | 249 | 2746 | (, , 155) | 0.0199 | 0.73375938 | |
| 16 | 0.21666474 | 244 | 2634 | (, , 152) | 9.80 | 0.75109777 | |
| 17 | 0.20867967 | 235 | 2422 | (, , 147) | 2.40 | 0.74030245 | |
| 18 | 0.20560465 | 231 | 2318 | (, , 144) | 1.30 | 0.76091887 | |
| 19 | 0.20560465 | 231 | 2318 | (, , 144) | 1.30 | 0.80319214 | |
| 20 | 0.19522401 | 220 | 2127 | (, , 137) | 3.76 | 0.76224829 | |
| 21 | 0.19039215 | 214 | 2026 | (, , 133) | 2.01 | 0.76123256 | |
| 22 | 0.18383303 | 207 | 1851 | (, , 129) | 6.29 | 0.7434808 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sawalmeh, A.; Othman, N.S.; Shakhatreh, H. Efficient Deployment of Multi-UAVs in Massively Crowded Events. Sensors 2018, 18, 3640. https://doi.org/10.3390/s18113640
Sawalmeh A, Othman NS, Shakhatreh H. Efficient Deployment of Multi-UAVs in Massively Crowded Events. Sensors. 2018; 18(11):3640. https://doi.org/10.3390/s18113640
Chicago/Turabian StyleSawalmeh, Ahmad, Noor Shamsiah Othman, and Hazim Shakhatreh. 2018. "Efficient Deployment of Multi-UAVs in Massively Crowded Events" Sensors 18, no. 11: 3640. https://doi.org/10.3390/s18113640
APA StyleSawalmeh, A., Othman, N. S., & Shakhatreh, H. (2018). Efficient Deployment of Multi-UAVs in Massively Crowded Events. Sensors, 18(11), 3640. https://doi.org/10.3390/s18113640







