1. Introduction
For over 30 years, Risk Assessment and Management has been a stand-alone scientific discipline, and several attempts have been made to establish widely accepted definitions of key terms and concepts related to the field of risk [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. In this respect, it is important to clarify the concept of risk first. The Society for Risk Analysis (SRA) gives both qualitative definitions of risk and risk metrics [
14,
15].
In terms of purely qualitative definitions, risk is defined as the possibility of an unfortunate event; the potential occurrence of negative consequences arising from an incident; the set of consequences deriving from an activity and associated uncertainties or, moreover, the deviation from a reference value and the corresponding uncertainty measures.
With regard to risk metrics, the risk R can be defined as a combination of the probability of an occurring event and the severity of the consequences arising from it.
where s
i indicates the i-th scenario, p
i is the probability that the i-th scenario takes place and c
i expresses the consequence of the i-th scenario, with i = 1, 2, 3, ..., N.
The following mathematical relationship is also valid:
being C’ consequences of the event, Q the likelihood of C’ (typically probability) where Q is expressed in probabilistic terms, and K the cognitive background connected to C’ and to Q.
The risk can also be measured according to the expected consequences, i.e., in terms of losses and/or damage, for example:
Number of expected fatalities in a specific time interval (Potential Loss of Life (PPL), that is the expected number of fatalities in a period of one year; or Fatal Accidental Rate, (FAR) which represents the expected number of fatalities per 100 million hours of exposure);
Product of the probability P that the risky event occurs, by the probability
of exposure to the risk and expected damage D
Expected disutility.
Finally, a further possibility is to express the risk R as a probability distribution related to the damage.
This last definition was shared by different Authors, according to which there is a risk when the occurrence of an event can be measured on a probabilistic basis; on the contrary, there is uncertainty when there are no significant data on the frequency of the phenomenon investigated [
16,
17,
18].
Knight F.H. focusing on the measurability of uncertainties, distinguishes between measurable uncertainties, properly defined risks, and unmeasurable uncertainties, which represent the true uncertainties: «It will appear that a measurable uncertainty, or “risk” proper, as we shall use the term, is so far different from an unmeasurable one that it is not in effect an uncertainty at all. We shall accordingly restrict the term “uncertainty” to cases of the non-quantitative type. It is this “true” uncertainty, and not risk, as has been argued, which forms the basis of a valid theory of profit and accounts for the divergence between actual and theoretical competition» [
19]. According to this interpretation, the consequences arising from risky events can have both negative and positive characters, thus configuring possible losses, but also opportunities that result in a higher value [
20].
Those described are widely shared concepts in fields of application that are also very different: From finance to security engineering, from health to transport sector, as well as in the supply chain management [
21]. Nonetheless, the risk assessment and management process are essential to express judgments of economic convenience on investment initiatives. This is especially true for civil engineering projects, where the risk components are not only of an economic nature, but also of an environmental, social and cultural character [
22].
Based on this premise, the aim of the paper is to define a risk management protocol in the economic evaluation of investments in the civil field. Specifically, the novelty of the model is related to the acceptability of the project risk, both as to the initiative as proposed by the investor, and to the project possibly modified providing for it mitigation actions to reduce the risk. Basically, it is important to measure the residual risk of the investment after having identified the mitigation interventions, through criteria that are methodologically robust and easily repeatable.
How to pursue the objectives of the study? Using the As Low as Reasonably Practicable (ALARP) logic in the Cost-Benefit Analysis (CBA) schemes.
Risk analysis that is the Cost-Benefit Analysis carried out in probabilistic terms, assigns a probability distribution to each of the critical variables of the project, defined in a precise range of values around the best estimate, used as the base case. From these basic assumptions, it therefore estimates the probability distribution of the Internal Return Rate (IRR) or net present value (NPV) of the investment. Thus, on the one hand, from this type of analysis it is possible to read the risk of investment failure. On the other hand, the literature does not provide any objective criteria for determining whether the investment risk calculated in this way is acceptable. The idea is to define two different thresholds: That of acceptability and that of tolerability of investment risk. The former represents the probability of failure that the investor is willing to broadly accept; the latter defines the probability of bankruptcy that the investor considers tolerable because the costs to increase the probability of success are excessive compared to the benefits obtainable. As described in
Section 3, these thresholds are widely used to assess the acceptability and tolerability of the risk of potential loss of human life in the nuclear, energy and oil and gas sectors [
23,
24,
25,
26]. The novelty of the research is therefore that of transferring the concept of the acceptability of investment risk to evaluate the financial profitability of civil engineering projects.
The paper is structured as follows. The first part describes the steps necessary for managing the risk associated with a project initiative (
Section 2) and analyses the ALARP logic (
Section 3). In the second part, contained in
Section 4, a protocol to manage the investment risk is defined, highlighting how the ALARP principle can be integrated into the logical schema of Cost-Benefit Analysis (CBA). By introducing the thresholds of acceptability and tolerability of the risk of bankruptcy. In other words, the literature has so far only suggested identifying the risk components of the project and studying the probability distribution of the economic performance indicator. Instead, with the present work we want to define if the risk of failure, before and after possible mitigation interventions, is acceptable or at least tolerable for the investor. Hence the definition of the two thresholds must be established both according to the specific investment sector and according to the geographical and socio-economic context in which the project falls. In the third part,
Section 5, the protocol is validated via a case study. It’s about a project of an ancient village in the province of Salerno (Italy) with the purpose to increase the touristic attraction. The application to the case study shows how the model makes it possible to express a judgment on the economic suitability of a project in probabilistic terms, taking into account the acceptability and tolerability of the risk of the decision makers. In the final part (
Section 6), the results obtained are analyzed and scenarios for future research are presented also in light of the relevant political implications. In particular, the construction of a dataset in order to define specific thresholds of acceptability and tolerability of risk on a statistical basis can represent the next step of the research.
2. Risk Management Process in the Economic Evaluation of Projects
The logical-operative process of risk management is divided into successive and strictly interdependent phases [
27,
28,
29,
30,
31,
32,
33], consisting of:
Definition of the objectives of the risk management activity
Identification of risks, which may influence the objectives already established in phase 1
Risk analysis in order to study the causes and consequences deriving from the risky events
Risk assessment, an activity necessary to define the actions aimed at managing the risk
Risk mitigation, through specific mitigation strategies
Assessment of the residual risk, i.e., the risk that remains despite the planned mitigation strategy.
The described process, which has already been mentioned above, is applied in very different fields, and is of paramount importance when it is necessary to evaluate the economic performance of civil engineering projects [
34,
35]. The rationale for this is that civil projects are characterized by profiles of complexity that arise from the multiple interrelations with the lived city, being of a nature that is not merely technical, but economic in a broad sense, thus covering the rates of financial, social, cultural and environmental risks that need to be assessed in order to conduct correct economic evaluations [
36,
37,
38,
39,
40,
41,
42]. For this reason, it is critical to evaluate the project risk that, as S. Savvides (1994) states, «depends, on the one hand, on our ability to identify and understand the nature of uncertainty surrounding the key project variables and on the other, on having the tools and methodology to process its risk implications on the return of the project» [
43]. In this sense, risk analysis or probabilistic simulation in the economic evaluation of projects is a methodology whereby the uncertainty encompassing the main variables projected in a forecasting model is processed in order to estimate the impact of risk on the expected results [
43,
44,
45,
46,
47,
48]
It should be noted that for major projects in civil works, the Guide to Cost-Benefit Analysis of Investment Projects 2014–2020 (European Commission, EC) requires the assessment of investment risks as a necessary condition for funding [
49].
However, the European Commission, although provides precise indications for the analysis and for the risk assessment; however, does not provide any useful criteria to decide on its tolerability. On the contrary, the definition of threshold limits of risk acceptability is systematically provided in other areas, such as health and safety. In these areas, the risk-reduction principle is the ALARP (As Low as Reasonably Practicable), according to which a specific reduction measure must be implemented until costs are too disproportionate compared to the benefits that can be obtained. The concrete possibility of applying ALARP principle also for the risk analysis of civil engineering projects, therefore in sectors different from those where it is commonly adopted, is the subject of discussion in the following sections.
3. ALARP Logic in the Decision-Making
According to the ALARP principle, the risks in decision-making regarding safety and health must be reduced to levels as low as reasonably practicable, after which a further reduction in risk would be excessively expensive [
50,
51,
52,
53,
54]. This principle, already explained in the Health and Safety Executive (HSE) regulations [
47,
48,
49,
50], can have applications of extreme importance in all cases where the primary objective is the triangular balancing between risks, costs to reduce them and potential benefits that can be achieved.
Figure 1 shows two different representations of the ALARP principle. The simplest one is shown in
Figure 1a, where the risk increases along the vertical axis.
Figure 1b, on the other hand, represents the “carrot” model defined by the HSE, which illustrates the obvious criterion according to which, the greater the residual risk, the greater the mitigation costs to make it tolerable [
55,
56,
57,
58]. In both cases, two horizontal lines delimit three risk regions: The bottom line represents the “broadly acceptable” threshold, up to which the risk does not need to be reduced; the upper one defines the “limit of tolerability” threshold that separates the risk tolerability zone from the unacceptability zone. Therefore, unlike the simpler model, shown in
Figure 1a, the carrot representation considers the magnitude of the risk that can be read horizontally: In fact, as the magnitude increases, the costs necessary to bring the risk at least to the threshold of tolerability increase.
The ALARP principle implicitly recognizes that the “zero” risk is not a feasible option, so much so that within the “safety risk” the “broadly acceptable” threshold is often considered as a “safe level”. Similarly, the “limit of tolerability” threshold is not a catastrophe, but represents the beginning of an “unsafe” area.
Note how the absence of specific numerical values for the thresholds suggests the need to calibrate the model. For example, HSE recommends a “broadly acceptable” threshold of 10−6 deaths per year (one in a million) and a “tolerability limit” between 10−3 and 10−4 victims per year.
It should be noted that within ALARP the disproportion between costs and benefits obtained results in the estimate of the Implied Cost of Averting one Fatality (ICAF). This indicator, which represents the cost of an investment, is the ratio of the cost of the investment made and the expected decrease in the number of deaths because of the mitigation action:
Comparing the estimated ICAF for the proposed option with reference ICAF values, specific according to the sector in question, it is verified whether there is a disproportionate between the costs for risk mitigation and the advantages obtained. The risk is tolerable if it falls in the ALARP area, as additional costs to bring the risk to the acceptability threshold would be excessive [
59,
60,
61].
Although mainly used in “safety risk”, it emerges that ALARP logic defines a general way of thinking, as well as a framework able to facilitate “risk communication” [
61]. In this sense, it is believed that the ALARP principle integrated with traditional evaluation techniques, may allow the definition of an innovative approach to risk management that characterizes civil engineering projects, as explained in the following section.
5. The Case Study: Rehabilitation Project for an Ancient Village in Cilento, Italy
The protocol for the analysis and assessment of the risk summarized in
Table 1 is applied to the recovery and transformation into a “country-hotel” of an ancient medieval village in the Province of Salerno (Italy). Located on the border between Campania and Basilicata, the village was abandoned after the earthquake of 1980 and the population moved to a new urban center. The project of redeveloping the country has as objectives both the conservation of its historical-architectural values and the revival of the economy through tourism activities.
The intervention in question has been chosen as representative of those interventions for the recovery and revitalization of the ancient abandoned villages. However, the definition of sensitive variables and risk mitigation interventions are strictly related to the specifics of the case study. In addition, the determination of the value to be attributed to the limits of acceptability and tolerability is a function of the specific sector of intervention and of the socio-economic characteristics of the area in which the project is located.
The analysis of the state of affairs shows that the building stock of the village is strongly degraded, with many residential units in a condition of ruin, as shown in
Figure 2. The conservation degree and the typological characteristics of the buildings are detailed in
Table 2 and
Table 3 respectively. The building capital is classified according to four different levels of degradation, as also derives from
Figure 3.
The investment project includes, in addition to the preliminary making safe of the entire area of the village, the construction of accommodation for tourists and works necessary to provide additional functions to that of widespread hospitality. The individual recovery actions provide for:
Tourist residences for a total offer of 144 beds;
An info-point and a consortium for the promotion of typical products;
Three restaurants and a bar with an observation deck;
Green area;
Parking space;
Spaces for the processing and marketing of typical local crafts (a mill, a dairy and a wine shop);
A movie theatre, to be located in a building that has already been restored;
A reading room;
Shops and premises for the rental of equipment necessary to carry out sports and recreational activities on site.
Figure 4 shows the planimetric distribution of the single functional destinations. The area in celestial color constitutes a portion of the village that is preserved in the original conditions, with the aim of recreating a historical
promenade in a real “open-air museum”.
The financial feasibility study of the synthetically described project is conducted. Following the six phases of the protocol summarized in
Table 1, the analysis and evaluation of the investment risk are carried out.
5.1. Definition of the Objectives of the Risk Management Process
The preparation of the financial plan and the consequent estimate of the economic performance indicators are operations necessary to verify the achievement of the goal of the risk management process, that is to assess the effective financial feasibility of the investment. For the case study,
Table 4 shows the main assumptions made based on the financial analysis and the values of the main parameters.
The analysis is therefore developed over a period of 25 years, a term deemed sufficient to assess the effects of the investment taking into account both the degree of stability of the scenarios (i.e., likelihood of the forecasts), and the importance of cash flows on the profitability of the project and the degree of risk inherent in the type of project.
Due to the nature of the intervention, the work is scheduled to be completed over two years (construction phase), with expenditure amounts for each year equal to about 50% of the total investment cost.
The valuation is carried out at constant prices, i.e., for any estimate the same prices are applied for the entire analysis period, specifically those for the evaluation reference year (2018).
Ordinary and extraordinary maintenance rates are introduced in the operating costs to ensure constant efficiency and capital value of the project’s works and plants, so that at the end of the analysis period a residual value of the works is not different from the investment cost.
As a discount rate for the cash flows discounting, the value of 4% is adopted according to the indications of the European Commission for the 2014–2020 programming period.
With regard to management, it is assumed that the widespread-hotel is entrusted to a company that manages exclusively the accommodation and that grants third parties the additional services provided.
To be able to produce the calculations related to the financial plan it is necessary to estimate:
Costs of the project;
Revenue of the project.
As regards costs, they are related to the implementation of the intervention and those for the management of the works to be carried out, namely investment costs and operating costs.
With specific reference to the project in question, investment costs include both those for the renovation of the village and those necessary for the inclusion of ancillary functions.
Operating costs include the management of functions, ordinary and extraordinary maintenance and financial amortization. In fact, it is expected to take a mortgage with a French amortization plan to cover 60% of investment costs. The annual interest rate is set at 6% and the duration of the plan is ten years.
Table 5 summarizes the amounts relating to the individual cost items. In order to evaluate the investment costs, estimates have been drawn up on the basis of the prices provided by the Campania Region 2017 price List and the current price List for the conservation and restoration of the cultural and landscape works and heritage of Campania. Management costs, on the other hand, have been estimated by analyzing similar country-hotel financial statements for both the socio-economic properties of the place in which they are located and for technical-functional characteristics.
The project’s revenue is due to the re-entries deriving from the offer of tourist residences based on an average annual housing filling index (Ihf), estimated at just over 60%. In particular, the tourist flows in the village were analyzed on a seasonal basis. From this study it was possible to estimate the number of hotel guests, the number of lodgings occupied during the year and, therefore, the value of the index Ihf as the annual average of the housing filling.
The annual revenue, for 144 beds divided into 47 rooms of different capacities, is just over one million euro. For the remaining assets, on the other hand, profits deriving from lease rentals are considered, estimated at around € 200,000/year based on market surveys. Specifically, as for the operating costs, revenues were also estimated by analyzing financial statements of country-hotel with similar characteristics assumed as benchmarks.
The financial plan of the investment is defined starting from the costs and profits respectively to be incurred and to be achieved during the evaluation period. From the plan so defined, it is possible to estimate the economic performance indicators:
Table 7 summarizes the values of the NPV and the IRR related to the project. The estimate is greater than zero, and the Internal Rate of Return is higher than the discount rate used, assumed equal to 4%.
5.2. Identification of the Risk Components of the Project
The risk variables of the project are identified through a sensitivity analysis, using which percentage changes to the values of the parameters from time to time taken into consideration are introduced in order to research the variables that most affect the investment performance.
The “critical” variables are the variable for which a variation of ± 1% of the value assumed in the base case gives rise to a variation of more than ± 1% of the value of the NPV. The elaborations allow for the identification of sensitive variables:
Table 8 summarizes the terms of sensitivity analysis for critical variables.
5.3. Risk Analysis
The sensitivity analysis evaluates the effects on the NPV of the change in the value of a single uncertain variable at a time. However, to assess the real risk of failure associated with the investment, changes in the values of economic performance indicators deriving from the simultaneous change of several project variables must be identified. This can be done through quantitative risk analysis, which consists of:
Estimate of the probability distribution associated with each of the identified critical variables;
Random generation of the probability distribution of the economic performance indicator. In fact, from the cumulative probability distribution of the indicator it is possible to evaluate the project risk, verifying whether the cumulative probability for a given value of VAN or TIR is higher or lower than a reference value considered critical.
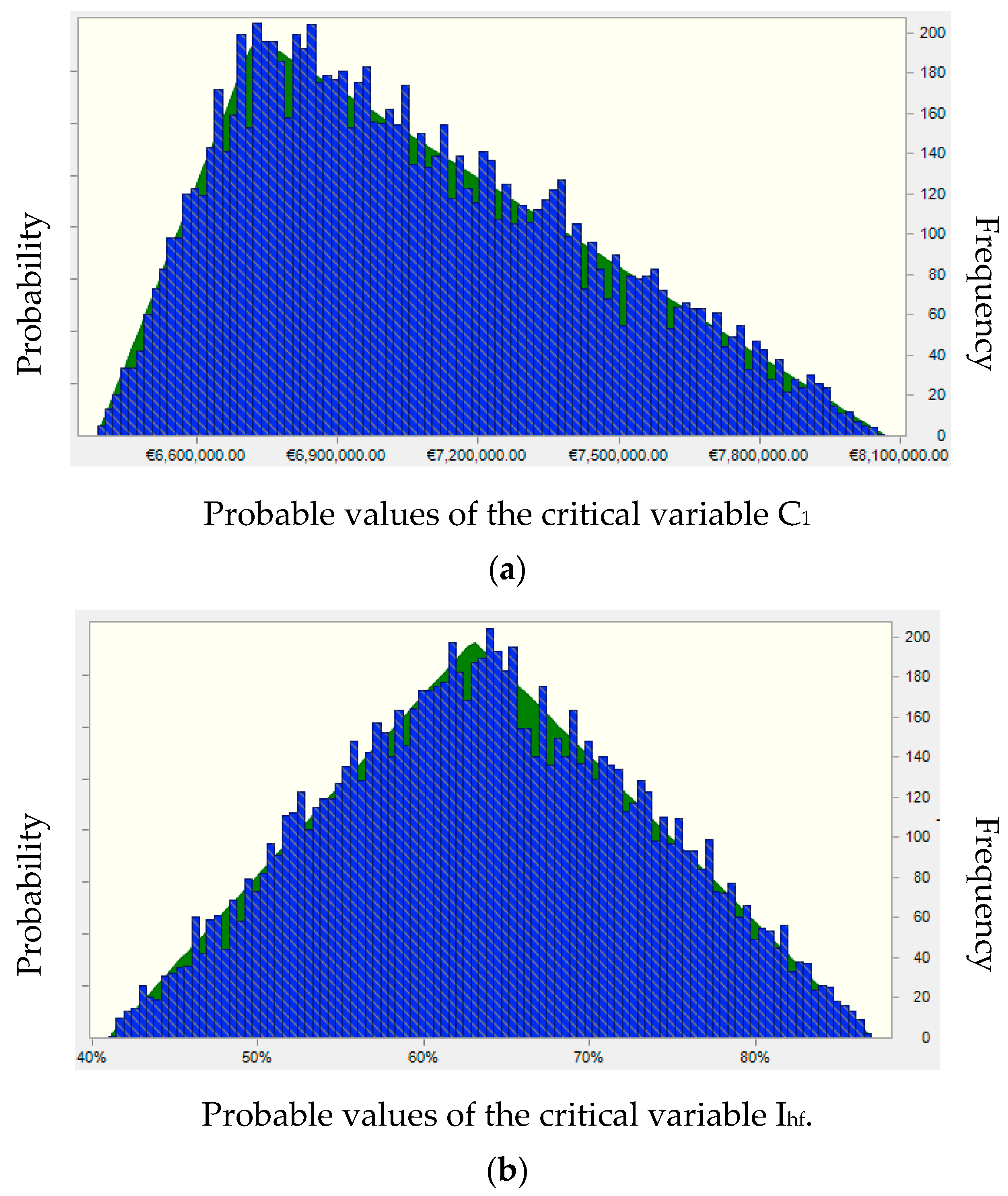
Table 9 summarizes the hypotheses assumed for the probability distribution of the critical variables detected in the case study. The distributions of the two variables are assumed triangular, since for both the average, minimum and maximum value of the critical variable can be estimated. The resulting probability distributions obtained are represented in
Figure 5a,b. The results of the risk analysis are in the numerical values of
Table 10, which summarizes the forecast values of the main static parameters relating to the Net Present Value (NPV) and the Internal Rate of Return (IRR). The same results are represented graphically in in
Figure 6a,b that show the probability distributions of the NPV and the IRR.
The analysis, obtained based on 10,000 random extrapolations through the Montecarlo method shows that the probability of having a negative NPV is almost zero, while the maximum value that the indicator can take is about € 1,200,000. Assuming the minimum IRRmin value of the performance indicator able to satisfy the investor equal to 4.5%, the probability of having IRR ≤ 4.5% is 62%. This demonstrates the high risk of the investment to make and the consequent need to intervene through mitigation actions.
5.4. Risk Assesment
It is at this step that the ALARP principle is applicable to analyze the triangular balance between risks, mitigation costs and achievable benefits. This makes the decision making process more transparent.
Operationally, it is necessary first of all to set the two thresholds for investment risk, namely: (1) Broadly acceptable threshold, understood as the limit value of the probability of failure that the economic operator is willing to “accept broadly”; (2) tolerability threshold, which represents the limit value of the probability of failure that the investor tolerates only because additional mitigation measures would have disproportionate costs in relation to the benefits obtainable.
The values of the two thresholds depend on the investment sector, on the socio-economic characteristics of the area in which the project is to be carried out, but certainly also on the risk appetite of the economic operator who intends to take charge of the execution and management of the works. In the case study, judgments of experts and information from investors lead to the following values:
Depending on these values, there is an unacceptable risk level for the country-hotel project. In fact, the probability of failure, ie the probability for which IRR ≤ IRR
lim = 4.5%, is 68%, that is higher than the tolerability threshold. This is shown in
Figure 7 in which, taking up the ALARP logic described in
Section 2, the three failure risk regions separated from the acceptability and tolerability threshold are represented. The inverted triangle shows the increase of the magnitude of the risk passing from the lower vertex to the upper base. Obviously the greater the risk, the higher the costs for its mitigation.
5.5. Definition of Risk Mitigation Interventions
Since the project risk is unacceptable to the investor, it is necessary to envisage mitigation measures able to increase the probability of success of the project initiative.
As a risk mitigation option, more investments in promotion and advertising are evaluated. These correspond to a relative increase in operating costs (see
Table 11 result in a rise of visitor flows and, therefore, in the average housing filling index, which goes from 63% to 80%.
5.6. Assesment of the Resisual Risk
At this point, the ALARP principle requires the assessment of the residual risk, i.e., the one that remains despite the actions taken to mitigate it. To this end, the new probability distribution of the IRR is estimated, as a result of the change in both the costs of promotion and advertising, and the index of housing filling.
Table 12 contains the new hypotheses assumed for the probability distribution of the critical variable “housing fill index”. In fact, the risk mitigation intervention consisting of the increase in cost of promoting the diffused hotel has consequently led to an increase in the modal value of the I
hf. By studying the functional relationship between costs of promotion and increase in tourist turnout, the mode of the index I
hf has gone from 63% to 80% The relative probability distribution obtained is shown in
Figure 8.
The results of the calculations are shown in
Table 13 which summarizes the forecast values of the main static parameters relating to the Internal Rate of Return (IRR) post mitigation intervention.
Figure 9 shows the new probability distribution of the IRR, which results in a significant reduction in the level of risk, which falls in the ALARP area after the mitigation intervention. In fact, the probability of failure, ie that for which IRR ≤ IRR
lim = 4.5%, drops to 38%, as shown in
Figure 10.
Subsequent calculations prove that further options for changing the structure of operating costs are not convenient, since they do not generate satisfactory increases in revenues. This means that the investment risk is tolerable as ALARP.
6. Discussion and Conclusive Remarks
To express a judgment of economic convenience on an investment project, it is essential to analyze and evaluate the risk components in probabilistic terms. This is requested to define actions useful to reduce the financial risk, also proposing changes to the intervention.
Both the reference literature and the current regulatory guidelines outline a risk management process that the phases of sensitivity analysis, qualitative risk analysis, risk probabilistic study, definition of mitigation actions. But for the civil engineering sector there are no specific indications to compare the levels of project risk before and after mitigation actions.
The idea of the paper is to integrate ALARP logic “As Low As Reasonably Practicable”, generally used in the evaluation of health and safety risks, in the methodological and procedural schemes of the Cost-Benefit Analysis as known and applied in the field civil, with the aim of introducing thresholds of acceptability and tolerability of the risk connected to the intervention. This attempt, in other words to use in the classic investment risk management procedures, the highly consolidated ALARP assessment approach in the industrial sector, leads to characterizing an investigation protocol that appears useful to improve the information panel on project profitability, with clear advantages for investors, who more consciously can decide on the implementation of the initiative.
The model of economic analysis is tested on the investment for the recovery and transformation of an ancient medieval village in the province of Salerno (Italy). The introduction of the acceptability and tolerability thresholds has, as a main advantage, the possibility of verifying in an objective and immediate manner the degree of riskiness of the intervention. Consequently, if the risk is unacceptable or ALARP it is necessary to plan or design and structural changes of the project or changes regarding the strict management phase. In other words, it is necessary to estimate the risk mitigation measures that will positively affect the economic performance indicator. In the case under consideration, the design constraints and the opportunity not to distort the planning guidelines, push to prefigure mitigation options regarding the strict management phase. Specifically, by increasing advertising and promotion costs, the probability of investment failure decreases, from 64%—already considered unacceptable to the investor—to 32%, the latter term considered tolerable. Further processing shows that other options for changing the structure of operating costs are not prospective, as they do not produce satisfactory increases in revenues. This means that the investment risk is tolerable as ALARP.
The case study shows, on one hand, that the joint use of the ALARP logic and the principles of the CBA in economic analyses in the civil field is concretely possible. On the other hand, the model outlined gives the risk analyst the opportunity to consistently evaluate the triangular balance between risks, costs and benefits, thus making the decision-making process more transparent and rational.
The novelty of the model concerns the use of the ALARP logic to evaluate the acceptability of investment risk, both the one related to the project as it was designed, and the one that still remains following the planned mitigation options. However, the research -highlights a substantial difference in the use of ALARP logic among industrial sectors, where it is generally necessary to limit the loss of human life risk, and the field of civil engineering. In fact, in the first case, the actions to mitigate the project risk and the consequent effect (for example the lower number of loss of life) are respectively independent and dependent variables according to a direct functional relationship. In fact, the disproportion in costs with respect to the achievable benefits is verified through the ICAF estimate as explained in
Section 3. On the contrary, in the second case, to know the link between the input variables (for example, the management costs) and the levels of risk, we pass through the output variables (IRR), where inputs and outputs are interrelated. In other words, the level of investment risk and the disproportion between the costs incurred and the benefits obtainable by the mitigation measures depend directly on the economic performance indicator. For this reason, in the civil field, this makes difficult to construct risk acceptance and tolerability thresholds on a probabilistic basis.
However, the construction of a dataset able to summarize the risk appetite of the ordinary investor may be the next step of the research. Therefore, the goal is to build a dataset on the basis of average levels of profitability of investments classified both for categories of investment projects and for specific socio-economic characteristics of the area where the initiative is located. This will make it easier to predict the thresholds of acceptability and tolerability of risk in probabilistic terms, giving greater rigor to the basic logic of the protocol.
In conclusion, one aspect emerges clearly. Although actually it is mainly used in “safety risk”, ALARP logic defines a general way of thinking, as well as a framework able to facilitate “risk communication” [
62]. In this sense, it is believed that the ALARP principle integrated with traditional evaluation techniques, can allow the assertion of an innovative approach for risk management of civil engineering projects.