Algorithm for Producing Rankings Based on Expert Surveys
Norwegian Institute of International Affairs (NUPI), 0130 Oslo, Norway
*
Author to whom correspondence should be addressed.
Algorithms 2019, 12(1), 19; https://doi.org/10.3390/a12010019
Submission received: 6 December 2018
/
Revised: 31 December 2018
/
Accepted: 3 January 2019
/
Published: 10 January 2019
Abstract
:This paper develops an automated algorithm to process input data for segmented string relative rankings (SSRRs). The purpose of the SSRR methodology is to create rankings of countries, companies, or any other units based on surveys of expert opinion. This is done without the use of grading systems, which can distort the results due to varying degrees of strictness among experts. However, the original SSRR approach relies on manual application, which is highly laborious and also carries a risk of human error. This paper seeks to solve this problem by further developing the SSRR approach by employing link analysis, which is based on network theory and is similar to the PageRank algorithm used by the Google search engine. The ranking data are treated as part of a linear, hierarchical network and each unit receives a score according to how many units are positioned below it in the network. This approach makes it possible to efficiently resolve contradictions among experts providing input for a ranking. A hypertext preprocessor (PHP) script for the algorithm is included in the article’s appendix. The proposed methodology is suitable for use across a range of social science disciplines, especially economics, sociology, and political science.
1. Introduction
Expert opinion can be useful for the creation of rankings when more objective data are not available [1]. An example of a ranking based on expert opinion is the Corruption Perception Index (CPI) published by Transparency International [2]. It is difficult to obtain objective data on corruption, so instead, CPI is created on the basis of expert opinion [3,4]. Although the views of the experts whose input is used for the CPI are based on imperfect information and carry a risk of bias [5,6,7], the resulting index is nonetheless a useful tool to inform the political choices of citizens, guide companies in their investment decisions, and help governments understand how their level of corruption is seen [2,8].
Most expert-based rankings involve experts grading units in some way or other [9]. However, experts are liable to apply grades with different degrees of strictness, and this can distort a ranking [10]. For example, if experts are asked to grade countries from 5 to 1, where 5 is best and 1 is worst, some experts will liberally dish out 5s, while others will strive to use the whole grading scale evenly, and yet others will be very strict and mostly give low grades. Individual experts may also vary in their strictness over time depending on their mood and other subjective factors.
The problem with grading is particularly severe when different clusters of units are assessed by different experts [11]. For example, if one expert assesses European countries and another assesses Latin American countries and one of the experts is generally stricter than the other, this may lead to countries from one region getting an unfair advantage.
In order to overcome this problem, some systems include elaborate criteria to ensure that all experts do their grading according to the same standards [11]. For example, the Academy of the Organization for Security and Cooperation in Europe (OSCE) uses the descriptions in Table 1 to guide experts—that is to say, professors grading student papers. This helps even out some differences among professors, but it is still up to each professor to define what counts as good organization, superior grasp of the subject matter, etc. Even if a professor manages to make fair judgements among the papers submitted by students taking his or her course, it is difficult to know whether a professor on a different course might be generally more strict or lenient. Especially if the courses are electives with some students taking one course and others taking another, this can distort the overall grade point averages (GPAs) of students.
The existing literature includes several techniques for addressing the weaknesses of the traditional way of dealing with criteria-based input e.g., [12,13]. Based on these improvements, criteria-based input has been effectively processed in several cases e.g., [14,15].
The segmented string relative ranking (SSRR) approach, first proposed by Overland [16], goes one step further and omits criteria altogether. However, SSRR remains unwieldy when applied manually, demanding a lot of work and carrying a risk of human error in calculations. There is thus a gap in the literature when it comes to increasing the efficiency of SSRRs, and this article seeks to fill that gap by developing an automated algorithm so that SSRRs can be produced using computers.
2. Basics of SSRR
The purpose of the SSRR methodology is to create rankings based on input from multiple experts while avoiding distortions due to differing standards among the experts. Rather than first generating grades and then translating them into a ranking, SSRR starts by ranking small groups of units relative to each other and subsequently merges these groups to create one comprehensive ranking. Thus, SSRR is a pure approach to ranking, starting with small ranking clusters and ending with an aggregate ranking.
The basic principle of SSRR is as follows. Experts compare and rank units in relation to other units. Each expert ranks only those units they are familiar with, creating a small ranking referred to as a segment. Subsequently, these segments are strung together into a combined ranking. For example, Expert I may say that she is familiar with units P, Q, and Y and rank them; whereas Expert II may say that he is familiar with units Y, H, and K and rank them. Combining the input from the two experts, we can create the larger ranking as shown in Figure 1.
One way of thinking about SSRR rankings is that they are based on inference. In Figure 1, combining the input from Experts I and II makes it possible to infer that Q and P should be ranked above H and K.
One premise for stringing together segments from different experts is that there is always some overlap between the segments, i.e., that at least one unit from each segment is ranked by two or more experts. This ensures that the segments can be strung together. In Figure 1, Y is ranked by both Experts I and II, providing a linkage between their two ranking segments and making it possible to string them together. If an expert ranks only units that nobody else has ranked, the input from this expert becomes an isolated island in the data and cannot be included in the ranking. It is therefore important to ensure that there is always some overlap between the input from experts.
3. Lessons Learned from the Public Brainpower Ranking
In Overland [16], the SSRR methodology was tried out in the creation of a ranking of the public brainpower of resource rich countries. “Public brainpower” was defined as the coexistence of many different public actors, all freely expressing their thoughts and thus ensuring good governance of natural resources through the creativity, dynamism, and flexibility of institutions for resource management [17]. The ranking was based on input from 19 experts and covered 33 resource-rich countries.
In the public brainpower ranking, the experts were requested to also rank their own competence on the countries they ranked, and this additional information was used to resolve contradictions between experts [16]. Thus, if Expert I stated that Angola had greater public brainpower than Azerbaijan, while Expert II stated that Azerbaijan had more than Angola, but Expert II assessed their competence on Angola and Azerbaijan as relatively low, the view of Expert I would carry greater weight than that of Expert II.
The data from the experts for the public brainpower ranking was processed manually, following the steps listed below:
- A cut-off point was selected for the self-assessed competence of the experts, and only those assessments that were above that point were included.
- The country that was most often rated as No. 1 among all experts was identified. This was not necessarily going to be the top country in the final ranking; it was just a starting point.
- The three countries most often placed directly below and above this country were identified. Each of these countries formed a dyad with the first country.
- For each of those dyads, it was calculated which of the two countries was most often placed higher than the other.
- If two countries were placed above each other the same number of times, the sum of the experts’ competence on the two countries was calculated, and the country which the experts had most competence on was placed highest.
- If the two countries still had the same number of points, the analysis was expanded to include the top 15 countries by competence rank. If they were still equal, the input was expanded to include all of the countries ranked.
- On this basis, it was worked out which country was No. 2.
- Then country No. 2 was subjected to the same treatment as country No. 1.
- Next, the same was repeated for the resulting country No. 3 and onwards until all countries were subsumed into the ranking.
Although the public brainpower ranking covered a small number of countries and used data from only a few experts, processing the data was highly laborious because it was necessary to check a large number of country dyads. This work process is illustrated in Figure 2, where the solid lines represent the final ranking, and the dotted lines represent all the other dyadic relationships that were assessed for each country. For rankings involving larger numbers of units and experts, it is much more efficient to automate the process. Automation also makes it possible to remove the risk of human error in calculations, which is not insignificant when they are carried out manually.
In the public brainpower ranking, it was also found that it was confusing for experts to both assess units and their own competence on those units at the same time, and it was difficult to process the additional data generated on competence. For the purposes of the algorithm developed in this paper, self-assessment of competence was therefore omitted.
4. Challenges
Several challenges can arise in connection with the creation of SSRRs. The most obvious of these is that experts may contradict each other, ranking the same units in a different order. Such contradictions can come in two forms: direct and indirect. Direct contradiction is when the experts rank the same units in a different order, as exemplified in Figure 3. There, Expert I has put Y above X, whereas Expert II has put X above Y.
Indirect contradiction is when three or more experts provide input and a contradiction arises between segments that are not directly linked to each other (see example in Figure 4).
Mathematically, this contradiction can be expressed as follows:
Q > P > X > Q
This type of problem is particularly intractable when there are multiple overlapping contradictions in a ranking of hundreds of units. Multiple overlapping contradictions are exemplified on a small scale in Figure 5, where contradictory input from different experts results in P being placed in three different locations and V being placed in two locations, one of which is between two of the locations of P. Thus, the resolution of the contradictions related to P may have a knock-on effect on the resolution of the contradiction related to V. If there are many such overlapping contradictions in expert input, they can become particularly intractable, as dealing with one contradiction can destabilize the context of another contradiction.
Another problem is that contradictions can result in a unit being placed in multiple locations that are far apart in the ranking. For example, in Figure 5 there are seven other units between the lowest and second lowest placement of V. Thus, when resolving the contradiction concerning V, it is not clear whether V should be placed either above C or below X (the two solutions simplest to calculate), or somewhere in the middle of the range between those two locations (which makes more sense in terms of a compromise between the divergent expert views on V).
Another problem that can arise is that patches of undefined units are left over between the data input from different experts. In the example in Figure 6, the input from Experts I and II can be strung together via unit X, which they both cover, but this leaves the relationship among units Q, P, and H undefined.
The challenges highlighted in this section are largely solved by using the algorithm outlined in the next section.
5. Link Analysis as a Basis for Ranking
In link analysis systems such as Google’s PageRank algorithm, it is assumed that the importance of a webpage is indicated by the number of other webpages that link to it [18]. For example, more webpages link to the Wikipedia page about energy policy than to the page on my personal blog about energy policy, so the Wikipedia page is probably more important than that on my blog. Thus, webpages are given scores based on how many other pages link to them (see Figure 7). However, not only are the number of incoming links counted, but also the importance of the internet pages they come from, that is to say, how many incoming links of their own they have. Accordingly, webpages pass on part of their own score from their incoming links to those pages they link to. Normally, they pass on 85% of their own score [19]. The reason why they pass on 85% rather than 100% of their incoming links—known as the “damping factor”—is that, if they were to pass on 100%, webpages linking back and forth among themselves would result in an infinitely rising value [19,20].
Figure 2 is a simplified illustration of how this works. Internet page R has no incoming links, and therefore has a score of zero. Internet page Q has one direct incoming link and therefore gets a score of 1. Internet page P has one direct link from R giving it a score of 1, another direct link from Q giving it another score of 1, and finally, Q passes on 0.85 of the score of 1 it received from R, giving P a total score of 2.85.
In developing an algorithm for SSRR, we treat rankings as link networks. Accordingly, we treat each unit in the ranking as having incoming links (and therefore scoring points) from the units below it, resulting in the highest score for the top-ranked unit and 0 for the lowest-ranked unit (see Figure 8). The difference between such a “ranking network” and the type of internet network analyzed by the PageRank algorithm is that our ranking is linear and hierarchical, while the internet network is sprawling and amorphous, and in the internet network many units can have the same score [21].
Now that we have classified the ranking as a network, we can use link analysis to string together the ranking segments received from different experts. When an expert ranks unit Q above P, and P above V, we treat this as a link from unit V to P, and then from P to Q (see Figure 8).
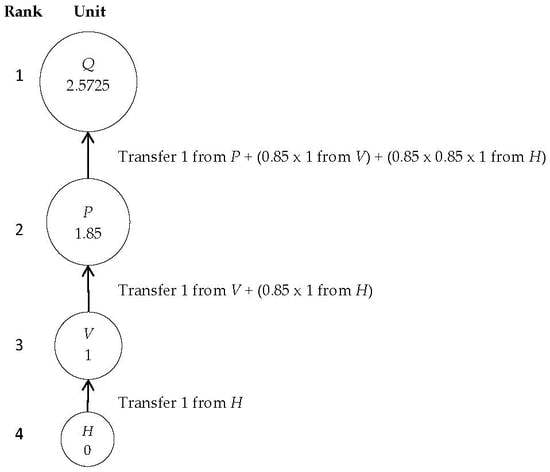
6. Building an Automated Algorithm
The full script of the algorithm is presented in the Appendix A at the end of this article. For reasons of personal preferences and practicality, we used the hypertext preprocessor (PHP) programing language, but the algorithm can easily be replicated in other programing languages.
Sample dummy data are presented in Table 2 to exemplify the operation of the algorithm. The first column of data represents the identification letter of the unit, the second column is the identification number of the expert, and the third column is the unit’s relative ranking within a segment, that is, among the units ranked by that expert.
Our dummy data include responses from five experts. The algorithm starts by reading data from the file and grouping the units into segments by experts. An array of segments is stored for later use. The segments in our dummy dataset are presented in Table 3.
Next, the script creates an array of all unique units present in a dataset; that is, it looks through all segments and collects all units into a separate list without repetition. With our dummy dataset, this step results in the following array:
The algorithm works its way through this array and calculates the score of each unit. As discussed above, a unit gains its score from its subordinates (i.e., units ranked directly or indirectly below it). A hierarchical tree of subordinates is built for each unit. For instance, the first unit in our example is Q. It has one direct subordinate in the segment from Expert I (namely P) and another one in the segment from Expert IV (namely R). Unit P, in turn, also has its own subordinates in the segments from Experts II and III (H, D and V). At this point, the script looks for subordinates of H, D, and V as well. However, it finds that H does not have any subordinates in any segment, D has three subordinates (V, Q, and R), and V has one subordinate (R) that is already included in the tree. Here, the algorithm moves on to the next unit, because all possible branches of the subordinate tree for unit Q have been built. Figure 9 shows the subordinate trees for all units:
Units that appear directly below the parent (along the blue axis) are level 0 subordinates, units that appear below direct subordinates (along the green axis) are level 1 subordinates, and the next units (along the orange axis) are level 2 subordinates. Subordinate trees can have many more levels, depending on the scope and complexity of data.
Each unit in the tree contributes to the final score of a parent at the top of the tree. Each level 0 subordinate delivers one point to the parent’s score, each level 1 subordinate delivers 85% of 1 point (or 1 × 0.85), each level 2 subordinate delivers 85% of 0.85 points (or 0.852 = 0.7225), and so on. The general rule is that each unit in a subordinate tree contributes 0.85L points to the score of the grandparent (where L is the level of subordination).
The precise damping factor one uses can have an impact on the final ranking. A number closer to 100% strengthens the relative scores of units with few level 0 subordinates and many level 1, 2, 3, etc. subordinates; whereas a number closer to 0 boosts the relative scores of units with many level 0 subordinates and fewer at other levels. There is no straightforward way to determine which damping factor is correct. In applying a damping factor of 85%, we simply follow the link analysis convention.
In our dummy data, Q has two level 0 subordinates and three level 1 subordinates. So, the final score for Q can be expressed as follows:
Final scores for P, D, and V are derived similarly:
H and R do not have subordinates (their trees are empty); hence, they have a score of 0:
The mathematics of multilevel subordination used to calculate the score of a unit, in most cases, resolves the challenges related to the direct and indirect contradictions discussed above. We can observe this in our dummy data. If we look at columns for Experts I, III, and IV in Table 3, we can see that there is an indirect contradiction between their rankings of units Q, P and D:
In other words, Expert I ranked Q above P, Expert III ranked P above D, and Expert IV ranked D above Q—a logical contradiction. The algorithm determines the position of unit Q in the final ranking to be below D, based on their cumulative scores derived from their subordinates:
This logic can also be easily observed in Figure 9: unit P has three level 0 and two level 1 subordinates; unit D has three level 0, one level 1, and one level 2 subordinate; whereas unit Q has only two level 0 and 3 level 1 subordinates. The unit with the most level 0 (direct) subordinates receives the greatest score and is positioned highest in the aggregate ranking.
In the final step, the algorithm saves the calculated scores of all units in a new array. The units are sorted from the highest to lowest score and displayed to the user. For our dummy data, the final ranking is as follows (scores of units in brackets):
7. Discussion
The algorithm has a significant labor-saving effect. Whereas manual calculation of SSRR rankings may take weeks or months to carry out—depending on the volume of expert input and the number of units ranked—the automated algorithm can do the same job in a matter of seconds, while also doing it more accurately.
Another important advantage of this algorithm-based SSRR approach is that it generates differentiated scores for almost all units ranked, ensuring that each unit has its own unique place in the ranking. This contrasts with grading-based rankings where some units are likely to get the same grades and thus to occupy the same place in the ranking. This is unfortunate because the whole purpose of a ranking is that it is strictly ordinal.
However, there is an important exception to the point above: while the algorithm gives unique positions in the ranking to almost all ranked units, the units at the very bottom sometimes cannot be ranked in relation to each other, because they have neither been ranked directly in relation to each other nor have other units below them that could indirectly help determine their ranks. If two or more units thus end up with equal scores of zero (as in the case of our dummy data happened with units H and R), the script tags them as unresolvable contradictions, places them next to each other, and colors them red. In such cases, the researchers have several options. They can consider collecting further input from experts on the unresolved units; or carry out their own in-depth evaluation of H and R; or appoint a committee to perform such an evaluation. Alternatively, they could simply omit the units grouped at the bottom of the ranking, but this would be unsatisfactory because it is often precisely the top and bottom of a ranking that are of greatest interest.
8. Conclusions
In this article, we propose a novel ranking algorithm based on network theory and link analysis. The algorithm turns subjective input from multiple experts into a unified and coherent ranking. It does so by calculating the rankings of units according to their cumulative scores. The cumulative score of a unit is the sum of points transferred to the unit by its subordinates: the algorithm decrements scores passed onwards with a damping factor of 85% at each level of subordination, in accordance with the link analysis convention.
The SSRR approach is an alternative to traditional criteria- and grading-based approaches to ranking. A major advantage of this approach is that it demands little from the experts who provide input for the ranking. All they need to do is rank those units they are familiar with; they do not need to think about specific grades, nor do they necessarily have to understand how their data are processed afterwards. This makes it significantly easier to elicit responses from expert respondents, something that is often a challenge [22,23,24].
Because the input data come from experts who are independent of each other, they may contain direct and indirect contradictions. The proposed algorithm resolves such contradictions by comparing the cumulative network-based scores of units.
The algorithm has several weaknesses, which form avenues for future research. Sometimes the algorithm is unable to rank the units at the very bottom of the ranking in relation to each other. Thus, these last units either have to be placed in a group; or they must be ranked through qualitative assessment; or a new round of data-gathering has to be carried out to cover them; or they have to be omitted from the ranking. Future research could try to find a more efficient and consistent way of dealing with such cases.
In its current form, the algorithm is a good tool for small- and medium-sized ranking lists. However, with complex data and a high frequency of contradictions in expert responses, it may be difficult to eliminate all contradictions. In future research it may be possible to further improve the algorithm to handle larger volumes of data with more serious inconsistencies.
The use of an 85% damping factor is in accordance with the link analysis convention. In future research, it would be worth looking into whether it is possible to work out a different damping factor that is optimal specifically for SSRR approach.
The original SSRR methodology developed by Overland [16] included self-assessment of competence by experts providing input for rankings. In the new version of SSRR in this article, this competence element has been omitted since it was found to be confusing for experts to both have to assess their own competence on countries and rank those same countries at the same time. However, for rankings where the level of competence among experts varies greatly it might be desirable to reintroduce some kind of assessment of competence and it might also be possible to find ways of gathering the necessary information without confusing experts.
Author Contributions
Conceptualization, I.O.; Formal analysis, I.O.; Funding acquisition, I.O.; Investigation, J.J.; Methodology, I.O. and J.J.; Project administration, I.O.; Software, J.J.; Visualization, I.O. and J.J.; Writing—original draft, I.O. and J.J.; Writing—review & editing, I.O.
Funding
This work is a product of the POLGOV project, funded by POLARPROG of the Research Council of Norway.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Algorithm Code
<?php
header(’Content-Type:text/html; charset=utf-8’);
$units = array();
$experts = array();
$ranking = array();
$segments = array();
if(($handle = fopen(’data.csv’, ’r’)) !== false) {
while(($data = fgetcsv($handle, 0, ",")) !== false)
{
$units[[] = $data[0 ];
$experts[[] = $data[1];
$ranking[[] = $data[2];
unset($data);
}
fclose($handle);
}
foreach (array_unique($experts) as $e) {
$segments[$e] = array();
}
foreach ($units as $k => $v) {
$segments[$experts[$k]][$v] = array($ranking[$k]);
}
foreach ($segments as $k => $v) {
asort($v);
$segments[$k] = $v;
}
$units = array_values(array_unique($units));
function findChildren($parent, $unit, $children, $level) {
global $segments;
$generation = array();
foreach($segments as $pool) {
if (isset($pool[$unit])) {
$unitRank = $pool[$unit][0];
foreach($pool as $pk => $pv) {
if ($pk != $parent
&& $pv[0] > $unitRank
&& !isset($children[$pk])) {
$children[$pk] = 1 * pow(0.85, $level);
$generation[[] = $pk;
}
}
}
}
if (sizeof($generation) > 0) {
$level++;
foreach($generation as $child) {
$children = findChildren($parent, $child, $children, $level);
}
}
return $children;
}
$rank = array();
foreach($units as $unit) {
$children = array();
$rank[$unit] = round(array_sum(findChildren($unit, $unit, $children, 0)), 5) * 100000;
}
arsort($rank);
$result = array();
foreach ($rank as $k => $v) { $result[$v][[] = $k; }
$numberOfSegments = sizeof($segments);
$numberOfUnits = sizeof($units);
$notice = false;
echo "<h4>Ranking for " . $numberOfUnits . " units in " . $numberOfSegments . " segments:</h4>";
echo "<ol>";
foreach ($result as $k => $v) {
if ( sizeof($v) > 1) {
$notice = true;
echo "<li>";
foreach($v as $vk => $vv){
echo (0 == $vk) ? "<span style=’color: red;’>" . $vv . "</span>" : " | <span style=’color: red;’>" . $vv . "</span>";
}
echo "</li>";
} else {
echo "<li><span>" . $v[0] . "</span></li>";
}
}
echo "</ol>";
if ($notice) {
echo "<h2>Notice:</h2><hr><p>The above list contains units with equal ranking (colored red). These units have the same position in the final list. Please, consider providing extra data with ranking of these units relative to each other.</p><hr>";
}
?>
References
- Aspinall, W. A route to more tractable expert advice. Nature 2010, 463, 294–295. [Google Scholar] [CrossRef] [PubMed]
- Beddow, R. Fighting Corruption, Demanding Justice: Impact Report; Transparency International: Berlin, Germany, 2015; ISBN 978-3-943497-88-5. [Google Scholar]
- Lambsdorff, J.G. The methodology of the TI Corruption Perceptions Index. Transparency International and University of Passau. 2006. Available online: https://www.transparency.org/files/content/tool/2006_CPI_LongMethodology_EN.pdf (accessed on 9 November 2018).
- Treisman, D. What have we learned about the causes of corruption from ten years of cross-national empirical research? Annu. Rev. Political Sci. 2007, 10, 211–244. [Google Scholar] [CrossRef]
- Langfeldt, L. Decision-Making in Expert Panels Evaluating Research: Constraints, Processes and Bias; NIFU: Oslo, Norway, 2002; ISBN 82-7218-465-6. [Google Scholar]
- Steenbergen, M.R.; Marks, G. Evaluating expert judgments. Eur. J. Political Res. 2007, 46, 347–366. [Google Scholar] [CrossRef] [Green Version]
- Serenko, A.; Bontis, N. A critical evaluation of expert survey-based journal rankings: The role of personal research interests. J. Assoc. Inf. Sci. Technol. 2018, 69, 749–752. [Google Scholar] [CrossRef]
- Wilhelm, G.P. International validation of the Corruption Perceptions Index: Implications for business ethics and entrepreneurship education. J. Bus. Ethics 2002, 35, 177–189. [Google Scholar] [CrossRef]
- Maestas, C. Expert surveys as a measurement tool: Challenges and new frontiers. In The Oxford Handbook of Polling and Survey Methods; Atkenson, L.R., Alvarez, R.M., Eds.; Oxford University Press: Oxford, UK, 2016; pp. 13–26. [Google Scholar] [CrossRef]
- Marquardt, K.L.; Pemstein, D. IRT models for expert-coded panel data. Political Anal. 2018, 26, 431–456. [Google Scholar] [CrossRef]
- Tofallis, C. Add or multiply? A tutorial on ranking and choosing with multiple criteria. INFORMS Trans. Educ. 2014, 14, 109–119. [Google Scholar] [CrossRef]
- Mukhametzyanov, I.; Pamucar, D. A sensitivity analysis in MCDM problems: A statistical approach. Decis. Mak. Appl. Manag. Eng. 2018, 1, 51–80. [Google Scholar] [CrossRef]
- Sremac, S.; Stević, Ž.; Pamučar, D.; Arsić, M.; Matić, B. Evaluation of a Third-Party Logistics (3PL) Provider Using a Rough SWARA–WASPAS Model Based on a New Rough Dombi Aggregator. Symmetry 2018, 10, 305. [Google Scholar] [CrossRef]
- Chatterjee, K.; Pamucar, D.; Zavadskas, E.K. Evaluating the performance of suppliers based on using the R’AMATEL-MAIRCA method for green supply chain implementation in electronics industry. J. Clean. Prod. 2018, 184, 101–129. [Google Scholar] [CrossRef]
- Liu, F.; Aiwu, G.; Lukovac, V.; Vukic, M. A multicriteria model for the selection of the transport service provider: A single valued neutrosophic DEMATEL multicriteria model. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–130. [Google Scholar] [CrossRef]
- Overland, I. (Ed.) Lonely minds: Natural resource governance without input from society. In Public Brainpower: Civil Society and Natural Resource Management; Palgrave: Cham, Switzerland, 2018; pp. 387–407. ISBN 978-3-319-60626-2. Available online: https://www.academia.edu/35377095 (accessed on 30 June 2018).
- Overland, I. (Ed.) Introduction: Civil society, public debate and natural resource management. In Public Brainpower: Civil Society and Natural Resource Management; Palgrave: Cham, Switzerland, 2018; pp. 1–22. ISBN 978-3-319-60626-2. Available online: https://www.researchgate.net/publication/320656629 (accessed on 17 July 2018).
- Borodin, A.; Roberts, G.O.; Rosenthal, J.S.; Tsaparas, P. Link analysis ranking: Algorithms, theory, and experiments. ACM Trans. Internet Technol. 2005, 5, 231–297. [Google Scholar] [CrossRef]
- Fu, H.H.; Lin, D.K.; Tsai, H.T. Damping factor in Google page ranking. Appl. Stoch. Models Bus. Ind. 2006, 22, 431–444. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Garg, R.; Mishra, P.K. Discussion on damping factor value in PageRank computation. Int. J. Intell. Syst. Appl. 2017, 9, 19–28. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Harzing, A.W.; Reiche, B.S.; Pudelko, M. Challenges in international survey research: A review with illustrations and suggested solutions for best practice. Eur. J. Int. Manag. 2013, 7, 112–134. [Google Scholar] [CrossRef]
- Moy, P.; Murphy, J. Problems and prospects in survey research. J. Mass Commun. Q. 2016, 93, 16–37. [Google Scholar] [CrossRef]
- Thomas, D.I. Survey research: Some problems. Res. Sci. Educ. 1974, 4, 173–179. [Google Scholar] [CrossRef]
Figure 1.
Input from Experts I and II combined into one ranking.
Figure 2.
Visual representation of steps in manual calculation of segmented string relative ranking (SSRR) of public brainpower (solid lines = final ranking; dotted lines = other relationships that were checked).
Figure 2.
Visual representation of steps in manual calculation of segmented string relative ranking (SSRR) of public brainpower (solid lines = final ranking; dotted lines = other relationships that were checked).
Figure 3.
Direct contradiction between Experts I and II.
Figure 4.
Indirect contradiction among Experts I, II, and III.
Figure 5.
Ranking with multiple contradictions.
Figure 6.
Patch of undefined units.
Figure 7.
Basic model of PageRank link analysis.
Figure 8.
Ranking as a hierarchical link network.
Figure 9.
Subordinate trees for dummy data.
Table 1.
An example of detailed grading guidance: grading system of the Academy of the Organization for Security and Cooperation in Europe (OSCE).
Table 1.
An example of detailed grading guidance: grading system of the Academy of the Organization for Security and Cooperation in Europe (OSCE).
| Grade | Description |
|---|---|
| A | Excellent performance: strong evidence of original thinking; good organization; capacity to analyze and synthesize; superior grasp of subject matter with sound critical evaluations; evidence of extensive knowledge base; high level of motivation. |
| B | Good performance: evidence of grasp of subject matter; some evidence of critical capacity and analytical ability; reasonable understanding of relevant issues; regular attendances of classes; productive contribution to the discussion by sharing thoughts and questions that demonstrate familiarity with the material; interest in other students’ contributions. |
| C | Average performance: understanding of the subject matter; ability to develop solutions to simple problems in the material; acceptable but uninspired work, not seriously faulty but lacking style and vigor; meeting the basic requirements of preparedness and regular attendance; rare participation in class discussion. |
| D | Poor performance: inconsistency in attendance and preparation for classes; lack of participation in class discussions; absence of respect for the contributions of other students. |
| E | Inadequate performance: little or no evidence of understanding of the subject matter; weakness in critical and analytic skills; limited or irrelevant use of the literature. |
Table 2.
Dummy dataset (for readability, the dummy data in the table are presented in tabular format; for actual processing by the hypertext preprocessor (PHP) algorithm, the data need to be reformatted as comma-separated values).
Table 2.
Dummy dataset (for readability, the dummy data in the table are presented in tabular format; for actual processing by the hypertext preprocessor (PHP) algorithm, the data need to be reformatted as comma-separated values).
| Unit | Expert | Ranking |
|---|---|---|
| Q | I | 1 |
| P | I | 2 |
| P | II | 1 |
| H | II | 2 |
| P | III | 1 |
| D | III | 2 |
| V | III | 3 |
| D | IV | 1 |
| Q | IV | 2 |
| R | IV | 3 |
| V | V | 1 |
| R | V | 2 |
Table 3.
Dummy dataset divided into segments.
| Expert I | Expert II | Expert III | Expert IV | Expert V |
|---|---|---|---|---|
| Q | P | P | D | V |
| P | H | D | Q | R |
| V | R |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Overland, I.; Juraev, J. Algorithm for Producing Rankings Based on Expert Surveys. Algorithms 2019, 12, 19. https://doi.org/10.3390/a12010019
AMA Style
Overland I, Juraev J. Algorithm for Producing Rankings Based on Expert Surveys. Algorithms. 2019; 12(1):19. https://doi.org/10.3390/a12010019
Chicago/Turabian StyleOverland, Indra, and Javlon Juraev. 2019. "Algorithm for Producing Rankings Based on Expert Surveys" Algorithms 12, no. 1: 19. https://doi.org/10.3390/a12010019
APA StyleOverland, I., & Juraev, J. (2019). Algorithm for Producing Rankings Based on Expert Surveys. Algorithms, 12(1), 19. https://doi.org/10.3390/a12010019
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
