Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data
Abstract
:1. Introduction
2. Materials and Methods
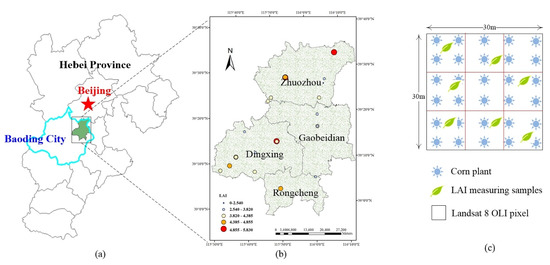
2.1. Study Area
2.2. Data Collection
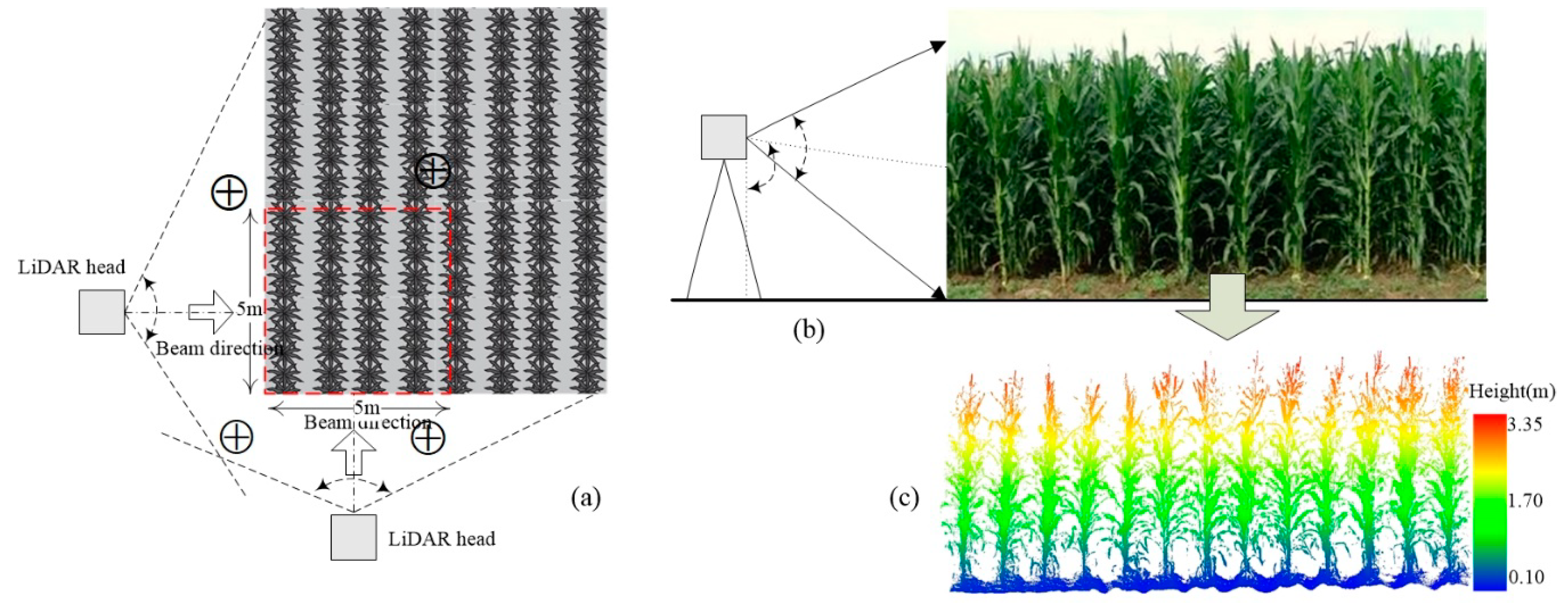
2.2.1. TLS Data Acquisition and Pre-Processing
2.2.2. Acquisition of Remote Sensing Images
2.2.3. Field Data Collection
2.3. LAI Retrieval
2.3.1. PROSAIL Model and Sensitivity Analysis
2.3.2. Leaf Angle Distribution Function Inferred from the TLS Data
2.3.3. LUT-Based LAI Retrieval Strategy Based on PROSAIL Model
- 1.
- LUT generation
- 2.
- Cost function
3. Results and Analysis
3.1. Sensitivity Analysis of PROSAIL for Simulating Corn Canopy Reflectance
3.2. Inferred Leaf Angle Distribution Function from the TLS Scanner Data
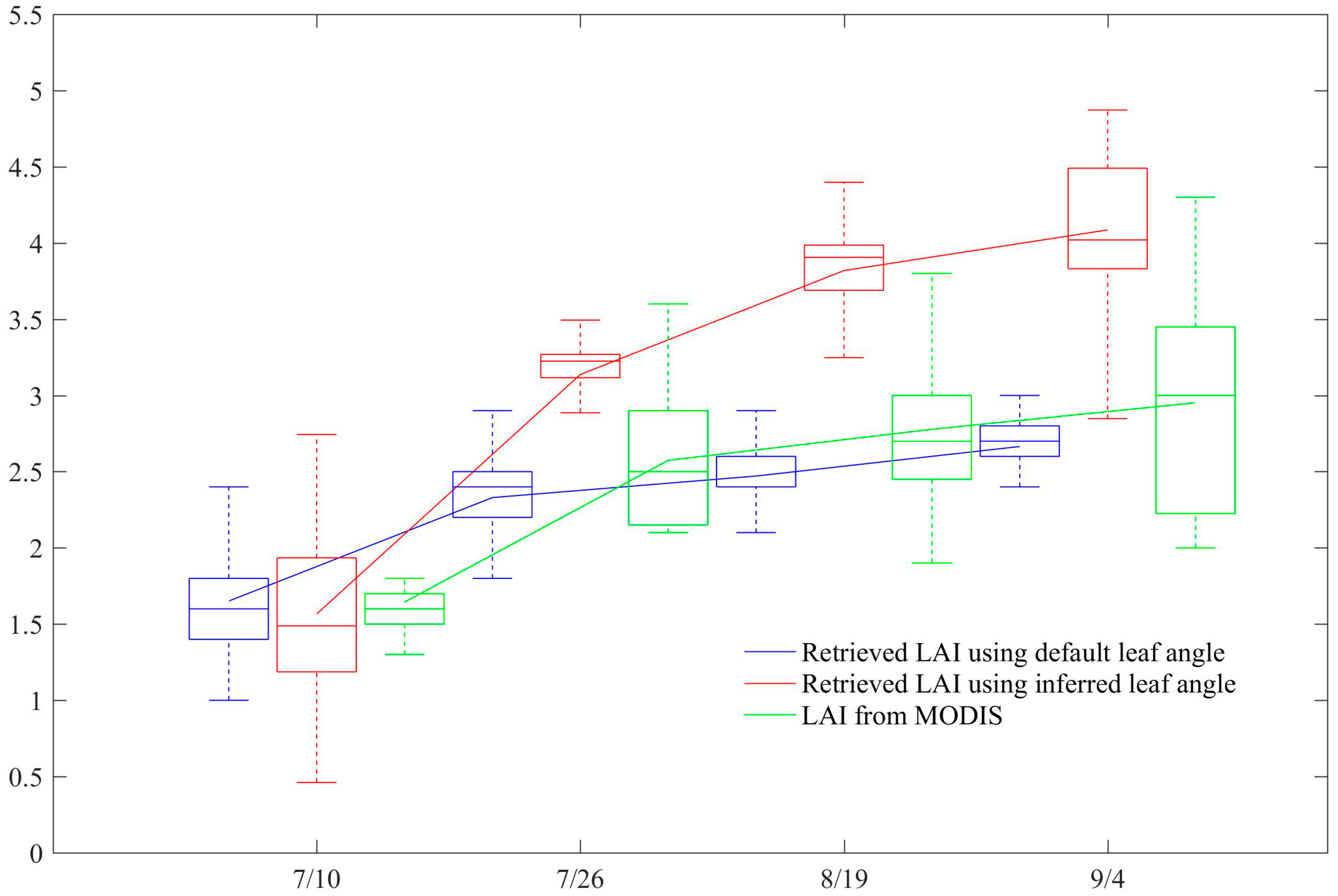
3.3. Retrieved Corn Canopy LAIs
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Huang, J.X.; Tian, L.Y.; Liang, S.L.; Ma, H.Y.; Becker-Reshef, I.; Su, W.; Huang, Y.B.; Zhang, X.D.; Zhu, D.H.; Wu, W.B. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Su, W.; Zhang, X.; Huang, Y.; Fan, J.; Wu, W.B. Jointly assimilating MODIS LAI and ET products into the SWAP model for winter wheat yield estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4060–4071. [Google Scholar] [CrossRef]
- Huang, J.X.; Sedano, F.; Huang, Y.B.; Ma, H.Y.; Li, X.L.; Liang, S.L.; Tian, L.Y.; Zhang, X.D.; Fan, J.L.; Wu, W.B. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to estimate regional winter wheat yield. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Rudolph, S.; Kruk, J.V.D.; Hebel, C.V.; Ali, M.; Herbst, M.; Montzka, C.; Pätzold, S.; Robinson, D.A.; Vereecken, H.; Weihermüller, L. Linking satellite derived LAI patterns with subsoil heterogeneity using large-scale ground-based electromagnetic induction measurements. Geoderma 2015, s241–s242, 262–271. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M.; Kim, S.H. Retrieval of effective leaf area index in heterogeneous forests with terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 777–786. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; García-Haro, F.J.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Crema, A.; Boschetti, M. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sens. Environ. 2016, 187, 102–118. [Google Scholar] [CrossRef]
- Fang, H.L.; Ye, Y.C.; Liu, W.L.; Wei, S.S.; Ma, L. Continuous estimation of canopy leaf area index (LAI) and clumping index over broadleaf crop fields: An investigation of the PASTIS-57 instrument and smartphone applications. Agric. For. Meteorol. 2018, 253, 48–61. [Google Scholar] [CrossRef]
- Bréda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.Q.; Liang, S.L.; Wang, J.D.; Chen, P.; Yin, X.J.; Zhang, L.Q.; Song, J.L. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarcotejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Guyot, G.; Leprieur, C. Modeled analysis of the biophysical nature of spectral shifts and comparison with information content of broad bands. Remote Sens. Environ. 1992, 41, 133–142. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Quantifying the effect of canopy architecture on optical measurements of leaf area index using two gap size analysis methods. IEEE Trans. Geosci. Remote Sens. 1995, 33, 777–787. [Google Scholar] [CrossRef]
- Campbell, G.S. Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol. 1990, 49, 173–176. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M. Sensitivity of Common Vegetation Indices to the Canopy Structure of Field Crops. Remote Sens. 2017, 9, 994. [Google Scholar] [CrossRef]
- Campbell, G.S. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agric. For. Meteorol. 1986, 36, 317–321. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Leaf orientation retrieval from terrestrial laser scanning (TLS) data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3970–3979. [Google Scholar] [CrossRef]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.H.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. Estimating aboveground biomass and leaf area of low-stature arctic shrubs with terrestrial lidar. Remote Sens. Environ. 2015, 164, 26–35. [Google Scholar] [CrossRef]
- Bailey, B.N.; Mahaffee, W.F. Rapid measurement of the three-dimensional distribution of leaf orientation and the leaf angle probability density function using terrestrial LiDAR scanning. Remote Sens. Environ. 2017, 194, 63–76. [Google Scholar] [CrossRef]
- Vicari, M.B.; Pisek, J.; Disney, M. New estimates of leaf angle distribution from terrestrial LiDAR Comparison with measured and modelled estimates from nine broadleaf tree species. Agric. For. Meteorol. 2019, 264, 322–333. [Google Scholar] [CrossRef]
- Hosoi, F.; Nakai, Y.; Omasa, K. Estimating the leaf inclination angle distribution of the wheat canopy using a portable scanning lidar. J. Agric. Meteorol. 2009, 65, 297–302. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.M.; Su, Y.J.; Hu, T.Y.; Xu, G.C.; Guo, Q.H. Retrieving 2-D leaf angle distributions for deciduous trees from terrestrial laser scanner data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4945–4955. [Google Scholar] [CrossRef]
- Xu, Q.F.; Cao, L.; Xue, L.F.; Chen, B.C.; An, F.; Yun, T. Extraction of leaf biophysical attributes based on a computer graphic-based algorithm using terrestrial laser scanning data. Remote Sens. 2019, 11, 15. [Google Scholar] [CrossRef]
- Li, D.; Pang, Y.; Yue, C.R.; Zhao, D.; Xu, G.C. Extraction of individual tree DBH and height based on terrestrial laser scanner data. J. Beijing For. Univ. 2012, 34, 79–86. [Google Scholar]
- Su, W.; Zhu, D.H.; Huang, J.X.; Guo, H. Estimation of the vertical leaf area profile of corn (Zea mays) plants using terrestrial laser scanning (TLS). Comput. Electron. Agric. 2018, 150, 5–13. [Google Scholar] [CrossRef]
- Su, W.; Zhang, M.Z.; Liu, J.M.; Sun, Z.P. Automated extraction of corn leaf points from unorganized terrestrial lidar point clouds. Int. J. Agric. Biol. Eng. 2018, 11, 166–170. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Su, W.; Jiang, F.F.; Zhu, D.H.; Zhan, J.G.; Ma, H.Y.; Zhang, X.D. Extraction of maize planting area based on decision tree and mixed-pixel unmixing methods. Trans. Chin. Soc. Agric. Mach. 2015, 46, 289–295. [Google Scholar]
- Markwell, J.; Osterman, J.C.; Mitchell, J.L. Calibration of the minolta spad-502 leaf chlorophyll meter. Photosynth. Res. 1995, 46, 467–472. [Google Scholar] [CrossRef]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Quan, X.; He, B.; Li, X.; Liao, Z. Retrieval of grassland live fuel moisture content by parameterizing radiative transfer model with interval estimated LAI. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 910–920. [Google Scholar] [CrossRef]
- Propastin, P.; Panferov, O. Retrieval of remotely sensed LAI using landsat ETM+ data and ground measurements of solar radiation and vegetation structure: Implication of leaf inclination angle. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 38–46. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Macé, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Ding, Y.L.; Zhang, H.Y.; Li, Z.W.; Xin, X.P.; Zheng, X.M.; Zhao, K. Comparison of fractional vegetation cover estimations using dimidiate pixel models and look-up table inversions of the PROSAIL model from Landsat 8 OLI data. J. Appl. Remote Sens. 2016, 10, 036022. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Wu, H.; Tang, B.H.; Ma, L.; Zhao, E.Y.; Li, C.R. Inversion of the prosail model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Laurent, V.C.E.; Gijsel, J.A.E.V. Visualizing the ill-posedness of the inversion of a canopy radiative transfer model: A case study for sentinel-2. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 7–18. [Google Scholar] [CrossRef]
- Chaabouni, S.; Kallel, A. Inversion of vegetation canopy reflectance based on variationnel multiscale approach. In Proceedings of the 2nd International Conference on Advanced Technologies for Signal and Image Processing—ATSIP, Monastir, Tunisia, 21–24 March 2016; pp. 494–498. [Google Scholar]
- Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of seasonal leaf area index from simulated EnMAP data through optimized LUT-based inversion of the PROSAIL model. Remote Sens. 2015, 7, 10321–10346. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.S. Jacquemoud. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Campos-Taberner, M.; Muñoz-Marí, J.; Laparra, V.; de Coca, F.C.; Sánchez-Zapero, J.; Camps-Valls, G. Derivation of global vegetation biophysical parameters from EUMETSAT Polar System. ISPRS J. Photogramm. Remote Sens. 2018, 139, 57–74. [Google Scholar] [CrossRef]
- Yang, F.; Sun, J.L.; Zhang, B.; Yao, Z.F.; Wang, Z.M.; Wang, J.L.; Yue, X.F. Assessment of MODIS LAI product accuracy based on the PROSAIL model, TM and field measurements. Trans. Chin. Soc. Agric. Eng. 2010, 26, 192–197. [Google Scholar]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS leaf area index products for land surface and climate modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res. Biogeosci. 2013, 118, 529–548. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.W.; Tang, H.; Zhang, B.H.; Yang, G.X.; Xin, X.P. Evaluation and intercomparison of MODIS and GEOV1 global leaf area index products over four sites in north China. Sensors 2015, 15, 6196–6216. [Google Scholar] [CrossRef]
- Xu, X.J.; Du, H.Q.; Zhou, G.M.; Li, P.H. Method for improvement of MODIS leaf area index products based on pixel-to-pixel correlations. Eur. J. Remote Sens. 2016, 49, 57–72. [Google Scholar] [CrossRef] [Green Version]
- Justice, C.; Belward, A.; Morisette, J.; Lewis, P.; Privette, J.; Baret, F. Developments in the ‘validation’ of satellite sensor products for the study of the land surface. Int. J. Remote Sens. 2000, 21, 3383–3390. [Google Scholar] [CrossRef]
- Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Shabanov, N.V.; Weiss, M.; Fernandes, R.A.; Leblanc, S.G.; et al. Validation of global moderate-resolution LAI products: A framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1804–1817. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR cyclopes global products derived from vegetation. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Jiang, C.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Zou, X.; Haikarainen, I.; Haikarainen, I.P.; Mäkelä, P.; Mõttus, M.; Pellikka, P. Effects of crop leaf angle on LAI-sensitive narrow-band vegetation indices derived from imaging spectroscopy. Appl. Sci.-Basel 2018, 8, 1435. [Google Scholar] [CrossRef]
- Huang, J.X.; Ma, H.Y.; Sedano, F.; Lewis, P.; Liang, S.L.; Wu, Q.L.; Su, W.; Zhang, X.D.; Zhu, D.H. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]







| Parameter | Range of Values |
|---|---|
| Scanning distance (m) | 0.6 to 330 |
| Scanning speed (points/s) | 122,000 to 976,000 |
| Ranging error (mm) | ±2 |
| Resolution (pixels) | 7 × 107 |
| Vertical field of view (°) | 300 |
| Horizontal field of view (°) | 360 |
| Laser class | Class 1 |
| Wavelength (nm) | 1550 |
| GPS | Integrated GPS receiver |
| Date | Sensor | UTM Time | Sun Elevation Angle (°) | Sun Azimuth Angle (°) | Viewing Zenith Angle (°) | Viewing Azimuth Angle (°) |
|---|---|---|---|---|---|---|
| 10 July | ETM+ | 02:51:27 | 64.77 | 124.82 | 0 | 90 |
| 26 July | ETM+ | 02:51:31 | 62.52 | 128.55 | 0 | 90 |
| 19 August | OLI | 02:53:59 | 58.03 | 138.33 | 0 | 90 |
| 4 September | OLI | 02:54:02 | 53.72 | 144.98 | 0 | 90 |
| Model Variables | Range or Value | Distribution | ||
|---|---|---|---|---|
| Canopy | LAI | Leaf area index (m2 m−2) | 0.1 to 7.0 | Uniform |
| LIDFa | Leaf angle distribution (º) | 0 to 90 | Gaussian | |
| hspot | Hotspot parameter (m m−1) | 0.1 | - | |
| Leaf | N | Leaf structural parameter in PROSPECT | 1.518 | - |
| Cab | Chlorophyll a+b content in PROSPECT (μg cm−2) | 0.1 to 60.0 | Uniform | |
| Car | Carotenoid content in PROSPECT (μg cm−2) | 8 | - | |
| Cw | Equivalent water thickness in PROSPECT (cm) | 0.05 to 0.3 | Gaussian | |
| Cm | Dry matter content in PROSPECT (g cm−2) | 0.002 to 0.012 | Gaussian | |
| Soil and sky | psoil | Soil reflectance assumed to be Lambertian (1) or not (0) | 0–1 | Gaussian |
| skyl | Ratio of diffuse to total incident radiation | Calculated by tts | - | |
| Sun-sensor | tts | Solar zenith angle (°) | / | / |
| tto | Viewing zenith angle (°) | / | / | |
| psi | Relative azimuth angle (v) | / | / | |
| Date | χ | Proportion of Leaf Angles (% of Total) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0°–10° | 10°–20° | 20°–30° | 30°–40° | 40°–50° | 50°–60° | 60°–70° | 70°–80° | 80°–90° | ||
| 10 July | 1.223 | 7.83 | 11.33 | 14.2 | 16.1 | 16.68 | 15.05 | 10.63 | 5.68 | 2.5 |
| 26 July | 1.206 | 6.49 | 8.98 | 10.73 | 12.42 | 14.18 | 15.41 | 14.67 | 11.1 | 6.02 |
| 19 August | 1.214 | 7.1 | 10.11 | 11.3 | 11.89 | 13.4 | 14.79 | 14.02 | 10.85 | 6.54 |
| 4 September | 1.195 | 6.17 | 8.76 | 10.02 | 10.73 | 12.19 | 14.54 | 15.79 | 13.53 | 8.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, W.; Huang, J.; Liu, D.; Zhang, M. Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data. Remote Sens. 2019, 11, 572. https://doi.org/10.3390/rs11050572
Su W, Huang J, Liu D, Zhang M. Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data. Remote Sensing. 2019; 11(5):572. https://doi.org/10.3390/rs11050572
Chicago/Turabian StyleSu, Wei, Jianxi Huang, Desheng Liu, and Mingzheng Zhang. 2019. "Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data" Remote Sensing 11, no. 5: 572. https://doi.org/10.3390/rs11050572
APA StyleSu, W., Huang, J., Liu, D., & Zhang, M. (2019). Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data. Remote Sensing, 11(5), 572. https://doi.org/10.3390/rs11050572