A Mechanistic Model for the Extraction of Phenolics from Grapes During Red Wine Fermentation
Abstract
:1. Introduction
2. Results
2.1. Model Development
2.2. Estimating Release and Reaction Model Parameters
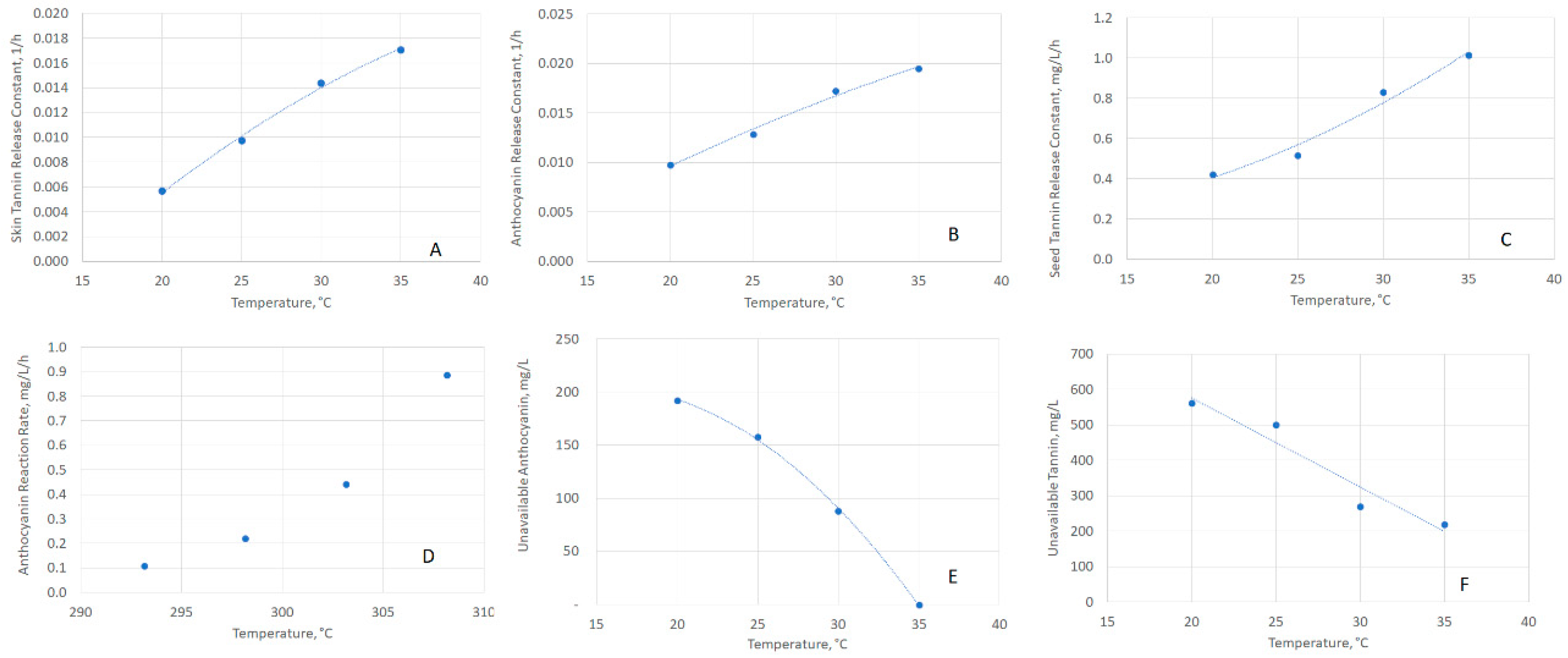
2.3. Examining the Temperature Dependence of Release and Reaction Parameters
2.4. Evaluating Model Fit to Experimental Data
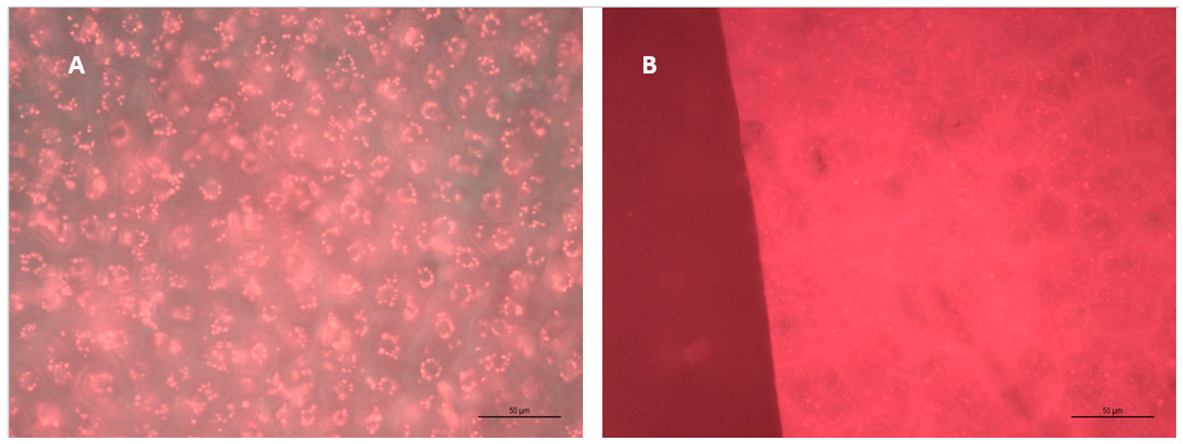
2.5. Physical Basis for Observed Form of Skin and Seed Release Expressions
3. Discussion
4. Material and Methods
4.1. Grape Skin and Seed Microscopy
4.2. Calculations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boulton, R.B.; Singleton, V.L.; Bisson, L.F.; Kunkee, R.E. Principles and Practices of Winemaking; Chapman & Hall: New York, NY, USA, 1996. [Google Scholar]
- Lerno, L.; Reichwage, M.; Ponangi, R.; Hearne, L.; Oberholster, A.; Block, D.E. Effects of Cap and Overall Fermentation Temperature on Phenolic Extraction in Cabernet Sauvignon Fermentations. Am. J. Enol. Vitic. 2015, 66, 444–453. [Google Scholar] [CrossRef]
- Lerno, L.; Panprivech, S.; Ponangi, R.; Hearne, L.; Blair, T.; Oberholster, A.; Block, D.E. Effect of Pump-over Conditions on the Extraction of Phenolic Compounds during Cabernet Sauvignon Fermentation. Am. J. Enol. Vitic. 2018, 69, 295–301. [Google Scholar] [CrossRef]
- Lerno, L.; Reichwage, M.; Panprivech, S.; Ponangi, R.; Hearne, L.; Oberholster, A.; Block, D.E. Chemical Gradients in Pilot-Scale Cabernet Sauvignon Fermentations and Their Effect on Phenolic Extraction. Am. J. Enol. Vitic. 2017, 68, 401–411. [Google Scholar] [CrossRef]
- Singleton, V.L.; Draper, D.E. The Transfer of Polyphenolic Compounds from Grape Seeds into Wines. Am. J. Enol. Vitic. 1964, 15, 34–40. [Google Scholar]
- Setford, C.S.; Jeffery, D.W.; Grbin, P.R.; Muhlack, R.A. Factors affecting extraction and evolution of phenolic compounds during red wine maceration and the role of process modelling. Trends Food Sci. Technol. 2017, 69, 106–117. [Google Scholar] [CrossRef]
- Bucic-Kojic, A.; Planinic, M.; Tomas, S.; Bilic, M.; Velic, D. Study of solid-liquid extraction kinetics of total polyphenols from grape seeds. J. Food Eng. 2006, 81, 234–242. [Google Scholar] [CrossRef]
- Setford, P.C.; Jeffery, D.W.; Grbin, P.R.; Muhlack, R.A. Mathematical modelling of anthocyanin mass transfer to predict extraction in simulated red wine fermentation scenarios. Food Res. Int. 2018. [Google Scholar] [CrossRef]
- Simeonov, E.; Yaneva, Z.; Chilev, C. Kinetics of green solid-liquid extraction of useful compounds from plant materials: Kinetics coefficients and modeling. Green Process. Synth. 2018, 7, 68–73. [Google Scholar] [CrossRef]
- Chilev, C.; Koleva, V.; Simeonov, E. A New Empirical Model for the Calculation of Effective Diffusion Coefficient for Solid-Liquid Extraction from Plants. Ind. Eng. Chem. Res. 2014, 53, 6288–6296. [Google Scholar] [CrossRef]
- Battista, F.; Tomasi, D.; Porro, D.; Caicci, F.; Giacosa, S.; Rolle, L. Winegrape Berry Skin Thickness Determination: Comparison Between Histological Observation and Texture Analysis Determination. Ital. J. Food Sci. 2014, 27, 136–141. [Google Scholar]
- Beaver, J.W.; Medina-Plaza, C.; Miller, K.V.; Oberholster, A.O.; Block, D.E.; Ponangi, R.; Blair, T. Investigating the effects of temperature and ethanol on the kinetics and composition of proanthocyanidin adsorption to cell wall material in model wine systems. J. Agric. Food Chem. 2019. under review. [Google Scholar]
- Medina-Plaza, C.; Beaver, J.W.; Miller, K.V.; Lerno, L.; Dokozzlian, N.; Ponangi, R.; Blair, T.; Block, D.E.; Oberholster, A. Influence of Ethanol and Temperature on Cell Wall-Anthocyanin Interactions. J. Food. Chem. 2019. under review. [Google Scholar]
- Rhim, J.W.; Nunes, R.V.; Jones, V.A.; Swartzel, K.R. Kinetics of Color Change of Grape Juice Generated Using Linearly Increasing Temperature. J. Food Sci. 1989, 54, 776–777. [Google Scholar] [CrossRef]
- Verbeyst, L.; Indrawati, O.; Van der Plancken, I.; Hendrickx, M.; Van Loey, A. Kinetic study on the thermal and pressure degradation of anthocyanins in strawberries. Food Chem. 2010, 123, 269–274. [Google Scholar] [CrossRef]
- Kechinski, C.P.; Guimaraes, P.V.R.; Norena, C.P.Z.; Tessaro, I.C.; Marczak, L.D.F. Degradation Kinetics of Anthocyanin in Blueberry Juice during Thermal Treatment. J. Food Sci. 2010, 75, 173–176. [Google Scholar] [CrossRef]
- Wang, W.D.; Xu, S.Y. Degradation kinetics of anthocyanins in blackberry juice and concentrate. J. Food Eng. 2007, 82, 271–275. [Google Scholar] [CrossRef]
- Drabent, R.; Pliszka, B.; Olszewska, T. Fluorescence properties of plant anthocyanin pigments. I. Fluorescence of anthocyanins in Brassica oleracea L. extracts. Photochem. Photobiol. 1999, 50, 53–58. [Google Scholar] [CrossRef]
- Okamoto, G.; Onishi, H.; Hirano, K. The effect of different fertilizer application levels on anthocyanoplast development in berry skin of Pione grapevines (V. vinifera x V. labrusca). Vitis 2003, 42, 117–121. [Google Scholar]
- Kolb, C.A.; Kopecky, J.; Riederer, M.; Pfundel, E.E. UV Screening by phenolics in berries of grapevine (Vitis vinifera). Funct. Plant Biol. 2003, 30, 1177–1186. [Google Scholar] [CrossRef]
- Thorngate, J.H.; Singleton, V.L. Localization of Procyanidins in Grape Seeds. Am. J. Enol. Vitic. 1994, 45, 259–262. [Google Scholar]
- Miller, K.V.; Oberholster, A.O.; Block, D.E. Creation and Predictions of a Reactor Engineering Model for Red Wine Fermentations. Biotechnol. Bioeng. 2019, in press. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.V.; Oberholster, A.O.; Block, D.E. Predicting the Impact of Red Winemaking Practices Using a Reactor Engineering Model. Am. J. Enol. Vitic. 2019, in press. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |





| Work | Substrate | Activation Energy, kJ/mol |
|---|---|---|
| This work | Grapes (Cabernet Sauvignon) | 107.3 |
| Rhim [14] | Grapes (Vitis Rotundifolia) | 92.8 |
| Verbeyst [15] | Strawberries | 94.4 |
| Kechinski [16] | Blackberries | 80.4 |
| Wang [17] | Blackberries | 59.0–75.5 |
| Parameter | Symbol (Unit) | Fit as a Function of T (°C) |
|---|---|---|
| Skin-Tannin Release Constant | kG,Tan,Skin (1/h) | y = −0.000014T2 + 0.001554T − 0.019916 |
| Skin-Anthocyanin Release Constant | kG,Anth,Skin (1/h) | y = −0.0000081T2 + 0.0011173T − 0.0095045 |
| Seed-Tannin Release Constant | kG,Tan,Seed (mg/L/h) | y = 0.00089T2 − 0.00703T + 0.19030 |
| Unavailable Anthocyanin Concentration | CAnth,U (mg/L) | y = −0.53615T2 + 16.57825T + 75.70350 |
| Unavailable Skin-Tannin Concentration | CTan,U (mg/L) | y = −25.1835T + 1080.7055 |
| Anthocyanin Reaction Rate | kR,Anth (mg/L/h) | See Arrhenius Parameters |
| Temperature | Anthocyanin Fit R2 | Tannin Fit R2 |
|---|---|---|
| 20 °C | 0.93 | 0.99 |
| 25 °C | 0.93 | 0.96 |
| 30 °C | 0.84 | 0.99 |
| 35 °C | 0.84 | 0.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, K.V.; Noguera, R.; Beaver, J.; Medina-Plaza, C.; Oberholster, A.; Block, D.E. A Mechanistic Model for the Extraction of Phenolics from Grapes During Red Wine Fermentation. Molecules 2019, 24, 1275. https://doi.org/10.3390/molecules24071275
Miller KV, Noguera R, Beaver J, Medina-Plaza C, Oberholster A, Block DE. A Mechanistic Model for the Extraction of Phenolics from Grapes During Red Wine Fermentation. Molecules. 2019; 24(7):1275. https://doi.org/10.3390/molecules24071275
Chicago/Turabian StyleMiller, Konrad V., Roberto Noguera, Jordan Beaver, Cristina Medina-Plaza, Anita Oberholster, and David E. Block. 2019. "A Mechanistic Model for the Extraction of Phenolics from Grapes During Red Wine Fermentation" Molecules 24, no. 7: 1275. https://doi.org/10.3390/molecules24071275
APA StyleMiller, K. V., Noguera, R., Beaver, J., Medina-Plaza, C., Oberholster, A., & Block, D. E. (2019). A Mechanistic Model for the Extraction of Phenolics from Grapes During Red Wine Fermentation. Molecules, 24(7), 1275. https://doi.org/10.3390/molecules24071275







