Thickness and Structure of Adsorbed Water Layer and Effects on Adhesion and Friction at Nanoasperity Contact
Abstract
:1. Introduction
2. Water Adsorption on Solid Surfaces
2.1. Effect of the Surface Atomic Structure on Water Adsorption
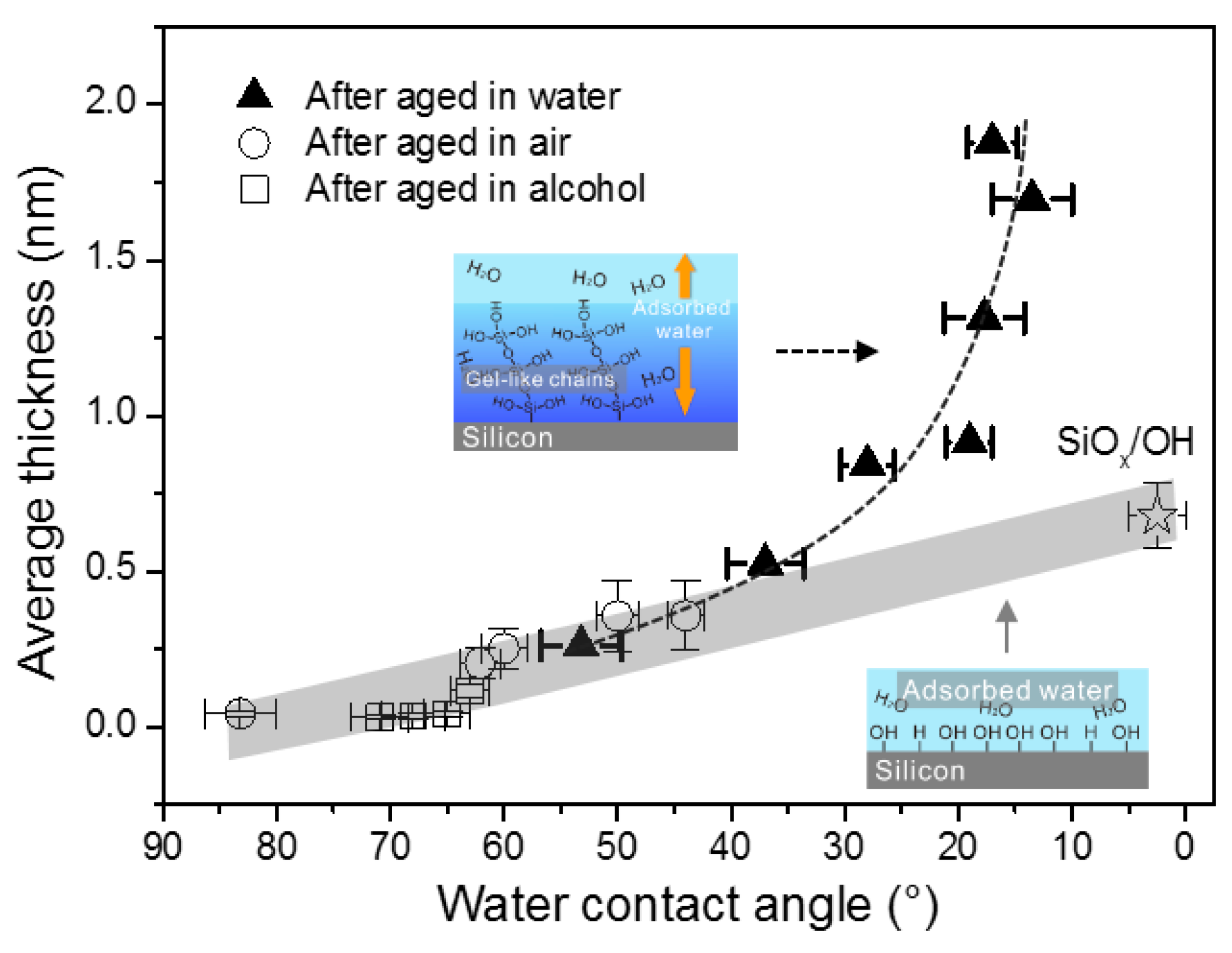
2.2. Effect of Surface Wettability on Water Adsorption
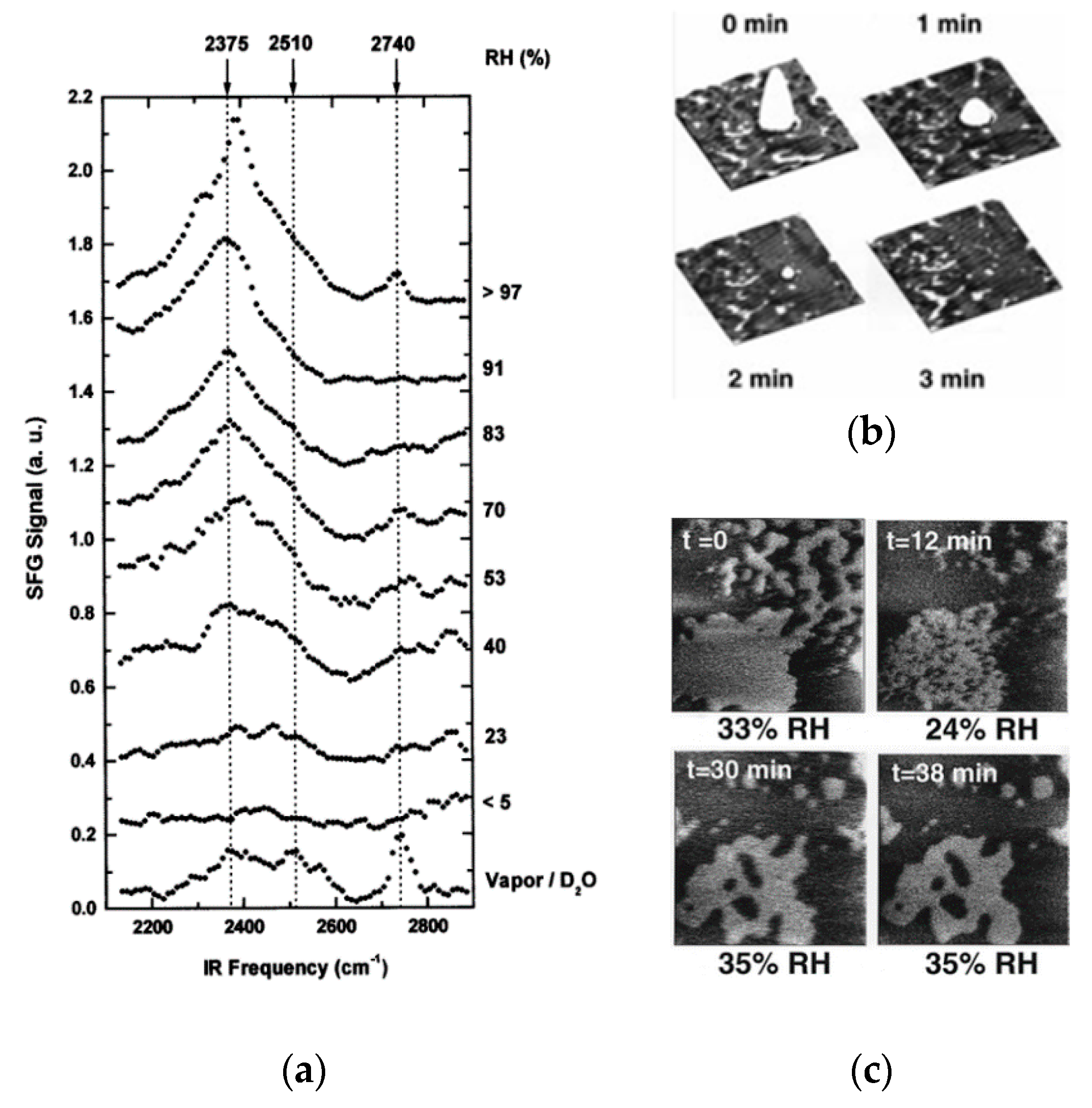
2.3. Effect of External Environments on Water Adsorption
3. Effect of Water Adsorption on Adhesion at Nanoasperity Contact
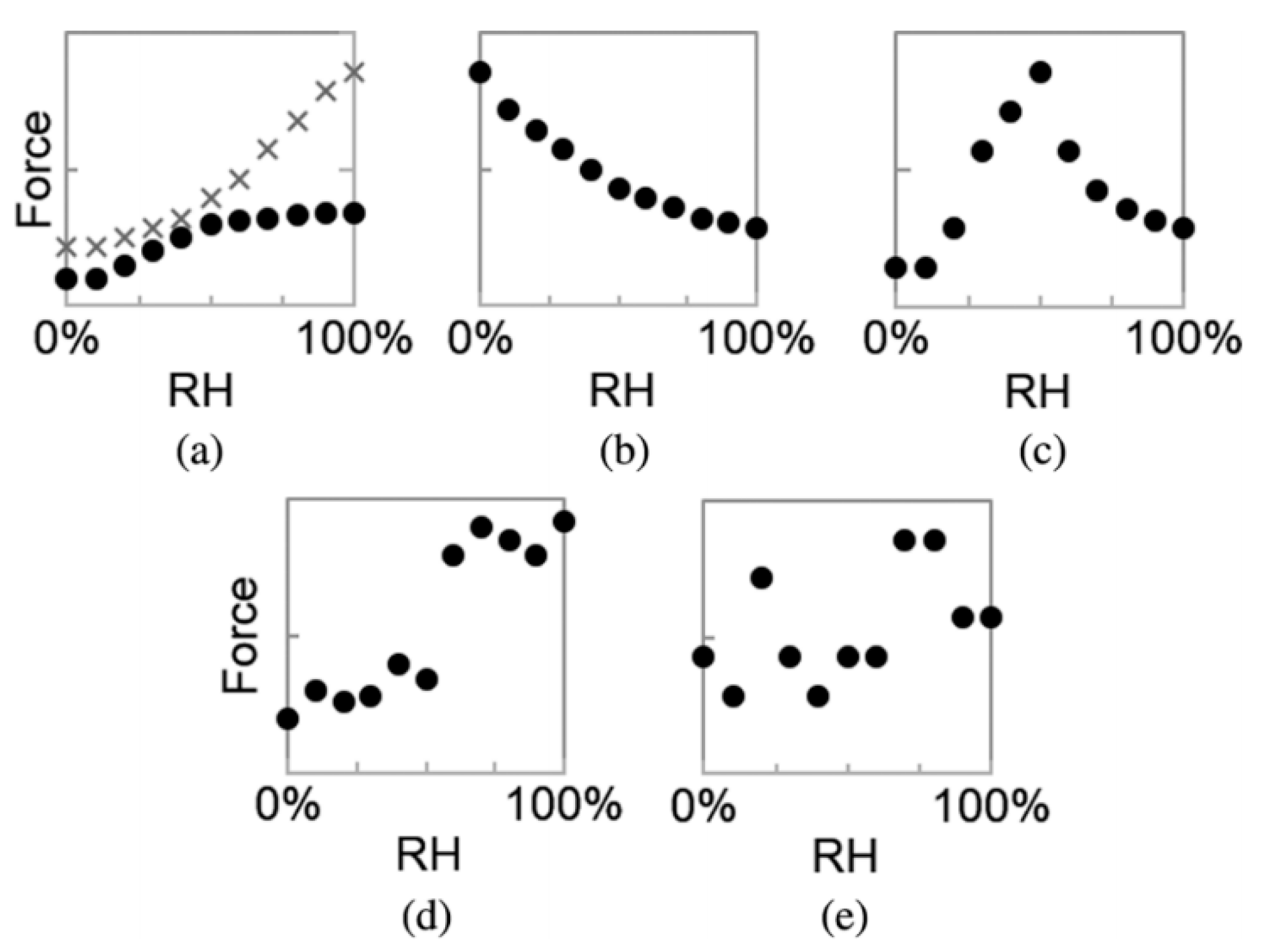
3.1. Brief Introduction of Water Adsorption-Dependent Adhesion Forces
3.2. Effect of Water Adsorption on van der Waals Force
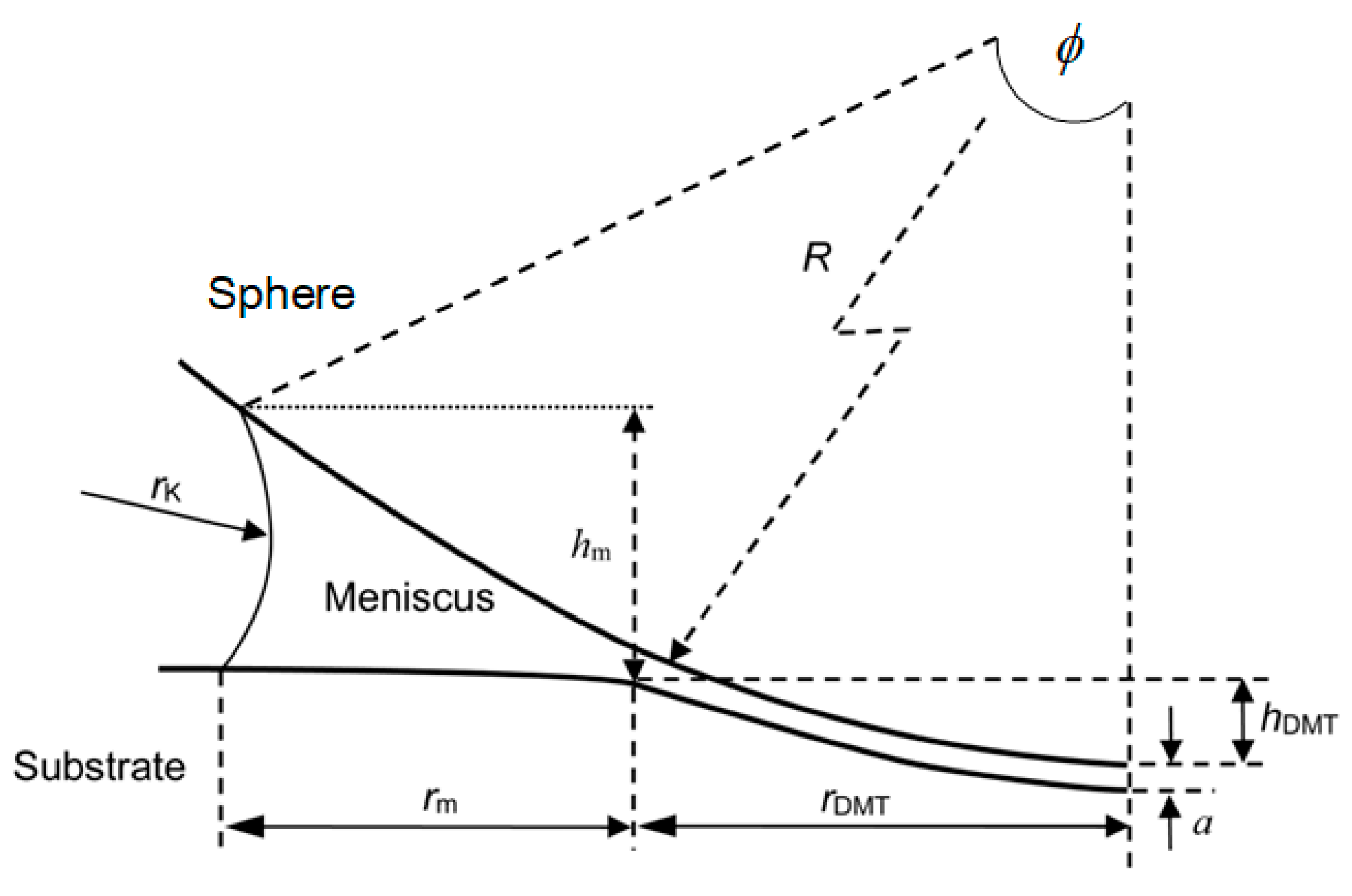
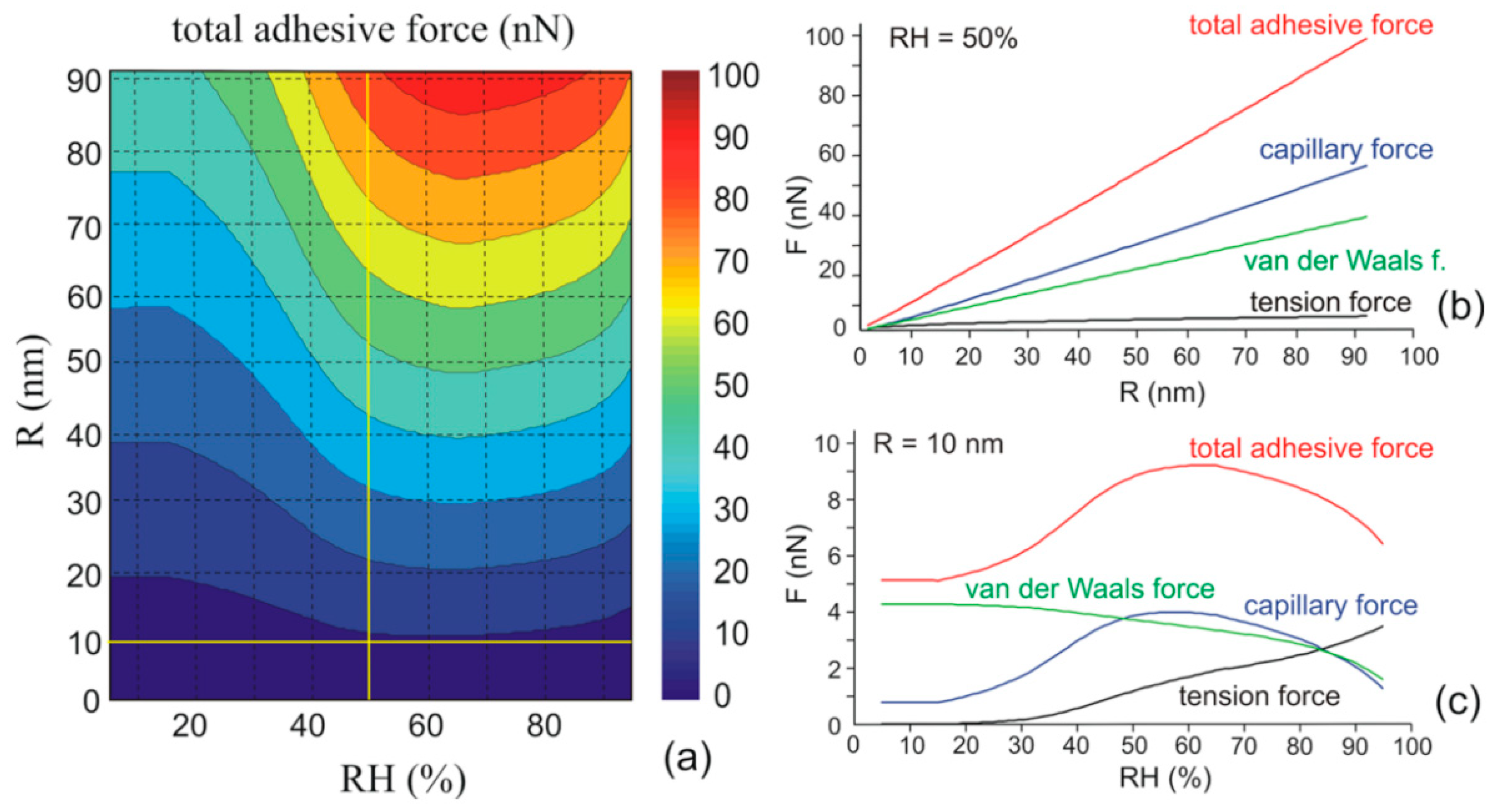
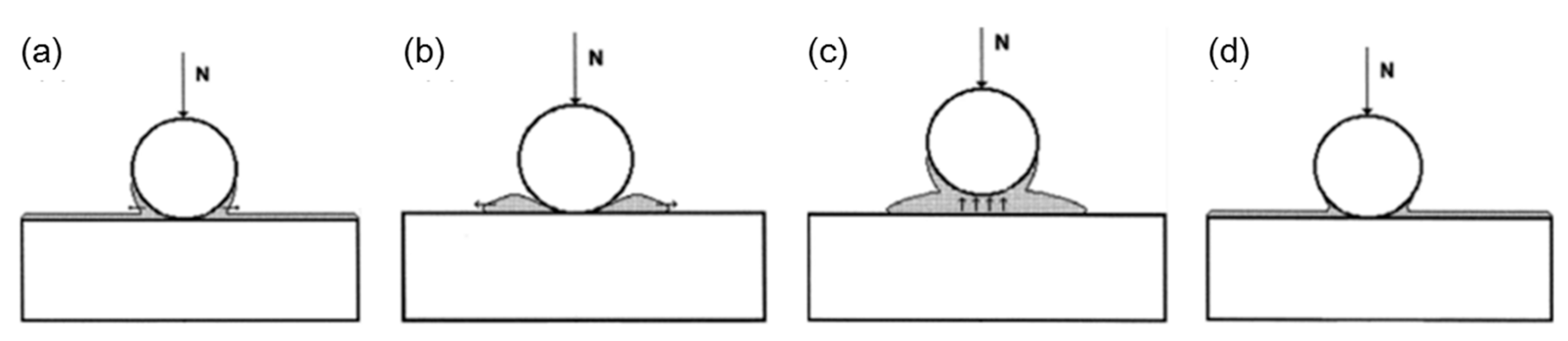
3.3. Effect of Water Condensation on Capillary Force
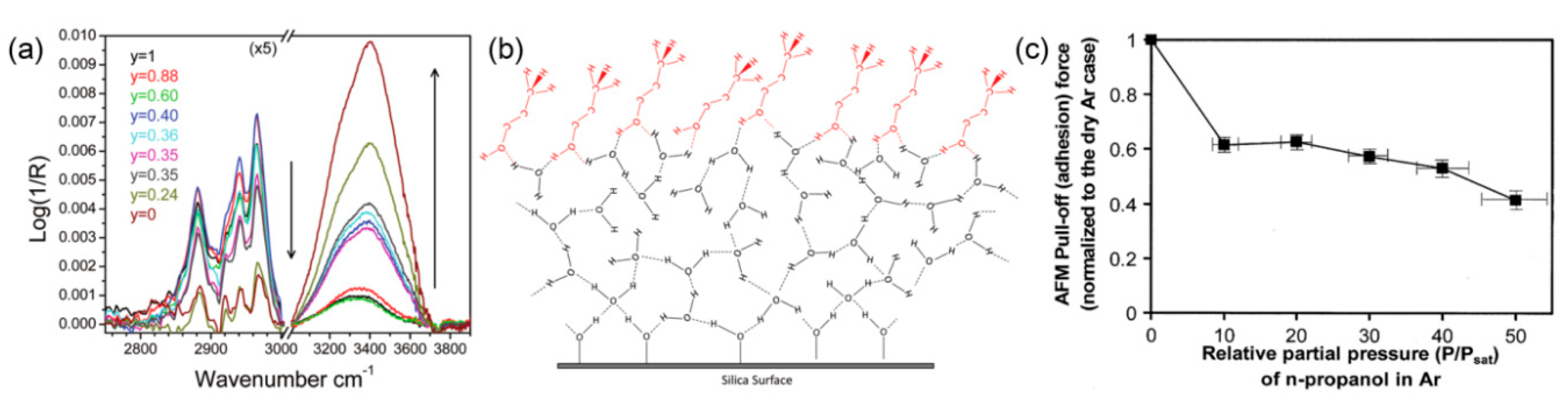
3.4. Effect of Adsorbed Water Structure on Adhesion
4. Effect of Water Adsorption on Friction Force at Nanoscale
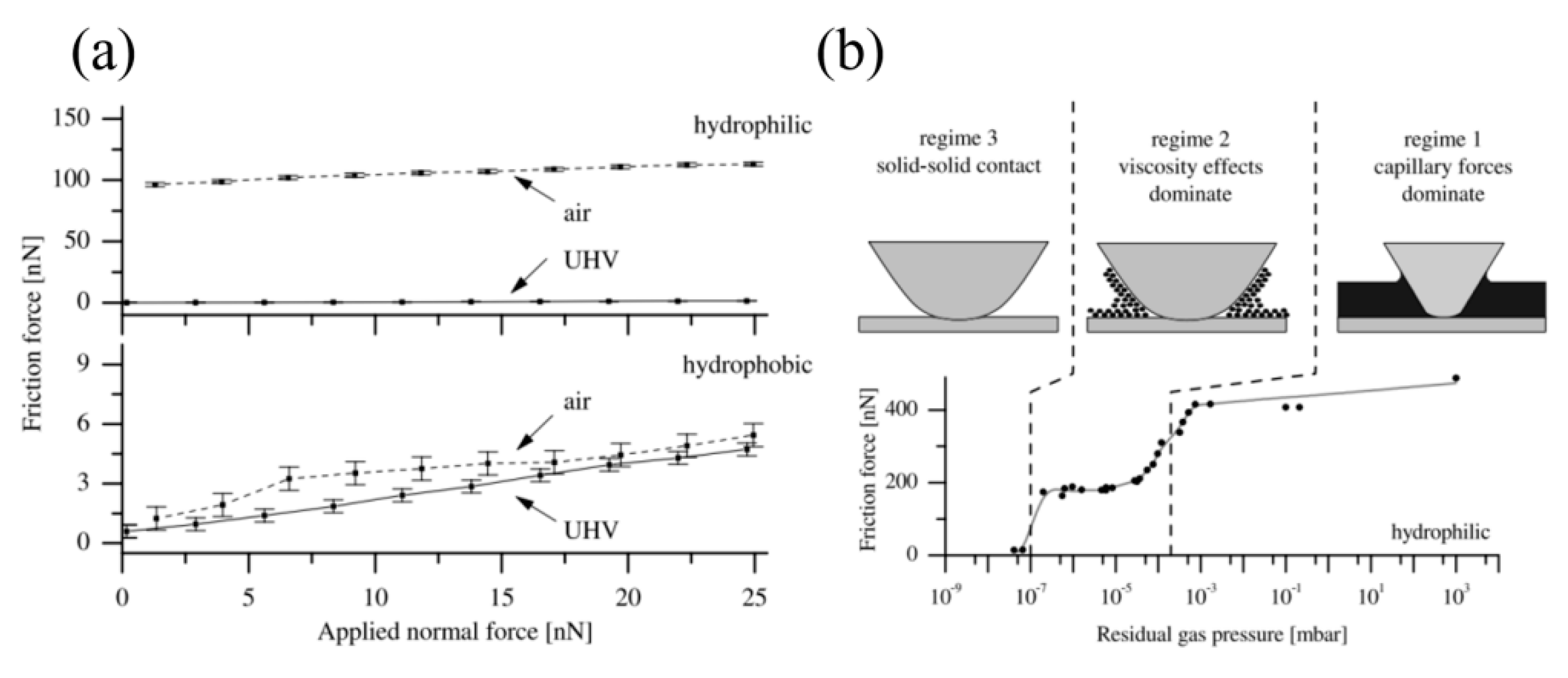
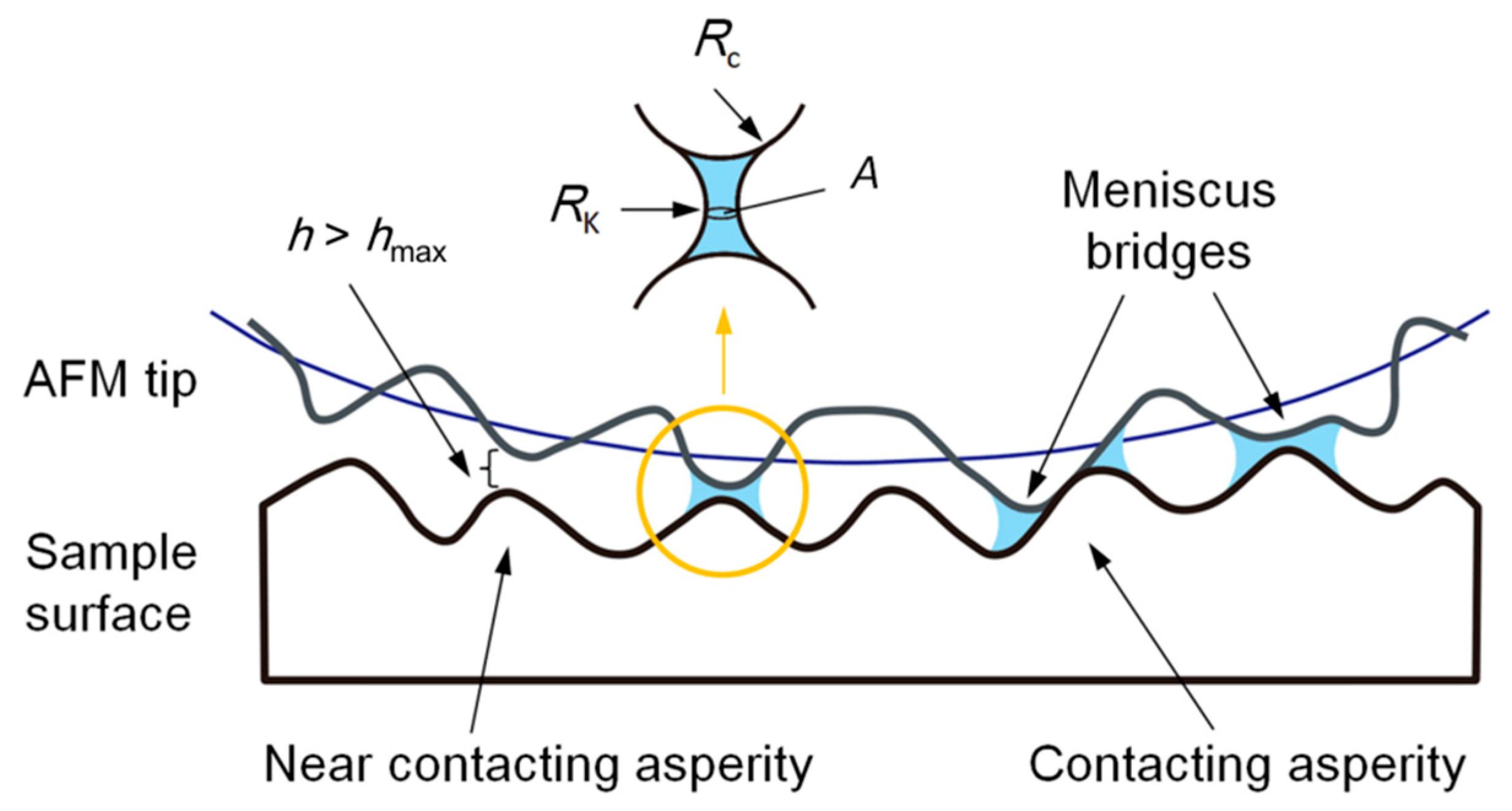
4.1. Nucleation of the Water Meniscus During Sliding Process
4.2. Effect of Surface Wettability on Water Condensation at Nanoasperity Contact
4.3. Effect of Water Condensation on Friction Force
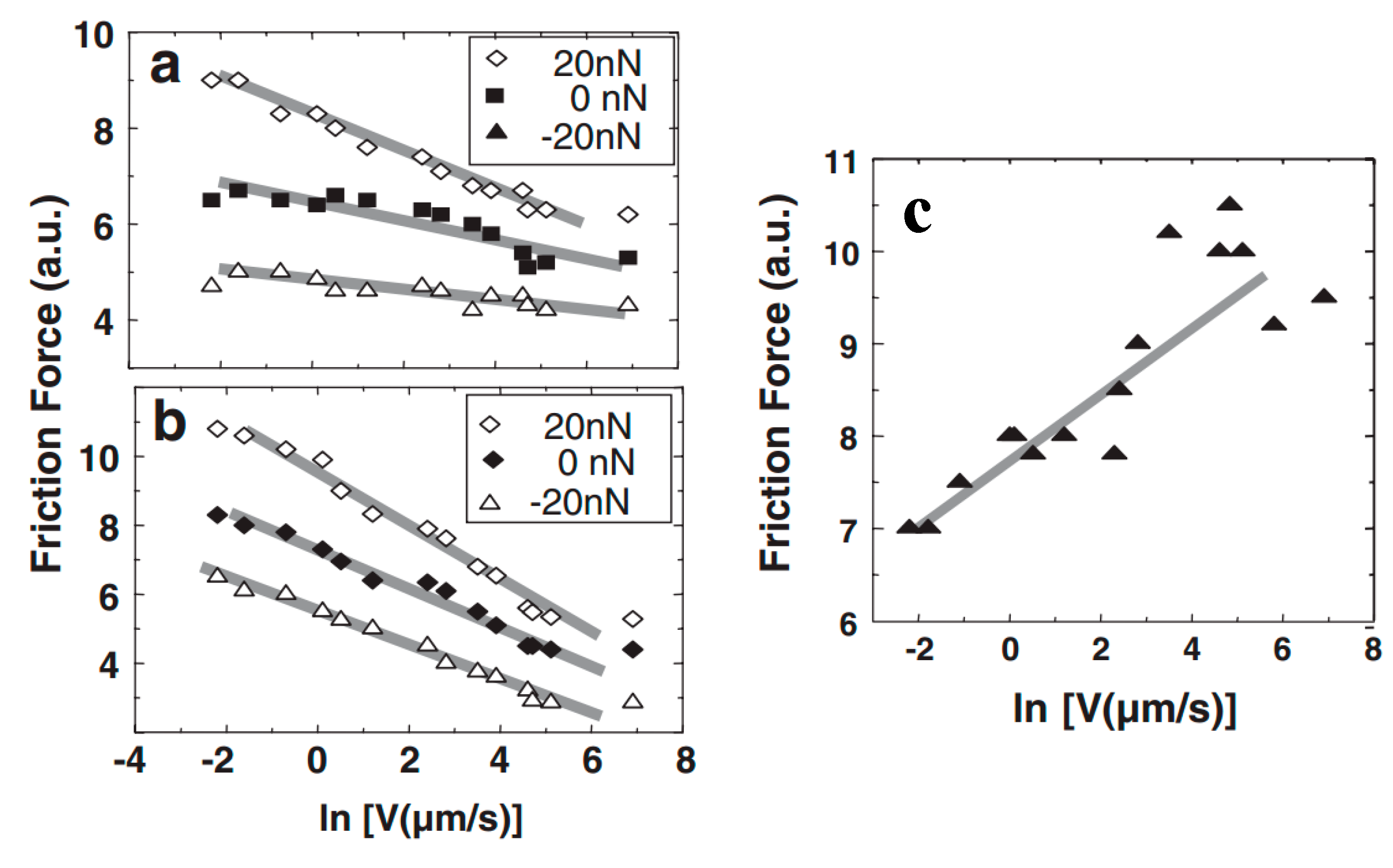
4.4. Effect of Adsorbed Water Structure on Friction Force at Single-Asperity Contact
5. Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, J.; Meng, X.; Chen, J.; Peng, J.; Sheng, J.; Li, X.Z.; Xu, L.; Shi, J.R.; Wang, E.; Jiang, Y. Real-space imaging of interfacial water with submolecular resolution. Nat. Mater. 2014, 13, 184–189. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, A.; Haq, S. Water adsorption and the wetting of metal surfaces. Surf. Sci. Rep. 2009, 64, 381–451. [Google Scholar] [CrossRef]
- Henderson, M. The interaction of water with solid surfaces: fundamental aspects revisited. Surf. Sci. Rep. 2002, 46, 1–308. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, C.; Wang, X.; Zhang, P.; Chen, L.; Qi, Y.; Qian, L. Role of water in the tribochemical removal of bare silicon. Appl. Surf. Sci. 2016, 390, 696–702. [Google Scholar] [CrossRef]
- Chen, L.; Wen, J.; Zhang, P.; Yu, B.; Chen, C.; Ma, T.; Lu, X.; Kim, S.H.; Qian, L. Nanomanufacturing of silicon surface with a single atomic layer precision via mechanochemical reactions. Nat. Commun. 2018, 9, 1542. [Google Scholar] [CrossRef] [PubMed]
- Michaelides, A. Density functional theory simulations of water–metal interfaces: Waltzing waters, a novel 2D ice phase, and more. Appl. Phys. A 2006, 85, 415–425. [Google Scholar] [CrossRef]
- Bhushan, B. Principles and Applications of Tribology; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bhushan, B.; Israelachvili, J.N.; Landman, U. Nanotribology: friction, wear and lubrication at the atomic scale. Nature 1995, 374, 607–616. [Google Scholar] [CrossRef]
- Bhushan, B.; Liu, H.; Hsu, S.M. Adhesion and friction studies of silicon and hydrophobic and Low friction films and investigation of scale effects. J. Tribol. 2004, 126, 583–590. [Google Scholar] [CrossRef]
- Asay, D.B.; Kim, S.H. Evolution of the adsorbed water layer structure on silicon oxide at room temperature. J. Phys. Chem. B 2005, 109, 16760–16763. [Google Scholar] [CrossRef]
- Argyris, D.; Cole, D.R.; Striolo, A. Dynamic behavior of interfacial water at the silica surface. J. Phys. Chem. C 2009, 113, 19591–19600. [Google Scholar] [CrossRef]
- Argyris, D.; Cole, D.R.; Striolo, A. Hydration structure on crystalline silica substrates. Langmuir 2009, 25, 8025–8035. [Google Scholar] [CrossRef] [PubMed]
- Verdaguer, A.; Weis, C.; Oncins, G.; Ketteler, G.; Bluhm, H.; Salmeron, M. Growth and structure of water on SiO2 films on Si investigated by kelvin probe microscopy and in situ X-ray spectroscopies. Langmuir 2007, 23, 9699–9703. [Google Scholar] [CrossRef] [PubMed]
- Butt, H.J.; Kappl, M. Normal capillary forces. Adv. Colloid Interface 2009, 146, 48–60. [Google Scholar] [CrossRef] [PubMed]
- Harrison, A.J.; Corti, D.S.; Beaudoin, S.P. Capillary forces in nanoparticle adhesion: a review of AFM methods. Part Sci. Technol. 2015, 33, 526–538. [Google Scholar] [CrossRef]
- Tambe, N.S.; Bhushan, B. Friction model for the velocity dependence of nanoscale friction. Nanotechnology 2005, 16, 2309–2324. [Google Scholar] [CrossRef] [PubMed]
- Ben-Naim, A. Hydrophobic interaction. Phys. Chem. Liq. 1978, 7, 375–386. [Google Scholar] [CrossRef]
- Raschke, T.M. Water structure and interactions with protein surfaces. Curr. Opin. Struct. Biol. 2006, 16, 152–159. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.J.; Xi, X.K.; Kleinhammes, A.; Wu, Y. Temperature-induced hydrophobic-hydrophilic transition observed by water adsorption. Science 2008, 322, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Fecko, C.J.; Sánchez-Villagra, M.R.; Aguilera, O.; Horovitz, I. Ultrafast hydrogen-bond dynamics in the infrared spectroscopy of water. Science 2003, 301, 1698–1702. [Google Scholar] [CrossRef]
- Midya, U.S.; Bandyopadhyay, S. Hydration behavior at the ice-binding surface of the tenebrio molitor antifreeze protein. J. Phys. Chem. B 2014, 118, 4743–4752. [Google Scholar] [CrossRef]
- Ruan, C.Y.; Lobastov, V.A.; Vigliotti, F.; Chen, S.; Zewail, A.H. Ultrafast electron crystallography of interfacial water. Science 2004, 304, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Ruan, C.Y.; Vigliotti, F.; Lobastov, V.A.; Chen, S.; Zewail, A.H. Ultrafast electron crystallography: transient structures of molecules, surfaces, and phase transitions. Proc. Natl. Acad. Sci. USA 2004, 101, 1123–1128. [Google Scholar] [CrossRef] [PubMed]
- Silvestrelli, P.L.; Toigo, F.; Ancilotto, F. Interfacial water on Cl- and H-terminated Si(111) surfaces from first-principles calculations. J. Phys. Chem. B 2006, 110, 12022–12028. [Google Scholar] [CrossRef] [PubMed]
- Dette, C.; Pérez-Osorio, M.A.; Mangel, S.; Giustino, F.; Jung, S.J.; Kern, K. Atomic structure of water monolayer on anatase TiO2(101) surface. J. Phys. Chem. C 2018, 122, 11954–11960. [Google Scholar] [CrossRef]
- Carrasco, J.; Hodgson, A.; Michaelides, A. A molecular perspective of water at metal interfaces. Nat. Mater. 2012, 11, 667–674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Motobayashi, K.; Matsumoto, C.; Kim, Y.; Kawai, M. Vibrational study of water dimers on Pt(111) using a scanning tunneling microscope. Surf. Sci. 2008, 602, 3136–3139. [Google Scholar] [CrossRef]
- Kumagai, T.; Kaizu, M.; Okuyama, H.; Hatta, S.; Aruga, T.; Hamada, I.; Morikawa, Y. Tunneling dynamics of a hydroxyl group adsorbed on Cu(110). Phys. Rev. B 2009, 79, 035423. [Google Scholar] [CrossRef]
- Cabrera-Sanfelix, P.; Arnau, A.; Mugarza, A.; Shimizu, T.K.; Salmeron, M.; Sánchez-Portal, D. Decisive role of the energetics of dissociation products in the adsorption of water on O/Ru(0001). Phys. Rev. B 2008, 78, 155438. [Google Scholar] [CrossRef] [Green Version]
- Maier, S.; Stass, I.; Mitsui, T.; Feibelman, P.J.; Thürmer, K.; Salmeron, M. Adsorbed water-molecule hexagons with unexpected rotations in islands on Ru(0001) and Pd(111). Phys. Rev. B 2012, 85, 155434. [Google Scholar] [CrossRef]
- Pelmenschikov, A.G.; Morosi, G.; Gamba, A. Adsorption of water and methanol on silica hydroxyls: ab initio energy and frequency calculations. J. Phys. Chem. A 1997, 101, 1178–1187. [Google Scholar] [CrossRef]
- Ostroverkhov, V.; Waychunas, G.A.; Shen, Y.R. New information on water interfacial structure revealed by phase-sensitive surface spectroscopy. Phys. Rev. Lett. 2005, 94, 046102. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.E.; Carter, E.A. First-principles study of the interfacial adhesion between SiO2 and MoSi2. Phys. Rev. B 2005, 72, 165410. [Google Scholar] [CrossRef]
- Park, S.H.; Sposito, G. Structure of water adsorbed on a mica surface. Phys. Rev. Lett. 2002, 89, 085501. [Google Scholar] [CrossRef] [PubMed]
- Hass, K.C.; Schneider, W.F.; Curioni, A.; Andreoni, W. First-principles molecular dynamics simulations of H2O on α-Al2O3(0001). J. Phys. Chem. B 2000, 104, 5527–5540. [Google Scholar] [CrossRef]
- Yang, J.; Meng, S.; Xu, L.; Wang, E.G. Water adsorption on hydroxylated silica surfaces studied using the density functional theory. Phys. Rev. B 2005, 71, 1123–1131. [Google Scholar] [CrossRef]
- Miller, J.D.; Zhang, X.; Wang, X. Wetting of selected fluorite surfaces by water. Surf. Innov. 2015, 3, 39–48. [Google Scholar]
- Yuan, Y.; Lee, T.R. Contact angle and wetting properties. In Surface Phonons; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013; Volume 51, pp. 3–34. [Google Scholar]
- Tidswell, I.M.; Rabedeau, T.A.; Pershan, P.S.; Kosowsky, S.D. Complete wetting of a rough surface: An X-Ray study. Phys. Rev. Lett. 1991, 66, 2108–2111. [Google Scholar] [CrossRef]
- Feng, L.; Li, S.; Li, Y.; Li, H.; Zhang, L.; Zhai, J.; Song, Y.; Liu, B.; Jiang, L.; Zhu, D. Super-hydrophobic surfaces: from natural to artificial. Adv. Mater. 2003, 34, 1857–1860. [Google Scholar] [CrossRef]
- Chen, L.; He, X.; Liu, H.; Qian, L.; Kim, S.H. Water adsorption on hydrophilic and hydrophobic surfaces of silicon. J. Phys. Chem. C 2018, 122, 11385–11391. [Google Scholar] [CrossRef]
- Tu, A.; Kwag, H.R.; Barnette, A.L.; Kim, S.H. Water adsorption isotherms on CH3-, OH-, and COOH-terminated organic surfaces at ambient conditions measured with PM-RAIRS. Langmuir 2012, 28, 15263–15269. [Google Scholar] [CrossRef]
- Asay, D.B.; Barnette, A.L.; Kim, S.H. Effects of surface chemistry on structure and thermodynamics of water layers at solid−vapor interfaces. J. Phys. Chem. C 2008, 113, 2128–2133. [Google Scholar] [CrossRef]
- Bertilsson, L.; Potje-Kamloth, K.; Liess, H.D.; Liedberg, B. On the adsorption of dimethyl methylphosphonate on self-assembled alkanethiolate monolayers: influence of humidity. Langmuir 1999, 15, 1128–1135. [Google Scholar] [CrossRef]
- Vogler, E.A. Structure and reactivity of water at biomaterial surfaces. Adv. Colloid Interface Sci. 1998, 74, 69–117. [Google Scholar] [CrossRef]
- Tadros, M.E.; Hu, P.; Adamson, A.W. Adsorption and contact angle studies: I. water on smooth carbon, linear polyethylene, and stearic acid-coated copper. J. Colloid. Interf. Sci. 1974, 49, 184–195. [Google Scholar] [CrossRef]
- Yang, J.; Meng, S.; Xu, L.F.; Wang, E.G. Ice tessellation on a hydroxylated silica surface. Phys. Rev. Lett. 2004, 92, 146102. [Google Scholar] [CrossRef] [PubMed]
- Willard, A.P.; Chandler, D. The molecular structure of the interface between water and a hydrophobic substrate is liquid-vapor like. J. Chem. Phys. 2014, 141, 18C159. [Google Scholar] [CrossRef] [PubMed]
- Gordillo, M.C.; Martí, J. Molecular dynamics description of a layer of water molecules on a hydrophobic surface. J. Chem. Phys. 2002, 117, 3425–3430. [Google Scholar] [CrossRef]
- Irvine, W.M.; Pollack, J.B. Infrared optical properties of water and ice spheres. Icarus 1968, 8, 324–360. [Google Scholar] [CrossRef]
- Du, Q.; Freysz, E.; Shen, Y.R. Surface vibrational spectroscopic studies of hydrogen bonding and hydrophobicity. Science 1994, 264, 826–828. [Google Scholar] [CrossRef]
- Mallamace, F.; Broccio, M.; Corsaro, C.; Faraone, A.; Majolino, D.; Venuti, V.; Liu, L.; Mou, C.Y.; Chen, S.H. Evidence of the existence of the low-density liquid phase in supercooled, confined water. Proc. Natl. Acad. Sci. USA 2007, 104, 424–428. [Google Scholar] [CrossRef] [Green Version]
- Ewing, G.E. Thin film water. J. Phys. Chem. B 2004, 108, 15953–15961. [Google Scholar] [CrossRef]
- Nijem, N.; Canepa, P.; Kaipa, U.; Tan, K.; Roodenko, K.; Tekarli, S.; Halbert, J.; Oswald, I.W.H.; Arvapally, R.K.; Yang, C.; et al. Water cluster confinement and methane adsorption in the hydrophobic cavities of a fluorinated metal–organic framework. J. Am. Chem. Soc. 2013, 135, 12615–12626. [Google Scholar] [CrossRef] [PubMed]
- Aarts, I.M.P.; Pipino, A.C.R.; Hoefnagels, J.P.M.; Kessels, W.M.M.; Van De Sanden, M.C.M. Quasi-ice monolayer on atomically smooth amorphous SiO2 at room temperature observed with a high-finesse optical resonator. Phys. Rev. Lett. 2005, 95, 166104. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, K.S. A molecular dynamics study of the interaction of water with the external surface of silicalite-1. Phys. Chem. Chem. Phys. 2017, 19, 2950–2960. [Google Scholar] [CrossRef] [PubMed]
- Thiel, P.A.; Madey, T.E. The interaction of water with solid surfaces: fundamental aspects. Surf. Sci. Rep. 1987, 7, 211–385. [Google Scholar] [CrossRef]
- Beaglehole, D.; Christenson, H.K. Vapor adsorption on mica and silicon: entropy effects, layering, and surface forces. J. Phys. Chem. 1992, 96, 3395–3403. [Google Scholar] [CrossRef]
- Odelius, M.; Bernasconi, M.; Parrinello, M. Two dimensional ice adsorbed on mica surface. Phys. Rev. Lett. 1997, 78, 2855–2858. [Google Scholar] [CrossRef]
- Nauta, K. Formation of cyclic water hexamer in liquid helium: The smallest piece of ice. Science 2000, 287, 293–295. [Google Scholar] [CrossRef]
- Cao, P.; Xu, K.; Varghese, J.O.; Heath, J.R. The microscopic structure of adsorbed water on hydrophobic surfaces under ambient conditions. Nano Lett. 2011, 11, 5581–5586. [Google Scholar] [CrossRef]
- Chen, L.; Ngo, D.; Luo, J.; Xiao, C.; He, X.; Yu, B.; Qian, L.; Kim, S.H. Dependence of water adsorption on surface structure of silicon wafer aged in different environmental conditions. 2018; in press. [Google Scholar]
- Salmeron, M.; Miranda, P.B.; Shen, Y.R.; Xu, L. Icelike water monolayer adsorbed on mica at room temperature. Phys. Rev. Lett. 1998, 81, 5876–5879. [Google Scholar]
- Du, Q.; Superfine, R.; Freysz, E.; Shen, Y.R. Vibrational spectroscopy of water at the vapor/water interface. Phys. Rev. Lett. 1993, 70, 2313–2316. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Lio, A.; Hu, J.; Ogletree, D.F.; Salmeron, M. Wetting and capillary phenomena of water on mica. J. Phys. Chem. B 1998, 102, 540–548. [Google Scholar] [CrossRef]
- Hatch, C.D.; Wiese, J.S.; Crane, C.C.; Harris, K.J.; Kloss, H.G.; Baltrusaitis, J. Water adsorption on clay minerals as a function of relative humidity: application of BET and freundlich adsorption models. Langmuir 2012, 28, 1790–1803. [Google Scholar] [CrossRef] [PubMed]
- Rahaman, A.; Grassian, V.H.; Margulis, C.J. Dynamics of water adsorption onto a calcite surface as a function of relative humidity. J. Phys. Chem. C 2008, 112, 2109–2115. [Google Scholar] [CrossRef]
- Xu, K.; Cao, P.; Heath, J.R. Graphene visualizes the first water adlayers on mica at ambient conditions. Science 2010, 329, 1188–1191. [Google Scholar] [CrossRef]
- Weiss, D.R.; Raschke, T.M.; Levitt, M. How hydrophobic buckminsterfullerene affects surrounding water structure. J. Phys. Chem. B 2008, 112, 2981–2990. [Google Scholar] [CrossRef]
- Striolo, A. The mechanism of water diffusion in narrow carbon nanotubes. Nano Lett. 2006, 6, 633–639. [Google Scholar] [CrossRef]
- Wang, J.; Kalinichev, A.G.; Kirkpatrick, R.J.; Cygan, R.T. Structure, energetics, and dynamics of water adsorbed on the muscovite (001) surface: a molecular dynamics simulation. J. Phys. Chem. B 2005, 109, 15893–15905. [Google Scholar] [CrossRef]
- Ketteler, G.; Yamamoto, S.; Bluhm, H.; Andersson, K.J.; Starr, D.E.; Ogletree, D.F.; Ogasawara, H.; Nilsson, A.; Salmeron, M. The nature of water nucleation sites on TiO2(110) surfaces revealed by ambient pressure X-ray photoelectron spectroscopy. J. Phys. Chem. C 2007, 111, 8278–8282. [Google Scholar] [CrossRef]
- Puibasset, J.; Pellenq, R.J. Water adsorption in disordered mesoporous silica (Vycor) at 300 K and 650 K: a grand canonical monte carlo simulation study of hysteresis. J. Chem. Phys. 2005, 122, 094704. [Google Scholar] [CrossRef]
- Hamaker, H. The London—van der Waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar] [CrossRef]
- Cappella, B.; Dietler, G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 1999, 34, 1–104. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Xiao, C.; Qian, L.; Cui, S. Detecting van der Waals forces between a single polymer repeating unit and a solid surface in high vacuum. Nano Res. 2018, 12, 57–61. [Google Scholar] [CrossRef]
- Barthel, A.J.; Al-Azizi, A.; Kim, S.H. Fundamental understanding of environmental effects on adhesion and friction: alcohol and water adsorption cases. Tribol. Lett. 2013, 50, 157–168. [Google Scholar] [CrossRef]
- Jones, R.; Pollock, H.M.; Cleaver, J.A.S.; Hodges, C.S. Adhesion forces between glass and silicon surfaces in air studied by AFM: Effects of relative humidity, particle size, roughness, and surface treatment. Langmuir 2002, 18, 8045–8055. [Google Scholar] [CrossRef]
- Binggeli, M.; Mate, C.M. Influence of capillary condensation of water on nanotribology studied by force microscopy. Appl. Phys. Lett. 1994, 65, 415–417. [Google Scholar] [CrossRef]
- Xiao, X.; Qian, L. Investigation of Humidity-Dependent Capillary Force. Langmuir 2000, 16, 8153–8158. [Google Scholar] [CrossRef]
- Asay, D.B.; Kim, S.H. Effects of adsorbed water layer structure on adhesion force of silicon oxide nanoasperity contact in humid ambient. J. Chem. Phys. 2006, 124, 174712. [Google Scholar] [CrossRef]
- Aston, D.E.; Buenviaje, C.; Overney, R.M.; He, M.; Blum, A.S.; Overney, R.M.; Luginbühl, R. Critical phenomena of water bridges in nanoasperity contacts. J. Chem. Phys. 2001, 114, 1355–1360. [Google Scholar] [Green Version]
- Tang, J.; Wang, C.; Liu, M.; Su, M.; Bai, C. Effect of humidity on the surface adhesion force of inorganic crystals by the force spectrum method. Chin. Sci. Bull. 2001, 46, 912–914. [Google Scholar] [CrossRef]
- Köber, M.; Sahagún, E.; Briones, F.; Luna, M.; Sáenz, J.J.; García-Mochales, P.; García-Mochales, P. Nanogeometry matters: unexpected decrease of capillary adhesion forces with increasing relative humidity. Small 2010, 6, 2725–2730. [Google Scholar] [CrossRef] [PubMed]
- Farshchi-Tabrizia, M.; Kappl, M.; Butt, H.J. Influence of humidity on adhesion: An atomic force microscope study. J. Adhes. Sci. Technol. 2008, 22, 181–203. [Google Scholar] [CrossRef]
- Ptak, A.; Gojzewski, H.; Kappl, M.; Butt, H.J. Influence of humidity on the nanoadhesion between a hydrophobic and a hydrophilic surface. Chem. Phys. Lett. 2011, 503, 66–70. [Google Scholar] [CrossRef]
- Zarate, N.V.; Harrison, A.J.; Litster, J.D.; Beaudoin, S.P. Effect of relative humidity on onset of capillary forces for rough surfaces. J. Colloid Interface Sci. 2013, 411, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Dzyaloshinskii, I.; Lifshitz, E.; Pitaevskii, L.; Priestley, M. The general theory of van der Waals forces. In Perspectives in Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 1992; pp. 443–492. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Yang, L.; Hu, J.; Xiao, H.; Quan, W. Analysis of humidity-dependent adhesion between a probe tip and a surface. Particuology 2017, 33, 91–97. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, C.; Yu, B.; Kim, S.H.; Qian, L. What governs friction of silicon oxide in humid environment: contact area between solids, water meniscus around the contact, or water layer structure? Langmuir 2017, 33, 9673–9679. [Google Scholar] [CrossRef] [PubMed]
- Senden, T.J.; Drummond, C.J. Surface chemistry and tip-sample interactions in atomic force microscopy. Colloids Surfaces A Physicochem. Eng. Asp. 1995, 94, 29–51. [Google Scholar] [CrossRef]
- Bartošík, M.; Kormoš, L.; Flajšman, L.; Kalousek, R.; Mach, J.; Lišková, Z.; Nezval, D.; Švarc, V.; Šamořil, T.; Šikola, T. Nanometer-sized water bridge and pull-off force in AFM at different relative humidities: reproducibility measurement and model based on surface tension change. J. Phys. Chem. B 2017, 121, 610–619. [Google Scholar] [CrossRef]
- Chen, M.; Kato, K.; Adachi, K. Friction and wear of self-mated SiC and Si3N4 sliding in water. Wear 2001, 250, 246–255. [Google Scholar] [CrossRef]
- Eastman, T.; Zhu, D.-M. Adhesion forces between surface-modified AFM tips and a mica surface. Langmuir 1996, 12, 2859–2862. [Google Scholar] [CrossRef]
- Ashraf, A.; Wu, Y.; Wang, M.C.; Yong, K.; Sun, T.; Jing, Y.; Haasch, R.T.; Aluru, N.R.; Nam, S. Doping-induced tunable wettability and adhesion of graphene. Nano Lett. 2016, 16, 4708–4712. [Google Scholar] [CrossRef] [PubMed]
- Orr, F.M.; Scriven, L.E.; Rivas, A.P. Pendular rings between solids: Meniscus properties and capillary force. J. Fluid Mech. 1975, 67, 723–742. [Google Scholar] [CrossRef]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Kralchevsky, P.; Nagayama, K. Particles at Fluid Interfaces and Membranes: Attachment of Colloid Particles and Proteins to Interfaces and Formation of Two-Dimensional Arrays; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Adamson, A.; Gast, A. Chemistry of Surfaces; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Douillard, J.; Henry, M. Calculation of surface enthalpy of solids from an ab initio electronegativity based model: case of ice. J. Colloid Interface Sci. 2003, 263, 554–561. [Google Scholar] [CrossRef]
- Szoszkiewicz, R.; Riedo, E. Nucleation time of nanoscale water bridges. Phys. Rev. Lett. 2005, 95, 135502. [Google Scholar] [CrossRef] [PubMed]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. [Google Scholar] [CrossRef]
- Barnette, A.L.; Kim, S.H. Coadsorption of n-propanol and water on SiO2: study of thickness, composition, and structure of binary adsorbate layer using attenuated total reflection infrared (ATR-IR) and sum frequency generation (SFG) vibration spectroscopy. J. Phys. Chem. C 2012, 116, 9909–9916. [Google Scholar] [CrossRef]
- Strawhecker, K.; Asay, D.B.; McKinney, J.; Kim, S.H. Reduction of adhesion and friction of silicon oxide surface in the presence of n-propanol vapor in the gas phase. Tribol. Lett. 2005, 19, 17–21. [Google Scholar] [CrossRef]
- Chen, L.; Yang, Y.; He, H.; Kim, S.; Qian, L. Effect of coadsorption of water and alcohol vapor on the nanowear of silicon. Wear 2015, 332, 879–884. [Google Scholar] [CrossRef]
- Singer, I.L.; Pollock, H. Fundamentals of Friction: Macroscopic and Microscopic Processes; Springer: Berlin, Germany, 2012. [Google Scholar]
- Persson, B.N. Sliding Friction: Physical Principles and Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- Bhushan, B. Handbook of Nanotechnology; Springer: Berlin, Germany, 2017. [Google Scholar]
- Tománek, D.; Zhong, W.; Thomas, H. Calculation of an atomically modulated friction force in atomic-force microscopy. EPL (Europhys. Lett.) 1991, 15, 887–892. [Google Scholar] [CrossRef]
- Gnecco, E.; Bennewitz, R.; Gyalog, T.; Loppacher, C.; Bammerlin, M.; Meyer, E.; Güntherodt, H.-J. Velocity dependence of atomic friction. Phys. Rev. Lett. 2000, 84, 1172–1175. [Google Scholar] [CrossRef]
- Sacha, G.M.; Verdaguer, A.; Salmeron, M. Induced water condensation and bridge formation by electric fields in atomic force microscopy. J. Phys. Chem. B 2006, 110, 14870–14873. [Google Scholar] [CrossRef] [PubMed]
- Sung, B.; Kim, J.; Stambaugh, C.; Chang, S.J.; Jhe, W. Direct measurement of activation time and nucleation rate in capillary-condensed water nanomeniscus. Appl. Phys. Lett. 2013, 103, 213107. [Google Scholar] [CrossRef]
- Greiner, C.; Felts, J.R.; Dai, Z.; King, W.P.; Carpick, R.W. Controlling nanoscale friction through the competition between capillary adsorption and thermally activated sliding. ACS Nano 2012, 6, 4305–4313. [Google Scholar] [CrossRef] [PubMed]
- Barel, I.; Filippov, A.E.; Urbakh, M. Formation and rupture of capillary bridges in atomic scale friction. J. Chem. Phys. 2012, 137, 164706. [Google Scholar] [CrossRef] [PubMed]
- Greiner, C.; Felts, J.R.; Dai, Z.; King, W.P.; Carpick, R.W. Local nanoscale heating modulates single-asperity friction. Nano Lett. 2010, 10, 4640–4645. [Google Scholar] [CrossRef] [PubMed]
- Bocquet, L.; Charlaix, E.; Ciliberto, S.; Crassous, J. Moisture-induced ageing in granular media and the kinetics of capillary condensation. Nature 1998, 396, 735–737. [Google Scholar] [CrossRef]
- Restagno, F.; Bocquet, L.; Crassous, J.; Charlaix, E. Slow kinetics of capillary condensation in confined geometry: experiment and theory. Colloids Surf. A Physicochem. Eng. Asp. 2002, 206, 69–77. [Google Scholar] [CrossRef] [Green Version]
- Biben, T.; Restagno, F.; Bocquet, L. Metastability and nucleation in capillary condensation. Phys. Rev. Lett. 2000, 84, 2433–2436. [Google Scholar]
- Yu, J.; Qian, L.; Yu, B.; Zhou, Z. Effect of surface hydrophilicity on the nanofretting behavior of Si(100) in atmosphere and vacuum. J. Appl. Phys. 2010, 108, 034314. [Google Scholar] [CrossRef]
- Opitz, A.; Ahmed, S.-U.; Schaefer, J.; Scherge, M. Friction of thin water films: A nanotribological study. Surf. Sci. 2002, 504, 199–207. [Google Scholar] [CrossRef]
- Roa, J.; Oncins, G.; Diaz, J.; Capdevila, X.; Sanz, F.; Segarra, M. Study of the friction, adhesion and mechanical properties of single crystals, ceramics and ceramic coatings by AFM. J. Eur. Ceram. Soc. 2011, 31, 429–449. [Google Scholar] [CrossRef]
- Borruto, A.; Crivellone, G.; Marani, F. Influence of surface wettability on friction and wear tests. Wear 1998, 222, 57–65. [Google Scholar] [CrossRef]
- Kaibara, Y.; Sugata, K.; Tachiki, M.; Umezawa, H.; Kawarada, H. Control wettability of the hydrogen-terminated diamond surface and the oxidized diamond surface using an atomic force microscope. Diam. Relat. Mater. 2003, 12, 560–564. [Google Scholar] [CrossRef]
- Opitz, A.; Ahmed, S.-U.; Schaefer, J.; Scherge, M. Nanofriction of silicon oxide surfaces covered with thin water films. Wear 2003, 254, 924–929. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, C.; He, X.; Yu, B.; Kim, S.H.; Qian, L. Friction and tribochemical wear behaviors of native oxide layer on silicon at nanoscale. Tribol. Lett. 2017, 65, 139. [Google Scholar] [CrossRef]
- Chen, L.; Kim, S.H.; Wang, X.; Qian, L. Running-in process of Si-SiOx/SiO2 pair at nanoscale—Sharp drops in friction and wear rate during initial cycles. Friction 2013, 1, 81–91. [Google Scholar] [CrossRef]
- Nevshupa, R.; Scherge, M.; Ahmed, S.U.; Nevshupa, R. Transitional microfriction behavior of silicon induced by spontaneous water adsorption. Surf. Sci. 2002, 517, 17–28. [Google Scholar] [CrossRef]
- Zeng, X.; Peng, Y.; Yu, M.; Lang, H.; Cao, X.; Zou, K.; Cao, X. Dynamic sliding enhancement on the friction and adhesion of graphene, graphene oxide, and fluorinated graphene. ACS Appl. Mater. Interfaces 2018, 10, 8214–8224. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Graphene: A new emerging lubricant. Mater. Today 2014, 17, 31–42. [Google Scholar] [CrossRef]
- Ko, J.H.; Kwon, S.; Byun, I.S.; Choi, J.S.; Park, B.H.; Kim, Y.H.; Park, J.Y. Nanotribological properties of fluorinated, hydrogenated, and oxidized graphenes. Tribol. Lett. 2013, 50, 137–144. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, K.E.; Lee, H.; Koh, S.J.; Ko, J.H.; Kim, Y.H.; Kim, S.O.; Park, J.Y. The effect of thickness and chemical reduction of graphene oxide on nanoscale friction. J. Phys. Chem. B 2017, 122, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Mitropoulos, A. The kelvin equation. J. Colloid Inter. Sci. 2008, 317, 643–648. [Google Scholar] [CrossRef] [PubMed]
- Riedo, E.; Lévy, F.; Brune, H. Kinetics of capillary condensation in nanoscopic sliding friction. Phys. Rev. Lett. 2002, 88, 185505. [Google Scholar] [CrossRef] [PubMed]
- Riedo, E.; Palaci, I.; Boragno, C.; Brune, H. The 2/3 power law dependence of capillary force on normal load in nanoscopic friction. J. Phys. Chem. B 2004, 108, 5324–5328. [Google Scholar] [CrossRef]
- Bouhacina, T.; Aimé, J.P.; Gauthier, S.; Michel, D.; Heroguez, V. Tribological behavior of a polymer grafted on silanized silica probed with a nanotip. Phys. Rev. B 1997, 56, 7694–7703. [Google Scholar] [CrossRef]
- Chen, J.; Ratera, I.; Park, J.Y.; Salmeron, M. Velocity dependence of friction and hydrogen bonding effects. Phys. Rev. Lett. 2006, 96, 236102. [Google Scholar] [CrossRef]
- Zwörner, O.; Hölscher, H.; Schwarz, U.; Wiesendanger, R. The velocity dependence of frictional forces in point-contact friction. Appl. Phys. A 1998, 66, S263–S267. [Google Scholar] [CrossRef]
- Paul, J.; Meltzer, C.; Braunschweig, B.; Peukert, W. Lubrication of individual microcontacts by a self-assembled alkyl phosphonic acid monolayer on α-Al2O3 (0001). Langmuir 2016, 32, 8298–8306. [Google Scholar] [CrossRef]
- Al-Azizi, A.A.; Eryilmaz, O.; Kim, S.H.; Erdemir, A. Effects of nanoscale surface texture and lubricant molecular structure on boundary lubrication in liquid. Langmuir 2013, 29, 13419–13426. [Google Scholar] [CrossRef]
- Weber, T.A.; Stillinger, F.H. Molecular dynamics study of ice crystallite melting. J. Phys. Chem. 1983, 87, 4277–4281. [Google Scholar] [CrossRef]
- Mu, R.; Zhao, Z.J.; Dohnálek, Z.; Gong, J. Structural motifs of water on metal oxide surfaces. Chem. Soc. Rev. 2017, 46, 1785–1806. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Tan, Q.; Xiang, L.; Cai, D.; Zeng, H.; Yi, H.; Ni, Z.; Chen, Y. Structure and properties of water film adsorbed on mica surfaces. J. Chem. Phys. 2015, 143, 104705. [Google Scholar] [CrossRef] [PubMed]
- Putman, C.A.J.; Igarashi, M.; Kaneko, R. Single-asperity friction in friction force microscopy: The composite-tip model. Appl. Phys. Lett. 1995, 66, 3221–3223. [Google Scholar] [CrossRef]
- Yu, J.; Chen, L.; Qian, L.; Song, D.; Cai, Y. Investigation of humidity-dependent nanotribology behaviors of Si(100)/SiO2 pair moving from stick to slip. Appl. Surf. Sci. 2013, 265, 192–200. [Google Scholar] [CrossRef]
- Guo, W.; Yin, J.; Qiu, H.; Guo, Y.; Wu, H.; Xue, M. Friction of low-dimensional nanomaterial systems. Friction 2014, 2, 209–225. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Li, Q.; Wang, X.; Li, J.; Zhang, S.; Kjems, J.; Besenbacher, F.; Dong, M. Evidence of Stranski–Krastanov growth at the initial stage of atmospheric water condensation. Nat. Commun. 2014, 5, 4837. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Ko, J.H.; Choi, J.S.; Hwang, J.H.; Kim, Y.H.; Salmeron, M.; Park, J.Y. Enhancement of friction by water intercalated between graphene and mica. J. Phys. Chem. Lett. 2017, 8, 3482–3487. [Google Scholar] [CrossRef]
- Lee, H.; Ko, J.H.; Song, H.C.; Salmeron, M.; Kim, Y.H.; Park, J.Y. Isotope- and thickness-dependent friction of water layers intercalated between graphene and mica. Tribol. Lett. 2018, 66, 36. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, H.; Suh, J.; Doh, W.H.; Baik, J.; Shin, H.J.; Ko, J.H.; Wu, J.; Kim, Y.H.; Park, J.Y. Nanoscale friction on confined water layers intercalated between MoS2 flakes and silica. J. Phys. Chem. C 2019, 123, 8827–8835. [Google Scholar] [CrossRef]
- Fisher, L.R.; Israelachvili, J.N. Direct measurement of the effect of meniscus forces on adhesion: A study of the applicability of macroscopic thermodynamics to microscopic liquid interfaces. Colloids Surf. 1981, 3, 303–319. [Google Scholar] [CrossRef]
- Chapel, J.P. Electrolyte species dependent hydration forces between silica surfaces. Langmuir 1994, 10, 4237–4243. [Google Scholar] [CrossRef]
- Donose, B.C.; Vakarelski, I.U.; Higashitani, K. Silica surfaces lubrication by hydrated cations adsorption from electrolyte solutions. Langmuir 2005, 21, 1834–1839. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Butt, H.J. Adhesion between solid surfaces in polymer melts: bridging of single chains. Macromolecules 2004, 37, 6086–6089. [Google Scholar] [CrossRef]
- Christenson, H.K.; Gruen, D.W.R.; Horn, R.G.; Israelachvili, J.N. Structuring in liquid alkanes between solid surfaces: Force measurements and mean-field theory. J. Chem. Phys. 1987, 87, 1834–1841. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Adhesion forces between surfaces in liquids and condensable vapours. Surf. Sci. Rep. 1992, 14, 109–159. [Google Scholar] [CrossRef]
- Palacio, M.; Bhushan, B. A review of ionic liquids for green molecular lubrication in nanotechnology. Tribol. Lett. 2010, 40, 247–268. [Google Scholar] [CrossRef]
- Xiao, C.; Li, J.; Chen, L.; Zhang, C.; Zhou, N.; Qian, L.; Luo, J. Speed dependence of liquid superlubricity stability with H3PO4 solution. RSC Adv. 2017, 7, 49337–49343. [Google Scholar] [CrossRef]
- Chen, L.; He, H.; Wang, X.; Kim, S.H.; Qian, L. Tribology of Si/SiO2 in humid air: Transition from severe chemical wear to wearless behavior at nanoscale. Langmuir 2015, 31, 149–156. [Google Scholar] [CrossRef]
- Xiao, C.; Guo, J.; Zhang, P.; Chen, C.; Chen, L.; Qian, L. Effect of crystal plane orientation on tribochemical removal of monocrystalline silicon. Sci. Rep. 2017, 7, 40750. [Google Scholar] [CrossRef] [Green Version]
- Xiao, C.; Xin, X.; He, X.; Wang, H.; Chen, L.; Kim, S.H.; Qian, L. Surface structure dependence of mechanochemical etching: scanning probe-based nanolithography study on Si(100), Si(110), and Si(111). ACS Appl. Mater. Interfaces 2019, 11, 20583–20588. [Google Scholar] [CrossRef]
- Gong, J.; Xiao, C.; Yu, J.; Peng, J.; Yu, B.; Chen, L.; Qian, L. Stress-enhanced dissolution and delamination wear of crystal CaF2 in water condition. Wear 2018, 418, 86–93. [Google Scholar] [CrossRef]
- Yu, J.; He, H.; Zhang, Y.; Hu, H. Nanoscale mechanochemical wear of phosphate laser glass against a CeO2 particle in humid air. Appl. Surf. Sci. 2017, 392, 523–530. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, C.; Guo, J.; Zhang, P.; Chen, L.; Qian, L. Threshold contact pressure for the material removal on monocrystalline silicon by SiO2 microsphere. Wear 2017, 376, 188–193. [Google Scholar] [CrossRef]
- Wen, J.; Ma, T.; Zhang, W.; Psofogiannakis, G.; Van Duin, A.C.; Chen, L.; Qian, L.; Hu, Y.; Lu, X. Atomic insight into tribochemical wear mechanism of silicon at the Si/SiO2 interface in aqueous environment: Molecular dynamics simulations using ReaxFF reactive force field. Appl. Surf. Sci. 2016, 390, 216–223. [Google Scholar] [CrossRef]
- Liu, Z.; Gong, J.; Xiao, C.; Shi, P.; Kim, S.H.; Chen, L.; Qian, L. Temperature-dependent mechanochemical wear of silicon in water: the role of Si-OH surfacial groups. Langmuir 2019, 35, 7735–7743. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Chen, L.; Jiang, S.; Yu, J.; Yu, B.; Xiao, C.; Qian, L. Investigation of silicon wear against non-porous and micro-porous SiO2 spheres in water and in humid air. RSC Adv. 2016, 6, 89627–89634. [Google Scholar] [CrossRef]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Shi, P.; Yan, W.; Chen, L.; Qian, L.; Kim, S.H. Thickness and Structure of Adsorbed Water Layer and Effects on Adhesion and Friction at Nanoasperity Contact. Colloids Interfaces 2019, 3, 55. https://doi.org/10.3390/colloids3030055
Xiao C, Shi P, Yan W, Chen L, Qian L, Kim SH. Thickness and Structure of Adsorbed Water Layer and Effects on Adhesion and Friction at Nanoasperity Contact. Colloids and Interfaces. 2019; 3(3):55. https://doi.org/10.3390/colloids3030055
Chicago/Turabian StyleXiao, Chen, Pengfei Shi, Wenmeng Yan, Lei Chen, Linmao Qian, and Seong H. Kim. 2019. "Thickness and Structure of Adsorbed Water Layer and Effects on Adhesion and Friction at Nanoasperity Contact" Colloids and Interfaces 3, no. 3: 55. https://doi.org/10.3390/colloids3030055
APA StyleXiao, C., Shi, P., Yan, W., Chen, L., Qian, L., & Kim, S. H. (2019). Thickness and Structure of Adsorbed Water Layer and Effects on Adhesion and Friction at Nanoasperity Contact. Colloids and Interfaces, 3(3), 55. https://doi.org/10.3390/colloids3030055





