An Efficient and Flexible Method for Deconvoluting Bulk RNA-Seq Data with Single-Cell RNA-Seq Data
Abstract
:1. Introduction
2. Methods and Materials
2.1. Model and Algorithm
2.2. Simulation Designs
2.3. Bulk RNA-Seq and scRNA-Seq Data for GBM
2.4. Bulk RNA-Seq and scRNA-Seq Data for CRC
2.5. Bulk RNA-Seq and scRNA-Seq Data for T2D
2.6. Software for Analyses
3. Results
3.1. Method Overview
3.2. Normalization Distorts Raw Expression Counts
3.3. Simulations
3.4. Human Glioblastoma (GBM) Data
3.5. Human Colorectal Cancer (CRC) Data
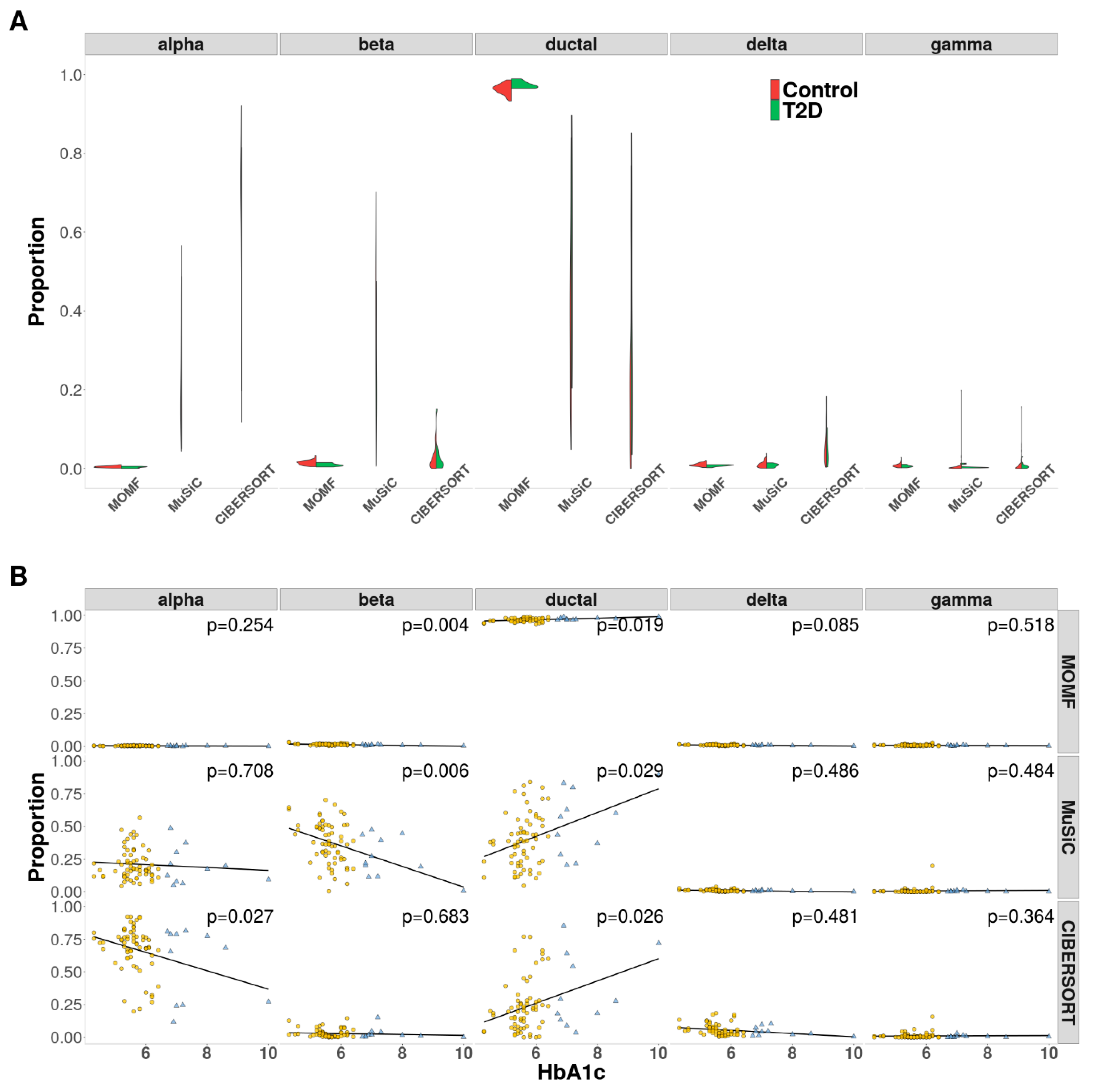
3.6. Human Type II Diabetes (T2D) Data
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Availability and Implementation
References
- Wagner, J.; Rapsomaniki, M.A.; Chevrier, S.; Anzeneder, T.; Langwieder, C.; Dykgers, A.; Rees, M.; Ramaswamy, A.; Muenst, S.; Soysal, S.D.; et al. A Single-Cell Atlas of the Tumor and Immune Ecosystem of Human Breast Cancer. Cell 2019, 177, 1330–1345.e1318. [Google Scholar] [CrossRef] [PubMed]
- Van Hove, H.; Martens, L.; Scheyltjens, I.; De Vlaminck, K.; Pombo Antunes, A.R.; De Prijck, S.; Vandamme, N.; De Schepper, S.; Van Isterdael, G.; Scott, C.L.; et al. A single-cell atlas of mouse brain macrophages reveals unique transcriptional identities shaped by ontogeny and tissue environment. Nat. Neurosci. 2019, 22, 1021–1035. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Guo, F.; Wang, L.; Zou, Q. Prediction of tumor metastasis from sequencing data in the era of genome sequencing. Brief. Funct. Genom. 2019. [Google Scholar] [CrossRef]
- Smolders, J.; Heutinck, K.M.; Fransen, N.L.; Remmerswaal, E.B.; Hombrink, P.; Ten Berge, I.J.; van Lier, R.A.; Huitinga, I.; Hamann, J. Tissue-resident memory T cells populate the human brain. Nat. Commun. 2018, 9, 4593. [Google Scholar] [CrossRef] [PubMed]
- Altschuler, S.J.; Wu, L.F. Cellular Heterogeneity: Do Differences Make a Difference? Cell 2010, 141, 559–563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, Y.; Guo, H.; Cao, C.; Li, X.; Hu, B.; Zhu, P.; Wu, X.; Wen, L.; Tang, F.; Huang, Y. Single-cell triple omics sequencing reveals genetic, epigenetic, and transcriptomic heterogeneity in hepatocellular carcinomas. Cell Res. 2016, 26, 304–319. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.M.; Mazutis, L.; Akartuna, I.; Tallapragada, N.; Veres, A.; Li, V.; Peshkin, L.; Weitz, D.A.; Kirschner, M.W. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 2015, 161, 1187–1201. [Google Scholar] [CrossRef]
- Hashimshony, T.; Senderovich, N.; Avital, G.; Klochendler, A.; de Leeuw, Y.; Anavy, L.; Gennert, D.; Li, S.; Livak, K.J.; Rozenblatt-Rosen, O. CEL-Seq2: Sensitive highly-multiplexed single-cell RNA-Seq. Genome Biol. 2016, 17, 77. [Google Scholar] [CrossRef]
- Ziegenhain, C.; Vieth, B.; Parekh, S.; Reinius, B.; Guillaumet-Adkins, A.; Smets, M.; Leonhardt, H.; Heyn, H.; Hellmann, I.; Enard, W. Comparative analysis of single-cell RNA sequencing methods. Mol. Cell 2017, 65, 631–643.e634. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.; Susztak, K.; Zhang, N.R.; Li, M. Bulk tissue cell type deconvolution with multi-subject single-cell expression reference. Nat. Commun. 2019, 10, 380. [Google Scholar] [CrossRef]
- Li, S.; Łabaj, P.P.; Zumbo, P.; Sykacek, P.; Shi, W.; Shi, L.; Phan, J.; Wu, P.-Y.; Wang, M.; Wang, C.; et al. Detecting and correcting systematic variation in large-scale RNA sequencing data. Nat. Biotechnol. 2014, 32, 888–895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lonsdale, J.; Thomas, J.; Salvatore, M.; Phillips, R.; Lo, E.; Shad, S.; Hasz, R.; Walters, G.; Garcia, F.; Young, N.; et al. The Genotype-Tissue Expression (GTEx) project. Nat. Genet. 2013, 45, 580–585. [Google Scholar] [CrossRef] [PubMed]
- Taliun, D.; Harris, D.N.; Kessler, M.D.; Carlson, J.; Szpiech, Z.A.; Torres, R.; Taliun, S.A.G.; Corvelo, A.; Gogarten, S.M.; Kang, H.M.; et al. Sequencing of 53,831 diverse genomes from the NHLBI TOPMed Program. bioRxiv 2019. [Google Scholar] [CrossRef]
- Baron, M.; Veres, A.; Wolock, S.L.; Faust, A.L.; Gaujoux, R.; Vetere, A.; Ryu, J.H.; Wagner, B.K.; Shen-Orr, S.S.; Klein, A.M.; et al. A Single-Cell Transcriptomic Map of the Human and Mouse Pancreas Reveals Inter- and Intra-cell Population Structure. Cell Syst. 2016, 3, 346–360.e344. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Zheng, S.C. Cell-type deconvolution in epigenome-wide association studies: A review and recommendations. Epigenomics 2017, 9, 757–768. [Google Scholar] [CrossRef]
- Mohammadi, S.; Zuckerman, N.; Goldsmith, A.; Grama, A. A critical survey of deconvolution methods for separating cell types in complex tissues. Proc. IEEE 2016, 105, 340–366. [Google Scholar] [CrossRef]
- Zuckerman, N.S.; Noam, Y.; Goldsmith, A.J.; Lee, P.P. A Self-Directed Method for Cell-Type Identification and Separation of Gene Expression Microarrays. PLoS Comput. Biol. 2013, 9, e1003189. [Google Scholar] [CrossRef]
- Roy, S.; Lane, D.T.; Allen, C.; Aragon, A.D.; Werner-Washburne, M. A Hidden-State Markov Model for Cell Population Deconvolution. J. Comput. Biol. 2006, 13, 1749–1774. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Y.; Kuang, Q.; Xie, F.; Hao, Y.; Wen, Z.; Li, M. Post-modified non-negative matrix factorization for deconvoluting the gene expression profiles of specific cell types from heterogeneous clinical samples based on RNA-sequencing data. J. Chemom. 2018, 32, e2929. [Google Scholar] [CrossRef]
- Wang, N.; Hoffman, E.P.; Chen, L.; Chen, L.; Zhang, Z.; Liu, C.; Yu, G.; Herrington, D.M.; Clarke, R.; Wang, Y. Mathematical modelling of transcriptional heterogeneity identifies novel markers and subpopulations in complex tissues. Sci. Rep. 2016, 6, 18909. [Google Scholar] [CrossRef]
- Li, B.; Severson, E.; Pignon, J.-C.; Zhao, H.; Li, T.; Novak, J.; Jiang, P.; Shen, H.; Aster, J.C.; Rodig, S.; et al. Comprehensive analyses of tumor immunity: Implications for cancer immunotherapy. Genome Biol. 2016, 17, 174. [Google Scholar] [CrossRef] [PubMed]
- Pollara, G.; Murray, M.J.; Heather, J.M.; Byng-Maddick, R.; Guppy, N.; Ellis, M.; Turner, C.T.; Chain, B.M.; Noursadeghi, M. Validation of Immune Cell Modules in Multicellular Transcriptomic Data. PLoS ONE 2017, 12, e0169271. [Google Scholar] [CrossRef] [PubMed]
- Finotello, F.; Mayer, C.; Plattner, C.; Laschober, G.; Rieder, D.; Hackl, H.; Krogsdam, A.; Loncova, Z.; Posch, W.; Wilflingseder, D.; et al. Molecular and pharmacological modulators of the tumor immune contexture revealed by deconvolution of RNA-seq data. Genome Med. 2019, 11, 34. [Google Scholar] [CrossRef] [PubMed]
- Gong, T.; Szustakowski, J.D. DeconRNASeq: A statistical framework for deconvolution of heterogeneous tissue samples based on mRNA-Seq data. Bioinformatics 2013, 29, 1083–1085. [Google Scholar] [CrossRef] [PubMed]
- Frishberg, A.; Steuerman, Y.; Gat-Viks, I. CoD: Inferring immune-cell quantities related to disease states. Bioinformatics 2015, 31, 3961–3969. [Google Scholar] [CrossRef] [PubMed]
- Newman, A.M.; Liu, C.L.; Green, M.R.; Gentles, A.J.; Feng, W.; Xu, Y.; Hoang, C.D.; Diehn, M.; Alizadeh, A.A. Robust enumeration of cell subsets from tissue expression profiles. Nat. Methods 2015, 12, 453–457. [Google Scholar] [CrossRef] [Green Version]
- Risso, D.; Perraudeau, F.; Gribkova, S.; Dudoit, S.; Vert, J.-P. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun. 2018, 9, 284. [Google Scholar] [CrossRef]
- Sun, S.; Hood, M.; Scott, L.; Peng, Q.; Mukherjee, S.; Tung, J.; Zhou, X. Differential expression analysis for RNAseq using Poisson mixed models. Nucleic Acids Res. 2017, 45, e106. [Google Scholar] [CrossRef]
- Amrhein, L.; Harsha, K.; Fuchs, C. A mechanistic model for the negative binomial distribution of single-cell mRNA counts. bioRxiv 2019. [Google Scholar] [CrossRef]
- Sun, S.; Zhu, J.; Mozaffari, S.; Ober, C.; Chen, M.; Zhou, X. Heritability estimation and differential analysis of count data with generalized linear mixed models in genomic sequencing studies. Bioinformatics 2019, 35, 487–496. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Li, H.; Courtois, E.T.; Sengupta, D.; Tan, Y.; Chen, K.H.; Goh, J.J.L.; Kong, S.L.; Chua, C.; Hon, L.K.; Tan, W.S. Reference component analysis of single-cell transcriptomes elucidates cellular heterogeneity in human colorectal tumors. Nat. Genet. 2017, 49, 708–718. [Google Scholar] [CrossRef] [PubMed]
- Maza, E.; Frasse, P.; Senin, P.; Bouzayen, M.; Zouine, M. Comparison of normalization methods for differential gene expression analysis in RNA-Seq experiments: A matter of relative size of studied transcriptomes. Commun. Integr. Biol. 2013, 6, e25849. [Google Scholar] [CrossRef] [PubMed]
- Cole, M.B.; Risso, D.; Wagner, A.; DeTomaso, D.; Ngai, J.; Purdom, E.; Dudoit, S.; Yosef, N. Performance Assessment and Selection of Normalization Procedures for Single-Cell RNA-Seq. Cell Syst. 2019, 8, 315–328. [Google Scholar] [CrossRef]
- Ding, B.; Zheng, L.; Wang, W. Assessment of Single Cell RNA-Seq Normalization Methods. G3 Genes Genomes Genet. 2017, 7, 2039–2045. [Google Scholar] [CrossRef] [Green Version]
- Vallejos, C.A.; Risso, D.; Scialdone, A.; Dudoit, S.; Marioni, J.C. Normalizing single-cell RNA sequencing data: Challenges and opportunities. Nat. Methods 2017, 14, 565–571. [Google Scholar] [CrossRef]
- Anders, S.; Huber, W. Differential expression analysis for sequence count data. Genome Biol. 2010, 11, R106. [Google Scholar] [CrossRef]
- Townes, F.W.; Hicks, S.C.; Aryee, M.J.; Irizarry, R.A. Feature Selection and Dimension Reduction for Single Cell RNA-Seq based on a Multinomial Model. bioRxiv 2019. [Google Scholar] [CrossRef]
- Llaguno, S.R.A.; Wang, Z.; Sun, D.; Chen, J.; Xu, J.; Kim, E.; Hatanpaa, K.J.; Raisanen, J.M.; Burns, D.K.; Johnson, J.E. Adult lineage-restricted CNS progenitors specify distinct glioblastoma subtypes. Cancer Cell 2015, 28, 429–440. [Google Scholar]
- Lindberg, N.; Kastemar, M.; Olofsson, T.; Smits, A.; Uhrbom, L. Oligodendrocyte progenitor cells can act as cell of origin for experimental glioma. Oncogene 2009, 28, 2266–2275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, X.; Curtin, J.; Xiong, Y.; Liu, G.; Waschsmann-Hogiu, S.; Farkas, D.L.; Black, K.L.; Yu, J.S. Isolation of cancer stem cells from adult glioblastoma multiforme. Oncogene 2004, 23, 9392–9400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takano, S. Glioblastoma angiogenesis: VEGF resistance solutions and new strategies based on molecular mechanisms of tumor vessel formation. Brain Tumor Pathol. 2012, 29, 73–86. [Google Scholar] [CrossRef] [PubMed]
- The Cancer Genome Atlas Research Network; McLendon, R.; Friedman, A.; Bigner, D.; Van Meir, E.G.; Brat, D.J.M.; Mastrogianakis, G.; Olson, J.J.; Mikkelsen, T.; Lehman, N.; et al. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature 2008, 455, 1061–1068. [Google Scholar] [CrossRef]
- Darmanis, S.; Sloan, S.A.; Zhang, Y.; Enge, M.; Caneda, C.; Shuer, L.M.; Gephart, M.G.H.; Barres, B.A.; Quake, S.R. A survey of human brain transcriptome diversity at the single cell level. Proc. Natl. Acad. Sci. USA 2015, 112, 7285–7290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zong, H.; Verhaak, R.G.W.; Canoll, P. The cellular origin for malignant glioma and prospects for clinical advancements. Expert Rev. Mol. Diagn. 2012, 12, 383–394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ricci-Vitiani, L.; Pallini, R.; Biffoni, M.; Todaro, M.; Invernici, G.; Cenci, T.; Maira, G.; Parati, E.A.; Stassi, G.; Larocca, L.M.; et al. Tumour vascularization via endothelial differentiation of glioblastoma stem-like cells. Nature 2010, 468, 824–828. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Chadalavada, K.; Wilshire, J.; Kowalik, U.; Hovinga, K.E.; Geber, A.; Fligelman, B.; Leversha, M.; Brennan, C.; Tabar, V. Glioblastoma stem-like cells give rise to tumour endothelium. Nature 2010, 468, 829–833. [Google Scholar] [CrossRef]
- The Cancer Genome Atlas Network; Muzny, D.M.; Bainbridge, M.N.; Chang, K.; Dinh, H.H.; Drummond, J.A.; Fowler, G.; Kovar, C.L.; Lewis, L.R.; Morgan, M.B.; et al. Comprehensive molecular characterization of human colon and rectal cancer. Nature 2012, 487, 330–337. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Qi, F.; Zhao, F.; Li, G.; Shao, S.; Zhang, X.; Yuan, L.; Feng, Y. Cancer-associated fibroblasts enhance tumor-associated macrophages enrichment and suppress NK cells function in colorectal cancer. Cell Death Dis. 2019, 10, 273. [Google Scholar] [CrossRef]
- Engblom, C.; Pfirschke, C.; Pittet, M.J. The role of myeloid cells in cancer therapies. Nat. Rev. Cancer 2016, 16, 447–462. [Google Scholar] [CrossRef] [PubMed]
- Ootani, A.; Li, X.; Sangiorgi, E.; Ho, Q.T.; Ueno, H.; Toda, S.; Sugihara, H.; Fujimoto, K.; Weissman, I.L.; Capecchi, M.R.; et al. Sustained in vitro intestinal epithelial culture within a Wnt-dependent stem cell niche. Nat. Med. 2009, 15, 701–706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Butler, A.; Galasso, R.; Matveyenko, A.; Rizza, R.; Dry, S.; Butler, P. Pancreatic duct replication is increased with obesity and type 2 diabetes in humans. Diabetologia 2010, 53, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Segerstolpe, Å.; Palasantza, A.; Eliasson, P.; Andersson, E.-M.; Andréasson, A.-C.; Sun, X.; Picelli, S.; Sabirsh, A.; Clausen, M.; Bjursell, M.K.; et al. Single-Cell Transcriptome Profiling of Human Pancreatic Islets in Health and Type 2 Diabetes. Cell Metab. 2016, 24, 593–607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, S.; Sun, X.; Zheng, Y. Higher-order partial least squares for predicting gene expression levels from chromatin states. BMC Bioinform. 2018, 19, 113. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Xing, F.; Wang, C.; Zeng, X.; Zou, Q. Investigation and development of maize fused network analysis with multi-omics. Plant Physiol. Biochem. 2019, 141, 380–387. [Google Scholar] [CrossRef]
- Sun, S.; Chen, Y.; Liu, Y.; Shang, X. A fast and efficient count-based matrix factorization method for detecting cell types from single-cell RNAseq data. BMC Syst. Biol. 2019, 13, 28. [Google Scholar] [CrossRef]
- Butler, A.; Hoffman, P.; Smibert, P.; Papalexi, E.; Satija, R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 2018, 36, 411–420. [Google Scholar] [CrossRef]




| Variables | COAD (N = 435) | READ (N = 155) | p |
|---|---|---|---|
| Age (years), mean ± SD | 67.30 ± 12.97 | 65.33 ± 11.49 | 0.089 |
| Gender, n (%) | 0.680 | ||
| Female | 202 (46.43) | 69 (44.52) | |
| Male | 233 (53.56) | 86 (55.48) | |
| Tumor stage (%) | 0.166 | ||
| 0-I | 240 (55.17) | 76 (49.68) | |
| II-IV | 184 (42.30) | 71 (45.81) | |
| Unknown | 11 (2.53) | 8 (5.16) | |
| Race (%) | 7.25 × 10−4 | ||
| White | 207 (45.59) | 77 (47.59) | |
| Non-white | 70 (41.08) | 6 (6.5) | |
| Unknown | 158 (13.33) | 71 (45.81) | |
| Survival year (month) | |||
| Median | 2532 | 1741 | 0.3 |
| Dead, n (%) | 97 (22.23) | 25 (16.13) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Sun, S.; Yang, S. An Efficient and Flexible Method for Deconvoluting Bulk RNA-Seq Data with Single-Cell RNA-Seq Data. Cells 2019, 8, 1161. https://doi.org/10.3390/cells8101161
Sun X, Sun S, Yang S. An Efficient and Flexible Method for Deconvoluting Bulk RNA-Seq Data with Single-Cell RNA-Seq Data. Cells. 2019; 8(10):1161. https://doi.org/10.3390/cells8101161
Chicago/Turabian StyleSun, Xifang, Shiquan Sun, and Sheng Yang. 2019. "An Efficient and Flexible Method for Deconvoluting Bulk RNA-Seq Data with Single-Cell RNA-Seq Data" Cells 8, no. 10: 1161. https://doi.org/10.3390/cells8101161
APA StyleSun, X., Sun, S., & Yang, S. (2019). An Efficient and Flexible Method for Deconvoluting Bulk RNA-Seq Data with Single-Cell RNA-Seq Data. Cells, 8(10), 1161. https://doi.org/10.3390/cells8101161






