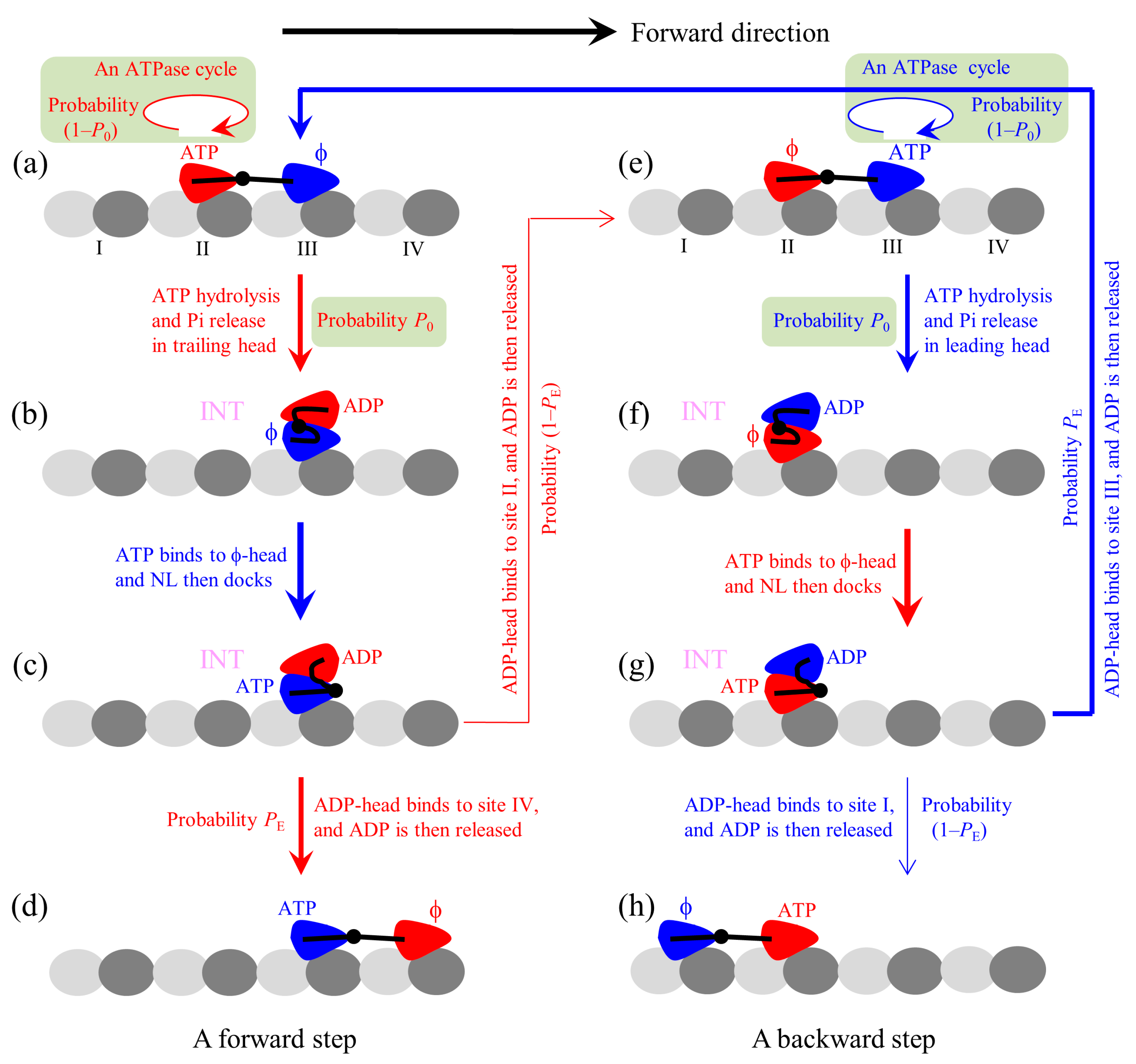
2.1. The Model
We first describe the model for the chemomechanical coupling pathway of kinesin dimer, based on which our theoretical analyses are made. The model is built up on the basis of the following three pieces of experimental and computational evidence and/or arguments.
(1) A kinesin head in nucleotide-free (
), ATP, or ADP.Pi state binds strongly to MT whereas in ADP state binds weakly to MT, as experimental data showed [
41,
42,
43,
44,
45]. Additionally, immediately after Pi release there is a very short time period
tr (in the order of μs) when the ADP-head has a lower affinity to the local binding site (denoted by
Ew1) on MT than that to other binding sites (denoted by
Ew2), as all-atom molecular dynamics (MD) simulations indicated [
46]. This can be understood as follows [
46,
47]. The large conformational changes in the local MT tubulin induced by the strong interaction with
-, ATP- or ADP.Pi-head [
48] result in the local tubulin having a further weaker interaction with the ADP-head than other unperturbed tubulins. As the weak interaction between the ADP-head and MT can hardly induce the conformational change of the MT-tubulin [
46], in the time
tr after Pi release from the MT-bound ADP.Pi head the local MT-tubulin returns to the normally unchanged conformation, with the binding energy of the local MT-tubulin to the ADP-head becoming the same as other tubulins.
(2) When an MT-bound head is in ATP or ADP.Pi state, its NL can dock into its motor domain whereas in
or ADP state its NL cannot dock [
49,
50]. Structural analyses showed that the NL docking involves NL strand
forming a cover-neck bundle with strand
of the motor domain [
22,
51], which can occur when the two strands are in proximity.
(3) An interaction exists between the MT-bound head and detached ADP-head. When the MT-bound head is in ADP or
state, with undocked NL, the two heads have a high binding energy, while when the MT-bound head is in ATP or ADP.Pi state, with docked NL, the binding energy is reduced greatly, as recent all-atom MD simulations indicated (see
Figure S1 in Supplementary Information, which is reproduced from Shi et al., to be published in Proteins).
The proposed chemomechanical coupling pathway at low ATP is schematically illustrated in
Figure 1. We begin with the trailing head in ATP state binding strongly to binding site II on MT while the leading head in
state binding strongly to site III (
Figure 1a). After an ATPase activity (ATP hydrolysis and Pi release) taking place in the trailing head, the ADP-head has a low affinity (
Ew1) to the local site II for a very short time period
tr in the order of μs. During
tr, it is most probable (with a probability
P0) that the ADP-head escapes from the potential well of depth
Ew1 and then diffuses to the intermediate (INT) position relative to the MT-bound head, where the two heads have a high binding energy (
Figure 1b). If the ADP-head has not escaped from the potential well of depth
Ew1 within
tr (with probability 1–
P0), after the depth of the potential well changes to
Ew2 the ADP-head is almost unable to escape from the potential well until ADP is released. Then, ATP binding, ATP hydrolysis, and Pi release take place in the trailing head (the transition shaded in light green). The trailing ADP-head then diffuses to the INT position with probability
P0 (
Figure 1b), as just mentioned above. This INT (or one-head-bound) state (
Figure 1b) is consistent with the available cryo-EM image [
52] and recent all-atom MD simulations (Shi et al., to be published in
Proteins) showing that one head in
state binds to MT and the other head is in the above position of the MT-bound head. After ATP binding to the MT-bound head, NL docking takes place, weakening the interaction between the two heads (
Figure 1c). Then, by overcoming the weak binding energy (
EI) between the two heads and the energy change (
) arising from the stretching of the NLs, the ADP-head (with a probability
PE) diffuses to and binds to the nearest front binding site IV on MT with affinity
Ew2, and ADP is released (
Figure 1d). From
Figure 1a to b to c to d, a forward step was made by hydrolyzing an ATP molecule. From
Figure 1c, it is also possible (with probability 1–
PE) that by overcoming
EI, NL-docking energy (
ED) of the MT-bound head and
, the ADP-head diffuses to and binds to the previous site II with affinity
Ew2 (noting that after Pi release the binding energy of site II for ADP-head changes rapidly from
Ew1 to
Ew2 in time
tr in the order of μs), and ADP is released (
Figure 1e). The transition (from
Figure 1a to b to c to e) gives a futile chemomechanical coupling cycle.
In
Figure 1e after the ATPase activity (ATP hydrolysis and then Pi release) taking place in the leading head, there are also two possible cases that can occur. There is a probability 1–
P0 that the head still binds to site III but an ATPase cycle (consisting of ADP release, ATP binding, ATP hydrolysis, and then Pi release) takes place (the transition shaded in light green). There is also a probability
P0 that the ADP-head diffuses to the INT position (
Figure 1f). ATP binding to the MT-bound head induces its NL docking, weakening its interaction with the ADP-head (
Figure 1g). Then, by overcoming
EI and
the ADP-head rebinds to the previous site III with affinity
Ew2, and releases ADP (
Figure 1a). The transition (from
Figure 1e to f to g to a) gives a futile chemomechanical coupling cycle. From
Figure 1g, it is also possible that by overcoming
EI,
ED, and
the ADP-head diffuses to and binds to site I with affinity
Ew2, and releases ADP (
Figure 1h). The transition (from
Figure 1e to f to g to h) gives a backward step by hydrolyzing one ATP molecule. Because the transitions of
Figure 1g to a and to h overcome the same energy barriers as the transitions of
Figure 1c to d and to e, respectively, the transition from
Figure 1g to a and that from
Figure 1c to d occur with the same probability
PE and the transition from
Figure 1g to h and that from
Figure 1c to e occur with the same probability 1–
PE.
It should be noted that besides the above-mentioned transitions, other possible transitions can also occur, which are not drawn in
Figure 1. For example, in
Figure 1e before ATP hydrolysis occurs in the leading head ATP can bind to the trailing head, becoming the state with both heads bound by ATP. Similarly, in
Figure 1a before ATP hydrolysis occurs in the trailing head ATP can bind to the leading head, also becoming the state with both heads bound by ATP. From the state with both heads in ATP state, if the ATPase activity (ATP hydrolysis and then Pi release) takes place in the trailing head the system becomes the state of
Figure 1c with probability
P0, while if the ATPase activity takes place in the leading head the system becomes the state of
Figure 1g with probability
P0.
As all-atom MD simulations showed [
39,
40,
53], for WT kinesin-1 with the NL of each head having 14 residues, when the two heads are bound to two successive binding sites on an MT filament that are 8.2-nm apart the internally stretched force on the NLs has a large value (about 30 pN). Driven by the large internally stretched force and the thermal noise, the ADP-head can escape from the potential well of depth
Ew1 within the time period
tr with nearly 100% probability [
39,
40]. Thus, for a good approximation, we take
P0 = 1. That is, the transitions shaded in light green cannot occur, with the pathway becoming identical to that presented before [
38]. By contrast, for mutant kinesin-1 with each NL being extended by six residues, when the two heads are bound to two successive binding sites on an MT filament that are 8.2-nm apart the internally stretched force in the NLs is nearly zero [
39,
40]. Thus, after Pi release, the ADP-head may not escape from the potential well of depth
Ew1 within the time period
tr with 100% probability, i.e., with
P0 < 1.
As done in the single-molecule optical trapping assays [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26], we consider a bead attached to the coiled-coil stalk that connects the NLs of the two heads and an external force,
F, acting on the bead. The force
F is defined to be positive when pointing backward. The available experimental data showed that extending the NLs of the kinesin-1 dimer by any length via inserting additional residues into the NLs has nearly no effect on the ATPase rate of the dimer during its processive movement on MT [
27]. Since changing the length of the NLs changes the strain on the NLs when the two heads are bound to MT, the experimental data thus imply that the strain on the NL has no effect on the ATPase rate (at least the rate constants of the rate-limiting steps of the ATPase activity such as ATP hydrolysis and Pi release) of the kinesin head. Consequently, we propose that changing the NL length has no effect on the ATPase rate, and the external force
F, which affects the strain on the NL, also has no effect on the ATPase rate. However, the orientation direction of the NL has an effect on the ATPase rate: the trailing head with the forward NL orientation has a much higher ATPase rate than the leading head with the backward NL orientation. This can be understood as follows. The NL with the forward orientation can interact with the head and the interaction enhances the ATPase rate, and by contrast, the NL with the backward orientation has no interaction with the head. This is consistent with the experimental data showing that by deleting the NL, equivalent to removing the interaction of the NL with the head, the ATPase rate is reduced greatly [
54].
2.2. The Simplified Model at Saturating ATP
At saturating ATP, the chemomechanical coupling pathway shown in
Figure 1 can be simplified to that shown in
Figure 2a–f. We begin with both heads in ATP state binding strongly to MT (
Figure 2a).
First, consider an ATPase activity (ATP hydrolysis and then Pi release) taking place in the trailing head. Then, two possible cases can occur, as discussed above. One case, with probability 1–
P0, is that the head still binds to site II but an ATPase cycle (consisting of ADP release, ATP binding, ATP hydrolysis and Pi release) takes place in the head (the transition shaded in light green). Another case, with probability
P0, is that the ADP-head diffuses to the INT position relative to the MT-bound head (
Figure 2b). In the INT state, with the MT-bound head in ATP state, NL docking takes place, weakening the interaction between the two heads (
Figure 2c). Then, the ADP-head (with probability
PE) diffuses to and binds to the nearest front site IV with affinity
Ew2, and ADP is released, which is followed immediately by ATP binding (
Figure 2d). From
Figure 2a to d, a forward step was made by hydrolyzing an ATP molecule. From
Figure 2c, it is also possible (with probability 1–
PE) that the ADP-head diffuses to and binds to the previous site II with affinity
Ew2, and ADP is released, which is followed immediately by ATP binding (
Figure 2a). The transition (from
Figure 2a to c and then returning to a) gives a futile chemomechanical coupling cycle.
Second, consider in
Figure 2a an ATPase activity (ATP hydrolysis and then Pi release) taking place in the leading head. Two possible cases can occur. One case, with probability 1–
P0, is that the head still binds to site III but an ATPase cycle (consisting of ADP release, ATP binding, ATP hydrolysis and Pi release) takes place in the head (the transition shaded in light green). Another case, with probability
P0, is that the ADP-head diffuses to the INT position (
Figure 2e). After the binding affinity of site III for ADP-head changes rapidly back to
Ew2 in time
tr, the detached ADP-head rebinds to site III, with probability
PE, and ADP is released, followed immediately by ATP binding (
Figure 2a). The transition (from
Figure 2a to e and then returning to a) gives a futile chemomechanical coupling cycle. From
Figure 2e, it is also possible that the ADP-head diffuses to and binds to site I with affinity
Ew2, with probability 1–
PE, and ADP is released, followed immediately by ATP binding (
Figure 2f). The transition (from
Figure 2a to e to f) gives a backward step by hydrolyzing an ATP molecule.
The pathway (
Figure 2a–f) can be simply described as follows. We denote by
k(+) and
k(−) the rate constants of ATP hydrolysis and Pi release in the trailing and leading heads at saturating ATP, respectively. Considering that the step of ATP hydrolysis and Pi release is rate limiting in the ATPase activity at saturating ATP, it is approximate that
k(+) and
k(−) are ATPase rates of the trailing and leading heads, respectively. Since under physiological conditions an ATP hydrolysis gives free energy
20
kBT and
k(+) and
k(−) are constants independent of the NL strain and external force (see above), it is a good approximation to consider the transitions of the ATPase activity to be irreversible under any external force, i.e., to ignore the reverse transitions of the ATPase activity. Since in the INT state with the MT-head bound with ATP (
Figure 2b) its NL docks rapidly [
55], we approximate that the NL docking occurs immediately. Thus, during processive movement of the dimer the total ATPase rate is
k(+) +
k(−), a constant independent of the NL length and external force, which is consistent with the available experimental data [
27]. When an ATPase activity with rate constant
k(+) takes place, the motor either takes a forward step with probability
P0PE or does not move with probability (1–
P0) +
P0(1–
PE). When an ATPase activity with rate constant
k(−) takes place, the motor either takes a backward step with probability
P0(1–
PE) or does not move with probability (1–
P0) +
P0PE. Since after detaching from MT the time for the ADP-head to diffuse from the binding site on MT to INT position and the time for the ADP-head to diffuse from the INT position to binding site on MT are much shorter than the inverse of the ATPase rates [
39], for a good approximation, the velocity of the motor is determined solely by the ATPase rates of the two heads. Hence, the overall forward stepping rate of the motor is
P0PEk(+), backward stepping rate is
P0(1–
PE)
k(−), and ATPase rate with no stepping is
ω0 = [(1–
P0) +
P0(1–
PE)]
k(+) + [(1–
P0) +
P0PE]
k(−), as schematically shown in
Figure 2g.
2.3. Dynamics of WT Kinesin-1 at Saturating ATP
For the case of WT kinesin dimer,
P0 = 1 (see above) and the transitions shaded in light green in
Figure 2 can be excluded, as studied in the previous work [
38]. Since NL is flexible it is reasonable to consider that when only one head is bound to MT the interaction between the attached bead and kinesin dimer acts only on the NL of the head having a larger distance to the bead. Thus, when only one head is bound to MT, the backward external force (
F > 0) acts only on the NL of the head in the leading position and the forward external force (
F < 0) acts only on the NL of the head in the trailing position. As a result, after the trailing head detaches from site II,
F > 0 has no effect on its movement to the INT position and
F < 0 facilitates its movement to the INT position, giving the transition from
Figure 2a to b with 100% probability for any
F. After the leading head detaches from site III,
F > 0 facilitates its movement to the INT position and
F < 0 has no effect on its movement to the INT position, giving the transition from
Figure 2a to e with 100% probability for any
F. When
F > 0 the force dependence of the rate for the detached ADP-head to move from the INT position to the front binding site on MT has the form
and the rate for the detached ADP-head to move from the INT position to the rear binding site on MT has the form
(see
Section S1 in Supplementary Information). Here,
C1 is a constant independent of
F,
, with
kB being the Boltzmann constant and
T the absolute temperature,
d(+) is the characteristic distance for the movement of the detached ADP-head from the INT position to the front binding site on MT, and
ED is the NL-docking energy and. Throughout we consider room temperature (
T = 298 K) unless otherwise pointed out.
With
kF and
kR, probability
PE can be calculated by
=
. Hence, the force dependence of the stepping ratio (defined as the ratio of the number of forward steps to that of backward steps) of the motor can be calculated by
r =
=
=
, where
r0 =
is the stepping ratio under no external force and
is independent of
F. Similarly, when
F < 0 the force dependence of the stepping ratio has the form,
, where
is independent of
F, with
d(−) being the characteristic distance for the movement of the detached ADP-head from the INT position to the rear binding site on MT. For approximation,
and
. Therefore, for both
F > 0 and
F < 0, the force dependence of the stepping ratio can be re-expressed as
where
is the stall force, at which
r = 1, and
ED is the NL-docking energy (see above). Using Equation (1) and relation
, probability
PE can be re-expressed as
From
Figure 2g with
P0 = 1, the velocity of the motor can be expressed as
where
d = 8.2 nm is the step size equal to the period of the MT filament. Substituting Equation (3) into Equation (4) we obtain
We then derive the equation for mean dwell time between two mechanical steps. If
n (
n > 0 is an integer) ATP molecules are hydrolyzed for the motor to make a mechanical step (either a forward or backward step), the dwell time before stepping is
. The probability for the motor to make a mechanical step after hydrolyzing
n ATP molecules can be expressed as
. Hence, the mean dwell time between two mechanical steps can be calculated by
Equation (6) can be reduced as
, which with Equation (3) can be re-expressed as
Using Equations (1), (5), and (7), the available single-molecule data on the force dependence of stepping ratio, velocity and dwell time at saturating ATP for WT kinesin-1 dimers can be reproduced quantitatively with only four adjustable parameters,
r0,
FS,
k(+) and
k(−). Each parameter has a clear physical meaning:
r0 is the stepping ratio under no external force,
FS is the stall force, and
k(+) and
k(−) are the ATPase rates of the trailing and leading heads, respectively. Using Equation (1) and taking
r0 = 900 and
FS = 7 pN, the single-molecule data of Carter and Cross [
23] on the force dependence of stepping ratio for
Drosophila kinesin (abbreviated as DmK) at saturating ATP (1 mM) can be reproduced (
Figure 3a). Adjusting
r0 = 220 and
FS = 7.6 pN, the single-molecule data of Nishiyama et al. [
20] on the force dependence of stepping ratio for bovine brain kinesin (abbreviated as Bovine) at saturating ATP (1 mM) can be reproduced (
Figure 3b). Using Equation (5), the single-molecule data of Andreasson et al. [
24] on the force dependence of velocity for DmK at saturating ATP (2 mM) can be fitted well by adjusting
r0 = 890,
FS = 8 pN,
k(+) = 95
and
k(−) = 3
(see
Table 1,
Figure 3c). Note here that
r0 = 890 is close to that used in
Figure 3a for DmK, and
FS = 8 pN is slightly larger than that used in
Figure 3a. The slight difference of
FS could be due to different buffer conditions in different experiments [
23,
24]. With
r0 = 220 and
FS = 7.6 pN (see
Figure 3b) and adjusting
k(+) = 138
and
k(−) = 3
(see
Table 1), the single-molecule data of Nishiyama et al. [
20] on the force dependence of velocity for Bovine at saturating ATP (1 mM) can be fitted well (
Figure 3d). Using Equation (7) and with parameter values given in
Table 1 for DmK, the theoretical results of dwell time versus force are shown in
Figure 3e. Using Equation (7) and with parameter values given in
Table 1 for Bovine, the theoretical results of dwell time versus force are in agreement with the single-molecule data of Nishiyama et al. [
20] at saturating ATP (1 mM) (
Figure 3f).
More interestingly, with above fitted parameter values and Equation (2) we can determine the NL-docking energy
ED and compare with the available experimental data [
56]. With
r0 = 890
120,
k(+) = 95
1
and
k(−) = 3
0.4
for DmK (see
Table 1), we obtain
ED = (3.34
0.28)
kBT. Here, from Equation (2), the error of
ED is calculated with
=
=
, where
,
and
represent errors of
r0,
k(−) and
k(+), respectively. With
r0 = 220
68,
k(+) = 138
20
and
k(−) = 3
1.1
for Bovine (see
Table 1), we obtain
ED = (1.56
0.82)
kBT. These small values of
ED = (3.34
0.28)
kBT and (1.56
0.82)
kBT are close to the available experimental data showing that the free energy change associated with the NL docking is only about (1 — 2)
kBT [
56]. It is noted that in the prevailing models presented in the literature proposing that the NL docking drives the forward movement of the ADP-head, a persistent problem is that the small NL-docking energy of (1 — 2)
kBT is only about 10% of the energy required to generate an 8.2-nm step against a load of 7 — 8 pN [
57,
58]. Here, with our model proposing that the NL docking provides an energy barrier to prevent the detached ADP-head in the INT position from moving backward and the ATPase rates of the two heads are independent of
F, this puzzling issue can be understandable easily. In addition, from the fitted curve in
Figure 3a we have
d(+) = 4 nm, which is understandable easily by considering that
d(+) should be smaller than or about half of
d = 8.2 nm. By contrast, with the prevailing models presented in the literature proposing that the force dependence of velocity is determined by the force dependence of ATPase rate, it is puzzling why the related characteristic distance is only about half of the movement distance of the motor in one step [
28].
In addition, other available single-molecule data, such as those on the dependence of the forward stepping rate, backward stepping rate and dwell time upon backward force (
F > 0) and temperature (
T) at saturating ATP [
59], can also be reproduced quantitatively (
Figure 4, see
Section S2 in Supplementary Information for related equations). As shown in
Table S1 (see
Supplementary Information), only four parameters are adjusted to fit all the single-molecule data (10 curves) shown in
Figure 4. Interestingly, the fitted value of
ED = 0.4 pN nm (see
Table S1) implies that the free energy change of NL docking is very small, also consistent with the experimental result [
56]. The analytical result of the stall force being independent of temperature (see
Equation (S15) in Section S2) is also in agreement with the available single-molecule data [
60].
It is mentioned that in the calculation here, we use the step size of a constant value of
d = 8.2 nm, which is equal to the periodicity of an MT filament. However, from the published experimental results, the step size fluctuated in a range of ±2 nm. The fluctuations of the step size could be due to the large fluctuations of the position of the attached bead which was detected in the experiments. Another point to note here is that for simplicity of analysis, we have not considered the effect of the length of the coiled-coil stalk on kinesin movement. With a model system simulating complex of kinesin dimer and MT, it was demonstrated that the interaction between the stalk and MT provides the force to drive the motion of the motor [
61]. Using single-molecule optical trapping, Asbury et al. [
21] found that WT kinesin-1 homodimer moves in an asymmetric hand-over-hand manner (called limping), and the length of the stalk affects the limping character. Although the effect of the stalk length on the limping effect of kinesin homodimers has been studied numerically based on our model (
Figure 2) [
40], it is interesting to have an analytical study on the effect of the stalk length on the kinesin movement, which will be studied in the future.
2.4. Dynamics of Kinesin-1 with Extended NLs at Saturating ATP
In the above section, we studied analytically the dynamics of WT kinesin-1 dimer, with
P0 = 1. In this section, we will study analytically the dynamics of mutant kinesin-1 dimer of extended NLs. For example, we consider that the NL is extended by inserting six additional residues AEQKLT into the C-terminal portion of the NL region of each head, as done in Clancy et al. [
26]. As all-atom MD simulations showed [
39,
40], for the mutant kinesin dimer with the extended NLs, when the two heads are bound to two successive binding sites on an MT filament the internally stretched force between the NLs is nearly equal to zero. Thus, after Pi release the ADP-head may not escape from the potential well of depth
Ew1 within the time period
tr with 100% probability, implying
P0 < 1 under no external force. In addition, since the NL is flexible and the internally stretched force is nearly equal to zero, the backward external force
F (> 0) acts only on the leading head while the forward external force
F (< 0) acts only on the trailing head. In the following we consider the backward force
F > 0 and forward force
F < 0, separately.
First, consider
F > 0. Since
F affects only the leading head while has no effect on the trailing head, at saturating ATP the forward stepping rate is
and the backward stepping rate is
(see
Figure 2g), where
P0(0) is the probability for the kinesin head to escape from the potential well of depth
Ew1 within the time period
tr under
F = 0. For approximation, the force dependence of
P0(
F) can be calculated by
where
is the characteristic distance, which should be equal to the Debye length of about 1 nm in solution, and thus we take
= 1 nm.
Probability
PE can still be calculated by
PE(
F) =
=
, where
C1 has the same form as that for the WT case except that the energy change
arising from NL stretching has a different value from that for the WT case (see
Section S1). As it is seen,
PE(
F) is independent of
C1. Thus, the above equation for
PE(
F) is the same as that for the WT case, which can also be written as Equation (3).
The stepping ratio can be calculated by
. Substitution of Equation (3) into above equation yields
Note that for the WT case,
P0(
F) =
P0(0) = 1 and Equation (9) becomes Equation (1). It should be emphasized that in Equation (9) only under
P0(0) =
P0(
F) the stall force is equal to
FS, whereas under
P0(0)
P0(
F) the stall force is no longer equal to
FS. In other words,
FS represents the stall force only under case of
P0(
F) =
P0(0) = 1 (i.e., the WT case). By contrast,
r0 is the stepping ratio at
F = 0 under any case.
The velocity can be calculated by
. Substitution of Equation (3) into above equation yields
Note that for the WT case,
P0(
F) =
P0(0) = 1 and Equation (10) becomes Equation (4).
The diffusion constant is calculated by
, where
x is the center-of-mass position of the motor along the movement direction in a movement trace. From this equation, we finally obtain
. Substitution of Equation (3) into above equation yields
The randomness parameter, which is defined as
, can be calculated by
. Substitution of Equations (10) and (11) into above equation yields
The mean number of ATP molecules consumed per forward step can be calculated by
. Substitution of Equation (3) into above equation yields
The mean number of ATP molecules consumed per step (either a forward or a backward step) can be calculated by
. Substitution of Equation (3) into above equation yields
Second, consider
F < 0, which affects only the trailing head while has no effect on the leading head. Similar to Equation (8) for
F > 0, the force dependence of
P0(
F) for
F < 0 can be calculated by
Similar to the derivation of Equations (9)–(14) for
F > 0, we can derive following equations for
F < 0. The stepping ratio has the form
The velocity has the form
The diffusion constant has the form
The randomness parameter has the form
The mean number of ATP molecules consumed per forward step has the form
The mean number of ATP molecules consumed per step (either a forward or a backward step) has the form
Now, we can use Equations (8)–(21) to calculate velocity, stepping ratio, randomness parameter, ATP number per step, etc., at saturating ATP. First, we consider WT human kinesin-1 (abbreviated as HsK) and the one with its two NLs being extended by inserting six additional amino acids AEQKLT into the C-terminal portion of the NL region of each head (abbreviated as HsK-6AA). In our model, although the extension of the NLs for HsK-6AA changes the strain on the NLs, it has no effect on the ATPase activity of the head, the NL docking of the MT-bound head and the interaction of the head with MT. In addition, the extension has the same effect on the movement of the detached ADP-head from the INT position to the front binding site on MT and to the rear binding site on MT, thus having no or little effect on
r0 and
FS. Hence, we have the same values of
r0,
FS,
k(+), and
k(−) for both HsK and HsK-6AA. As mentioned above,
P0 = 1 for HsK and
P0 < 1 for HsK-6AA under
F = 0. By taking
r0 = 900 and
FS = 7 pN, as done in
Figure 3a for DmK, and adjusting
k(+) = 90.5
,
k(−) = 4
, and
P0(0) = 0.33 (see
Table 1), the single-molecule data of Andreasson et al. [
24] on the force dependence of velocity for both HsK and HsK-6AA at saturating ATP (2 mM) can be fitted well (
Figure 5a). In other words, with the same four parameters
r0,
FS,
k(+), and
k(−) for both HsK and HsK-6AA and an additional parameter
P0(0) for HsK-6AA, the calculated results for both HsK and HsK-6AA shown in
Figure 5a are in quantitative agreement with the single-molecule data. The calculated results of the stepping ratio versus external force for HsK and HsK-6AA at saturating ATP are shown in
Figure 5b. As expected, the stepping ratio for HsK-6AA at a given backward force (
F > 0) is smaller than that for HsK whereas at a given forward force (
F < 0) is larger than that for HsK.
Second, we consider human kinesin-1 with a residue cysteine in each of the two NL domains being mutated (abbreviated as HsK-CL) and the one with its two NLs being extended by inserting six additional residues AEQKLT into the C-terminal portion of the NL region of each head (abbreviated as HsK-CL-6AA). For the leading head with the backward orientation of its NL, no interaction would be present between the head and its NL. Thus, the mutation of a residue cysteine in the NL domain (HsK-CL and HsK-CL-6AA) would have no effect on the ATPase activity of the leading head and the interaction of the leading head with MT. Consequently, value of
k(−) and value of
P0(0) for HsK-CL and HsK-CL-6AA should be equal to those for HsK and HsK-6AA, respectively. As a result, we still take
k(−) = 4
for HsK-CL and HsK-CL-6AA,
P0(0) = 1 for HsK-CL, and
P0(0) = 0.33 for HsK-CL-6AA, same as those for HsK and HsK-6AA. However, since the mutation of the NL would affect the NL docking and the interaction between the NL and the trailing head with the forward orientation of the NL, values of parameters
r0,
FS and
k(+) for HsK-CL and HsK-CL-6AA would be different from those of HsK and HsK-6AA. By adjusting
r0 = 600,
FS = 5 pN, and
k(+) = 107
(see
Table 1), the calculated results for dynamics of both HsK-CL and HsK-CL-6AA such as the force dependence of velocity (
Figure 6a), stepping ratio (
Figure 6b), and randomness parameter (
Figure 6c) are in agreement with the single-molecule data of Clancy et al. [
26] and Andreasson et al. [
24]. In particular, the calculated data show that about 3.3 ATP molecules consumed per forward step under no load for HsK-CL-6AA (
Figure 6d), which is in quantitative agreement with the experimental data of about 3.5 [
26]. The calculated data of nearly 1 ATP molecule consumed per forward step under no load for HsK-CL is also in quantitative agreement with the experimental data [
27] (
Figure 6d).
Taken together,
with only three adjustable parameters r0,
FS and
k(+), the calculated results for both HsK-CL and HsK-CL-6AA shown in
Figure 6 are in quantitative agreement with the single-molecule data. In addition, it is noted that
r0 = 600 and
FS = 5 pN for HsK-CL and HsK-CL-6AA are smaller than
r0 = 900 and
FS = 7 pN for HsK and HsK-6AA (see
Table 1). This is understandable easily, because the mutation of the NL reduces the NL-docking energy, decreasing and increasing the probabilities for the detached ADP-head to move from the INT position to the front and rear binding sites on MT, respectively, under the backward load.
2.5. Dynamics of Kinesin-1 with Extended NLs at Non-Saturating ATP
At low ATP, the pathway for the chemomechanical coupling of mutant kinesin-1 with extended NLs is schematically shown in
Figure 1, with
P0 < 1. Since it is difficult to obtain exactly analytical solutions for the dynamics of the motor at non-saturating ATP, here we use Monte-Carlo (MC) algorithm (see
Section 3) to study numerically the dynamics of the mutant kinesin-1. At non-saturating ATP, besides parameters
r0,
FS,
k(+),
k(−), and
P0(0) (see above section), two additional parameters
kb and
k−1 are also required to study the dynamics. Parameter
kb (also independent of force) is the second-order rate constant of ATP binding to the
-head in any position on MT (whether it is in the leading or INT or trailing position) and parameter
k−1 (also independent of force) is the rate constant of ATP dissociation from the leading head with the backward NL orientation (see
Section 3). Note that when the head is in the trailing or INT position, without the backward NL orientation, we take zero ATP dissociation rate (see
Section 3).
In our previous work [
38], using MC simulations and with six parameters
r0,
FS,
k(+),
k(−),
kb, and
k−1, diverse and even contradictory available single-molecule data on dynamics of different species of WT kinesin-1 dimers such as squid optic lobe kinesin, DmK, and Bovine (with
P0 = 1) under varying external force and ATP concentrations were reproduced well. Here, we focus on dynamics of the mutant kinesin-1 dimer with extended NLs such as HsK-CL-6AA under varying external force and ATP concentrations. For HsK-CL-6AA, we have values of
r0,
FS,
k(+),
k(−), and
P0(0) (see
Table 1), as given in
Figure 6. To study its dynamics at non-saturating ATP, we take
kb = 3.3
and
k−1 = 30
(see
Table 1).
In
Figure 7a we show the MC simulated and single-molecule results of the velocity versus
F at 2 mM and 10
ATP concentrations.
Figure 7b shows the MC simulated and single-molecule results of the stepping ratio versus
F at 2 mM and 10
ATP concentrations using the method described in
Section 3. In
Figure 7c we show the MC simulated and single-molecule results of the reciprocal randomness,
, versus
F at 2 mM and 10
ATP concentrations.
Figure 7d shows the MC simulated and single-molecule results of the velocity versus ATP concentration under no external force (i.e.,
F = 0).
Figure 7e shows the MC simulated and single-molecule results of the backstepping velocity versus ATP concentration under
F = 7 pN.
Figure 7f shows the MC simulated results of the mean number of ATP molecules consumed per step (either a forward or a backward step) versus
F at 2 mM and 10
ATP concentrations, where to check the MC simulation we also show the analytical solution of Equation (14) at saturating ATP (line). From
Figure 7a–e, it is seen that all the simulated results are in quantitative agreement with the single-molecule data [
26].
It should be mentioned here that the results for HsK-CL and HsK-CL-6AA shown in both
Figure 6 and
Figure 7 are calculated with the same parameters
r0,
FS,
k(+),
k(−),
kb, and
k−1 and an additional parameter
P0(0) for HsK-CL-6AA (see
Table 1). In addition, the two parameters
k(−) and
P0(0) related to the leading head for HsK-CL and HsK-CL-6AA have the same values as those given in
Figure 5 for HsK and HsK-6AA. Thus,
only five parameters r0,
FS,
k(+),
kb, and
k−1 are adjustable here to make all of the analytical and MC simulated results for both HsK-CL and HsK-CL-6AA shown in
Figure 6 and
Figure 7 be in quantitative agreement with the single-molecule data.
By contrast, using models presented in the literature to fit the single-molecule data, many more adjustable parameters are required for a species of the kinesin and moreover, different parameters values are required for the WT case and the corresponding case with extension of its NLs. For example, 10 and 13 parameters were adjustable in References [
26] and [
36], respectively, to fit the single-molecule data shown in
Figure 7 for only HsK-CL-6AA. Moreover, with those fitted parameter values, the calculated numbers of ATP molecules consumed per forward step under no load are far away from the experimental value of 3.5 [
26]. In addition, with those fitted parameters, the calculated ATPase rate of the motor during its processive movement is changed significantly as the force is varied in the small range from 0 to 4 pN (near the stall force), implying that variation of the NL strain by only 4 pN can result in a significant change in the ATPase rate. This is in contrast to the available experimental data showing that extending NLs of kinesin-1 dimer via adding different numbers (2–26) of residues in each NL (implying variation of the NL strain from about 30 pN to 0 pN [
39,
40]) has nearly no effect on the ATPase rate of the motor during its processive movement [
27].
2.6. Dynamics of Kinesin-2
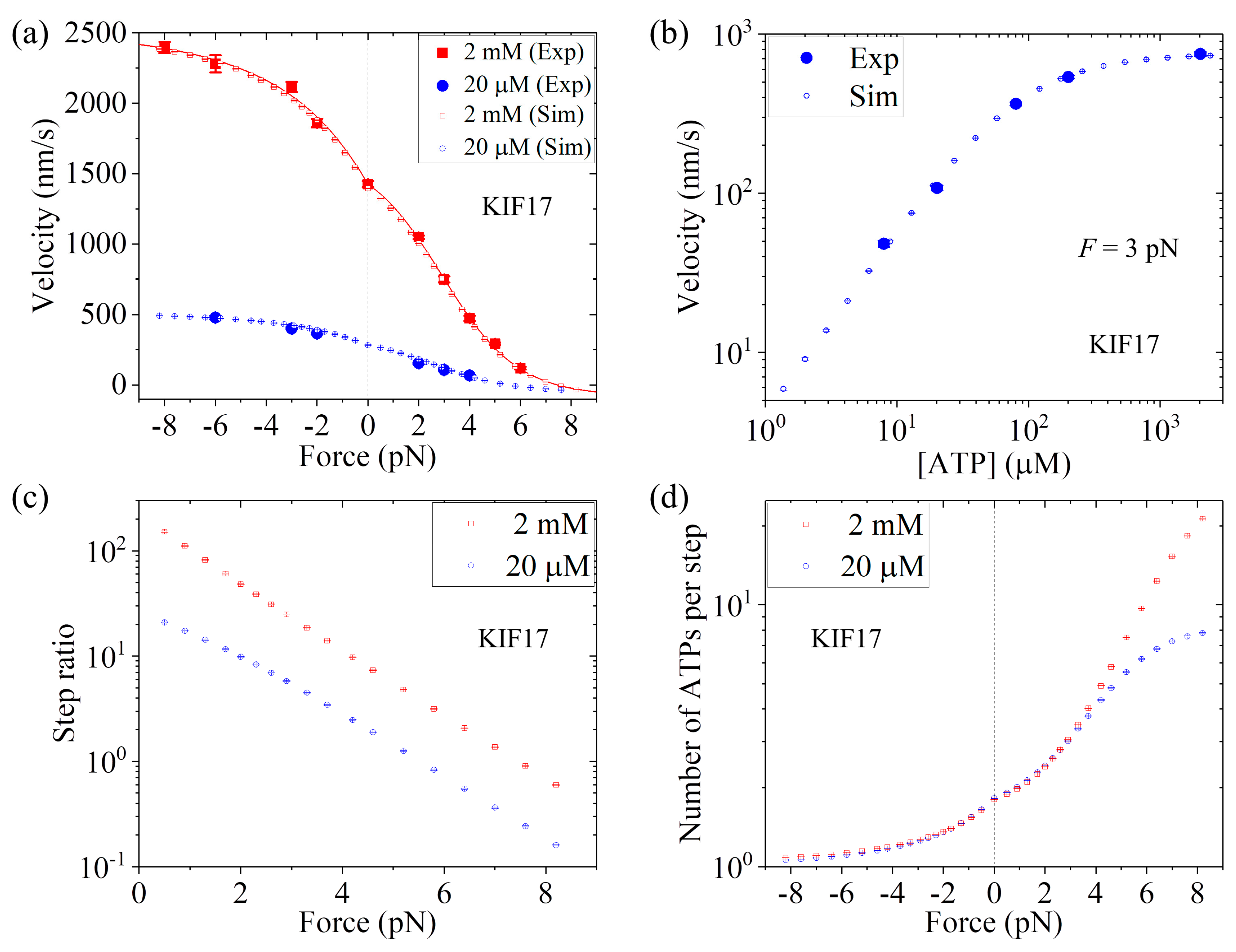
Up to now, we have focused on kinesin-1 homodimers. In this section, we study dynamics of kinesin-2 homodimer KIF17, comparing with the single-molecule data of Milic et al. [
25]. For KIF17, the NL in each head has 17 residues. Previous all-atom MD simulations indicated that when the two heads are bound to MT the internally stretched force on the NLs has a very small value, close to zero [
39,
53], as in the case of HsK-CL-6AA. Thus, we also take
P0 < 1 under no external force for KIF17.
First, we consider saturating ATP. We take
r0 = 220, same as that for Bovine (see
Table 1), and
FS = 8 pN, also close to that for Bovine (see
Table 1). Then, by adjusting
k(+) = 307
,
k(−) = 9.8
, and
P0(0) = 0.65 (see
Table 1), the analytical results of the velocity versus external force (line in
Figure 8a) reproduce the single-molecule data at 2 mM ATP [
25] very well (
Figure 8a). Then, we consider non-saturating ATP. By taking
kb = 3.3
and
k−1 = 30
(see
Table 1), the MC simulated results of both the velocity versus external force
F at [ATP] = 20
(
Figure 8a) and the velocity versus [ATP] under
F = 3 pN (
Figure 8b) are in good agreement with the single-molecule data [
25]. Moreover, in
Figure 8c we show the MC simulated results of the stepping ratio versus backward force at 2 mM and 20
concentrations, where the stepping ratio is calculated as done in
Figure 7b (see
Section 3). These predicted results of
Figure 8c can be test easily by using single-molecule optical trappings. In
Figure 8d we show the MC simulated results of the mean number of ATP molecules consumed per step (either a forward or a backward step) versus external force at 2 mM and 20
ATP concentrations. From
Figure 8d we see that under no external force, about 1.8 ATP molecules are consumed to make a mechanical step.
2.7. Power Production and Efficiency of Kinesin Dimers
One of important factors that characterize the performance of a molecular motor is the work production per unit time (power). To compare the performance among different species of kinesin motors, we calculate the power that the motor can provide at saturating ATP.
Under backward force
F > 0, the power production can be calculated by
. Substitution of Equation (3) into above equation yields
where
P0(
F) is calculated by Equation (8). Similarly, under forward force
F < 0, the power production has the form
where
P0(
F) is calculated by Equation (15).
Using Equation (22) and with parameter values given in
Table 1, the calculated results of the power versus backward force for different species of kinesin motors are shown in
Figure 9a. From
Figure 9a we see that the maximum power (in units of
kBT/s) decreases in the following order: 552.6 (KIF17) > 388.5 (DmK) > 362.4 (HsK) > 300.1 (Bovine) > 265.1 (HsK-CL) > 117.0 (HsK-6AA) > 86.0 (HsK-CL-6AA). Among the seven kinesin molecular motors studied here, KIF17 has the best performance by providing the highest power of about 552.6
kBT/s, whereas HsK-CL-6AA has the worst performance by providing the lowest power of about 86
kBT/s. These results indicate that the power provided by WT kinesin-2 (KIF17) is larger than that by WT kinesin-1 (DmK, HsK, and Bovine). The power by WT kinesin-1 is larger than that by the mutant with a residue cysteine in the NL domain being mutated (HsK-CL). The extension of the NLs (HsK-6AA and HsK-CL-6AA) reduces the power relative to that without the extension of the NLs (HsK and HsK-CL).
The efficiency of kinesin motors can be calculated by
, where
is the energy input per unit time. In our model,
, where
is the free energy change provided by hydrolysis of an ATP molecule. With parameter values given in
Table 1 and taking
= 20
kBT under physiological conditions, the calculated results of
versus backward force for seven species of kinesin motors are shown in
Figure 9b. It is noted that the calculated efficiency of about 16% for HsK is in agreement with the available single-molecule value determined recently at
F = 2 pN [
62]. Comparing
Figure 9a with
Figure 9b, we see that except for KIF17 that can provide the highest power production but has a mediate efficiency, in general, the motor that can provide a high (low) power production has a high (low) efficiency.