Accelerated Aging Characterization of Lithium-ion Cells: Using Sensitivity Analysis to Identify the Stress Factors Relevant to Cyclic Aging
Abstract
:1. Introduction
1.1. Motivation
1.2. Objective and Content of This Study
- Theoretical investigation on the cause–effect chain of aging: To provide a basic understanding, the cause–effect chain of aging is presented. To demonstrate the need for a sensitivity analysis, existing controversies on the sensitivity of cyclic aging are discussed (Section 2).
- Experimental test procedure for sensitivity analyses on lithium-ion cells: The experimental set-up for sensitivity analyses on cyclic aging with two distinct acceleration levels is presented. For the practical implementation of the sensitivity analyses, standard battery testing hardware is required, i.e., a battery tester and a temperature chamber (Section 3).
- Analytical implementation of the sensitivity analyses: The experimental results are evaluated regarding their statistical significance as well as the identifiable effects of the stress factors on cyclic aging. Thereupon, the accelerated approaches are critically questioned. This evaluation is conducted using available statistical software (Section 4).
2. Cause–Effect Chain of Aging
2.1. Stress Factors, Mechanisms, Modes, and Effects of Aging
2.2. Mapping by Semi-Empirical Aging Models
2.3. Sensitivity Analysis as an Essential Step
2.4. Consideration of Disturbance Factors
3. Methods and Experimental Set-Up
3.1. Test Designs
3.2. Cell Candidates
3.3. Testing Procedure
4. Results of Sensitivity Analyses
4.1. Null and Alternative Hypothesis
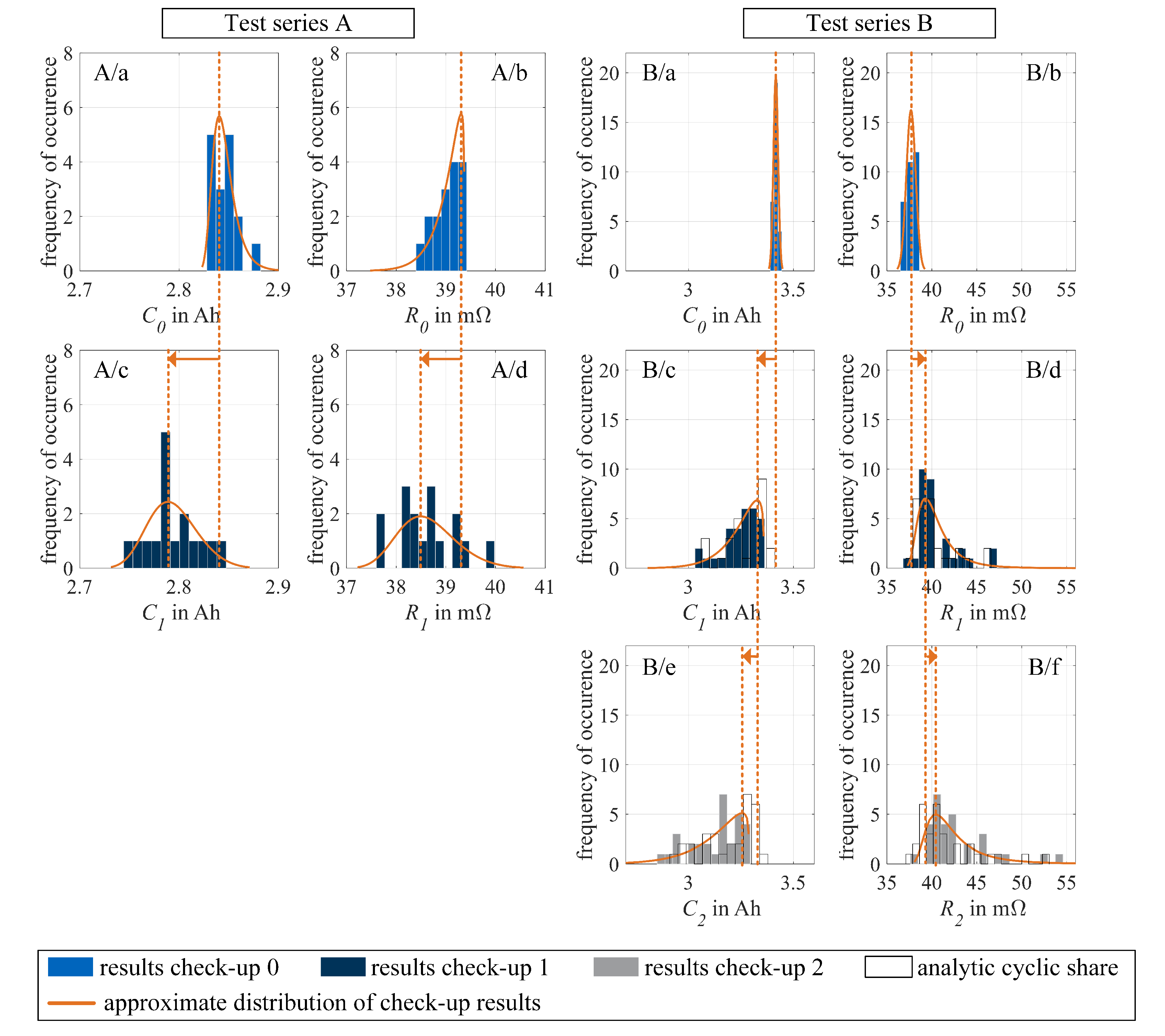
4.2. Analysis on Test Series A
4.3. Analysis on Test Series B
5. Summary and Conclusions
5.1. Accelerated Sensitivity Analyses for the Aging Characterization of Lithium-Ion Cells
5.2. Application Potentials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sour. 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Marongiu, A.; Rocher, M.; Sauer, D.U. Influence of the vehicle-to-grid strategy on the aging behavior of lithium battery electric vehicles. Appl. Energy 2015, 137, 899–912. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Sour. 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Grolleau, S.; Delaille, A.; Gualous, H.; Gyan, P.; Revel, R.; Bernard, J.; Redondo-Iglesias, E.; Peter, J. Calendar aging of commercial graphite/LiFePO4 cell—Predicting capacity fade under time dependent storage conditions. J. Power Sour. 2014, 255, 450–458. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukiazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M. Degradation of lithium ion batteries employing graphite negatives and nickel-cobalt-manganese oxide + spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sour. 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Petit, M.; Prada, E.; Sauvant-Moynot, V. Development of an empirical aging model for Li-ion batteries and application to assess the impact of Vehicle-to-Grid strategies on battery lifetime. Appl. Energy 2016, 172, 398–407. [Google Scholar] [CrossRef]
- de Hoog, J.; Timmermans, J.M.; Stroe, D.I.; Swierczynski, M.; Jaguemont, J.; Goutam, S.; Omar, N.; van Mierlo, J.; van den Bossche, P. Combined cycling and calendar capacity fade modeling of a Nickel-Manganese-Cobalt Oxide Cell with real-life profile validation. Appl. Energy 2017, 200, 47–61. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sour. 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Wright, R.; Christophersen, J.; Motloch, C.; Belt, J.; Ho, C.; Battaglia, V.; Barnes, J.; Duong, T.; Sutula, R. Power fade and capacity fade resulting from cycle-life testing of Advanced Technology Development Program lithium-ion batteries. J. Power Sour. 2003, 119–121, 865–869. [Google Scholar] [CrossRef]
- Canals Casals, L.; Schiffer Gonzalez, A.M.; Garcia, B.; Llorca, J. PHEV Battery Aging Study Using Voltage Recovery and Internal Resistance From Onboard Data. IEEE Trans. Veh. Technol. 2016, 65, 4209–4216. [Google Scholar] [CrossRef] [Green Version]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sour. 2013, 241, 680–689. [Google Scholar] [CrossRef] [Green Version]
- Lewerenz, M. Dissection and Quantitative Description of Aging of Lithium-Ion Batteries Using Non-Destructive Methods Validated by Post-Mortem-Analyses. Ph.D. Thesis, Institut für Stromrichtertechnik und Elektrische Antriebe (ISEA), Aachen, Germany, 2018. [Google Scholar]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sour. 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Waldmann, T.; Hogg, B.I.; Wohlfahrt-Mehrens, M. Li plating as unwanted side reaction in commercial Li-ion cells—A review. J. Power Sour. 2018, 384, 107–124. [Google Scholar] [CrossRef]
- Bach, T.C.; Schuster, S.F.; Fleder, E.; Müller, J.; Brand, M.J.; Lorrmann, H.; Jossen, A.; Sextl, G. Nonlinear aging of cylindrical lithium-ion cells linked to heterogeneous compression. J. Energy Storage 2016, 5, 212–223. [Google Scholar] [CrossRef]
- Ebert, F.; Sextl, G.; Lienkamp, M. Effect of a flexible battery module bracing on cell aging. In Proceedings of the 2017 Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 13 April 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Somerville, L.; Bareño, J.; Trask, S.; Jennings, P.; McGordon, A.; Lyness, C.; Bloom, I. The effect of charging rate on the graphite electrode of commercial lithium-ion cells: A post-mortem study. J. Power Sour. 2016, 335, 189–196. [Google Scholar] [CrossRef] [Green Version]
- Broussely, M.; Biensan, P.; Bonhomme, F.; Blanchard, P.; Herreyre, S.; Nechev, K.; Staniewicz, R.J. Main aging mechanisms in Li ion batteries. J. Power Sour. 2005, 146, 90–96. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Aging of Lithium-Ion Batteries in Electric Vehicles: Impact of Regenerative Braking. World Electr. Veh. J. 2015, 7, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Herb, F. Ageing Mechanisms in Lithium-ion Batteries and PEM Fuel Cells and Their Influence on the Properties of Hybrid Systems: (dt. Originaltitel: Alterungsmechanismen in Lithium-Ionen-Batterien und PEM-Brennstoffzellen und deren Einfluss auf die Eigenschaften von Daraus Bestehenden Hybrid-Systemen). Ph.D. Thesis, University of Ulm, Ulm, Germany, 2010. [Google Scholar]
- Paul, S.; Diegelmann, C.; Kabza, H.; Tillmetz, W. Analysis of ageing inhomogeneities in lithium-ion battery systems. J. Power Sour. 2013, 239, 642–650. [Google Scholar] [CrossRef]
- Guan, T.; Zuo, P.; Sun, S.; Du, C.; Zhang, L.; Cui, Y.; Yang, L.; Gao, Y.; Yin, G.; Wang, F. Degradation mechanism of LiCoO2/mesocarbon microbeads battery based on accelerated aging tests. J. Power Sour. 2017, 268, 816–823. [Google Scholar] [CrossRef]
- Scrosati, B.; Garche, J.; Tillmetz, W. (Eds.) Advances in Battery Technologies for Electric Vehicles, 1st ed.; Woodhead Publishing series in energy; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- Pistoia, G. (Ed.) Lithium-Ion Batteries: Advances and Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Schmitt, J.; Maheshwari, A.; Heck, M.; Lux, S.; Vetter, M. Impedance change and capacity fade of lithium nickel manganese cobalt oxide-based batteries during calendar aging. J. Power Sour. 2017, 353, 183–194. [Google Scholar] [CrossRef]
- Sun, S.; Guan, T.; Shen, B.; Leng, K.; Gao, Y.; Cheng, X.; Yin, G. Changes of Degradation Mechanisms of LiFePO 4 /Graphite Batteries Cycled at Different Ambient Temperatures. Electrochim. Acta 2017, 237, 248–258. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sour. 2011, 196, 3492–3948. [Google Scholar] [CrossRef]
- Baghdadi, I.; Briat, O.; Delétage, J.Y.; Gyan, P.; Vinassa, J.M. Lithium battery aging model based on Dakin’s degradation approach. J. Power Sour. 2016, 325, 273–285. [Google Scholar] [CrossRef]
- Dakin, T.W. Electrical Insulation Deterioration Treated as a Chemical Rate Phenomenon. Trans. Am. Inst. Electr. Eng. 1948, 67, 113–122. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sour. 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Kar, S.K.; Teodorescu, R. Degradation Behavior of Lithium-Ion Batteries During Calendar Ageing—The Case of the Internal Resistance Increase. IEEE Trans. Ind. Appl. 2018, 54, 517–525. [Google Scholar] [CrossRef] [Green Version]
- Bauer, M.; Guenther, C.; Kasper, M.; Petzl, M.; Danzer, M.A. Discrimination of degradation processes in lithium-ion cells based on the sensitivity of aging indicators towards capacity loss. J. Power Sour. 2015, 283, 494–504. [Google Scholar] [CrossRef]
- Cui, Y.; Du, C.; Yin, G.; Gao, Y.; Zhang, L.; Guan, T.; Yang, L.; Wang, F. Multi-stress factor model for cycle lifetime prediction of lithium ion batteries with shallow-depth discharge. J. Power Sour. 2015, 279, 123–132. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A. Battery durability and reliability under electric utility grid operations: Representative usage aging and calendar aging. J. Energy Storage 2018, 18, 185–195. [Google Scholar] [CrossRef]
- Edouard, C.; Petit, M.; Bernard, J.; Forgez, C.; Revel, R. Sensitivity Analysis of an Electrochemical Model of Li-ion Batteries and Consequences on the Modeled Aging Mechanisms. ECS Trans. 2015, 66, 37–46. [Google Scholar] [CrossRef]
- Su, L.; Zhang, J.; Wang, C.; Zhang, Y.; Li, Z.; Song, Y.; Jin, T.; Ma, Z. Identifying main factors of capacity fading in lithium ion cells using orthogonal design of experiments. Appl. Energy 2016, 163, 201–210. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.M.; Liu, Z.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J. Power Sour. 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Eichner, T. Degradations in Lithium-ion Batteries under the Demands of the Automotive Application: (Dt. Originaltitel: Degradationen in Lithium-Ionen-Batterien unter Anforderungen im Automobilen Umfeld). Ph.D. Thesis, University of Ulm, Ulm, Germany, 2014. [Google Scholar]
- Selvamuthu, D.; Das, D. Introduction to Statistical Methods, Design of Experiments and Statistical Quality Control; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Baumann, M.; Wildfeuer, L.; Rohr, S.; Lienkamp, M. Parameter variations within Li-Ion battery packs—Theoretical investigations and experimental quantification. J. Power Sour. 2018, 18, 295–307. [Google Scholar] [CrossRef]
- Lewerenz, M.; Fuchs, G.; Becker, L.; Sauer, D.U. Irreversible calendar aging and quantification of the reversible capacity loss caused by anode overhang. J. Energy Storage 2018, 18, 149–159. [Google Scholar] [CrossRef]
- Rumpf, K.; Naumann, M.; Jossen, A. Experimental investigation of parametric cell-to-cell variation and correlation based on 1100 commercial lithium-ion cells. J. Energy Storage 2017, 14, 224–243. [Google Scholar] [CrossRef]
- Prochazka, W.; Pregartner, G.; Cifrain, M. Design-of-Experiment and Statistical Modeling of a Large Scale Aging Experiment for Two Popular Lithium Ion Cell Chemistries. J. Electrochem. Soc. 2013, 160, A1039–A1051. [Google Scholar] [CrossRef]
- Mathieu, R.; Baghdadi, I.; Briat, O.; Gyan, P.; Vinassa, J.M. D-optimal design of experiments applied to lithium battery for ageing model calibration. Energy 2017, 141, 2108–2119. [Google Scholar] [CrossRef]
- Schweiger, H.G.; Obeidi, O.; Komesker, O.; Raschke, A.; Schiemann, M.; Zehner, C.; Gehnen, M.; Keller, M.; Birke, P. Comparison of several methods for determining the internal resistance of lithium ion cells. Sensors 2010, 10, 5604–5625. [Google Scholar] [CrossRef] [Green Version]
- Gewald, T.; Lienkamp, M.; Lehmkuhl, D.; Hahn, A. Accelerated Aging Characterization of Lithium-Ion Cells: Limitation of Arrhenius Dependency. In Proceedings of the 2019 Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 8 May 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Knudesn Kaer, S.; Martinez Laserna, E.; Sarasketa Zabala, E. Accelerated Aging of Lithium-Ion Batteries based on Electric Vehicle Mission Profile. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1 October 2017; pp. 5631–5637. [Google Scholar] [CrossRef] [Green Version]
- Schuster, S.F.; Bach, T.; Fleder, E.; Müller, J.; Brand, M.; Sextl, G.; Jossen, A. Nonlinear aging characteristics of lithium-ion cells under different operational conditions. J. Energy Storage 2015, 1, 44–53. [Google Scholar] [CrossRef]
- Gewald, T.; Lienkamp, M. A Systematic Method for Accelerated Aging Characterization of Lithium-Ion Cells in Automotive Applications. Eng. Res. 2019, 83, 831–841. [Google Scholar] [CrossRef]


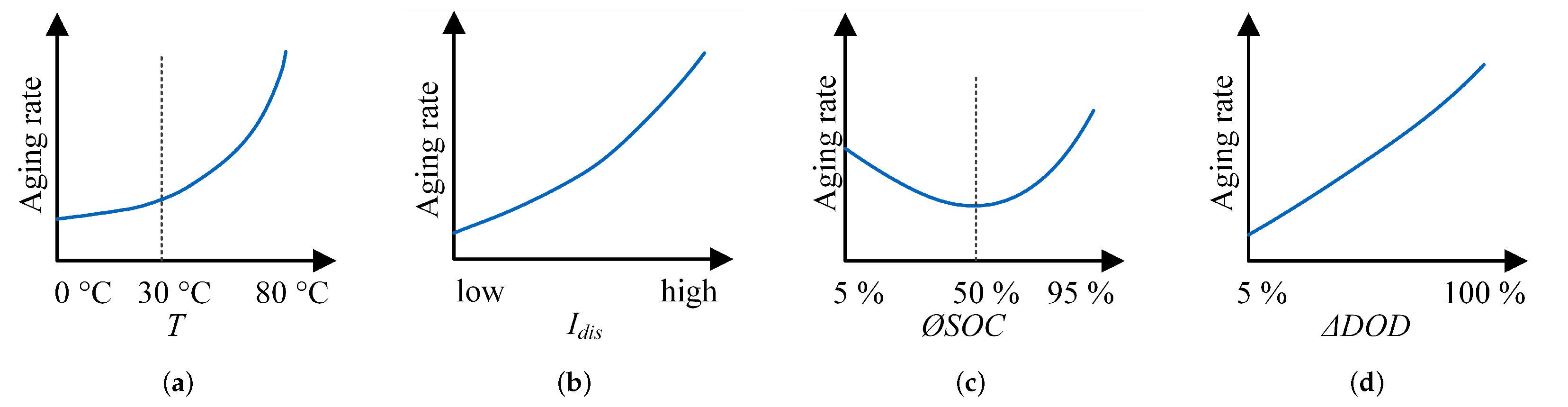


| Stress Factor | Chemistry | Factor Range | Reference | ||
|---|---|---|---|---|---|
| Effects on Calendar Aging | |||||
| T | NCA | 10–40C | ● | - | Keil & Jossen, 2015 [19] |
| NCA | ● | ● | Broussely et al., 2005 [18] | ||
| NMC | 0–5C | ● | ● | Schmitt et al., 2017 [25] | |
| NMC, LFP | 40–70C | - | ● | Marongiu et al., 2015 [2] | |
| LFP | ● | ● | Herb, 2010 [20] | ||
| ● | ● | Vetter et al., 2005 [13] | |||
| ● | ● | Barré et al., 2013 [11] | |||
| Fluctuations in T | LFP | ○ | ◑ | Herb, 2010 [20] | |
| NCA | if T high ●, else ○ | if T high ●, else ○ | Broussely et al., 2005 [18] | ||
| NCA | 0–100% | ● | - | Keil & Jossen, 2015 [19] | |
| NMC | 0–100% | ● | ● | Schmitt et al., 2017 [25] | |
| NMC, LFP | 20–100% | - | ● | Marongiu et al., 2015 [2] | |
| ● | ● | Vetter et al., 2005 [13] | |||
| 80–100% | ● | ● | Barré et al., 2013 [11] | ||
| Effects on Cyclic Aging | |||||
| T | NCA | 10–40C | ● | - | Keil & Jossen, 2015 [19] |
| LFP | 25–55C | ● | - | Sun et al., 2017 [26] | |
| LFP | ● | ● | Herb, 2010 [20] | ||
| 10–40C | ● | if T high ●, else ○ | Vetter et al., 2005 [13] | ||
| - | ● | Barré et al., 2013 [11] | |||
| Fluctuations in T | LFP | ○ | ◑ | Herb, 2010 [20] | |
| NCA, NMC | ● | - | Broussely et al., 2005 [18] | ||
| NMC | 1.0–2.0C | ○ | ○ | Marongiu et al., 2015 [2] | |
| LFP | 1.0–6.0C | ○ | ○ | Marongiu et al., 2015 [2] | |
| LFP | ◑ | ● | Herb, 2010 [20] | ||
| LCO | 0.6–3.0C | ◑ | - | Guan et al., 2017 [22] | |
| ● | ● | Vetter et al., 2005 [13] | |||
| NCA | 33–78% | ● | - | Keil & Jossen, 2015 [19] | |
| LFP | if high ●, else ○ | ● | Vetter et al., 2005 [13] | ||
| LFP | ○ | ◑ | Herb, 2010 [20] | ||
| 80–100% | - | ● | Barré et al., 2013 [11] | ||
| LFP | ○ | ○ | Herb, 2010 [20] | ||
| LFP | ◑ | ● | Herb, 2010 [20] | ||
| NCA | ≈25% | ● | - | Keil & Jossen, 2015 [19] | |
| NMC, LFP | 20–80% | ◑ | ◑ | Marongiu et al., 2015 [2] | |
| LFP | - | ◑ | Barré et al., 2013 [11] | ||
| LFP | ● | ● | Herb, 2010 [20] | ||
| - | ● | Paul et al., 2013 [21] | |||
| ● | - | Vetter et al., 2005 [13] | |||
| Reference | Chemistry | Modelling Approach | Input | Output | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Petit et al., 2016 [6] | NCA, LFP | (c) | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Baghdadi et al., 2016 [28] | NCA, NMC | (b) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Wang et al., 2014 [5] | NMC | (a) | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Ecker et al., 2012 [30] | NMC | ✓ | ✓ | ✓ | ✓ | |||||
| Schmalstieg et al., 2014 [1] | NMC | (a) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Hoog et al., 2017 [7] | NMC | (a) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Marongiu et al., 2015 [2] | NMC, LFP | (a) | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Wang et al., 2011 [27] | LFP | (b) | ✓ | ✓ | ✓ | ✓ | ||||
| Herb et al., 2010 [20] | LFP | (a) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Grolleau et al., 2014 [4] | LFP | ✓ | ✓ | ✓ | ||||||
| Stroe et al., 2018 [31] | LFP | ✓ | ✓ | ✓ | ||||||
| Disturbance Factors for Calendar Aging | Disturbance Factors for Cyclic Aging |
|---|---|
| Production fluctuations | Production fluctuations |
| Fluctuations of storage temperature | Fluctuation of ambient temperature |
| Fluctuations of storage SOC | Cell self-heating |
| Cycling during check-up testing | Cell temperature interference with neighbored cells |
| Reversible capacity loss due to anode overhang | Current measurement error |
| Humidity | Voltage drift during charge-based cycling |
| Vibrations | Charge drift during voltage-based cycling |
| Clamping | Rest time during cycling |
| Humidity | |
| Vibrations | |
| Clamping |
| Test Point | Factor T | Factor | Factor | Factor |
|---|---|---|---|---|
| 1 | 40C | 2.0C | ||
| 2 | 40C | |||
| 3 | 40C | |||
| 4 | 40C | |||
| 5 | 40C | |||
| 6 | 40C | |||
| 7 | 40C | |||
| 8 | 40C | |||
| 9 | 25C | |||
| 10 | 25C | |||
| 11 | 25C | |||
| 12 | 25C | |||
| 13 | 25C | |||
| 14 | 25C | |||
| 15 | 25C | |||
| 16 | 25C |
| Test Point | Factor T | Factor | Factor | Factor |
|---|---|---|---|---|
| 1 | 25C | 2.0C | ||
| 2 | 45C | |||
| 3 | 35C | |||
| 4 | 25C | |||
| 5 | 25C | |||
| 6 | 45C | |||
| 7 | 45C | |||
| 8 | 45C | |||
| 9 | 25C | |||
| 10 | 25C | |||
| 11 | 25C | |||
| 12 | 25C | |||
| 13 | 45C | |||
| 14 | 35C | |||
| 15 | 25C | |||
| 16 | 45C | |||
| 17 | 45C | |||
| 18 | 45C | |||
| 19 | 35C | |||
| 20 | 25C | |||
| 21 | 45C | |||
| 22 | 45C | |||
| 23 | 45C | |||
| 24 | 35C | |||
| 25 | 35C | |||
| 26 | 35C | |||
| 27 | 25C | |||
| 28 | 25C | |||
| 29 | 25C | |||
| 30 | 45C |
| Header | Test Series A | Test Series B |
|---|---|---|
| Manufacturer | Panasonic | Sony (Murata) |
| Type | NCR18650PF | US18650VC7 |
| High-energy | High-energy | |
| Nom. Capacity | 2.9 Ah | 3.5 Ah |
| Nom. Voltage | 3.6 V | 3.6 V |
| Geometry | Cylindrical (18650) | Cylindrical (18650) |
| Anode | Graphite | Graphite, Si-doped |
| Cathode | NCA | NCA |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gewald, T.; Candussio, A.; Wildfeuer, L.; Lehmkuhl, D.; Hahn, A.; Lienkamp, M. Accelerated Aging Characterization of Lithium-ion Cells: Using Sensitivity Analysis to Identify the Stress Factors Relevant to Cyclic Aging. Batteries 2020, 6, 6. https://doi.org/10.3390/batteries6010006
Gewald T, Candussio A, Wildfeuer L, Lehmkuhl D, Hahn A, Lienkamp M. Accelerated Aging Characterization of Lithium-ion Cells: Using Sensitivity Analysis to Identify the Stress Factors Relevant to Cyclic Aging. Batteries. 2020; 6(1):6. https://doi.org/10.3390/batteries6010006
Chicago/Turabian StyleGewald, Tanja, Adrian Candussio, Leo Wildfeuer, Dirk Lehmkuhl, Alexander Hahn, and Markus Lienkamp. 2020. "Accelerated Aging Characterization of Lithium-ion Cells: Using Sensitivity Analysis to Identify the Stress Factors Relevant to Cyclic Aging" Batteries 6, no. 1: 6. https://doi.org/10.3390/batteries6010006
APA StyleGewald, T., Candussio, A., Wildfeuer, L., Lehmkuhl, D., Hahn, A., & Lienkamp, M. (2020). Accelerated Aging Characterization of Lithium-ion Cells: Using Sensitivity Analysis to Identify the Stress Factors Relevant to Cyclic Aging. Batteries, 6(1), 6. https://doi.org/10.3390/batteries6010006





