Non-Gaussian Quadrature Integral Transform Solution of Parabolic Models with a Finite Degree of Randomness
Abstract
:1. Introduction
2. Preliminaries and Formal Solution
- (i)
- is m.s. locally integrable,
- (ii)
- , if ,
- (iii)
- The 2-norm of is of exponential order, i.e., there exist real constants , called the abscissa of convergence, and such that
3. Random Numerical Solutions
| Algorithm1 Procedure to compute the expectation and the standard deviation of the approximate solution s.p. (32) of the problem (1)–(5). |
|
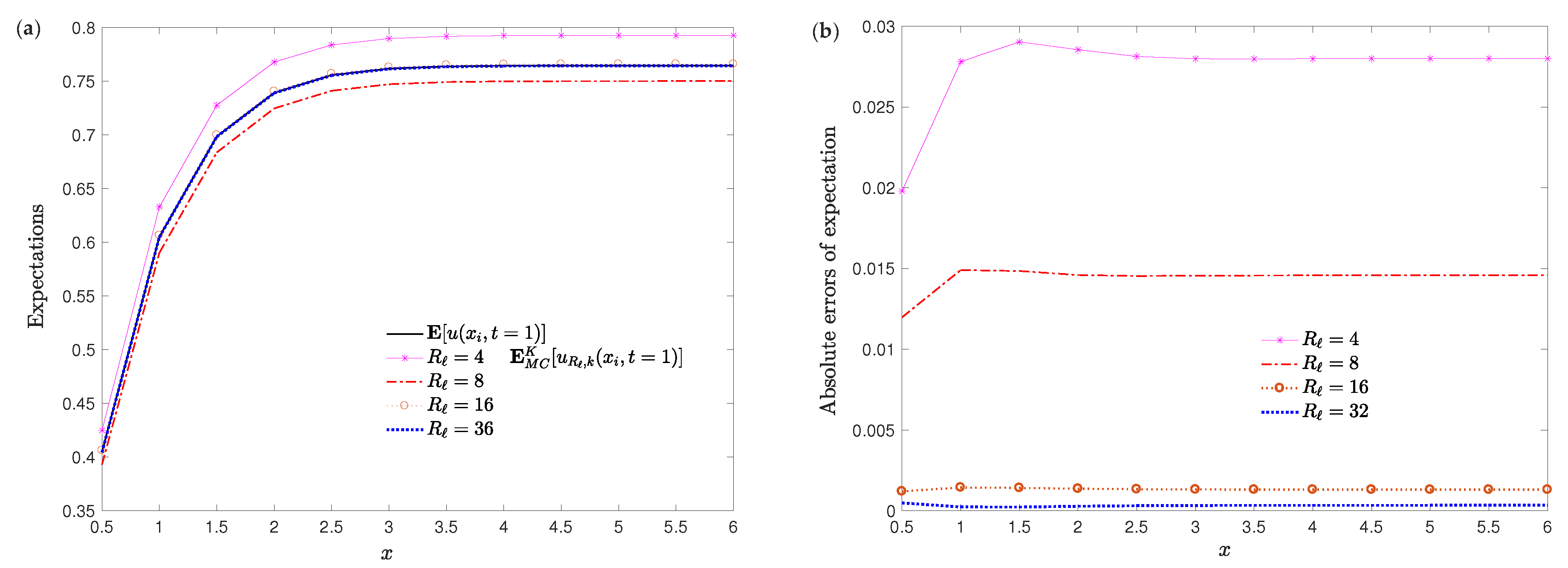
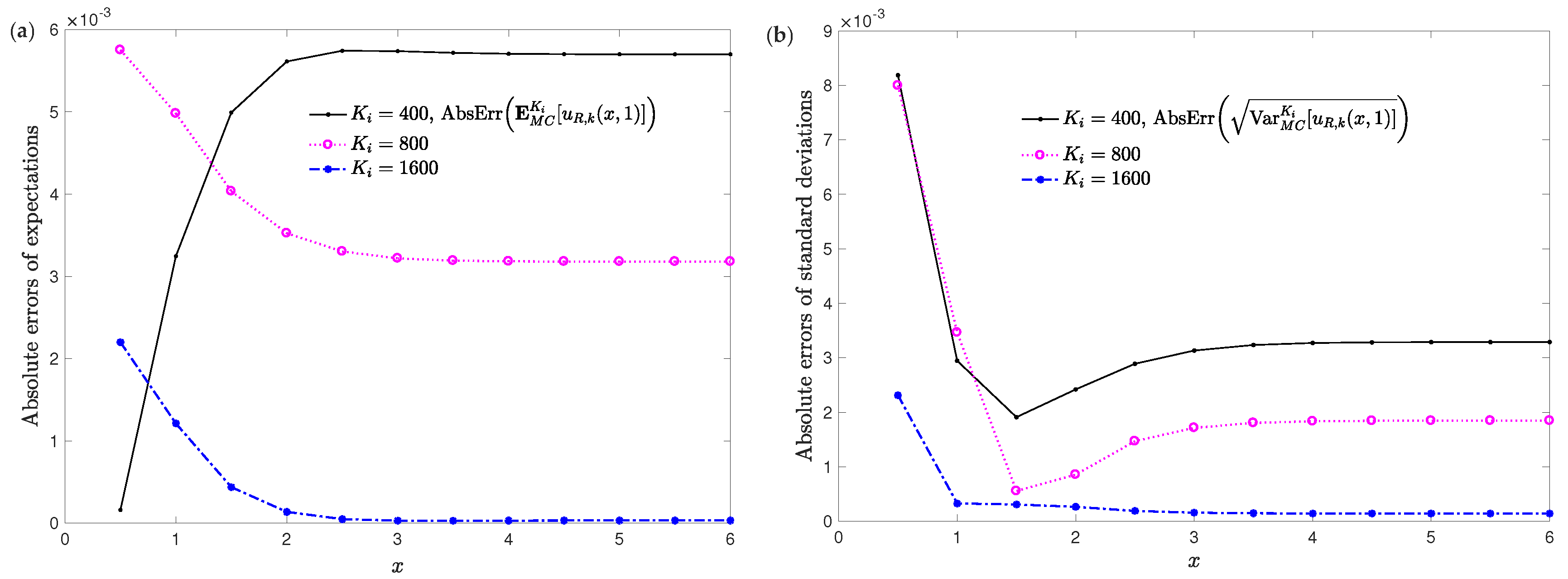
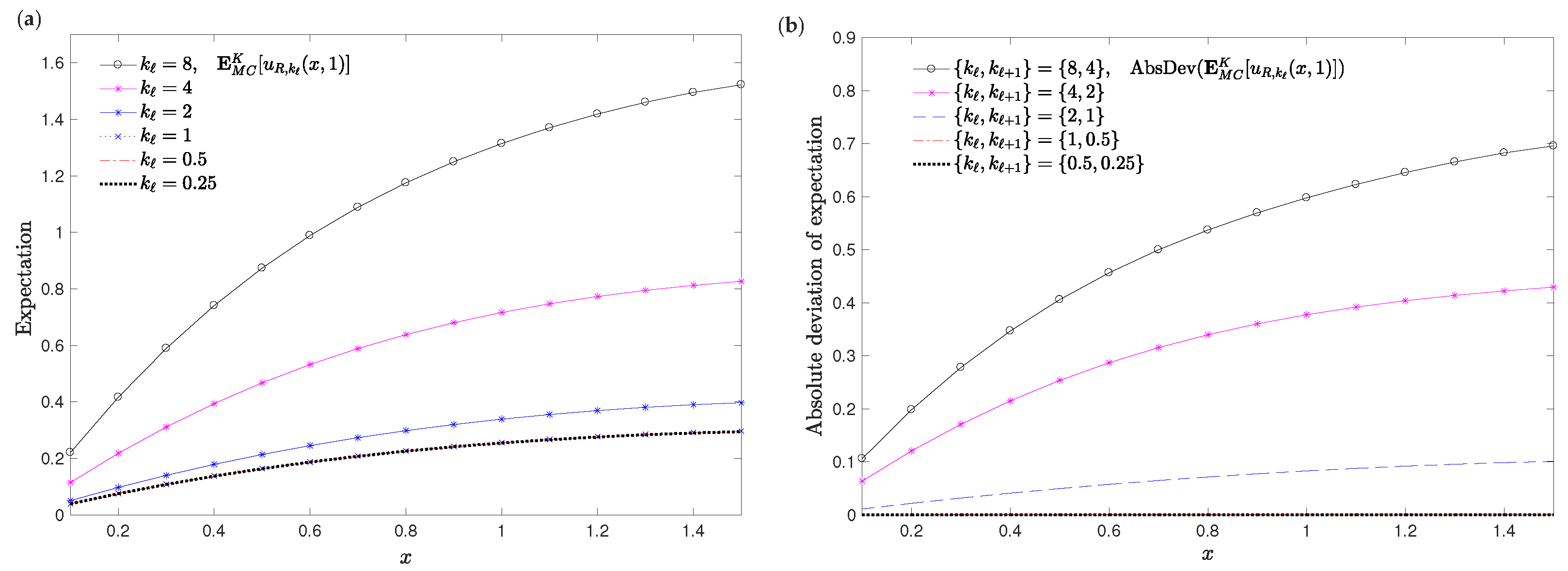
4. Numerical Examples and Simulations
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bharucha-Reid, A.T. On the Theory of Random Equations, Stochastic Processes in Mathematical Physics and Engineering. In Proceedings of Symposia in Applied Mathematics, American Mathematical Society XVI; American Mathematical Society: Providence, RI, USA, 1964; pp. 40–69. [Google Scholar]
- Bharucha-Reid, A.T. Probabilistic Methods in Applied Mathematics; Academic Press, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Bäck, J.; Nobile, F.; Tamellini, L.; Tempone, R. Stochastic Spectral Galerkin and Collocation Methods for PDEs with Random Coefficients: A Numerical Comparison. In Spectral and High Order Methods for Partial Differential Equations. Lecture Notes in Computational Science and Engineering; Hesthaven, J., Rønquist, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 76, pp. 43–62. [Google Scholar]
- Ernst, O.; Sprungk, B.; Tamellini, L. Convergence of Sparse Collocation for Functions of Countably Many Gaussian Random Variables (with Application to Elliptic PDEs). SIAM J. Numer. Anal. 2018, 56, 877–905. [Google Scholar] [CrossRef] [Green Version]
- Casabán, M.-C.; Cortés, J.-C.; Jódar, L. Analytic-Numerical Solution of Random Parabolic Models: A Mean Square Fourier Transform Approach. Math. Model. Anal. 2018, 23, 79–100. [Google Scholar] [CrossRef]
- Casabán, M.-C.; Company, R.; Jódar, L. Numerical Integral Transform Methods for Random Hyperbolic Models with a Finite Degree of Randomness. Mathematics 2019, 7, 853. [Google Scholar] [CrossRef] [Green Version]
- Nouri, K.; Ranjbar, H. Mean Square Convergence of the Numerical Solution of Random Differential Equations. Mediterr. J. Math. 2015, 12, 1123–1140. [Google Scholar] [CrossRef]
- Casabán, M.-C.; Cortés, J.-C.; Jódar, L. A random Laplace transform method for solving random mixed parabolic differential problems. Appl. Math. Comput. 2015, 259, 654–667. [Google Scholar] [CrossRef]
- Iserles, A. On the numerical quadrature of highly oscillating integrals I: Fourier transforms. IMA J. Numer. Anal. 2004, 24, 365–391. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: Orlando, FL, USA, 1984. [Google Scholar]
- Casabán, M.-C.; Company, R.; Egorova, V.N.; Jódar, L. Integral transform solution of random coupled parabolic partial differential models. Math. Method Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Farlow, S.J. Partial Differential Equations for Scientists and Engineers; Dover: New York, NY, USA, 1993. [Google Scholar]
- Jódar, L.; Pérez, J. Analytic numerical solutions with a priori error bounds of initial value problems for the time dependent coefficient wave equation. Util. Math. 2002, 62, 95–115. [Google Scholar]
- Soong, T.T. Random Differential Equations in Science and Engineering; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Özişik, M.N. Boundary Value Problems of Heat Conduction; Dover Publications, Inc.: New York, NY, USA, 1968. [Google Scholar]
- Polyanin, A.D.; Nazaikinskii, V.E. Handbook of Linear Partial Differential Equations for Engineers and Scientists, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Casabán, M.-C.; Company, R.; Cortés, J.-C.; Jódar, L. Solving the random diffusion model in an infinite medium: A mean square approach. Appl. Math. Model. 2014, 38, 5922–5933. [Google Scholar] [CrossRef]
- Casabán, M.-C.; Cortés, J.-C.; Jódar, L. Solving linear and quadratic random matrix differential equations using: A mean square approach. The non-autonomous case. J. Comput. Appl. Math 2018, 330, 937–954. [Google Scholar] [CrossRef]
- Davies, B.; Martin, B. Numerical Inversion of the Laplace Transform: A Survey and Comparison of Methods. J. Comput. Phys. 1979, 33, 1–32. [Google Scholar] [CrossRef]
- Cohen, A.M. Numerical Methods for Laplace Transform Inversion; Springer: New York, NY, USA, 2007. [Google Scholar]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; Wiley Series in Probability and Statistics; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Asmussen, S.; Glynn, P.W. Stochastic Simulation: Algorithms and Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 57. [Google Scholar]
- Ng, E.W.; Geller, M. A Table of Integrals of the Error Functions. Natianal Bur. Stand.-B Math. Sci. 1969, 73B, 1–20. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Armstrong, J.S.; Collopy, F. Error measures for generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Mathematica, Version 11.3; Wolfram Research, Inc.: Champaign, IL, USA, 2018.



| RMSE | CPU,s | RMSE | CPU,s | |
|---|---|---|---|---|
| 4 | 2.75343 × | 4.21989 × | ||
| 8 | 1.44244 × | 7.36449 × | ||
| 16 | 1.33445 × | 4.23940 × | ||
| 32 | 3.36898 × | 4.27797 × |
| RMSE | CPU,s | RMSE | CPU,s | |
|---|---|---|---|---|
| 1.28377 × 10 | 4.75391× | |||
| 4.23282 × | 9.02170 × | |||
| 1.33445 × | 4.23940 × | |||
| 1.14283 × | 4.25683 × | |||
| 1.04648 × | 4.26453 × |
| RMSE | CPU, s | RMSE | CPU, s | |
|---|---|---|---|---|
| 100 | 2.16541 × | 2.97642 × | ||
| 200 | 1.19892 × | 5.94483 × | ||
| 400 | 5.22902 × | 3.73953 × | ||
| 800 | 3.74892 × | 2.92100 × | ||
| 1600 | 7.37703 × | 6.96690 × | ||
| 3200 | 7.94225 × | 7.89259 × |
| RMSD | RMSD | |
|---|---|---|
| 4.08921 × | 2.39328 × | |
| 2.72959 × | 2.57692 × | |
| 1.03896 × | 8.86479 × | |
| 1.61474 × | 3.36047 × | |
| 8.11820 × | 2.62627 × |
| RMSD | RMSD | |
|---|---|---|
| 5.18967 × 10 | 2.57413 × | |
| 3.24473 × 10 | 1.88253 × | |
| 7.14500 × | 8.83031 × | |
| 1.03254 × | 3.25342 × | |
| 6.92989 × | 2.62627 × |
| CPU,s | CPU,s | |
|---|---|---|
| 2 | ||
| 4 | ||
| 8 | ||
| 16 | ||
| 32 | ||
| 64 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casabán, M.-C.; Company, R.; Jódar, L. Non-Gaussian Quadrature Integral Transform Solution of Parabolic Models with a Finite Degree of Randomness. Mathematics 2020, 8, 1112. https://doi.org/10.3390/math8071112
Casabán M-C, Company R, Jódar L. Non-Gaussian Quadrature Integral Transform Solution of Parabolic Models with a Finite Degree of Randomness. Mathematics. 2020; 8(7):1112. https://doi.org/10.3390/math8071112
Chicago/Turabian StyleCasabán, María-Consuelo, Rafael Company, and Lucas Jódar. 2020. "Non-Gaussian Quadrature Integral Transform Solution of Parabolic Models with a Finite Degree of Randomness" Mathematics 8, no. 7: 1112. https://doi.org/10.3390/math8071112
APA StyleCasabán, M.-C., Company, R., & Jódar, L. (2020). Non-Gaussian Quadrature Integral Transform Solution of Parabolic Models with a Finite Degree of Randomness. Mathematics, 8(7), 1112. https://doi.org/10.3390/math8071112







