On the Surface Residual Stress Measurement in Magnesium Alloys Using X-Ray Diffraction
Abstract
:1. Introduction
2. Material, Experiments and Methods
2.1. Material
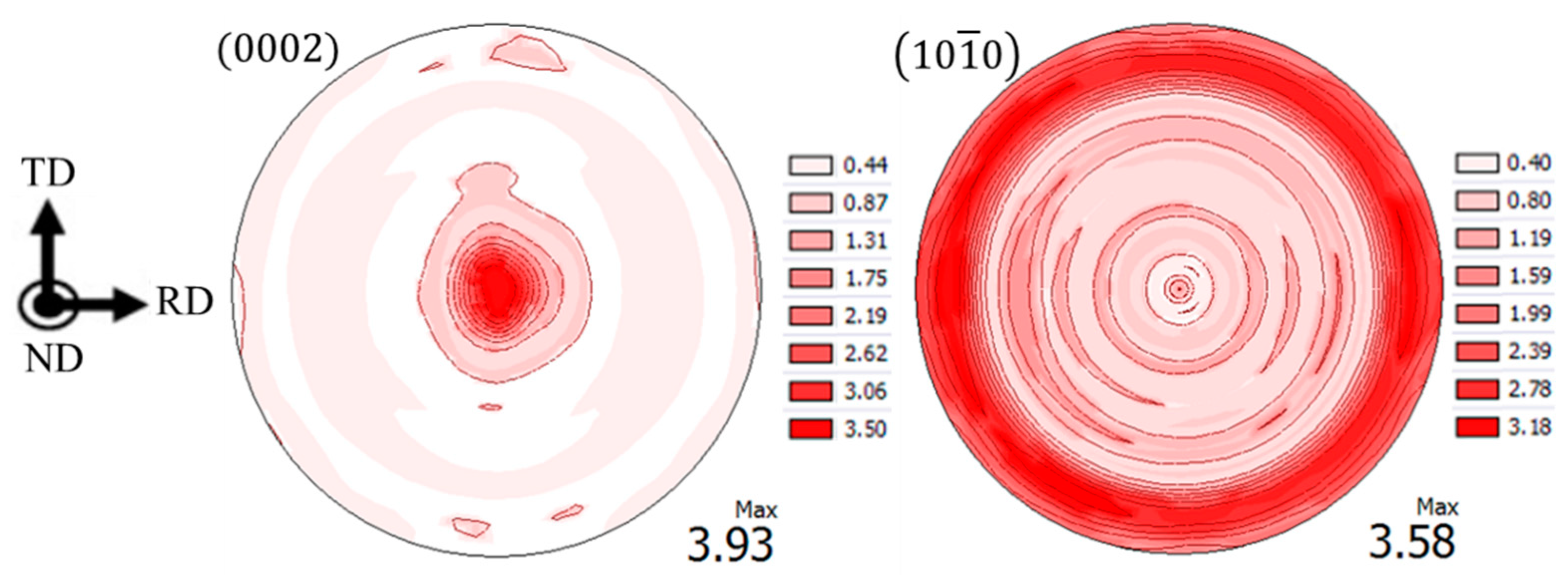
2.2. Texture Measurement
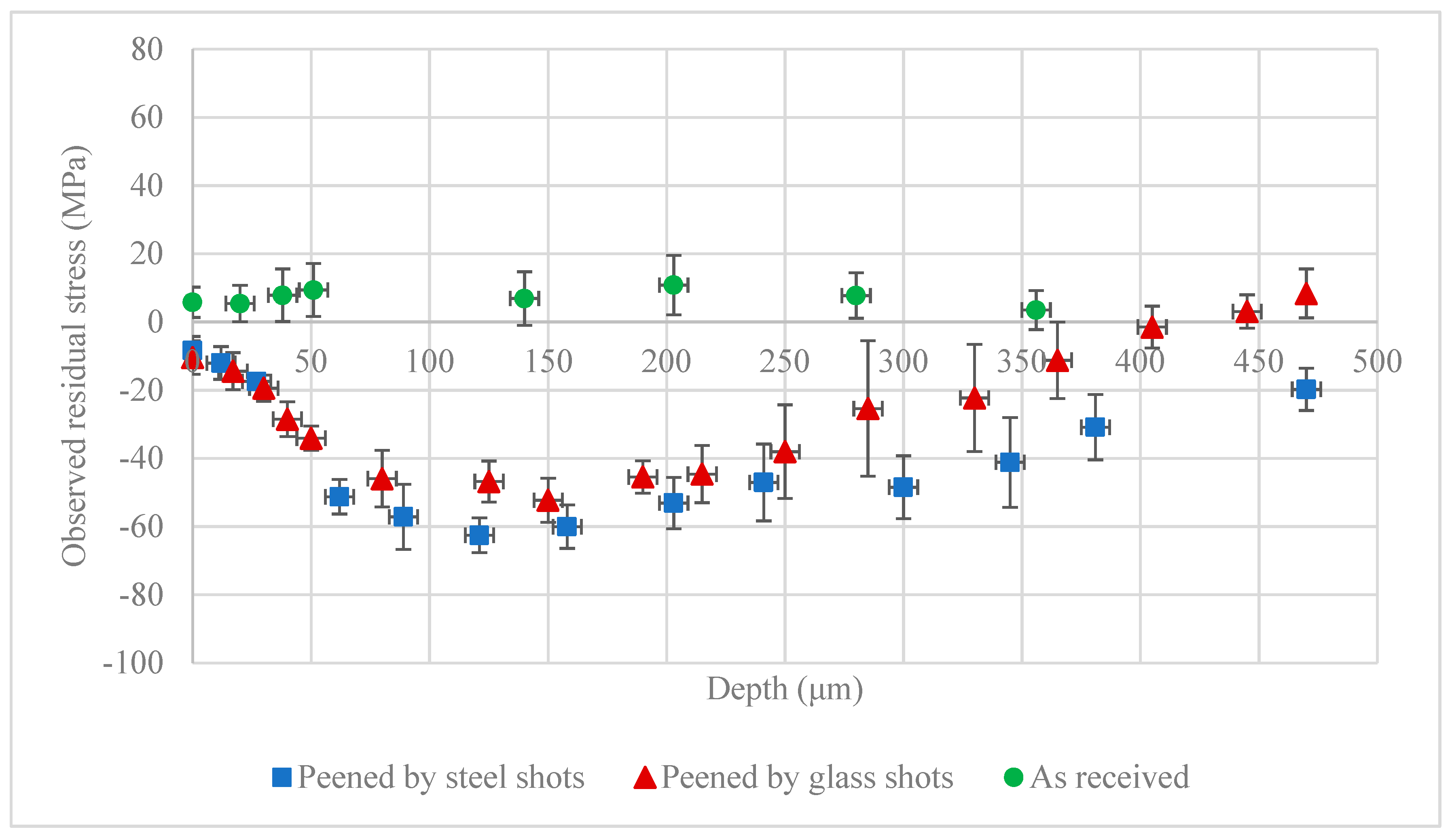
2.3. Shot Peening
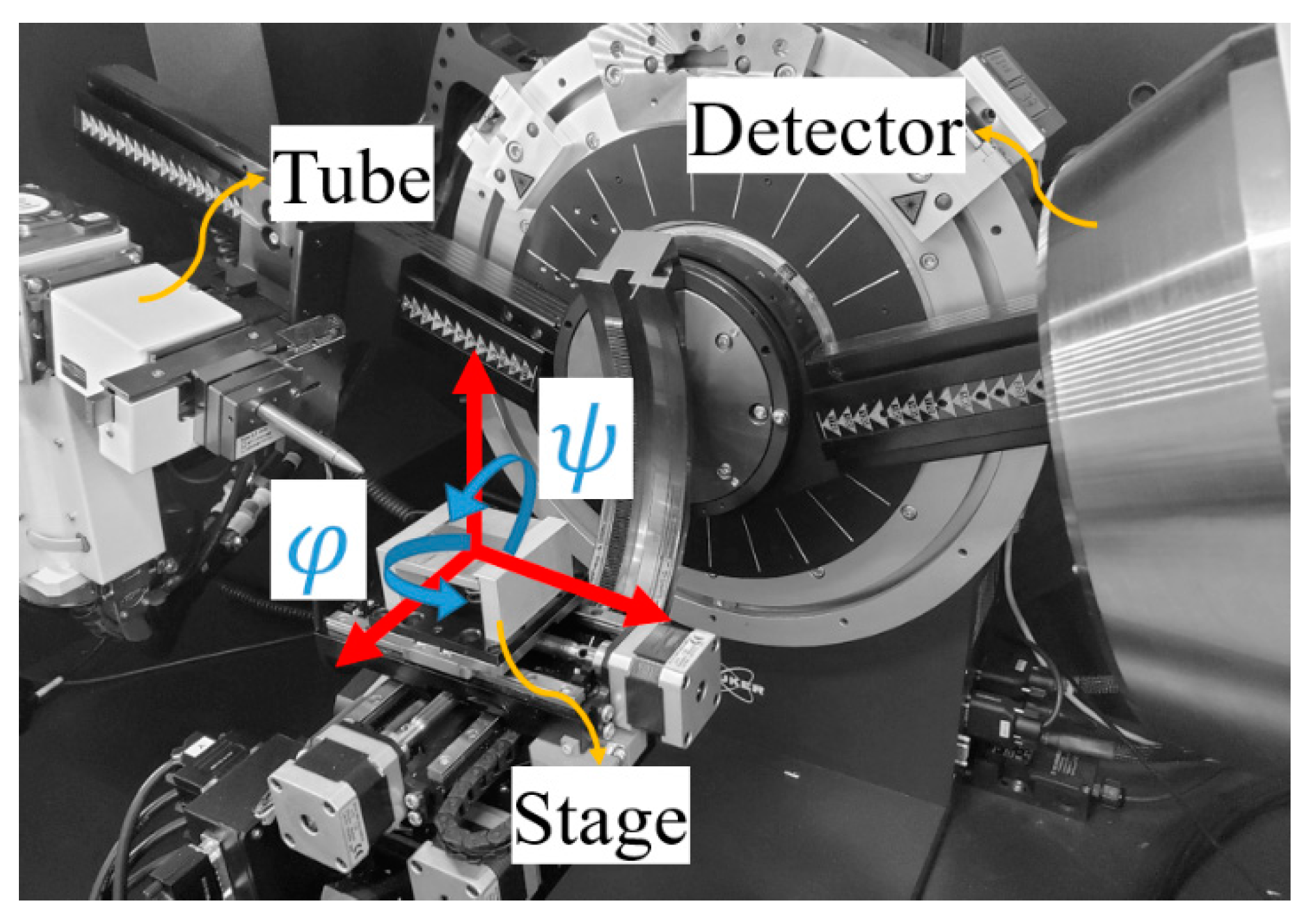
2.4. X-Ray Diffraction
2.5. Layer Removal for Through-Depth Measurement
2.6. Stress Correction Methods
2.7. Grazing-Incidence X-Ray Diffraction Method (GIXD)
2.8. Error Calculation
2.9. Hole Drilling
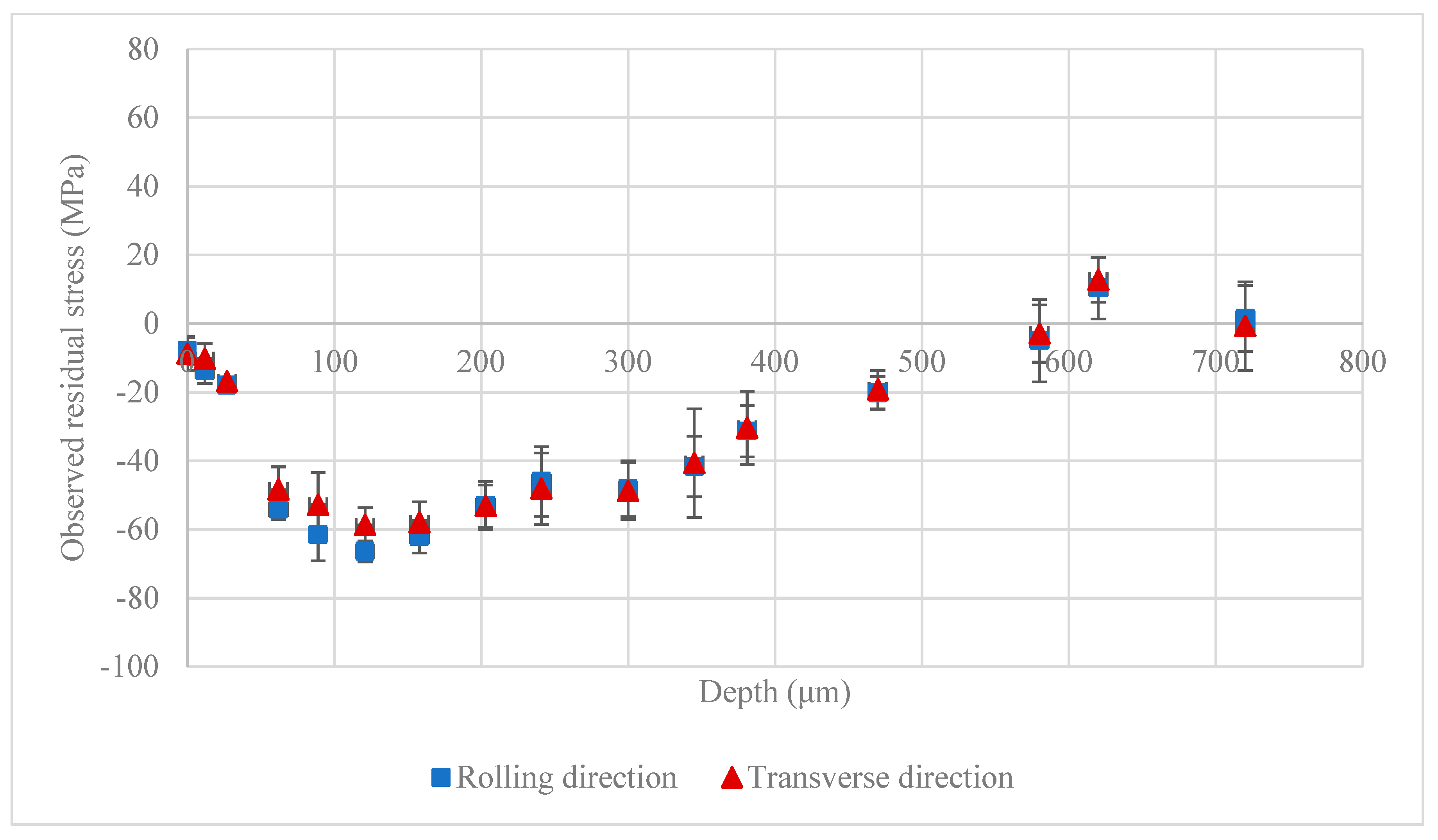
3. Results and Discussion
4. Conclusions and Further Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Evans, W.P. Residual Stress Measurement by X-Ray Diffraction. Soc. Automot. Eng. SAE HS784 2003, 74–79. [Google Scholar]
- Zhang, P.; Lindemann, J. Influence of shot peening on high cycle fatigue properties of the high-strength wrought magnesium alloy AZ80. Scr. Mater. 2005, 52, 485–490. [Google Scholar] [CrossRef]
- Liu, W.C.; Dong, J.; Zhang, P.; Korsunsky, A.M.; Song, X.; Ding, W.J. Improvement of fatigue properties by shot peening for Mg-10Gd-3Y alloys under different conditions. Mater. Sci. Eng. A 2011, 528, 5935–5944. [Google Scholar] [CrossRef]
- Liu, W.C.; Dong, J.; Zheng, X.W.; Zhang, P.; Ding, W.J. Influence of shot peening on notched fatigue properties of magnesium alloy ZK60. Mater. Sci. Technol. 2011, 27, 201–207. [Google Scholar] [CrossRef]
- Zinn, W.; Scholtes, B. Mechanical surface treatments of lightweight materials—Effects on fatigue strength and near-surface microstructures. J. Mater. Eng. Perform 1999, 8, 145–151. [Google Scholar] [CrossRef]
- Bagherifard, S.; Hickey, D.J.; Fintová, S.; Pastorek, F.; Fernandez-Pariente, I.; Bandini, M.; Webster, T.J.; Guagliano, M. Effects of nanofeatures induced by severe shot peening (SSP) on mechanical, corrosion and cytocompatibility properties of magnesium alloy AZ31. Acta Biomater. 2018, 66, 93–108. [Google Scholar] [CrossRef] [Green Version]
- Commin, L.; Dumont, M.; Masse, J.E.; Barrallier, L. Friction stir welding of AZ31 magnesium alloy rolled sheets: Influence of processing parameters. Acta Mater. 2009, 57, 326–334. [Google Scholar] [CrossRef] [Green Version]
- da Silva, E.P.; Oliveira, V.B.; Pereira, V.F.; Maluf, O.; Buzolin, R.H.; Pinto, H.C. Microstructure and Residual Stresses in a Friction Stir Welded Butt Joint of as-cast ZK60 Alloy Containing Rare Earths. Mater. Res. 2017, 20, 775–779. [Google Scholar] [CrossRef] [Green Version]
- Nitschke-Pagel, T.; Dilger, K. Residual Stress Condition of Tubular Laser Welds of an AZ31 Magnesium Alloy. Mater. Res. Proc. 2016, 2, 277–282. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Z.; Li, X.; Miao, Y.; Wu, G.; Zhao, Z. Numerical and experiment analysis of residual stress on magnesium alloy and steel butt joint by hybrid laser-TIG welding. Comput. Mater. Sci. 2011, 50, 1763–1769. [Google Scholar] [CrossRef]
- Coelho, R.S.; Kostka, A.; Pinto, H.; Riekehr, S.; Koçak, M.; Pyzalla, A.R. Microstructure and mechanical properties of magnesium alloy AZ31B laser beam welds. Mater. Sci. Eng. A 2008, 485, 20–30. [Google Scholar] [CrossRef]
- Kouadri, A.; Barrallier, L. Study of mechanical properties of AZ91 magnesium alloy welded by laser process taking into account the anisotropy microhardness and residual stresses by X-ray diffraction. Metall. Mater. Trans. A 2011, 42, 1815–1826. [Google Scholar] [CrossRef] [Green Version]
- Outeiro, J.C.; Batista, A.C.; Marques, M.J. Residual Stresses Induced by Dry and Cryogenic Cooling during Machining of AZ31B Magnesium Alloy. Adv Mater. Res. 2014, 996, 658–663. [Google Scholar] [CrossRef] [Green Version]
- Pu, Z.; Outeiro, J.C.; Batista, A.C.; Dillon, O.W.; Puleo, D.A.; Jawahir, I.S. Enhanced surface integrity of AZ31B Mg alloy by cryogenic machining towards improved functional performance of machined components. Int. J. Mach. Tools Manuf. 2012, 56, 17–27. [Google Scholar] [CrossRef]
- Hosaka, T.; Yoshihara, S.; Amanina, I.; Macdonald, B.J. Influence of Grain Refinement and Residual Stress on Corrosion Behavior of AZ31 Magnesium Alloy Processed by ECAP in RPMI-1640 Medium. Procedia Eng. 2017, 184, 432–441. [Google Scholar] [CrossRef]
- Kalatehmollaei, E.; Mahmoudi-Asl, H.; Jahed, H. An asymmetric elastic-plastic analysis of the load-controlled rotating bending test and its application in the fatigue life estimation of wrought magnesium AZ31B. Int. J. Fatigue 2014, 64, 33–41. [Google Scholar] [CrossRef] [Green Version]
- Marzbanrad, B.; Jahed, H.; Toyserkani, E. On the evolution of substrate’s residual stress during cold spray process: A parametric study. Mater. Des. 2018, 138, 90–102. [Google Scholar] [CrossRef]
- Shayegan, G.; Mahmoudi, H.; Ghelichi, R.; Villafuerte, J.; Wang, J.; Guagliano, M.; Jahed, H. Residual stress induced by cold spray coating of magnesium AZ31B extrusion. Mater. Des. 2014, 60, 72–84. [Google Scholar] [CrossRef]
- Shaha, S.K.; Marzbanrad, B.; Jahed, H. Influence of Cold Spray on the Microstructure and Residual Stress of Resistance Spot Welded Steel-Mg. In TMS Annual Meeting & Exhibition 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 635–644. [Google Scholar]
- Zhang, Y.; You, J.; Lu, J.; Cui, C.; Jiang, Y.; Ren, X. Effects of laser shock processing on stress corrosion cracking susceptibility of AZ31B magnesium alloy. Surf. Coatings Technol. 2010, 204, 3947–3953. [Google Scholar] [CrossRef]
- Behravesh, S.B.; Jahed, H.; Lambert, S. Fatigue characterization and modeling of AZ31B magnesium alloy. Int. J. Fatigue 2014, 64, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Behravesh, S.B. Fatigue Characterization and Cyclic Plasticity Modeling of Magnesium Spot-Welds. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2013. [Google Scholar]
- Toscano, D.; Shaha, S.K.; Behravesh, B.; Jahed, H.; Williams, B. Effect of Forging on Microstructure, Texture, and Uniaxial Properties of Cast AZ31B Alloy. J. Mater. Eng. Perform 2017, 26, 3090–3103. [Google Scholar] [CrossRef]
- Mos, Y.M.; Vermeulen, A.C.; Buisman, C.J.N.; Weijma, J. X-Ray Diffraction of Iron Containing Samples: The Importance of a Suitable Configuration. Geomicrobiol. J. 2018, 35, 511–517. [Google Scholar] [CrossRef] [Green Version]
- Bunaciu, A.A.; Udriştioiu, E.G.; Aboul-Enein, H.Y. X-Ray Diffraction: Instrumentation and Applications. Crit. Rev. Anal. Chem. 2015, 45, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Bisen, D.P.; Shukla, U.; Sharma, B.G. X-ray diffraction: A powerful method of characterizing nanomaterials. Recent Res. Sci. Technol. 2012, 4, 77–79. [Google Scholar]
- Takakuwa, O.; Soyama, H. Optimizing the Conditions for Residual Stress Measurement Using a Two-Dimensional XRD Method with Specimen Oscillation. Adv. Mater. Phys. Chem. 2013, 3, 8–18. [Google Scholar] [CrossRef] [Green Version]
- He, B. Two-Dimensional X-Ray Diffraction, 2nd ed; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- ASTM International. E1558-09. Standard Guide for Electrolytic Polishing of Metallographic Specimens, E1558-09. ASTM Int. 2014, 9, 1–13. [Google Scholar] [CrossRef]
- Hubbell, J.H.; Seltzer, S.M. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients (Version 1.4); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2004. [Google Scholar]
- Azanza Ricardo, C.L.; D’Incau, M.; Scardi, P. Revision and extension of the standard laboratory technique for X-ray diffraction measurement of residual stress gradients. J. Appl. Crystallogr. 2007, 40, 675–683. [Google Scholar] [CrossRef]
- Marciszko, M.; Baczmanski, A.; Wierzbanowski, K.; Wróbel, M.; Braham, C.; Chopart, J.-P.; Lodini, A.; Bonarski, J.; Tarkowski, L.; Zazi, N. Application of multireflection grazing incidence method for stress measurements in polished Al-Mg alloy and CrN coating. Appl. Surf. Sci. 2013, 266, 256–267. [Google Scholar] [CrossRef] [Green Version]
- Kania, B.; Indyka, P.; Tarkowski, L.; Beltowska-Lehman, E. X-ray diffraction grazing-incidence methods applied for gradient-free residual stress profile measurements in electrodeposited Ni coatings. J. Appl. Crystallogr. 2015, 48, 71–78. [Google Scholar] [CrossRef]
- Klaus, M.; Genzel, C. X-ray residual stress analysis on multilayer systems: An approach for depth-resolved data evaluation. J. Appl. Crystallogr. 2013, 46, 1266–1276. [Google Scholar] [CrossRef]
- Withers, P.J.; Preuss, M.; Webster, P.; Hughes, D.; Korsunsky, A.M. Residual strain measurement by synchrotron diffraction. Mater. Sci. Forum 2002, 1–12. [Google Scholar] [CrossRef]
- He, B. Measurement of Residual Stresses in Thin Films by Two-Dimensional XRD. Mater. Sci. Forum 2006, 524–525, 613–618. [Google Scholar] [CrossRef]
- Marciszko, M.; Baczmański, A.; Braham, C.; Wróbel, M.; Wroński, S.; Cios, G. Stress measurements by multi-reflection grazing-incidence X-ray diffraction method (MGIXD) using different radiation wavelengths and different incident angles. Acta Mater. 2017, 123, 157–166. [Google Scholar] [CrossRef]
- Baczmanski, A.; Braham, C.; Seiler, W.; Shiraki, N. Multi-reflection method and grazing incidence geometry used for stress measurement by X-ray diffraction. Surf. Coat. Technol. 2004, 182, 43–54. [Google Scholar] [CrossRef]
- Schajer, G.S. Measurement of Non-Uniform Residual Stresses Using the Hole-Drilling Method. Part II—Practical Application of the Integral Method. J. Eng. Mater. Technol. 1988, 110, 344–349. [Google Scholar] [CrossRef]
- ASTM E 837:08. Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gages. AIP Conf. Proc. 2008, 1, 1–17. [Google Scholar] [CrossRef]
- Honeycombe, R. The Plastic Deformation of Metals; St. Martin’s Press: New York, NY, USA, 1975. [Google Scholar]
- Stouffer, D.; Dame, L. Inelastic Deformation of Metals: Models, Mechanical Properties, and Metallurgy; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Guo, Z. The Deformation and Processing of Structural Materials; Woodhead Pub Limited: Sawston, UK; Cambridge, UK, 2005. [Google Scholar]






| Reference | Material | Process | Surface/In-Depth Measurement | X-Ray Source | Correction Applied |
|---|---|---|---|---|---|
| Zhang and Lindemann [2] | AZ80, Forged | Shot peening | In-depth | Cu-Kα | NA |
| Liu et al. [3] | Mg–10Gd–3Y, Extrusion | Shot peening | In-depth | NA | NA |
| Liu et al. [4] | ZK 60, Extrusion | Shot peening | In-depth | NA | NA |
| Zinn and Scholtes [5] | AZ31, Rolled | Shot peening | In depth | NA | NA |
| Bagherifard et al. [6] | AZ31, Rolled | Shot peening | In-depth | Cr-Kα | Yes |
| Commin et al. [7] | AZ31, Rolled | Friction stir welding | Surface | Cr-Kα | NA |
| Silva et al. [8] | ZK60, Cast | Friction stir welding | Surface | Co-Kα | NA |
| Nitschke-Pagel and Dilger [9] | AZ31B | Tubular laser welding | Surface | Cu-Kα | NA |
| Zeng et al. [10] | AZ31B, Rolled | Hybrid laser-TIG welding | Surface | NA | NA |
| Coelho et al. [11] | AZ31B, Rolled | Laser beam welding | Surface | NA | NA |
| Kouadri and Barrallier [12] | AZ91, Rolled | Laser beam welding | In-depth/Surface | Cr-Kα | NA |
| Outeiro et al. [13] | AZ31B, Rolled | Machining | In-depth | Cr-Kα | NA |
| Pu et al. [14] | AZ31B, Rolled | Machining | In-depth | Mn-Kα | NA |
| Hosaka et al. [15] | AZ31B, Extrusion | Equal-channel angular pressing | Surface | NA | NA |
| Kalatehmollaei et al. [16] | AZ31B, Extrusion | Machining | Surface | NA | NA |
| Marzbanrad et al. [17] | AZ31B, Rolled | Cold spray | Surface | Cu-Kα | NA |
| Shayegan et al. [18] | AZ31B, Extrusion | Cold spray | In-depth | Cr-Kα | Yes |
| Shaha et al. [19] | Mg alloy | Resistance spot welding | In-depth | NA | NA |
| Zhang et al. [20] | AZ31B, Rolled | Laser shock peening | In-depth | Cr-Kα | NA |
| Composition | Al | Zn | Mn | Mg |
|---|---|---|---|---|
| Weight% | 2.73 | 0.915 | 0.375 | Bal. |
| ψ (°) | φ (°) |
|---|---|
| 0 | 0 |
| 25 | 0, 45, 90, 135, 180, 225, 270, 315 |
| 50 | 0, 45, 90, 135, 180, 225, 270, 315 |
| ω (°) | z (μm) |
|---|---|
| 5 | 7.7 |
| 10 | 14.3 |
| 15 | 19.8 |
| 25 | 28.3 |
| 35 | 33.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yazdanmehr, A.; Jahed, H. On the Surface Residual Stress Measurement in Magnesium Alloys Using X-Ray Diffraction. Materials 2020, 13, 5190. https://doi.org/10.3390/ma13225190
Yazdanmehr A, Jahed H. On the Surface Residual Stress Measurement in Magnesium Alloys Using X-Ray Diffraction. Materials. 2020; 13(22):5190. https://doi.org/10.3390/ma13225190
Chicago/Turabian StyleYazdanmehr, Amir, and Hamid Jahed. 2020. "On the Surface Residual Stress Measurement in Magnesium Alloys Using X-Ray Diffraction" Materials 13, no. 22: 5190. https://doi.org/10.3390/ma13225190





