Analysis of Teacher-Student Interaction in the Joint Solving of Non-Routine Problems in Primary Education Classrooms
Abstract
:1. Introduction
- As regards cognitive processes, the greater the level of complexity of the task, the greater the proportion of the interaction devoted to reasoning.
- As regards level of participation of teachers and students, there will be a high participation of students in the cognitive processes aimed at reasoning in the resolution process, especially in tasks with a higher level of complexity.
2. Materials and Methods
2.1. Participants
2.2. Materials
2.3. Procedure and Analysis
- b.
2.4. Reliability
2.5. Measures
3. Results
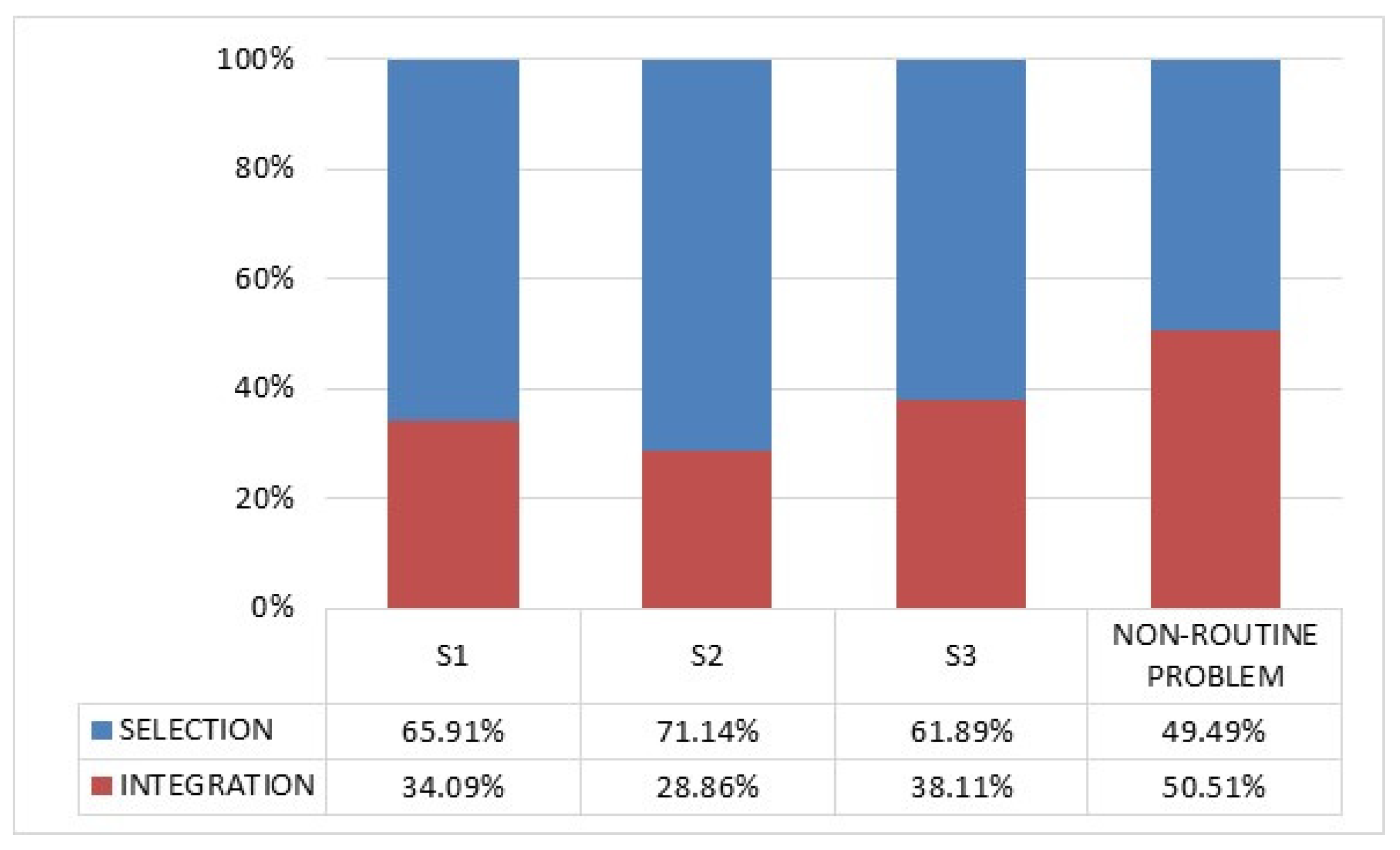
3.1. In Relation to Cognitive Processes
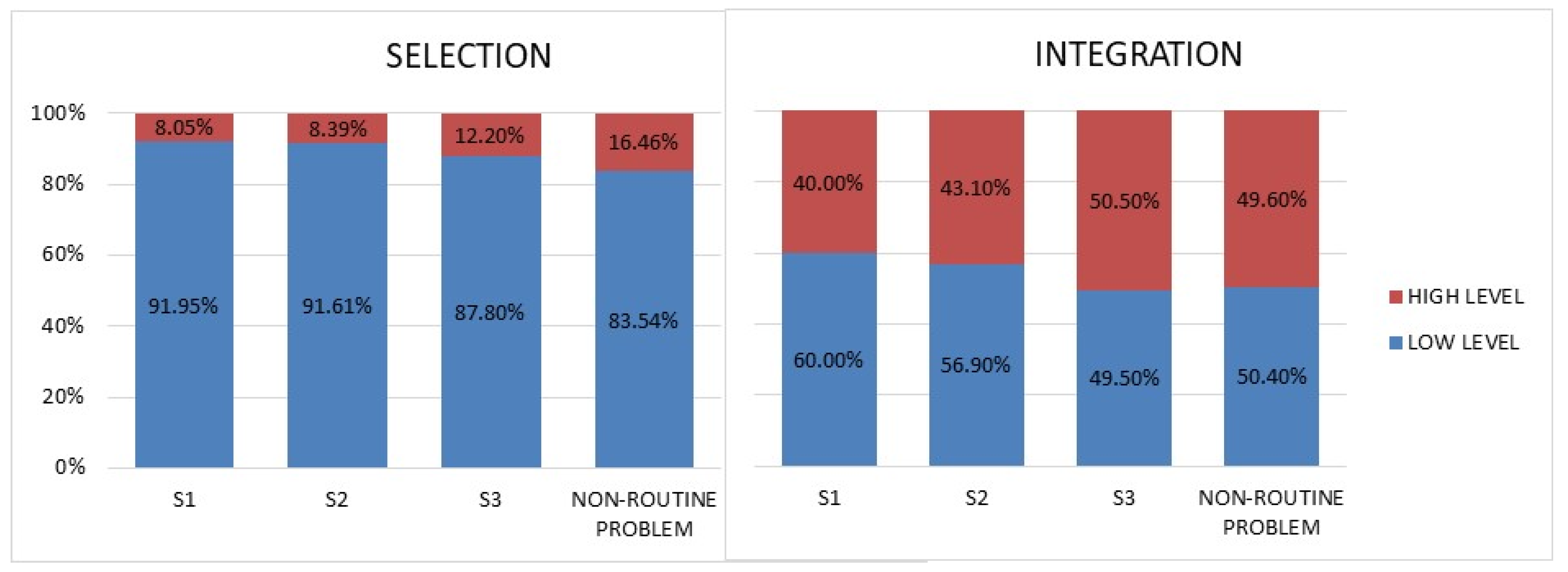
3.2. In Relation to Level of Participation
4. Discussion
4.1. In Relation to Process Cognitives
4.2. In Relation to Level of Participation
5. Conclusions
- Nonroutine problems pose a challenge for teachers and students as they are not used to working in the classroom with these types of problems [2,3]. When solving the nonroutine problem, reasoning was promoted to a greater extent by elaborating a more interesting interaction than when solving the routine problem [47]. In the latter, the differentiation established by the TIMSS to define its cognitive domains—knowing, applying, and reasoning—was so subtle that changes in teacher–students behavior in the solving process barely took place.
- In the solving of the nonroutine problem, students collaborated more. Furthermore, this collaboration was aimed at promoting reasoning. As has been said in the previous point, the concern or interest that this type of challenging task arouses causes the student’s interest to materialize in a question aimed at the promotion of reasoning [2,3].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Chapman, O. Classroom practices for context of mathematics Word problems. Educ. Stud. Math. 2006, 62, 211–230. [Google Scholar] [CrossRef]
- Depaepe, F.; De Corte, E.; Verschaffel, L. Teachers’ approaches towards Word problem solving: Elaborating or restricting the problem context. Teach. Teach. Educ. 2010, 26, 152–160. [Google Scholar] [CrossRef]
- Rosales, J.; Vicente, S.; Chamoso, J.M.; Muñez, D.; Orrantia, J. Teacher-student interaction in joint Word problem solving. The role of situational and mathematical knowledge in mainstream classrooms. Teach. Teach. Educ. 2012, 28, 1185–1195. [Google Scholar] [CrossRef]
- Kolovou, A.; van den Heuvel-Panhuizen, M.; Bakker, A. Non-routine problem solving tasks in Primary School Mathematics textbooks-a needle in a Haystack. Mediterr. J. Math. 2009, 8, 31–68. [Google Scholar]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Aksoy, Y.; Bayazit, I.; Kirnap, S.M. Prospective Primary school teachers’ proficiencies in solving real-words problems: Approaches, strategies and models. Eurasia J. Math. Sci. Technol. Educ. 2015, 11, 827–839. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Lester, F. Why is Teaching with Problem Solving Important to Student Learning? National Council of Teachers of Mathematics: Reston, VA, USA, 2010. [Google Scholar]
- Reusser, K.; Stebler, R. Every word problem has a solution: The suspension of reality and sense-making in the culture of school mathematics. Learn. Instr. 1997, 7, 309–328. [Google Scholar] [CrossRef]
- Webb, N.M.; Nemer, K.M.; Ing, M. Small group-reflections: Parallels between teacher discourse and student behavior in peer-directed groups. J. Learn. Sci. 2006, 15, 63–119. [Google Scholar] [CrossRef]
- Verschaffel, L.; De Corte, E.; Borghart, I. Pre-service teachers’ conceptions and beliefs about the role of real-world knowledge in mathematical modelling of school word problems. Learn. Instr. 1997, 7, 339–359. [Google Scholar] [CrossRef]
- Vicente, S.; Orrantia, J. Word problem solving and situational knowledge. Cult. Educ. 2007, 19, 61–85. [Google Scholar] [CrossRef]
- UNESCO. Education for Sustainable Development Goals—Learning Objectives; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2017. [Google Scholar]
- Verschaffel, L.; Depaepe, F.; Van Dooren, W. Word Problems in Mathematics Education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Arlsan, C.; Yazgan, Y. Common and flexible use of mathematical non routine problem solving strategies. Am. J. Educ. Res. 2015, 3, 1519–1523. [Google Scholar] [CrossRef]
- Verschaffel, L.; De Corte, E.; Lasure, S. Realistic considerations in mathematical modelling of school arithmetic word problems. Learn. Instr. 1994, 4, 273–294. [Google Scholar] [CrossRef]
- Inoue, N. Rehearsing to teach: Content-specific deconstruction of instructional explanations in pre-service teacher training. J. Educ. Teach. 2009, 35, 47–60. [Google Scholar] [CrossRef]
- Jiménez, L.; Ramos, F.J. The negative impact of the didactic contract in realistic problem solving: A study with second- and third-grade students. Rev. Electron. Investig. Psicoeduc. Psicopedag. 2011, 9, 1155–1182. [Google Scholar]
- Jiménez, L.; Verschaffel, L. Development of Children’s solutions of non-standard arithmetic word problem solving. Rev. Psicodidáctica 2014, 1, 93–123. [Google Scholar] [CrossRef] [Green Version]
- Woodward, J.; Beckmann, S.; Driscoll, M.; Franke, M.; Herzig, P.; Jitendra, A.; Koedinger, K.R.; Ogbuehi, P. Improving Mathematical Problem Solving in Grades 4 Through 8. Educator’s Practice Guide; U.S. Department of Education: Washington, DC, USA, 2012.
- Saygılı, S. Examining The Problem Solving Skills and The Strategies Used by High School Students in Solving Non-routine Problems. E-Int. J. Educ. Res. 2017, 8, 91–114. [Google Scholar]
- Mullis, I.V.S.; Martin, M.O.; Foy, P.; Hooper, M. TIMSS 2015 International Results in Mathematics. Retrieved from Boston College, TIMSS & PIRLS International Study Center. 2016. Available online: http://timssandpirls.bc.edu/timss2015/international-results/ (accessed on 11 July 2020).
- Hogan, K.; Pressley, M. Scaffolding Student Learning: Instructional Approaches and Issues; Brookline Books: Cambridge, MA, USA, 1997. [Google Scholar]
- Elbers, E. Classrroom interaction as reflection: Learning and teaching mathematics in a community of inquiri. Educ. Stud. Math. 2003, 54, 77–99. [Google Scholar] [CrossRef]
- Hiebert, J.; Wearne, D. Instructional task, classroom discourse and students’ learning in second grade. Am. Educ. Res. J. 1993, 30, 393–425. [Google Scholar] [CrossRef]
- Redfield, D.L.; Rousseau, E.W. A meta-analysis of experimental research on teacher questioning behavior. Rev. Educ. Res. 1981, 51, 237–245. [Google Scholar] [CrossRef]
- Franke, M.L.; Webb, N.M.; Chan, A.G.; Ing, M.; Freund, D.; Battey, D. Teacher questioning to elicit students’ mathematical thinking in elementary school classrooms. J. Teach. Educ. 2009, 60, 380–392. [Google Scholar] [CrossRef] [Green Version]
- Katalin, Z.; Körtesi, P.; Guncaga, J.; Szabo, D.; Neag, R. Examples of problem-solving strategies in Mathematics Education supporting the Sustainability of 21 st-Century Skills. Sustainability 2020, 12, 10113. [Google Scholar] [CrossRef]
- Mercer, N.; Littleton, K. Dialogue and the Development of Children’s Thinking; Routledge: London, UK, 2007. [Google Scholar]
- Radovic, D.; Preiss, D. Patrones de discurso observados en el aula de Matemáticas de segundo ciclo de básico en Chile. Psykhe 2010, 10, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Ames, C. Classrooms: Goals, structures, and student motivation. J. Educ. Psychol. 1992, 84, 261. [Google Scholar] [CrossRef]
- Deci, E.L.; Ryan, R.M.; Williams, G.C. Need satisfaction and the self-regulation of learning. Learn. Individ. Differ. 1996, 8, 165–183. [Google Scholar] [CrossRef]
- Bakker, A.; Smit, J.; Wegerif, R. Scaffolding and dialogic teaching in mathematics education: Introduction and review. ZDM 2015, 47, 1047–1065. [Google Scholar] [CrossRef] [Green Version]
- Nystrand, M. Research on the role of classroom discourse as it as affects Reading comprehension. Res. Teach. Engl. 2006, 40, 392–412. [Google Scholar]
- Wegerif, R. Dialogic: Education for the Internet Age; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Rosales, J.; Orrantia, J.; Vicente, S.; Chamoso, J.M. Studying mathematics problem-solving classrooms. A comparision between the discourse of in-service teachers and student teachers. Eur. J. Psychol. Educ. 2008, 23, 275–294. [Google Scholar] [CrossRef]
- Vicente, S.; Rosales, J.; Chamoso, J.M.; Múñez, D. Analyzing educational practice in Spanish Primary Education mathematics classes: A tentative explanation for students’ mathematical ability. Cult. Educ. 2013, 25, 535–548. [Google Scholar] [CrossRef]
- Nathan, M.J.; Knuth, E.J. A study of whole classroom mathematical discourse and teacher change. Cogn. Instr. 2003, 21, 175–207. [Google Scholar] [CrossRef]
- González, G.; DeJarnette, A.F. Teachers’ and students’ negotiation moves when teachers scaffold group work. Cogn. Instr. 2015, 33, 1–45. [Google Scholar] [CrossRef]
- Praetorius, A.K.; Pauli, C.; Reusser, K.; Rakoczy, K.; Klieme, E. One lesson is all you need? Stability of instructional quality across lessons. Learn. Instr. 2014, 31, 2–12. [Google Scholar] [CrossRef]
- Smart, J.B.; Marshall, J.C. Interactions between classroom discourse, teacher questioning, and student cognitive engagement in middle school science. J. Sci. Teach. Educ. 2013, 24, 249–267. [Google Scholar] [CrossRef]
- Turner, J.C.; Midgley, C.; Meyer, D.K.; Gheen, M.; Anderman, E.M.; Kang, Y.; Patrick, H. The classroom environment and students’ reports of avoidance strategies in mathematics: A multimethod study. J. Educ. Psychol. 2020, 94, 88–106. [Google Scholar] [CrossRef]
- Sánchez-Barbero, B.; Calatayud, M.; Chamoso, J.M. Analysis of the interaction of teachers when they solve realistic problems along with their students in primary classrooms, taking into account their teaching experience. Uni-pluri 2019, 19, 40–59. [Google Scholar] [CrossRef] [Green Version]
- Tahan, M. The Man Who Counted; EE.UU: New York, NY, USA, 1993. [Google Scholar]
- Wells, G. Dialogic Inquiry: Toward a Sociocultural Practice and Theory of Education; CUP: Cambridge, UK, 1999. [Google Scholar]
- Ilany, B.; Margolin, B. Language and Mathematics: Bridging between Natural Language and Mathematical Language in Solving Problems in Mathematics. Creat. Educ. 2010, 1, 138–148. [Google Scholar] [CrossRef] [Green Version]
- Paredes, S.; Cáceres, M.J.; Diego-Matecón, J.M.; Blanco, T.F.; Chamoso, J.M. Creating realistid mathematics tasks involving authenticity cognitive domains, and openness characteristics: A study with pre-service teachers. Sustainability 2020, 12, 9656. [Google Scholar] [CrossRef]
- Rosales, J.; Orrantia, J.; Vicente, S.; Chamoso, J.M. Arithmetic problema solving in the classroom: What do teachers do when they work jointly with students? Cult. Educ. 2008, 20, 423–439. [Google Scholar] [CrossRef]
- Verschaffel, L.; Greer, B.; De Corte, E. Making Sense of Word Problems; Swets y Zeitlinger: Leiden, The Netherlands, 2000. [Google Scholar]
- Gillies, R.M.; Khan, A. Promoting reasoned argumentation, problem-solving and learning during small-group work. Camb. J. Educ. 2009, 39, 7–27. [Google Scholar] [CrossRef]
- Hiebert, J.; Gallimore, R.; Garnier, H.; Givvin, K.B.; Hollingsworth, H.; Jacobs, J.; Chui, A.M.-Y.; Wearne, D.; Smith, M.; Kersting, N.; et al. Understanding and improving mathematics teaching: Highlights from the TIMSS 1999 Video Study. Phi Delta Kappan 2003, 84, 768–775. [Google Scholar]
- Cai, J. What research tells us about teaching mathematics through problem solving. In Research and Issues in Teaching Mathematics through Problem Solving; Lester, F., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 241–254. [Google Scholar]
- Lambdin, D.V. Benefits of teaching through problem solving. In Teaching Mathematics through Problem Solving: Prekindergarten-Grade 6; Lester, F., Charles, R.I., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 3–13. [Google Scholar]
- Kaur, B.; Yeap, B.H. Mathematical Problem Solving in Singapore School. In Mathematical Problem Solving: Yearbook; Kaur, B., Yeap, B.H., Kapur, M., Eds.; Association of Mathematics Education and World Scientific: Singapore, 2009; pp. 3–13. [Google Scholar]
- Singer, F.M.; Voica, C.; Pelczer, I. Cognitive styles in posing geometry problems: Implications for assessment of mathematical creativity. Int. J. Math. Educ. 2017, 49, 37–52. [Google Scholar] [CrossRef]
- Mabilangan, R.A.; Limpjap, A.A.; Belecina, R.R. Problem Solving Strategies of High School Students on non-rotuine problems. Alipato J. Basic Educ. 2011, 5, 23–47. [Google Scholar]
- Boston, M.D. Connecting changes in secondary mathematics teachers’ knowledge to their experiences in a profesional development workshop. J. Math. Teach. Educ. 2013, 16, 7–31. [Google Scholar] [CrossRef]
- Sullivan, P.; Askew, M.; Cheeseman, J.; Clarke, D.; Mornane, A.; Roche, A.; Walker, N. Supporting teachers in structuring mathematics lessons involving challenging tasks. J. Math. Teach. Educ. 2015, 18, 123–140. [Google Scholar] [CrossRef]

| Teacher | Experience (Years) | Geographical Scope | Students in Each Class (Number) |
|---|---|---|---|
| Teacher 1 | 32 | Rural 1 | 20 |
| Teacher 2 | 33 | Rural 2 | 22 |
| Teacher 3 | 28 | Urban 1 | 14 |
| Teacher 4 | 23 | Urban 2 | 23 |
| Teacher 5 | 23 | Urban 3 | 24 |
| Teacher 6 | 13 | Urban 4 | 11 |
| Teacher 7 | 13 | Urban 5 | 13 |
| Teacher 8 | 30 | Rural 3 | 21 |
| Teacher 9 | 25 | Rural 4 | 25 |
| Teacher 10 | 30 | Rural 5 | 22 |
| Categories | Definition | |
|---|---|---|
| Cognitive Processes | Selection | Aspects that are explicitly included in the problem’s statement or that arise, unjustified, in the solving process. |
| Integration | Aspects that relate or compare information or data that are explicitly included in the problem’s statement or that arise in the solving process in an adequate and justified way. | |
| Metacognitive Processes | Generalization | Aspects of the solving process that are more general than those considered in the problem. |
| Regulation | Aspects of the solving process that are related to planning (organization of the process), monitoring (assessment and observation of the process), and evaluation (definition of the advance and progress in producing the solution as well as assessment of the development of the process). | |
| Other Processes | Control | Aspects related to keeping attention focused and classroom order, or related to organization, with no relation whatsoever to the solving process. |
| Reading | Aspects related to the reading of the problem, which includes vocabulary definition prior to the solving process. |
| Categories | Indicators | |
|---|---|---|
| Low Level | T Level (teacher): Teacher autonomously. | The teacher begins the cycle, develops it individually during the entire intervention and can end it. |
| Ts Level (teacher–students): Teacher and student with greater teacher participation. | The teacher begins the cycle with a question or closed or invasive intervention. The teacher may end the cycle providing feedback. | |
| High Level | St Level (students–teacher): Teacher and student with greater student participation. | The teacher begins the cycle with an open-ended question or intervention that is adequately answered by the student. If the teacher ends the building of the main idea of the cycle, it will be St Level. The teacher may end the cycle providing feedback. |
| S Level (students): Student autonomously. | The student begins the cycle, although the teacher can also do so by returning to the participation of a student in a previous cycle and can end it. | |
| Cycles (0.99) | Transcription | Processes | Level of Participation (0.94) | |
|---|---|---|---|---|
| Public Content (0.84) | Category (0.94) | |||
| 1 | Teacher: It is about completing with the tables, isn’t it? Let’s see. Student: Mountain bike rental.1 h, price 8; 2 h, price 11. Teacher: Price 11. | “Mountain bikes 1 h, €8; 2 h, €11, …” | Selection | Low Level |
| 2 | Teacher: Why is the price 11? Let’s see, Pablo. How do we know that the price is 11? Student: Because you must add 8 plus 3. Teacher: 8 plus 3. Student: Yes. Teacher: That is, 8 that is the price of an hour, the first one. | “Two hours are €11 because the first hour costs €8 and the second €3, so €8 plus €3, €11” | Integration | High Level |
| 3 | Teacher: And the second hour, how much does it cost? Student: 3. Teacher: 3. So that you already pay €11, don’t you? For two hours, €11. | “The second hour is €3, and two hours are €11” | Selection | Low Level |
| 4 | Teacher: Then, after 3 h? Student: 14 Teacher: 14. | “3 h are €14” | Selection | Low Level |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Barbero, B.; Chamoso, J.M.; Vicente, S.; Rosales, J. Analysis of Teacher-Student Interaction in the Joint Solving of Non-Routine Problems in Primary Education Classrooms. Sustainability 2020, 12, 10428. https://doi.org/10.3390/su122410428
Sánchez-Barbero B, Chamoso JM, Vicente S, Rosales J. Analysis of Teacher-Student Interaction in the Joint Solving of Non-Routine Problems in Primary Education Classrooms. Sustainability. 2020; 12(24):10428. https://doi.org/10.3390/su122410428
Chicago/Turabian StyleSánchez-Barbero, Beatriz, José María Chamoso, Santiago Vicente, and Javier Rosales. 2020. "Analysis of Teacher-Student Interaction in the Joint Solving of Non-Routine Problems in Primary Education Classrooms" Sustainability 12, no. 24: 10428. https://doi.org/10.3390/su122410428






