Preliminary Evaluation of a Rooftop Grid-Connected Photovoltaic System Installation under the Climatic Conditions of Texas (USA)

Abstract

Solar photovoltaic (PV) systems have demonstrated growing competitiveness as a viable alternative to fossil fuel-based power plants to mitigate the negative impact of fossil energy sources on the environment. Notwithstanding, solar PV technology has not made yet a meaningful contribution in most countries globally. This study aims to encourage the adoption of solar PV systems on rooftop buildings in countries which have a good solar energy potential, and even if they are oil or gas producers, based on the obtained results of a proposed PV system. The performance of a rooftop grid-tied 3360 kW_p PV system was analyzed by considering technical, economic, and environmental criteria, solar irradiance intensity, two modes of single-axis tracking, shadow effect, PV cell temperature impact on system efficiency, and Texas A&M University as a case study. The evaluated parameters of the proposed system include energy output, array yield, final yield, array and system losses, capacity factor, performance ratio, return on investment, payback period, Levelized cost of energy, and carbon emission. According to the overall performance results of the proposed PV system, it is found to be a technically, economically, and environmentally feasible solution for electricity generation and would play a significant role in the future energy mix of Texas.

1. Introduction

Solar photovoltaic (PV) systems are a promising technology through offering a significant potential for providing energy in a sustainable way. Access to PV energy will play a critical role in shifting consumption toward low-carbon electricity. Thus, PV systems on the roof of buildings can be adopted as one of the major future sources of electricity generation mix due to drastic reduction in PV module cost, faster installation than other renewable energy technologies, avoidance of land costs, minimized grid transmission line cost and lessening dependence on fossil fuels. According to the International Energy Agency (IEA), the cost of PV modules and systems have declined by 80% and 67% of their initial cost, respectively. Furthermore, PV systems’ contribution to global electricity generation is forecast to increase to 16% by 2050, compared with 11% in 2010, and this would avoid up to 4 gigatons of annual greenhouse gases (GHGs) emissions [1].

The feasibility, proper design, and operating performance of PV systems at a selected site are influenced by the meteorological and geographic parameters such as solar radiation intensity, temperature, relative humidity, wind speed, sunshine duration, cleanness index, cloud cover, geographical site, etc. [2]. PV module characteristics, sun-tracker system, inverter and control systems, and wiring are factors that also affect the performance of PV systems [3]. The most common solar PV systems are stand-alone systems (off-grid systems) and grid-connected systems (on-grid systems) [4]. Each type of system shares roughly half of the global market. PV expansion in self-consumption of using PV electricity directly at the same site, especially on the rooftop of buildings, may raise concerns for recovering the fixed capital costs of grids, therefore, the deployment of PV systems on rooftops should be designed to ensure a fair allocation of costs and full grid cost recovery [1]. Many studies have been conducted on various solar PV systems installed on building rooftops in different sites around the world. The performance evaluation of a 1.72 kW_p photovoltaic system installed on the flat roof of a 12 m high building in Dublin (Ireland) was carried out based on a monthly, seasonal and annual basis by [5], including the calculation of parameters such as final yield, reference yield, array yield, system losses, array capture losses, cell temperature losses, PV module efficiency, system efficiency, inverter efficiency, performance ratio and capacity factor. Performance predictions were performed in [6] to study energy loss, energy outputs, and degradation of a 200 kW roof-integrated crystalline photovoltaic (PV) system in India based on an evaluation of the capacity factor (CF), performance ratio (PR), and efficiencies. The findings of a performance assessment for a grid-connected PV system with capacity of 2.07 kW_p installed on the roof of a building in Norway indicated that the PV system is technically feasible and could play a significant role in the future energy mix of the country [7]. To encourage the use of solar PV systems in government, commercial and residential buildings in Morocco [8], the performance of a 5 kW_p grid-connected PV system installed on the roof of a government building was assessed daily. The assessment included energy output, final yield, modules temperature, efficiency module, performance ratio (PR), etc. The annual performance parameters of an 11.2 kW_p grid-connected PV system installed on the rooftop of a constituent institute of Siksha ‘O’Anusandhan University (Bhubaneswar, India) were studied. The notable finding from this study is the PV system can be a feasible solution for power supply in eastern India and other states [9]. An analysis of economic performance and energy loss of 80 kW_p grid-connected installed on a rooftop on the GRT IET Campus (Thiruthani, India) was performed [10] through calculating the performance ratio and the various power losses (power electronics, temperature, soiling, internal, network, grid availability, and interconnection). The solar PV system showed a remarkable annual reduction of CO₂ emissions (i.e., eco-friendly for the environment). The long-term assessment of operating and feasibility for grid-tied PV systems on the roof-top of buildings at Najah National University in Palestine was carried out by [11]. Data from three years of electrical supply to the grid showed that the system performance and its output were steady during the operation period. The central role of operating temperature in the PV conversion process was discussed by [12,13]. The studies show that the power output of a PV module and its efficiency depend linearly on the operating temperature, which is presented in algebraic form in suitable tabulations, and their values will decrease with increasing cell/module operating temperature. Study [14] offers a tool to evaluate the performances of a 960 kWp photovoltaic system, which is divided into two subfields with different tilt angle (3–15°) and different nominal powers (353.3 kW_p and 606.6 kW_p). The system was installed on the parking lots on the campus of the University of Salento (Apulia, Italy) or it can be used for any PV system that would be installed in sites with climatic characteristics similar to southeastern Italy. Additionally, the tool is also useful to make a comparison by investigating the productivity of PV plants placed in various sites. According to another study in Kuwait [15], installing PV systems on the rooftop of buildings can be considered a unique and important feature. These systems could provide a combination of relatively large, unutilized, proper areas. Therefore, they would make the process of distribution and generation of solar power is possible on the national level. a general overview of one of the European projects in the PV sector located on the campus of the University of Jaen (Spain) was presented. The project consists of four grid-connected PV systems of 200 kW_p that fully integrated into the university buildings to provide more than 8% of its electricity needs. Furthermore, the possibilities of replicating the application of architectural integration of the PV system in other regional places were discussed [16]. Multiple studies were conducted to analyze the PV systems performance in Saudi Arabia; the effect of some factors on the PV system’s performance on the building rooftops was analyzed by considering structural, services, accessibility, maintenance, and others. The PVsyst software was used to optimize the system efficiency and space utilization and it found that tilted installations are more efficient (i.e., by about 9%) than horizontal ones [17]. The performance of various PV module technologies including sc-Si, mc-Si, and a-Si/μc-Si was evaluated in three Peruvian sites under desert climate conditions. This study was carried out to overcome the lack of outdoor behavior data of this technology specific to Peru in the literature and define the detrimental impact of high temperature and low irradiance losses on the PV system performance [18]. Another study at the King Fahd University of Petroleum and Minerals campus (Dhahran, Saudi Arabia) showed that installing environmentally-friendly technologies like PV systems on the rooftop of buildings can significantly help the building and energy sectors become more sustainable due to the notable savings in greenhouse gas emissions and meeting over 16% of the total energy requirements of the campus [19].

This work aims to study the solar potential at a selected site and the performance of the proposed solar PV system that is roof-mounted and grid-connected to encourage countries or regions which have a good potential for solar energy, even if they are oil or gas producers as is the case of Texas (USA), for implementing PV systems. These PV systems could contribute effectively to reducing reliance on fossil-fuel-burning power plants and addressing the energy and environmental challenges of the rapid growth of the building sector. The performance evaluation is carried out using technical, economic, and environmental criteria. To consider the effect of the incidence angle on the amount of the total solar radiation falling on PV module surface, two tracking modes are adopted. The effect of shadow and climatic conditions on the PV system are investigated by considering the required space between PV arrays and PV cell temperature variations. The performance results of this study are compared with other PV systems installed in different sites globally. Furthermore, it is worth noting that this work is the first study that is done hypothetically in Texas based on theoretical analysis whereas all previous studies, which are used for comparison with this study, have been done based on experimental results.

2. General Description

2.1. Site and Meteorological Data

The grid-connected system (on-grid system) is proposed to install on the rooftops of buildings located in the east part of Texas A&M University (TAMU, College Station, TX, USA). This location is known for its relatively high solar energy potential with a subtropical climate and mild temperature. Summers are mostly hot and humid, while the winters are short. The wind speed is commonly in the range of light breeze or gentle breeze. Geographic information of the city of College Station is presented in

Table 1. Geographic information of College Station.

Area	132.87 km2
Altitude	100 m
Latitude	30.6280° N
Longitude	96.3344° W

.

The meteorological data for College Station as extracted from National Solar Radiation Data Base (NSRDB) are summarized in Appendix A, which presents average hourly dry bulb temperature (^◦C), average hourly direct solar irradiance (W/m²), average hourly diffuse solar irradiance (W/m²), average hourly solar incidence angle (degree), monthly mean relative humidity (%), and monthly mean wind speed (mph).

2.2. PV System

The grid-connected systems proposed in the present study are installed on the rooftops of buildings on the east campus of Texas A&M University. This type of PV system can be competitive economically and technically through eliminating the expense of storage devices like batteries by connecting the PV system, which consists of PV arrays, inverters, and transformers as shown in Figure 1, directly to the grid and the surplus or deficiency in the energy production may be manipulated by the mutual feeding (forward and backward feed).

Each PV system consists of monocrystalline silicon modules (each of 350 W capacity) that are connected in series to make an array and such arrays are arranged in parallel. The PV module and inverter specifications are given in Appendix B The entire PV systems can be mounted on metal frames, which may be supported by concrete pillars. To enable the PV systems to track the sun and to raise the amount of solar radiation falling on a PV module surface per unit area in proportion to the cosine of the incidence angle, two modes of tracking are employed based on their movements: horizontal E–W axis with N–S track, and horizontal N–S axis with E–W track.

3. Performance Analysis Methodologies

The performance analysis of the PV system can be performed by considering different parameters for technical, economic, and environmental aspects.

3.1. Technical Analysis

3.1.1. Calculation of Utilizable Rooftop Area

The calculation of areas available on the rooftop of buildings is the first step toward meeting the design requirements. In terms of roof construction, most TAMU buildings have flat rooftops that offer a significant advantage to facilitate the installation of PV systems.

3.1.2. Calculation of PV Modules Number Considering Shading Effect and Air Circulation

In order to determine properly the number of PV modules required for installation on the rooftop of each building, a roof spacing analysis is performed to calculate the actual space that is required for installing solar panels considering the shadow effect and air circulation behind the modules. The shading impact of neighboring PV modules is critical for obtaining the optimal design of PV systems, especially in a certain period of the day (i.e., near sunrise and sunset). Therefore, the disregarding of the shading effect can be contributing to reducing the efficiency of PV modules by approximately 20% [20]. The shading effect on the PV system can be considered by identifying several parameters such as the dimensions of modules, space between modules, tilt angle, latitude, etc. [21]. To avoid the shading effect in this work, the spacing between adjacent PV modules, which are arranged one behind another in rows to face the sun as shown in Figure 2, is calculated by using the solar angles and spacing distance expressions [22].

The solar angles are calculated as follows:

$$\mathrm{Solar}\mathrm{altitude}\mathrm{angle}\left(\mathsf{\alpha }\right)=90-\mathrm{Solar}\mathrm{zenith}\mathrm{angle}(\mathsf{\varphi })$$

(1)

$$\mathrm{Solar}\mathrm{altitude}\mathrm{angle}\left(\mathsf{\alpha }\right)=90-\left|\mathrm{Solar}\mathrm{zenith}\mathrm{angle}(\mathsf{\varphi })-\mathrm{Declination}\left(\mathsf{\delta }\right)\right|$$

(2)

$$\cos \mathsf{\varphi }=\sin \mathsf{\alpha }=\sin \mathrm{L}\times \sin \mathsf{\delta }+\cos \mathrm{L}\times \cos \mathsf{\delta }\times \cos \mathrm{h}$$

(3)

$$\mathsf{\delta }=23.45\sin [\frac{360}{365}\left(284+\mathrm{N}\right)]$$

(4)

$$\mathrm{h}=\pm 0.25\times \left(\mathrm{Number}\mathrm{of}\mathrm{minutes}\mathrm{from}\mathrm{local}\mathrm{solar}\mathrm{noon}\right)$$

(5)

where L is the Latitude, $\mathrm{h}$ is the hour angle, δ = 0° (Fall and Spring Equinox), δ = ± 23.45° (Winter and Summer Solstice).

The spacing distance (m) is given by the following expression:

$${\mathrm{D}}_{\mathrm{S}}={\mathrm{H}}_m\times \left(\cos \mathsf{\alpha }/\sin \mathsf{\alpha }\right)$$

(6)

where ${\mathrm{D}}_{\mathrm{S}}$ is the spacing distance between two rows, and ${\mathrm{H}}_m$ is the height of a module from ground.

In addition, the module tilt angle (β) will be considered equal to the latitude (L) of the proposed site. However, the solar radiation on the tilted module increases with latitude. The maximum shadow length in the northern hemisphere will be determined on December 22 that can be considered the worst scenario of the shading effect.

The total space area required for each module can be calculated by:

$${\mathrm{A}}_{\mathrm{spa}}=({\mathrm{D}}_{\mathrm{s}}+{\mathrm{D}}_{\mathrm{m}})\times \mathrm{Y}$$

(7)

where ${\mathrm{A}}_{\mathrm{spa}}$, ${\mathrm{D}}_{\mathrm{s}}$, ${\mathrm{D}}_{\mathrm{m}}$, and Y denote the total space of a PV module, spacing distance between two rows, spacing distance under a PV module, length of a PV module, respectively. Therefore, the total number of PV modules is calculated by the following general formula:

$${\mathrm{N}}_{\mathrm{m}}=({\mathrm{A}}_{\mathrm{R}}\times {\mathrm{F}}_{\mathrm{U}})/{\mathrm{A}}_{\mathrm{spa}}$$

(8)

where ${\mathrm{N}}_{\mathrm{m}}$, ${\mathrm{A}}_{\mathrm{R}}$, and ${\mathrm{F}}_{\mathrm{U}}$ denote the total number of PV modules, total roof area, utilization factor, respectively.

3.1.3. Calculation of Total Solar Radiation on Tilted PV Modules

An increase in the amount of incident solar radiation (including beam, diffuse, and ground-reflected irradiance) on PV modules and reduce reflection and cosine losses require installing the modules in an inclined setting. However, most solar estimated or measured data are obtainable for horizontal surfaces or for normal incidence [22]. For that reason, there is a necessity to alter these data properly by using the following equations [22] to calculate the amount of radiation on tilted modules.

The monthly average hourly beam irradiance on a tilted surface (Wh/m²) is given by [22]:

$${\mathrm{I}}_{\mathrm{B}}={\mathrm{I}}_{\mathrm{B},\mathrm{n}}\times \cos \mathsf{\theta }$$

(9)

where ${\mathrm{I}}_{\mathrm{B},\mathrm{n}}$ is the monthly average hourly beam irradiance for normal incidence (Wh/m²), and $\mathsf{\theta }$ is the incident angle (°).

The monthly average hourly diffuse irradiance on a tilted surface (Wh/m²) is given by [22]:

$${\mathrm{I}}_{\mathrm{D}}={\mathrm{I}}_{\mathrm{D},\mathrm{n}}\times \left[ \frac{1+\cos \mathsf{\beta }}{2}\right]$$

(10)

where ${\mathrm{I}}_{\mathrm{D},\mathrm{n}}$ is the monthly average hourly diffuse irradiance for normal incidence (Wh/m²), $\mathsf{\beta }$ is the tilt angle (°).

The monthly average hourly ground-reflected irradiance on a tilted surface (Wh/m²) is given by [22]:

$${\mathrm{I}}_{\mathrm{GR}}={\mathsf{\rho }}_{\mathrm{G}}\times \left({\mathrm{I}}_{\mathrm{B},\mathrm{n}}+{\mathrm{I}}_{\mathrm{D},\mathrm{n}}\right).\left[\frac{1-\cos \mathsf{\beta }}{2}\right]$$

(11)

where, ${\mathsf{\rho }}_{\mathrm{G}}$ = Ground albedo (based on surface type).

Consequently, the total absorbed solar irradiance on a tilted surface (Wh/m²) is calculated as follows:

$${\mathrm{I}}_{\mathrm{t}}={\mathrm{I}}_{\mathrm{B}}+{\mathrm{I}}_{\mathrm{D}}+{\mathrm{I}}_{\mathrm{GR}}$$

(12)

Additionally, the tracking systems can contribute efficiently to enable PV modules to track the sun and enhance their performance by utilizing various modes of tracking. These tracking mechanisms are classified into a single-axis tracking mode and two axes tracking mode based on their motion. A single-axis mode can be controlled to move in various tracks: parallel to the earth’s axis, east-west, and north-south [22]. In this study, two tracking modes, which represent horizontal E–W axis with N–S tracking and horizontal N–S axis with E–W tracking, have been adopted to consider the effect of the incidence angle on calculation of the amount of the total solar radiation that strikes PV arrays’ surface per unit area, as in the following expressions [22]:

$$\cos {\mathsf{\theta }}_{\mathrm{E}-\mathrm{W}}=\sqrt{{\sin }^2\left(\mathsf{\alpha }\right)+{\cos }^2\left(\mathsf{\delta }\right)\times {\sin }^2\left(\mathrm{h}\right)}$$

(13)

$$\cos {\mathsf{\theta }}_{\mathrm{N}-\mathrm{S}}=\sqrt{{\sin }^2\left(\mathsf{\delta }\right)+{\cos }^2\left(\mathsf{\delta }\right)\times {\sin }^2\left(\mathrm{h}\right)}$$

(14)

where ${\mathsf{\theta }}_{\mathrm{E}-\mathrm{W}}$ is the incidence angle for a tilted surface rotated about horizontal N–S axis with E W tracking (o), and ${\mathsf{\theta }}_{\mathrm{N}-\mathrm{S}}$ is the Incidence angle for a tilted surface rotated about horizontal E–W axis with N–S tracking (o).

3.1.4. Calculation of Operating Temperature Effect on PV Modules Efficiency

The operating temperature of a solar PV module plays a significant role in determining its efficiency and electric power output. Therefore, the performance of the PV module can be impacted negatively by elevated temperatures, causing it to dissipate some of the absorbed solar energy to the environment in the form of heat, instead of being converted into electricity [12]. The PV electrical efficiency of modules can be defined as the ratio of the electrical output of the cell to the cell irradiation, and it is assumed to decrease linearly with PV module temperature [23], as in the following expression:

$${\mathsf{\eta }}_{\mathrm{e}}={\mathsf{\eta }}_{\mathrm{ref}}\times \left[1-{\mathsf{\beta }}_{\mathrm{ref}}\times ({\mathrm{T}}_{\mathrm{c}}-{\mathrm{T}}_{\mathrm{ref}})\right]$$

(15)

where ${\mathsf{\eta }}_{\mathrm{ref}}$ is the module efficiency evaluated at the reference temperature ${\mathrm{T}}_{\mathrm{ref}}$, which is equal to the normal operating cell temperature ${\mathrm{T}}_{\mathrm{NOCT}},{\mathsf{\beta }}_{\mathrm{ref}}$ is the fractional decrease of module efficiency per unit temperature increase, and ${\mathrm{T}}_{\mathrm{c}}$ is module operating temperature, which is calculated as in the expression 16. ${\mathsf{\eta }}_{\mathrm{ref}}$ and ${\mathsf{\beta }}_{\mathrm{ref}}$ are normally offered by the PV module manufacturer:

$${\mathrm{T}}_{\mathrm{c}}={\mathrm{T}}_{\mathrm{a}}+\left(\frac{{\mathrm{T}}_{\mathrm{ref}}-20}{800}\right)\times {\mathrm{I}}_{\mathrm{t}}$$

(16)

where ${\mathrm{T}}_{\mathrm{a}}$ is the air temperature.

3.1.5. Calculations of PV System Energy Output

The solar thermal power which is absorbed per unit area of a PV system, can be determined using the following expression:

$${\mathrm{E}}_{\mathrm{sun}\to \mathrm{PV}\mathrm{system}}\left(\frac{\mathrm{kWh}}{\mathrm{d}}\right)={\mathrm{I}}_{\mathrm{t}}\times {\mathrm{A}}_{\mathrm{m}}\times {\mathrm{N}}_{\mathrm{m}}$$

(17)

where ${\mathrm{I}}_{\mathrm{t}}$ is monthly average daily of total absorbed solar irradiance on a tilted surface, and ${\mathrm{A}}_{\mathrm{m}}$ is the area of a PV module.

The DC energy output generated from a PV system is obtained by:

$${\mathrm{E}}_{\mathrm{PV}\mathrm{system}\to \mathrm{DC}\mathrm{energy}}\left(\frac{\mathrm{kWh}}{\mathrm{d}}\right)={\mathrm{I}}_{\mathrm{t}}\times {\mathrm{A}}_{\mathrm{m}}\times {\mathrm{N}}_{\mathrm{m}}\times {\mathsf{\eta }}_{\mathrm{e}}$$

(18)

The electrical grid is designed to transport alternating current (AC). However, the energy generated by a PV system is direct current (DC) that needs to be converted to AC before injecting it into the grid. Inverters with a variety of designs and sizes can be utilized for this purpose to be the most appropriate to the nominal PV system power [22]. The AC energy output from the inverter, which is available to the grid, can be determined from:

$${\mathrm{E}}_{\mathrm{DC}\mathrm{energy}\to \mathrm{AC}\mathrm{energy}}\left(\mathrm{kWh}/\mathrm{d}\right)={\mathrm{E}}_{\mathrm{PV}\mathrm{system}\to \mathrm{DC}\mathrm{energy}}\times {\mathsf{\eta }}_{\mathrm{inv}}$$

(19)

where ${\mathsf{\eta }}_{\mathrm{inv}}$ is the inverter efficiency.

Therefore, the actual energy delivered to the distribution grid is calculated by accounting for the system efficiency that is comprised of the PV module efficiency, electrical efficiency (operating temperature effect), inverter efficiency, distribution losses ${\mathsf{\eta }}_{\mathrm{dist}.\mathrm{loss}}$ [14], and grid absorption rate ${\mathsf{\eta }}_{\mathrm{grid}\mathrm{abs}.}$ [14], as in the following expression:

$${\mathrm{E}}_{\mathrm{AC}\mathrm{energy}\to \mathrm{distribution}\mathrm{grid}}\left(\frac{\mathrm{kWh}}{\mathrm{d}}\right)={\mathrm{E}}_{\mathrm{DC}\mathrm{energy}\to \mathrm{AC}\mathrm{energy}}\times {\mathsf{\eta }}_{\mathrm{dist}.\mathrm{loss}}\times {\mathsf{\eta }}_{\mathrm{grid}\mathrm{abs}.}$$

(20)

3.1.6. Performance Analysis of PV System

There are several significant parameters that can be computed to analyze the performance of the grid-connected PV system of a given site. These parameters include array yield (${\mathrm{Y}}_{\mathrm{a}}$), final yield (${\mathrm{Y}}_{\mathrm{f}}$), reference yield (${\mathrm{Y}}_{\mathrm{r}}$), performance ratio ($\mathrm{PR}$), and capacity factor ($\mathrm{CF}$).

The array yield is defined as the DC energy output from a PV array during the monitored period (kWh/d) divided by its rated power (kW), as follows [5]:

$${\mathrm{Y}}_{\mathrm{a}}=\frac{{\mathrm{E}}_{\mathrm{PV}\mathrm{system}\to \mathrm{DC}\mathrm{energy}}}{{\mathrm{P}}_{\mathrm{nominal}}}$$

(21)

The reference yield is the ratio of the total absorbed solar irradiance on a tilted surface (Wh/m²/d) and the PV’s reference irradiance (1000 W/m² in STC conditions), as follows [5]:

$${\mathrm{Y}}_{\mathrm{f}}=\frac{{\mathrm{E}}_{\mathrm{DC}\mathrm{energy}\to \mathrm{AC}\mathrm{energy}}}{{\mathrm{P}}_{\mathrm{nominal}}}$$

(22)

The reference yield is the ratio of the total absorbed solar irradiance on a tilted surface (Wh/m²/d) and the PV’s reference irradiance (1000 W/m² in STC conditions), as follows [5]:

$${\mathrm{Y}}_{\mathrm{r}}=\frac{{\mathrm{I}}_{\mathrm{t}}}{{\mathrm{I}}_{\mathrm{r}}}$$

(23)

The performance ratio (PR) is the ratio of final yield and the reference yield, as in the following expression [5,24]:

$$\mathrm{PR}=\frac{{\mathrm{Y}}_{\mathrm{f}}}{{\mathrm{Y}}_{\mathrm{r}}} \times 100$$

(24)

The capacity factor during the nominated period is the AC energy output from the inverter divided by the AC energy that can be produced if the PV system operated with its nominal power during that same period (t), as in the following expression [5,25]:

$$\mathrm{CF}=\frac{{\mathrm{E}}_{\mathrm{DC}\mathrm{energy}\to \mathrm{AC}\mathrm{energy}}}{{\mathrm{P}}_{\mathrm{nominal}}.\mathrm{t}} \times 100$$

(25)

Additionally, the loss analysis is necessary to evaluate its influence on reducing system performance and provide obvious information about the loss values such as array capture losses (${\mathrm{L}}_{\mathrm{a}}$) that are due to the PV module losses, and system capture losses (${\mathrm{L}}_{\mathrm{s}}$) that are due to the inverter losses, as follows [5]:

$${\mathrm{L}}_{\mathrm{a}}={\mathrm{Y}}_{\mathrm{r}}-{\mathrm{Y}}_{\mathrm{a}}$$

(26)

$${\mathrm{L}}_{\mathrm{s}}={\mathrm{Y}}_{\mathrm{a}}-{\mathrm{Y}}_{\mathrm{f}}$$

(27)

3.2. Economic and Environmental Analysis

Most of the cost of a solar PV system is incurred at the beginning of the project’s implementation. Therefore, once a PV system is built, it generates electricity mostly for free. This feature is critical if synchronized with the reducing initial capital costs of PV modules and other supplemental materials because initial cost investments can be recovered based on future income streams. A financial analysis of a solar PV system is essential for determining the economic feasibility by considering the expected cost requirements that include capital expenditure (CAPEX) and operating and maintenance expenditure (OPEX). The CAPEX of a solar PV system includes the initial capital expense of equipment (including the module cost, support structure (mounting hardware) cost, and circuit cost, breakers cost, and cables cost), initial labor cost (including site design, installation, supply chain, permitting and interconnection), and grid connection cost (including inverter cost, transformer cost, and transmission cost to the nearest grid), while the OPEX represents yearly scheduled operation costs that include screening, maintenance, repairs, panel cleaning, insurance, additional operational and overhead. It is worth noting that the above costs are very sensitive to panel efficiency. The abovementioned expenses are very sensitive to module efficiency. Modules that are 12% efficient will require 50% more modules, 50% more inverters, 50% more space area, etc. versus those that are 18% efficient [26]. There are some quantitative parameters such as return on investment (ROI), payback period (PBP), and levelized cost of energy (LCOE) that can be used to evaluate the feasibility of a solar PV system, as in the expressions 28–35 [27,28]. The most attractive system for investment which has a higher ROI, lower PBP, and lower LCOE.

$$\mathrm{Returen}\mathrm{on}\mathrm{investment}\left(\mathrm{ROI}\right)=\frac{\mathrm{Annual}\mathrm{Net}\left(\mathrm{After}-\mathrm{Tax}\right)\mathrm{Profit}}{\mathrm{TCI}}$$

(28)

$$\begin{array}{l}\mathrm{Annual}\mathrm{net}\left(\mathrm{after}-\mathrm{tax}\right)\mathrm{profit}\left(\$/\mathrm{year}\right)\\ =\left(\mathrm{Annual}\mathrm{income}-\mathrm{Total}\mathrm{annualized}\mathrm{cost}\right)\times \left(1-\mathrm{Tax}\mathrm{rate}\right)\\ +\mathrm{Depreciation}\end{array}$$

(29)

$$\begin{array}{l}\mathrm{Annual}\mathrm{income}\left(\frac{\$}{\mathrm{year}}\right)\\ =\mathrm{Avoided}\cos \mathrm{t}\mathrm{of}\mathrm{purchasing}\mathrm{electricity}\left(\mathrm{EC}\right)\\ +\mathrm{Avoided}\cos \mathrm{t}\mathrm{of}\mathrm{a}\mathrm{fuel}\mathrm{needed}\mathrm{during}\mathrm{the}\mathrm{production}\mathrm{of}\mathrm{electric}\mathrm{energy}\left(\mathrm{FC}\right)\end{array}$$

(30)

$$\begin{array}{l}\mathrm{Total}\mathrm{capital}\mathrm{investment}\left(\mathrm{TCI}\right)(\$)\\ =\mathrm{Fixed}\mathrm{capital}\mathrm{investment}\mathrm{or}\mathrm{CAPEX}\left(\mathrm{FCI}\right)+\mathrm{Working}\mathrm{capital}\mathrm{investment}\left(\mathrm{WCI}\right)\end{array}$$

(31)

$$\begin{array}{l}\mathrm{Annualized}\mathrm{fixed}\mathrm{cost}\left(\mathrm{Annual}\mathrm{FCI}\mathrm{depreciation}\right)\left(\text{AFC}\right)(\$/\mathrm{year})\\ =\frac{\mathrm{Initial}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{depreciable}\mathrm{FCI}\left({\mathrm{FCI}}_{\mathrm{o}}\right)-\mathrm{Salvage}\mathrm{or}\mathrm{scrap}\mathrm{value}\mathrm{of}\mathrm{the}\mathrm{FCI}\mathrm{at}\mathrm{the}\mathrm{end}\mathrm{of}\mathrm{the}\mathrm{sevice}\mathrm{life}({\mathrm{FCI}}_{\mathrm{s}})}{\mathrm{Service}\mathrm{life}\mathrm{of}\mathrm{the}\mathrm{property}\mathrm{in}\mathrm{years}\left(\mathrm{N}\right)}\end{array}$$

(32)

$$\begin{array}{l}\mathrm{Total}\mathrm{annualized}\mathrm{cost}\left(\mathrm{TAC}\right)(\$/\mathrm{year})\\ =\mathrm{AFC}+\mathrm{Annualized}\mathrm{operating}\mathrm{cost}\left(\mathrm{AOC}\right)\left(\frac{\$}{\mathrm{year}}\right)\end{array}$$

(33)

$$\mathrm{Payback}\mathrm{period}\left(\mathrm{PBP}\right)\left(\mathrm{year}\right)=\frac{\mathrm{Depreciable}\mathrm{FCI}}{\mathrm{Annual}\mathrm{Net}\left(\mathrm{After}-\mathrm{Tax}\right)\mathrm{Profit}}$$

(34)

$$\mathrm{Levelized}\cos \mathrm{t}\mathrm{of}\mathrm{energy}\left(\mathrm{LCOE}\right)\left(\frac{\$}{\mathrm{kWh}}\right)=\frac{\mathrm{Total}\mathrm{life}\mathrm{cycle}\mathrm{cost}}{\mathrm{Total}\mathrm{lifetime}\mathrm{energy}\mathrm{production}}=\frac{{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{N}}\frac{{\mathrm{IC}}_{\mathrm{t}}+{\mathrm{OMC}}_{\mathrm{t}}+{\mathrm{F}}_{\mathrm{t}}}{{(1+{\mathrm{D}}_{\mathrm{r}})}^{\mathrm{t}}}}{{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{N}}\frac{{\mathrm{E}}_{\mathrm{t}}}{{(1+{\mathrm{D}}_{\mathrm{r}})}^{\mathrm{t}}}}$$

(35)

where ${\mathrm{IC}}_{\mathrm{t}}\mathrm{is}\mathrm{the}\mathrm{investment}\cos \mathrm{t}\mathrm{in}\mathrm{the}\mathrm{year}\mathrm{t}(\$)$, ${\mathrm{OMC}}_{\mathrm{t}}\mathrm{is}\mathrm{the}\mathrm{Operting}\mathrm{and}\mathrm{maintenance}\cos \mathrm{t}\mathrm{in}\mathrm{the}\mathrm{year}\mathrm{t}(\$)$, ${\mathrm{F}}_{\mathrm{t}}\mathrm{is}\mathrm{the}\mathrm{fuel}\cos \mathrm{t}\mathrm{in}\mathrm{the}\mathrm{year}\mathrm{t}(\$)$, ${\mathrm{E}}_{\mathrm{t}}\mathrm{is}\mathrm{the}\mathrm{electrical}\mathrm{energy}\mathrm{generated}\mathrm{in}\mathrm{the}\mathrm{year}\mathrm{t}\left(\mathrm{kWh}\right)$, and ${\mathrm{D}}_{\mathrm{r}}\mathrm{is}\mathrm{the}\mathrm{discount}\mathrm{rate}$.

Solar PV systems are considered environmentally friendly. To measure the environmental feasibility for the system, a measurable indicator, as in the simple form of CE in the expression 36 [29], is used to estimate the total carbon emissions that can be avoided due to utilizing solar PV technologies rather than fossil fuels.

$$\mathrm{CE}=\mathrm{E}\times \mathrm{N}\times n_s\times \mathsf{\alpha }$$

(36)

where CE is the carbon emission, E is the electrical energy production of PV system (kWh/day), ${\mathrm{n}}_{\mathrm{s}}\mathrm{is}\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{sunny}\mathrm{days}$, and α is the average carbon emission generated in the production of 1 kWh of electricity.

4. Results and Discussion

4.1. Total Number of Modules

The first step toward implementing the design requirements for installing solar PV modules is how to estimate available installation areas on the rooftops of buildings. The rooftop areas of 33 buildings on the campus have been estimated based on using Google Earth and Google Maps as shown in

Table 2. Total modules number and rooftop areas for TAMU buildings.

Building	Total Roof Area (m2)	Utilization Factor (%)	Total PV Utilized Area (m2)	Number of Modules	Total Area of Modules (m2)
Emerging Technologies (ETB)	3834.04	50	1917.02	405	783.48
Zachry Engineering Education Complex	6927.69	50	3463.84	731	1415.66
WEB	4560.84	50	2280.42	481	932.00
Dwight Look Engineering	1334.13	50	667.06	140	272.62
Zachry Department of Civil and Environmental Engineering	1746.86	50	873.43	184	356.96
Haynes Engineering (HEB)	869.86	50	434.93	91	177.75
Ernest Langford Architecture Center Department of Visualization	1513.35	50	756.67	159	309.25
Preston Geren Auditorium Architecture Building B	835.99	50	417.99	88	170.83
Department of Computer Science Engineering	1800.44	50	900.22	190	367.91
Department of Biological and Agricultural Engineering	744.43	50	372.21	78	152.12
Department of Architecture	2546.32	50	1273.16	268	520.33
Liberal Arts and Humanities Department of Performance studies	2395.16	50	1197.58	253	489.44
Help Desk Central	1673.69	50	836.84	176	342.01
Texas A&M University Press	2181.61	50	1090.80	230	445.80
Music Activities Center	1982.1793	50	991.08	209	405.05
John J Koldus	4052.84	50	2026.42	428	828.19
Rudder Complex	4654.47	50	2327.23	491	951.13
Memorial Student Center	4483.33	50	2241.66	473	916.16
Corps of Cadets &Trigon	1024.62	50	512.31	108	209.37
Psychology	1739.6	50	869.8	183	355.48
Department of Biology	679.2	50	339.6	71	138.79
Heldenfels Hall	2252	50	1126	237	460.19
Student Computing Center	4104.82	50	2052.41	433	838.81
Evans Library	10,604.67	50	5302.33	1120	2167.05
Department of History	981.92	50	490.96	103	200.65
Department of Construction Science	995.35	50	497.67	105	203.39
College of Liberal Arts	694.8	50	347.4	73	141.98
Department of Philosophy (YMCA)	678.77	50	339.38	71	138.70
Student Health Services	1681.66	50	840.83	177	343.64
Hullabaloo Hall	4616.19	50	2308.095	487	943.31
Department of Communication	847.7	50	423.85	89	173.22
Cushing Memorial Library and Archives	1147.61	50	573.80	121	234.51
KANM	2844.87	50	1422.43	300	581.34
Department of Mechanical Engineering	1005.76	50	502.88	106	205.52
Blocker	4905.11	50	2452.55	518	1002.35
Mitchell Physics	1009.14	50	504.57	106	206.21
Artie McFerrin Department of Chemical Engineering	938	50	469	99	191.67
Total	-	-	-	9601	18,573.06

. It is necessary to determine the utilizable area of a rooftop based on several factors such as support structure features, spacing required for avoiding shadow on modules, tracking system type, suitable space for maintenance purposes to calculate the number of modules that can be installed on available areas. Table 2 shows the total number of modules and their areas that have been calculated for each building by using Section 3.1.2 analysis, utilization factor of 50% for the rooftop area, and Appendix B.

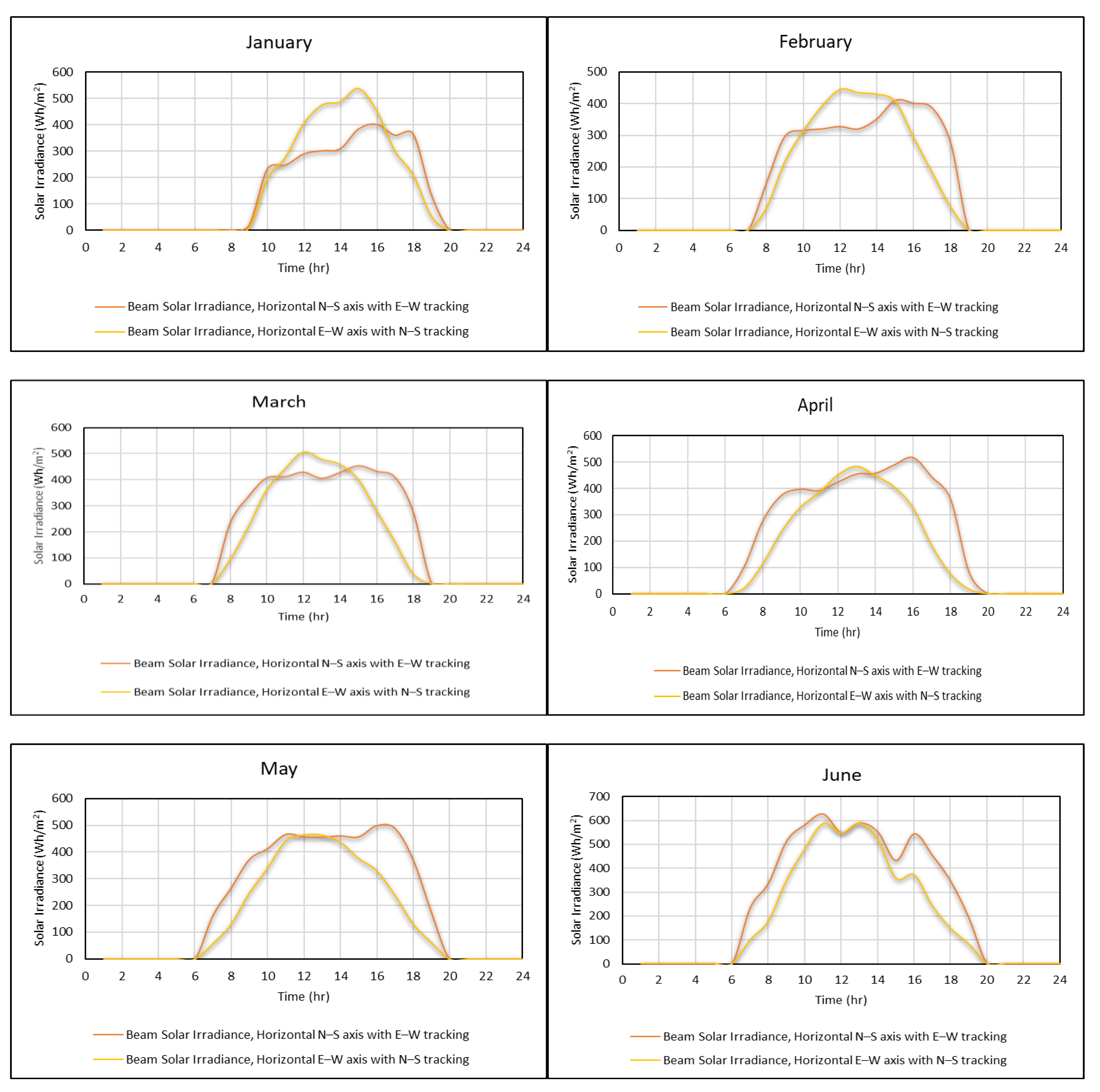
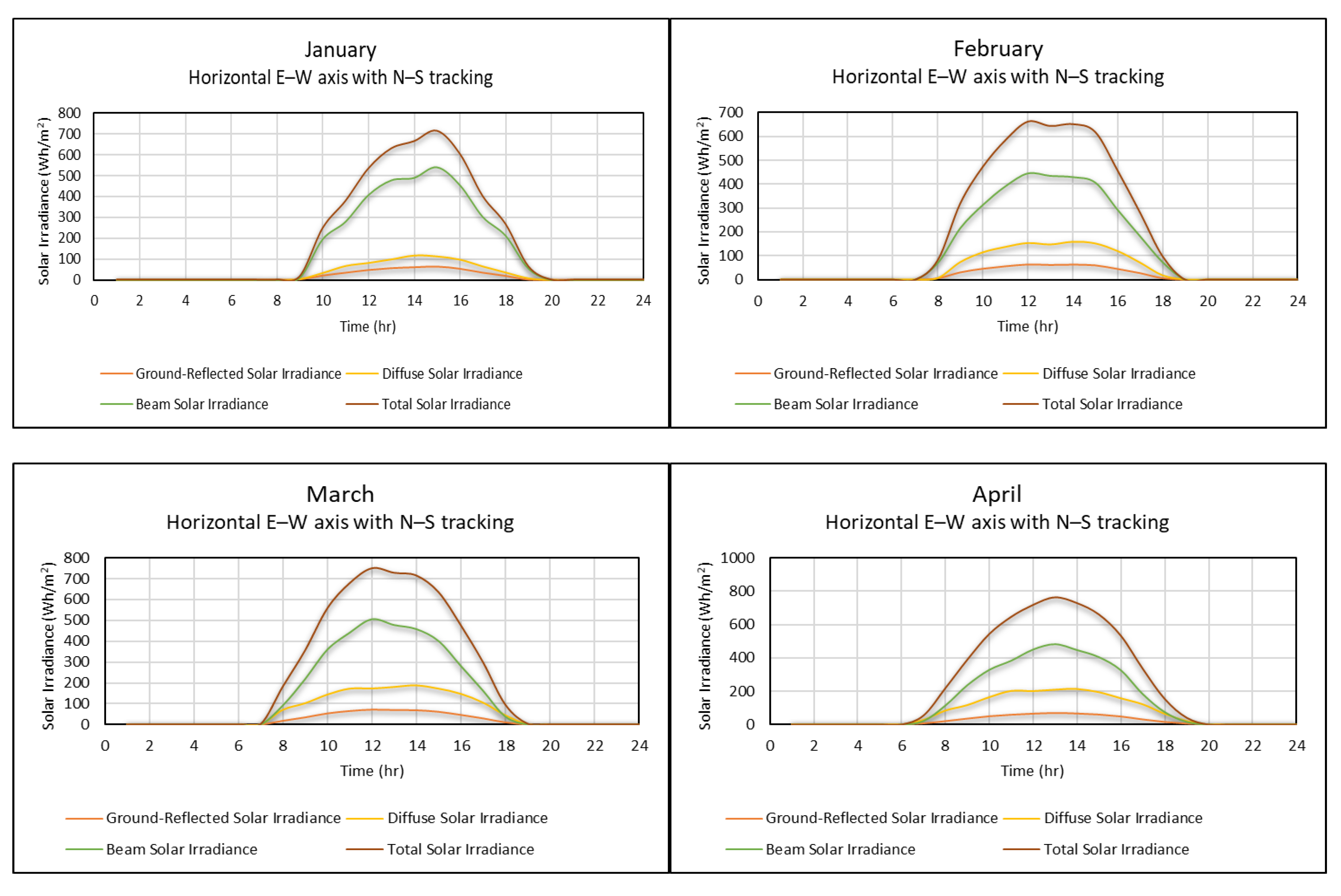
4.2. Estimation of Various Solar Irradiances

A preliminary assessment for the potential of solar energy is another important step toward making a proper decision for installing solar PV modules at a selected site. The amount of solar irradiation falling on a surface per unit area of the PV module can be increased remarkably and the economic feasibility improved by employing tracking systems to enable the PV system to track the Sun considering the effect of incidence angle, which has a different formula for each tracking mode. The solar irradiance and tracking modes equations in Section 3.1.3 have been used to perform a reasonable comparison between the two tracking modes that have been adopted in this study. From Figure 3, it is obvious that the performance of the solar PV system, which is used the mode of horizontal N–S axis with E–W tracking, is more effective for capturing more amount of beam irradiance falling on the PV modules surface than the mode of horizontal E–W axis with N–S tracking in proportion to the cosine of the incidence angle, especially from the month of February to October. While the mode of horizontal E–W axis with N–S tracking provides the higher performance during the winter season including November, December, and January.

It is worth noting that the most relevant solar irradiance component for most solar power technologies is beam irradiance. Thus, the performance of these technologies reduces dramatically with growing cloud cover; whereas photovoltaics can continue generating electric power from diffuse and ground reflected solar irradiation. Consequently, the diffuse radiation is undoubtedly a significant component besides beam irradiance for assessing the modules’ performance. Accordingly, various forms of solar irradiance: direct (beam), diffuse, and reflected (scattered) radiation have been estimated, as shown in Figure 4 and Figure 5, to show the amount of contribution of each type of solar irradiance in the total energy amount that may be received by PV modules at the selected site.

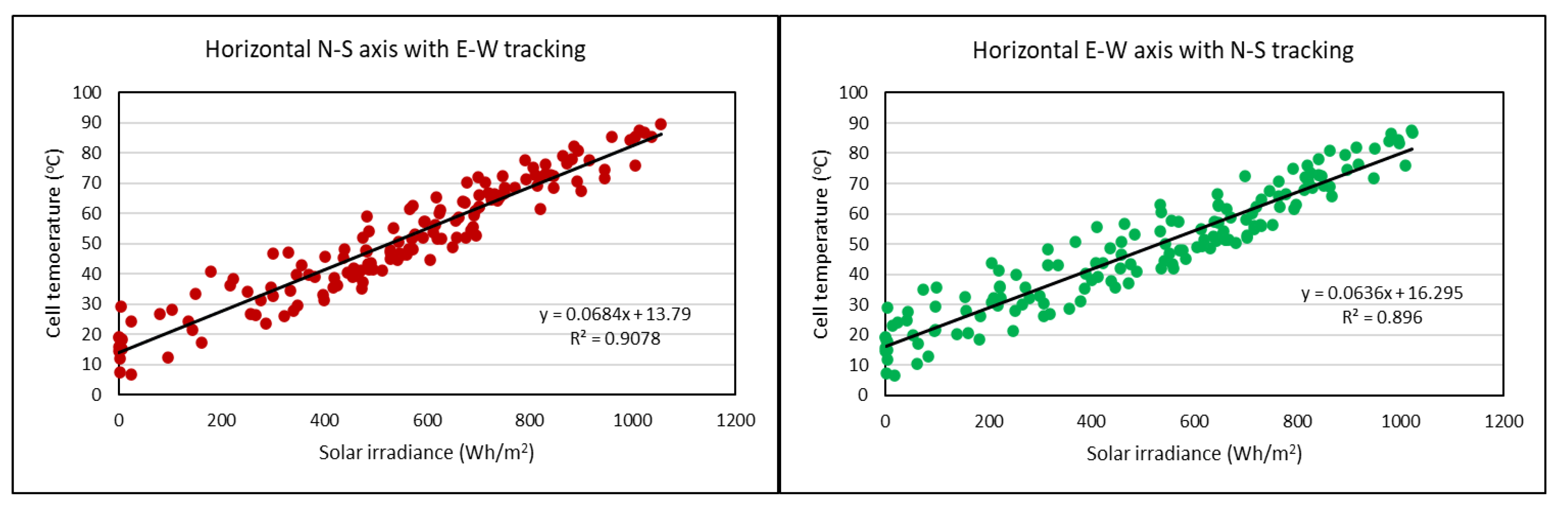
4.3. Temperature Effect on PV Module Performance

A typical PV module can convert 6–20% of the total incident solar irradiance into electric energy based on the type of solar cells and climatic conditions [30], while the rest of the incident solar irradiance is dissipated to the surrounding or converted into heat causing a notable increase in the temperature of the PV module and a reduction in its efficiency. The variation of cell temperature with the total absorbed solar irradiance on its surface is shown in Figure 6 for both tracking modes. It is seen that the cell temperature increased linearly with growing the intensity of solar irradiance. The mode of horizontal N–S axis with E–W tracking has shown a higher value of the linear correlation coefficient (R² = 0.9078) than the value of the mode of horizontal E–W axis with N–S tracking (R² = 0.896) due to the somewhat convergence between the values. To consider the uncertain nature of correcting the PV module efficiency according to its temperature. The low, average, and high values of module efficiency have been estimated depending on equations of Section 3.1.4, as shown in Figure 7. The box plots show that the minimum and maximum values of the PV electrical efficiency of module are 15.05 and 20.65%, respectively, using a horizontal N–S axis with E–W tracking, while they are 15.26 and 20.67%, respectively, using a horizontal E–W axis with N–S tracking.

4.4. Energy Output

The predicted DC energy outputs of the PV system and AC energy injected into the grid for each month are shown in Figure 8. The calculations have been carried out using the analysis described in Section 3.1.5. The DC energy outputs of the PV system vary from 13.12 MWh/day in December to 36.24 MWh/day in June with using horizontal N–S axis with E–W tracking, and from 14.53 MWh/day to 32.08 MWh/day with using horizontal E–W axis with N–S tracking. Using the inverter can be helping to convert DC energy to AC energy. The AC energy delivered to the grid varies from 12.46 MWh/day in December to 34.43 MWh/day in June with using horizontal N–S axis with E–W tracking, and from 13.80 MWh/day to 30.48 MWh/day with using horizontal E–W axis with N–S tracking. The observed variation in these values and between DC and AC outputs represents the impacts of different factors on the PV system performance such as the influence of climatic conditions including temperature, wind, cloud cover, the effect of the reduced number of sun hours in several months, and energy losses from the production stage to end-users.

4.5. Technical Assessment Results

The performance evaluation of the solar PV system has been carried out by using several technical criteria in accordance with the IEC 61724 standard. Figure 9 presents the daily final yield, array losses, and system losses. The highest, average, and lowest final yield (${\mathrm{Y}}_{\mathrm{f}}$), which is used to measure the productivity of the system, were found to being in the range of 4.139–10.247 kWh/kW_p/day, 3.855–8.364 kWh/kW_p/day, and 3.710–7.925 kWh/kW_p/day, respectively, for a horizontal N–S axis with E–W tracking, while 4.776–9.071 kWh/kW_p/day, 4.375–7.584 kW h/kW_p/day, and 4.108–7.072 kWh/kW_p/day, respectively, for a horizontal E–W axis with N–S tracking. The observed variation in ${\mathrm{Y}}_{\mathrm{f}}$ values during the year months is due to the change in solar irradiance intensity, the number of sunny hours per day, climatic conditions and various types of losses. There is no typical ${\mathrm{Y}}_{\mathrm{f}}$ value for comparison purposes, as each area around the world has its ${\mathrm{Y}}_{\mathrm{f}}$ value [31]. It is obvious that the high value of ${\mathrm{Y}}_{\mathrm{f}}$ of the proposed system in Texas will make it has the best performance in comparison with other countries mentioned in

Table 3. Economic indicators.

Economic Indictor Type	Economic Indictor Value
LCOE	5.38 c/kWh
ROI	22.64%
PBP	3.75 years

. Furthermore, system performance can be affected by two main categories of losses: array capture losses (${\mathrm{L}}_{\mathrm{a}}$) and system losses (${\mathrm{L}}_{\mathrm{s}}$). These losses cause a marked reduction in the system’s performance, as shown in Figure 9. Array capture losses vary from a minimum of 0.0288 h/d in January to a maximum of −1.131 h/d in July for horizontal N–S axis with E–W tracking, and from a minimum of 0.135 h/d in December to a maximum of −0.956 h/d in July for horizontal E–W axis with N–S tracking. The negative capture loss values in some cases represent an improvement in the capture. The capture losses are a typical indicator of excessive losses and failures at the DC part of the PV system. It can be divided into thermal capture losses and miscellaneous capture losses [28]. If the PV array does not work under standard test conditions (STC) of operating temperature (25 °C), it will cause thermal capture losses. Miscellaneous capture losses may occur because of wiring losses, soiling losses, diodes, shading, and component failure [32]. To estimate losses at the AC side of the conversion, system losses can be used for this purpose. Most of these losses occur in the inverter, transformer, and wire resistance [33]. System losses vary from a minimum of 0.195 h/d in December to a maximum of 0.539 h/d in June for a horizontal N–S axis with E–W tracking, and from a minimum of 0.216 h/d in December to a maximum of 0.477 h/d in June for a horizontal E–W axis with N–S tracking.

As seen in Figure 10, the average array yield $\left({\mathrm{Y}}_{\mathrm{a}}\right)$, reference yield $({\mathrm{Y}}_{\mathrm{r}})$, and final yield $\left({\mathrm{Y}}_{\mathrm{f}}\right)$ vary from a minimum of 4.058 kWh/kW_p/day, 3.89 kWh/kW_p/day, and 3.855 kWh/kW_p/day, respectively, in December to a maximum of 8.805 kWh/kW_p/day, 10.2 kWh/kW_p/day, and 8.364 kWh/kW_p/day, respectively, in June for a horizontal N–S axis with E–W tracking, and from a minimum of 4.605 kWh/kWp/day, 4.46 kWh/kWp/day, and 4.37 kWh/kWp/day, respectively, in December to a maximum of 7.983 kWh/kWp/day, 8.87 kWh/kWp/day, and 7.584 kWh/kWp/day, respectively, in June for a horizontal E–W axis with N–S tracking. The solar irradiance intensity and sunny hours during the day are critical contributor factors for the noticed changes in yield values. Additionally, the notable difference between the values of ${\mathrm{Y}}_{\mathrm{a}}$ and ${\mathrm{Y}}_{\mathrm{f}}$ maybe attributed to DC/AC conversion losses that occurred in the inverter. Regardless of the climatic conditions, where the dry bulb temperature in College Station, Texas varies approximately from 6 to 35 °C, the monthly energy process conversion of the inverter is a fairly constant period. It is observed that the inverter efficiency may be dropped 1% when the ambient temperature rises about 12 °C [34].

The capacity factor (CF) is another technical criterion that can be used to evaluate the usage of the power source. The maximum real CF is slightly less than 50% and the typical CF for a PV system in the range of 15–40% [35]. The variation of the CF of the PV system varied between 16.1% in December and 34.85% in June for a horizontal N–S axis with E–W tracking, 18.23% in December, and 31.60% in June for a horizontal E–W axis with N–S tracking, as presented in Figure 11. On the other hand, the performance ratio (PR) is affected by the total losses in the system depending on several factors that resulted from conversion operations for various components such as PV modules, inverters, and cables, in addition to other impacting factors like climatic conditions. The PR of a PV system measures how its performance close to ideal performance during the real operational period. PR factor also allows making a comparison between PV systems apart from location, tilt angle, orientation, and nominal rated power capacity [5]. From Figure 11, the proposed system shows a reasonable performance based on PR value that varies between 82–98.91% compared with other PV systems around the world, as shown in Table 3.

4.6. Economic Assessment Results

The financial evaluation is a significant criterion for making-decision on the economic feasibility of the proposed system. In addition, to use a levelized cost of energy (LCOE) metric to compare the cost of energy generation from different energy source options, two criteria have been used for assessing the profitability of a project without including interest or the time-value of money that are known as return on investment (ROI) and payback period (PBP) [27]. The values of ROI, PBP, and LCOE have been estimated by using Section 3.2, Appendix B, and the following assumptions: PV system lifetime = 20 years, discount rate = 7%, tax rate = 30%, investment cost = 1.13 $/W [36], operating and maintenance cost = 14 $/kW-year [36], cost of purchasing electricity = 0.078 $/kWh_e, and cost of natural gas for generating 1 kWh of electricity in Texas = 0.105 $/kWh [37]. The estimated values of LCOE, ROI, and PBP for the proposed system (without subsidy) were presented in Table 3. These three economical indictors values refer that the system is worth for investment compared to the traditional power plant. These three economical indictors values refer that the system is worth for investment compared to the traditional power plants, especially if LCOE E of the system was compared with other LCOE values of PV systems that have one-axis tacking, and installed on the rooftop: 4.91–6.05 c/kWh [38], 3.9–6.8 c/kWh [39], and 4–6 c/kWh [36].

4.7. Environmental Assessment Results

The effects of using the roof-mounted and grid-connected PV system on the environment when it can be utilized to replace or minimize the use of other traditional energy sources have been investigated. The avoided amount of carbon emissions from using the system has been estimated by using equation 35 and assumptions that are: Average carbon emission generated in the production of 1 kWh of electricity = 0.449 kgCO₂/kWh_e [40], and an average number of sunny days = 209 days. Consequently, the positive impact of 3360 kWhp PV system on the environment by mitigating carbon emissions will be as shown in

Table 4. Environmental Indicator.

PV System Type	Avoided Amount of Carbon Emissions
Horizontal N–S axis with E–W tracking	20,077 metric tonCO2/year
Horizontal E–W axis with N–S tracking	18,217 metric tonCO2/year

.

5. Comparison with Existing Roof-Mounted and Grid-Connected PV Systems

The estimated performance results of this study are compared with other roof-mounted and grid-connected PV systems depending on their performance data extracted from the available literature. The comparison has been carried out by using parameters such as PV cell type, tracking modes, PV module efficiency, inverter efficiency, PV system size, final yield, and performance ratio. Despite the fact the roof-mounted and grid-connected PV system of this study is merely a proposed idea compared with other PV systems that are in operating mode, its preliminary results indicate promising performance that place it in line with other PV systems or it can be better in some respects, as shown in

Table 5. Performance parameters for various roof-mounted and grid-connected PV systems.

Location	PV Type	Tracking System	PV Module Efficiency (%)	Inverter Efficiency (%)	PV System Size (kWp)	Final Yield (kWh/kWp-day)	Performance Ratio (%)	Reference
Ballymena, Ireland	Monocrystalline silicon	Fixed	7.5–10	87	13	1.7	60–62	[41]
Dublin, Ireland	Monocrystalline silicon	Fixed	14.9	89.2	1.27	2.40	81.50	[5]
Singapore	Polycrystalline silicon	-	11.80	-	-	3.12	81.00	[42]
Abu Dhabi-UAE	Amorphous silicon and Polycrystalline silicon	-	-	94.80	142.5	-	-	[43]
Bangalore, India	Polycrystalline silicon	Fixed	13.71	-	20	4.1	85.00	[25]
India	Multicrystalline Silicon	Fixed	15.53	-	80	4.45	83.2	[10]
Bhopal, India	Crystalline silicon, Amorphous silicon	Fixed	-	93.5–97.5	110	2.67–3.36	71.6–79.5	[44]
College Station, Texas	Monocrystalline silicon	E-W Tracking, N-S Tracking	17.63–18.83	95	3360.35	3.71–10.24	82–98.91	Present study
Jaén, Spain	Polycrystalline silicon	Fixed	8.9	88.1	200	2.4	62.7	[16]
Warsaw, Poland	Amorphous silicon	Fixed	4.5–5.5	92–93	1	2.3	60–80	[45]
Umbertide, Italy	Polycrystalline silicon	Fixed	9	-	15	-	-	[46]
Chandig, India	Monocrystalline silicon	Fixed	-	-	200	-	77.27	[6]
Dhahran, KSA	Monocrystalline silicon	Fixed	15.38	97.7	4800	4.82	78.9	[19]
Nablus, Palestine	Polycrystalline silicon	Fixed	16.49	98–98.5	40.96	4.6	78.4	[11]
Norway	Multicrystalline Silicon and Polycrystalline silicon	Fixed	14	53–94	2.07	2.55	83.03
Tangier, Morocco	-	Fixed	15.2	96.7–96.8	5	4.45	58–98	[8]
Sohar, Oman	-	Fixed	13.9	94.1	1.4	5.2	84.6	[35]
Bhubaneswar, India	Polycrystalline silicon	Fixed	13.42	89.83	11.2	3.67	78	[9]

.

6. Conclusions

A comprehensive performance analysis of a rooftop grid-tied 3360 kW_p PV system was carried out in this study. The technical, economic, and environmental criteria were used to evaluate the capability of the proposed system to become environmentally friendly and economically promising alternative to today’s conventional power plants and help in mitigating the harmful impact of fossil energy sources on the environment. The performance of the PV system was examined using two modes of single-axis tracking: horizontal N–S axis with E–W tracking and horizontal E–W axis with N–S tracking. The following key conclusions can be drawn from the study:

• The prospects of the implementation of a PV system on rooftop buildings in Texas was investigated for the first time in this study to overcome the lack of performance behavior data of this technology, specifically for the selected location.
• With the lack of abundant studies for evaluating the rooftop grid-tied PV systems in the existing literature over a few decades ago, the potential of the proposed PV system in this study has been evaluated by comparing its technical, economic, and environmental indicators to other PV solar systems in the existing literature that are fairly similar to the proposed system.
• The simplicity and precision of the followed performance analysis and models in the study over a broad range of climatic conditions would provide confidence that the analysis can be easily generalized to other regions in Texas or around the world.
• The major challenge of installing PV modules is the availability of sufficient area for this purpose. The number of PV modules was calculated to be 9601 along with considering sufficient space for shadow avoidance, maintenance service, and other facilities. According to the utilization factor of 50% for the rooftop, the utilized area can be exploited to install the PV system avoiding the land cost of 18,573.0673 m² that may be used for other purposes such as agricultural and urban activities.
• It seems that the performance of the solar PV system, which is used the mode of horizontal N–S axis with E–W tracking, is more effective for capturing more amount of the beam, diffuse, and ground-reflected irradiance falling on the PV modules surface than the mode of horizontal E–W axis with N–S tracking in proportion to the cosine of the incidence angle, especially for months of February to October. While the mode of horizontal E–W axis with N–S tracking provides the higher performance during the winter season including November, December, and January.
• The amount of contribution of each type of solar irradiance in the total energy amount that may be received by PV modules at the selected site has been estimated.
• The obtained values for minimum and maximum of the PV cell efficiency have indicated fairly good performance compared to available PV systems in the current literature. The variation of cell temperature and the total absorbed solar irradiance on its surface has been considered to calculate efficiencies that are 15.05 and 20.65 % respectively using horizontal N–S axis with E–W tracking, while 15.26 and 20.67% respectively using horizontal E–W axis with N–S tracking.
• The amount of electricity generated is fine to mitigate adopting fossil fuels. The predicted DC energy outputs of the PV system varies from 13.12 MWh/day in December to 36.24 MWh/day in June with using a horizontal N–S axis with E–W tracking, and from 14.53 MWh/day to 32.08 MWh/day with using a horizontal E–W axis with N–S tracking. The predicted AC energy injected into the grid for each month varies from 12.46 MWh/day in December to 34.43 MWh/day in June with using a horizontal N–S axis with E–W tracking, and from 13.80 MWh/day to 30.48 MWh/day with using a horizontal E–W axis with N–S tracking.
• It is obvious that the high value of ${\mathrm{Y}}_{\mathrm{f}}$ for the proposed system in Texas will make it has the best performance in comparison with PV systems installed in other countries around the world. The highest, average, and lowest final yield (${\mathrm{Y}}_{\mathrm{f}}$), which is used to measure the productivity of the system, were found to being in the range of 4.139–10.247 kWh/kW_p/day, 3.855–8.364 kWh/kW_p/day, and 3.710–7.925 kWh/kW_p/day, respectively for horizontal N–S axis with E–W tracking, while 4.776–9.071 kWh/kW_p/day, 4.375–7.584 kW h/kW_p/day, and 4.108–7.072 kWh/kW_p/day respectively for horizontal E–W axis with N–S tracking.
• The capacity factor (CF) was found to vary between 16.1% in December and 34.85% in June for a horizontal N–S axis with E–W tracking, 18.23% in December, and 31.60% in June for a horizontal E–W axis with N–S tracking. While the performance ratio (PR) was between 82–98.91%, which is higher than PR values of existing roof-mounted and grid-connected PV systems around the world.
• The economic evaluation has been performed using technical results and three economic criteria. The estimated values of LCOE, ROI, and PBP were 5.38 c/kWh, 22.64%, and 3.75 years for the proposed system (without subsidy). These three economic indicators values refer that the system is worthy of investment compared to existing roof-mounted and grid-connected PV systems and traditional power plants.
• The proposed PV system can result in a harmful emission reduction of 20,077 metric tonCO₂/year using a horizontal N–S axis with E–W tracking, and 18,217 metric tonCO₂/year using a horizontal E–W axis with N–S tracking.
• The result of the comparison for the proposed PV system with other PV systems located in different sites around the world showed that their performance does not only depend on solar radiation intensity, but the operational and climatic conditions should be considered for any site which is selected to install the PV system.

According to the overall performance results of the proposed PV system, it is found to be a feasible solution for electric power supply in countries which have a good potential for solar energy and even if they are oil or gas producers as is Texas, to reduce their reliance on fossil-fuel-burning power plants and address the energy and environmental challenges of the rapid growth of the building sector. The results obtained in this study can be used as a future vision, especially the economic analysis, for estimating the potential of investment incentives, subsidies, and feed-in-tariff to make implementing solar PV systems more attractive around the world. In any case the long-term performance of the rooftop grid-tied technologies in Texas requires further research.