Forecast of Hourly Airport Visibility Based on Artificial Intelligence Methods
Abstract
:1. Introduction
2. Methodology
2.1. Data
2.2. Methods
2.2.1. Trend Test
2.2.2. Artificial Intelligence Algorithms
Partial Least Squares Regression (PLS)
Classification and Regression Tree (CART)
K-Nearest Neighbor (KNN)
Least Angle Regression (LAR)
Multi-Layer Perceptron (MLP)
Random Forest (RF)
Ridge Regressor (RR)
Stochastic Gradient Descent Regression (SGD)
Linear Support Vector Regression (SVR)
3. Results
3.1. Mean and Trends of Monthly and Annual Airport Visibility
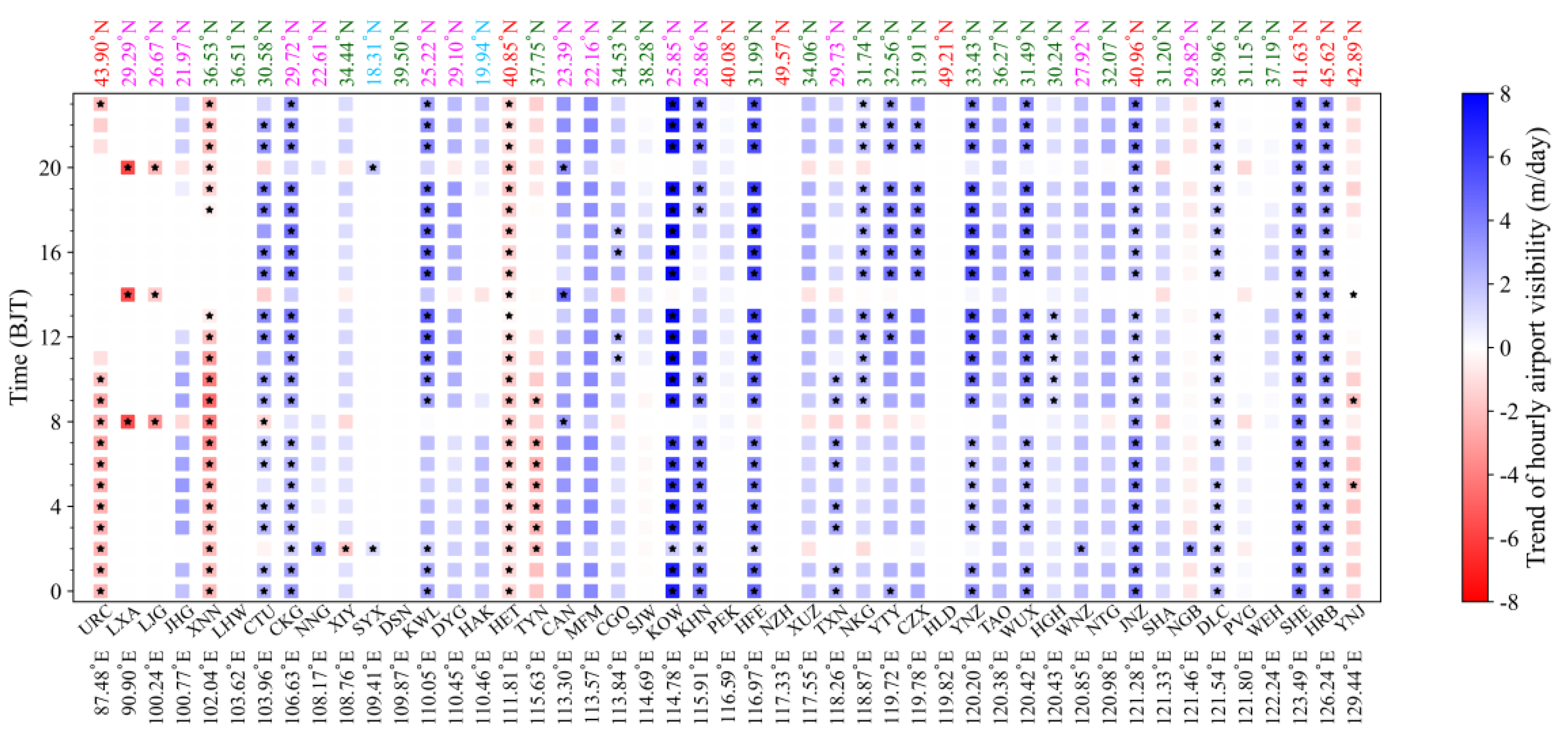
3.2. Diurnal Mean and Trends of Hourly Airport Visibility
3.3. Model Training and Testing
4. Discussions
4.1. Distributions and Changes of Airport Visibility in Different Time Scales
4.2. Prediction Performances of Different Models
5. Conclusions
- The visibility of airports in eastern and central China is at a poor level all year round, and LXA has good visibility all year round. Airports in south and northwest China have better visibility from May to October and poorer visibility from November to April.
- In all months, the increasing visibility mainly occurs in the central, northeast and coastal areas of China, while decreasing visibility mainly appears in the western and northern parts of China. In spring, summer and autumn, the changes difference between east and west is particularly obvious. This East–West distribution of trends is obviously different from the North–South distribution shown by the mean.
- For all airports, good visibility mainly occurs from 14:00–18:00 p.m., while poor visibility mainly concentrates from 22:00 p.m. to 12:00 p.m. the next day, especially between 3:00–9:00 a.m.
- Our proposed artificial intelligence algorithm models can be reasonably used in airport visibility prediction. In particular, most algorithm models have the best results in the visibility prediction over HFE (in Hefei) and SJW (in Shijiazhuang). On the contrary, the worst forecast results appear at LXA and LHW (in Lanzhou) airports. The prediction results of airport visibility in cold seasons (October–December) are better than those in warm seasons (May–September). Among the algorithm models, the prediction performance of the RF-based model is the best.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kneringer, P.; Dietz, S.J.; Mayr, G.J.; Zeileis, A. Probabilistic Nowcasting of Low-Visibility Procedure States at Vienna International Airport During Cold Season. Pure Appl. Geophys. 2018, 176, 2165–2177. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Jiang, T.; Zhang, Y.; Wang, Y.; Pan, X.; Wu, J. Forecast model of airport haze visibility and meteorological factors based on SVR-RBF model. IOP Conf. Ser. Earth Environ. Sci. 2021, 657, 012029. [Google Scholar] [CrossRef]
- Abbey, D.E.; Ostro, B.E.; Fraser, G.; Vancuren, T.; Burchette, R.J. Estimating fine particulates less than 2.5 microns in aerodynamic diameter (pm2.5) from airport visibility data in california. J. Expo. Anal. Environ. Epidemiol. 1995, 5, 161–180. [Google Scholar] [CrossRef] [PubMed]
- Iwakura, S.; Okada, K. Dependence of Prevailing Visibility on Relative Humidity at Tokyo International Airport. Pap. Meteorol. Geophys. 1999, 50, 81–90. [Google Scholar] [CrossRef]
- Shu, Z.; Yang, S.; Xu, W. The System of the Calibration for Visibility Measurement Instrument Under the Atmospheric Aerosol Simulation Environment. EPJ Web Conf. 2016, 119, 23005. [Google Scholar] [CrossRef] [Green Version]
- Won, W.-S.; Oh, R.; Lee, W.; Kim, K.-Y.; Ku, S.; Su, P.-C.; Yoon, Y.-J. Impact of Fine Particulate Matter on Visibility at Incheon International Airport, South Korea. Aerosol Air Qual. Res. 2020, 20, 1048–1061. [Google Scholar] [CrossRef] [Green Version]
- Wei, G.; Zhang, Z.; Ouyang, X.; Shen, Y.; Jiang, S.; Liu, B.; He, B.-J. Delineating the spatial-temporal variation of air pollution with urbanization in the Belt and Road Initiative area. Environ. Impact Assess. Rev. 2021, 91, 106646. [Google Scholar] [CrossRef]
- França, G.B.; Carmo, L.F.R.D.; De Almeida, M.V.; Neto, F.L.A. Fog at the Guarulhos International Airport from 1951 to 2015. Pure Appl. Geophys. 2018, 176, 2191–2202. [Google Scholar] [CrossRef]
- Kutty, S.G.; Agnihotri, G.; Dimri, A.P.; Gultepe, I. Fog Occurrence and Associated Meteorological Factors Over Kempegowda International Airport, India. Pure Appl. Geophys. 2018, 176, 2179–2190. [Google Scholar] [CrossRef]
- Dutta, D.; Chaudhuri, S. Nowcasting visibility during wintertime fog over the airport of a metropolis of India: Decision tree algorithm and artificial neural network approach. Nat. Hazards 2015, 75, 1349–1368. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, G.; Han, L.; Wang, N. The Application of Deep Learning in Airport Visibility Forecast. Atmos. Clim. Sci. 2017, 7, 314–322. [Google Scholar] [CrossRef] [Green Version]
- Oğuz, K.; Pekin, M.A. Predictability of fog visibility with artificial neural network for esenboga airport. Eur. J. Sci. Technol. 2019, 15, 542–551. [Google Scholar] [CrossRef] [Green Version]
- Goswami, S.; Chaudhuri, S.; Das, D.; Sarkar, I.; Basu, D. Adaptive neuro-fuzzy inference system to estimate the predictability of visibility during fog over Delhi, India. Meteorol. Appl. 2020, 27, e1900. [Google Scholar] [CrossRef]
- Cornejo-Bueno, S.; Casillas-Pérez, D.; Cornejo-Bueno, L.; Chidean, M.I.; Caamaño, A.J.; Sanz-Justo, J.; Casanova-Mateo, C.; Salcedo-Sanz, S. Persistence Analysis and Prediction of Low-Visibility Events at Valladolid Airport, Spain. Symmetry 2020, 12, 1045. [Google Scholar] [CrossRef]
- Marzban, C.; Leyton, S.; Colman, B. Ceiling and Visibility Forecasts via Neural Networks. Weather. Forecast. 2007, 22, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Fabbian, D.; de Dear, R.; Lellyett, S.C. Application of Artificial Neural Network Forecasts to Predict Fog at Canberra International Airport. Weather. Forecast. 2007, 22, 372–381. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Ghalhari, G.F.; Dastjerdi, J.K.; Nokhandan, M.H. Using Mann Kendal and t-test methods in identifying trends of climatic elements: A case study of northern parts of Iran. Manag. Sci. Lett. 2012, 2, 911–920. [Google Scholar] [CrossRef]
- Rehman, S. Long-Term Wind Speed Analysis and Detection of its Trends Using Mann–Kendall Test and Linear Regression Method. Arab. J. Sci. Eng. 2012, 38, 421–437. [Google Scholar] [CrossRef]
- Tekleab, S.; Mohamed, Y.; Uhlenbrook, S. Hydro-climatic trends in the Abay/Upper Blue Nile basin, Ethiopia. Phys. Chem. Earth Parts A/B/C 2013, 61–62, 32–42. [Google Scholar] [CrossRef]
- Sa’Adi, Z.; Shahid, S.; Ismail, T.; Chung, E.-S.; Wang, X.-J. Trends analysis of rainfall and rainfall extremes in Sarawak, Malaysia using modified Mann–Kendall test. Theor. Appl. Clim. 2017, 131, 263–277. [Google Scholar] [CrossRef]
- Elnesr, M.N.; Alazba, A.A. Seasonal trends of air temperature and diurnal range in the Arabian Peninsula, the Levant, and Iraq: A spatiotemporal study and development of an online data visualization tool. Theor. Appl. Climatol. 2019, 137, 1271–1287. [Google Scholar] [CrossRef]
- Serencam, U. Innovative trend analysis of total annual rainfall and temperature variability case study: Yesilirmak region, Turkey. Arab. J. Geosci. 2019, 12, 704. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Babamiri, O. Trends in reference crop evapotranspiration in Urmia Lake basin. Arab. J. Geosci. 2020, 13, 372. [Google Scholar] [CrossRef]
- de Jesus, A.L.; Thompson, H.; Knibbs, L.D.; Hanigan, I.; De Torres, L.; Fisher, G.; Berko, H.; Morawska, L. Two decades of trends in urban particulate matter concentrations across Australia. Environ. Res. 2020, 190, 110021. [Google Scholar] [CrossRef]
- Mallick, J.; Talukdar, S.; Alsubih, M.; Salam, R.; Ahmed, M.; Ben Kahla, N.; Shamimuzzaman, M. Analysing the trend of rainfall in Asir region of Saudi Arabia using the family of Mann-Kendall tests, innovative trend analysis, and detrended fluctuation analysis. Theor. Appl. Clim. 2021, 143, 823–841. [Google Scholar] [CrossRef]
- Ding, J.; Cuo, L.; Zhang, Y.; Zhang, C. Varied spatiotemporal changes in wind speed over the Tibetan Plateau and its surroundings in the past decades. Int. J. Clim. 2021, 41, 5956–5976. [Google Scholar] [CrossRef]
- Ding, J.; Cuo, L.; Zhang, Y.; Zhang, C.; Liang, L.; Liu, Z. Annual and Seasonal Precipitation and Their Extremes over the Tibetan Plateau and Its Surroundings in 1963–2015. Atmosphere 2021, 12, 620. [Google Scholar] [CrossRef]
- Zheng, X.B.; Zhao, T.L.; Luo, Y.X.; Duan, C.C.; Chen, J. Trends in sunshine duration and atmospheric visibility in the yunnan-guizhou plateau, 1961–2015. Sci. Cold Arid. Reg. 2011, 3, 179–184. [Google Scholar] [CrossRef]
- Araghi, A.; Mousavi-Baygi, M.; Adamowski, J.; Martinez, C.J. Analyzing trends of days with low atmospheric visibility in Iran during 1968–2013. Environ. Monit. Assess. 2019, 191, 249. [Google Scholar] [CrossRef]
- Alhathloul, S.H.; Khan, A.A.; Mishra, A.K. Trend analysis and change point detection of annual and seasonal horizontal visibility trends in Saudi Arabia. Theor. Appl. Clim. 2021, 144, 127–146. [Google Scholar] [CrossRef]
- Ding, J.; Cuo, L.; Zhang, Y.; Zhu, F. Monthly and annual temperature extremes and their changes on the Tibetan Plateau and its surroundings during 1963–2015. Sci. Rep. 2018, 8, 11860. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Research on Spatial and Temporal Variation Characteristics, Factors, and Source Apportionment of PM2. Master’s Thesis, Zhejiang University, Hangzhou, China, 2014. (In Chinese). [Google Scholar]
- Shi, D.; Li, C.; Shi, Y.; Zhang, Y. Study on the localization diagnosis of extra heavy fog on the background of the fog weather based on machine learning algorithms. J. Catastrophol. 2018, 33, 193–199. [Google Scholar] [CrossRef]
- Xie, Y. Deep Learning Architectures for PM2.5 and Visibility Predictions. Master’s Thesis, The Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Feng, R.; Gao, H.; Luo, K.; Fan, J.-R. Analysis and accurate prediction of ambient PM2.5 in China using Multi-layer Perceptron. Atmos. Environ. 2020, 232, 117534. [Google Scholar] [CrossRef]
- Li, J.; Garshick, E.; Hart, J.E.; Li, L.; Shi, L.; Al-Hemoud, A.; Huang, S.; Koutrakis, P. Estimation of ambient PM2.5 in Iraq and Kuwait from 2001 to 2018 using machine learning and remote sensing. Environ. Int. 2021, 151, 106445. [Google Scholar] [CrossRef]
- Shogrkhodaei, S.Z.; Razavi-Termeh, S.V.; Fathnia, A. Spatio-temporal modeling of PM2.5 risk mapping using three machine learning algorithms. Environ. Pollut. 2021, 289, 117859. [Google Scholar] [CrossRef] [PubMed]
- Avila, J.; Hauck, T. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Calle, M.L.; Urrea, V. Letter to the Editor: Stability of Random Forest importance measures. Brief. Bioinform. 2011, 12, 86–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Micheletti, N.; Foresti, L.; Robert, S.; Leuenberger, M.; Pedrazzini, A.; Jaboyedoff, M.; Kanevski, M. Machine Learning Feature Selection Methods for Landslide Susceptibility Mapping. Math. Geosci. 2014, 46, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Pham, Q.B.; Mukherjee, K.; Norouzi, A.; Linh, N.T.T.; Janizadeh, S.; Ahmadi, K.; Cerdà, A.; Doan, T.N.C.; Anh, D.T. Head-cut gully erosion susceptibility modelling based on ensemble Random Forest with oblique decision trees in Fareghan watershed, Iran. Geomat. Nat. Hazards Risk 2020, 11, 2385–2410. [Google Scholar] [CrossRef]
- Abu El-Magd, S.A.; Ali, S.A.; Pham, Q.B. Spatial modeling and susceptibility zonation of landslides using random forest, naïve bayes and K-nearest neighbor in a complicated terrain. Earth Sci. Inform. 2021, 14, 1227–1243. [Google Scholar] [CrossRef]
- Farebrother, R.W. Further Results on the Mean Square Error of Ridge Regression. J. R. Stat. Soc. Ser. B 1976, 38, 248–250. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Amari, S. A Theory of Adaptive Pattern Classifiers. IEEE Trans. Electron. Comput. 1967, EC-16, 299–307. [Google Scholar] [CrossRef]
- Bottou, L. Online Algorithms and Stochastic Approximations. In Online Learning and Neural Networks; Saad, D., Ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Cristianini, N.; Taylor, J.S. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Printed in the United Kingdom at the University Press: Cambridge, UK, 2000. [Google Scholar]
- Zhao, D.; Arshad, M.; Wang, J.; Triantafilis, J. Soil exchangeable cations estimation using Vis-NIR spectroscopy in different depths: Effects of multiple calibration models and spiking. Comput. Electron. Agric. 2021, 182, 105990. [Google Scholar] [CrossRef]
- Zhao, D.; Li, N.; Zare, E.; Wang, J.; Triantafilis, J. Mapping cation exchange capacity using a quasi-3d joint inversion of EM38 and EM31 data. Soil Tillage Res. 2020, 200, 104618. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, X.; Khongnawang, T.; Arshad, M.; Triantafilis, J. A Vis-NIR Spectral Library to Predict Clay in Australian Cotton Growing Soil. Soil Sci. Soc. Am. J. 2018, 82, 1347–1357. [Google Scholar] [CrossRef]
- Yang, J.; Li, Z.; Huang, S. Influence of relative humidity on shortwave radiative properties of atmosphere aerosol particles. Chin. J. Atmos. Sci. 1993, 23, 239–247. (In Chinese) [Google Scholar]
- Boudala, F.S.; Isaac, G.A.; Crawford, R.W.; Reid, J. Parameterization of runway visual range as a function of visibility: Implications for numerical weather prediction models. J. Atmos. Ocean. Technol. 2011, 29, 177–191. [Google Scholar] [CrossRef]
- Ren, J.; Liu, J.; Li, F.; Cao, X.; Ren, S.; Xu, B.; Zhu, Y. A study of ambient fine particles at Tianjin International Airport, China. Sci. Total Environ. 2016, 556, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ding, W. Change Characteristics and Its Influence Mechanism of Low RVR at Shanghai Pudong Airport. J. Arid. Meteorol. 2016, 34, 873–880. (In Chinese) [Google Scholar] [CrossRef]
- Chen, J.L.; Qiu, X.; Pan, J.; Bian, Q.G.; Tang, M.; Jiang, F.; Wang, H.M. Analysis of air pollution in shanghai hongqiao airport. Adm. Tech. Environ. Monit. (In Chinese). 2018, 30, 39–43. [Google Scholar] [CrossRef]
- Masiol, M.; Harrison, R.M. Aircraft engine exhaust emissions and other airport-related contributions to ambient air pollution: A review. Atmos. Environ. 2014, 95, 409–455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, P.; Zhang, Y.; Wu, T.; Shen, Z.; Xu, H. Acid-extractable heavy metals in PM2.5 over Xi’an, China: Seasonal distribution and meteorological influence. Environ. Sci. Pollut. Res. 2019, 26, 34357–34367. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Wang, W.; Li, L.; Li, J.; Wei, L.; Chi, W.; Hong, L.; Zhao, Q.; Jiang, J. Seasonal concentration distribution of PM1.0 and PM2.5 and a risk assessment of bound trace metals in Harbin, China: Effect of the species distribution of heavy metals and heat supply. Sci. Rep. 2020, 10, 8160. [Google Scholar] [CrossRef]
- Mahowald, N.M.; Ballantine, J.A.; Feddema, J.; Ramankutty, N. Global trends in visibility: Implications for dust sources. Atmos. Chem. Phys. Discuss. 2007, 7, 3309–3339. [Google Scholar] [CrossRef] [Green Version]
- Diaz-Uriarte, R.; Alvarez De Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hastie, T.; Tibshirani, R.J.; Friedman, J.H. The elements of statistical learning: Springer. Elements 2009, 1, 267–268. [Google Scholar]









| ID | Airport Code | Airport Name | City | ID | Airport Code | Airport Name | City |
|---|---|---|---|---|---|---|---|
| 1 | CAN | Baiyun | Guangzhou | 25 | NKG | Lukou | Nanjing |
| 2 | CGO | Xinzheng | Zhengzhou | 26 | NNG | Wuwei | Nanning |
| 3 | CKG | Jiangbei | Chongqing | 27 | NTG | Xingdong | Nantong |
| 4 | CTU | Shuangliu | Chengdu | 28 | NZH | Xijiao | Manzhouli |
| 5 | CZX | Benniu | Changzhou | 29 | PEK | Shoudu | Beijing |
| 6 | DLC | Zhoushuizi | Dalian | 30 | PVG | Pudong | Shanghai |
| 7 | DSN | Yijinhuoluo | Erdos | 31 | SHA | Honqiao | Shanghai |
| 8 | DYG | Hehua | Zhangjiajie | 32 | SHE | Taoxian | Shenyang |
| 9 | HAK | Meilan | Haikou | 33 | SJW | Zhengding | Shijiazhuang |
| 10 | HET | Baita | Hohhot | 34 | SYX | Fenghuang | Sanya |
| 11 | HFE | Xinqiao | Hefei | 35 | TAO | Liuting | Qingdao |
| 12 | HGH | Xiaoshan | Hangzhou | 36 | TXN | Tunxi | Huangshan |
| 13 | HLD | Dongshan | Hailar | 37 | TYN | Wusu | Taiyuan |
| 14 | HRB | Taiping | Harbin | 38 | URC | Diwobu | Urumqi |
| 15 | JHG | Gasa | Xishuangbanna | 39 | WEH | Dashuipo | Weihai |
| 16 | JNZ | Jinzhou | Jinzhou | 40 | WNZ | Longwan | Wenzhou |
| 17 | KHN | Changbei | Nanchang | 41 | WUH | Tianhe | Wuhan |
| 18 | KOW | Huangjin | Ganzhou | 42 | XIY | Xianyang | Xian |
| 19 | KWL | Liangjiang | Guilin | 43 | XNN | Caojiabu | Xining |
| 20 | LHW | Zhongchuan | Lanzhou | 44 | XUZ | Guanyin | Xuzhou |
| 21 | LJG | Sanyi | Lijiang | 45 | YNJ | Chaoyangchuan | Yanji |
| 22 | LXA | Gongga | Lhasa | 46 | YNZ | Nanyang | Yancheng |
| 23 | MFM | Aomen | Macao | 47 | YTY | Taizhou | Yangzhou |
| 24 | NGB | Lishe | Ningbo |
| Abbreviation | Full Name |
|---|---|
| visibility | Average horizontal visibility every 10 min in an hour (m) |
| TEM | Air temperature (°C) |
| TEM_Min | Minimum temperature (°C) |
| TEM_Max | Maximum temperature (°C) |
| DPT | Dew point temperature (°C) |
| PRS | Pressure (hPa) |
| PRS_Sea | Sea level pressure (hPa) |
| VAP | Vapor pressure (hPa) |
| RHU | Relative humidity (%) |
| PRE_1h | Precipitation in the past hour (mm) |
| PRE_6h | Precipitation in the past 6 h (mm) |
| PRE_12h | Precipitation in the past 12 h (mm) |
| GST | Ground surface temperature (°C) |
| GST_5cm | Ground temperature at 5 cm depth (°C) |
| GST_10cm | Ground temperature at 10 cm depth (°C) |
| GST_15cm | Ground temperature at 15 cm depth (°C) |
| GST_20cm | Ground temperature at 20 cm depth (°C) |
| WIN_S_Avg_2min | 2-min average wind speed (m/s) |
| WIN_S_Avg_10min | 10-min average wind speed (m/s) |
| WIN_S_Max | Maximum wind speed (m/s) |
| WIN_D_S_Max | Wind direction of maximum wind speed (degree) |
| WIN_S_Inst_Max | Extreme instantaneous wind speed (m/s) |
| WIN_D_Inst_Max | Direction with extreme wind speed (degree) |
| WIN_S_Inst_Max_6h | Maximum instantaneous wind speed in the past 6 h (m/s) |
| WIN_D_Inst_Max_6h | Direction of maximum instantaneous wind speed in the past 6 h (degree) |
| WIN_S_Inst_Max_12h | Maximum instantaneous wind speed in the past 12 h (m/s) |
| WIN_D_Inst_Max_12h | Direction of maximum instantaneous wind speed in the past 12 h (degree) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Zhang, G.; Wang, S.; Xue, B.; Yang, J.; Gao, J.; Wang, K.; Jiang, R.; Zhu, X. Forecast of Hourly Airport Visibility Based on Artificial Intelligence Methods. Atmosphere 2022, 13, 75. https://doi.org/10.3390/atmos13010075
Ding J, Zhang G, Wang S, Xue B, Yang J, Gao J, Wang K, Jiang R, Zhu X. Forecast of Hourly Airport Visibility Based on Artificial Intelligence Methods. Atmosphere. 2022; 13(1):75. https://doi.org/10.3390/atmos13010075
Chicago/Turabian StyleDing, Jin, Guoping Zhang, Shudong Wang, Bing Xue, Jing Yang, Jinbing Gao, Kuoyin Wang, Ruijiao Jiang, and Xiaoxiang Zhu. 2022. "Forecast of Hourly Airport Visibility Based on Artificial Intelligence Methods" Atmosphere 13, no. 1: 75. https://doi.org/10.3390/atmos13010075






