Fission Mechanism of 235U+n Reaction According to the Symmetrical Atomic Nucleus Model
Abstract
:1. Introduction
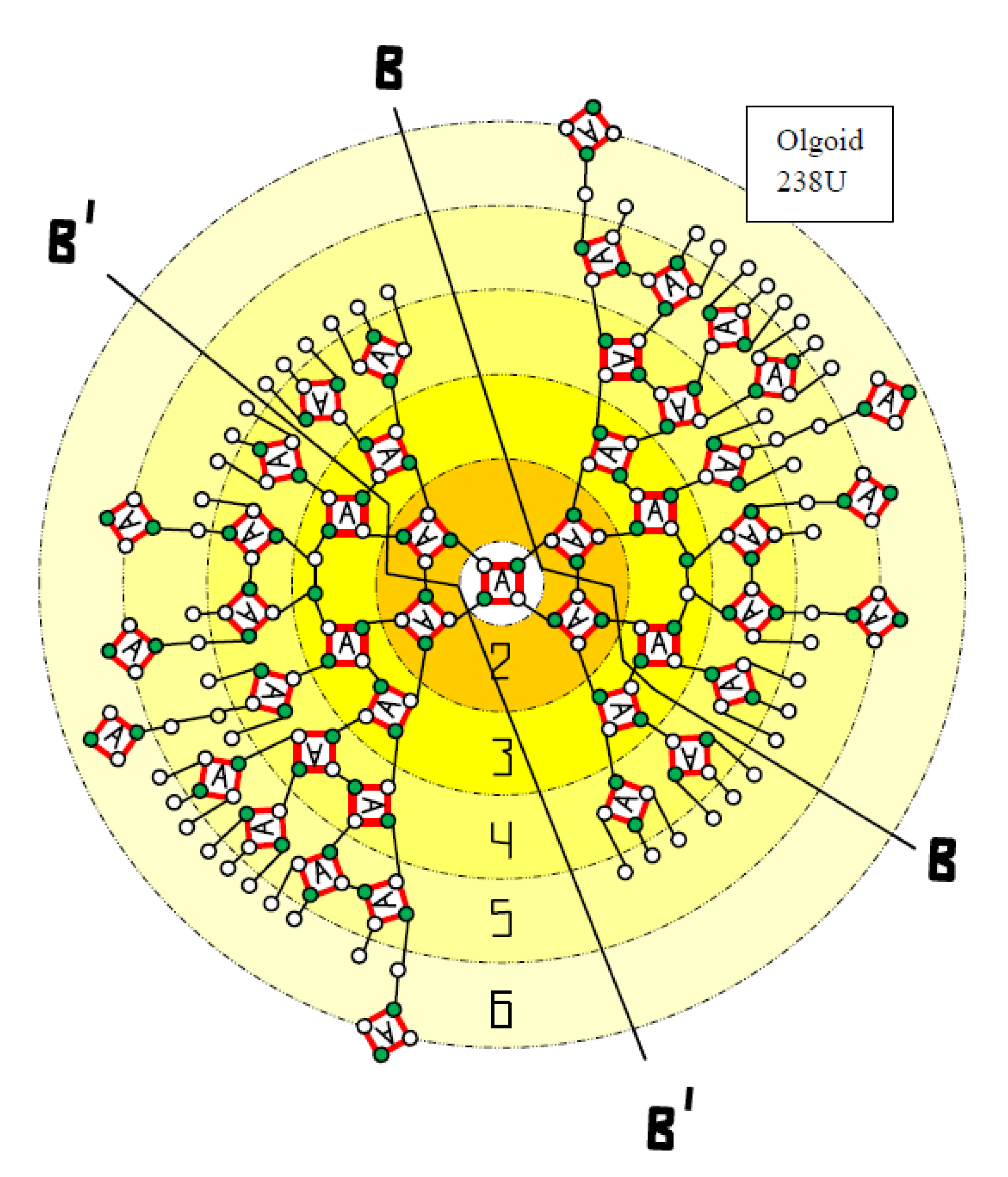
2. Brief Characteristics of Symmetrical Atomic Nucleus Model
3. 235U Nucleus Reaction Fission Mechanism
3.1. Equations of 235U Nucleus Fission Reactions
3.2. 235U Nucleus Fission Reaction into Less Probable Fragments
3.3. Analysis of Fragment Binding Energy in the 235U+n Reaction
3.4. Conclusions Based on Investigations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baba, H.; Takahashi, N.; Yokoyama, A.; Saito, T. Fast fission mechanism and duality of the diffusion process. Eur. Phys. J. 1998, 3, 281–292. [Google Scholar] [CrossRef]
- Gontchar, I.; Morjean, M.; Basnary, S. Nuclear dissipation from fission time. Eur. Lett. 2002, 57, 355–361. [Google Scholar] [CrossRef] [Green Version]
- Goutte, H.; Berger, J.F.; Casoli, P.; Gogny, D. Microscopic approach of fission dynamics applied to fragment kinetic energy and mass distributions in 238U. Phys. Rev. C 2005, 71, 024316. [Google Scholar] [CrossRef] [Green Version]
- Krappe, H.J. Cluster model versus Fermi-fluid approach to fission theory. Int. J. Mod. Phys. E 2007, 16, 396–401. [Google Scholar] [CrossRef]
- Royer, G.; Bonilla, C. Multiple-humped fission and fusion barriers of actinide and superheavy elements. J. Radioanal. Nucl. Chem. Artic. 2007, 272, 237–242. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, K.-H.; Kelić, A.; Ricciardi, M.V. Experimental evidence for the separability of compoundnucleus and fragment properties in fission. Eur. Lett. 2008, 83, 32001. [Google Scholar] [CrossRef] [Green Version]
- Sargsyan, V.V.; Kanokov, Z.; Adamian, G.G.; Antonenko, N.V. Quantum statistical effects in nuclear reactions, fission and open quantum systems. Phys. Part. Nucl. 2010, 41, 175–229. [Google Scholar] [CrossRef]
- Umar, A.S.; Oberacker, V.E.; Maruhn, J.A.; Reinhard, P.G. Microscopic description of nuclear fission dynamics. J. Phys. G Nucl. Part. Phys. 2010, 37, 064037. [Google Scholar] [CrossRef]
- Randrup, J.; Möller, P.; Sierk, A.J. Fission-fragment mass distributions from strongly damped shape evolution. Phys. Rev. C 2011, 84, 034613. [Google Scholar] [CrossRef] [Green Version]
- Al-Adili, A.; Hambsch, F.-J.; Pomp, S.; Oberstedt, S. Impact of prompt-neutron corrections on final fission-fragment distributions. Phys. Rev. C 2012, 86, 054601. [Google Scholar] [CrossRef]
- Schmidt, K.-H.; Jurado, B. Global view on fission observables–new insights and new puzzles. Phys. Procedia 2012, 31, 147–157. [Google Scholar] [CrossRef] [Green Version]
- Aritomo, Y.; Chiba, S.; Ivanyuk, F. Fission dynamics at low excitation energy. Phys. Rev. C 2014, 90, 054609. [Google Scholar] [CrossRef]
- Goriely, S. The fundamental role of fission during r-process nucleosynthesis in neutron star mergers. Eur. Phys. J. A 2015, 51, 22. [Google Scholar] [CrossRef] [Green Version]
- Imanishi, N.; Fujiwara, I.; Nishi, T. Independent isomer yields of Sb and Te isotopes in thermal-neutron fission of 233U, 235U and 239Pu. Nucl. Phys. A 1976, 263, 141–149. [Google Scholar] [CrossRef]
- Glendenin, L.E.; Gindler, J.E.; Henderson, D.J.; Meadows, J.W. Mass distributions for monoenergeticneutron-induced fission of 235U. Phys. Rev. C 1981, 24, 2600–2605. [Google Scholar] [CrossRef]
- Quade, U.; Rudolph, K.; Skorka, S.; Armbruster, P.; Clerc, H.-G.; Lang, W.; Mutterer, M.; Schmitt, C.; Theobald, J.; Gönnenwein, F.; et al. Nuclide yields of light fission products from thermal-neutron induced fission of 233U at different kinetic energies. Nucl. Phys. A 1988, 487, 1–36. [Google Scholar] [CrossRef]
- Laurec, J.; Adam, A.; de Bruyne, T.; Bauge, E.; Granier, T.; Aupiais, J.; Bersillon, O.; Le Petit, G.; Authier, N.; Casoli, P. Fission Product Yields of 233U, 235U, 238U and 239Pu in Fields of Thermal Neutrons, Fission Neutrons and 14.7-MeV Neutrons. Nucl. Data Sheets 2010, 111, 2965–2980. [Google Scholar] [CrossRef]
- Innes, M.M.; Chadwick, M.B.; Kawano, T. Fission product yields for 14 MeV neutrons on 235U, 238U and 239Pu. Nucl. Data Sheets 2011, 112, 3135–3152. [Google Scholar] [CrossRef]
- Schmitt, C.; Möller, P. On the isotopic composition of fission fragments. Phys. Lett. B 2020, 812, 136017. [Google Scholar] [CrossRef]
- Pleasonton, F. Prompt γ-rays emitted in the thermal-neutron induced fission of 233U and 239Pu. Nucl. Phys. A 1973, 213, 413–425. [Google Scholar] [CrossRef]
- Oberstedt, S.; Belgya, T.; Billnert, R.; Borcea, R.; Bryś, T.; Geerts, W.; Göök, A.; Hambsch, F.-J.; Kis, Z.; Martinez, T.; et al. Improved values for the characteristics of prompt-fission gamma-ray spectra from the reaction 235U(nth,f). Phys. Rev. C 2013, 87, 051602(R). [Google Scholar] [CrossRef] [Green Version]
- Vogt, R.; Randrup, J. Event-by-event study of photon observables in spontaneous and thermal fission. Phys. Rev. C 2013, 87, 044602. [Google Scholar] [CrossRef] [Green Version]
- Zucker, M.S.; Holden, N.E. Energy Dependence of Neutron Multiplicity in Fast-Neutron-Induced Fission for 235,238U and 239Pu. In Proceedings of the American Nuclear Society Annual Meeting, Reno, NV, USA, 15 June 1986. [Google Scholar]
- Naik, H.; Dange, S.P.; Singh, R.J. Angular momentum of fission fragments in low energy fission of actinides. Phys. Rev. C 2005, 71, 014304. [Google Scholar] [CrossRef]
- Schmidt, K.-H.; Jurado, B. Final excitation energy of fission fragments. Phys. Rev. C 2011, 83, 061601. [Google Scholar] [CrossRef] [Green Version]
- Maslov, V.M.; Tetereva, N.A.; Pronyaev, V.G.; Kagalenko, A.B.; Zolotarev, K.I.; Capote, R.; Granier, T.; Morillon, B.; Hambsch, F.-J.; Sublet, J.-C. 235U(n, f), 233U(n, f) and 239Pu(n, f) Prompt Fission Neutron Spectra. J. Korean Phys. Soc. 2011, 59, 1337–1342. [Google Scholar] [CrossRef]
- Ebran, A.; Taieb, J.; Belier, G.; Chatillon, A.; Laurent, B.; Martin, J.-F.; Pellereau, E. Picosecond resolution on relativistic heavy ions time-of-flight measurement. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 728, 40–46. [Google Scholar] [CrossRef]
- Stetcu, I.; Talou, P.; Kawano, T.; Jandel, M. Isomer production ratios and the angular momentum distribution of fission fragments. Phys. Rev. C 2013, 88, 044603. [Google Scholar] [CrossRef]
- Kadmensky, S.G. Mechanisms of binary and ternary low-energy fission of nuclei with allowance for nonsphericity effects. Phys. Atomic Nucl. 2004, 67, 170–182. [Google Scholar] [CrossRef]
- Gönnenwein, F.; Tsekhanovich, I.; Rubchenya, V. Angular momenta of near-spherical fission fragments. Int. J. Mod. Phys. E 2007, 16, 410–424. [Google Scholar] [CrossRef]
- Kadmensky, S.G. Quantum properties of deformation modes of fissile-nucleus motion. Phys. At. Nucl. 2008, 71, 1193–1199. [Google Scholar] [CrossRef]
- Schmidt, K.-H.; Jurado, B.; Amouroux, C.; Schmitt, C. General Description of Fission Observables: GEF Model Code. Nucl. Data Sheets 2016, 131, 107–221. [Google Scholar] [CrossRef] [Green Version]
- Kadmensky, S.G.; Lyubashevsky, D.E. Description of true and delayed ternary nuclear fission accompanied by the emission of various third particles. Phys. At. Nucl. 2010, 73, 1436–1442. [Google Scholar] [CrossRef]
- Santhosh, K.P.; Krishnan, S.; Priyanka, B. Light charged particle accompanied ternary fission of 242Cm using the Coulomb and proximity potential. Eur. Phys. J. A 2014, 50, 66. [Google Scholar] [CrossRef]
- Kadmensky, S.G.; Bulychev, A.O. Sequential character of low-energy ternary and quaternary nuclear fission. Phys. At. Nucl. 2016, 79, 793–797. [Google Scholar] [CrossRef]
- Holmvall, P.; Köster, U.; Heinz, A.; Nilsson, T. Collinear cluster tri-partition: Kinematics constraints and stability of collinearity. Phys. Rev. C 2017, 95, 014602. [Google Scholar] [CrossRef]
- Adamian, G.G.; Antonenko, N.V.; Bezbakh, A.N.; Malov, L.A. Manifestation of the structure of heavy nuclei in their alpha decays. Phys. At. Nucl. 2016, 79, 951–962. [Google Scholar] [CrossRef]
- Kapitonov, I.M. Vvedenie v Fiziku Yadra i Chastits: Textbook, 5th ed.; Revised by Lenand, M.; 2017; 544p. [Google Scholar]
- Cook, N.D. Models of the Atomic Nucleus; Springer: New York, NY, USA, 2010. [Google Scholar]
- Ebran, J.-P.; Khan, E.; Nikšić, T.; Vretenar, D. Density functional theory studies of cluster states in nuclei. Phys. Rev. C 2014, 90, 054329. [Google Scholar]
- Dubovichenko, S.B.; Burkova, N.A. Does the Excited Cluster 14N* Exist in the 15O Nucleus? Russ. Phys. J. 2019, 61, 2105–2112. [Google Scholar] [CrossRef]
- Pauling, L. The Close-packed-spheron model of atomic nuclei and its relation to the shell model. Proc. Natl. Acad. Sci. USA 1965, 54, 989–994. [Google Scholar] [CrossRef] [Green Version]
- Cook, N.D. LENR theory requires a proper understanding of nuclear structure. J. Condens. Matter Nucl. Sci. 2017, 24, 60–74. [Google Scholar]
- Wigner, E. On the consequences of the symmetry of the nuclear Hamiltonian on the spectroscopy of nuclei. Phys. Rev. 1937, 51, 106. [Google Scholar] [CrossRef]
- Sukhanov, A.D. Lektsii po kvantovoi fizike: Teaching Aid; Sukhanov, A.D., Golubeva, O.N., Eds.; Vysshaya shkola: Moscow, Russia, 2006; 528p. [Google Scholar]
- Nordling, C.; Osterman, J. Physics Handbook for Science and Engineering, 8th ed.; Professional Publishing House: Los Angeles, CA, USA, 2006; p. 503. [Google Scholar]



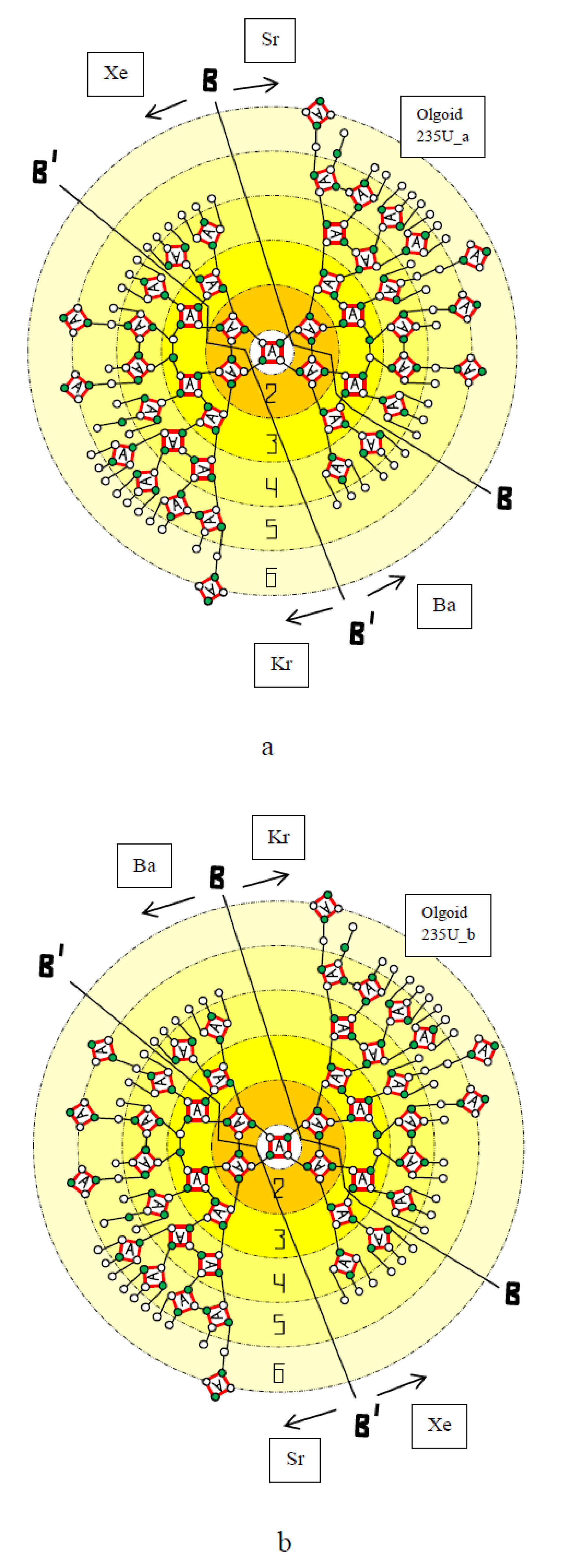
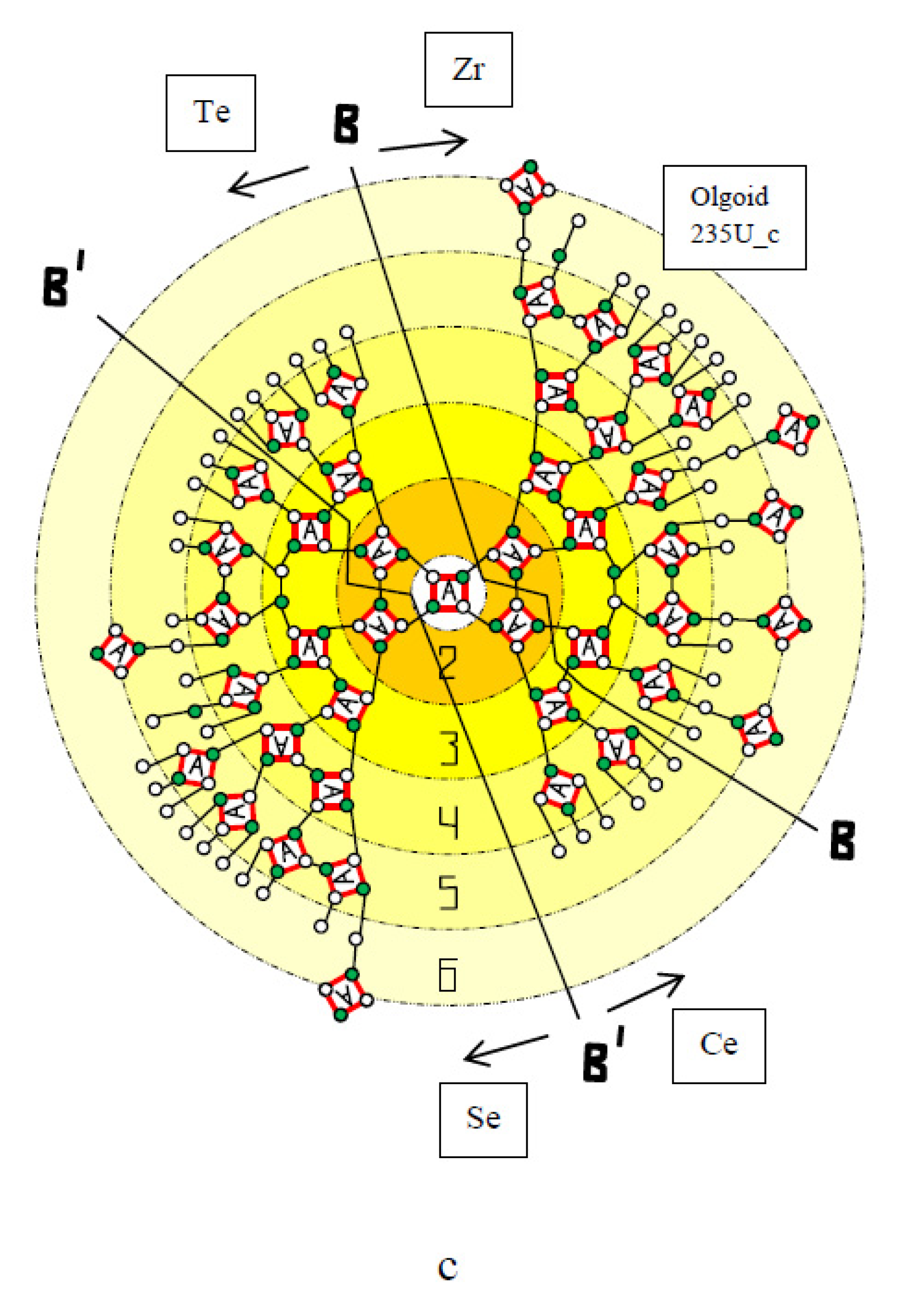
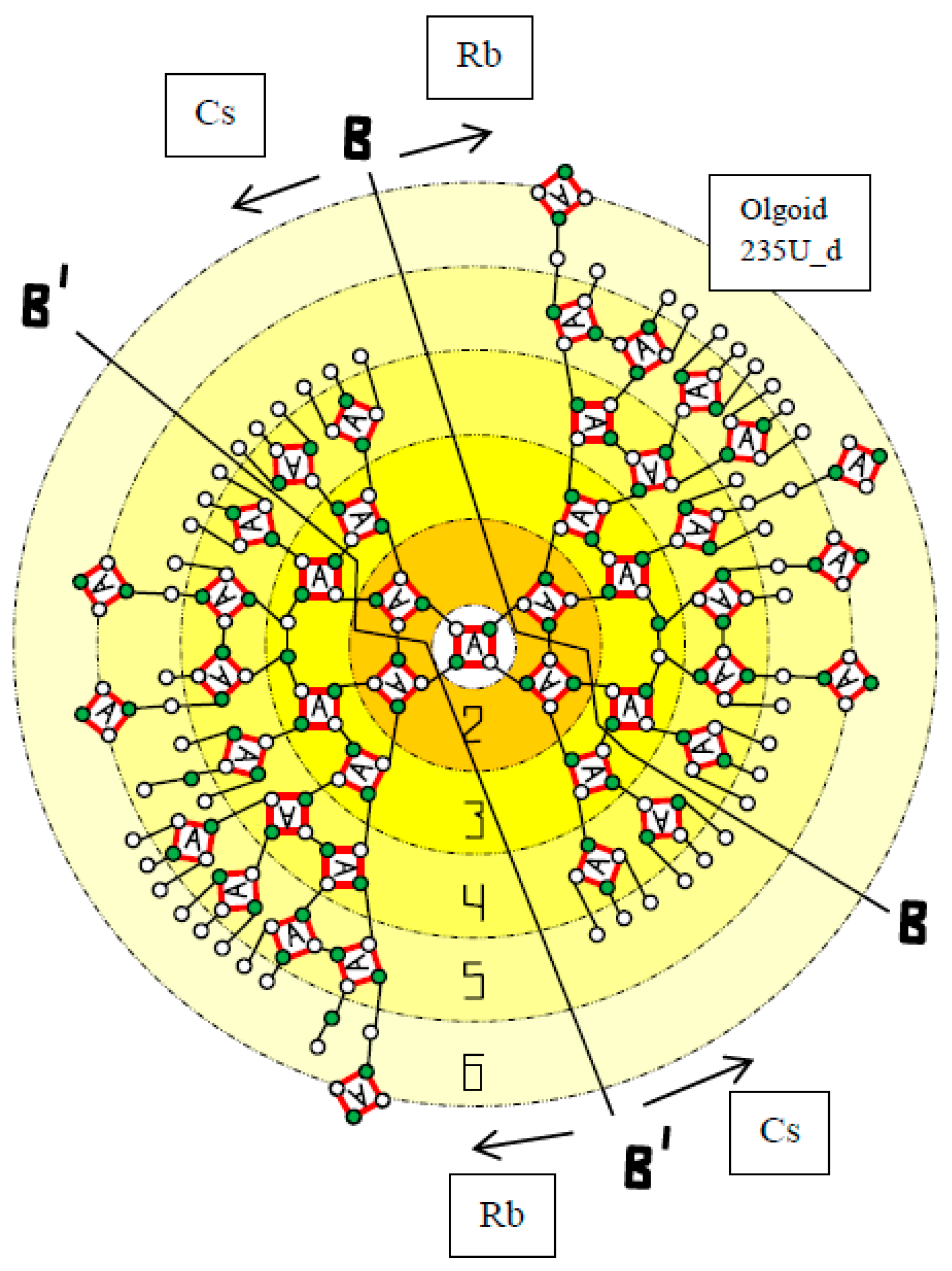
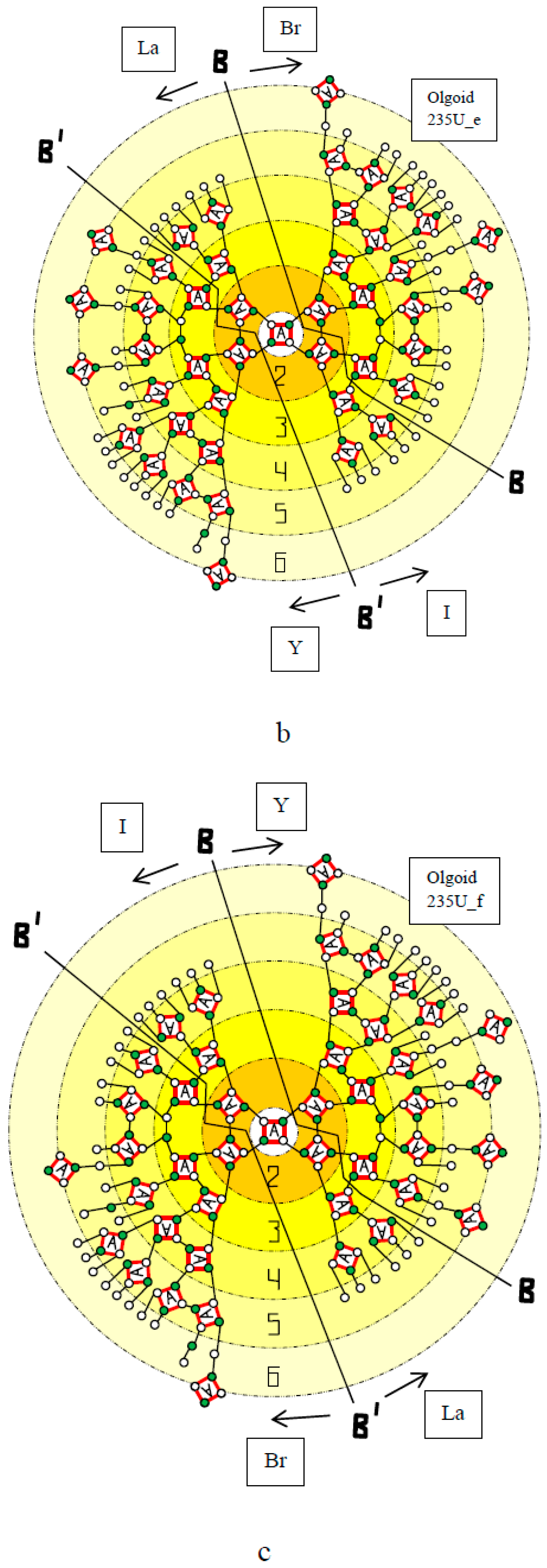

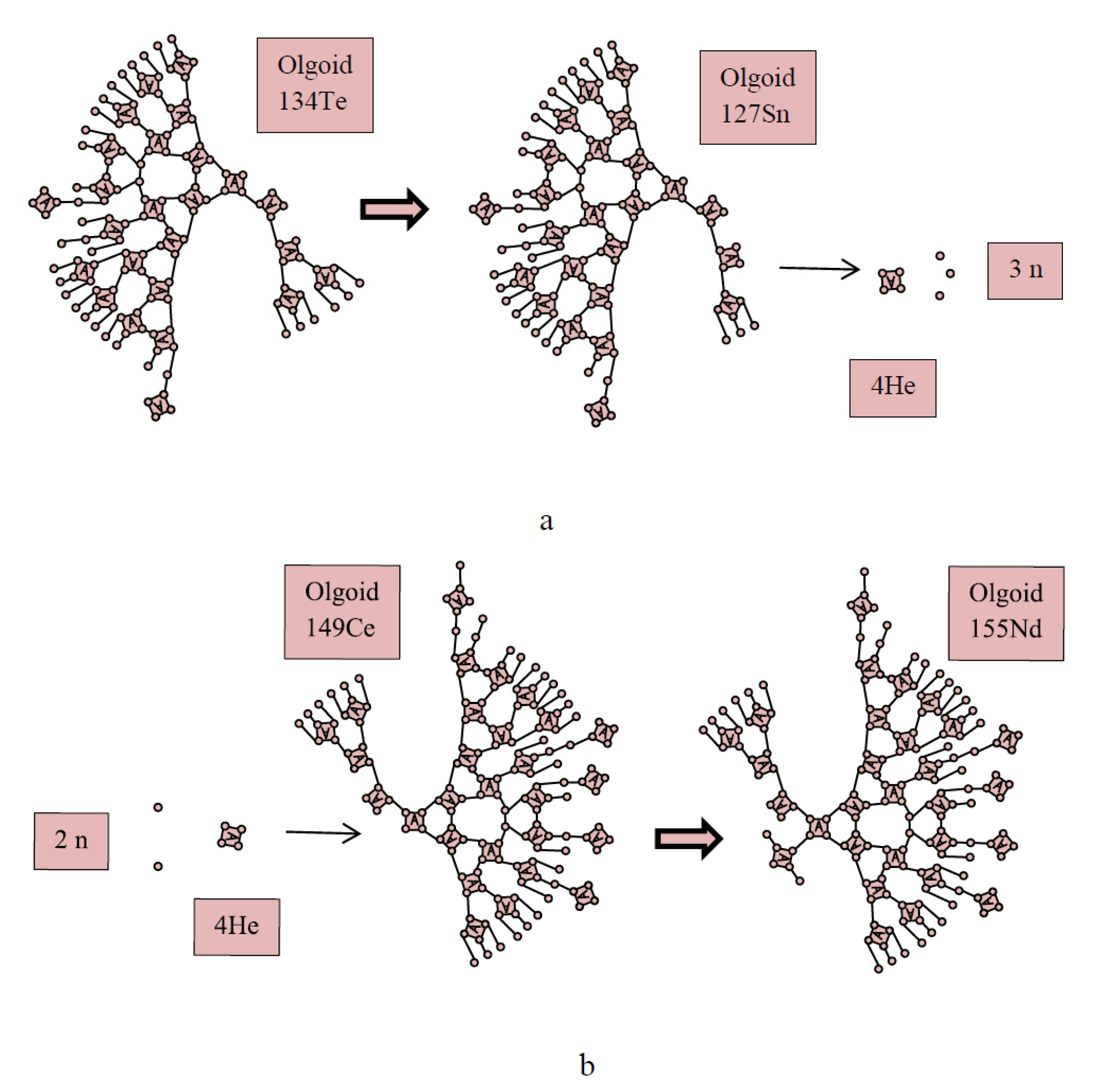
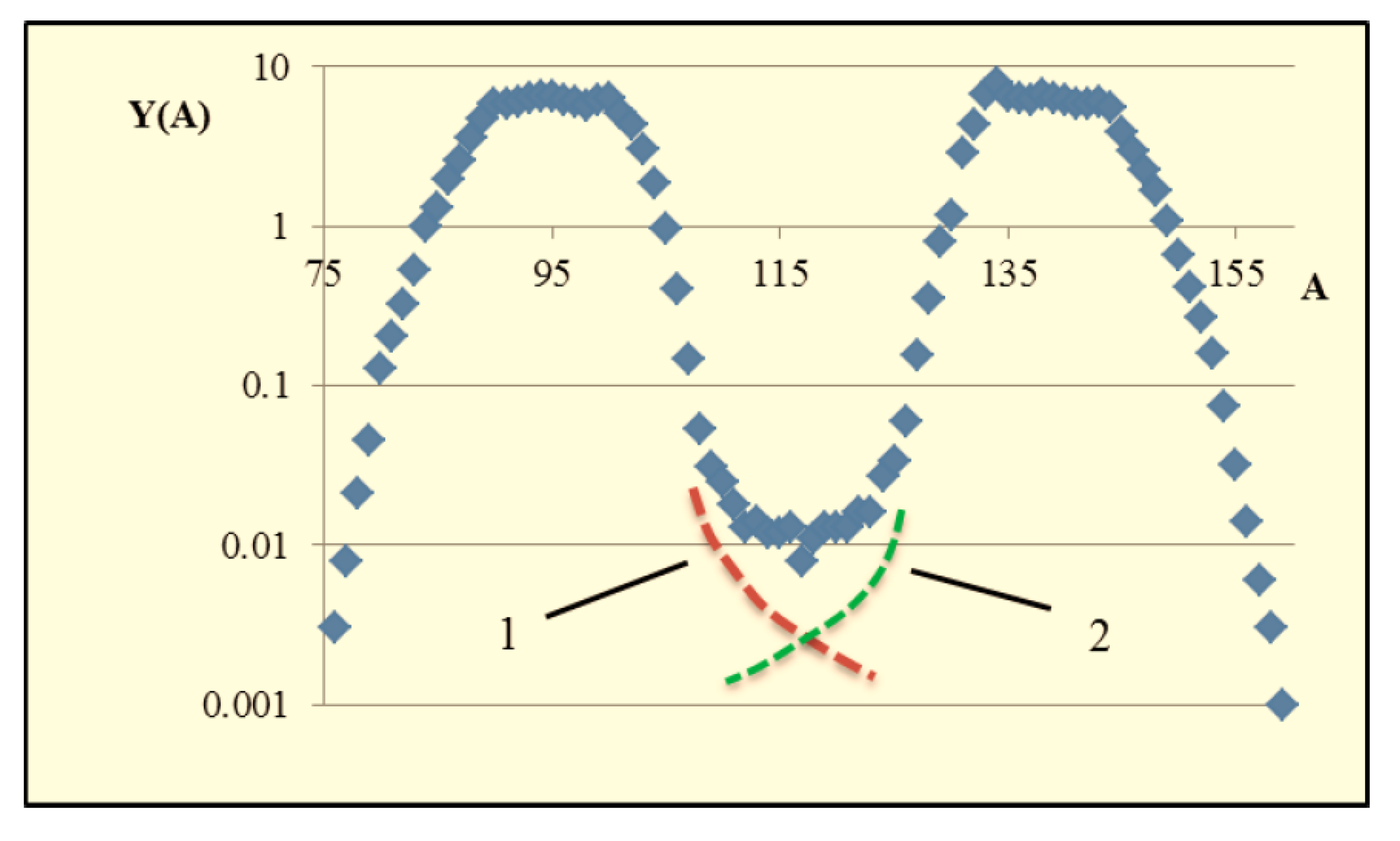
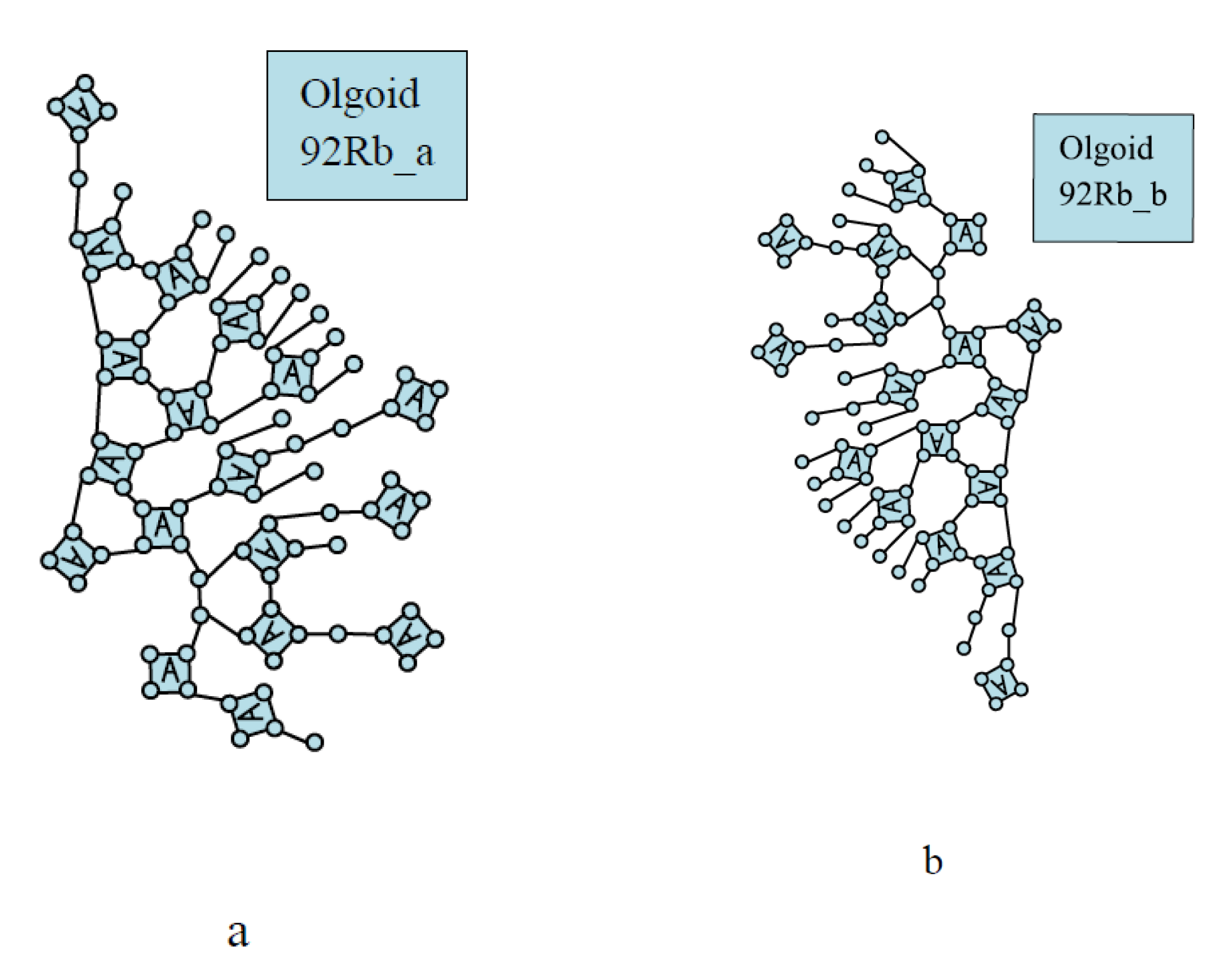
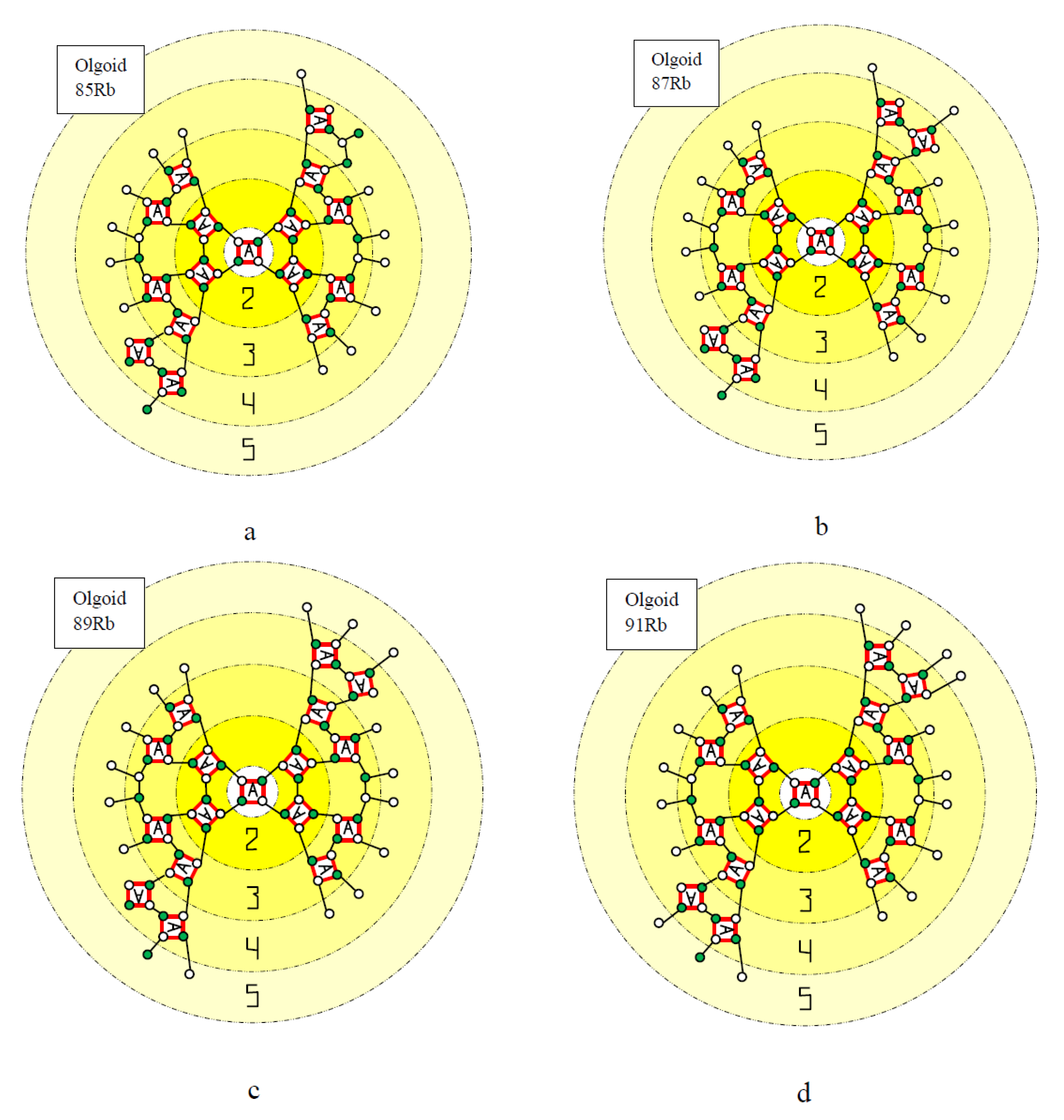
| Olgoid | Z | N | BS | NA | BA | BC = BS − BA | NcC | BC/NcC | NcS |
|---|---|---|---|---|---|---|---|---|---|
| MeV | MeV | MeV | MeV | ||||||
| 1H | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4He | 2 | 2 | 28.296 | 1 | 28.296 | 0 | 0 | 0 | 4 |
| 7Li | 3 | 4 | 39.244 | 1 | 28.296 | 10.948 | 3 | 3.649 | 7 |
| 12C | 6 | 6 | 92.162 | 3 | 84.888 | 7.274 | 2 | 3.637 | 14 |
| 16O | 8 | 8 | 127.619 | 4 | 113.183 | 14.436 | 3 | 4.812 | 19 |
| 20Ne | 10 | 10 | 160.645 | 5 | 141.478 | 19.167 | 4 | 4.792 | 24 |
| 23Na | 11 | 12 | 186.564 | 5 | 141.478 | 45.086 | 9 | 5.009 | 29 |
| 30Si | 14 | 16 | 255.620 | 7 | 198.07 | 57.55 | 10 | 5.755 | 38 |
| 40Ar | 18 | 22 | 343.810 | 9 | 254.661 | 89.149 | 16 | 5.572 | 52 |
| 41K | 19 | 22 | 351.619 | 9 | 254.661 | 96.958 | 17 | 5.703 | 53 |
| 86Kr | 36 | 50 | 749.234 | 17 | 481.026 | 268.208 | 44 | 6.096 | 112 |
| 85Rb | 37 | 48 | 739.282 | 16 | 452.731 | 286.551 | 46 | 6.229 | 110 |
| 87Rb | 37 | 50 | 757.856 | 17 | 481.026 | 276.830 | 45 | 6.152 | 113 |
| 89Rb | 37 | 52 | 771.113 | 17 | 481.026 | 290.087 | 47 | 6.172 | 115 |
| 91Rb | 37 | 54 | 783.288 | 17 | 481.026 | 302.262 | 49 | 6.169 | 117 |
| 132Xe | 54 | 78 | 1112.448 | 25 | 707.392 | 405.056 | 70 | 5.787 | 170 |
| 133Cs | 55 | 78 | 1118.527 | 25 | 707.392 | 411.135 | 71 | 5.791 | 171 |
| 204Hg | 80 | 124 | 1608.651 | 37 | 1046.939 | 561.712 | 106 | 5.299 | 254 |
| 235U | 92 | 143 | 1783.86 | 44 | 1245.02 | 538.836 | 116 | 4.645 | 292 |
| 238U | 92 | 146 | 1801.69 | 45 | 1273.32 | 528.37 | 116 | 4.555 | 296 |
| Kinetic Energy of Fragments | 167 MeV |
|---|---|
| Kinetic energy of neutrons | 5 MeV |
| Electrons of β-decay of fission products | 7 MeV |
| Anti-neutrino of β-decay of fission products | 9 MeV |
| Instantaneous γ-radiation | 8 MeV |
| γ-radiation of fission products | 7 MeV |
| Total energy of fission | 203 MeV |
| (a) Light Fragments | (b) Heavy Fragments | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A | Y(A) % | Nuclide X | Y(X) % | t(X) | A | Y(A) % | Nuclide X | Y(X) % | t(X) |
| 76 | 0.003 | 76Zn | 0.0018 | 5.7s | 118 | 0.011 | 118Ag | 0.0064 | 4.0s |
| 77 | 0.008 | 77Ga | 0.0041 | 13c | 119 | 0.013 | 119Ag | 0.0073 | 2.1s |
| 78 | 0.021 | 78Ga | 0.0103 | 5.1s | 120 | 0.013 | 120Cd | 0.0084 | 51s |
| 79 | 0.045 | 79Ge | 0.0233 | 19s | 121 | 0.013 | 121Cd | 0.0072 | 13.5s |
| 80 | 0.129 | 80Ge | 0.102 | 29.5s | 122 | 0.016 | 122Cd | 0.012 | 5.3s |
| 81 | 0.204 | 81Ge | 0.126 | 7.6s | 123 | 0.016 | 123Cd | 0.010 | 2.1s |
| 82 | 0.325 | 82As | 0.129 | 19s | 124 | 0.027 | 124Cd | 0.012 | 1.24s |
| 83 | 0.535 | 83As | 0.291 | 13.4s | 125 | 0.034 | 125Sn | 0.011 | 9.63d |
| 84 | 1.00 | 84Se | 0.631 | 3.3s | 126 | 0.059 | 126Sn | 0.045 | 0.1My |
| 85 | 1.32 | 85Se | 0.894 | 39s | 127 | 0.157 | 127Sn | 0.095 | 2.1h |
| 86 | 1.95 | 86Ge | 0.629 | 0.25s | 128 | 0.35 | 128Sn | 0.301 | 59m |
| 87 | 2.56 | 87Br | 1.27 | 56s | 129 | 0.79 | 129Sn | 0.43 | 6.9m |
| 88 | 3.58 | 88Kr | 1.73 | 2.84h | 130 | 1.18 | 130Sn | 1.08 | 3.7m |
| 89 | 4.74 | 89Kr | 3.44 | 3.15m | 131 | 2.89 | 131Sb | 1.65 | 39s |
| 90 | 5.78 | 90Kr | 4.40 | 32.3s | 132 | 4.31 | 132Sb | 2.16 | 4.2m |
| 91 | 5.83 | 91Kr | 3.16 | 8.6s | 133 | 6.70 | 133Te | 4.14 | 55.4m |
| 92 | 6.01 | 92Rb | 3.13 | 4.5s | 134 | 7.84 | 134Te | 6.22 | 42m |
| 93 | 6.36 | 93Rb | 3.07 | 5.85s | 135 | 6.54 | 135Te | 3.22 | 19s |
| 94 | 6.47 | 94Sr | 4.51 | 1.25m | 136 | 6.32 | 136I | 2.57 | 1.39m |
| 95 | 6.50 | 95Sr | 4.54 | 25.1s | 137 | 6.19 | 137Xe | 3.19 | 3.82m |
| 96 | 6.27 | 96Sr | 3.57 | 1.06s | 138 | 6.71 | 138Xe | 4.81 | 14.1m |
| 97 | 6.00 | 97Y | 3.14 | 3.76s | 139 | 6.41 | 139Xe | 4.32 | 39.7s |
| 98 | 5.76 | 98Zr | 2.57 | 30.7s | 140 | 6.22 | 140Xe | 3.51 | 13.6s |
| 99 | 6.11 | 99Zr | 3.58 | 2.2s | 141 | 5.85 | 141Cs | 2.92 | 25s |
| 100 | 6.29 | 100Zr | 4.98 | 7.1s | 142 | 5.84 | 142Ba | 3.01 | 10.7m |
| 101 | 5.18 | 101Zr | 2.79 | 2.1s | 143 | 5.95 | 143Ba | 4.10 | 14.3s |
| 102 | 4.29 | 102Zr | 1.78 | 2.9s | 144 | 5.50 | 144Ba | 3.98 | 11.4s |
| 103 | 3.03 | 103Nb | 1.41 | 1.5s | 145 | 3.93 | 145La | 1.92 | 24s |
| 104 | 1.88 | 104Mo | 1.13 | 60s | 146 | 3.00 | 146La | 1.49 | 6.3s |
| 105 | 0.96 | 105Mo | 0.668 | 36s | 147 | 2.25 | 147Ce | 1.00 | 56s |
| 106 | 0.402 | 106Mo | 0.359 | 8.4s | 148 | 1.67 | 148Ce | 1.24 | 56s |
| 107 | 0.146 | 107Mo | 0.121 | 3.5s | 149 | 1.08 | 149Ce | 0.70 | 5.2s |
| 108 | 0.054 | 108Mo | 0.030 | 1.5s | 150 | 0.653 | 150Ce | 0.39 | 4.4s |
| 109 | 0.031 | 109Mo | 0.0155 | 1.4s | 151 | 0.419 | 151Pr | 0.24 | 22s |
| 110 | 0.025 | 110Tc | 0.012 | 0.83s | 152 | 0.267 | 152Nd | 0.141 | 11.4m |
| 111 | 0.018 | 111Ru | 0.012 | 1.5s | 153 | 0.158 | 153Nd | 0.111 | 29s |
| 112 | 0.013 | 112Ru | 0.0099 | 4.5s | 154 | 0.074 | 154Nd | 0.058 | 26s |
| 113 | 0.014 | 113Rh | 0.0064 | 2.7s | 155 | 0.032 | 155Nd | 0.018 | 8.9s |
| 114 | 0.012 | 114Rh | 0.0050 | 1.8s | 156 | 0.014 | 156Pm | 0.0071 | 27s |
| 115 | 0.012 | 115Rh | 0.0036 | 0.99s | 157 | 0.006 | 157Pm | 0.0029 | 11s |
| 116 | 0.013 | 116Pd | 0.0068 | 12.7s | 158 | 0.003 | 158Sm | 0.0024 | 5.5s |
| 117 | 0.008 | 117Ag | 0.0030 | 1.2m | 159 | 0.001 | Sm159 | 0.0007 | 11c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denisov, V.A.; Razinkin, V.P.; Atuchin, V.V. Fission Mechanism of 235U+n Reaction According to the Symmetrical Atomic Nucleus Model. Atoms 2022, 10, 134. https://doi.org/10.3390/atoms10040134
Denisov VA, Razinkin VP, Atuchin VV. Fission Mechanism of 235U+n Reaction According to the Symmetrical Atomic Nucleus Model. Atoms. 2022; 10(4):134. https://doi.org/10.3390/atoms10040134
Chicago/Turabian StyleDenisov, Vladimir A., Vladimir P. Razinkin, and Victor V. Atuchin. 2022. "Fission Mechanism of 235U+n Reaction According to the Symmetrical Atomic Nucleus Model" Atoms 10, no. 4: 134. https://doi.org/10.3390/atoms10040134
APA StyleDenisov, V. A., Razinkin, V. P., & Atuchin, V. V. (2022). Fission Mechanism of 235U+n Reaction According to the Symmetrical Atomic Nucleus Model. Atoms, 10(4), 134. https://doi.org/10.3390/atoms10040134






