Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission
Abstract
:1. Introduction
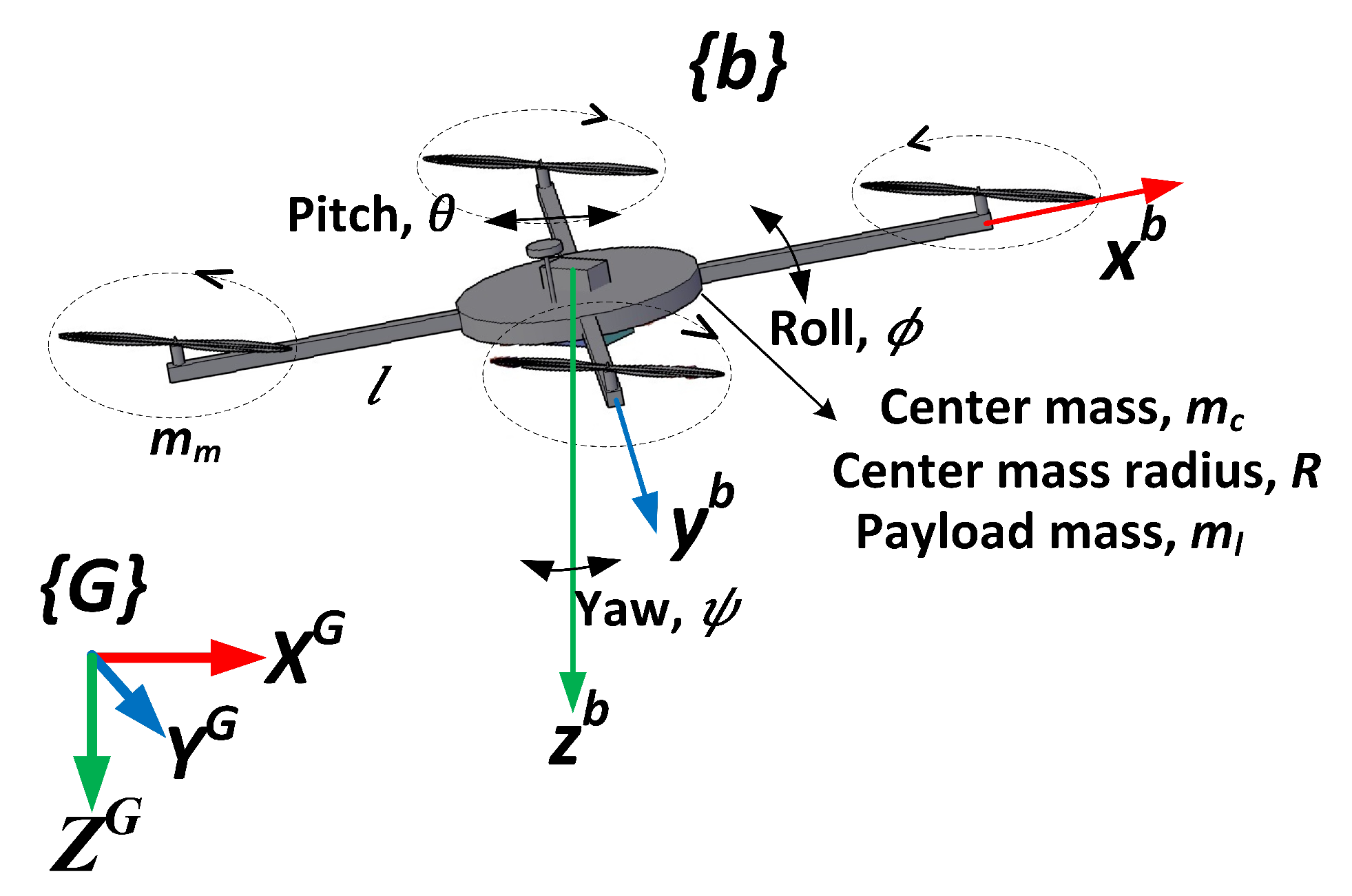
2. Dynamic Model of Quadcopter
- The frame of the quadcopter is symmetrical and the center of gravity is in the middle of the fuselage;
- The thrust and friction of each motor of a quadcopter is proportional to the square of their motor speed;
- Moment of inertia of the propellers;
- During the flight of the qudcopter, the Earth is flat and non-rotating.
3. Proposed Control Approach for Path Planning and Tracking
3.1. Controller Design
3.1.1. Translational Position Control
3.1.2. Attitude–Altitude Control
3.1.3. Angular Velocity Control
3.1.4. Motor Control
3.2. Three-Dimensional Path Planning Model of the Quadcopter
| Algorithm 1: Pseudo-code of proposed 3D path-planning algorithm. |
 |
3.3. Proposed Path Planning and Tracking Optimization Algorithm
3.3.1. Particle Swarm Optimization
| Algorithm 2: Pseudo-code of PSO algorithm. |
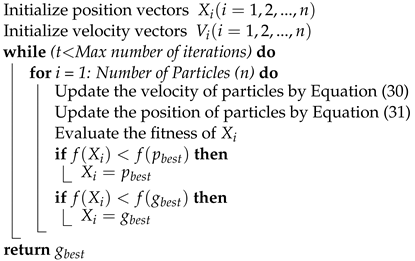 |
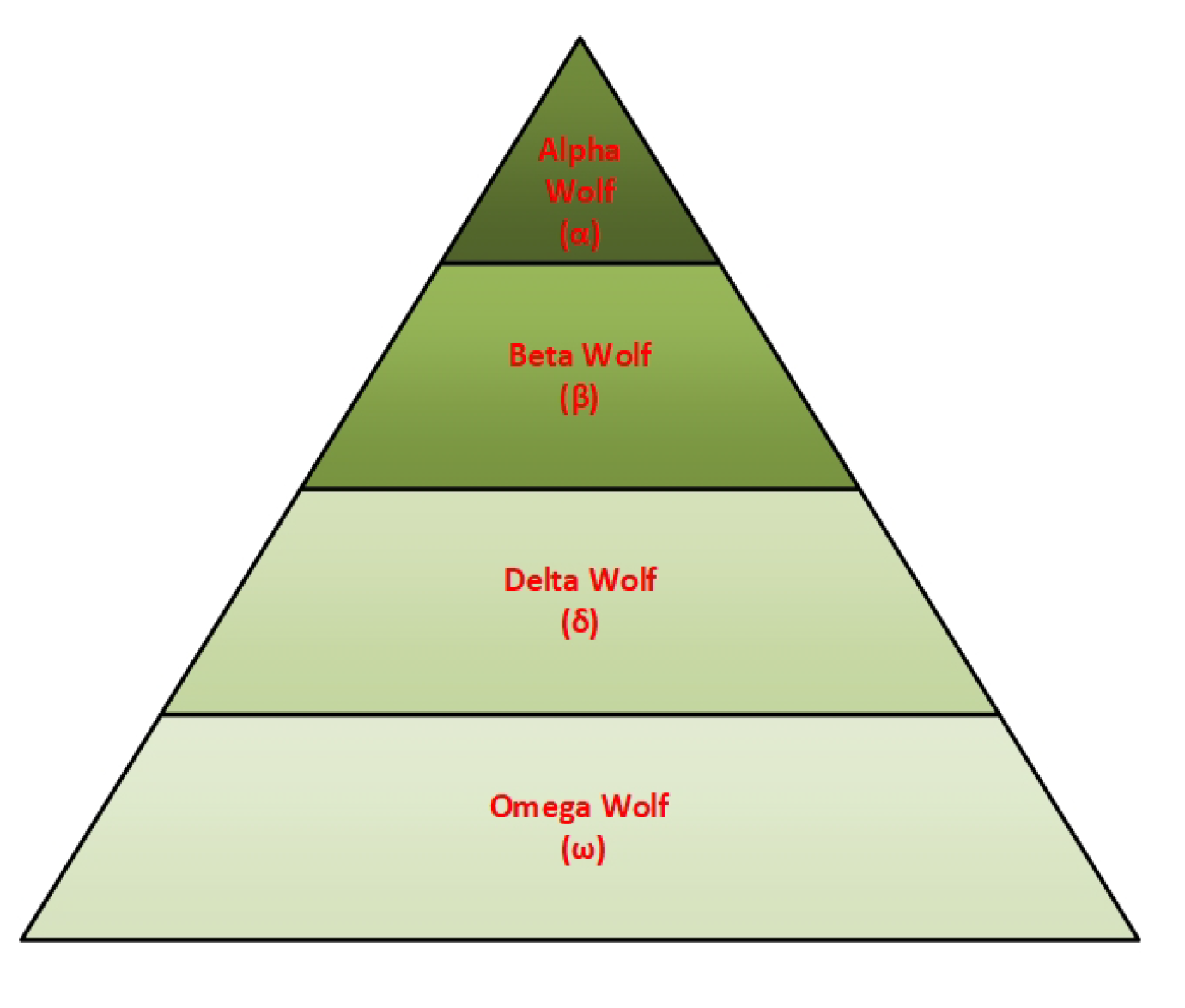
3.3.2. Grey Wolf Optimization
| Algorithm 3: Pseudo-code of GWO algorithm. |
 |
3.3.3. Harris Hawk Optimization
- Exploration phase: Although Harris hawks have strong eyes, sometimes they may not be able to detect their prey easily. In this situation, Harris hawks often wait in the desert area and observe their surroundings. This process continues in a loop. Harris hawks in each loop are identified as candidate solutions. The hawk, who is in the best position in relation to the rabbit in the loop, represents the optimum solution. The HHO algorithm uses two different strategies in the hunt search process. These strategies can be described by [45]:where represents the position of Harris hawks in the next iteration ; denotes the current position of Harris hawks; indicates the position of the rabbit; is the average position of the current population of Harris Hawks; represents a randomly selected Harris hawk from the current population; , and q are random numbers between ; and and show the upper and lower bounds of the variables, respectively. The average position of hawks is determined by:where N represents the total number of Harris hawks, and indicates the location of each Harris hawk in iteration t.
- Transition from exploration to exploitation phase: Harris hawks begin the exploitation phase by developing different attack models according to the energy of the prey after the exploration process is completed. This process is modelled in [45] as:where is the initial energy value of the prey randomly defined in the range of , E is the energy of the escaping prey, and T is the maximum number of iterations.
- Exploitation phase: At this phase, the Harris hawk attacks its prey and makes the surprise attack move. In response to this situation, the prey tries to escape. In this case, the Harris hawk basically develops four different strategies. The energy of the prey and the chance of catching the escaping prey are indicated by E and r, respectively:
- –
- Soft besiege ( and )In this strategy, the Harris hawk makes misleading jumps at its prey and tries to reduce the energy of its prey. This soft besiege strategy is mathematically described by:where is the difference between the current position in the t-th iteration and the current position of the prey, and J is a value that changes with each iteration to simulate the natural motion of the prey.
- –
- Hard besiege ( and )In this strategy, the energy of the prey is very low. The hawk hardly makes any besiege to throw his surprise claws on its prey. This strategy can be mathematically modeled as:where represents the current position of prey, is the difference between the current position in the t-th iteration and the current position of the prey.
- –
- Soft besiege with progressive rapid dives ( and )In this strategy, the prey has enough energy to escape. The Harris hawk is still performing the soft besiege strategy before the surprise jump. This process is smarter than the previous strategy. Before the hawks start their soft besiege, they decide their next move based on the following calculation:where indicates the current position of the prey, and J is a value that changes with each iteration to simulate the natural motion of the prey. This situation is compared with the previous dive to decide whether such a move would be a good dive. If the situation is unfavorable, the hawks dive into their prey suddenly. When deciding on this, a Levy-flight-based movement structure is used. This situation is defined by:where Z is the variable that decides whether the hawk will make a move on its prey, Y indicates its position in relation to the decreasing energy of the prey, D is the size of the problem, S is a random vector of size , and is the Levy flight function and is defined by:where u and v are the random numbers between (0, 1), and is 1.5. Note that the Levy flight algorithm is added to the exploitation phase to ensure that the local search process can be continued without becoming stuck at local optimum points. The positions of the hawks in the soft besiege phase are updated by:where Y and Z are obtained using Equations (40) and (41).
- –
- Hard besiege with progressive rapid dives ( and ) In this strategy, the prey does not have enough energy to escape. The Harris hawk makes a fierce siege before its surprise jump to catch its prey. The hard besiege situation is expressed by:where and are defined as:
3.3.4. The Proposed Optimization Algorithm
| Algorithm 4: Pseudo-code of hybrid HHO–GWO algorithm |
 |
4. Payload Hold-Release Mission Planning
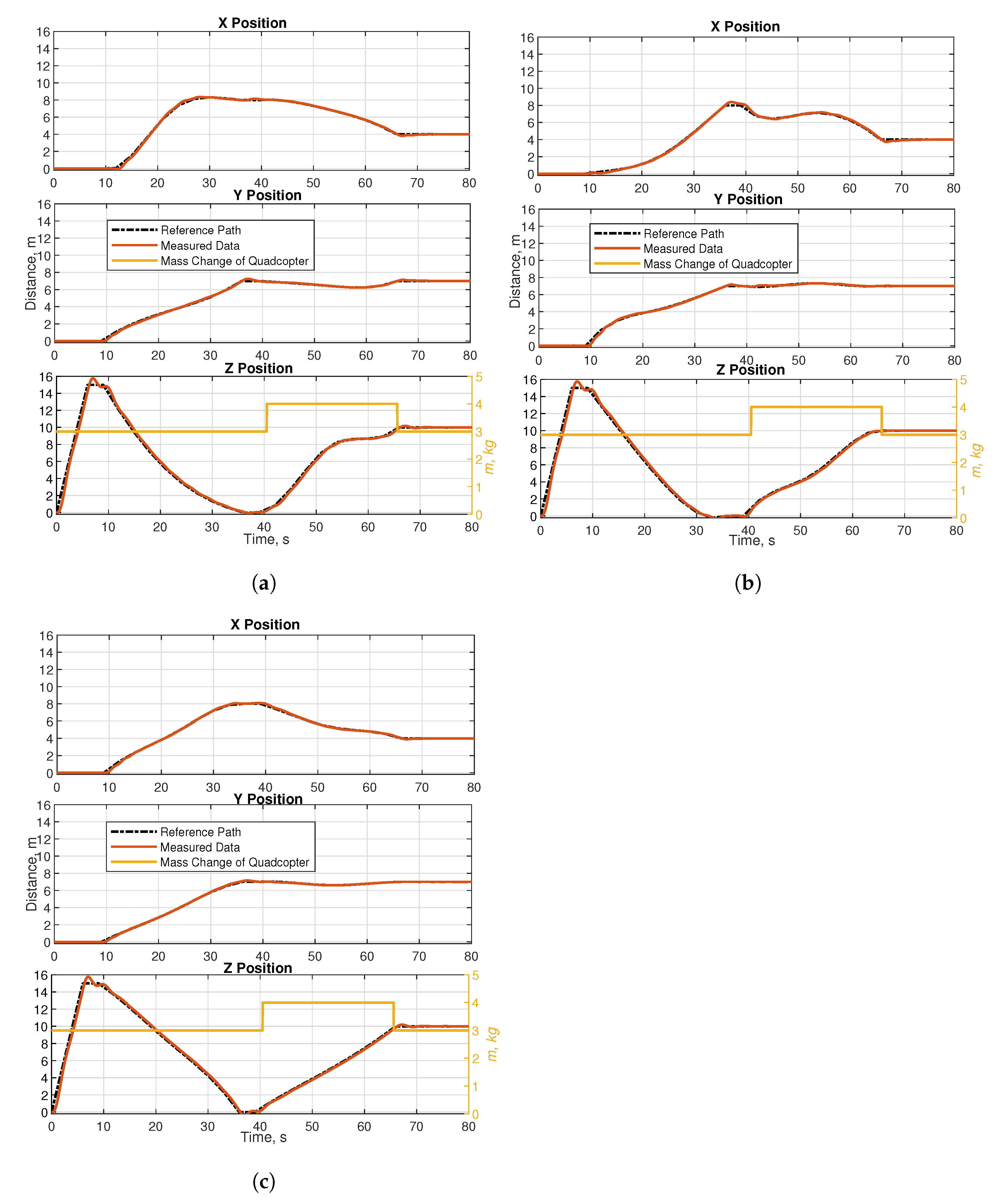
5. Experimental Results and Discussion
- A hybrid HHO–GWO optimization algorithm with high convergence speed for path planning has been proposed,
- The position error of the quadcopter caused by the sudden change during payload holding and releasing is examined;
- The errors that occur in path tracking under sudden payload changes are minimized with the newly proposed control strategy.
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Yu, X.; Li, C.; Zhou, J. A constrained differential evolution algorithm to solve UAV path planning in disaster scenarios. Knowl.-Based Syst. 2020, 204, 106209. [Google Scholar] [CrossRef]
- Ropero, F.; Muñoz, P.; R-Moreno, M.D. TERRA: A path planning algorithm for cooperative UGV–UAV exploration. Eng. Appl. Artif. Intell. 2019, 78, 260–272. [Google Scholar] [CrossRef]
- Sivčev, S.; Rossi, M.; Coleman, J.; Omerdić, E.; Dooly, G.; Toal, D. Collision detection for underwater ROV manipulator systems. Sensors 2018, 18, 1117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Vivo, F.; Battipede, M.; Johnson, E. Infra-red line camera data-driven edge detector in UAV forest fire monitoring. Aerosp. Sci. Technol. 2021, 111, 106574. [Google Scholar] [CrossRef]
- Altan, A.; Hacıoğlu, R. Model predictive control of three-axis gimbal system mounted on UAV for real-time target tracking under external disturbances. Mech. Syst. Signal Process. 2020, 138, 106548. [Google Scholar] [CrossRef]
- Silvagni, M.; Tonoli, A.; Zenerino, E.; Chiaberge, M. Multipurpose UAV for search and rescue operations in mountain avalanche events. Geomat. Nat. Hazards Risk 2017, 8, 18–33. [Google Scholar] [CrossRef] [Green Version]
- Cui, L.; Zhang, R.; Yang, H.; Zuo, Z. Adaptive super-twisting trajectory tracking control for an unmanned aerial vehicle under gust winds. Aerosp. Sci. Technol. 2021, 115, 106833. [Google Scholar] [CrossRef]
- Causa, F.; Fasano, G. Multiple UAVs trajectory generation and waypoint assignment in urban environment based on DOP maps. Aerosp. Sci. Technol. 2021, 110, 106507. [Google Scholar] [CrossRef]
- Sun, P.; Boukerche, A. Performance modeling and analysis of a UAV path planning and target detection in a UAV-based wireless sensor network. Comput. Netw. 2018, 146, 217–231. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Wang, J. Sequential convex programming for nonlinear optimal control problems in UAV path planning. Aerosp. Sci. Technol. 2018, 76, 280–290. [Google Scholar] [CrossRef]
- Huang, Y.; Mei, W.; Xu, J.; Qiu, L.; Zhang, R. Cognitive UAV communication via joint maneuver and power control. IEEE Trans. Commun. 2019, 67, 7872–7888. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, R.; Li, H. Graph-based path decision modeling for hypersonic vehicles with no-fly zone constraints. Aerosp. Sci. Technol. 2021, 116, 106857. [Google Scholar] [CrossRef]
- Radmanesh, R.; Kumar, M.; French, D.; Casbeer, D. Towards a PDE-based large-scale decentralized solution for path planning of UAVs in shared airspace. Aerosp. Sci. Technol. 2020, 105, 105965. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Baumann, M.; Leonard, S.; Croft, E.A.; Little, J.J. Path planning for improved visibility using a probabilistic road map. IEEE Trans. Robot. 2010, 26, 195–200. [Google Scholar] [CrossRef]
- Bayili, S.; Polat, F. Limited-Damage A*: A path search algorithm that considers damage as a feasibility criterion. Knowl.-Based Syst. 2011, 24, 501–512. [Google Scholar] [CrossRef]
- Moon, C.B.; Chung, W. Kinodynamic planner dual-tree RRT (DT-RRT) for two-wheeled mobile robots using the rapidly exploring random tree. IEEE Trans. Ind. Electron. 2014, 62, 1080–1090. [Google Scholar] [CrossRef]
- Battulwar, R.; Winkelmaier, G.; Valencia, J.; Naghadehi, M.Z.; Peik, B.; Abbasi, B.; Parvin, B.; Sattarvand, J. A Practical Methodology for Generating High-Resolution 3D Models of Open-Pit Slopes Using UAVs: Flight Path Planning and Optimization. Remote. Sens. 2020, 12, 2283. [Google Scholar] [CrossRef]
- Huang, L.; Qu, H.; Ji, P.; Liu, X.; Fan, Z. A novel coordinated path planning method using k-degree smoothing for multi-UAVs. Appl. Soft Comput. 2016, 48, 182–192. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H.; Hang, W.B. Cooperative path planning of multiple UAVs by using max–min ant colony optimization along with cauchy mutant operator. Fluct. Noise Lett. 2021, 20, 2150002. [Google Scholar] [CrossRef]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef] [PubMed]
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Three dimensional path planning using grey wolf optimizer for UAVs. Appl. Intell. 2019, 49, 2201–2217. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Ganguly, S. Multi-objective distributed generation penetration planning with load model using particle swarm optimization. Decis. Mak. Appl. Manag. Eng. 2020, 3, 30–42. [Google Scholar] [CrossRef]
- Negi, G.; Kumar, A.; Pant, S.; Ram, M. Optimization of complex system reliability using hybrid grey wolf optimizer. Decis. Mak. Appl. Manag. Eng. 2021, 4, 241–256. [Google Scholar] [CrossRef]
- Das, M.; Roy, A.; Maity, S.; Kar, S.; Sengupta, S. Solving fuzzy dynamic ship routing and scheduling problem through new genetic algorithm. Decis. Mak. Appl. Manag. Eng. 2021. [Google Scholar] [CrossRef]
- Sasongko, R.A.; Rawikara, S.; Tampubolon, H.J. UAV obstacle avoidance algorithm based on ellipsoid geometry. J. Intell. Robot. Syst. 2017, 88, 567–581. [Google Scholar] [CrossRef]
- Singla, A.; Padakandla, S.; Bhatnagar, S. Memory-based deep reinforcement learning for obstacle avoidance in UAV with limited environment knowledge. IEEE Trans. Intell. Transp. Syst. 2019, 22, 107–118. [Google Scholar] [CrossRef]
- Iacono, M.; Sgorbissa, A. Path following and obstacle avoidance for an autonomous UAV using a depth camera. Robot. Auton. Syst. 2018, 106, 38–46. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, P.; Tan, J.; Li, F. The obstacle detection method of UAV based on 2D LIDAR. IEEE Access 2019, 7, 163437–163448. [Google Scholar] [CrossRef]
- Liu, Y.; Rajappa, S.; Montenbruck, J.M.; Stegagno, P.; Bülthoff, H.; Allgöwer, F.; Zell, A. Robust nonlinear control approach to nontrivial maneuvers and obstacle avoidance for quadrotor UAV under disturbances. Robot. Auton. Syst. 2017, 98, 317–332. [Google Scholar] [CrossRef]
- Altan, A.; Aslan, Ö.; Hacıoğlu, R. Real-time control based on NARX neural network of hexarotor UAV with load transporting system for path tracking. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–6. [Google Scholar]
- Shirani, B.; Najafi, M.; Izadi, I. Cooperative load transportation using multiple UAVs. Aerosp. Sci. Technol. 2019, 84, 158–169. [Google Scholar] [CrossRef]
- Lee, H.I.; Yoo, D.W.; Lee, B.Y.; Moon, G.H.; Lee, D.Y.; Tahk, M.J.; Shin, H.S. Parameter-robust linear quadratic Gaussian technique for multi-agent slung load transportation. Aerosp. Sci. Technol. 2017, 71, 119–127. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, D.; Heidari, H. Trajectory planning of quadrotor UAV with maximum payload and minimum oscillation of suspended load using optimal control. J. Intell. Robot. Syst. 2020, 100, 1369–1381. [Google Scholar] [CrossRef]
- Kuantama, E.; Vesselenyi, T.; Dzitac, S.; Tarca, R. PID and Fuzzy-PID control model for quadcopter attitude with disturbance parameter. Int. J. Comput. Commun. Control. 2017, 12, 519–532. [Google Scholar] [CrossRef] [Green Version]
- Selby, W.C. Autonomous Navigation and Tracking of Dynamic Surface Targets On-Board a Computationally Impoverished Aerial Vehicle. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2011. [Google Scholar]
- Luukkonen, T. Modelling and control of quadcopter. Indep. Res. Proj. Appl. Math. Espoo 2011, 22, 22. [Google Scholar]
- Wang, P.; Man, Z.; Cao, Z.; Zheng, J.; Zhao, Y. Dynamics modelling and linear control of quadcopter. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 498–503. [Google Scholar]
- Beard, R. Quadrotor Dynamics and Control Rev 0.1. 2008. Available online: https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=2324&context=facpub (accessed on 10 April 2022).
- Koksal, N.; Jalalmaab, M.; Fidan, B. Adaptive linear quadratic attitude tracking control of a quadrotor UAV based on IMU sensor data fusion. Sensors 2019, 19, 46. [Google Scholar] [CrossRef] [Green Version]
- Abhishek, B.; Ranjit, S.; Shankar, T.; Eappen, G.; Sivasankar, P.; Rajesh, A. Hybrid PSO-HSA and PSO-GA algorithm for 3D path planning in autonomous UAVs. SN Appl. Sci. 2020, 2, 1805. [Google Scholar] [CrossRef]
- Ghambari, S.; Lepagnot, J.; Jourdan, L.; Idoumghar, L. A comparative study of meta-heuristic algorithms for solving UAV path planning. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 174–181. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]


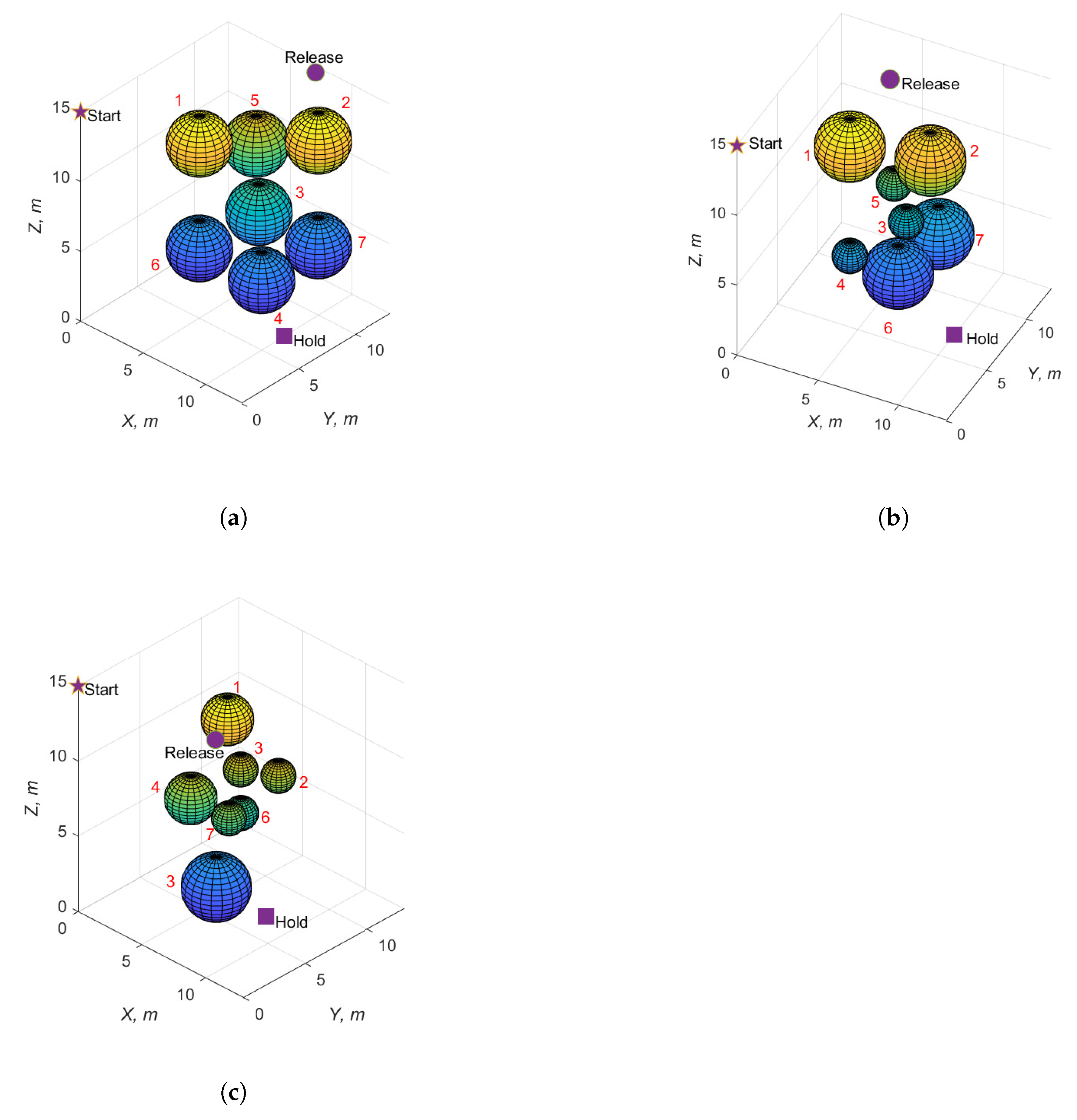


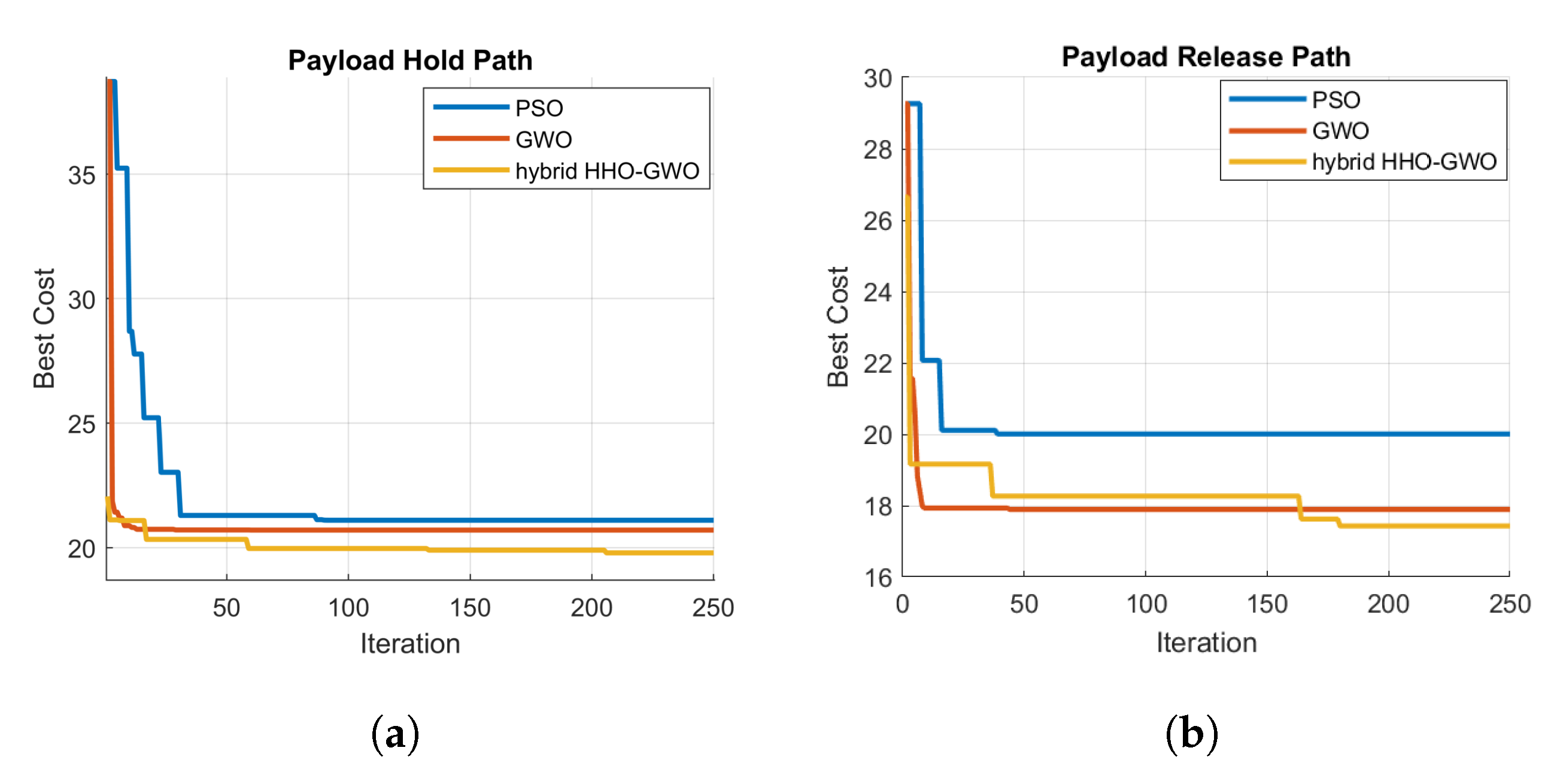
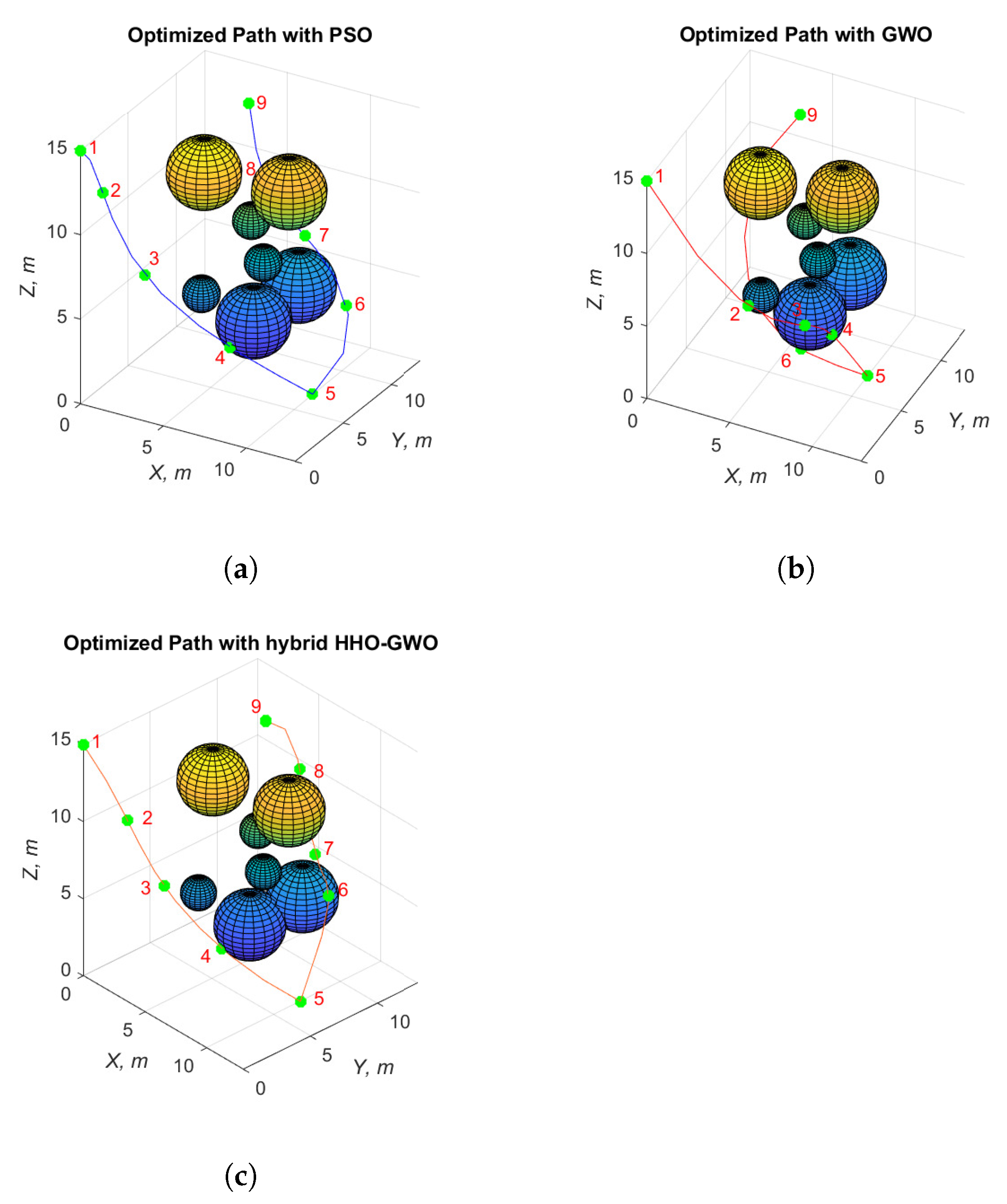
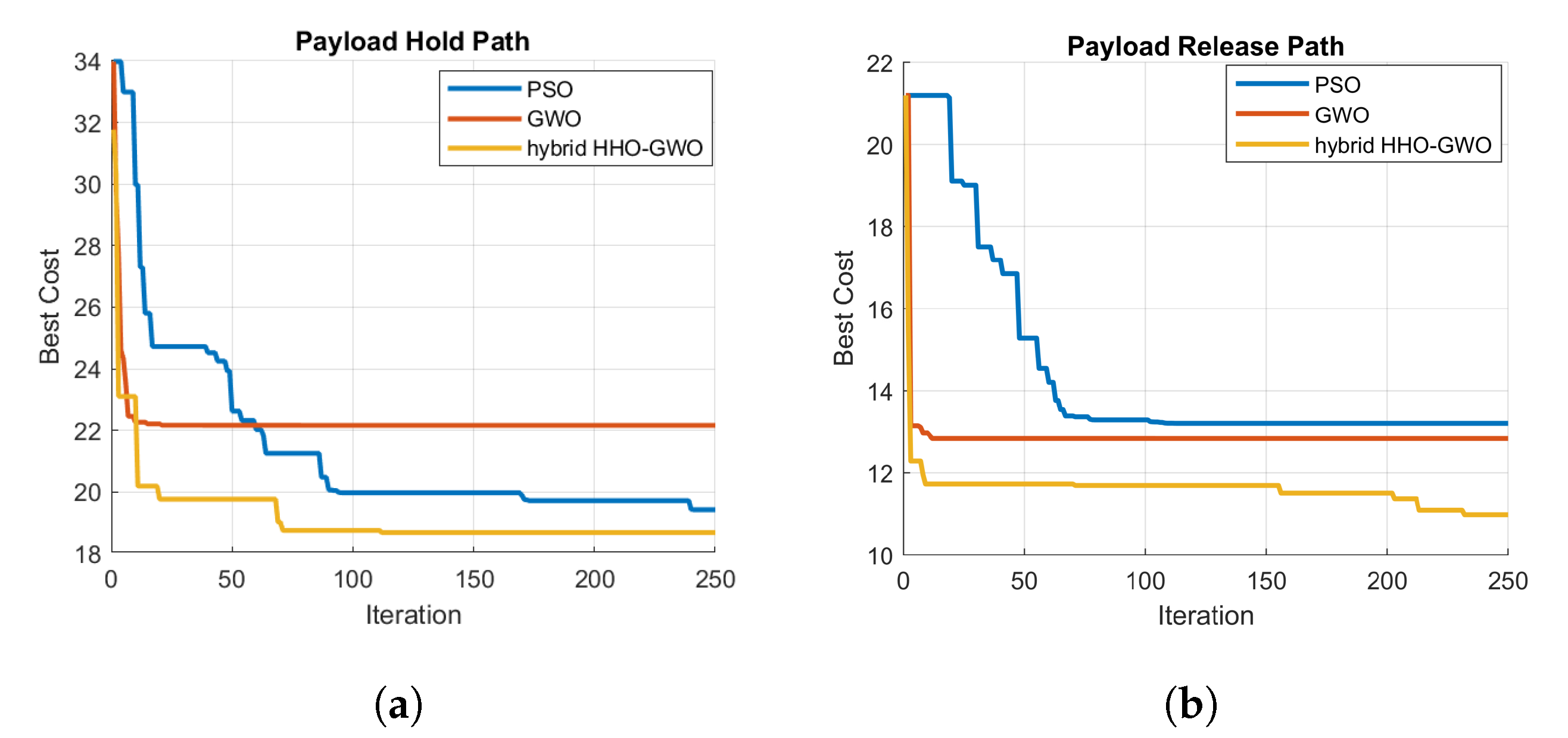

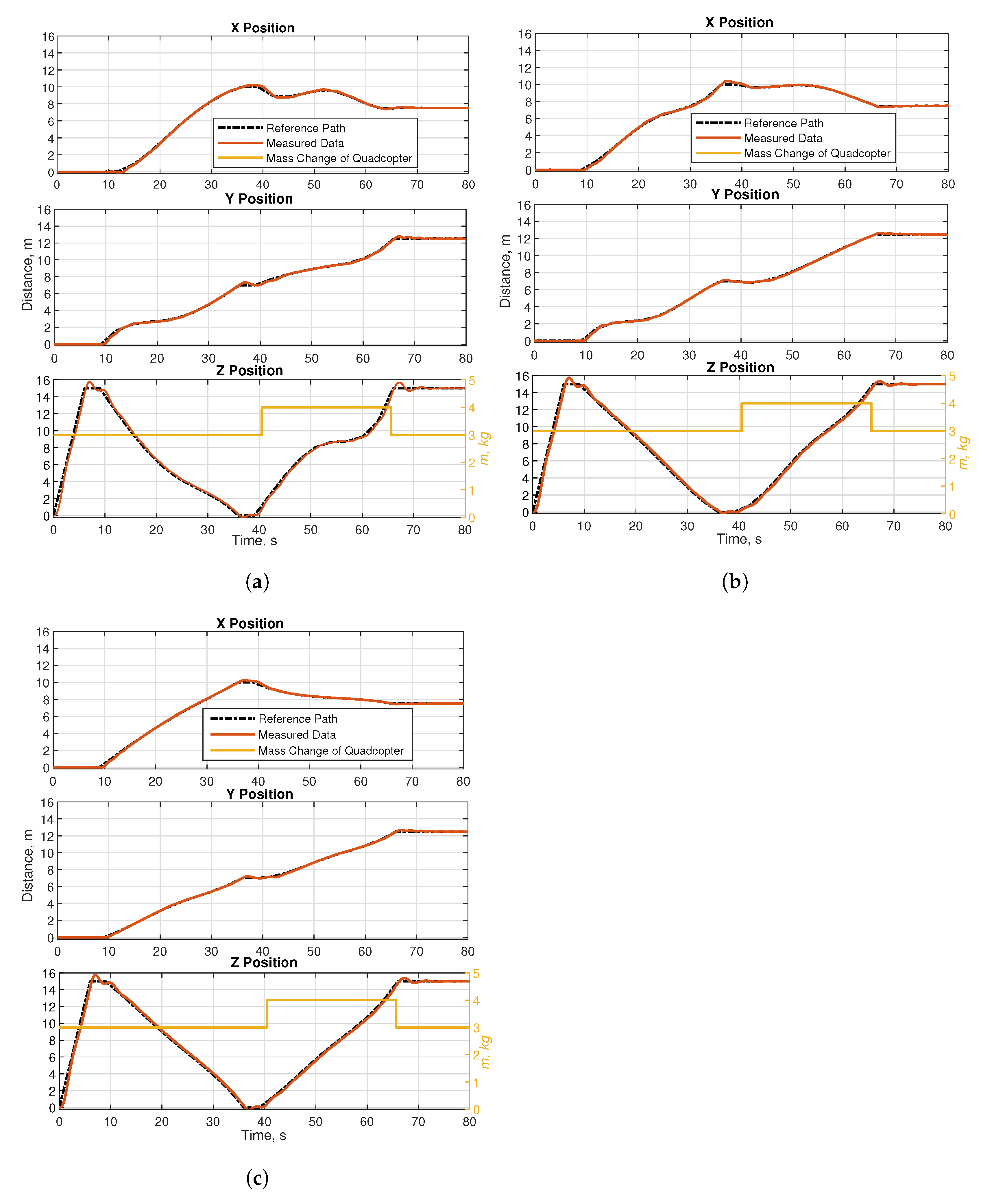

| Obstacle Number | Map 1 | Map 2 | Map 3 |
|---|---|---|---|
| (xobs, yobs, zobs, robs), (m) | |||
| 1 | (5, 5, 12.5, 2) | (4, 6, 12, 2) | (3, 9, 10, 1.5) |
| 2 | (10, 10, 12.5, 2) | (8, 8, 11, 2) | (7, 9, 8, 1) |
| 3 | (7.5, 7.5, 7.5, 2) | (7, 7, 7, 1) | (6, 5, 2, 2) |
| 4 | (10, 5, 5, 2) | (5, 4, 6, 1) | (4, 5, 7, 1.5) |
| 5 | (5, 10, 10, 2) | (6, 7.5, 9, 1) | (5, 8, 8, 1) |
| 6 | (5, 5, 5, 2) | (7, 6, 4, 2) | (6, 7, 6, 1) |
| 7 | (10, 10, 5, 2) | (8, 9, 5, 2) | (7, 5, 7, 1) |
| Waypoint Number | PSO | GWO | Hybrid HHO–GWO |
|---|---|---|---|
| (m), (m), (m) | |||
| 1 | (0, 0, 15) | (0, 0, 15) | (0, 0, 15) |
| 2 | (1.23, 2.44, 9.35) | (2.89, 2.14, 11.10) | (2.94, 1.85, 11.37) |
| 3 | (4.78, 2.90, 5.13) | (5.90, 2.62, 7.38) | (5.60, 3.82, 7.69) |
| 4 | (8.05, 4.45, 2.82) | (7.29, 4.62, 3.30) | (7.82, 5.26, 4.30) |
| 5 | (10, 7, 0) | (10, 7, 0) | (10, 7, 0) |
| 6 | (8.9, 8.33, 5.26) | (9.71, 7.21, 2.81) | (8.74, 7.85, 3.39) |
| 7 | (9.63, 9.16, 8.48) | (9.93, 8.81, 7.32) | (8.25, 9.41, 7.05) |
| 8 | (8.23, 9.97, 9.05) | (9.02, 10.74, 10.6) | (8, 10.68, 10.31) |
| 9 | (7.5, 12.5, 15) | (7.5, 12.5, 15) | (7.5, 12.5, 15) |
| Path Distance | 37.53 m | 36.26 m | 35.68 m |
| Waypoint Number | PSO | GWO | Hybrid HHO–GWO |
|---|---|---|---|
| (m), (m), (m) | |||
| 1 | (0, 0, 15) | (0, 0, 15) | (0, 0, 15) |
| 2 | (0.85, 0.84, 12.33) | (5.32, 1.71, 6.99) | (1.96, 1.51, 10.33) |
| 3 | (2.71, 2.08, 7.35) | (8.25, 2.73, 5.90) | (4.17, 2.21, 6.81) |
| 4 | (6.72, 4.05, 3.26) | (8.77, 4.99, 3.89) | (6.77, 4.14, 3.13) |
| 5 | (10, 7, 0) | (10, 7, 0) | (10, 7, 0) |
| 6 | (10.75, 9.24, 4.44) | (6.63, 5.61, 1.71) | (10.01, 9.11, 5.95) |
| 7 | (8.2, 9.3, 7.85) | (4.23, 4.71, 5.16) | (8.7, 9.32, 7.94) |
| 8 | (5.9, 9.49, 10) | (2.52, 7.58, 8.98) | (6.43, 10.25, 12.01) |
| 9 | (5, 9, 15) | (5, 9, 15) | (5, 9, 15) |
| Path Distance | 37.47 m | 40.72 m | 36.73 m |
| Waypoint Number | PSO | GWO | Hybrid HHO–GWO |
|---|---|---|---|
| (m), (m), (m) | |||
| 1 | (0, 0, 15) | (0, 0, 15) | (0, 0, 15) |
| 2 | (1.98, 2.19, 8.8) | (0.51, 3.15, 9.64) | (1.96, 1.51, 10.33) |
| 3 | (6.71, 3.59, 4.31) | (1.71, 4.16, 4.62) | (4.17, 2.21, 6.81) |
| 4 | (8.32, 4.95, 1.54) | (4.48, 5.41, 0.74) | (6.77, 4.14, 3.13) |
| 5 | (8, 7, 0) | (8, 7, 0) | (8, 7, 0) |
| 6 | (7.82, 6.76, 3.22) | (6.44, 7.01, 3.07) | (10.01, 9.11, 5.95) |
| 7 | (6.95, 6.45, 7.77) | (7.12, 7.33, 4.89) | (8.7, 9.32, 7.94) |
| 8 | (5.82, 6.24, 8.66) | (6.48, 7.1, 8.27) | (6.43, 10.25, 12.01) |
| 9 | (4, 7, 10) | (4, 7, 10) | (4, 7, 10) |
| Path Distance | 31.32 m | 32.24 m | 29.59 m |
| Map Number | Algorithms | Total Path (m) | RMSE (m) | Target Time (s) | Energy Efficiency (%) |
|---|---|---|---|---|---|
| 1 | PSO | 53.03 | 21.76 | 66.15 | 64.51 |
| 1 | GWO | 51.63 | 19.98 | 65.01 | 67.41 |
| 1 | hybrid HHO–GWO | 50.70 | 19.57 | 64.12 | 68.08 |
| 2 | PSO | 52.92 | 19.86 | 66.18 | 67.92 |
| 2 | GWO | 56.52 | 22.70 | 65.24 | 63.33 |
| 2 | hybrid HHO–GWO | 52.11 | 19.35 | 64.76 | 68.74 |
| 3 | PSO | 46.87 | 17.65 | 65.99 | 66.74 |
| 3 | GWO | 47.80 | 18.49 | 65.01 | 65.50 |
| 3 | hybrid HHO–GWO | 44.72 | 16.92 | 64.71 | 68.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belge, E.; Altan, A.; Hacıoğlu, R. Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission. Electronics 2022, 11, 1208. https://doi.org/10.3390/electronics11081208
Belge E, Altan A, Hacıoğlu R. Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission. Electronics. 2022; 11(8):1208. https://doi.org/10.3390/electronics11081208
Chicago/Turabian StyleBelge, Egemen, Aytaç Altan, and Rıfat Hacıoğlu. 2022. "Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission" Electronics 11, no. 8: 1208. https://doi.org/10.3390/electronics11081208
APA StyleBelge, E., Altan, A., & Hacıoğlu, R. (2022). Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission. Electronics, 11(8), 1208. https://doi.org/10.3390/electronics11081208








