Prediction of Solid Conversion Process in Direct Reduction Iron Oxide Using Machine Learning
Abstract
:1. Introduction
| Authors | Modeling/Simulation | Shaft Furnace Name | Remark | Reference |
|---|---|---|---|---|
| Parisi and Laborde | USCM/Numerical (Rung–Kutta and Dormand–Prince) | Gilmore Siderca | The model fits the data from two MIDREX plants successfully. Furthermore, they enable investigation of the reactor’s behavior under various operating situations. In terms of metallization, it has been determined that if it increases to 100 (a 6 increase in metallization), the output must reduce to 70 (A 30% loss in production). | [13] |
| Valipour and Saboohi | USCM/CFD (FVM) | Gilmore | They concluded that hematite was reduced entirely to magnetite during the reduction of the haematite pellets in a shaft furnace. However, wustite was transformed into iron in the lower section of the bed. Additionally, magnetite was changed into wustite in the center of the bed. Because there was more hydrogen in syngas than carbon monoxide, endothermic reactions were avoided, and as a result, the temperature along the bed was reduced. | [26,27] |
| Nouri et al. | USCM and Grain model with product layer resistance/Numerical Rung–Kutta | Mobarakeh | The impact of reducing gas parameters and pellet properties on the degree of reduction has been examined. They observed that the grain model predicted plant data better than the shrinking unreacted core model. Their calculations demonstrate that even at the lowest flow rate, the Sherwood number is large enough to eliminate the mass transfer resistance effectively. | [15] |
| Alamsari et al. | USCM/CFD (FEM) | Krakatau | The increase in H2 composition is predicted, whereas the attenuation of CO results in a higher metallization degree. The degree of metallization increases as the gas inlet temperature rises. It was discovered that lowering the gas temperature below 973 °C (1246 K) is not suggested because sticky iron production would occur. They also investigated the impact of lowering the iron’s temperature on the generation of total carbon in the cooling zone and isobaric iron reactor. | [28] |
| Khalid Alhumaizi et al. | USCM/Numerical (Developed computer code) | Saudi Arabia | The simulation of a complete MIDREX unit (shaft furnace, reformer, and recuperator) and the study of complex mass–energy interactions between the reformer and the reduction furnace were investigated in an iron plant based on MIDREX technology. According to their parametric study, the scrubber’s exit temperature might be lowered in order to create sufficient water vapor to avoid carbon formation, subject to the limitations placed on preventing carbon deposition in the reformer tubes. The same constraint should apply to the optimization of the recycle ratio. The ratio of natural gas to iron ore is optimal. If we want to improve the natural gas flow rate, it is best to do so at the transition zone, where methane breaks down into carbon and hydrogen and boosts metalization and carburization. | [29] |
| Shams and Moazeni | USCM/Numerical (Rung–Kutta and Gill) | Gilmore | Complete shaft furnace simulation (reduction zone, cooling zone, transition zone) and validation using Gilmore unit data. The pressure drop for the reduction zone’s 9.75 m length was demonstrated to be approximately 0.87 bar. The length of the reduction zone is the only length that has any bearing on pressure drop because of the upward gas flow. Methane causes the production of carbon. The final product has a carbon content of 1.4%. A small portion of the cooling gas that helps produce carbon flows upward and mixes with the reducing gas to cool the solid to about 56 °C. | [30] |
| Ghandi et al. | USCM/CFD (FVM) | Mobarakeh Gilmore | It was discovered that using the twin gas injection approach increases the radial average hydrogen concentration. As a result of the addition of a new gas entrance that injects hot and fresh reducing gas, the overall degree of reduction increases when operating a reactor with a dual injection system. | [31] |
| Mirzajani et al. | Three-interface USCM/Numerical (Rung-Kutta- Dormand–Prince) | Khorasan | According to this study, the two factors that impact the conversion of iron oxide are particle size and gas flow rate. This study has several limitations because most industrial data is only available for the top and bottom of the reactor, not all along the reactor. | [14] |
| Hamadeh et al. | Grain model with Crystallite/CFD (FVM) | Contrecoeur Gilmore | A multi-scale approach accurately describes the principal physical, chemical, and thermal phenomena. The moving bed is assumed to be composed of pellets with grain and crystallites. Eight heterogeneous chemical reactions and two homogeneous chemical reactions are also considered. One of their important findings is that they found a central area with a lower temperature and conversion. | [4] |
| Béchara et al. | Grain model/Aspen Plus model (FDM) | Contrecoeur Gilmore | They built the aspen plus model of the DR shaft derived from the REDUCTOR. Reduced CO2 emissions were investigated. Computer-aided optimization was used to adjust a set of ten operating parameters at the same time. The results revealed a 15% improvement over the original emissions for comparable output values. | [3,32] |
| This Study | ML | Gilmore Siderca Khorasan Mobarakeh | The first modeling was performed using ML, SGD, Adam, and LBFG optimization methods and optimization functions, and the best network for modeling was found. |
| Authors | Modeling/Simulation | Shaft Furnace Name | Remark | Ref. |
|---|---|---|---|---|
| Hara et al. | Three-interface USCM/Numerical | Pilot Plant | This model is used for the modeling of the variations in the degree of reduction in an experimental shaft furnace with a diameter of 0.1 m and a height of 4.0 m. It has been discovered that the model can accurately simulate the reduction behavior in the furnace and that the rate constants obtained from the simulation calculation of the experimental data are very close to those found in the previous literature on the fundamental research of iron ore pellet reduction. | [33] |
| Szekely and Evanse | Grain model and Pore model/Numerical | Pilot Plant | Part I and II series articles “a structural model for gas-solid reactions with a moving boundary” introduce two porous models for non-catalytic solid and gas reactions. They investigate the effects of porosity, grain size, and temperature on the reduction. | [34,35] |
| Takenaka et al. | Grain model/Numerical (Rung–Kutta and Gill) | Pilot Plant (Commercial-scale) | They concluded that by increasing the temperature of the reducing gas, the gas ratio required to produce the desired degree of reduction of product is decreased, thereby improving the gas economy. When the H/CO ratio of the reducing gas is high, the endothermic process due to reduction with hydrogen occurs more strongly, decreasing the temperature within the furnace and so retarding the reduction. In this case, either the temperature of the reducing gas needs to be raised, or the gas ratio needs to be raised. | [36] |
| Negri et al. | Three-interface USCM/Numerical | Pilot Plant Yanagiya [37] and Takenaka [36]. | The consumption of hydrogen is greater than that of carbon monoxide; this is consistent with the higher reduction rate expected by the given kinetic data for the first reactant. | [22] |
| Usai | Zone and Grain model/Experimental and Numerical | Pilot Plant | Based on the grain model, they explored the isothermal reduction of wustite pellet with hydrogen under pseudo-steady state and unsteady state circumstances. They said that the pseudo-steady state solution of their model performed well when compared to the unsteady state solution. | [18] |
| Kang et al. | USCM/Experimental and Analytical | Pilot Plant | Using Ishida–Mathematical Wen’s model, the effect of the size and form of iron oxide samples during reduction with CO–CO2 mixtures at 800 and 900 °C were discussed. | [38,39] |
| Bonalde et al. | Grain model/Experimental and Numerical | Pilot Plant | Using the grain model, the kinetics of reducing hematite pellets using hydrogen–carbon monoxide mixtures as the reducing agent was characterized. The experimental results were compared to the model’s predictions. | [40] |
| Rahimi and Niksiar | Grain Model/Numerical | Pilot Plant Takenaka [36]. | Their findings indicate that the feed temperature appears to have little effect on reactor performance. On the other hand, it is expected that the incoming gas flow rate will have a significant influence. It has also been explained that the significant interconnection of the reactor’s different zones may prevent general expression. | [41] |
| Ranzani da Costa et al. | Grain model with Crystallite/CFD (FVM) | Pilot Plant | They simulated a two-dimensional model of hydrogen-based DRI. Their results show that the use of hydrogen accelerates the reduction in comparison to the CO reaction, and CO2 emissions would be reduced by more than 80%. They made the REDUCTOR model, which is the most accurate shaft model (2D, 3 zones, 10 reactions). | [42] |
| Ponugoti et al. | USCM/Experimental and Numerical | Pilot Plant | They et al. took a new strategy, solving physical governing equations for the solid phase at the same time as gas phase transport equations. The shrinking core model is used to determine the reaction rate, and the genetic method is used to estimate the parameters for the kinetic term. | [43] |
| Yongliang Yan et al. | Experimental | National Energy Technology Laboratory | This was determined using the iron Fe3O4-to-Fe and FeO-to-Fe, H2 kinetic rate constants (for green hydrogen). The response rate of magnetite to iron was demonstrated. They discovered that the Fe3O4 to Fe reduction is a 1D growth with a slower nucleation rate, but the FeO to Fe reduction is a 1D to 2D development process that occurs more rapidly. | [44] |
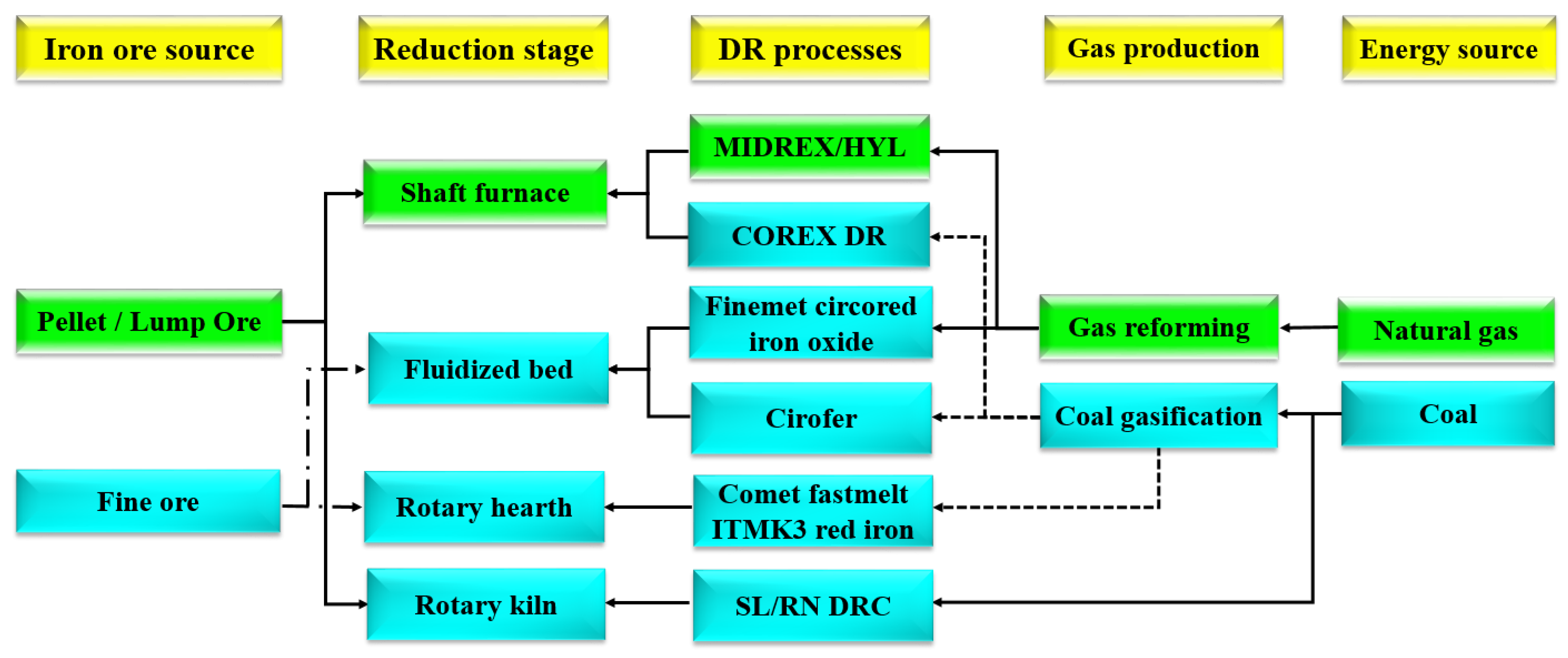
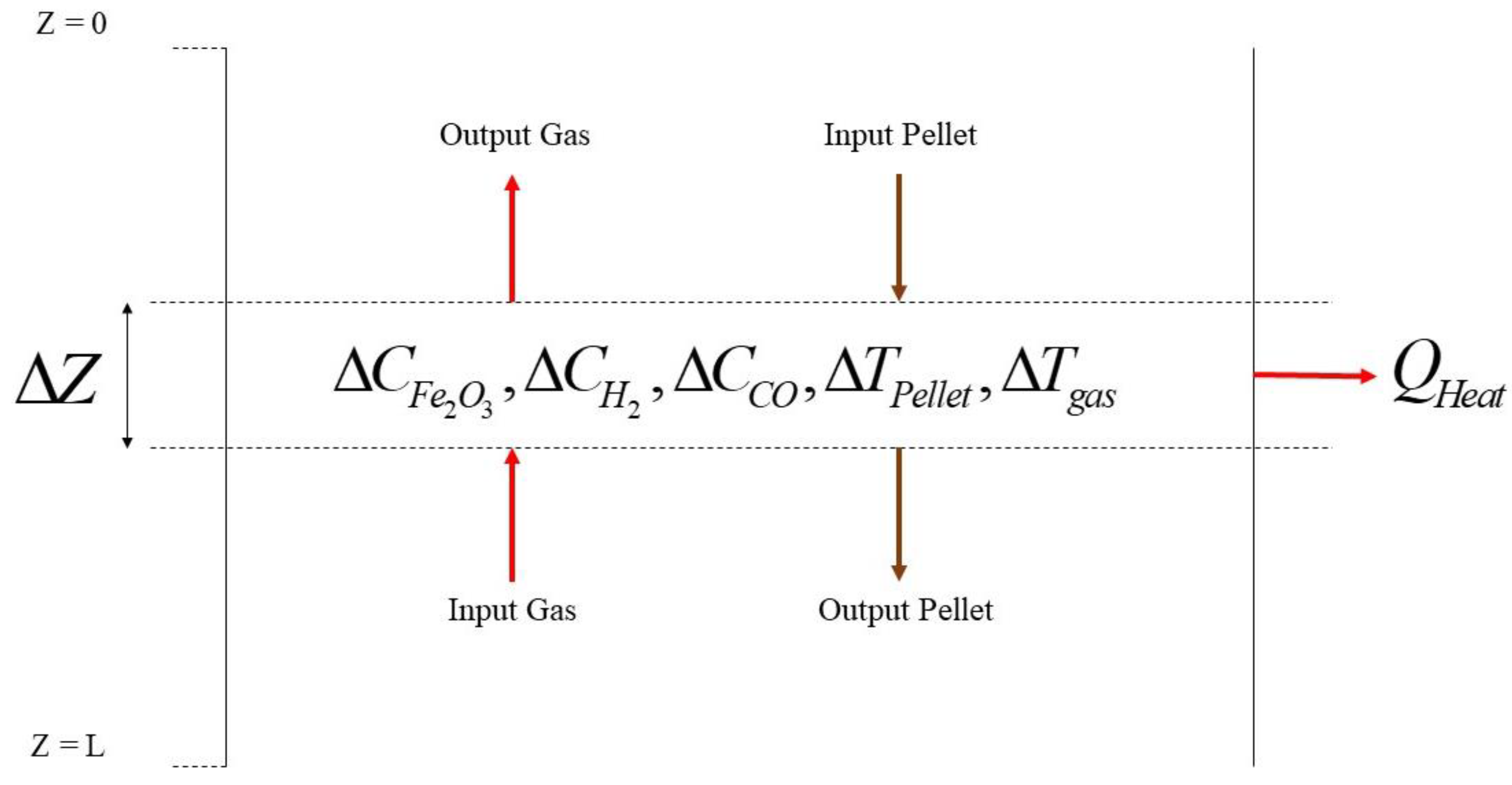
2. Numerical Modeling
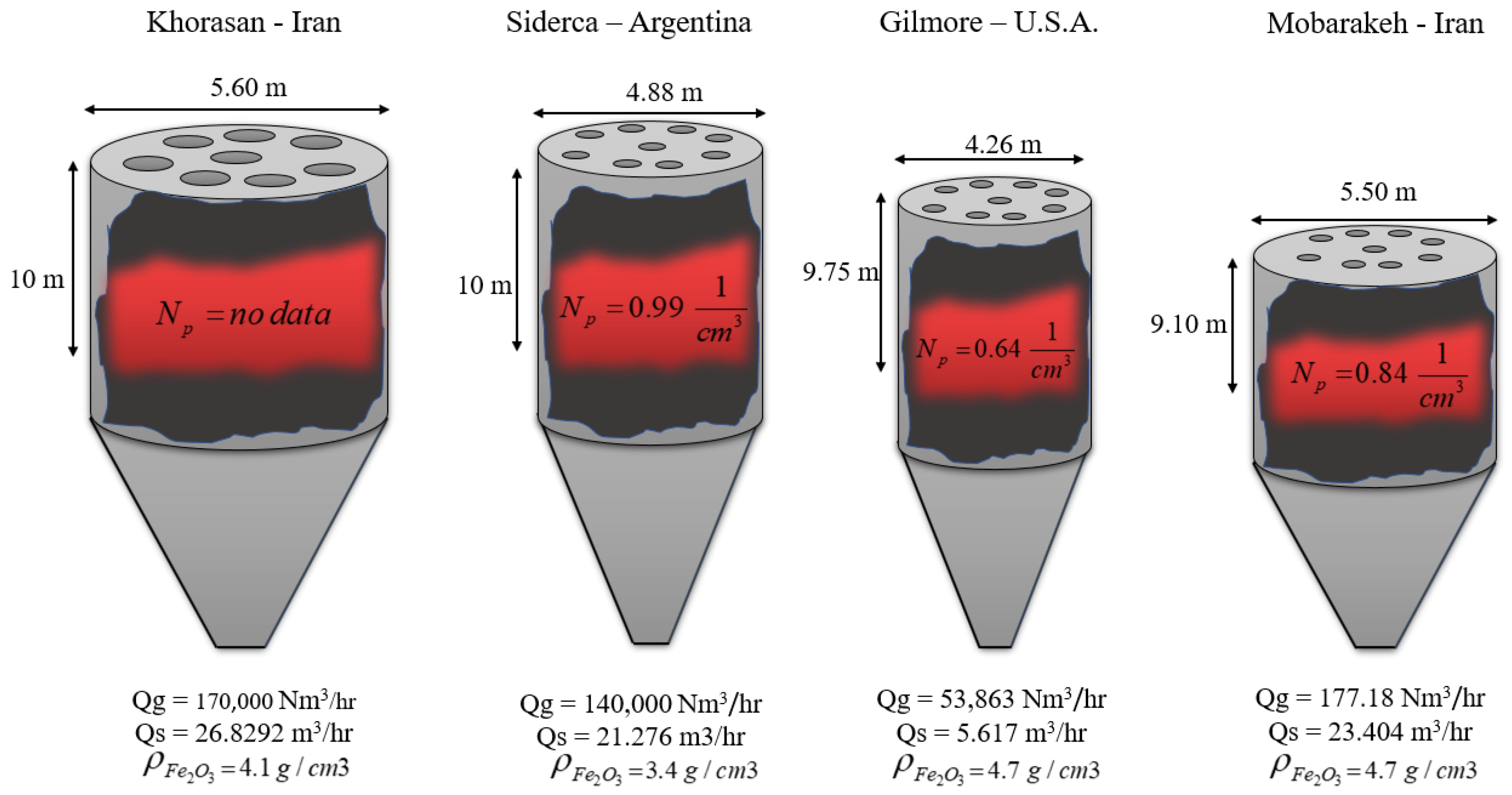
Case Studies
| Shaft Furnace Name | (−) | (−) | (−) | (−) | (−) | (−) | (−) | (−) | (−) | (%) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Gilmore | 0–2.2887 | 0.5268–0.37 | 0.2997–0.189 | 0.0465–0.212 | 0.048–0.143 | 0.71–1.08 | 0.33–1.15 | 9589.24 | 93 | 0.215 | [13] |
| Siderca | 0–2.0491 | 0.529–0.49 | 0.347–0.236 | 0.0517–0.124 | 0.0247–0.213 | 0.8–1.01 | 0.36–1.04 | 6580 | 93.7 | 0.106 | [13] |
| Mobarakeh | 0–1.6545 | 0.5357–3292 | 0.3425–2332 | 0.0583–0.2638 | 0.021–0.1373 | 0.7–1.04 | 0.32–1.09 | 7570.41 | 94.8 | 0.949 | [15] |
| Khorasan | 0–1.7857 | 0.53–0.4 | 0.345–0.197 | 0.048–0.180 | 0.022–0.171 | 0.52–1.08 | 0.32–1.11 | 6336.36 | 95.86 | 0.469 | [14] |
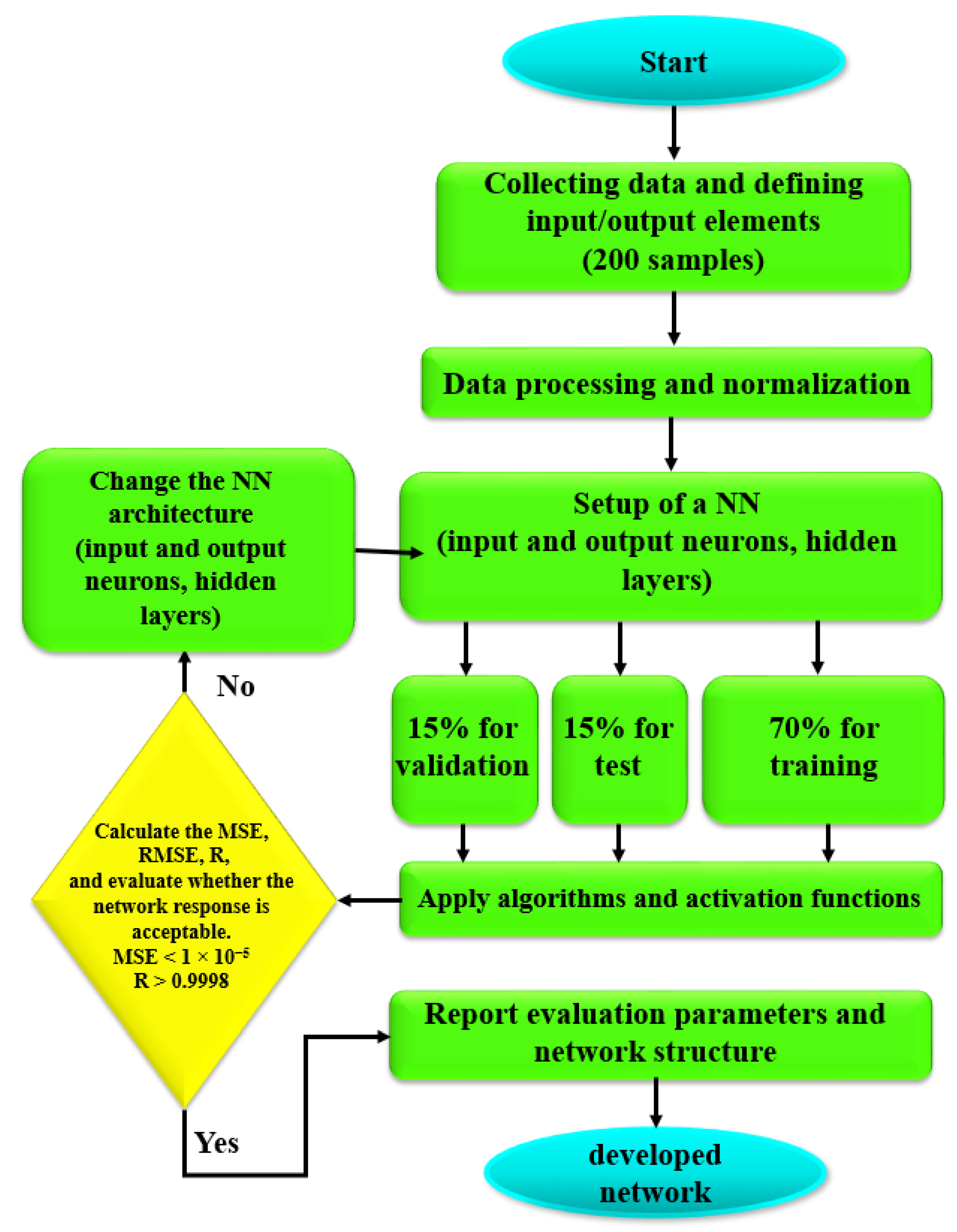
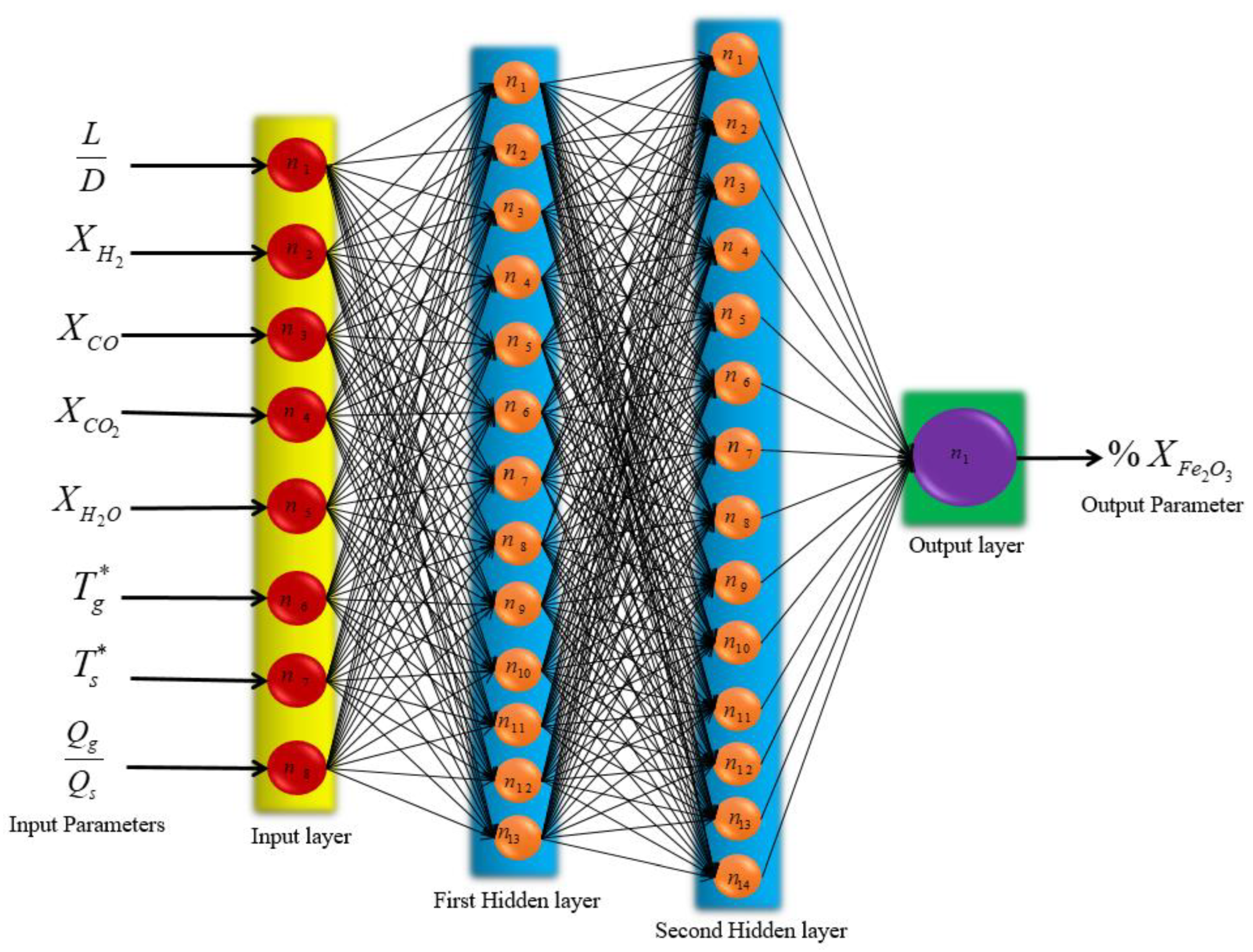
3. Artificial Neural Network (ANN)
4. Results and Discussion
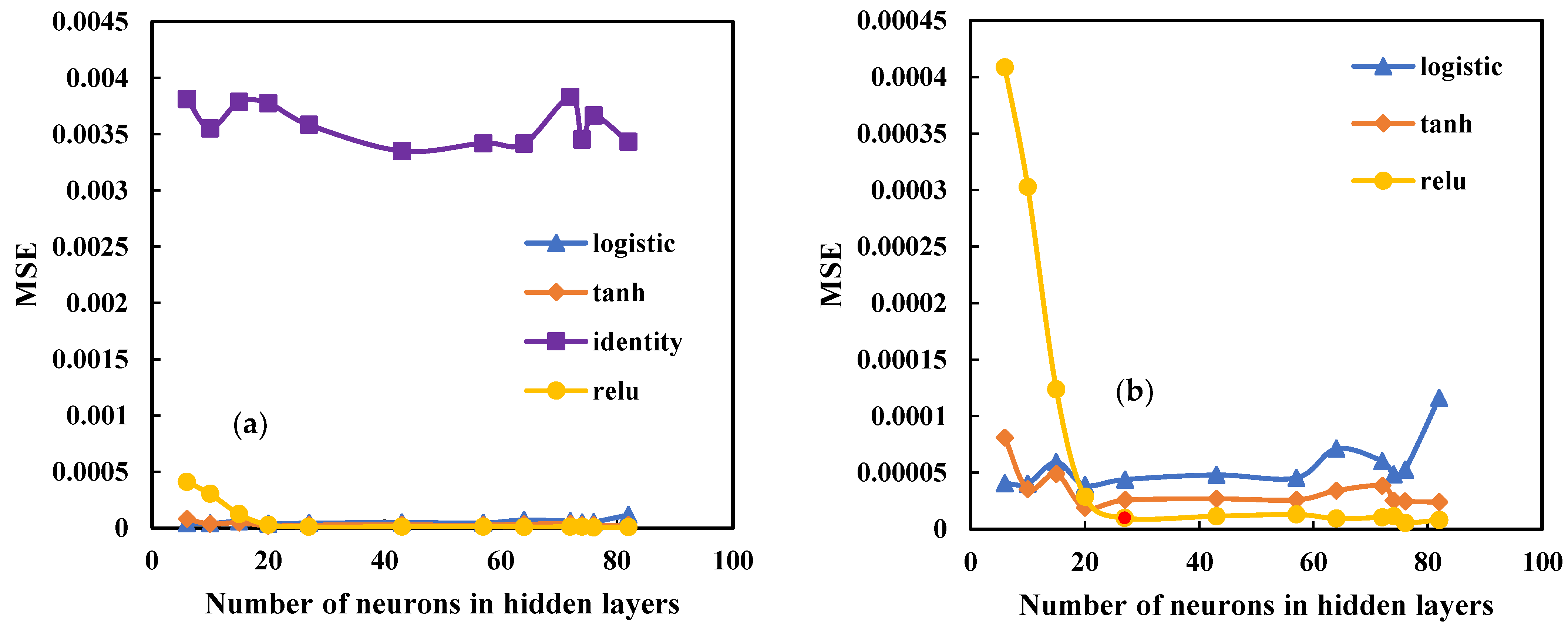
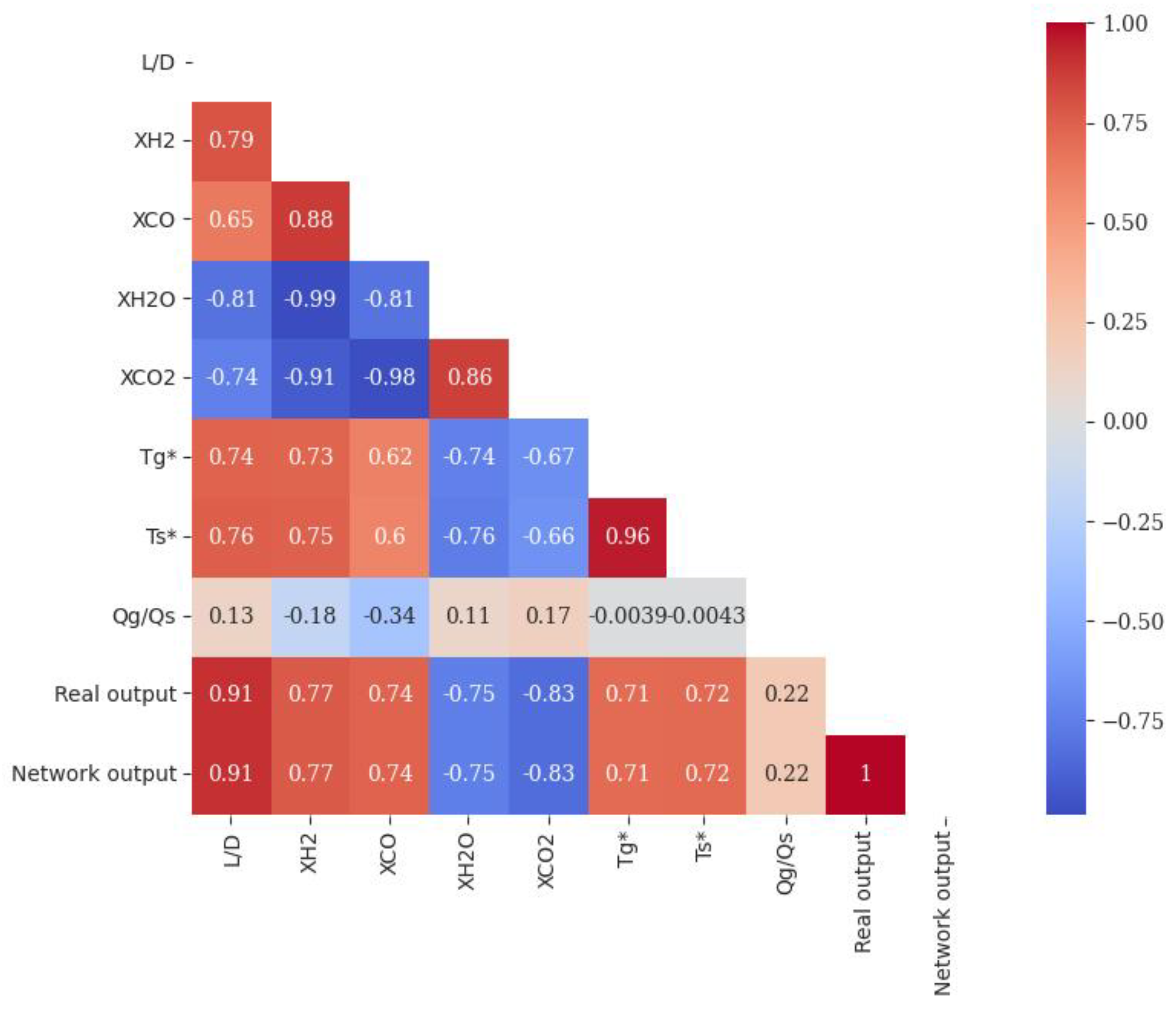
4.1. Comparative Analysis of ANN Models
| Optimization Algorithms | Training Function | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(−) | (−) | (%) | (%) | Neurons in Hidden Layers | (−) | (−) | (%) | (%) | Neurons in Hidden Layers | ||
| Adam | Relu | 3.05 × 10−4 | 1.74 × 10−2 | 0.9985 | 0.9986 | 6 | 8.67 × 10−5 | 9.3 × 10−3 | 0.9995 | 0.9996 | 57 |
| 1.67 × 10−4 | 1.29 × 10−2 | 0.9992 | 0.9993 | 10 | 2.48 × 10−5 | 4.9 × 10−3 | 0.9998 | 0.9998 | 64 | ||
| 1.41 × 10−4 | 1.18 × 10−2 | 0.9993 | 0.9995 | 15 | 1.77 × 10−5 | 4.2 × 10−3 | 0.9999 | 0.9999 | 72 | ||
| 1.35 × 10−4 | 1.16 × 10−2 | 0.9993 | 0.9994 | 20 | 3.76 × 10−5 | 6.1 × 10−3 | 0.9998 | 0.9998 | 74 | ||
| 1.13 × 10−4 | 1.06 × 10−2 | 0.9994 | 0.9994 | 27 | 9.61 × 10−5 | 9.8 × 10−3 | 0.9995 | 0.9996 | 76 | ||
| 7.04 × 10−5 | 8.3 × 10−3 | 0.9996 | 0.9997 | 43 | 1.94 × 10−5 | 4.4 × 10−3 | 0.9999 | 0.9999 | 82 | ||
| Broyden, Fletcher, Goldfarb, and Shanno | Relu | 4.09 × 10−4 | 2.02 × 10−2 | 0.9980 | 0.9983 | 6 | 1.29 × 10−5 | 3.6 × 10−3 | 0.9999 | 0.9999 | 57 |
| 3.03 × 10−4 | 1.74 × 10−2 | 0.9985 | 0.9987 | 10 | 1.7 × 10−5 | 4.13 × 10−3 | 0.9999 | 0.9999 | 64 | ||
| 1.24 × 10−4 | 1.11 × 10−2 | 0.9994 | 0.9996 | 15 | 1.05 × 10−5 | 3.25 × 10−3 | 0.9999 | 0.9999 | 72 | ||
| 2.88 × 10−5 | 5.37 × 10−3 | 0.9998 | 0.9998 | 20 | 1.78 × 10−5 | 4.21 × 10−3 | 0.9999 | 0.9999 | 74 | ||
| 8.95 × 10−6 | 2.99 × 10−3 | 0.9999 | 0.9999 | 27 | 5.63 × 10−6 | 2.37 × 10−3 | 0.9999 | 0.9999 | 76 | ||
| 1.15 × 10−5 | 3.39 × 10−3 | 0.9999 | 0.9999 | 43 | 8.15 × 10−6 | 2.85 × 10−3 | 0.9999 | 0.9999 | 82 | ||
| Scaled Conjugate Gradient | Relu | 6.37 × 10−3 | 3.94 × 10−2 | 0.9693 | 0.9695 | 6 | 3.4 × 10−4 | 1.84 × 10−2 | 0.9984 | 0.9985 | 57 |
| 5.2 × 10−3 | 3.31 × 10−2 | 0.9734 | 0.9735 | 10 | 1.46 × 10−4 | 1.21 × 10−2 | 0.9992 | 0.9992 | 64 | ||
| 2.59 × 10−3 | 4.19 × 10−2 | 0.9877 | 0.9878 | 15 | 3.39 × 10−4 | 1.84 × 10−2 | 0.9983 | 0.9984 | 72 | ||
| 9.1 × 10−4 | 3.02 × 10−2 | 0.9952 | 0.9955 | 20 | 1.53 × 10−4 | 1.24 × 10−2 | 0.9992 | 0.9993 | 74 | ||
| 6.81 × 10−4 | 2.61 × 10−2 | 0.9966 | 0.9967 | 27 | 1.38 × 10−4 | 1.18 × 10−2 | 0.9993 | 0.9994 | 76 | ||
| 3.9 × 10−4 | 1.97 × 10−2 | 0.9981 | 0.9984 | 43 | 2.34 × 10−4 | 1.53 × 10−2 | 0.9988 | 0.9990 | 82 | ||
| Broyden, Fletcher, Goldfarb, and Shanno | tanh | 8.08 × 10−5 | 8.99 × 10−3 | 0.9996 | 0.9997 | 6 | 2.59 × 10−5 | 5.09 × 10−3 | 0.9998 | 0.9998 | 57 |
| 3.53 × 10−5 | 5.94 × 10−3 | 0.9998 | 0.9998 | 10 | 3.41 × 10−5 | 5.84 × 10−3 | 0.9998 | 0.9998 | 64 | ||
| 4.86 × 10−5 | 6.97 × 10−3 | 0.9997 | 0.9997 | 15 | 3.82 × 10−5 | 6.18 × 10−3 | 0.9998 | 0.9998 | 72 | ||
| 1.87 × 10−5 | 4.33 × 10−3 | 0.9999 | 0.9999 | 20 | 2.53 × 10−5 | 5.03 × 10−3 | 0.9998 | 0.9998 | 74 | ||
| 2.56 × 10−5 | 5.06 × 10−3 | 0.9998 | 0.9998 | 27 | 2.45 × 10−5 | 4.95 × 10−3 | 0.9998 | 0.9998 | 76 | ||
| 2.69 × 10−5 | 5.18 × 10−3 | 0.9998 | 0.9998 | 43 | 2.39 × 10−5 | 4.89 × 10−3 | 0.9998 | 0.9999 | 82 | ||
| Broyden, Fletcher, Goldfarb, and Shanno | identity | 3.81 × 10−3 | 6.17 × 10−2 | 0.9823 | 0.9825 | 6 | 3.42 × 10−3 | 5.85 × 10−2 | 0.9837 | 0.9839 | 57 |
| 3.55 × 10−3 | 5.96 × 10−2 | 0.9831 | 0.9833 | 10 | 3.41 × 10−3 | 5.84 × 10−2 | 0.9841 | 0.9843 | 64 | ||
| 3.79 × 10−3 | 6.15 × 10−2 | 0.9815 | 0.9818 | 15 | 3.83 × 10−3 | 6.19 × 10−2 | 0.9817 | 0.9817 | 72 | ||
| 3.78 × 10−3 | 6.14 × 10−2 | 0.9828 | 0.9830 | 20 | 3.45 × 10−3 | 5.87 × 10−2 | 0.9835 | 0.9836 | 74 | ||
| 3.58 × 10−3 | 5.99 × 10−2 | 0.9829 | 0.9831 | 27 | 3.67 × 10−3 | 6.06 × 10−2 | 0.9810 | 0.9812 | 76 | ||
| 3.35 × 10−3 | 5.79 × 10−2 | 0.9841 | 0.9844 | 43 | 3.43 × 10−3 | 5.86 × 10−2 | 0.9841 | 0.9842 | 82 | ||
| Broyden, Fletcher, Goldfarb, and Shanno | logistic | 4.05 × 10−5 | 6.37 × 10−3 | 0.9997 | 0.9998 | 6 | 4.54 × 10−5 | 6.74 × 10−3 | 0.9997 | 0.9997 | 57 |
| 4.03 × 10−5 | 6.35 × 10−3 | 0.9998 | 0.9998 | 10 | 7.12 × 10−5 | 8.44 × 10−3 | 0.9996 | 0.9996 | 64 | ||
| 5.92 × 10−5 | 7.7 × 10−3 | 0.9997 | 0.9998 | 15 | 6.02 × 10−5 | 7.76 × 10−3 | 0.9997 | 0.9997 | 72 | ||
| 3.89 × 10−5 | 6.23 × 10−3 | 0.9998 | 0.9998 | 20 | 4.84 × 10−5 | 6.96 × 10−3 | 0.9997 | 0.9997 | 74 | ||
| 4.39 × 10−5 | 6.62 × 10−3 | 0.9997 | 0.9998 | 27 | 5.25 × 10−5 | 7.25 × 10−3 | 0.9997 | 0.9997 | 76 | ||
| 4.8 × 10−5 | 6.93 × 10−3 | 0.9997 | 0.9997 | 43 | 1.16 × 10−4 | 1.08 × 10−2 | 0.9994 | 0.9994 | 82 | ||
| Optimization Algorithms | Training Function | (−) | (−) | (%) | (%) | Neurons in Hidden Layers | (−) | (−) | (%) | (%) | Neurons in Hidden Layers |
|---|---|---|---|---|---|---|---|---|---|---|---|
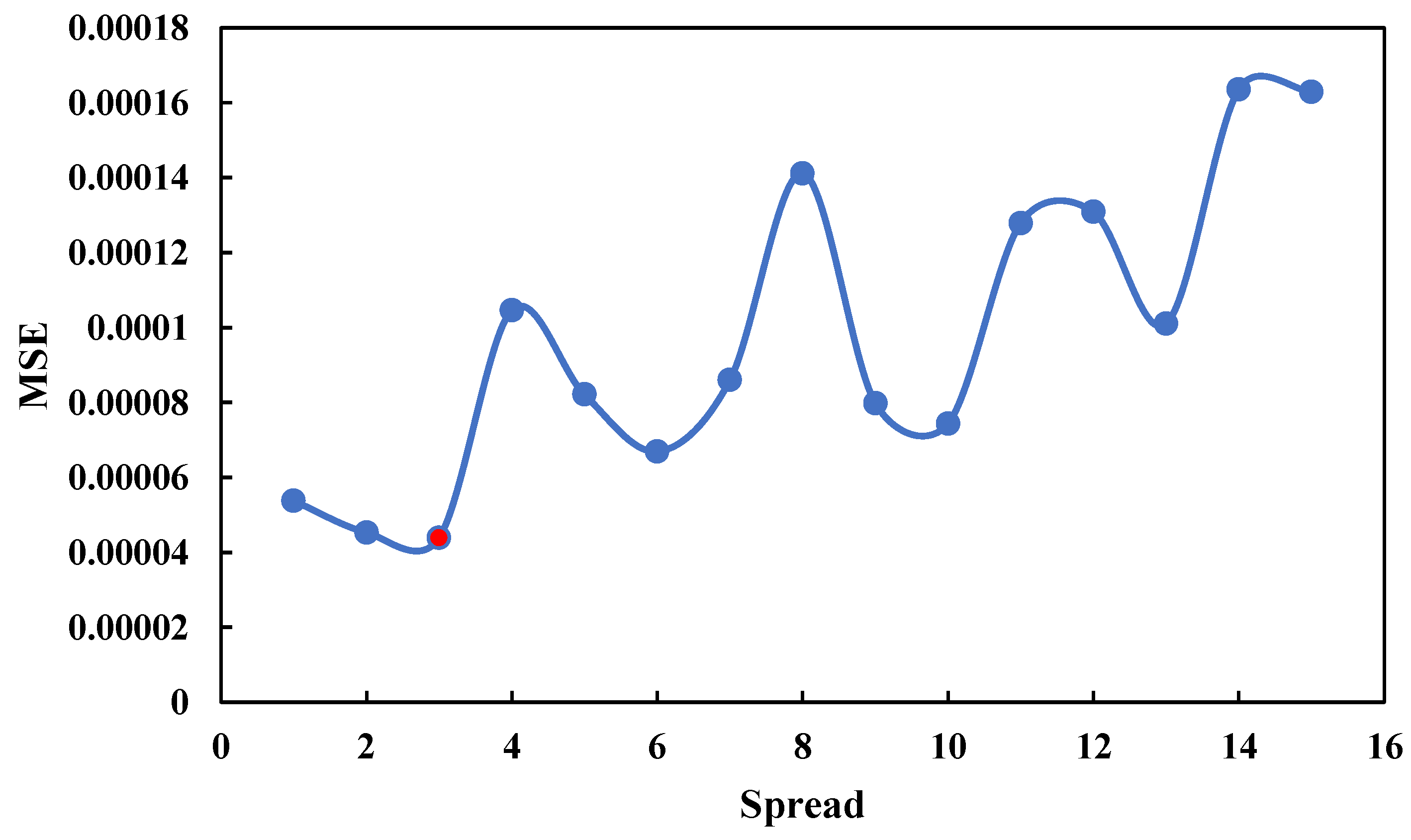
| RBF | Gaussian function | 7.57 × 10−3 | 8.7 × 10−2 | 0.9908 | 0.9908 | 6 | 1.15 × 10−5 | 3.39 × 10−3 | 0.9999 | 0.9999 | 57 |
| 3.66 × 10−3 | 6.6 × 10−2 | 0.9956 | 0.9956 | 10 | 9.8 × 10−6 | 3.14 × 10−3 | 0.9999 | 0.9999 | 64 | ||
| 3.73 × 10−4 | 1.93 × 10−2 | 0.9995 | 0.9995 | 15 | 7.8 × 10−6 | 2.79 × 10−3 | 0.9999 | 0.9999 | 72 | ||
| 1.29 × 10−4 | 1.13 × 10−2 | 0.9998 | 0.9998 | 20 | 7.6 × 10−6 | 2.75 × 10−3 | 0.9999 | 0.9999 | 74 | ||
| 4.38 × 10−5 | 6.61 × 10−3 | 0.9999 | 0.9999 | 27 | 7.2 × 10−6 | 2.68 × 10−3 | 0.9999 | 0.9999 | 76 | ||
| 1.58 × 10−5 | 3.97 × 10−3 | 0.9999 | 0.9999 | 43 | 6.3 × 10−6 | 2.5 × 10−3 | 0.9999 | 0.9999 | 82 |
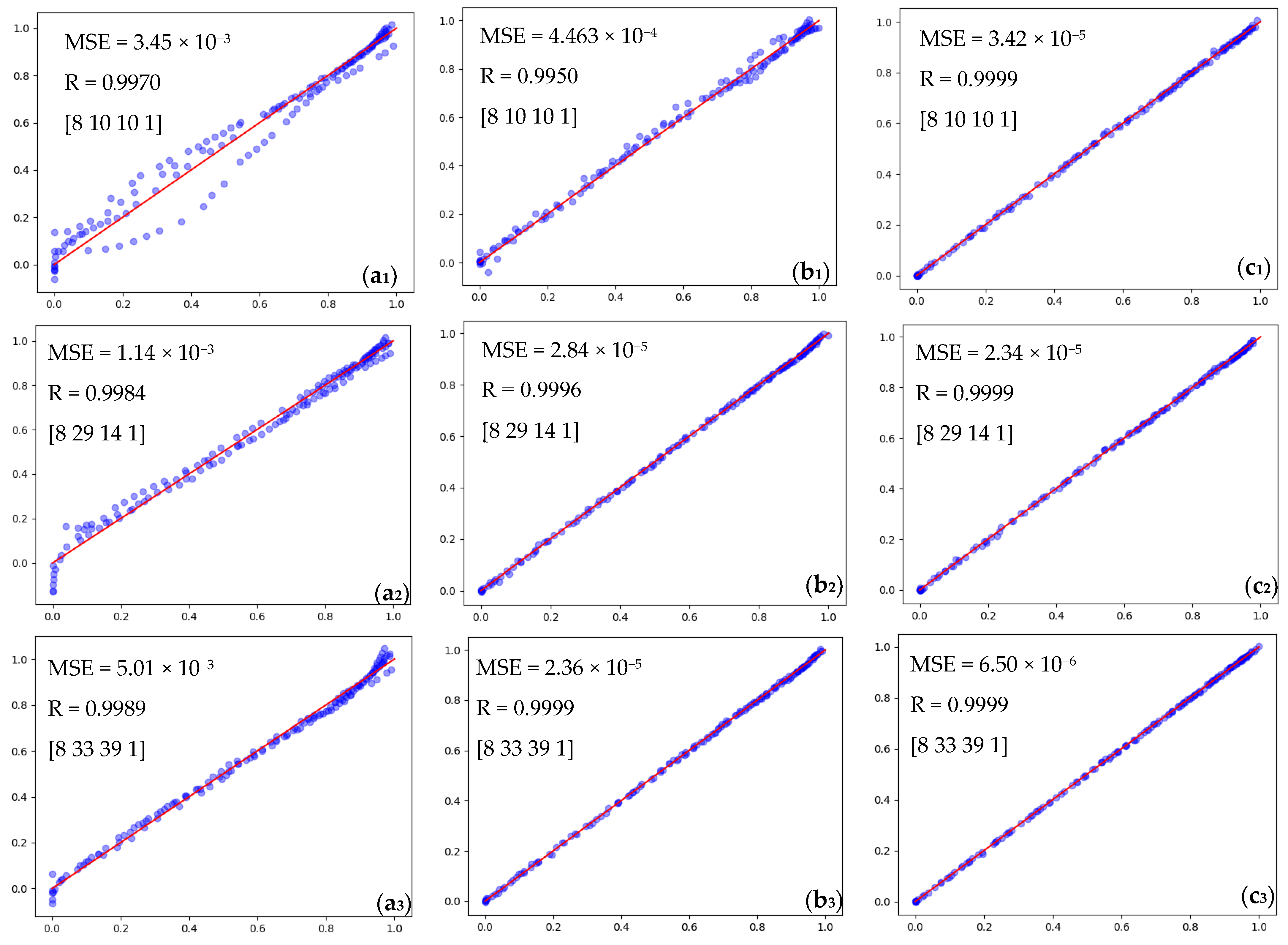
4.2. Optimum ANN Results for Prediction of Solid Conversion for DRI Process
4.2.1. Effect of Dimensions on Pellet Conversion Rate
4.2.2. The Effect of Gaseous Compounds on Pellet Conversion
4.2.3. The Effect of Flow Rate on Pellet Conversion Rate
4.2.4. The Effect of Temperature on the Pellet Conversion Rate
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Pellet external area [] | |
| Bias [] | |
| , | The heat capacity of solids and gases [] |
| Reduction zone diameter | |
| Cost function | |
| Nonlinear functions of activation transmission | |
| Function of Gaussian | |
| Function | |
| gas molar flow | |
| heat transfer coefficient [W ] | |
| Reaction enthalpy [] | |
| Approximate of the Hussein matrix | |
| Number of neurons in the hidden layer | |
| Position vector | |
| Reduction zone length | |
| first moment (the mean) | |
| Number of data sets for training | |
| number of pellets per unit volume of the bed | |
| n | Neurons |
| Direction of search | |
| Flow-rate | |
| Reaction rate per pellet [ | |
| , | Correlation coefficient [] |
| Direction vector | |
| Dimensionless temperature [] | |
| Dimensionless gas temperature [] | |
| Dimensionless solid temperature [] | |
| Velocity | |
| Second moment (the uncentered variance) | |
| Factor of weight [] | |
| Weight-related to each hidden neuron [] | |
| Input variable [] | |
| The extent of reaction/extent of reactant conversion for [ | |
| The extent of reaction/extent of reactant conversion for [ | |
| Extent of reaction/extent of reactant conversion for [ | |
| Output vector [] | |
| Target output | |
| Greek symbols | |
| Constants in turbulence models [] | |
| Weight of bias for neuron in layer | |
| The output of neuron from the layer of | |
| Step size | |
| Threshold limit [] | |
| Radial Basis Function (RBF) kernel width [] | |
| Gaussian function distribution [] | |
| Subscripts | |
| Characteristic | |
| Reactive solid () | |
| Gas | |
| Gaseous reactant | |
| Pellet | |
| Solid | |
| Acronyms | |
| ANN | Artificial Neural Networks |
| MSE | Mean Square Error |
| Terminology | |
| Neurons | Neurons are the fundamental components of the vast neural network. |
| Bias | Bias is a constant that allows the model to be optimally fitted to the available data. |
| Activation function | This function is a mathematical function between the input that feeds the current neuron and its output that travels to the next layer. |
| Weight | demonstrates the significance and ability of the characteristic/input to the neurons. |
| Epoch | In the training process, each training step’s inputs produce an output that is compared to the goal in order to determine an error. Weights and biases are calculated and adjusted in each epoch using this method. |
| Batch size | For stochastic optimizers, the size of mini-batches is important. (The classifier will not use minibatch if the solver is lbfgs.) |
| Momentum | Update on gradient descending momentum. Only when the solver is sgd. |
| Learning rate | For weight updates, we have to learn a rate schedule (used for SGD). |
Appendix A
| Neuron | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First hidden layer | −0.5261 | 0.3122 | 0.3003 | −0.3842 | −0.1168 | −0.4217 | −0.4679 | 0.5963 | −0.5029 | 0.2167 | 0.1923 | 0.2747 | −0.0355 | - | - | |
| 0.1414 | −0.6600 | 0.3918 | −0.4975 | −0.1184 | −0.0795 | −0.2839 | 0.2968 | −0.1454 | −0.3495 | 0.1552 | 0.2744 | −0.5067 | ||||
| −0.4716 | 0.1534 | 0.1572 | 0.0499 | −0.1170 | −0.5092 | 0.0669 | 0.3481 | 0.3992 | −0.3800 | −0.0519 | 0.2840 | 0.3226 | - | - | ||
| −0.4195 | 0.2306 | 0.4402 | 0.3055 | −0.3375 | −0.2342 | 0.4835 | 0.5569 | −0.0585 | −0.0243 | 0.3713 | 0.2479 | −0.4035 | - | - | ||
| −0.3103 | −0.4300 | −0.4428 | −0.3570 | −0.1607 | −0.3180 | 0.3841 | 0.3178 | 0.4336 | 0.2486 | −0.0613 | −0.1156 | 0.1871 | - | - | ||
| 0.1264 | 0.2072 | −0.1894 | 0.3279 | −0.4434 | −0.3503 | 0.2591 | −0.1250 | −0.0045 | −0.2883 | −0.1393 | 0.5487 | 0.1746 | - | - | ||
| −0.0399 | 0.4145 | −0.1454 | 0.4606 | 0.4224 | −0.4450 | 0.4078 | 0.1576 | −0.2562 | −0.3226 | −0.4084 | 0.4207 | −0.4346 | - | - | ||
| −0.2834 | 0.6741 | −0.3418 | 0.3441 | 0.1340 | 0.1127 | −0.0791 | −0.1540 | −0.3525 | −0.2026 | −0.2172 | −0.3762 | −0.0161 | - | - | ||
| −0.1834 | −0.1580 | −0.0837 | −0.2541 | 0.1330 | 0.4629 | −0.1553 | −0.2419 | −0.4652 | −0.1960 | −0.3441 | −0.1922 | −0.1461 | - | - | ||
| Second hidden layer | 0.0312 | 0.0689 | 0.4262 | 0.2687 | −0.0318 | 0.1865 | −0.2655 | −0.0196 | 0.1368 | −0.3179 | −0.3118 | −0.0888 | −0.2162 | 0.3304 | - | |
| 0.0045 | 0.2990 | −0.0313 | 0.3231 | 0.0983 | 0.2352 | 0.2577 | 0.3021 | −0.5072 | 0.3468 | −0.0712 | −0.6618 | 0.0328 | 0.3322 | - | ||
| −0.1573 | 0.1815 | 0.1161 | −0.0604 | 0.0848 | −0.4078 | 0.2779 | 0.1774 | −0.1519 | −0.2078 | −0.4528 | −0.3158 | 0.3392 | −0.0341 | - | ||
| 0.5107 | 0.2276 | −0.0847 | 0.3726 | −0.4047 | 0.0170 | 0.2782 | −0.3967 | 0.0856 | 0.2555 | −0.0656 | 0.1127 | −0.0742 | −0.1451 | - | ||
| −0.0711 | −0.4243 | 0.4544 | 0.4096 | 0.1945 | 0.2685 | −0.1691 | 0.2535 | 0.1275 | −0.1207 | 0.0698 | 0.2671 | −0.0571 | 0.3847 | - | ||
| 0.4588 | −0.1143 | 0.1844 | 0.4392 | 0.0310 | 0.0494 | 0.2749 | −0.2550 | −0.3050 | 0.2182 | −0.1881 | −0.0108 | −0.3532 | 0.3005 | - | ||
| 0.2885 | 0.2154 | 0.1225 | 0.0524 | 0.3704 | −0.3282 | 0.3586 | −0.4109 | 0.3636 | −0.3674 | −0.0109 | −0.2198 | 0.3213 | 0.4504 | - | ||
| −0.0564 | 0.2155 | −0.1700 | −0.1756 | −0.0896 | −0.1456 | 0.1221 | −0.1117 | −0.3548 | −0.1415 | 0.1060 | −0.0106 | 0.2727 | −0.5645 | - | ||
| 0.0639 | −0.1984 | −0.1939 | 0.3111 | −0.3191 | −0.3805 | 0.2158 | 0.0610 | −0.2565 | 0.2141 | 0.4456 | −0.2957 | −0.0531 | −0.1954 | - | ||
| −0.2476 | 0.0253 | −0.0674 | −0.0173 | −0.4643 | 0.1050 | 0.1627 | −0.4444 | −0.3693 | 0.3759 | −0.2169 | 0.2445 | 0.3126 | 0.1138 | - | ||
| −0.2510 | 0.3462 | −0.4332 | 0.3669 | −0.4641 | 0.3092 | 0.4015 | 0.0386 | 0.0139 | 0.2427 | −0.3794 | −0.1944 | −0.2762 | −0.1957 | - | ||
| 0.34032 | 0.1627 | −0.0866 | 0.4185 | −0.2898 | −0.3095 | 0.2176 | 0.1026 | 0.1285 | 0.4677 | 0.24473 | 0.0041 | 0.14404 | 0.0999 | - | ||
| −0.4088 | 0.1685 | −0.1742 | 0.4011 | −0.0112 | 0.4490 | 0.1211 | −0.1369 | −0.0108 | 0.2971 | −0.2613 | 0.4224 | 0.2733 | −0.1892 | - | ||
| 0.0027 | 0.3390 | −0.1864 | −0.3606 | −0.3528 | −0.0716 | 0.2954 | −0.3802 | 0.2887 | 0.0372 | 0.3559 | 0.3273 | 0.0601 | 0.2710 | - | ||
| Output layer | 0.1855 | |||||||||||||||
| 0.5334 | ||||||||||||||||
| −0.1828 | ||||||||||||||||
| 0.1919 | ||||||||||||||||
| 0.2326 | ||||||||||||||||
| −0.3029 | ||||||||||||||||
| −0.0028 | ||||||||||||||||
| −0.2619 | ||||||||||||||||
| −0.6629 | ||||||||||||||||
| 0.0341 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | ||
References
- Berg, K.; Olsen, S. Kinetics of manganese ore reduction by carbon monoxide. Metall. Mater. Trans. B 2000, 31, 477–490. [Google Scholar] [CrossRef]
- Szekely, J.; Lin, C.; Sohn, H. A structural model for gas—Solid reactions with a moving boundary—V an experimental study of the reduction of porous nickel-oxide pellets with hydrogen. Chem. Eng. Sci. 1973, 28, 1975–1989. [Google Scholar] [CrossRef]
- Béchara, R.; Hamadeh, H.; Mirgaux, O.; Patisson, F. Carbon impact mitigation of the iron ore direct reduction process through computer-aided optimization and design changes. Metals 2020, 10, 367. [Google Scholar] [CrossRef] [Green Version]
- Hamadeh, H.; Mirgaux, O.; Patisson, F. Detailed modeling of the direct reduction of iron ore in a shaft furnace. Materials 2018, 11, 1865. [Google Scholar] [CrossRef] [Green Version]
- Cavaliere, P. Clean ironmaking and steelmaking processes: Efficient technologies for greenhouse emissions abatement. In Clean Ironmaking and Steelmaking Processes; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–37. [Google Scholar]
- Cavaliere, P.; Perrone, A.; Silvello, A.; Stagnoli, P.; Duarte, P. Integration of Open Slag Bath Furnace with Direct Reduction Reactors for New-Generation Steelmaking. Metals 2022, 12, 203. [Google Scholar] [CrossRef]
- Statistics, W.D.R. Midrex the World Leader in Direct Reduction Technology; © 2021 Midrex Technologies, Inc.: Charlotte, NC, USA, 2020; pp. 1–15. [Google Scholar]
- Rechberger, K.; Spanlang, A.; Sasiain Conde, A.; Wolfmeir, H.; Harris, C. Green hydrogen-based direct reduction for low-carbon steelmaking. Steel Res. Int. 2020, 91, 2000110. [Google Scholar] [CrossRef]
- Pimm, A.J.; Cockerill, T.T.; Gale, W.F. Energy system requirements of fossil-free steelmaking using hydrogen direct reduction. J. Clean. Prod. 2021, 312, 127665. [Google Scholar] [CrossRef]
- Szekely, J.; El-Tawil, Y. The reduction of hematite pellets with carbon monoxide-hydrogen mixtures. Metall. Trans. B 1976, 7, 490–492. [Google Scholar] [CrossRef]
- Towhidi, N. Reduction kinetics of commercial low-silica hematite pellets with CO-H_2 mixtures over temperature range 600–1234 °C. Ironmak. Steelmak. 1981, 6, 237–249. [Google Scholar]
- Turkdogan, E.; Vinters, J. Gaseous reduction of iron oxides: Part I. Reduction of hematite in hydrogen. Metall. Mater. Trans. B 1971, 2, 3175–3188. [Google Scholar] [CrossRef]
- Parisi, D.R.; Laborde, M.A. Modeling of counter current moving bed gas-solid reactor used in direct reduction of iron ore. Chem. Eng. J. 2004, 104, 35–43. [Google Scholar] [CrossRef]
- Mirzajani, A.; Ebrahim, H.; Nouri, S. Simulation of a direct reduction moving bed reactor using a three interface model. Braz. J. Chem. Eng. 2018, 35, 1019–1028. [Google Scholar] [CrossRef] [Green Version]
- Nouri, S.; Ebrahim, H.A.; Jamshidi, E. Simulation of direct reduction reactor by the grain model. Chem. Eng. J. 2011, 166, 704–709. [Google Scholar] [CrossRef]
- Kazemi, M.; Pour, M.S.; Sichen, D. Experimental and modeling study on reduction of hematite pellets by hydrogen gas. Metall. Mater. Trans. B 2017, 48, 1114–1122. [Google Scholar] [CrossRef] [Green Version]
- McKewan, W. Reduction kinetics of hematite in hydrogen-water vapor-nitrogen mixtures. Trans. Metal Soc. AIME 1962, 224, 2–5. [Google Scholar]
- Usui, T.; Ohmi, M.; Yamamura, E. Analysis of rate of hydrogen reduction of porous wustite pellets basing on zone-reaction models. ISIJ Int. 1990, 30, 347–355. [Google Scholar] [CrossRef]
- Mondal, K.; Lorethova, H.; Hippo, E.; Wiltowski, T.; Lalvani, S. Reduction of iron oxide in carbon monoxide atmosphere—Reaction controlled kinetics. Fuel Process. Technol. 2004, 86, 33–47. [Google Scholar] [CrossRef]
- Tien, R.; Turkdogan, E. Gaseous reduction of iron oxides: Part IV. Mathematical analysis of partial internal reduction-diffusion control. Metall. Trans. 1972, 3, 2039–2048. [Google Scholar] [CrossRef]
- Kam, E. A Model for the Direct Reduction of Iron Ore by Mixtures of Hydrogen and Carbon Monoxide in a Moving Bed; Pascal and Francis: Lawrence, KS, USA, 1981. [Google Scholar]
- Negri, E.D.; Alfano, O.M.; Chiovetta, M.G. Direct reduction of hematite in a moving-bed reactor. Analysis of the water gas shift reaction effects on the reactor behavior. Ind. Eng. Chem. Res. 1991, 30, 474–482. [Google Scholar] [CrossRef]
- Abualigah, L.; Abu Zitar, R.; Almotairi, K.H.; Hussein, A.M.; Elaziz, M.A.; Nikoo, M.R.; Gandomi, A.H. Wind, solar, and photovoltaic renewable energy systems with and without energy storage optimization: A survey of advanced machine learning and deep learning techniques. Energies 2022, 15, 578. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Aslfattahi, N.; Ghodbane, M. Experimental analysis of novel ionic liquid-MXene hybrid nanofluid’s energy storage properties: Model-prediction using modern ensemble machine learning methods. J. Energy Storage 2022, 52, 104858. [Google Scholar] [CrossRef]
- Forootan, M.M.; Larki, I.; Zahedi, R.; Ahmadi, A. Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability 2022, 14, 4832. [Google Scholar] [CrossRef]
- Valipour, M.S.; Saboohi, Y. Numerical investigation of nonisothermal reduction of hematite using Syngas: The shaft scale study. Model. Simul. Mater. Sci. Eng. 2007, 15, 487. [Google Scholar] [CrossRef]
- Valipour, M.S.; Saboohi, Y. Modeling of multiple noncatalytic gas–solid reactions in a moving bed of porous pellets based on finite volume method. Heat Mass Transf. 2007, 43, 881–894. [Google Scholar] [CrossRef]
- Alamsari, B.; Torii, S.; Trianto, A.; Bindar, Y. Heat and mass transfer in reduction zone of sponge iron reactor. Int. Sch. Res. Not. 2011, 2011, 324659. [Google Scholar] [CrossRef] [Green Version]
- Alhumaizi, K.; Ajbar, A.; Soliman, M. Modelling the complex interactions between reformer and reduction furnace in a midrex-based iron plant. Can. J. Chem. Eng. 2012, 90, 1120–1141. [Google Scholar] [CrossRef]
- Shams, A.; Moazeni, F. Modeling and simulation of the MIDREX shaft furnace: Reduction, transition and cooling Zones. JOM 2015, 67, 2681–2689. [Google Scholar] [CrossRef]
- Ghadi, A.Z.; Valipour, M.S.; Biglari, M. CFD simulation of two-phase gas-particle flow in the Midrex shaft furnace: The effect of twin gas injection system on the performance of the reactor. Int. J. Hydrogen Energy 2017, 42, 103–118. [Google Scholar] [CrossRef]
- Béchara, R.; Hamadeh, H.; Mirgaux, O.; Patisson, F. Optimization of the iron ore direct reduction process through multiscale process modeling. Materials 2018, 11, 1094. [Google Scholar] [CrossRef] [Green Version]
- Hara, Y.; Sakawa, M.; Kondo, S.-I. Mathematical model of the shaft furnace for reduction of iron-ore pellet. Tetsu-Hagané 1976, 62, 315–323. [Google Scholar] [CrossRef] [Green Version]
- Szekely, J.; Evans, J. A structural model for gas-solid reactions with a moving boundary-II: The effect of grain size, porosity and temperature on the reaction of porous pellets. Chem. Eng. Sci. 1971, 26, 1901–1913. [Google Scholar] [CrossRef]
- Szekely, J.; Evans, J. A structural model for gas—Solid reactions with a moving boundary. Chem. Eng. Sci. 1970, 25, 1091–1107. [Google Scholar] [CrossRef]
- Takenaka, Y.; Kimura, Y.; Narita, K.; Kaneko, D. Mathematical model of direct reduction shaft furnace and its application to actual operations of a model plant. Comput. Chem. Eng. 1986, 10, 67–75. [Google Scholar] [CrossRef]
- Yanagiya, T.; Yagi, J.; Omori, Y. Reduction of iron oxide pellets in moving bed. Ironmak. Steelmak. 1979, 6, 93–100. [Google Scholar]
- Kang, H.W.; Chung, W.S.; Murayama, T.; Ono, Y. Effect of iron ore shape on gaseous reduction rate. ISIJ Int. 1998, 38, 1194–1200. [Google Scholar] [CrossRef] [Green Version]
- Kang, H.W.; Chung, W.S.; Murayama, T. Effect of iron ore size on kinetics of gaseous reduction. ISIJ Int. 1998, 38, 109–115. [Google Scholar] [CrossRef]
- Bonalde, A.; Henriquez, A.; Manrique, M. Kinetic analysis of the iron oxide reduction using hydrogen-carbon monoxide mixtures as reducing agent. ISIJ Int. 2005, 45, 1255–1260. [Google Scholar] [CrossRef] [Green Version]
- Rahimi, A.; Niksiar, A. A general model for moving-bed reactors with multiple chemical reactions part I: Model formulation. Int. J. Miner. Process. 2013, 124, 58–66. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Wagner, D.; Patisson, F. Modelling a new, low CO2 emissions, hydrogen steelmaking process. J. Clean. Prod. 2013, 46, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Ponugoti, P.V.; Garg, P.; Geddam, S.N.; Nag, S.; Janardhanan, V.M. Kinetics of iron oxide reduction using CO: Experiments and Modeling. Chem. Eng. J. 2022, 434, 134384. [Google Scholar] [CrossRef]
- Tang, Q.; Huang, K. Determining the kinetic rate constants of Fe3O4-to-Fe and FeO-to-Fe reduction by H2. Chem. Eng. J. 2022, 434, 134771. [Google Scholar] [CrossRef]
- Ajbar, A.; Alhumaizi, K.; Soliman, M. Modeling and simulations of a reformer used in direct reduction of iron. Korean J. Chem. Eng. 2011, 28, 2242–2249. [Google Scholar] [CrossRef]
- Parisi, D.R.; Laborde, M.A. Modeling steady-state heterogeneous gas–solid reactors using feedforward neural networks. Comput. Chem. Eng. 2001, 25, 1241–1250. [Google Scholar] [CrossRef]
- Parisi, D.R.; Mariani, M.a.C.; Laborde, M.A. Solving differential equations with unsupervised neural networks. Chem. Eng. Process. Process Intensif. 2003, 42, 715–721. [Google Scholar] [CrossRef]
- Wu, S.; Xu, J.; Yang, S.; Zhou, Q.; Zhang, L. Basic characteristics of the shaft furnace of COREX® smelting reduction process based on iron oxides reduction simulation. ISIJ Int. 2010, 50, 1032–1039. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Wu, S.; Kou, M.; Du, K. Numerical analysis of the characteristics inside pre-reduction shaft furnace and its operation parameters optimization by using a three-dimensional full scale mathematical model. ISIJ Int. 2013, 53, 576–582. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Xu, J.; Yagi, J.-I.; Guo, X.; Zhang, L. Prediction of pre-reduction shaft furnace with top gas recycling technology aiming to cut down CO2 emission. ISIJ Int. 2011, 51, 1344–1352. [Google Scholar] [CrossRef] [Green Version]
- Nield, D.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Yusufaly, T.I.; Kallis, K.; Simon, A.; Mayadev, J.; Yashar, C.M.; Einck, J.P.; Mell, L.K.; Brown, D.; Scanderbeg, D.; Hild, S.J.; et al. A knowledge-based organ dose prediction tool for brachytherapy treatment planning of patients with cervical cancer. Brachytherapy 2020, 19, 624–634. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, K.; Bagheri, M.; Burken, J.G.; Gu, A.; Li, B.; Ma, X.; Marrone, B.L.; Ren, Z.J.; Schrier, J.; et al. Machine learning: New ideas and tools in environmental science and engineering. Environ. Sci. Technol. 2021, 55, 12741–12754. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, J.; Realff, M.J. Machine learning: Overview of the recent progresses and implications for the process systems engineering field. Comput. Chem. Eng. 2018, 114, 111–121. [Google Scholar] [CrossRef]
- Hegde, J.; Rokseth, B. Applications of machine learning methods for engineering risk assessment–A review. Saf. Sci. 2020, 122, 104492. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Gholami, R.; Ridha, S. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models. J. Pet. Sci. Eng. 2021, 200, 108182. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques Elsevier Science; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Mashhadimoslem, H.; Vafaeinia, M.; Safarzadeh, M.; Ghaemi, A.; Fathalian, F.; Maleki, A. Development of predictive models for activated carbon synthesis from different biomass for CO2 adsorption using artificial neural networks. Ind. Eng. Chem. Res. 2021, 60, 13950–13966. [Google Scholar] [CrossRef]
- Kolbadinejad, S.; Mashhadimoslem, H.; Ghaemi, A.; Bastos-Neto, M. Deep learning analysis of Ar, Xe, Kr, and O2 adsorption on Activated Carbon and Zeolites using ANN approach. Chem. Eng. Process.-Process Intensif. 2022, 170, 108662. [Google Scholar] [CrossRef]
- Mashhadimoslem, H.; Ghaemi, A. Machine learning analysis and prediction of N2, N2O, and O2 adsorption on activated carbon and carbon molecular sieve. Environ. Sci. Pollut. Res. 2022, 1–21. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Egghe, L.; Leydesdorff, L. The relation between Pearson’s correlation coefficient r and Salton’s cosine measure. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 1027–1036. [Google Scholar] [CrossRef] [Green Version]
- Salemi, S.; Torabi, M.; Haghparast, A.K. Technoeconomical investigation of energy harvesting from MIDREX® process waste heat using Kalina cycle in direct reduction iron process. Energy 2022, 239, 122322. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseinzadeh, M.; Mashhadimoslem, H.; Maleki, F.; Elkamel, A. Prediction of Solid Conversion Process in Direct Reduction Iron Oxide Using Machine Learning. Energies 2022, 15, 9276. https://doi.org/10.3390/en15249276
Hosseinzadeh M, Mashhadimoslem H, Maleki F, Elkamel A. Prediction of Solid Conversion Process in Direct Reduction Iron Oxide Using Machine Learning. Energies. 2022; 15(24):9276. https://doi.org/10.3390/en15249276
Chicago/Turabian StyleHosseinzadeh, Masih, Hossein Mashhadimoslem, Farid Maleki, and Ali Elkamel. 2022. "Prediction of Solid Conversion Process in Direct Reduction Iron Oxide Using Machine Learning" Energies 15, no. 24: 9276. https://doi.org/10.3390/en15249276
APA StyleHosseinzadeh, M., Mashhadimoslem, H., Maleki, F., & Elkamel, A. (2022). Prediction of Solid Conversion Process in Direct Reduction Iron Oxide Using Machine Learning. Energies, 15(24), 9276. https://doi.org/10.3390/en15249276












