Energy Autonomy Simulation Model of Solar Powered UAV

Abstract

The energy autonomy of UAVs is an important direction in the field of aerospace. Long-endurance aerial vehicles allow for continuous flight; however, to meet the guidelines, the power supply system has to be able to harvest energy from outside. Solar cells allow the production of electricity during the day when the sun shines on their surface. Depending on the location, time, weather, and other external factors, the energy produced by PV panels will change. In order to calculate as accurately as possible the energy obtained by solar cells, we developed a simulation model that took into account all of the external restrictions and the UAV’s limits during flight. The conducted analysis made it possible to obtain information for the specific input data on whether the UAV is able to fly for 24 h in a specific flight scenario. The UAV powered by solar cells developed by us and the performed aviation missions have shown that the UAV is capable of continuous flight without the need to land.

1. Introduction

Unmanned Aerial Vehicles (UAVs) are increasingly used in everyday life. The scope of their work is constantly enlarged from casual filming [1] to advanced military use [2]. UAVs are used for distributing shipments, mapping, surveillance, and monitoring borders or crops [3,4]. The limited duration of the UAV flight causes the necessity to land and the resulting loss of time in terms of interrupting the mission, charging or replacing the batteries. Designers of UAVs are looking for opportunities to obtain energy from outside; if this is achieved, the time of flight will be extended [5]. The goal is to achieve full energy autonomy. The energy autonomy of UAVs is an important direction in the field of aerospace because, in addition to the possibility of continuous operation, another advantage is the lower cost of this kind of application in comparison to using a satellite. One of the most used sources is a solar cell [4,5].

Solar-powered UAVs are not a new concept of aerial vehicles. We can distinguish many types of solar-powered UAVs, for example: Atlantic Solar [5,6], Solar Impulse 2 [7], Airbus zephyr [8], PHASA-35 [9], and Odysseus [10]. Each of these aircrafts is based on a lightweight composite structure and is equipped with photovoltaic (PV) panels. Depending on the purpose of the UAV, the payload aspect, as well as the weight of the measuring, detection, and control devices should be taken into account. A UAV’s weight should be as low as possible. The load-bearing structure then enables a larger payload or an increase in the capacity of the batteries, which allows for an extension in the applications of the UAV [3,5].

The possibility of obtaining electricity from solar cells makes them the main substitute or complementary source of energy [11]. The use of PV panels can be found in small devices, such as lights or toys, on the roofs of houses to provide partial electricity to houses, or in a large area of desert, lake or farmland where they play the role of new power plants [11,12]. The ease of generating electricity, the relatively low cost of such a power supply system, and the newer materials of solar cells have seen them gain recognition in new technology industries.

There are a number of different technologies are used for manufacturing solar cells with different materials that are used in various industries [4]. The most commonly used material for solar cells is silicon. Other materials used for the construction of photovoltaic cells are gallium arsenide, cadmium telluride, and copper indium gallium selenide. However, this technology is restricted by the scarcity of the required materials. The most popular silicon PV panels are rigid and breakable [13,14]. These kinds of solar cells are not resistant to working under stresses where forces act on the PV panel. The wings, fuselages, tail are curved surfaces. This makes it impossible to fit the silicon solar cell into the construction of the UAV. For UAVs, aerospace, and aviation, we have to take into account flexible solar cells, which are able to bend and are more durable than standard silicon solar cells [15,16]. Under the influence of stresses and forces during operation, the PV panel will not break and will still be able to produce electricity. In this group, we can distinguish several types of solar cells that could be used in the aviation industry. The most popular is the GaAs (Gallium arsenide) solar cell, which provides the highest efficiency, exceeding 30% [4,17]. The disadvantage of GaAs is the high cost, meaning designers often cannot afford to build a prototype. GaAs is used primarily in the space industry as probes, satellites and in the military industry due to their flexibility, efficiency and weight. Another kind of solar cell that can be used in aviation is flexible silicon solar cells [18]. This kind of PV panel provides an efficiency of around 25%, at a much lower cost compared to GaAs. A DSSC (Dye-sensitized solar cell) is a type of solar cell that has different properties than the previous two types [19]. Their maximum efficiency is around 13%, but they make up for this with long service life, low production costs, high resistance to mechanical damage, and a wide-angle range of sunlight [19,20]. In addition to low efficiency, another is its poor resistance to operation at low and high temperatures [19,20].

To strengthen solar cells mounted on the UAV structure and to prevent mechanical damage, various protective coatings are used on their upper surface, e.g., films and resins to extend the service life of the system. Solar cells can be mounted to the wing via several types of technology [21]:

• Adhering to the existing wing—this method is good for the retrofit of existing UAVs. The advantage is the possibility of replacement in case of damage. The disadvantage of this solution is sealing the gap between the two modules [21,22].
• Solar modules into the mold—this method is good for new UAVs. Solar cells are a direct part of the wing. The advantage is its easy to arrange wiring, however, the PV modules cannot be swapped in case of damage.
• Solar modules as wing surface—PV panels are used as the upper surface of the wings. The advantage is its easy to arrange wiring, however, it requires additional ribs inside the structure of the wing to strengthen the structure of the UAV [8,23,24,25].

UAV’s power supply system can be built using many different storage sources. The current predominant battery energy storage technology for UAVs is the Li-ion battery [3,5,22,24]. The type of battery cell should take into account temperature range, lifespan, energy density, safety, and performance. Another issue is the shape of the battery cell. We can distinguish three main shapes of battery cells: prismatic, cylindrical, and pouch [26,27]. The cylindrical cell has good mechanical strength, specific energy, and energy density. The disadvantage of the cylindrical cell is its bad heat management. The prismatic cell has good mechanical strength, heat management, specific energy, and energy density but they have a heavy shell, which leads to certain restrictions on the energy density of the battery pack. Pouch cells have good heat management, energy density, and specific energy. The disadvantage is its low mechanical strength [26,27].

To provide solar cells and battery cells that are fully functional, the power supply system should be equipped with MPPT (Maximum Power Point Tracking) and a BMS (Battery Management System). MPPT ensures the continuous supply of the maximum power generated by the PV [28]. A photovoltaic module has non-linear I–V (current–voltage) characteristics and its P–V (power–voltage) characteristics show that it possesses only one point (P_mpp). This point also varies with the change in insolation and temperature. MPPT is used to maximize the value of the solar energy produced by the PV module. BMS is responsible for the proper work of the batteries. The BMS controls the charging and discharging currents, the uniform voltage of cells, and the overall temperature of the system [29].

As part of the research work, a team of scientists and designers developed and built a family of UAVs called TwinStratos (TS), which are suitable for continuous flight missions.

As part of this work, several scale-up units have been built so far and are intended to be built for the testing and verification of individual subsystems, as well as for the implementation of planned research missions.

• TwinStratos 110 (TS110) scaled 1:10—UAV for testing general layout and specific simplified control system;
• TS17 scaled 1:7—UAV for testing the power supply system, energy consumption simulation model, and technology of manufacturing;
• TS12 scaled 1:2—UAV for long endurance tests, verification flight parameters and performance ranges in operation mode, designated for service use and research tests;
• TS—target UAV intended for the research and implementation of commercial services.

The correct selection of solar cells, batteries, energy converters and energy management devices with the simultaneous use of energy-saving propulsion systems should enable the long-endurance flight of the UAV [5,6,30]. The aim of this article is to illustrate the complexity of the issues of a solar-powered UAV. The simulation model developed as part of this work was used to verify whether the aircraft is able to fly over 24 h under the given conditions. In this research, the Model-Based Design (MBD) methodology was used. The approach is characterized by placing the simulation models of the analyzed system in the center of the development process. Using MBD is beneficial, particularly in designing dynamic and complex systems, as it allows for a better understanding and reduction of the complexity of UAVs [31,32]. Additionally, the MBD allows us to design and optimize the technical parameters, work more efficiently in designing systems and ease cooperation between specialists in different fields [33]. Such an integrated design approach based on the MBD methodology was developed by the project team and applied to the design and testing of ultra-efficient racing vehicles [34], Automated Guided Vehicles AGVs [33], as well as for the design of General Aviation class aircraft [35].

2. Solar Energy Production

2.1. Irradiation

Irradiation is a key element in obtaining solar energy for PV cells. Solar cells can produce energy when the sun is shining on the upper surface. The value of the energy differs and depends on several factors. The most important factors, which cause the most significant differences, are location and date (time) [11,12,36]. Whilst the sun always produces the same value of energy, the circular and rotational movement of the earth means that we cannot obtain this same value of energy in one place for 24 h. To calculate the volume of energy we can produce in solar cells, we have to use equations that allow us to calculate the value of the energy that can be transferred to the solar cells [36,37,38,39]. Solar constant G_SC = 1367 W/m². To calculate the energy to the specific location, we have to use equations connected with the position of the earth, relative to the sun [39]. Declination (δ) is the angle between the line to the sun and the equatorial plane.

$$\delta =23.45\times \sin \left(360\times \frac{284+\mathrm{n}}{365} \right)$$

(1)

where n is the day of the year. The range of declination is −23.45° ≪ δ ≪ 23.45°. The maximum positive value is during the summer solstice and the maximum negative value is during the winter solstice. The declination is the same across the world. The hour angle (ω) changes all the time, by 15° per hour. We can write it with the following formula:

$$\omega =15°\times \left(Solar time-12\right)$$

(2)

The range of the hour angle is −180° ≪ ω ≪ 180°. The negative value is before solar noon. Zenith angle ${\theta }_z$ is the angle between the line to the sun and the horizontal surface. The formula of the zenith angle can be written as:

$${\theta }_z=\cos \left(\phi \right)\times \cos (\delta )\times \cos (\omega )+\sin \left(\phi \right)\times \sin \left(\delta \right)$$

(3)

where φ = latitude $\times$ π/180. The range of the zenith angle is 0° ≪ ${\theta }_z$ ≪ 90°. When zenith angle ${\theta }_z=0°$ is sunrise, ${\theta }_z=90°$ is sunset. Day length (N) can be calculated by the formula:

$$\mathrm{N}=\frac{2}{15}\times \mathrm{Arccos}\left(-\tan \phi \times \tan \delta \right)$$

(4)

The irradiation on surface G_on when θ_Z = 0 just outside the atmosphere is calculated from constant G_SC and the day number as follows:

$${\mathrm{G}}_{\mathrm{o}\mathrm{n}}={\mathrm{G}}_{\mathrm{s}\mathrm{c}}\times \left[1+0.033\times \cos \frac{360\times \mathrm{n}}{365}\right]$$

(5)

The solar constant G_SC is a mean value. The earth’s orbit is elliptical and the distance between the sun and earth varies by 3.3%.

The hourly radiation ${\mathrm{I}}_{\mathrm{o}}$ and the daily radiation ${\mathrm{H}}_{\mathrm{o}}$ can be calculated by the formulas below:

$$\begin{gathered} {\mathrm{I}}_{\mathrm{o}}=\frac{12\times 3600}{\mathsf{\pi }}\times {\mathrm{G}}_{\mathrm{sc}}\times \left[1+0.033\times \cos \frac{360\times \mathrm{n}}{365}\right] \\ \times \left[\cos \left(\phi \right)\times \cos (\delta )\times \left(\sin {\omega }_2-\sin {\omega }_1\right)+\frac{\mathsf{\pi }\times \left({\omega }_2-{\omega }_1\right)}{180}\times \sin \phi \times \sin \delta \right] \end{gathered}$$

(6)

where ${\omega }_2, {\omega }_1$ is the hour angle in the considered hours.

$$\begin{gathered} {\mathrm{H}}_{\mathrm{o}}=\frac{24\times 3600}{\mathsf{\pi }}\times {\mathrm{G}}_{\mathrm{sc}}\times \left[1+0.033\times \cos \frac{360\times \mathrm{n}}{365}\right]\times \cos \left(\phi \right)\times \cos (\delta )\times \sin {\omega }_s \\ +\frac{\mathsf{\pi }\times {\omega }_s}{180}\times \sin \phi \times \sin \delta \end{gathered}$$

(7)

The unit of the hourly radiation is J/m². The daily radiation unit is J/day $\times$ m². To calculate these values to watt-hours (Wh), we had to convert this unit.

Air mass (AM) is the distance travelled by the atmosphere by the sun’s rays on the Earth and can be calculated by the below formula [36,39]:

$$\mathrm{AM}=\frac{\mathrm{path}\mathrm{length}\mathrm{travelled}}{\mathrm{vertical}\mathrm{depth}\mathrm{of}\mathrm{the}\mathrm{atmosphere}}=\frac{1}{\cos {\theta }_z}$$

(8)

An explanation of air mass is posted below in Figure 1.

Hottel [40] has presented a method for estimating the beam radiation transmitted through clear atmospheres, which takes into account the zenith angle and altitude for a standard atmosphere and for four climate types [39].

Beam and diffuse radiation are the two types of radiation that are the most important in the case of irradiance solar cells. Beam (direct) radiation is the solar radiation that falls straight to the surface. This radiation is not scattered by the atmosphere. Diffuse radiation is scattered by the atmosphere in all directions. Only some of this radiation arrives at the Earth’s surface. Beam radiation can be calculated by the following formula:

$${\mathrm{G}}_{\mathrm{c}\mathrm{b}}={\tau }_b\times {\mathrm{G}}_{\mathrm{o}\mathrm{n}}\times \left[\cos \left(\phi \right)\times \cos (\delta )\times \cos (\omega )+\sin \left(\phi \right)\times \sin \left(\delta \right)\right]$$

(9)

where ${\tau }_b$ is the ratio of the transmitted direct radiation to the total radiation incident at the top of the atmosphere. This ratio can be calculated as follows:

$${\tau }_b=\frac{{\mathrm{G}}_{\mathrm{c}\mathrm{b}}}{{\mathrm{G}}_{\mathrm{o}}}={\mathrm{a}}_0+{\mathrm{a}}_1\times {\mathrm{e}}^{\left(\frac{-\mathrm{k}}{\cos {\theta }_z}\right)}$$

(10)

where ${\mathrm{G}}_{\mathrm{o}}={\mathrm{G}}_{\mathrm{o}\mathrm{n}}\times \cos {\theta }_z$ and ${\mathrm{a}}_0, {\mathrm{a}}_1, \mathrm{k}$ are the constant, calculated using next equations:

$${\mathrm{a}}_0={\mathrm{r}}_0\times \left(0.4237-0.00821\times {\left(6-\mathrm{A}\right)}^2\right)$$

(11)

$${\mathrm{a}}_1={\mathrm{r}}_1\times \left(0.5055-0.00595\times {\left(6.5-\mathrm{A}\right)}^2\right)$$

(12)

$$\mathrm{k}={\mathrm{r}}_{\mathrm{k}}\times \left(0.2711-0.01858\times {\left(2.5-\mathrm{A}\right)}^2\right)$$

(13)

where A is the altitude of the site above sea level. These equations can be used only for A < 2.5; ${\mathrm{r}}_0,{\mathrm{r}}_1,{\mathrm{r}}_{\mathrm{k}}$ are constant values from

Table 1. Coefficients for climate type and sample location.

Climate Type	${\mathbf{r}}_0$	${\mathbf{r}}_1$	${\mathbf{r}}_{\mathbf{k}}$	Sample location
Tropical	0.95	0.98	1.02	Nairobi
Midlatitude summer	0.97	0.99	1.02	Rome
Subarctic summer	0.99	0.99	1.01	Ny-Ålesund
Midlatitude winter	1.03	1.01	1.00	Gliwice

. Data for the Table 1 was develop based on the Hottel estimation method [40].

The diffuse radiation can be calculated by the following formula:

$${\mathrm{G}}_{\mathrm{c}\mathrm{d}}={\tau }_d\times {\mathrm{G}}_{\mathrm{o}\mathrm{n}}\times \left[\cos \left(\phi \right)\times \cos (\delta )\times \cos (\omega )+\sin \left(\phi \right)\times \sin \left(\delta \right)\right]$$

(14)

where ${\tau }_d$ is the ratio of the transmitted diffuse radiation to the total radiation incident at the top of the atmosphere. This coefficient can be calculated as follows:

$${\tau }_d=\frac{{\mathrm{G}}_{\mathrm{c}\mathrm{d}}}{{\mathrm{G}}_{\mathrm{o}}}=0.271-0.294\times {\tau }_b$$

(15)

Using all of the previous equations, we can calculate the total radiation, which is necessary to calculate the energy, which can be obtained by solar cells. The total radiation received on a horizontal surface at the ground surface can be calculated as follows:

$$\begin{gathered} {\mathrm{G}}_{\mathrm{c}}={\mathrm{G}}_{\mathrm{c}\mathrm{b}}+{\mathrm{G}}_{\mathrm{c}\mathrm{d}}=\left({\tau }_b+{\tau }_d\right)\times {\mathrm{G}}_{\mathrm{s}\mathrm{c}}\times \left[1+0.033\times \cos \frac{360\times \mathrm{n}}{365}\right] \\ \times \left[\cos \left(\phi \right)\times \cos (\delta )\times \cos (\omega )+\sin \left(\phi \right)\times \sin \left(\delta \right)\right] \end{gathered}$$

(16)

The hourly radiation on a horizontal surface is written as follows:

$$\begin{gathered} {\mathrm{I}}_{\mathrm{c}}=\frac{12\times 3600}{\mathsf{\pi }}\times \left({\tau }_b+{\tau }_d\right)\times {\mathrm{G}}_{\mathrm{s}\mathrm{c}}\times \left[1+0.033\times \cos \frac{360\times \mathrm{n}}{365}\right] \\ \times [\cos \left(\phi \right)\times \cos (\delta )\times \left(\sin {\omega }_2-\sin {\omega }_1\right) \\ +\frac{\mathsf{\pi }\times \left({\omega }_2-{\omega }_1\right)}{180}\times \sin \phi \times \sin \delta ] \end{gathered}$$

(17)

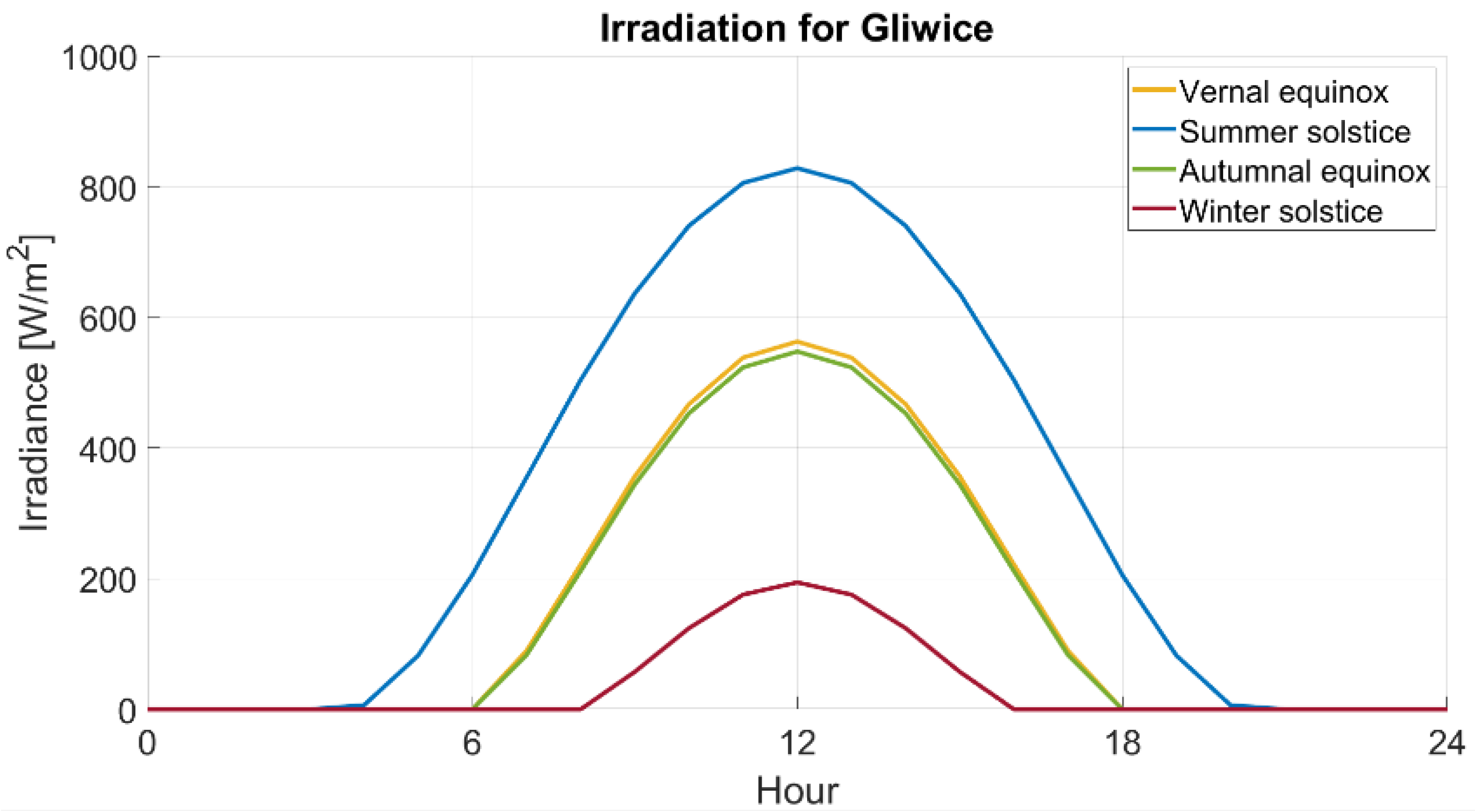
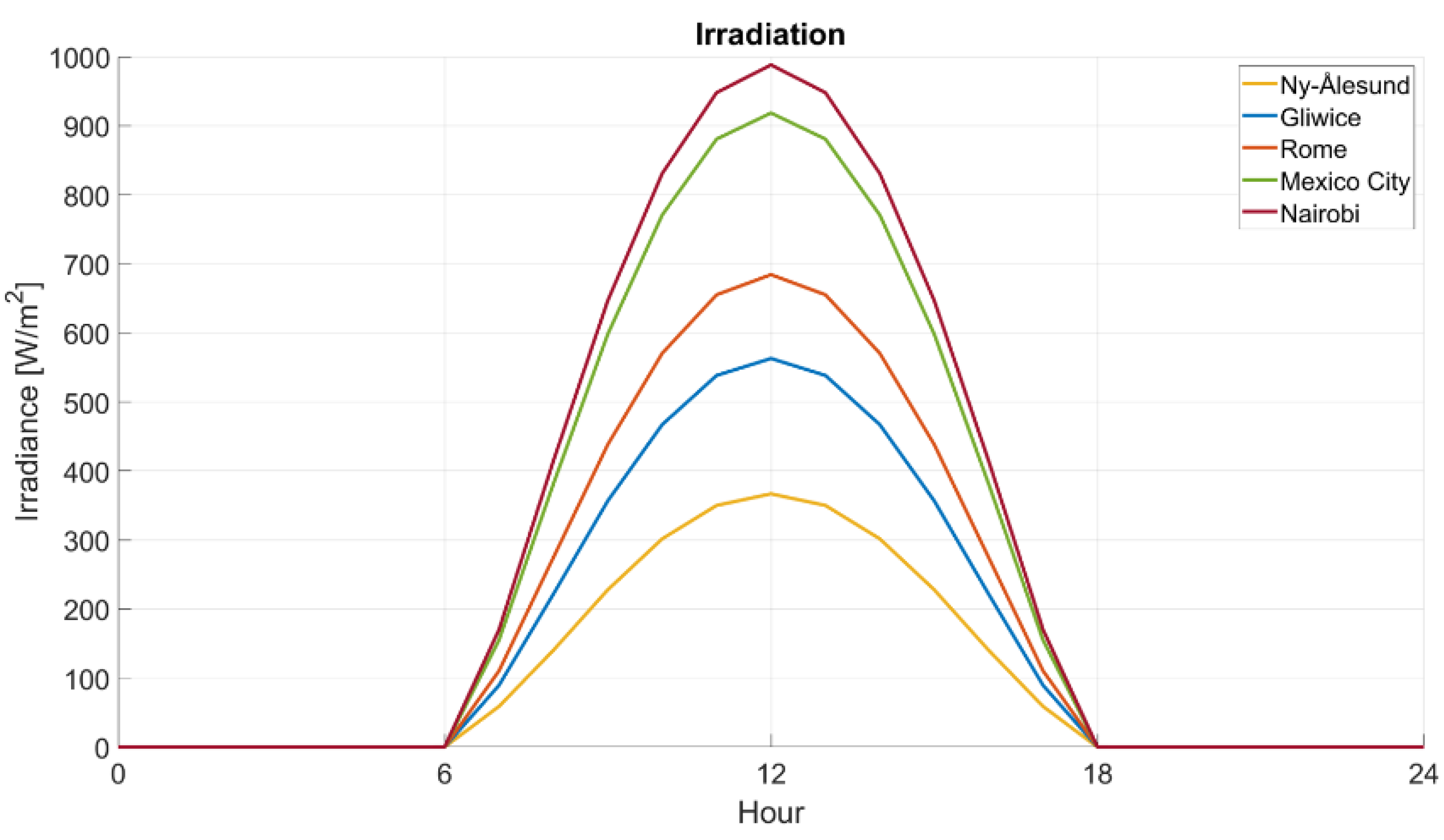
The above equations will be the basis for the source code, which will then be implemented into the simulation environment. The equations allow us to obtain the value of irradiation for a given time and location.

2.2. External Restrictions on Solar Energy Production

In the case of UAVs powered by solar energy, the power supply system is subject to many dependencies and limitations. It can be divided into two groups. The first is related to factors that are beyond human control, i.e., weather conditions, temperature, cloud cover, air pollution. The second is related to the variable parameters that can be changed in the UAV, e.g., electric motor power, mass, payload, flight path planning. The individual elements are divided into subsequent components and each of them has an impact on the energy balance. The general diagram of dependencies is presented in Figure 2.

Obtaining a negative energy balance makes it necessary to change the flight conditions or the construction of the drone, reduce energy consumption, and reduce the weight of the UAV [41]. Energy harvesting, in the case of solar powered UAVs, primarily depends on the irradiation level. During the flight, we also have to take into account other external restrictions, such as cloudiness, temperature, solar and air pollution.

2.2.1. Cloudiness

The calculations related to irradiation allow us to obtain the results for a given location and on a specific day. This value shows the results for perfect conditions. In a real environment, clouds often restrict the available sunlight. There are three main types of clouds [42]:

• cirrus clouds;
• cumulus clouds;
• stratus clouds.

Different types of clouds cause the scale of cloudiness to change. The cloudiness is measured on the okta scale (from 0—no cloud cover, to 8—full cloud cover). The percentage value that lowers the obtained energy can be written as: 0—100%, 1—98%, 2—94%, 3—88%, 4—79%, 5—70%, 6—54%, 7—50%, 8—27%. Cloudiness scale equal 9/8 is sky obscured—9—0% [43,44,45].

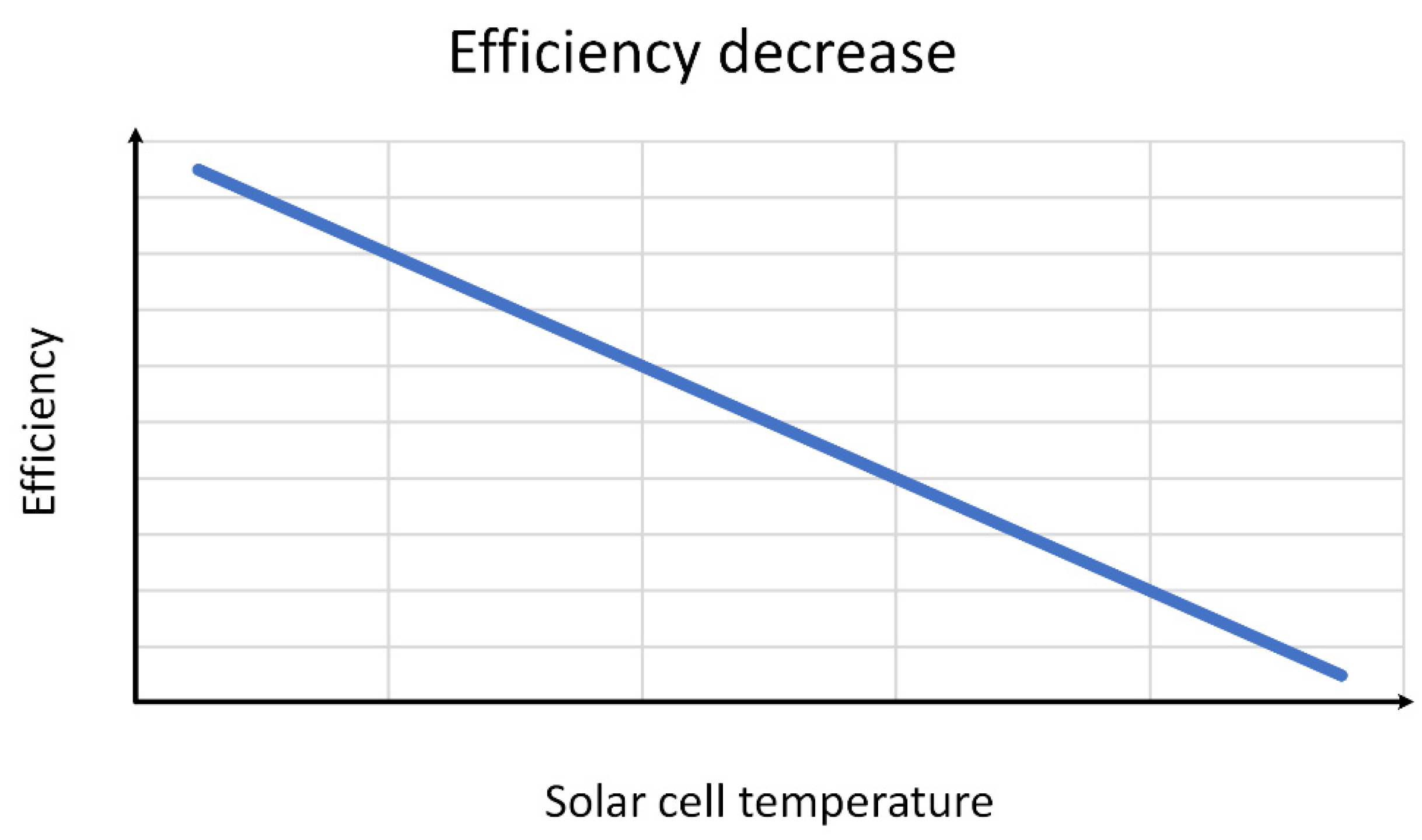
2.2.2. Temperature

Temperature is a variable that is important in the case of the efficiency of solar cells. The higher the temperature, the lower the efficiency [36,39,46]. Every solar cell has a temperature coefficient, which is connected with the voltage, current, and power [39]. The increase in temperature causes the deterioration of the solar cell parameters, reducing its power and efficiency (Figure 3).

For the UAV, we used a drop of air temperature between 0.5–1 °C, every 100 m [47]. The air temperature distribution depends mainly on: latitude, altitude, season, and topography. This kind of calculation for the temperature drop we can use up to the tropopause. Tropopause has this same temperature in the vertical section and amounts to −51 °C [47]. This temperature is maintained up to an altitude of 20 km.

The efficiency decrease in the solar cell with the increase in temperature is related to the heating of the solar cell under the influence of sunlight and the reduction in the heat dissipation capacity of the solar cell in the case of operation in high ambient temperature. The operation of the PV panels at high temperatures not only results in lower electrical power but also accelerates the degradation process of the solar cells.

In the simulation model, the current ambient temperature is connected with the height of the flight. To calculate the current temperature we can use the below formula.

$${\mathrm{T}}_{\mathrm{C}}={\mathrm{T}}_{\mathrm{I}}-\left[{\mathrm{H}}_{\mathrm{R}}\times \left({\mathrm{T}}_{\mathrm{D}}\times 100\right)\right]$$

(18)

where T_C is the current temperature on the height of the flight, T_I is the temperature on the ground, H_R—is the relative height of the flight in meters, and T_D is the temperature drop. We can assume ~1 °C for a dry-adiabatic temperature gradient and ~0.6 °C for a humid adiabatic temperature gradient [48].

2.2.3. Air and Solar Cell Pollutions

Air pollution and pollutions on the solar cells’ surfaces reduce the efficiency of the solar cells. These data are difficult to measure. The dust layer, smog from chimneys, soot, and hoarfrost cannot be precisely defined, particularly in the still changing conditions. In order to define more precisely the pollutants that may appear on the surface of the PV panels, it is necessary to group them. The purpose of this grouping is to facilitate the identification of the locations and seasons of such pollution. The intensity and impact on the operation of the solar-powered UAV power supply system should also be defined. Sometimes, these kinds of pollutions are momentary and, in terms of the entire mission, will not be of significant importance.

3. Materials and Methods—Numerical Model Data

The factors that were presented in the previous section are the first group of the numerical model. These data can help us to calculate the energy balance, but we have no influence on these variables. The second group is directly related to the power supply system components; namely, the solar cells and battery cells. We can freely change these elements and modify their connections in such a way as to obtain an energy surplus that allows for a continuous UAV flight of at least 24 h.

To provide a flight for 24 h we have to take into account both the outside data (e.g., weather) and the inside data (e.g., battery capacity, UAV design, solar cells). All of the requirements should be fulfilled to allow us to complete the planned flight scenario. The process of carrying out the concept selection is presented in Figure 4.

To verify the numerical model, we took into account two types of TwinStratos: TS17 (Figure 5) and TS12. The parameters of both UAVs are given in

Table 2. Parameters of TS17 and TS12.

Parameter	TS17	TS12
Mass [kg]	9.4	45
Wingspan [m]	3.6	12.4
Payload [kg]	2.5	2.5
Wing area [m2]	0.896	8.6
Rate of Climb (ROC) [m/s]	0.999	1.5
Rate of Descent (ROD) [m/s]	0.41	0.26
Climb speed [m/s]	13.3	11.1
Cruise speed [m/s]	13	13.9
Descend speed [m/s]	6.5	9.5
Angle of Attack range [°]	−3 to 8	−3 to 5
Maximum altitude [km]	8	20
Power supply system parameters—described in the below subchapters
Battery capacity [kWh]	0.622	2.797
Battery connection	4S12P	12S18P
Battery mass [kg]	2.4	10.8
Number of solar cells	40	350
Solar cell connection	40S1P	70S5P

, below:

3.1. Power Consumption

The UAV requires energy for its propulsion and additional systems, e.g., navigation, control, safety, measurement. Electric motors consume the majority of the energy. This value range can be wide due to the operational state of the flight. Take-off and climbing consume the most energy during flight at this same height and descent lower. During gliding, the electric motors do not consume energy; therefore, this stage of flight can be used as an energy buffer.

When the power consumption of the motors is variable, for the peripheral devices (control, navigation), we can use a constant value as the power consumption. The power consumption of the system on the UAV board is difficult to define. Due to the low percentage of the whole energy consumption, we can take into account the maximum value of the power consumption of the additional systems. In our case, this value is equal to 20 W for TS17 and 50 W for TS12. To assess the energy consumption of the analyzed UAVs, we used the simulation model developed in our previous study on the potential of General Aviation electric aircrafts, which is widely described [35]. Due to the higher altitudes reached by the UAVs, the COESA Atmosphere Model block responsible for calculating the changes in the atmospheric parameters was replaced by the ISA Atmosphere Model block. The model uses a backward approach. This approach allows us to assess the energy demand in order to perform the movement of the vehicle with the predefined parameters and it does not require control. Additionally, this approach performs calculations faster than the forward approach [49].

The model consists of the following subsystems, which are responsible for different calculations and behavior simulations (Figure 6):

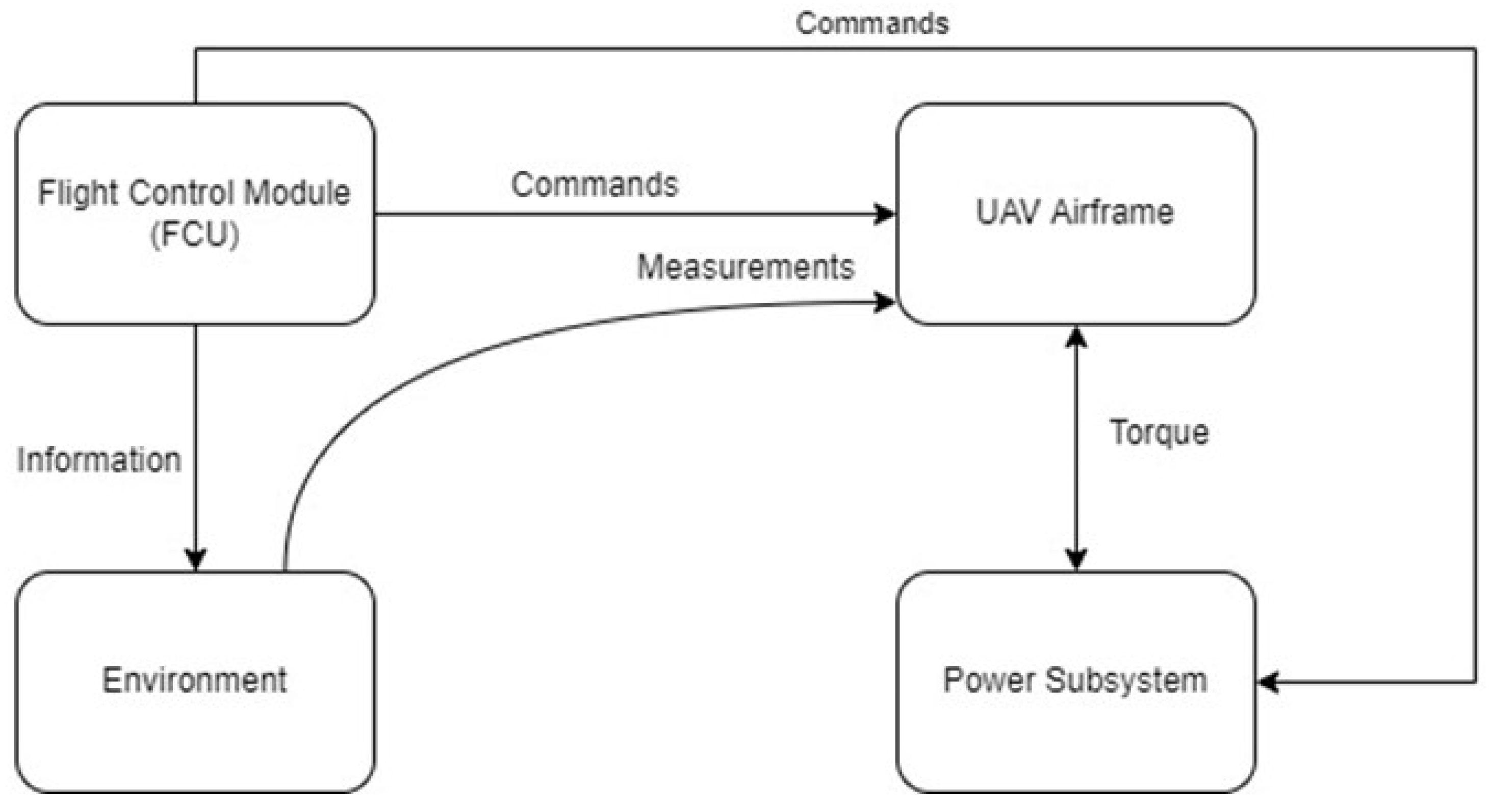
• Flight Control Module (FCM): controls the UAV and carries out the prepared mission scenario;
• Environment: calculates the changes in the atmospheric parameters due to changes in the UAV altitude;
• Airframe: calculates, based on the information from Flight Control Module and Environment, the required torque and energy demand of the UAV to fly with the given parameters;
• Power Subsystem: consists of the following subsystems: Battery, Electric Motor and Loads, which are responsible for simulating the power demand for avionics.

The model’s working principle can be described as follows: the Flight Control Module passes the information regarding the changes in the UAV altitude to the Environment to calculate the changes in the atmospheric parameters. Then, these subsystems send the flight and atmospheric parameters to the Airframe, which, after calculating the torque demand, “forces” the electric motor to produce the ordered value, which affects the battery power consumption.

In our simulation model, we used the following simplifications:

• The electric motor runs on a direct current;
• The flight takes place in nonthermal and nonwind conditions;
• The battery operation is not affected by the temperature;
• The UAV is considered to be a mass point;
• The UAV is not equipped with solar cells.

In the case of the last simplification, the task of this model is only to assess the energy demand of the UAV, not its flight performance (e.g., range).

3.2. Power Supply System Elements

3.2.1. Solar Cells

As a base for our UAV, we decided to use flexible SunPower Maxeon Ne3 solar cells [50]. The manufacturer ensures that the efficiency of this solar cell is over 24.34% and the generated power is around 3.77 W. To check if the parameters included in the datasheet are reliable, we decided to check the current-voltage (I-V) and power-voltage (P-V) characteristics on the test stand. The tests were carried out both for the non-laminated solar cells and for the solar cells laminated with 100 μm PVC (Polyvinyl Chloride) film (Figure 7). Lamination decreases the efficiency of the solar cell but this coating increases its durability and resistance to the mechanical damage that may occur during UAV flight [51].

The test stand allows us to test solar cells in the STC (Standard Test Conditions): irradiate with the power 1000 W/m² in the temperature 25 °C, and Air mass 1.5 spectrum (AM 1.5) defined by European standard IEC 60904-3 [52]. The system for the I-V characteristic measurements of the solar cells meets all of the requirements of the IEC 60904-1 standard [53].

On the wings of the TS17, we could place a maximum of 40 pcs solar cells and, on the TS12, 350 pcs. The exact type of solar cell connection also took into account the nominal voltage of the battery and the voltage range of the MPPT converters. We decided to use a connection 40S1P for TS17, and 70S5P for TS12. In a parallel connection, the disadvantage is that, in case of damaging a single solar cell and lowering the current value, the whole chain will generate this low current. By increasing the number of parallel connections, we increased the redundancy of the system, and in the event of a single cell failure, we increased the value of the generated energy.

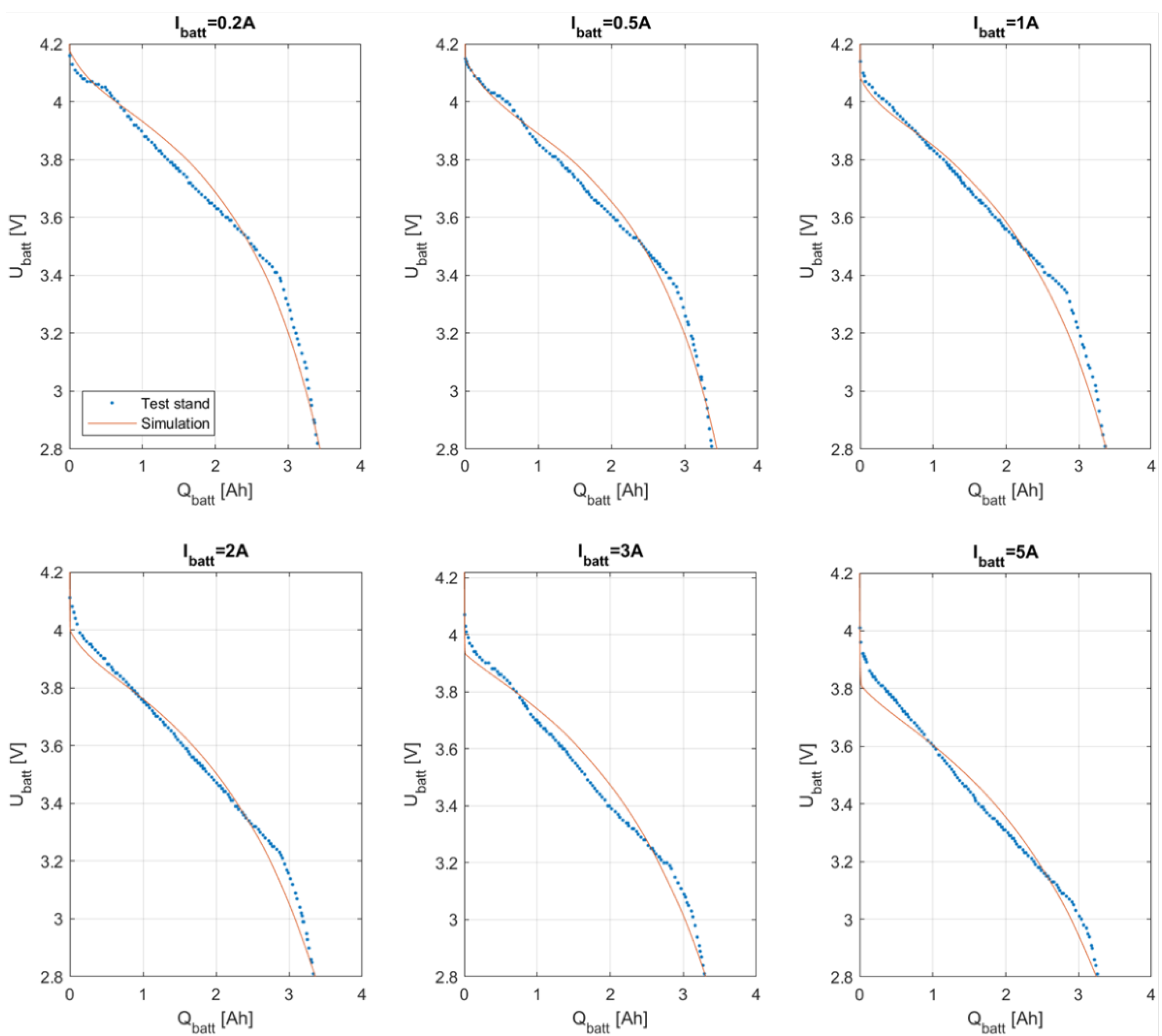
3.2.2. Battery Cells

The battery was selected in such a way as to best meet the following criteria: the lowest possible weight with the highest possible specific energy and energy density. The initial parameters of the power supply system were determined on the basis of simplified analytical calculations. Taking into account the number of solar cells and the energy that can be obtained, the capacity of the battery was calculated. We chose Gliwice as the location for the calculation. The vernal equinox was used for the irradiation equations.

For TS17 and TS12, we decided to use this same battery cell: Samsung INR18650-35E (Figure 8). The chosen battery cell generates 3.7 V, with a capacity of 3.5 Ah. The weight is equal to 50 g. As the connection, we used 4S12P for TS17 and 12S18P for TS12. A wide range of operating temperatures is essential in case of wide varying temperatures during flight. The Samsung INR18650-35E continues to work, even at −20 °C. The storage system was designed in such a way as to provide battery heating for long flights at high altitudes and at low temperatures. The heater starts to heat up the battery pack space if the temperature drops below the set level.

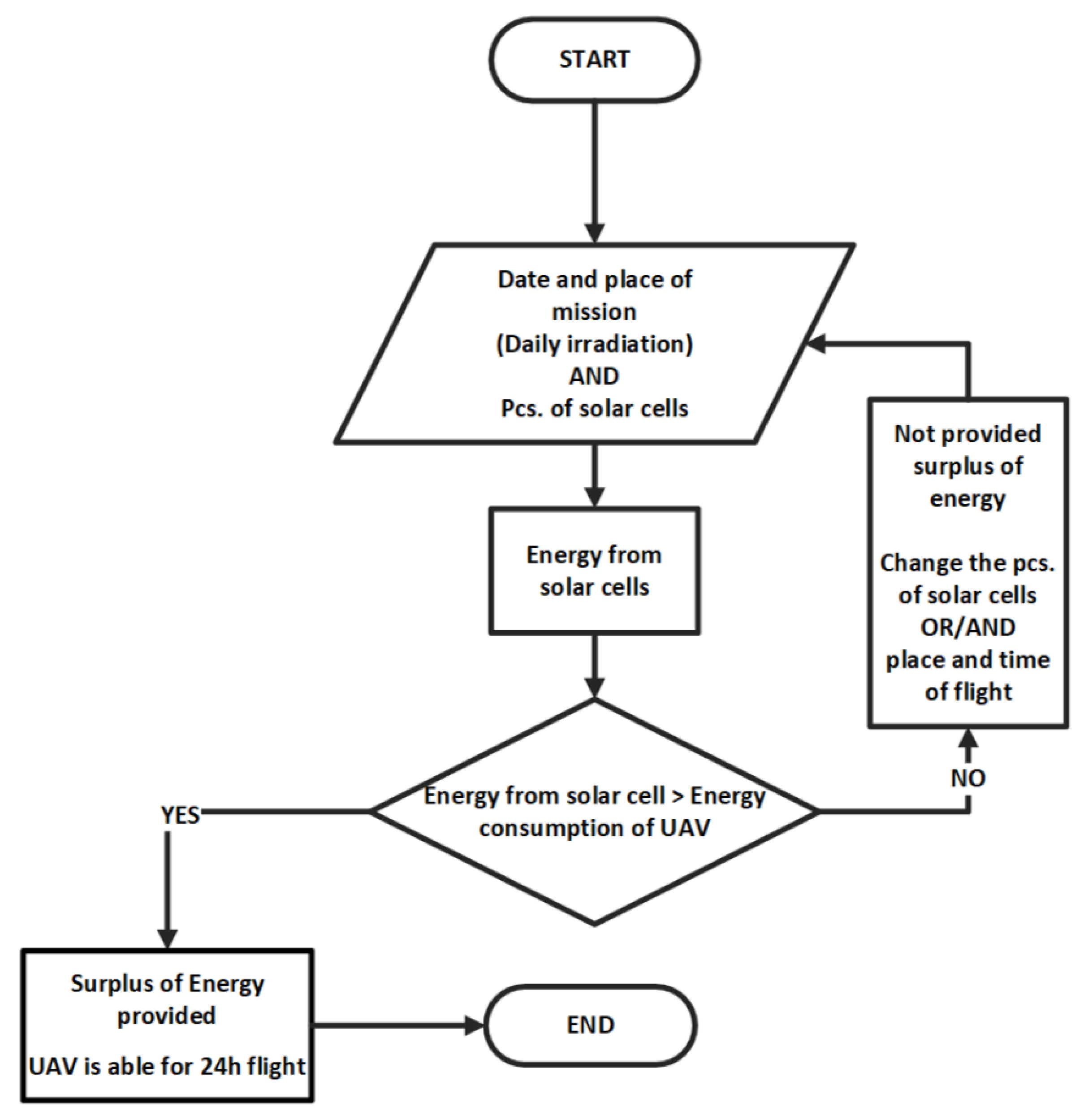
3.3. Simulation Model

A simulation model of the TwinStratos power supply system was prepared analogically, similar to the general diagram in Figure 2 (Figure 9). The main goal of the simulation model is to obtain the output data, such as the energy from the PV, the SoC (State of Charge), and time to discharge. Simulation allows us to check whether the given parameters in the adopted scenario will be feasible.

The scenarios that took into consideration time and location were either able or not able to achieve a 24 h flight. The flow chart (Figure 10) shows the change procedure for achieving a 24 h flight.

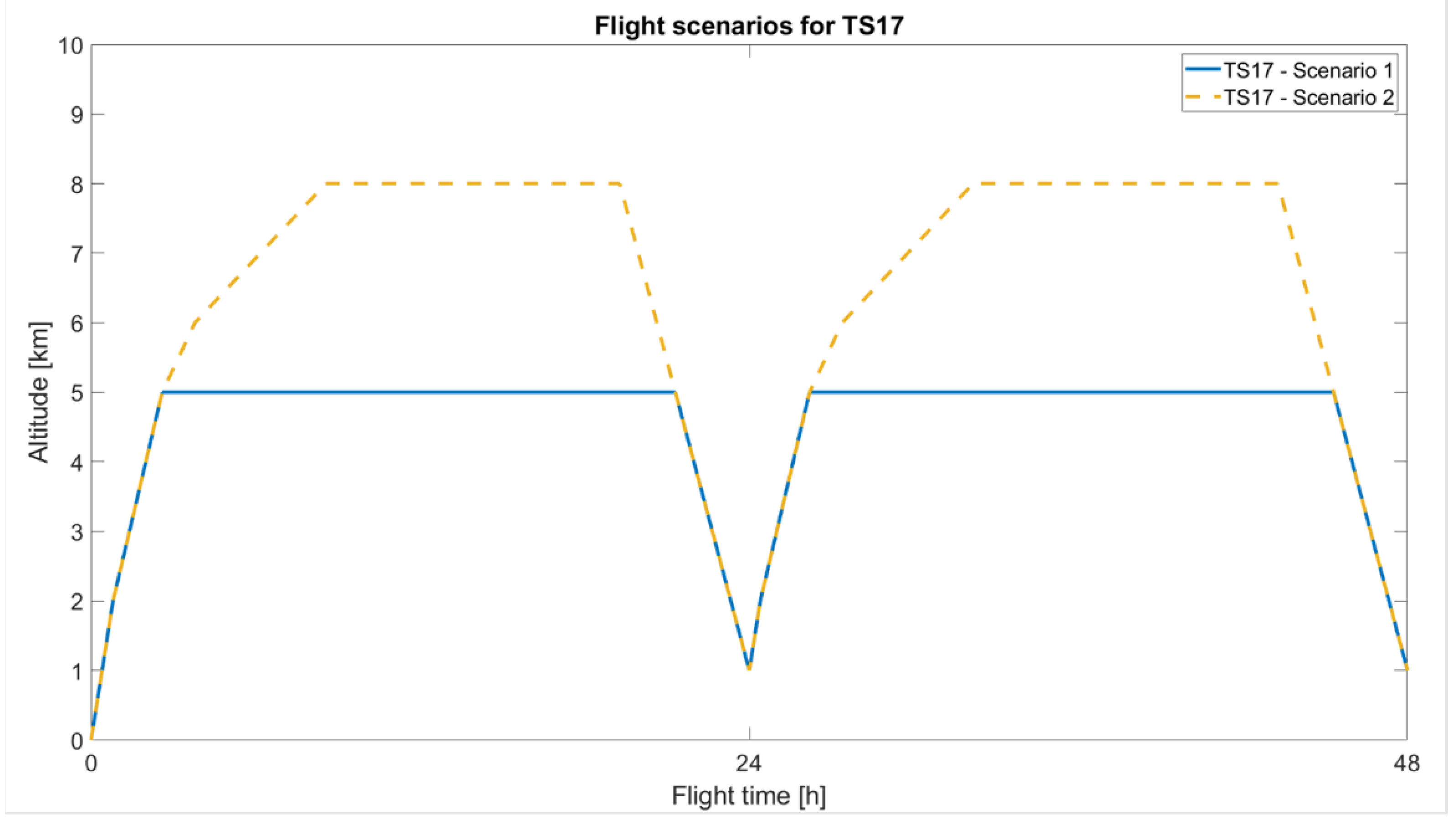
3.4. Scenarios of Path of Flight

To develop the UAV flight scenarios, we took into account the basic operations: take-off, climbing, gliding. The scenario helps to define the UAV energy demand so that it is possible to determine the power needed for each stage of flight. In the simulation model, we decided to prepare two main flight scenarios. Flight paths allow us to optimize the power consumption during the flight and increase the working time of the power supply system. The properly prepared scenarios for the UAV, in combination with the properly selected solar cells, batteries, and power consumption devices, allow for obtaining long endurance, which should ultimately achieve full energy autonomy of the UAV. The flight planning paths are mainly based on reaching the set altitude and then, depending on the needs, we can start the gliding or supporting the flight at a certain altitude. The goal of the simulation is to achieve a milestone in the form of a flight over 24 h. All of the scenarios were developed to take-off at sunrise. The single scenario is 24 h and it repeats every day thereafter.

The TwinStratos 1:7 scenarios were divided into two parts (Figure 11):

• Ascending to a height of 5 km and then holding that ceiling. We start gliding to 1 km in this way to finish gliding in 24 h from the take-off
• Ascending to a height of 8 km and then holding that ceiling. We start gliding to 1 km in this way to finish gliding in 24 h from the take-off

The TwinStratos 1:2 scenarios were divided for three parts (Figure 12):

• Ascending to a height of 10 km and then holding that ceiling. We start gliding to 1 km in this way to finish gliding in 24 h from the take-off.
• Ascending to a height of 15 km and then holding that ceiling. We start gliding to 1 km in this way to finish gliding in 24 h from the take-off.
• Ascending to a height of 20 km and then gliding to 1 km.

Figure 12. Flight scenarios for TS12.

Figure 12. Flight scenarios for TS12.

For the initial scenarios, we used a location of Gliwice. At the time of the first flights, we decided to set to the vernal equinox. If the UAV was unable to fly in this season, we would change the time to summer solstice to compare the results. As the temperature for the vernal equinox, we take a temperature of 15 °C, and for the summer solstice, 25 °C.

The data (partially included in Table 2) for the simulation model of the power consumption were developed by aviation designers. These parameters were entered into the model. In the simulation model, we used data where the flight path angle is 4.3° for TS17 and 7.7° for TS12. To provide enough lift force, the angle of attack is equal to 6° for TS17 and 3.5° for TS12.

As in the initial stage of flight (take-off), we can climb fast with a high flight path angle; in further climbing to the higher levels, this value will be lower due to the air density decrease and pressure decrease. It can cause lower energy consumption.

The lower the air density, the higher the speed required by the UAV to fly. We assumed that to simplify the simulation model, the power consumption data will be the same as in the simulation model of the propulsion system. Increasing the airspeed at a reduced flight path angle should, to some degree, increase the power consumption.

Table 3. Flight path angle included in the simulation.

Altitude [km]	TS17	Altitude [km]	TS12
From 0 to 2	3°	From 0 to 10	5°
From 2 to 5	2°	From 10 to 15	4°
From 5 to 6	1°	From 15 to 17	2°
From 6 to 8	0.5°	From 17 to 20	1°

contains the flight path angle used in the power supply system simulation model.

4. Results and Discussion

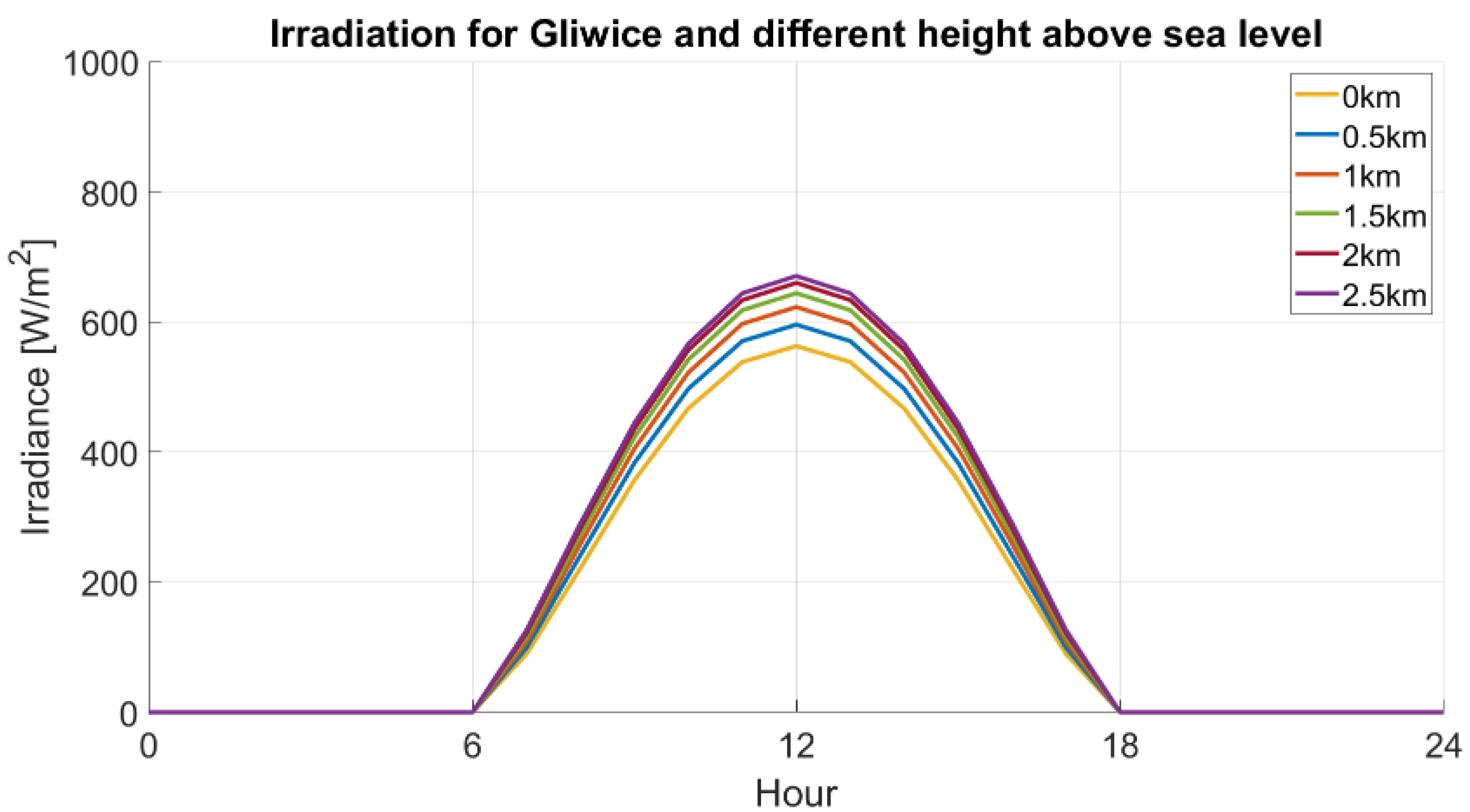
4.1. Irradiation Value in the Model

The irradiation, which is able to reach the solar cells, depends on time, location, and weather conditions. The formulas included in Section 2 allowed us to prepare a script that calculates the value of irradiation for the given parameters. We are planning to perform the first flights of TS12 and TS12 in Gliwice (Poland). As the initial assumption, we chose the vernal equinox as the time point for the mission. Depending on the season, we obtain different values of irradiation for Gliwice (Figure 13).

In the case of different places of flight at this same time, we obtain an irradiance parabola with a different peak value and time of solar insolation. To compare the location of Gliwice with different places—in both directions to the equator and to the pole—we chose four additional locations to see results. The geographical coordinates of all of the places are presented below:

• Ny-Ålesund—latitude: 78°55′0″ N; longitude: 11°56′0″ E;
• Gliwice—latitude: 50°17′32″ N; longitude: 18°40′3″ E;
• Rome—latitude: 41°53′0″ N; longitude: 12°29′0″ E;
• Mexico City—latitude: 19°26′0″ N; longitude: 99°8′0″ W;
• Nairobi—latitude: 1°16′0″ S; longitude: 36°48′0″ E;

For each location, we prepared an irradiation plot for the vernal equinox (Figure 14). On this day, across the globe, the day lasts 12 h. Figure 14 shows how important the location of a flight with a solar-powered UAV is.

In all of these places, we use a 0 level as height above sea level. The results will vary if the data take into account the altitude above sea level. To show how the altitude affects the irradiation, we prepared another analysis. Figure 15 shows the difference between 0 and 2.5 km altitude for Gliwice in the vernal equinox. For the 0–2.5 km range of height, the peak values were as follows:

• 0 km—563 W/m²
• 0.5 km—596 W/m²
• 1 km—623 W/m²
• 1.5 km—644 W/m²
• 2 km—660 W/m²
• 2.5 km—670 W/m²

Figure 15. Irradiation for Gliwice in vernal equinox for different altitude.

Figure 15. Irradiation for Gliwice in vernal equinox for different altitude.

The difference is the highest in the first 0.5 km and 1km. It is equal to 6 and 10.5%, respectively. In the last range, between 2 and 2.5 km, the difference is significantly smaller, and it is equal to 1.5%. The difference between the peak values from 0 and 2.5 km is equal to 19%.

In our simulation model, we used 0-level data as the input for the solar-powered power supply system. More precise data will be used in the model after the first flights.

4.2. Solar cells

The P-V and I-V characteristics of the solar cells allow us to obtain the exact parameters of the SunPower Maxeon Ne3. The obtained data are shown in

Table 4. Electrical specification of tested solar cells.

Data	Manufacturer Data (Non-Laminated)	Non-Laminated	Laminated (100 μm Film)
Voc [V]	>0.731	0.733	0.726
Isc [A]	>6.382	6.330	6.061
Vmp [V]	>0.625	0.627	0.624
Imp [A]	>6.050	5.92	5.747
Pmpp [Wp]	>3.77	3.71	3.589
Efficiency [%]	>24.34	24.29	23.33

. The I-V and P-V characteristics are presented in Figure 16.

We researched non-laminated and laminated solar cells. In the case of TS17 and TS12, we used laminated solar cells, which have lower efficiency than non-laminated ones. In the simulation model, we used parameters of this type of solar cell. Figure 17 shows the characteristics with a different irradiation level, Figure 18 shows the characteristics of a different temperature solar cell.

Table 5. MPPT data of tested solar cell.

Laminated SunPower Maxeon Ne3
Irradiation [W/m2]	Voltage [V]	Current [A]	Power [W]	Fill Factor [%]
1000	0.624	5.748	3.588	81
750	0.622	4.317	2.684	61
500	0.618	2.872	1.776	40
250	0.606	1.437	0.871	19.8

and

Table 6. MPPT data for tested solar cell in different temperatures.

Laminated SunPower Maxeon Ne3
Temperature	Voltage [V]	Current [A]	Power [W]	Fill Factor [%]
0	0.671	5.706	3.827	87
25	0.624	5.748	3.588	81
50	0.578	5.779	3.343	76
75	0.532	5.813	3.092	70.2

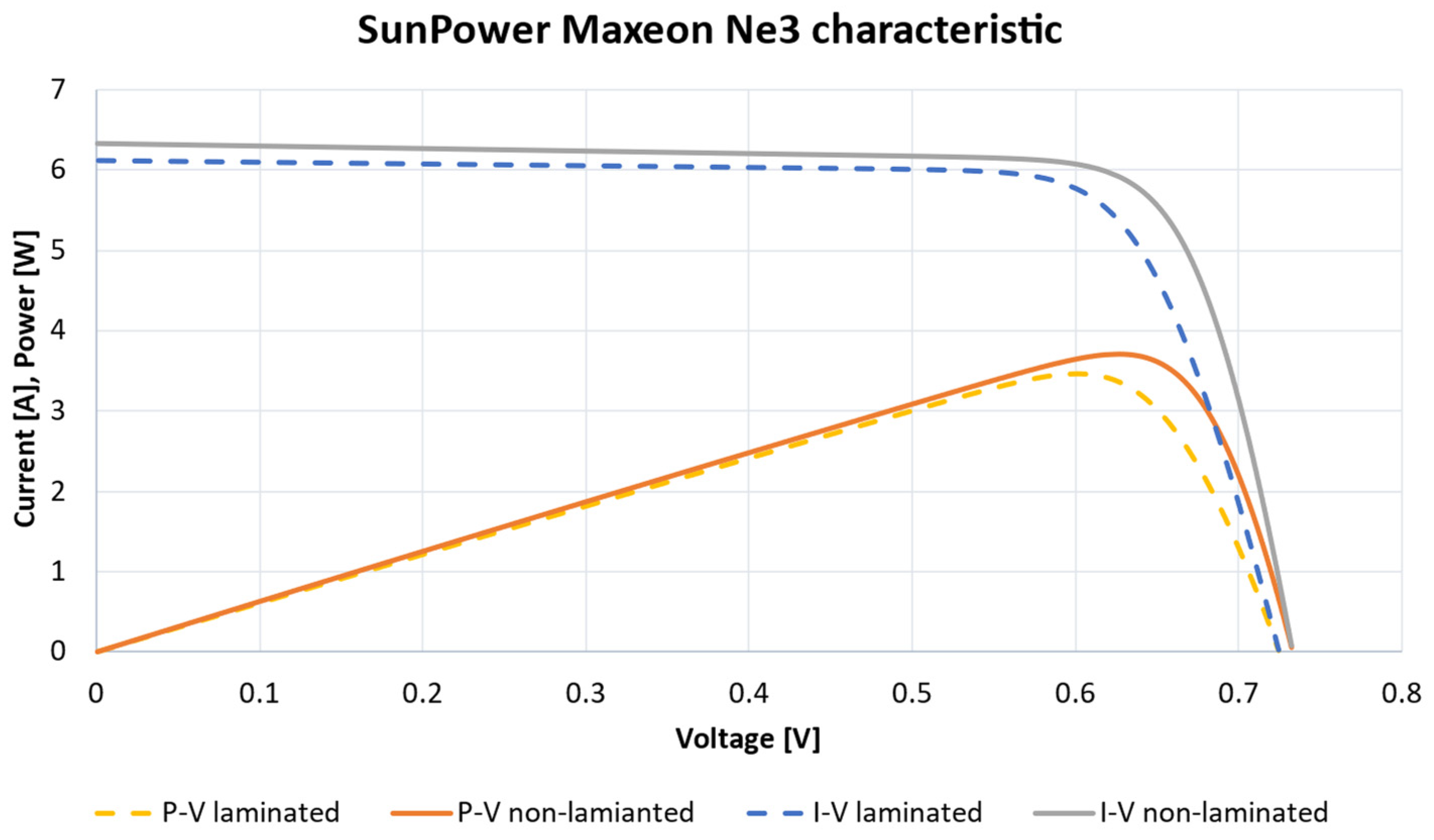
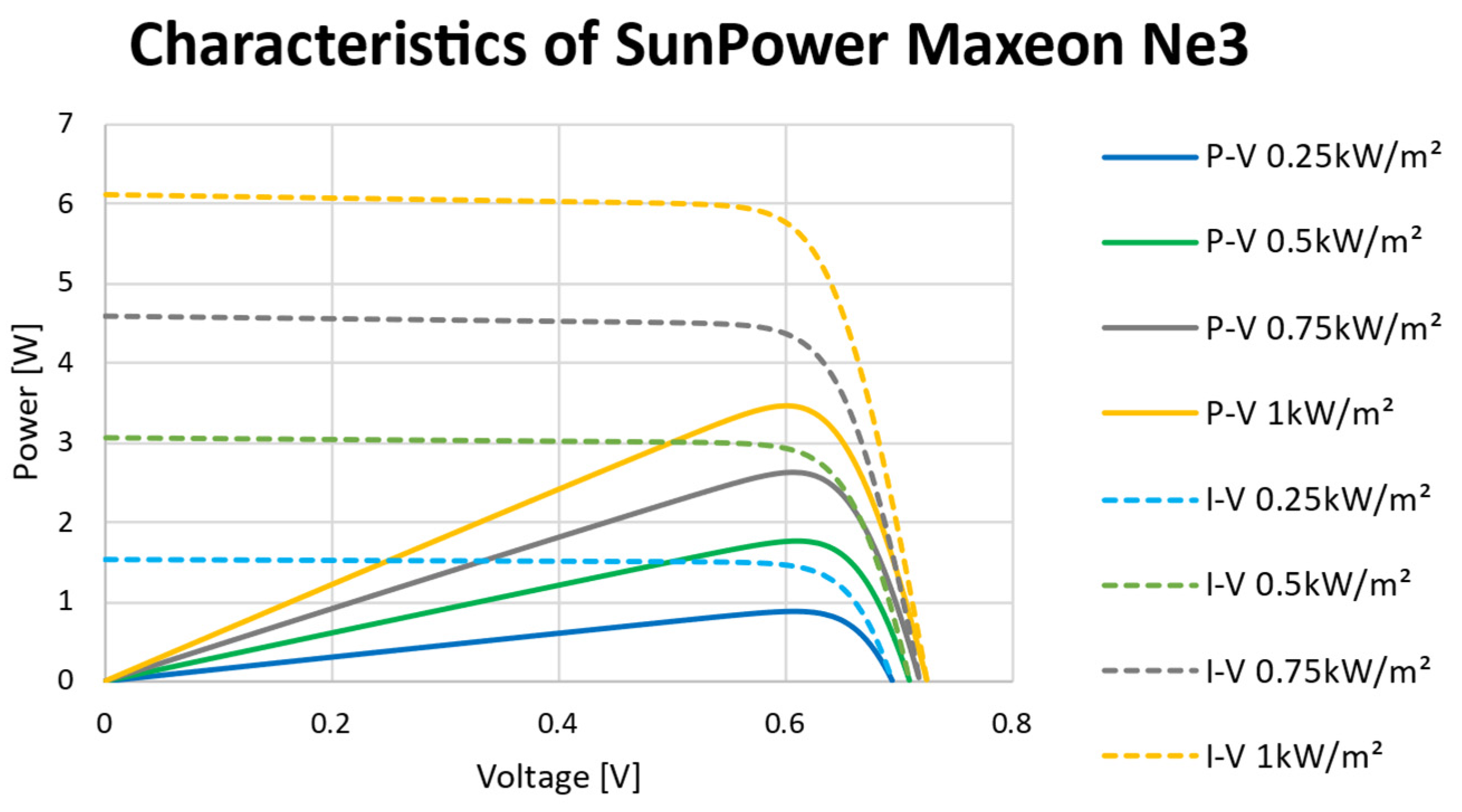
present the parameters of the laminated solar cells.

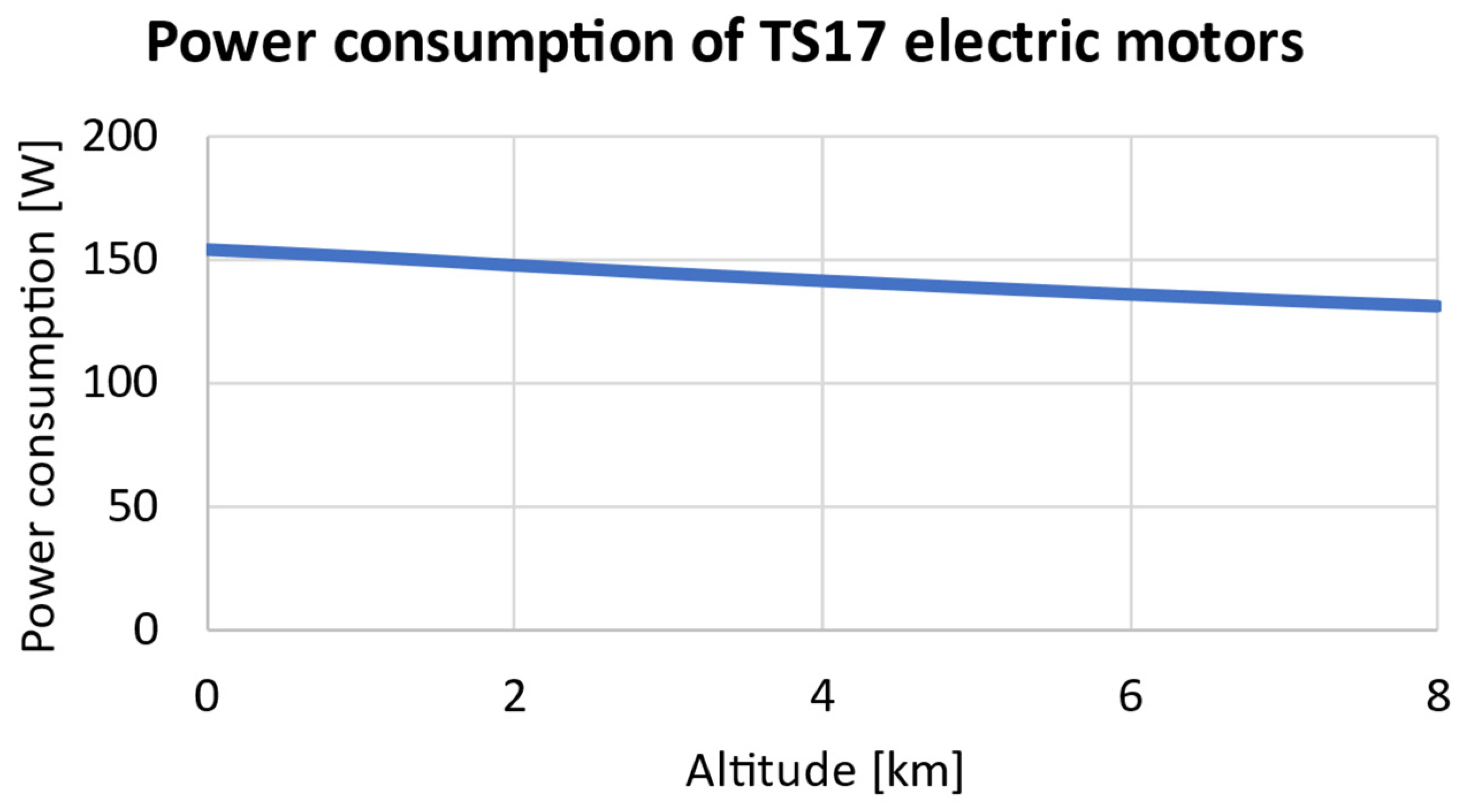
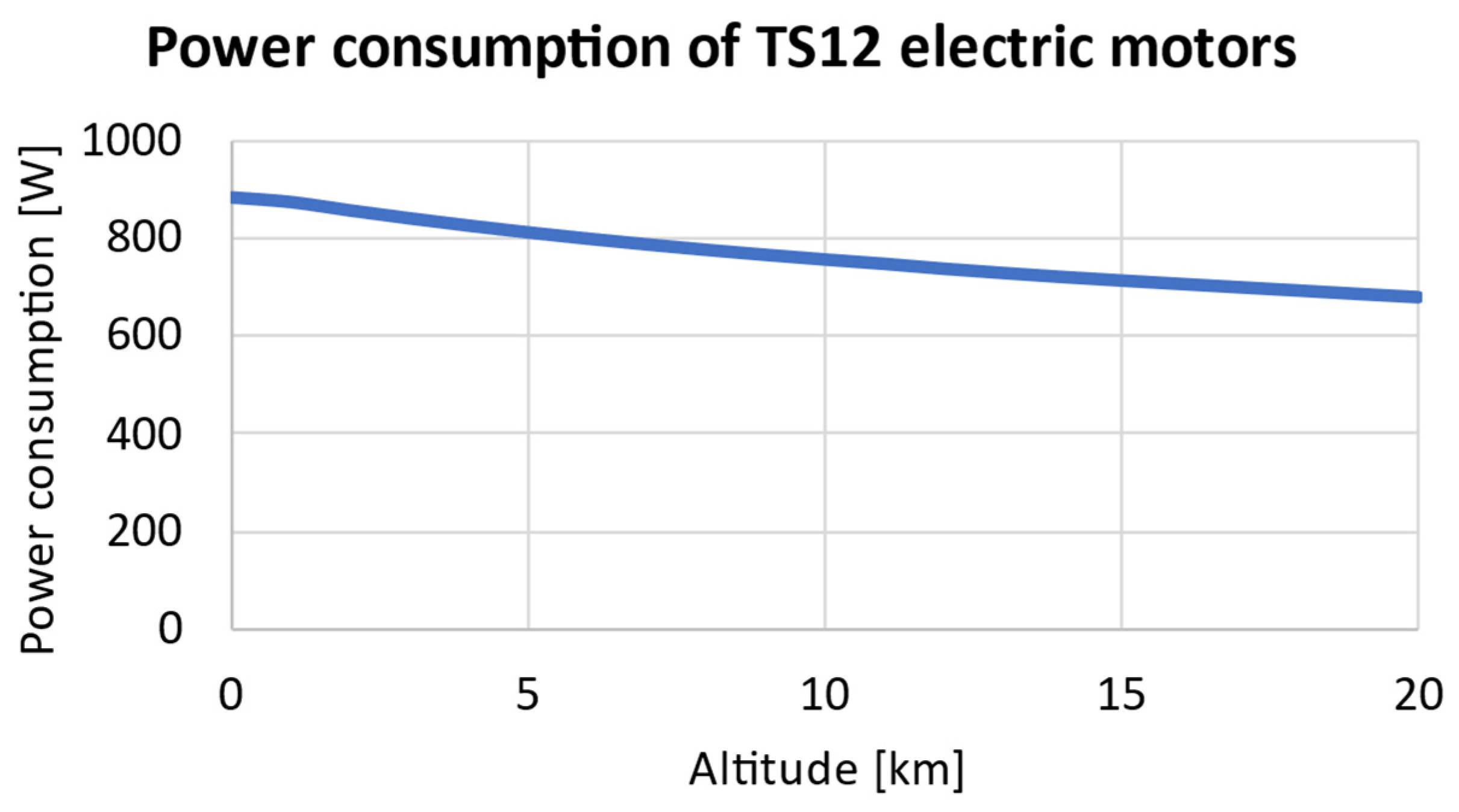
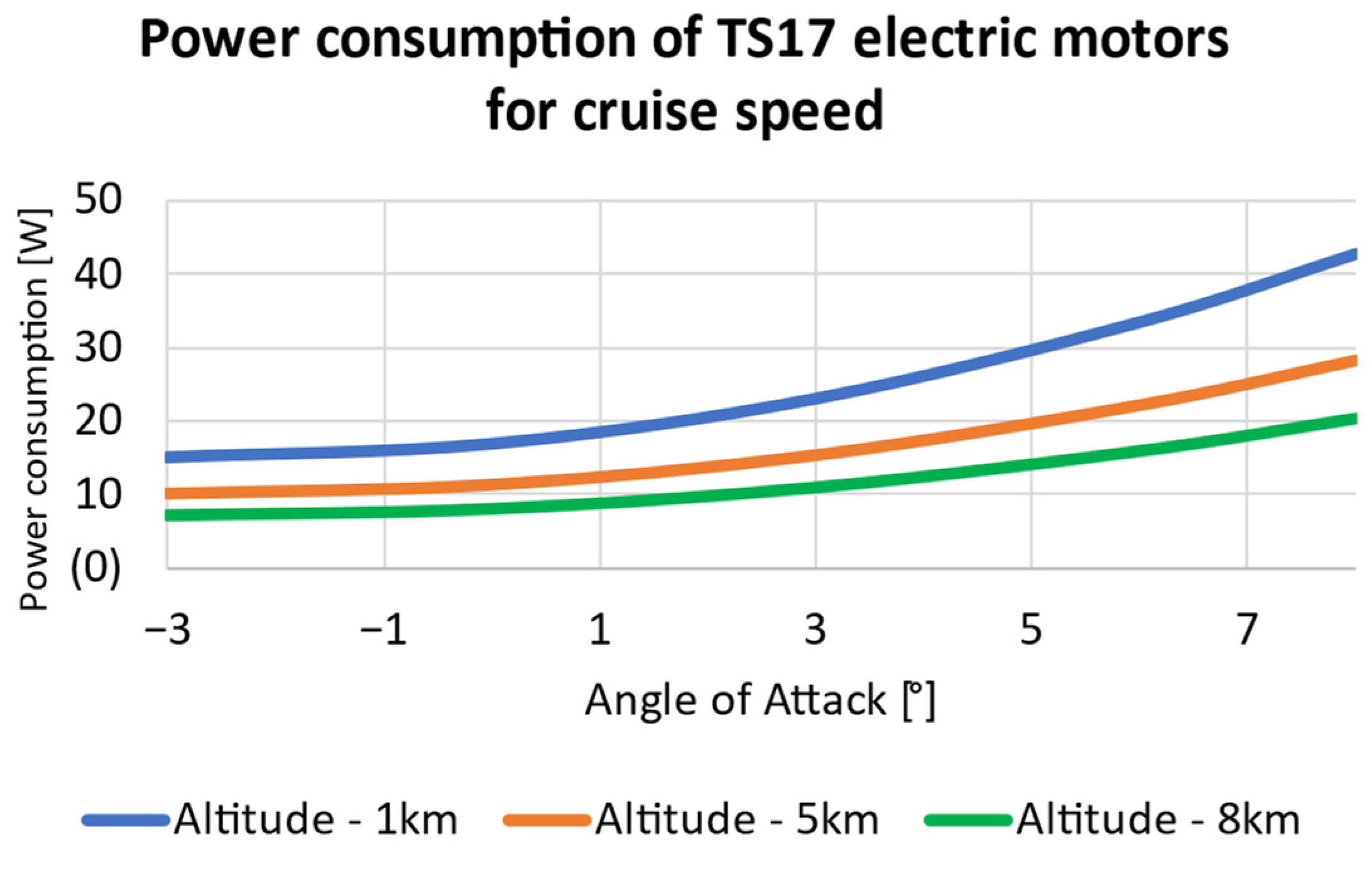
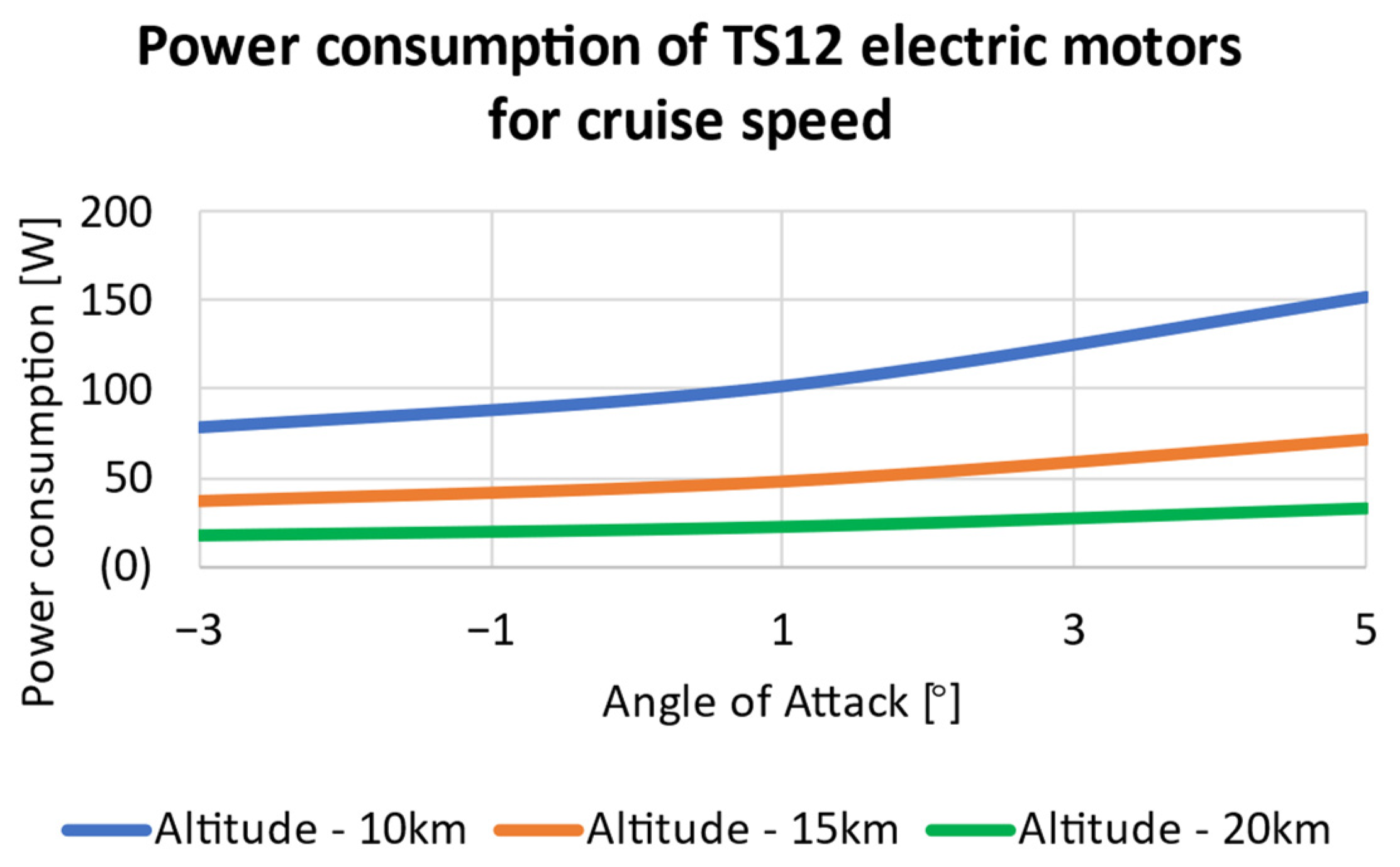
4.3. Power Consumption

The power consumption data for climbing are shown in Figure 19 for TS17 and in Figure 20 for TS12. The data obtained by the simulation model allows us to obtain the value of the power consumption of the electric motors. The low power of the electric motors is caused by a specific and very light UAV.

The cruise speed for TS17 was defined as 13 m/s and 13.9 m/s for TS12. Changes to the Angle of Attack (AoA) cause either greater or less aerodynamic drag. Figure 21 and Figure 22 show the differences in the power consumption caused by changing AoA. Depending on the altitude, the range of the cruise speed may be significantly wider; to simplify the calculations, we present the data on the power consumption for these cruise speeds.

In the simulation model of the power supply system, the value of the power consumption was additionally multiplied by the efficiency of the electric motors. The climbing efficiency of the electric motors was 90% both for TS17 and TS12; the cruise efficiency was 50%.

4.4. Battery Cell

To obtain the precise parameters of the power supply system, the model was adjusted to the parameters obtained on real systems. On the test stand, we received the data and tuned the simulation model. For each range of the discharge current, the model is adjusted separately due to significant changes in the discharge characteristics of the battery cells. The research was conducted for six discharge currents in the range 0.2–5 A (Figure 23).

To simplify the simulation model, we did not use a temperature effect and an ageing effect. By using the heater in the battery pack, we want to provide the optimal condition of work for the batteries. The ageing effect was omitted. When building the prototype, the decrease in the capacity after a few hundred charging cycles is redundant.

The developed calculations of the power consumption show that the power supply system will be discharged with low currents. For both of the UAVs, these values are similar and they are presented in

Table 7. Discharging currents during the flight.

Stage of Flight	TS17	TS12
Cruise flight	0.28 A	0.25 A
Climbing	~1.1 A	~1.1 A
Descend—without work of electric motors (avionics)	0.11 A	0.06 A

.

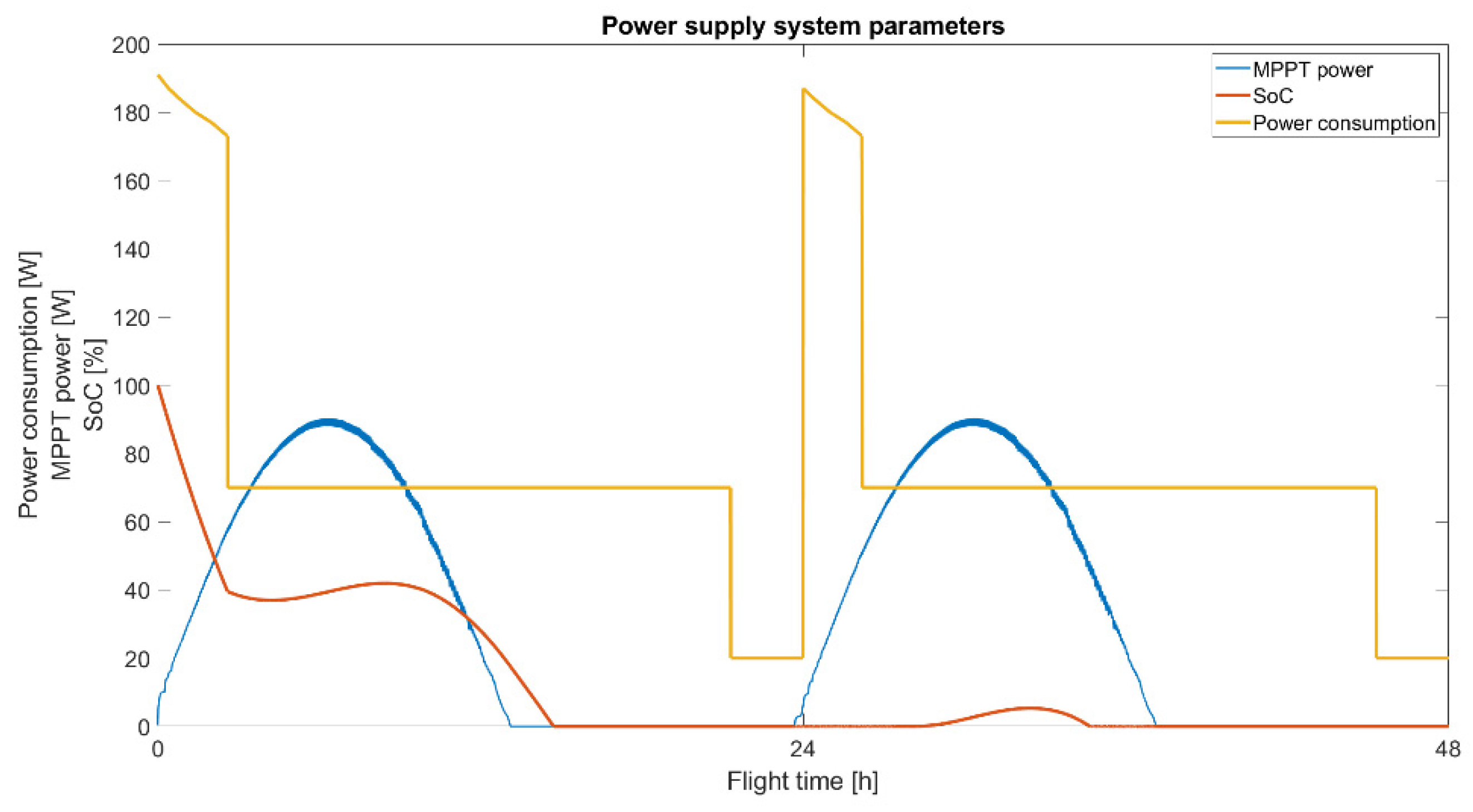
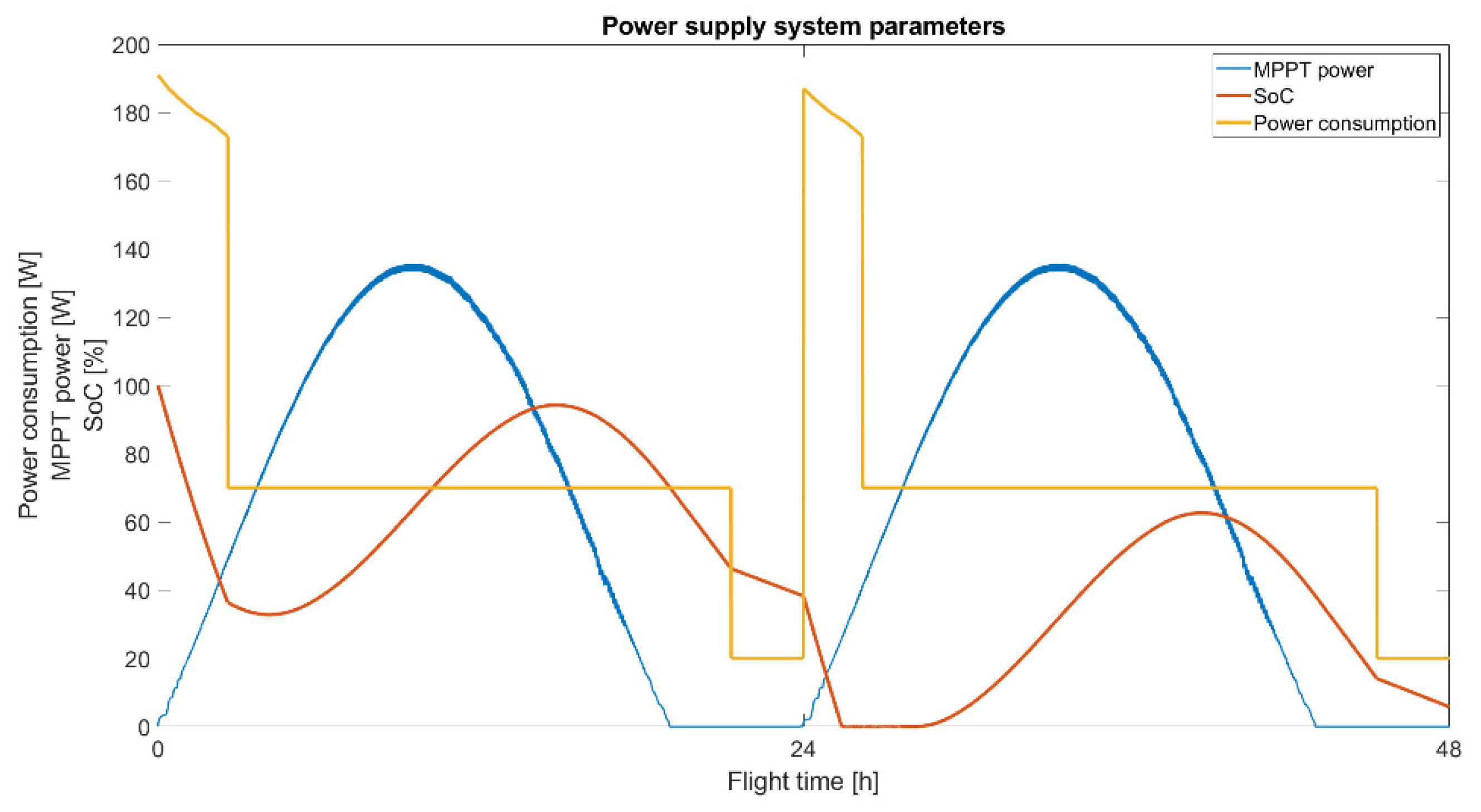
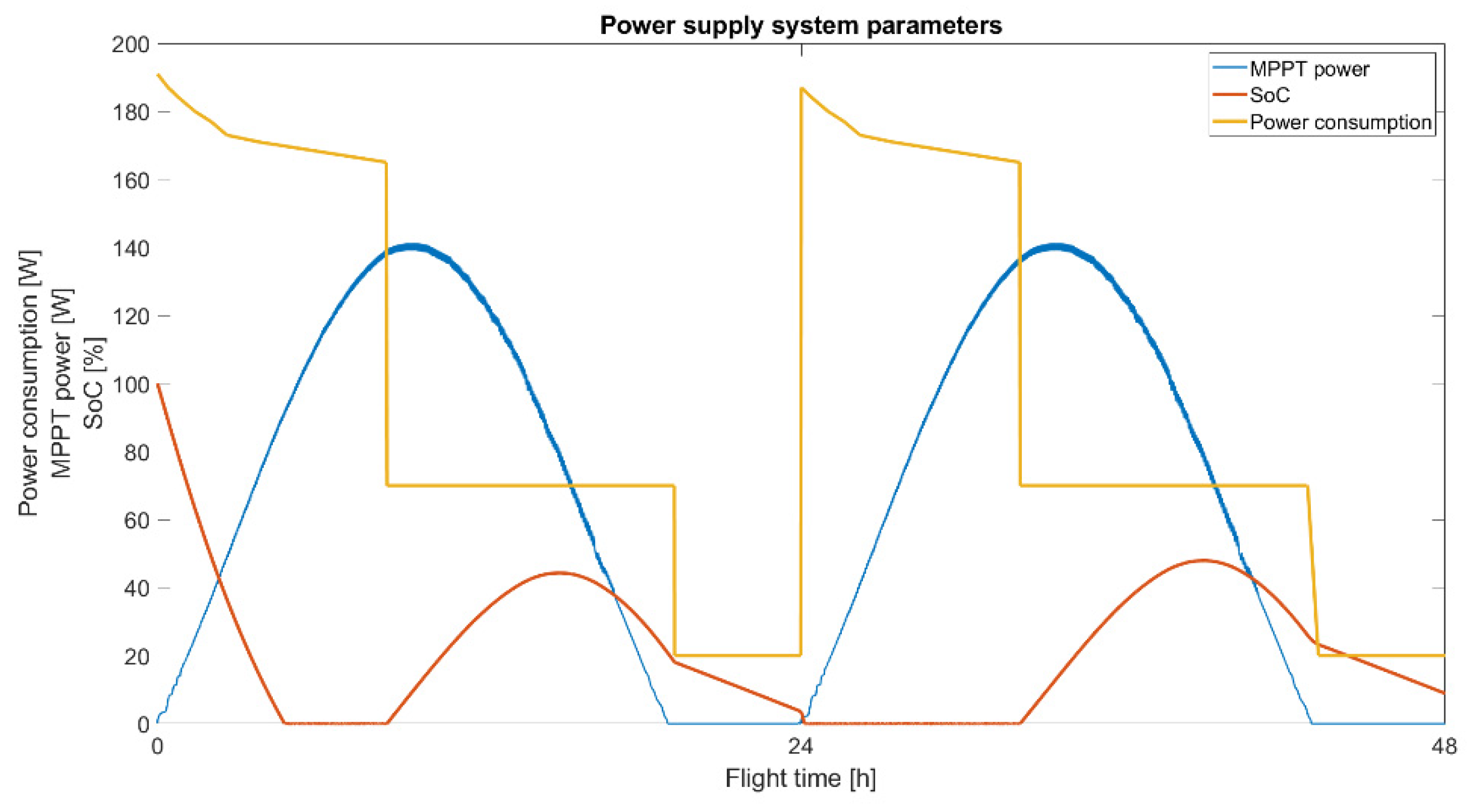
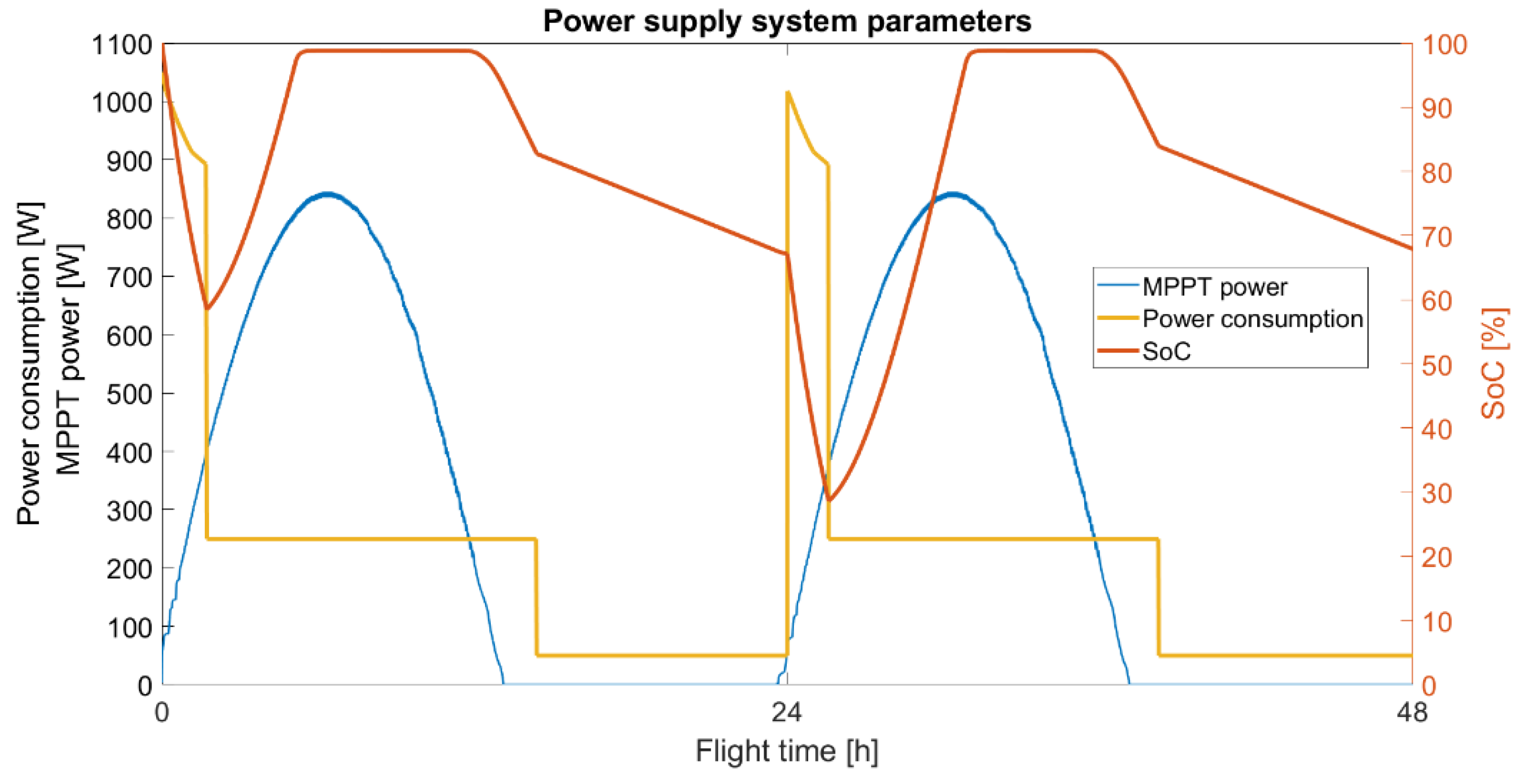
4.5. Power Supply System Simulation Model

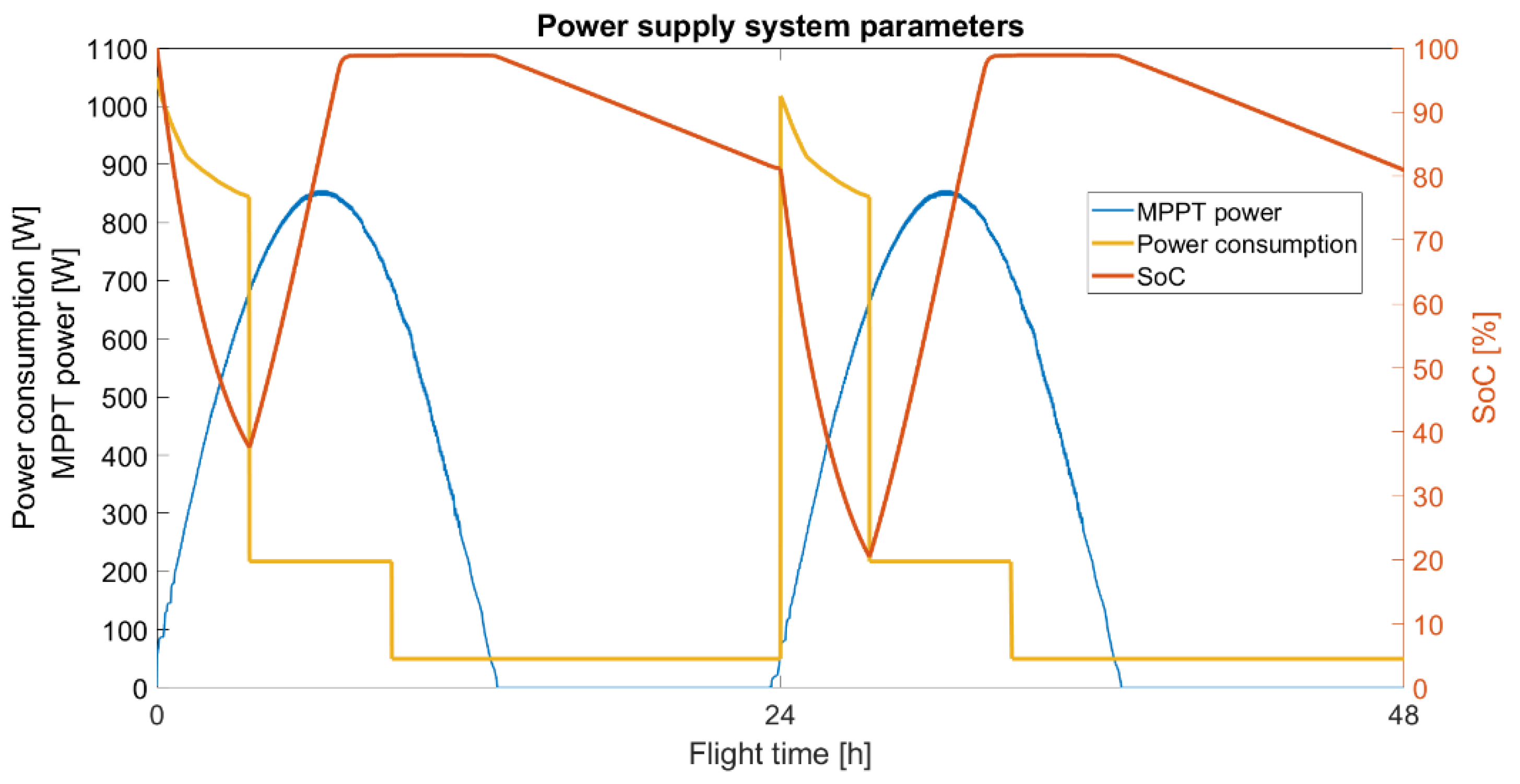
4.5.1. Twin Stratos 17

We have a three main points for changing the power consumption. At these points, there is a fundamental change in the flight state. The UAV goes from climbing to cruise flight and then to gliding.

The power consumption for the 5 km and 8 km scenarios reflects the scenario shown in Figure 11. During the climb, the power supply system drew the most energy with a gradual decrease in the power consumption (reflection of Figure 19). Flight at a certain altitude (5 km or 8 km) allows for a reduction in energy consumption. Both the climb and cruise values take into account the efficiency of the electric motors. Starting gliding saves energy, then only the control measuring devices consume energy.

MPPT power is the power that is provided to the power supply system from the PV panels. We can see a significant difference between the energy delivered at the vernal equinox and the summer solstice. The power obtained by the PV panels during the summer solstice is 92% higher than in the vernal equinox for Gliwice.

In the vernal equinox, TS17 is not able to ensure full energy autonomy (Figure 24). The battery was drained after 14 h and 30 min from take-off. The battery is discharged at a height of 5 km. This gives the UAV time for gliding, but it is a dangerous situation because the UAV is not able to rotate and change the direction of descent. To ensure the continuity of the mission, the battery cannot become entirely unloaded.

During the summer solstice, TS17 was able to fly for over 24 h at the maximum altitude of 5 km (Figure 25). The lowest SOC was equal to 11.5% and it occurred in the morning of the second day, at an altitude of 5 km. At this height, the UAV starts charging the battery because the energy from the PV is higher than the power consumption during cruising.

In the case of the flight to the highest altitude equal to 8 km, TS17 was not able to achieve this height (Figure 26). This was a result of the PV providing less energy and less energy storage and this caused the battery to be drained after 6 h and 30 min from take-off.

In Figure 24 and Figure 26, we can see recharging the battery on the second day. This shows that the simulation model of the power supply system works correctly, but the position of the UAV in space is not noticeable through this system. The system only recognizes the energy demand and the energy balance.

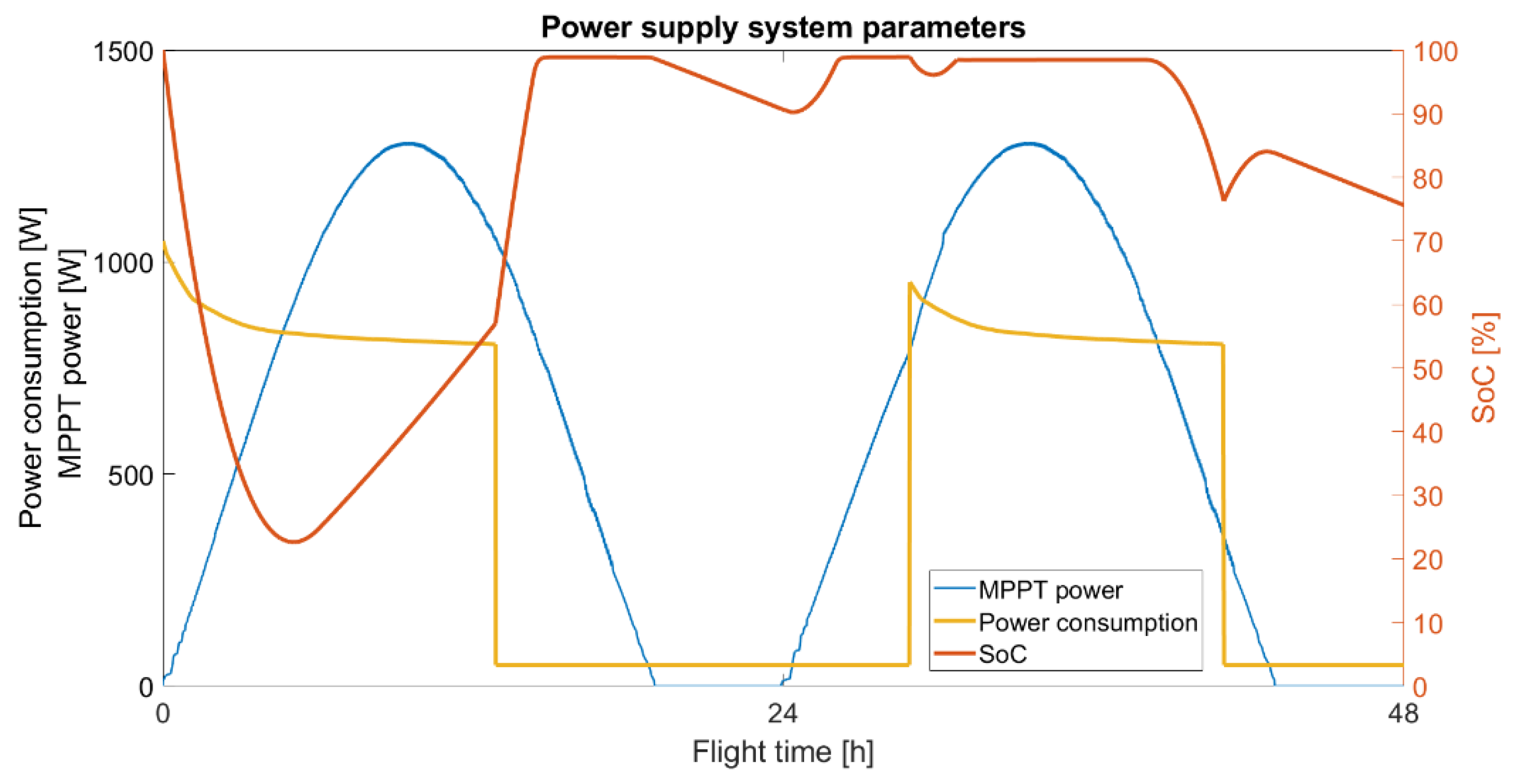
4.5.2. Twin Stratos 12

For TS12, the energy consumption was analogous to Figure 12. The climb values were taken from Figure 20. All of the values include the efficiency of the electric motors. During the vernal equinox, we can observe that the power from the PV is higher than the power consumption in the 10 km (Figure 27) and 15 km (Figure 28) scenarios, when the TwinStratos begin cruising. Higher flight altitude and longer gliding time allows for longer energy saving than in the case of the TS17. The power consumption spikes again after the glide phase ends and the climb phase resumes. We can observe it returning to the set altitude. Then, the SoC of the battery reaches its lowest value. The value of the SoC was correspondingly equal to 29% for the 10 km scenario and 20.5% for the 15 km scenario. In the TS12 scenarios, during flights up to altitudes of 10 km and 15 km, the UAV obtained its energy autonomy in the vernal equinox.

For the flight up to 20 km, the energy accumulated in the batteries and produced by the PV were not able to provide a surplus energy balance in the vernal equinox. The energy needed to achieve an altitude of 20 km was too high at the stage of climbing; 11 h after take-off, the battery was drained (Figure 29). The last two kilometers were achieved with a low degree of climb, equal to 1°. To achieve an altitude equal to 20 km, we had to change the time of the flight.

During the summer solstice, TS12 was able to fly for over 24 h (Figure 30). The lowest SoC was at the beginning of the flight, up to the moment when the power from the PV was higher than the current power consumption, which occurred about 4 h and 30 min after take-off. The lowest value of SoC was equal to 22.5%. On the second day, the battery began to lower the SoC when the power from the PV was lower than the power consumption.

As it was written in the previous case (for TS17), the power obtained by the PV panels during the summer solstice is 92% higher than in the vernal equinox for Gliwice. For our location, almost twice as much energy from the PV allows for a flight to an altitude of 20 km. Changing the flight time to the summer solstice allowed us to obtain a positive energy balance for the 20 km scenario.

5. Conclusions

By analyzing the simulation graphs, it can be concluded that the most important issue when planning a long-endurance flight is the flight path and the appropriate weather conditions. The simulations show that a 24 h flight is feasible for the location of Gliwice during the spring equinox for TS12 and during the summer solstice for TS17. For both scenarios, sunny weather was adopted without cloud cover, which additionally allowed the UAVs to obtain more energy from the PV.

As the altitude increases, the energy obtained from the solar cells increases. However, due to the impossibility of obtaining the data from the real environment, the increase in this value was omitted and the data from 0 m above sea level were adopted.

The falling speed of TS12 and TS17 depends on the altitude, but for the calculations, this value has been simplified to one constant value for TS12 — 0.26 m/s — and0.41 m/s for TS17.

By analyzing the numerical simulations and the prepared flight scenarios, it can be concluded that the best ways to achieve a long endurance flight (at least 24 h) are the following elements:

• The flight begins at sunrise. Take-off and climb are the stages that consume the most energy, so it is good to compensate for high energy consumption with energy produced from the photovoltaic system;
• The potential energy accumulated in the form of height should be used as a time buffer, which is best used at night, when the photovoltaic system does not produce energy and the drive system does not consume energy from the power supply system;
• Continuous, gradual increase in altitude during the day and keeping the altitude as high as possible until sunset or even more depending on the type of mission;
• Commencement of the UAV gliding stage with sunset or supporting a specific altitude in such a way as to complete the stage of gliding to a given altitude with sunrise or later depending on the type of mission;
• Flight sustain should be performed at the highest altitudes due to the lower energy demand of UAV propulsion systems;
• When it is not possible to obtain a long endurance flight for the UAV, it may be necessary to change the flight duration, location, time of flight, or flight path;
• If it is not possible to obtain flight-long endurance for the key set parameters, it may be necessary to change the design of the UAV, the number of solar cells, the capacity of the battery, or the weight of the payload.

It can be concluded that the TS17 scale is a bit too small for full energy autonomy. TS12 shows a greater degree of energy autonomy by achieving higher ceilings and a lower value of the ROD (Rate of Descent) than in the case of TS17. The TS12 has almost ten times more wing area than the TS17, as a result of which it is able to obtain ten times more energy during the flight than the TS17. An additional advantage in the energy balance of the TS12 is that the maximum power consumption is seven times higher than in the case of TS17. Comparing the energy that can be produced by the TwinStratos 1:2 and 1:7 and their energy demand, it can be seen that a better energy balance is achieved by TS12.

Another milestone that our team has taken into account is the highest possible altitude to be achieved. When analyzing the flight duration, we noticed that sometimes the maximum altitude of TS is not possible to reach, particularly when starting the flight at sunrise (e.g., Figure 26 and Figure 29), or during the not appropriate period. In the event that the energy demand during take-off and climb is the highest, and the PV energy is insufficient at some point, the battery discharges, preventing the UAV from continue to climb.

By analyzing the energy demand and PV power, it can be concluded that the best time to complete the mission aimed at achieving the highest ceiling is not sunrise, but around noon, when the sun is at its highest. In this case, the energy obtained from the PV will partially cover the energy demand of the electric motors and the UAV’s control systems. The limitations are also related to the time needed to reach a given altitude. These considerations should be taken into account when we are choosing the time of the UAV’s take-off.

The full set of equipment depends on the mission being performed, which is not fully defined at this stage of the work; therefore, simplifications have been made in the model after defining the mission and the various sets of measuring/observation devices. Another reason for simplifying the model is the lack of detailed data for many on-board subsystems with energy consumption characteristics. For many, only the maximum power of the device is given and the load characteristics are not analyzed. In laboratory tests, it is also difficult to confirm the characteristics of many subsystems. The team is planning intensive work on the problem indicated by the reviewer during the flight tests. Therefore, the entire power supply system has been measured in detail and is equipped with controllers and accessories that allow for connecting and disconnecting individual power supply systems.

TS17 and TS12 will be made with the technology of ultra-light composite structures. Currently, TS17 is at the construction stage and the prototype is shown in Figure 5. Only flights in the real environment will allow the correctness of the simulation and its results to be verified. The completed missions will provide the necessary data to fine-tune the simulation model. Another stage will be the intended use of the UAV, taking into consideration its equipment and the weight of its on-board devices. In the event that, in a given mission, it is not possible to perform a long-endurance flight, the mission can be postponed until the summer solstice or the 24 h flight stage can be avoided, with an emphasis on the implementation of a specific mission.