Slicing Algorithm and Partition Scanning Strategy for 3D Printing Based on GPU Parallel Computing
Abstract
:1. Introduction
2. Slicing Algorithm Based on Reverse Ray Tracing
2.1. Reverse Ray Tracing Algorithm
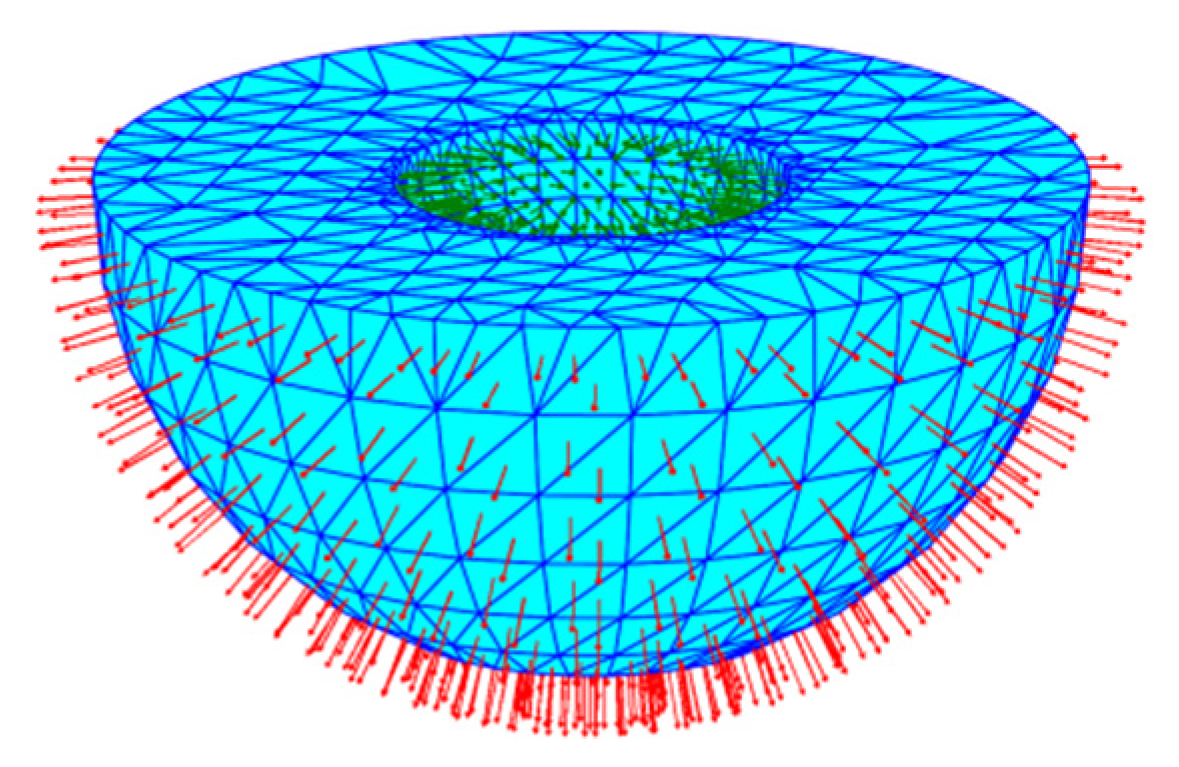
2.2. Fast Extraction of the Slice Contour
- (1)
- Load the STL file, obtain the bounding box information (length, width, and height) of the 3D model, initialize the field of view according to the length and width of the model, and enable the write function of the template cache;
- (2)
- Specify the slice height, and fill the template buffer with unsigned integer data 0, which means that the entire field of view does not need to be drawn;
- (3)
- Select the ray emitted from the viewpoint to intersect with all grids in the field of view. When the ray intersects with the forward grid, the value of the template buffer increases by 1, indicating that the pixel needs to be drawn; when the ray intersects with the reverse grid, the value of the stencil buffer decreases by 1, indicating that the pixel does not need to be drawn;
- (4)
- After the traversal is completed, the fragments with the value 1 or 2 in the buffer are rendered, and the fragments with the value 0 are discarded.
3. Contour Extraction and NURBS Fitting Optimization
3.1. Marching Square Contour Extraction Algorithm
3.2. Slice Data Fitting Based on the NURBS Basis Function
4. Contour Partition and Scan Filling Strategy
4.1. The Smallest Enclosing Rectangle of Contour Data
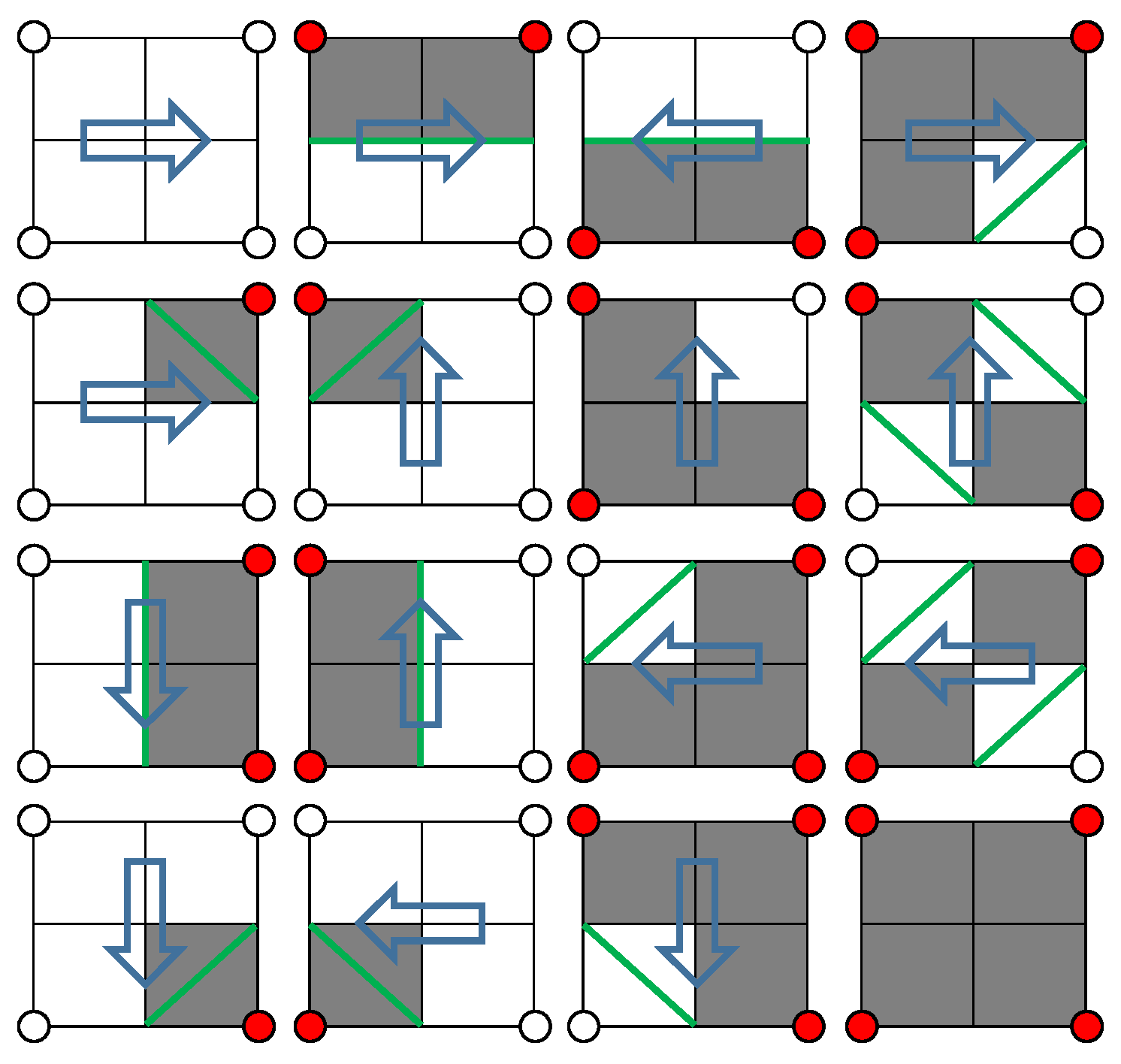
4.2. Partition Filling and Scanning Strategy
5. Discussion
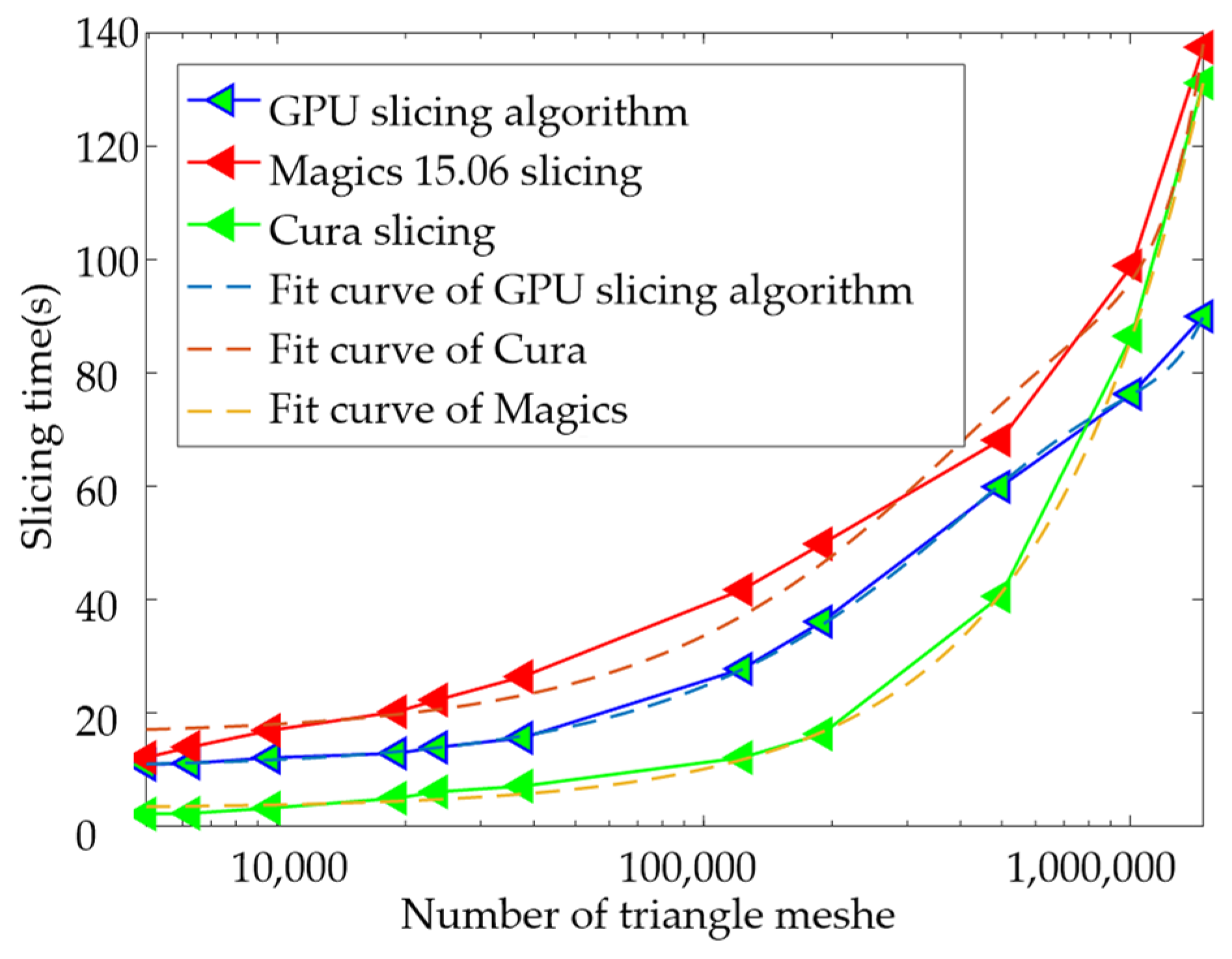
5.1. Slicing Efficiency
5.2. Analysis of Curve Fitting Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Panin, A.V.; Kazachenok, M.S.; Sinyakova, E.A.; Builuk, A.O.; Martynov, S.A.; Panin, S.V.; Berto, F. Improving mechanical properties of wire-based EBAM Til parts by adding TiC powders. Mater. Des. Process. Commun. 2021, 3, e136. [Google Scholar]
- Astafurova, E.G.; Panchenko, M.Y.; Moskvina, V.A.; Maier, G.G.; Astafurov, S.V.; Melnikov, E.V.; Fortuna, A.S.; Reunova, K.A.; Rubtsov, V.E.; Kolubaev, E.A. Microstructure and grain growth inhomogeneity in austenitic steel produced by wire-feed electron beam melting: The effect of post-building solid-solution treatment. J. Mater. Sci. 2020, 55, 1–14. [Google Scholar] [CrossRef]
- Raaj, R.K.; Anirudh, P.V.; Karunakaran, C.; Kannan, C.; Jahagirdar, A.; Joshi, S.; Balan, A.S. Exploring grinding and burnishing as surface post-treatment options for electron beam additive manufactured Alloy 718. Surf. Coat. Technol. 2020, 397, 126063. [Google Scholar] [CrossRef]
- Wang, P.; Nai, M.L.; Sin, W.J.; Lu, S.; Zhang, B.; Bai, J.; Song, J.; Wei, J. Realizing a full volume component by in-situ welding during electron beam melting process. Addit. Manuf. 2018, 22, 375–380. [Google Scholar] [CrossRef]
- Günther, J.; Brenne, F.; Droste, M.; Wendler, M.; Volkova, O.; Biermann, H.; Niendorf, T. Design of novel materials for additive manufacturing—Isotropic microstructure and high defect tolerance. Sci. Rep. 2018, 8, 1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Basile, G.; Baudana, G.; Marchese, G.; Lorusso, M.; Lombardi, M.; Ugues, D.; Fino, P.; Biamino, S. Characterization of an Additive Manufactured TiAl Alloy—Steel Joint Produced by Electron Beam Welding. Materials 2018, 11, 149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terrazas, C.A.; Murr, L.E.; Bermudez, D.; Arrieta, E.; Roberson, D.A.; Wicker, R.B. Microstructure and mechanical properties of Ti-6Al-4V-5% hydroxyapatite composite fabricated using electron beam powder bed fusion. J. Mater. Sci. Technol. 2019, 35, 309–321. [Google Scholar] [CrossRef]
- Zhang, W.; Tong, M.; Harrison, N.M. Scanning strategies effect on temperature, residual stress and deformation by multi-laser beam powder bed fusion manufacturing. Addit. Manuf. 2020, 36, 101507. [Google Scholar] [CrossRef]
- Bian, P.; Shi, J.; Liu, Y.; Xie, Y. Influence of laser power and scanning strategy on residual stress distribution in additively manufactured 316L steel. Opt. Laser Technol. 2020, 132, 106477. [Google Scholar] [CrossRef]
- Demir, K.; Zhang, Z.; Ben-Artzy, A.; Hosemann, P.; Gu, G.X. Laser scan strategy descriptor for defect prognosis in metal additive manufacturing using neural networks. J. Manuf. Process. 2021, 67, 628–634. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Zhu, H. Effect of scanning strategy on geometric accuracy of the circle structure fabricated by selective laser melting. J. Manuf. Process. 2021, 64, 907–915. [Google Scholar] [CrossRef]
- Vasilev, M.; MacLeod, C.; Javadi, Y.; Pierce, G.; Gachagan, A. Feed forward control of welding process parameters through on-line ultrasonic thickness measurement. J. Manuf. Process. 2021, 64, 576–584. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, D.; Dai, D.; Ma, C.; Li, Y.; Peng, R.; Li, S.; Liu, G.; Yang, B. Influence of scanning strategy and parameter on microstructural feature, residual stress and performance of Sc and Zr modified Al–Mg alloy produced by selective laser melting. Mater. Sci. Eng. A 2020, 788, 139593. [Google Scholar] [CrossRef]
- Riaz, M.Q.; Caputo, M.; Ferraro, M.M.; Ryu, J.J. Influence of Process-Induced Anisotropy and Synovial Environment on Wear of EBM Built Ti6Al4V Joint Implants. J. Mater. Eng. Perform. 2018, 27, 3460–3471. [Google Scholar] [CrossRef]
- Jaiswal, P.; Rai, R. A geometric reasoning approach for additive manufacturing print quality assessment and automated model correction. Comput. Aided Des. 2018, 109, 3460–3471. [Google Scholar] [CrossRef]
- Pandey, P.M.; Reddy, N.V.; Dhande, S.G. Real time adaptive slicing for fused deposition modelling. Int. J. Mach. Tools Manuf 2003, 43, 61–71. [Google Scholar] [CrossRef]
- Song, Y.; Yang, Z.; Liu, Y.; Deng, J. Function representation based slicer for 3D printing. Comput. Aided Geom. Des. 2018, 62, 276–293. [Google Scholar] [CrossRef]
- Manmadhachary, A.; Ravi, K.Y.; Krishnanand, L. Improve the accuracy, surface smoothing and material adaption in STL file for RP medical models. J. Manuf. Process. 2016, 21, 46–55. [Google Scholar]
- Song, J.; Wu, W.; Zhang, L.; He, B.; Lu, L.; Ni, X.; Long, Q.; Zhu, G. Role of scanning strategy on residual stress distribution in Ti-6Al-4V alloy prepared by selective laser melting. Optik 2018, 170, 342–352. [Google Scholar] [CrossRef]
- Ghouse, S.; Babu, S.; Van Arkel, R.J.; Nai, K.; Hooper, P.A.; Jeffers, J.R. The influence of laser parameters and scanning strategies on the mechanical properties of a stochastic porous material. Mater. Des. 2017, 131, 498–508. [Google Scholar] [CrossRef]
- Tsai, C.Y.; Cheng, C.W.; Lee, A.C.; Tsai, M.C. Synchronized multi-spot scanning strategies for the laser powder bed fusion process. Addit. Manuf. 2019, 27, 1–7. [Google Scholar] [CrossRef]
- Piegl, L.A.; Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Strantza, M.; Ganeriwala, R.K.; Clausen, B.; Phan, T.Q.; Levine, L.E.; Pagan, D.C.; Ruff, J.P.; King, W.E.; Johnson, N.S.; Martinez, R.M.; et al. Effect of the scanning strategy on the formation of residual stresses in additively manufactured Ti-6Al-4V. Addit. Manuf. 2021, 45, 102003. [Google Scholar]
- Lee, Y.S.; Kirka, M.M.; Dinwiddie, R.B.; Raghavan, N.; Turner, J.; Dehoff, R.R.; Babu, S.S. Role of scan strategies on thermal gradient and solidification rate in electron beam powder bed fusion. Addit. Manuf. 2018, 22, 516–527. [Google Scholar] [CrossRef]
- PaPatil, N.; Ganeriwala, R.; Solberg, J.M.; Hodge, N.E.; Ferencz, R.M. Benchmark multi-layer simulations for residual stresses and deformation in small additively manufactured metal parts. Addit. Manuf 2021, 45, 102015. [Google Scholar]
- Vatti, B.R. A Generic Solution to Polygon Clipping. Commun. ACM 1992, 35, 56–63. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, X.; Wei, Z. Slicing Algorithm and Partition Scanning Strategy for 3D Printing Based on GPU Parallel Computing. Materials 2021, 14, 4297. https://doi.org/10.3390/ma14154297
Lai X, Wei Z. Slicing Algorithm and Partition Scanning Strategy for 3D Printing Based on GPU Parallel Computing. Materials. 2021; 14(15):4297. https://doi.org/10.3390/ma14154297
Chicago/Turabian StyleLai, Xuhui, and Zhengying Wei. 2021. "Slicing Algorithm and Partition Scanning Strategy for 3D Printing Based on GPU Parallel Computing" Materials 14, no. 15: 4297. https://doi.org/10.3390/ma14154297
APA StyleLai, X., & Wei, Z. (2021). Slicing Algorithm and Partition Scanning Strategy for 3D Printing Based on GPU Parallel Computing. Materials, 14(15), 4297. https://doi.org/10.3390/ma14154297





