Short-Time Fatigue Life Estimation for Heat Treated Low Carbon Steels by Applying Electrical Resistance and Magnetic Barkhausen Noise
Abstract
:1. Introduction
2. Materials and Methods
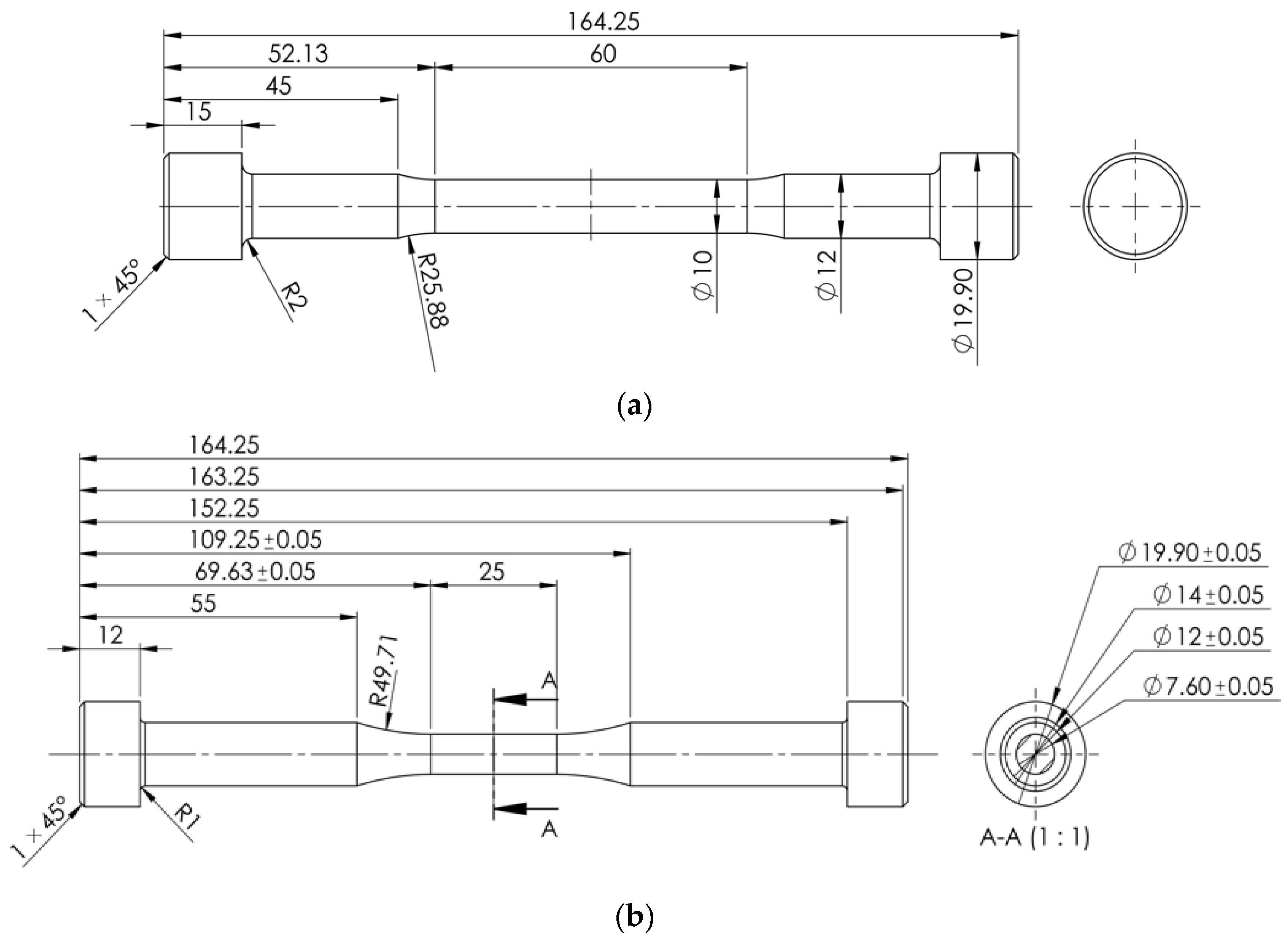
2.1. Material and Machining of Specimens
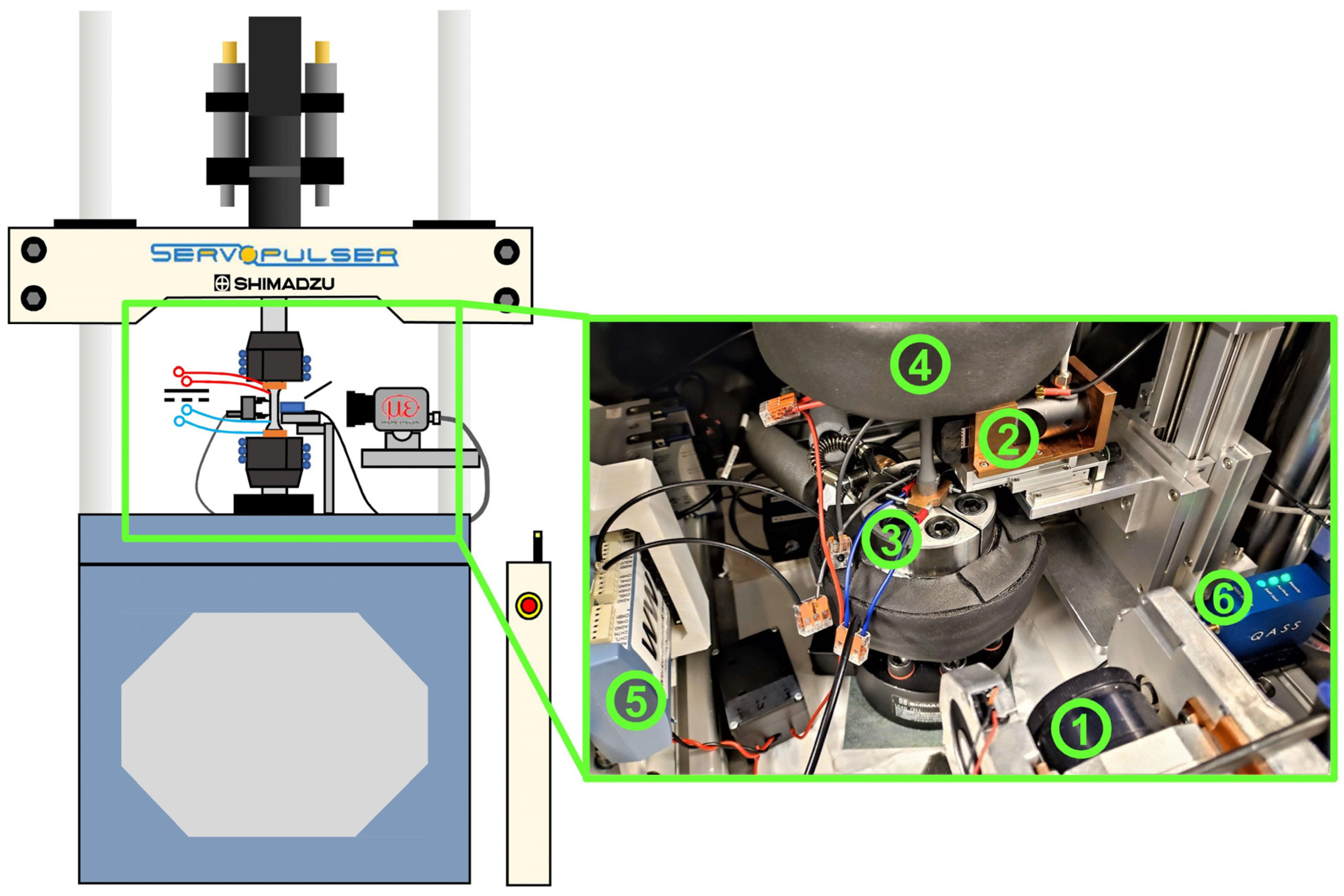
2.2. Test Setup
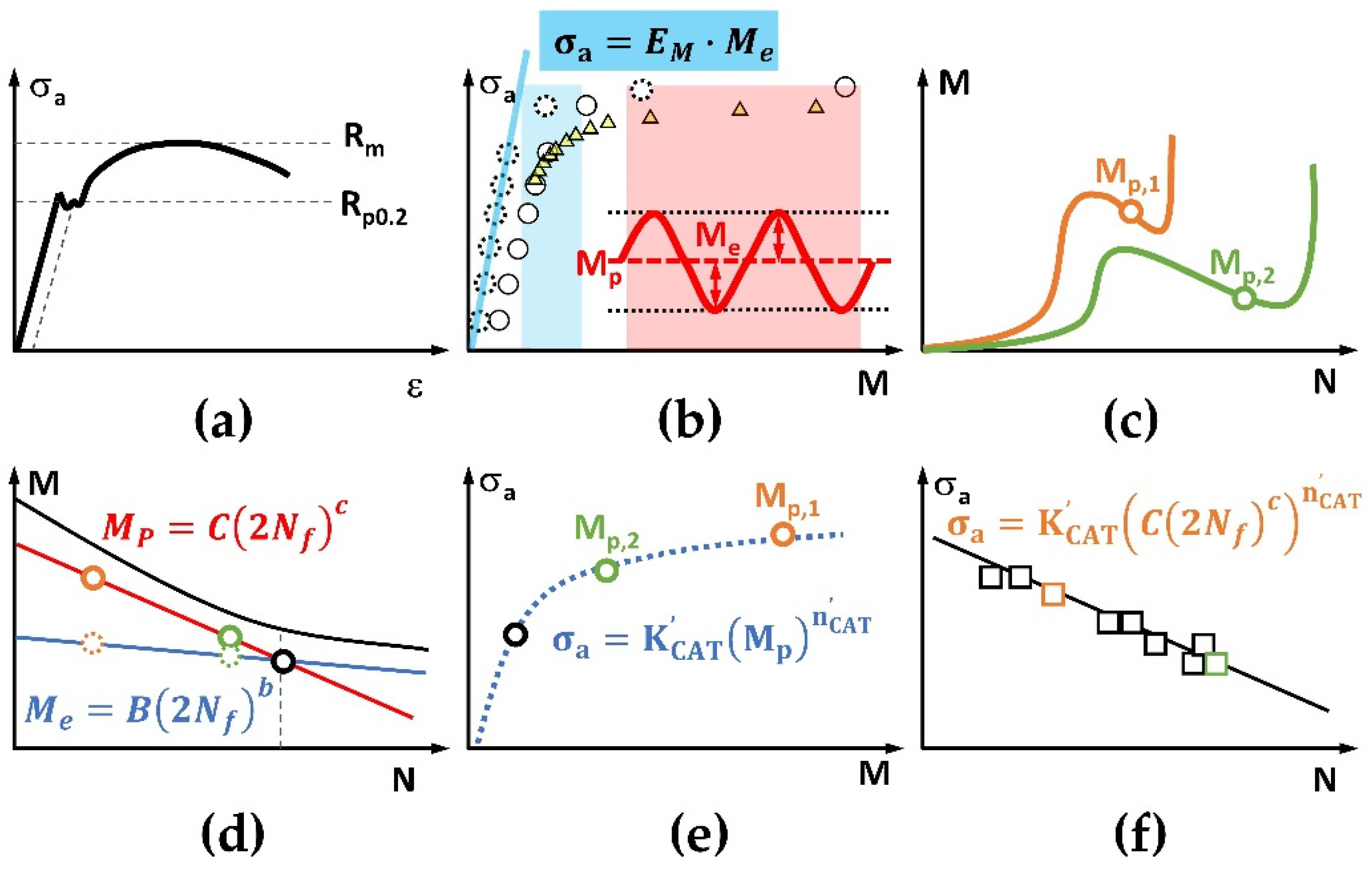
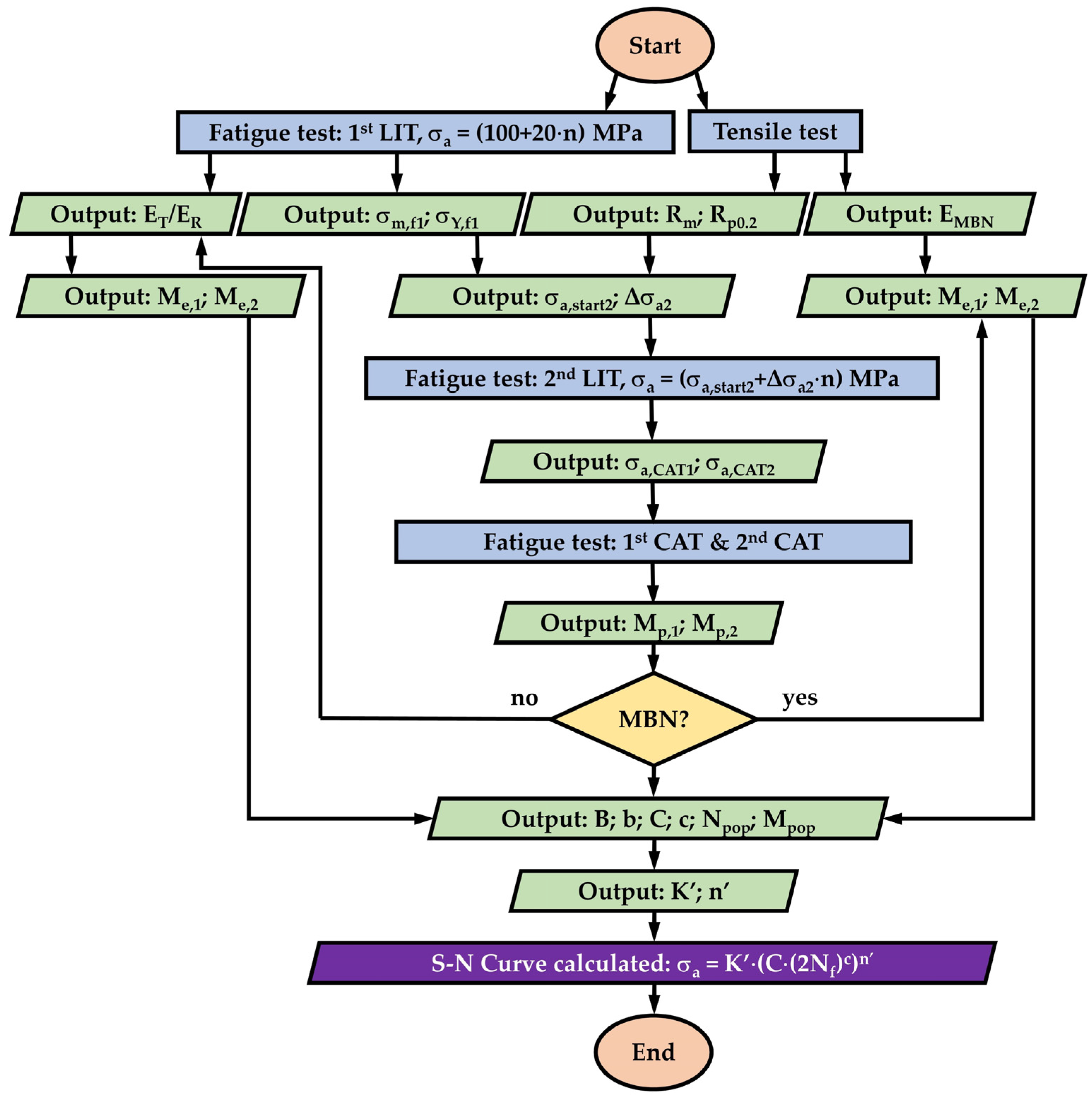
2.3. MaRePLife: Principles
3. Results
3.1. Tensile Tests
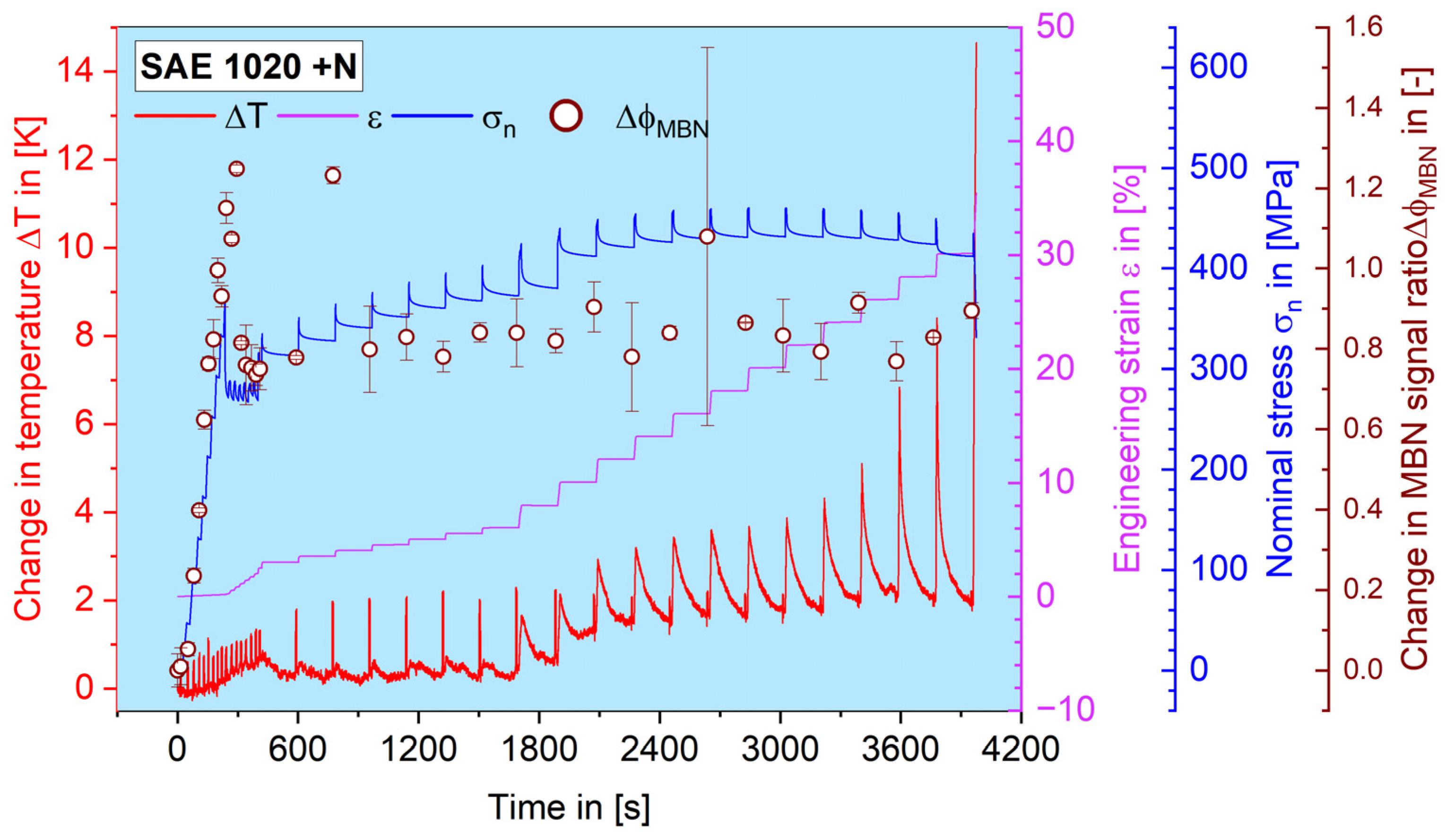
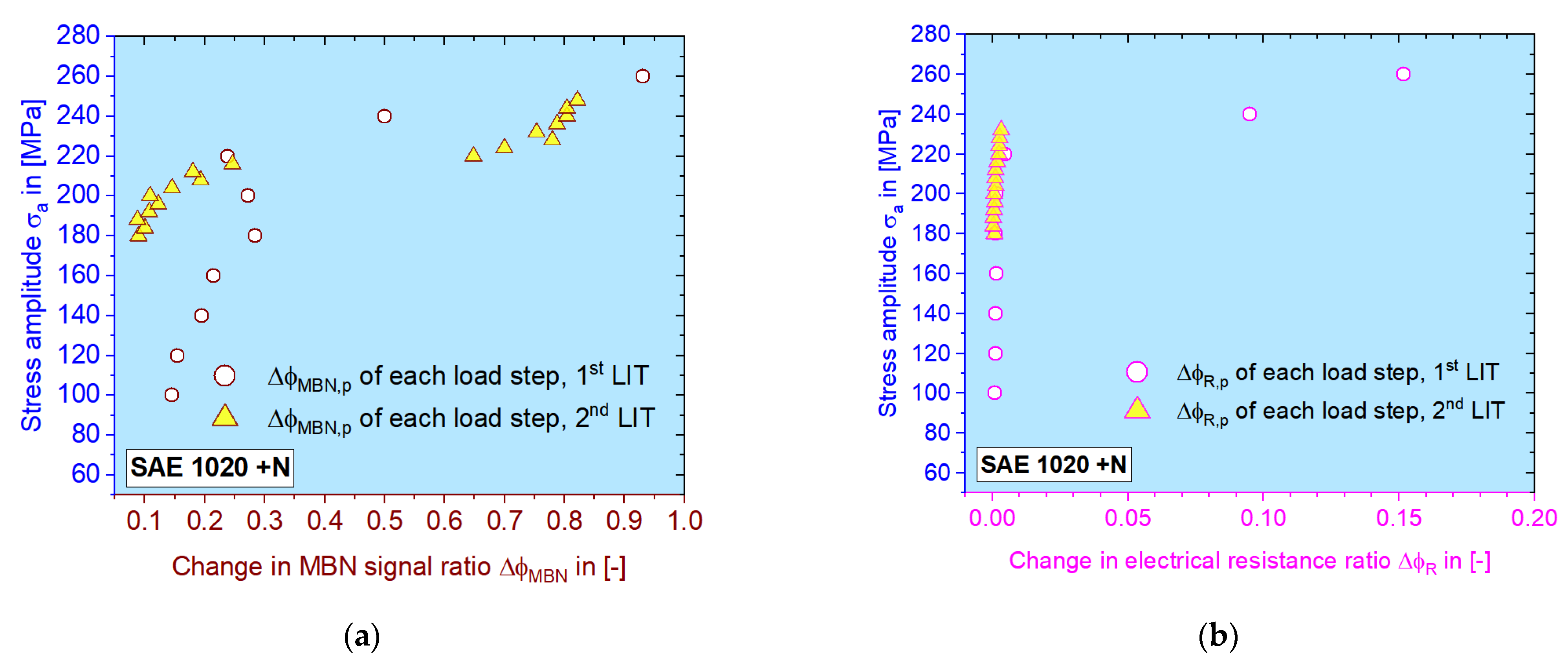
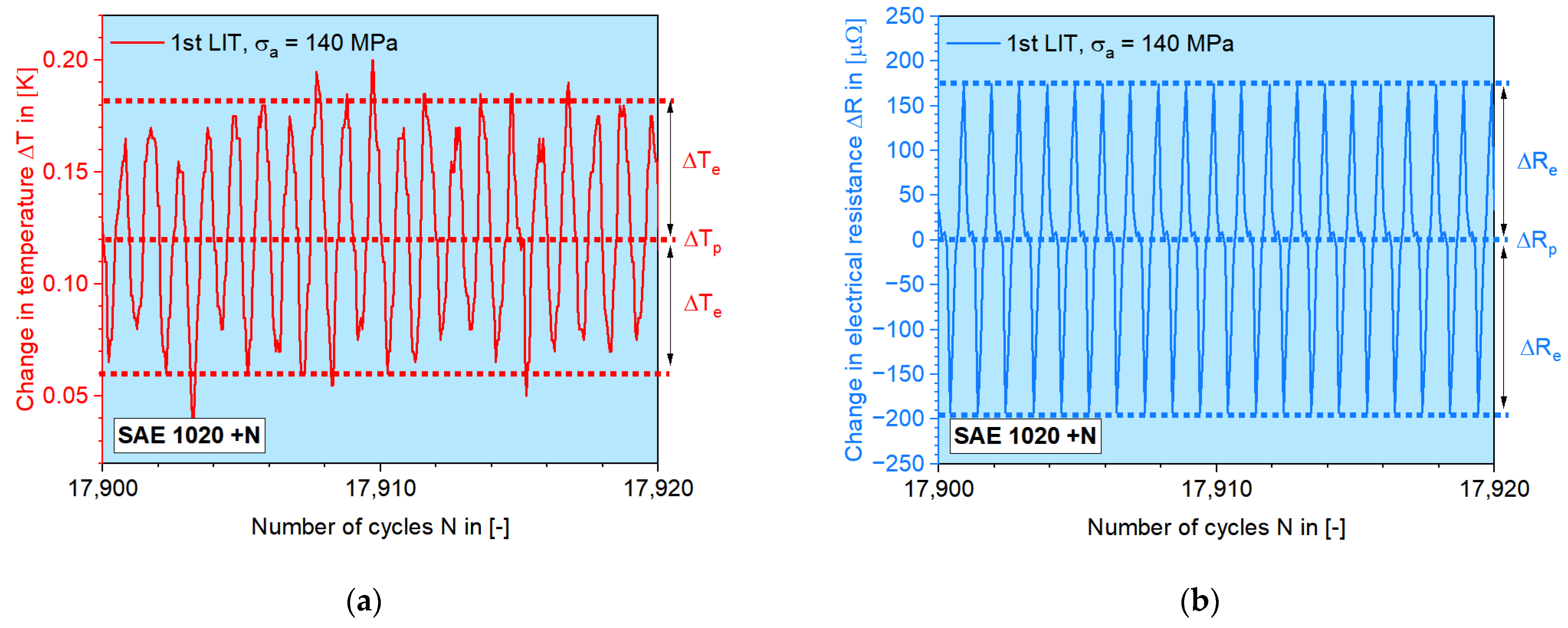
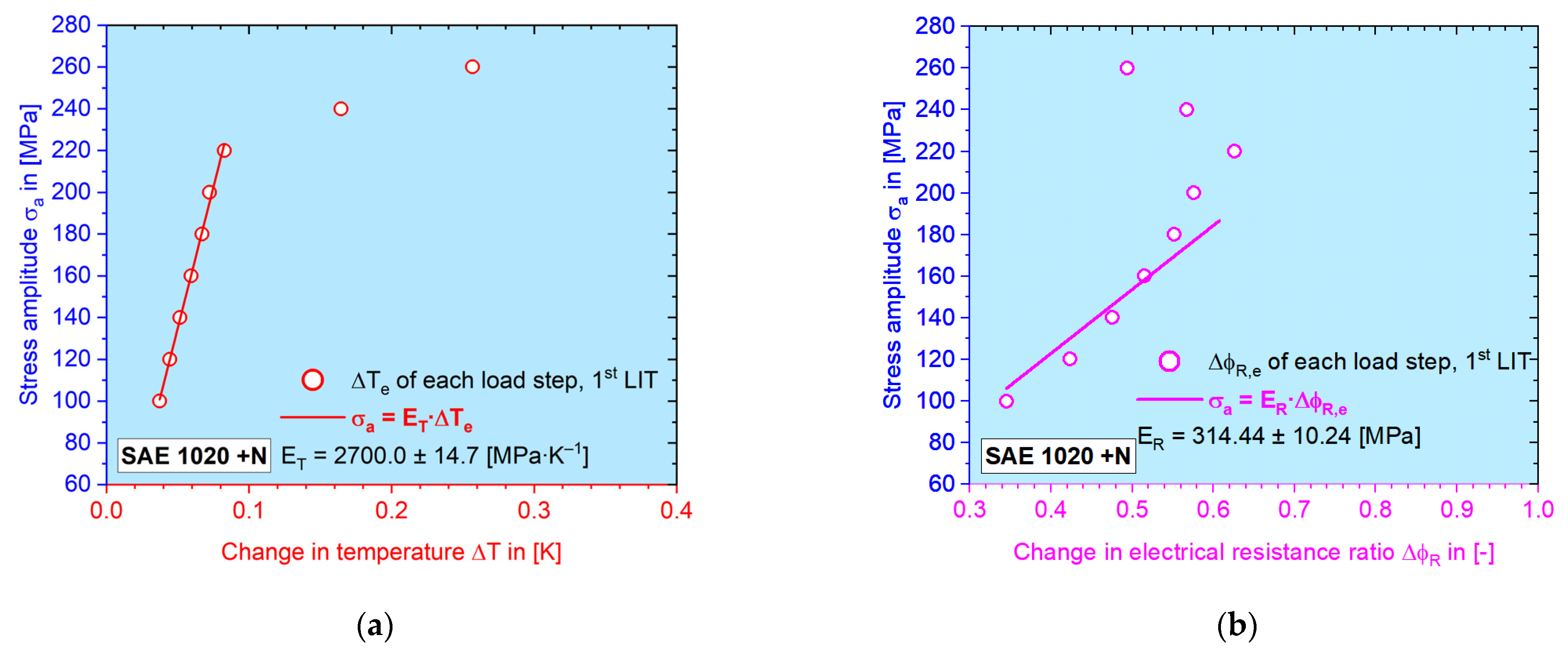
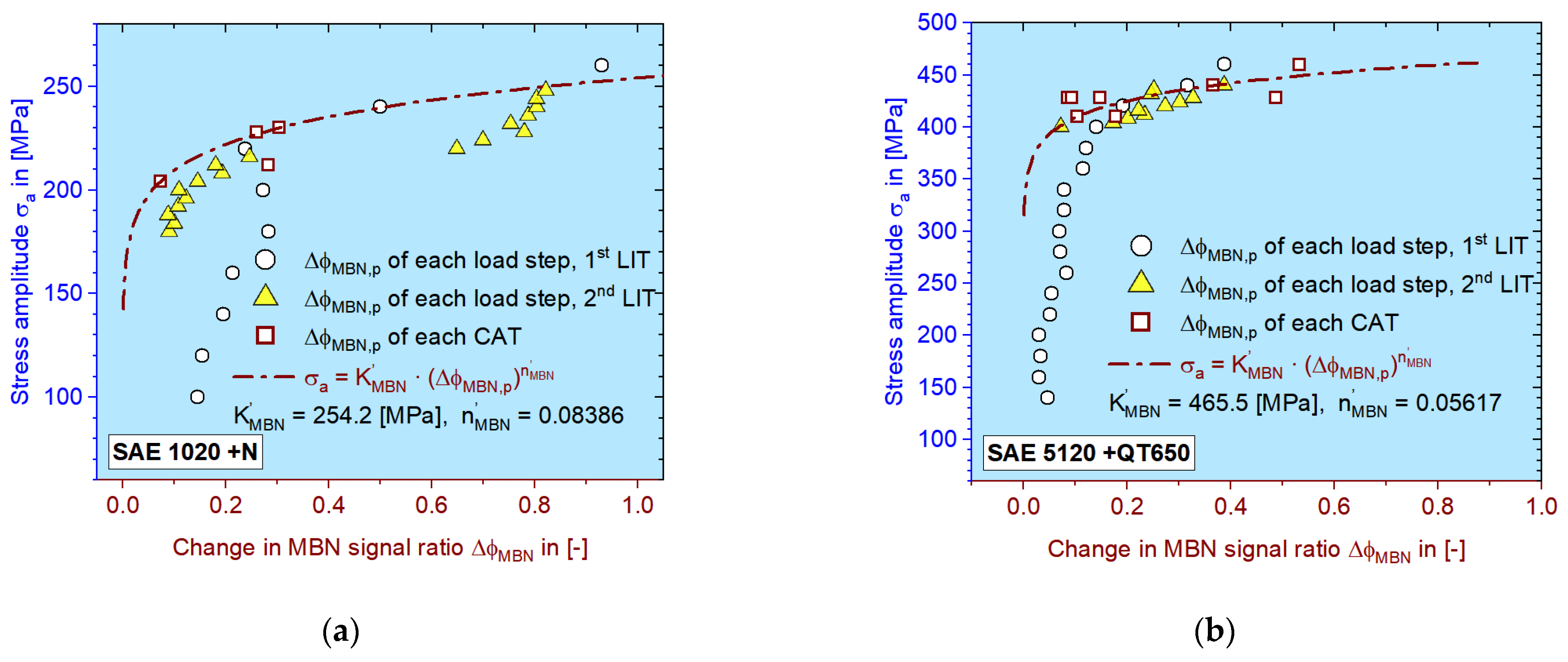
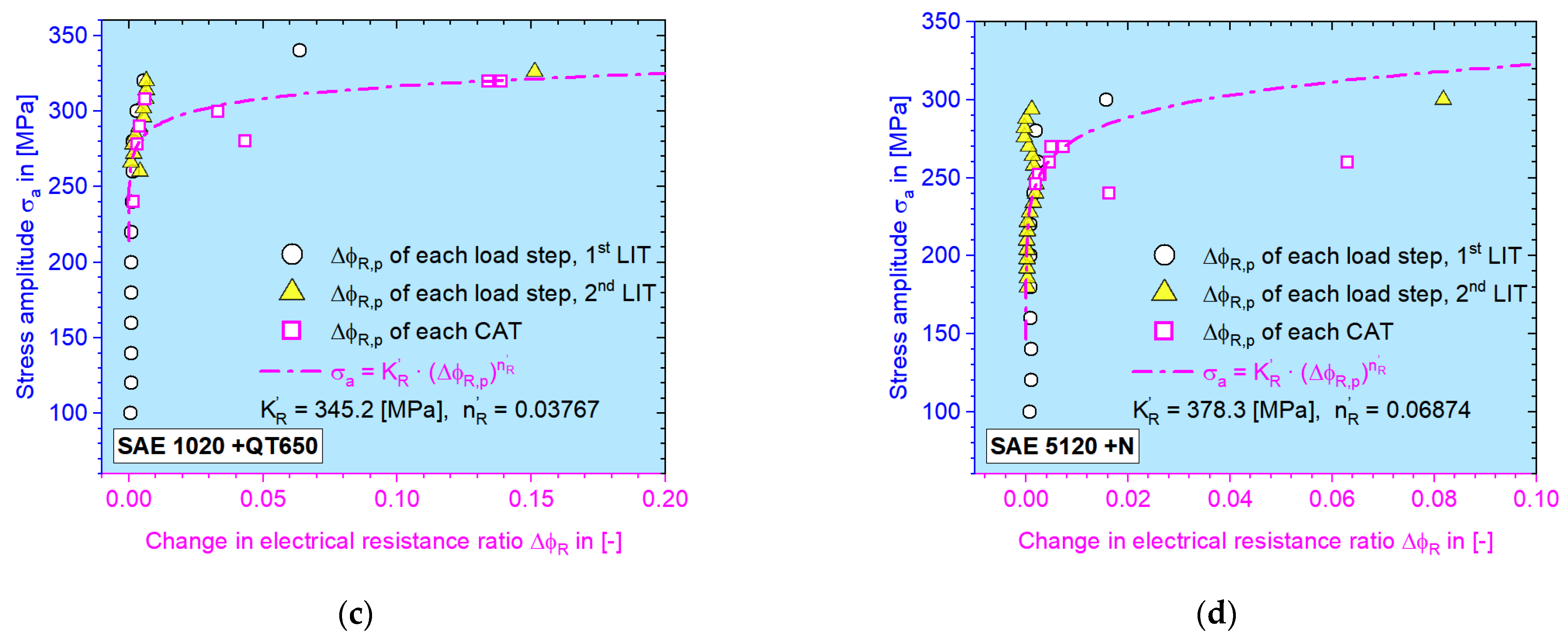
3.2. Load Increase Tests
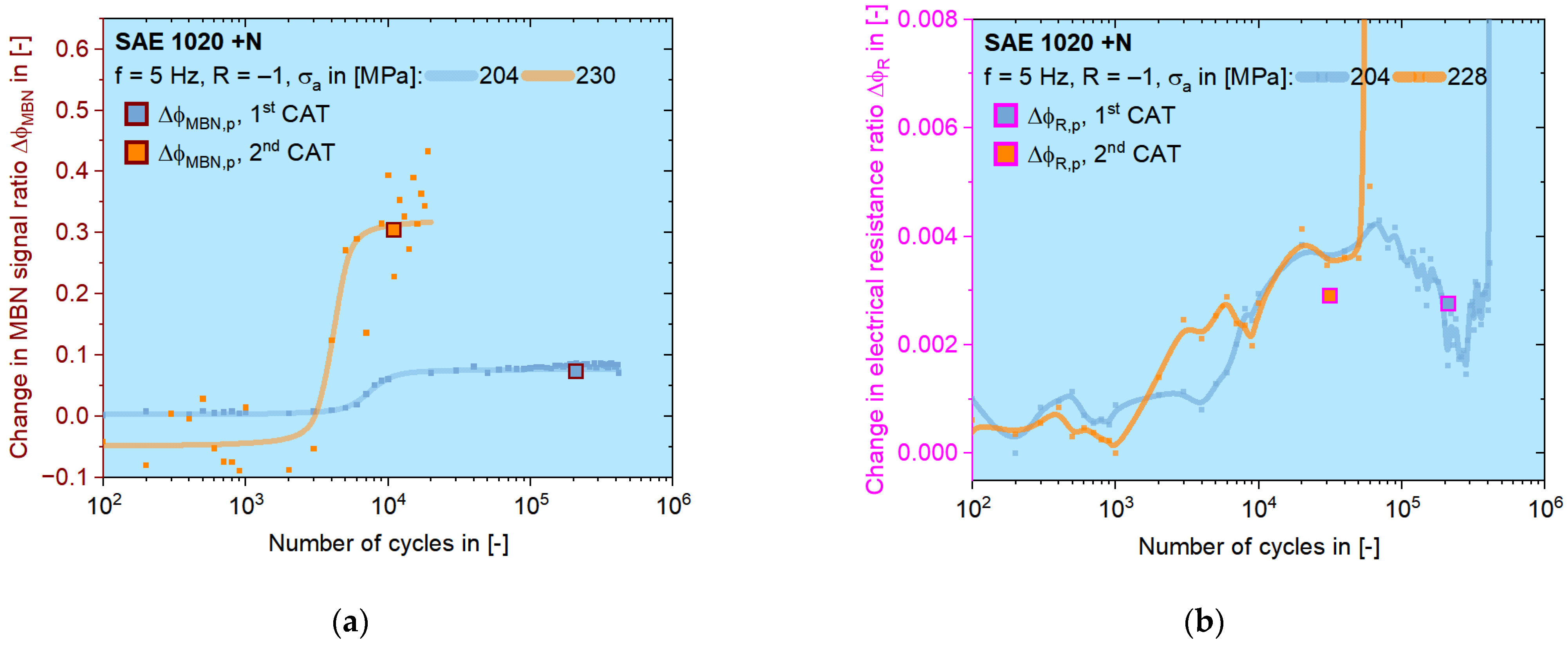
3.3. Constant Amplitude Tests
3.4. MaRePLife
4. Discussion
5. Conclusions
- It is essential to perform tensile and load increase tests (LIT) in order to determine the parameters of constant amplitude tests (CAT), which is the key to conduct short-time fatigue calculations. A method depending on Rm, Rp0.2 and the values from the first LIT (σY,f1 and σY,m1) has been proposed, which is suitable for the common materials to be investigated.
- The elastic modulus of material responses is defined by calculating the slopes of σa–Me data points in the elastic region from a single LIT or a tensile test. The latter is ideal for measurands acquired with discrete measuring methods, such as MBN.
- By applying the idea of material response partitioning for MBN and ER, we could maximize the information we acquired from single fatigue tests and use this as input to calculate the S–N curve in the HCF regime, so that the total cost of time can be reduced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basquin, O.H. The exponential law of endurance tests. In Proc. ASTM; ASTM International: West Conshohocken, PA, USA, 1910; pp. 625–630. [Google Scholar]
- Coffin, J.L.F. A Study of the Effects of Cyclic Thermal Stresses on a Ductile Metal. J. Fluids Eng. 1954, 76, 931–949. [Google Scholar] [CrossRef]
- Manson, S.S. Behavior of Materials under Conditions of Thermal Stress; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954. Available online: http://hdl.handle.net/2060/19930092197 (accessed on 30 November 2022).
- Matthiessen, A.L. On the specific resistance of the metals in terms of the B. A. unit (1864) of electric resistance, together with some remarks on the so-called mercury unit. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1865, 29, 361–370. [Google Scholar] [CrossRef]
- The effects of mechanical stress on the electrical resistance of metals. Proc. R. Soc. Lond. 1894, 54, 283–300. [CrossRef]
- Bridgman, P.W. The Effect of Tension on the Electrical Resistance of Certain Abnormal Metals. Proc. Am. Acad. Arts Sci. 1922, 57, 41. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Effect of Tension on the Thermal and Electrical Conductivity of Metals. Proc. Am. Acad. Arts Sci. 1923, 59, 119. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Effect of Homogeneous Mechanical Stress on the Electrical Resistance of Crystals. Phys. Rev. (Ser. I) 1932, 42, 858–863. [Google Scholar] [CrossRef]
- Reeves, C.A., Jr. Electrical Conductivity and Mechanical Property Measurements on a Cold Worked Sustenitic Stainless Steel; Union Carbide Corp: Oak Ridge, TN, USA, 1972. Available online: https://www.osti.gov/servlets/purl/4664017 (accessed on 28 November 2022).
- Stadnyk, B.I.; Motalo, V.P. Electrical resistivity and mechanical stresses in metals. Meas. Technol. 1987, 30, 608–611. [Google Scholar] [CrossRef]
- Carballo, M.; Pu, Z.J.; Wu, K.H. Variation of Electrical Resistance and the Elastic Modulus of Shape Memory Alloys under Different Loading and Temperature Conditions. J. Intell. Mater. Syst. Struct. 1995, 6, 557–565. [Google Scholar] [CrossRef]
- Gonzalez, C.H.; Morin, M.; Guénin, G. Behaviour of electrical resistivity in single crystals of Cu-Zn-Al and Cu-Al-Be under stress. Le J. de Phys. Colloq. 2001, 11, Pr8–167. [Google Scholar] [CrossRef]
- Gonzalez, C.H.; De Quadros, N.F.; De Araújo, C.J.; Morin, M.; Guénin, G. Coupled stress-strain and electrical resistivity measurements on copper based shape memory single crystals. Mater. Res. 2004, 7, 305–311. [Google Scholar] [CrossRef]
- Rudolf, C.; Goswami, R.; Kang, W.; Thomas, J. Effects of electric current on the plastic deformation behavior of pure copper, iron, and titanium. Acta Mater. 2021, 209, 116776. [Google Scholar] [CrossRef]
- Saberi, S.; Stockinger, M.; Stoeckl, C.; Buchmayr, B.; Weiss, H.; Afsharnia, R.; Hartl, K. A new development of four-point method to measure the electrical resistivity in situ during plastic deformation. Measurement 2021, 180, 109547. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Tan, K.; Zhang, H.; Qian, J.; Liu, H.; Liao, L. A prestress testing method for the steel strands inside in-service structures based on the electrical resistance. Measurement 2021, 184, 109930. [Google Scholar] [CrossRef]
- Esin, A.; Jones, W. A theory of fatigue based on the microstructural accumulation of strain energy. Nucl. Eng. Des. 1966, 4, 292–298. [Google Scholar] [CrossRef]
- Polák, J. The effect of intermediate annealing on the electrical resistivity and shear stress of fatigued copper. Scr. Met. 1970, 4, 761–764. [Google Scholar] [CrossRef]
- Piotrowski, A.; Eifler, D. Bewertung zyklischer Verformungsvorgänge metallischer Werkstoffe mit Hilfe mechanischer, ther-mometrischer und elektrischer Meßverfahren, Mat.-Wiss. u. Werkstofftech 1995, 26, 121–127. [Google Scholar]
- Chung, D.D.L. Structural health monitoring by electrical resistance measurement. Smart Mater. Struct. 2001, 10, 624–636. [Google Scholar] [CrossRef]
- Sun, B.; Guo, Y. High-cycle fatigue damage measurement based on electrical resistance change considering variable electrical resistivity and uneven damage. Int. J. Fatigue 2004, 26, 457–462. [Google Scholar] [CrossRef]
- Wakuda, D.; Suganuma, K. Stretchable fine fiber with high conductivity fabricated by injection forming. Appl. Phys. Lett. 2011, 98, 073304. [Google Scholar] [CrossRef]
- Omari, M.A.; Sevostianov, I. Estimation of changes in the mechanical properties of stainless steel subjected to fatigue loading via electrical resistance monitoring. Int. J. Eng. Sci. 2013, 65, 40–48. [Google Scholar] [CrossRef]
- Omari, M.A.; Sevostianov, I. Evaluation of the Growth of Dislocations Density in Fatigue Loading Process via Electrical Resistivity Measurements. Int. J. Fract. 2012, 179, 229–235. [Google Scholar] [CrossRef]
- Glushko, O.; Cordill, M. Electrical Resistance of Metal Films on Polymer Substrates Under Tension. Exp. Technol. 2014, 2014. 40, 1–8. [Google Scholar] [CrossRef]
- Starke, P.; Walther, F.; Eifler, D. Fatigue assessment and fatigue life calculation of quenched and tempered SAE 4140 steel based on stress–strain hysteresis, temperature and electrical resistance measurements. Fat. Frac. Eng. Mater. Struct. 2007, 30, 1044–1051. [Google Scholar] [CrossRef]
- Wu, H.; Bill, T.; Teng, Z.; Pramanik, S.; Hoyer, K.-P.; Schaper, M.; Starke, P. Characterization of the fatigue behaviour for SAE 1045 steel without and with load-free sequences based on non-destructive, X-ray diffraction and transmission electron microscopic investigations. Mater. Sci. Eng. A 2020, 794, 139597. [Google Scholar] [CrossRef]
- Kasai, N.; Koshino, H.; Sekine, K.; Kihira, H.; Takahashi, M. Study on the Effect of Elastic Stress and Microstructure of Low Carbon Steels on Barkhausen Noise. J. Nondestruct. Evaluation 2013, 32, 277–285. [Google Scholar] [CrossRef]
- Pal’A, J.; Stupakov, O.; Bydžovský, J.; Tomáš, I.; Novák, V. Magnetic behaviour of low-carbon steel in parallel and perpendicular directions to tensile deformation. J. Magn. Magn. Mater. 2007, 310, 57–62. [Google Scholar] [CrossRef]
- Karjalainen, L.; Moilanen, M. Detection of plastic deformation during fatigue of mild steel by the measurement of Barkhausen noise. NDT Int. 1979, 12, 51–55. [Google Scholar] [CrossRef]
- Karjalainen, L.; Moilanen, M. Fatigue softening and hardening in mild steel detected from Barkhausen noise. IEEE Trans. Magn. 1980, 16, 514–517. [Google Scholar] [CrossRef]
- Lachmann, C.; Nitschke-Pagel, T.; Wohlfahrt, H. Charakterisierung des Ermüdungszustandes in zyklisch beanspruchten Schweißverbindungen durch röntgenographische und mikromagnetische Kenngrößen. Mater. und Werkst. 1998, 29, 686–693. [Google Scholar] [CrossRef]
- Sagar, S.P.; Parida, N.; Das, S.; Dobmann, G.; Bhattacharya, D. Magnetic Barkhausen emission to evaluate fatigue damage in a low carbon structural steel. Int. J. Fatigue 2005, 27, 317–322. [Google Scholar] [CrossRef]
- Palma, E.; Mansur, T.; Silva, S.F.; Alvarenga, A. Fatigue damage assessment in AISI 8620 steel using Barkhausen noise. Int. J. Fatigue 2005, 27, 659–665. [Google Scholar] [CrossRef]
- Baak, N.; Schaldach, F.; Nickel, J.; Biermann, D.; Walther, F. Barkhausen Noise Assessment of the Surface Conditions Due to Deep Hole Drilling and Their Influence on the Fatigue Behaviour of AISI 4140. Metals 2018, 8, 720. [Google Scholar] [CrossRef] [Green Version]
- Baak, N.; Nickel, J.; Biermann, D.; Walther, F. Barkhausen noise-based fatigue life prediction of deep drilled AISI 4140. Procedia Struct. Integr. 2019, 18, 274–279. [Google Scholar] [CrossRef]
- Wu, H.; Raghuraman, S.R.; Ziman, J.A.; Weber, F.; Hielscher, T.; Starke, P. Characterization of the Fatigue Behaviour of Low Carbon Steels by Means of Temperature and Micromagnetic Measurements. Metals 2022, 12, 1838. [Google Scholar] [CrossRef]
- Starke, P. StressLifetc—NDT-related assessment of the fatigue life of metallic materials. Mater. Test. 2019, 61, 297–303. [Google Scholar] [CrossRef]
- Morrow, J.D. Cyclic plastic strain energy and fatigue of metals. In Internal Friction, Damping, and Cyclic Plasticity; ASTM International: West Conshohocken, PA, USA, 1965; pp. 45–87. [Google Scholar] [CrossRef]
- Thomson, W. On the thermo-elastic and thermomagnetic properties of matter. Q. J. Pure Appl. Math. 1857, 1, 57–77. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curve by Three Parameters; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. Available online: https://ntrs.nasa.gov/api/citations/19930081614/downloads/19930081614.pdf (accessed on 13 November 2022).
- O’Sullivan, D.; Cotterell, M.; Tanner, D.; Mészáros, I. Characterisation of ferritic stainless steel by Barkhausen techniques. NDT E Int. 2004, 37, 489–496. [Google Scholar] [CrossRef]
- Benitez, J.A.P.; Le Manh, T.; Alberteris, M. Barkhausen noise for material characterization. In Barkhausen Noise for Nondestructive Testing and Materials Characterization in Low-Carbon Steels; Woodhead Publishing: Sawston, UK, 2020; pp. 115–146. [Google Scholar] [CrossRef]







| Symbol or Abbreviation | Meaning | Symbol or Abbreviation | Meaning |
|---|---|---|---|
| CAT | Constant amplitude test | E | E-modulus |
| DAQ | Data acquisition | Imax | Maximum MBN signal intensity |
| ER | Electrical resistometry | Imax,0 | Initial maximum MBN signal intensity |
| HCF | High cycle fatigue | K’ | Cyclic strength coefficient |
| IR | Infrared | L0 | Measuring length at tensile specimen |
| LCF | Low cycle fatigue | Me(Me,1/Me,2) | Elastic material response (of first/second CAT) |
| LIT | Load increase test | Mp(Mp,1/Mp,2) | Plastic material response (of first/second CAT) |
| MaRePLife | Material response partitioning fatigue life evaluation | Mpop | Material response at point of partitioning |
| MBN | Magnetic Barkhausen noise | Nf | Fatigue life/number of cycles to failure |
| NDT | Non-destructive testing | Npop | Number of load cycle at point of partitioning |
| +N | Normalized state | n’ | Cyclic strain hardening exponent |
| +QT | Quenched and tempered state | R0 | Initial electrical resistance |
| αf | Ratio between the stress increases of both LITs | Rm | Tensile strength |
| b | Fatigue strength exponent | Rp0.2 | Yield strength |
| c | Fatigue ductility exponent | σ’f | Cyclic strength |
| Δεt/Δεe/Δεp | Change in total/elastic/plastic strain | Taust. | Austenitization temperature |
| ΔφMBN | Change in MBN signal ratio | Ttemp. | Tempering temperature |
| ΔφR | Change in ER ratio | vc | Crosshead speed |
| Δσa1 | Stress increase of the first LIT | σa/σa,t | (Total) stress amplitude |
| Δσa2 | Stress increase of the second LIT | σa,start1 | Initial stress amplitude of the first LIT |
| ΔT | Change in temperature | σa,start2 | Initial stress amplitude of the second LIT |
| ε a,t/ε a,e/εa,p | Total/elastic/plastic strain amplitude | σm,f1 | Stress amplitude at which the specimen breaks during LIT |
| ε’f | Cyclic ductility | σY,f1 | Stress amplitude at which the first obvious increment of material response is observed during LIT |
| EM/EMBN/ER | E-modulus regarding material response/MBN/R |
| Material | Fe | C | Si | Mn | P | S | Cr | Mo | Ni | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.1149 SAE 1020 | DIN EN 10083-2 | - | 0.17–0.24 | ≤0.4 | 0.40–0.70 | ≤0.030 | 0.020–0.040 | ≤0.40 | ≤0.10 | ≤0.40 |
| Producer | - | 0.21 | 0.24 | 0.46 | 0.013 | 0.023 | 0.12 | 0.013 | 0.12 | |
| * +N | bal. | 0.234 | 0.286 | 0.481 | 0.014 | 0.018 | 0.118 | 0.014 | 0.112 | |
| * +QT650 | bal. | 0.237 | 0.288 | 0.478 | 0.014 | 0.019 | 0.118 | 0.014 | 0.114 | |
| * +QT250 | bal. | 0.236 | 0.286 | 0.479 | 0.014 | 0.019 | 0.119 | 0.016 | 0.115 | |
| 1.7149 SAE 5120 | DIN EN 10084 | - | 0.17–0.22 | ≤0.4 | 1.10–1.40 | ≤0.025 | 0.020–0.040 | 1.00–1.30 | - | - |
| Producer | - | 0.18 | 0.24 | 1.23 | 0.015 | 0.026 | 1.05 | 0.022 | 0.10 | |
| * +N | bal. | 0.196 | 0.274 | 1.324 | 0.017 | 0.023 | 1.065 | 0.025 | 0.093 | |
| * +QT650 | bal. | 0.194 | 0.274 | 1.309 | 0.016 | 0.024 | 1.056 | 0.022 | 0.093 | |
| * +QT250 | bal. | 0.195 | 0.271 | 1.310 | 0.016 | 0.024 | 1.060 | 0.024 | 0.094 |
| Material Number after EN/SAE | Heat Treatment | Rm [MPa] | [MPa] | [MPa] | [MPa] | [-] | [MPa] | [MPa] |
|---|---|---|---|---|---|---|---|---|
| 1.1149SAE 1020 | +N | 460 | 290 | 260 | 220 | 0.2 | 180 | 4 |
| +QT650 | 580 | 440 | 340 | 300 | 0.3 | 260 | 6 | |
| +QT250 | 470 | 595 | 360 | 300 | 0.5 | 240 | 10 | |
| 1.7149SAE 5120 | +N | 540 | 340 | 300 | 240 | 0.3 | 180 | 6 |
| +QT650 | 700 | 600 | 460 | 440 | 0.2 | 420 | 4 | |
| +QT250 | 1200 | 905 | 760 | 580 | 0.6 | 400 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Ziman, J.A.; Raghuraman, S.R.; Nebel, J.-E.; Weber, F.; Starke, P. Short-Time Fatigue Life Estimation for Heat Treated Low Carbon Steels by Applying Electrical Resistance and Magnetic Barkhausen Noise. Materials 2023, 16, 32. https://doi.org/10.3390/ma16010032
Wu H, Ziman JA, Raghuraman SR, Nebel J-E, Weber F, Starke P. Short-Time Fatigue Life Estimation for Heat Treated Low Carbon Steels by Applying Electrical Resistance and Magnetic Barkhausen Noise. Materials. 2023; 16(1):32. https://doi.org/10.3390/ma16010032
Chicago/Turabian StyleWu, Haoran, Jonas Anton Ziman, Srinivasa Raghavan Raghuraman, Jan-Erik Nebel, Fabian Weber, and Peter Starke. 2023. "Short-Time Fatigue Life Estimation for Heat Treated Low Carbon Steels by Applying Electrical Resistance and Magnetic Barkhausen Noise" Materials 16, no. 1: 32. https://doi.org/10.3390/ma16010032
APA StyleWu, H., Ziman, J. A., Raghuraman, S. R., Nebel, J.-E., Weber, F., & Starke, P. (2023). Short-Time Fatigue Life Estimation for Heat Treated Low Carbon Steels by Applying Electrical Resistance and Magnetic Barkhausen Noise. Materials, 16(1), 32. https://doi.org/10.3390/ma16010032








