Evaluation of CBR of Graded Crushed Stone of Flexible Base Structural Layer Based on Discrete Element Model
Abstract
:1. Introduction
2. Basic Principles of Discrete Element Method
2.1. Force–Displacement Equation and Motion Relationship
2.2. Contact Constitutive Model
3. Basic Principles of Discrete Element Method
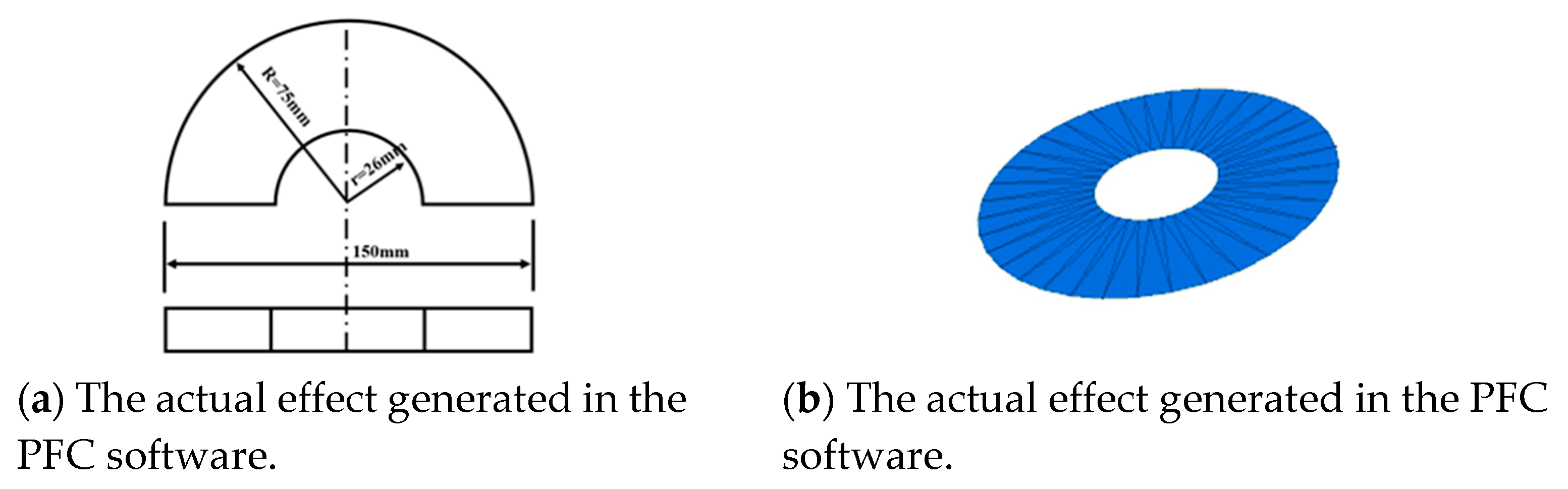
3.1. Virtual Mold Setting
3.2. Specimen Setting of Graded Particles
3.2.1. Calculation of The Number of Particles Corresponding to Gradation
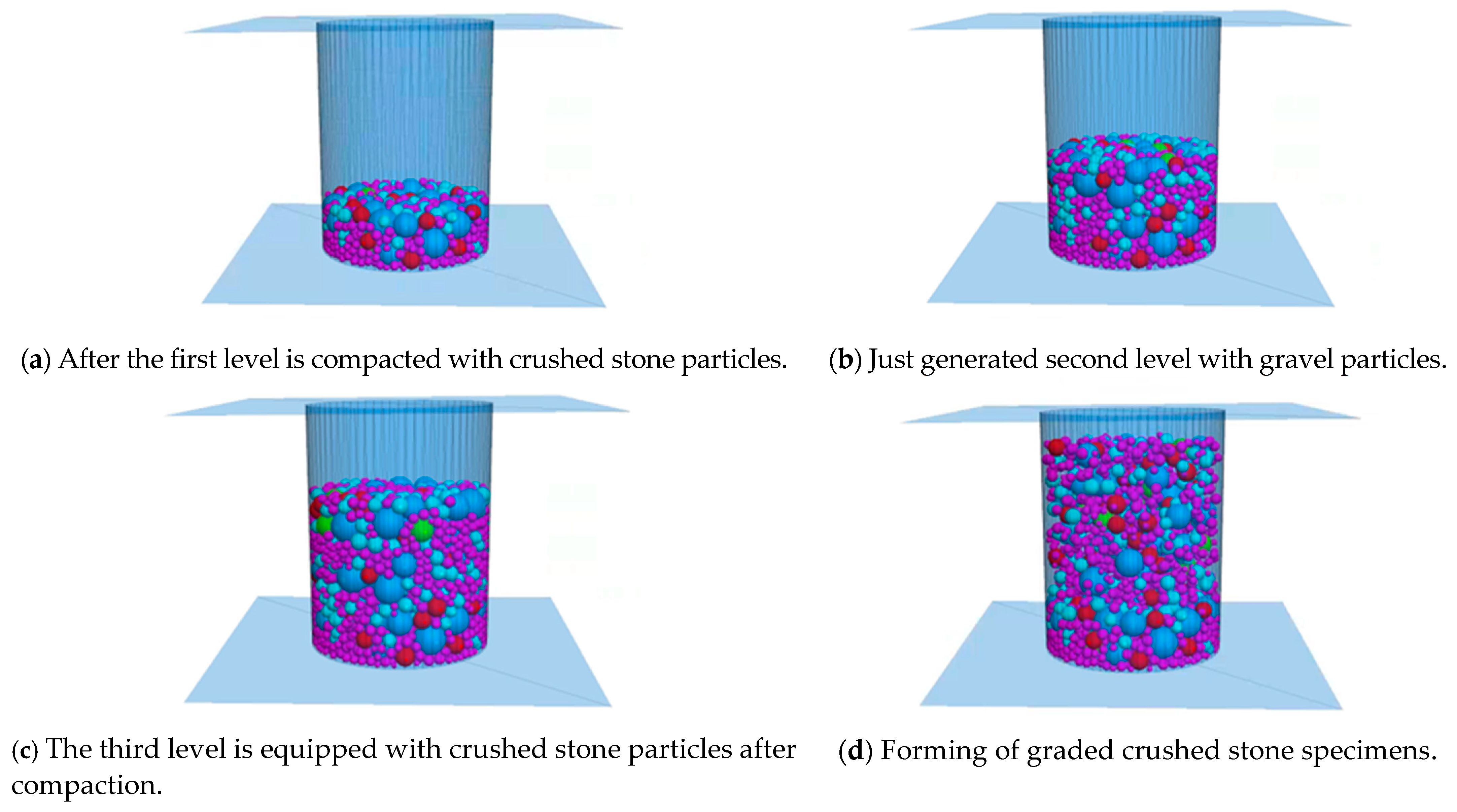
3.2.2. Generation Process of Target Graded Crushed Stone Specimens
3.3. Setting of Wall Speed and Confining Pressure
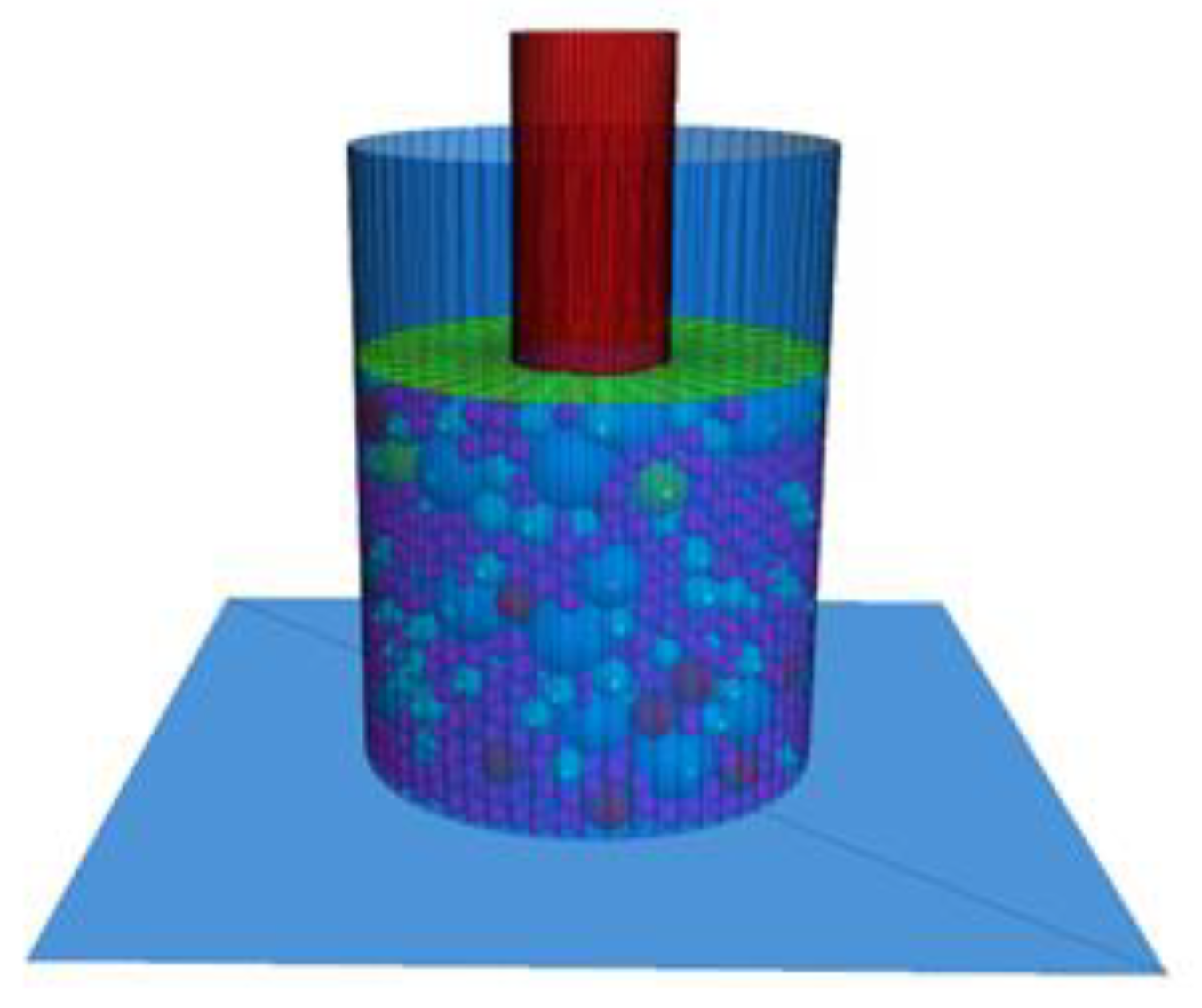
3.4. Simulation of CBR Loading Conditions
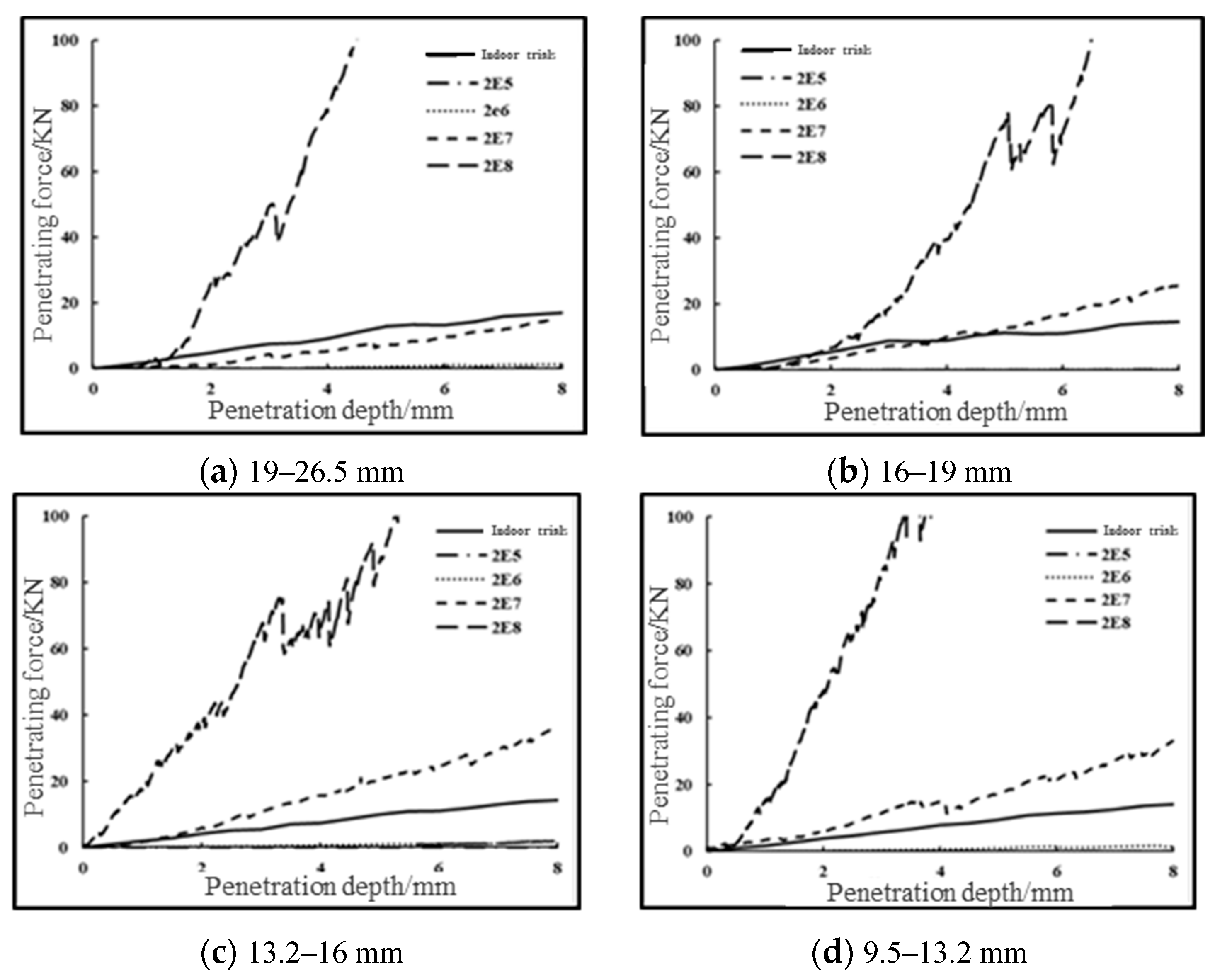
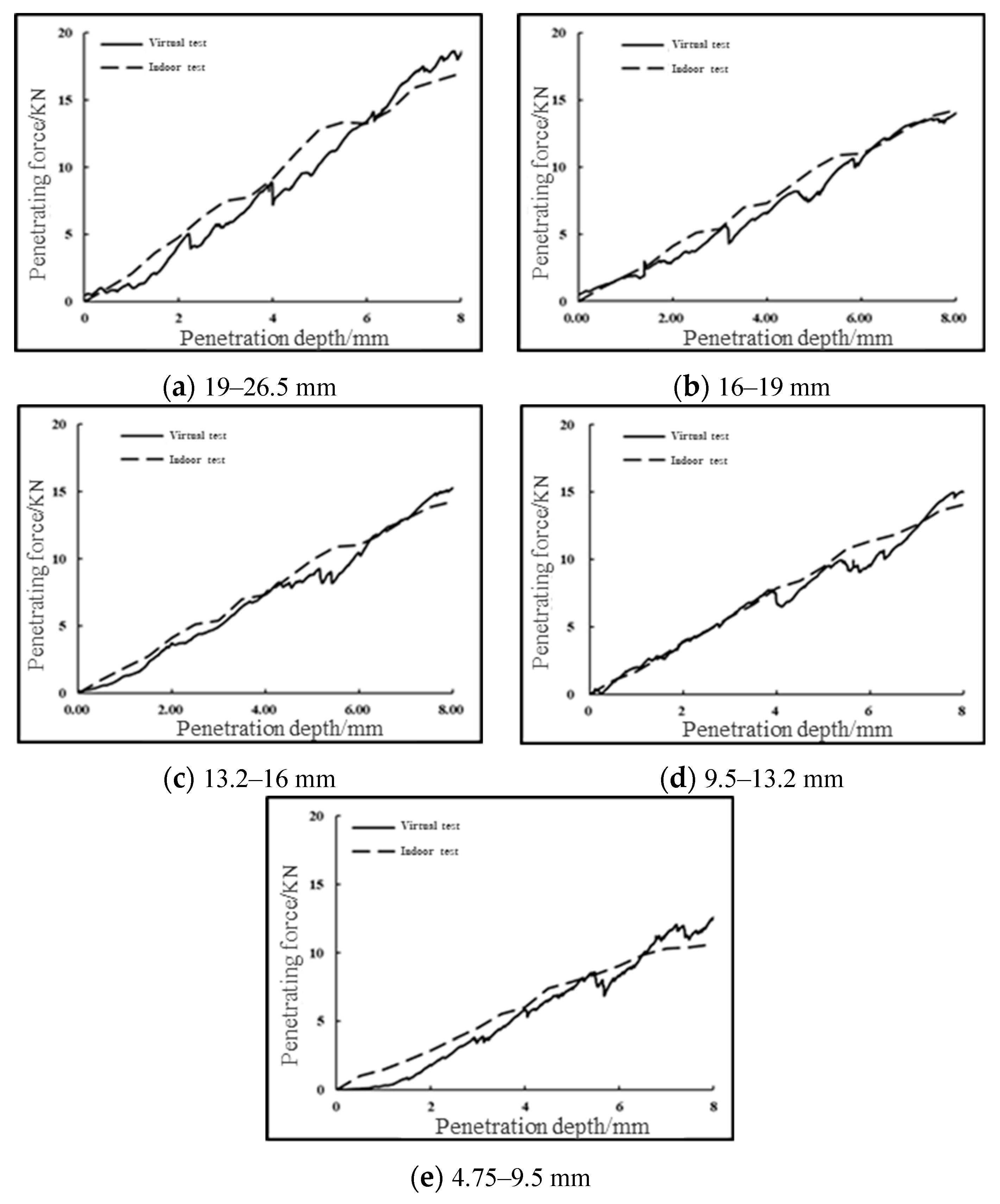
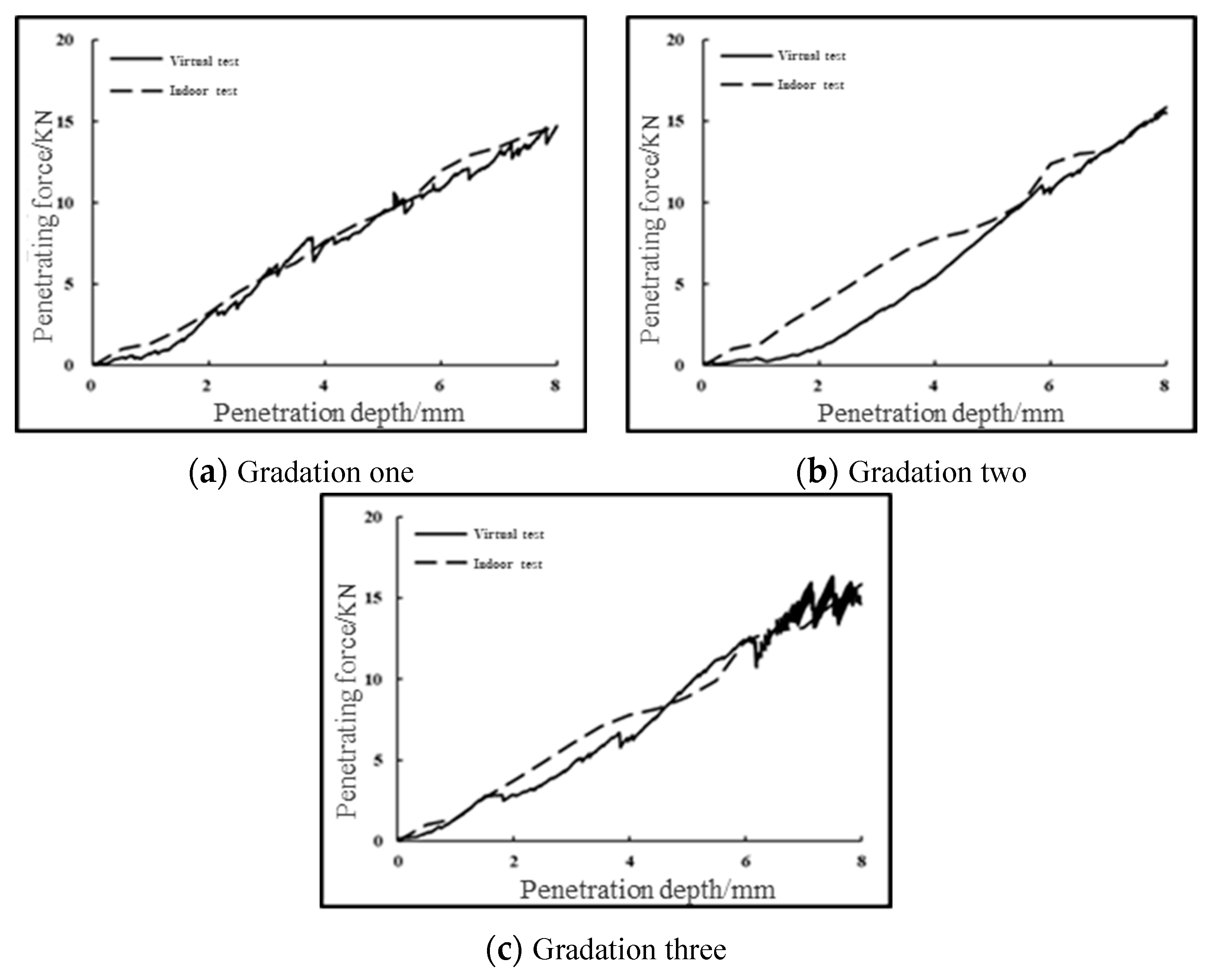
4. Calibration of microscopic parameters
4.1. Indoor CBR Test
4.1.1. Material selection and specimen grading
4.1.2. Forming Steps of The Test Piece
4.1.3. Indoor CBR Test
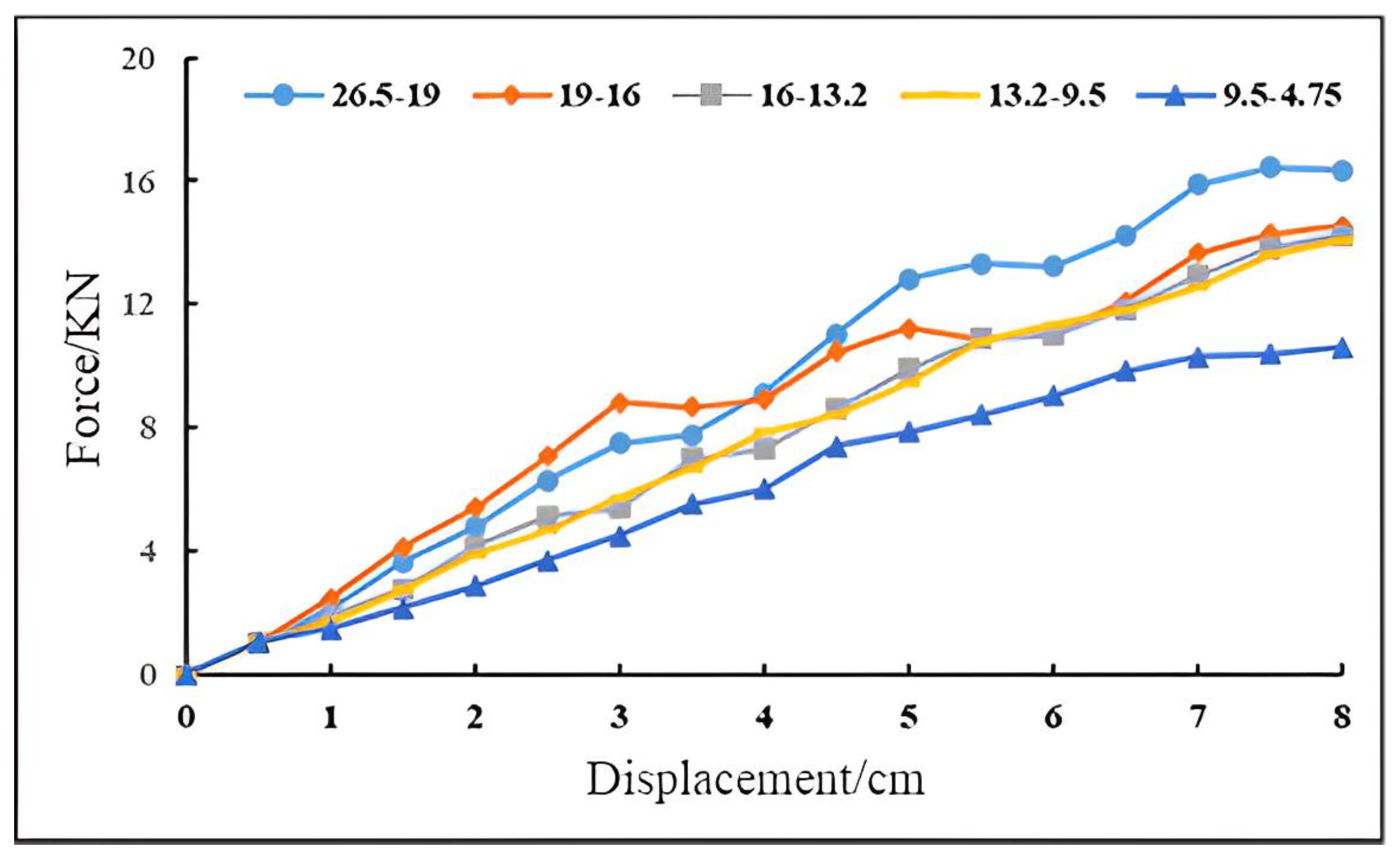
4.2. Calibration Results of Microscopic Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Feng, D.C. Methods to improve the use performance of graded gravel base. China J. Highw. Transp. 2016, 4, 40–45. [Google Scholar]
- Jiang, Y.L.; Li, D.; Ma, Q.W.; Cao, H.H.; Ren, J.L. Experimental study on the factors influencing the mechanical properties of graded aggregates. J. Transp. Sci. Eng. 2010, 26, 6–13. [Google Scholar]
- Chen, L.B.; Yan, E.H.; Xu, J.; Ma, T.; Zeng, J.C.; Gong, Y. Research on Design Indicators for Graded Crushed Stone Mixture Based on Vibration Molding Method. Adv. Mater. Sci. Eng. 2020, 2020, 5179563. [Google Scholar] [CrossRef]
- Lima, C.; Motta, L. Study of Permanent Deformation and Granulometric Distribution of Graded Crushed Stone Pavement Material. Procedia Eng. 2016, 143, 854–861. [Google Scholar] [CrossRef] [Green Version]
- Falla, G.C.; Leischner, S.; Blasl, A.; Erlingsson, S. Characterization of unbound granular materials within a mechanistic design framework for low volume roads. Transp. Geotech. 2017, 13, 2–12. [Google Scholar] [CrossRef]
- Xiao, Y.; Tutumluer, E.; Siekmeier, J. Mechanistic-Empirical Evaluation of Aggregate Base and Granular Subbase Quality Affecting Flexible Pavement Performance in Minnesota. Transp. Res. Rec. 2011, 2227, 97–106. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, H.; Yuan, K.; Li, M.; Yang, M.; Yi, Y.; Fan, J.; Tian, T. Research on Mechanical Properties and Influencing Factors of Cement-Graded Crushed Stone Using Vertical Vibration Compaction. Materials 2022, 15, 2132. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Yao, Y.; Zheng, J.; Gu, F. Geometric anisotropy modeling and shear behavior evaluation of graded crushed rocks. Constr. Build. Mater. 2018, 183, 346–355. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, X.M.; Tian, F. Experimental study on the factors influencing the mechanical properties of graded aggregates. J. Highw. Transp. Res. Dev. 2014, 31, 39–42+49. [Google Scholar]
- Li, J.; Zhang, J.; Qian, G.; Zheng, J.; Zhang, Y. Three-Dimensional Simulation of Aggregate and Asphalt Mixture Using Parameterized Shape and Size Gradation. J. Mater. Eng. C 2019, 31, 04019004. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Yu, H. Characterize packing of aggregate particles for paving materials: Particle size impact. Constr. Build. Mater. 2011, 25, 1362–1368. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.M. Evaluation of skeletal structure of aggregates using discrete element method. J. Southeast Univ. Nat. Sci. Ed. 2012, 42, 761–765. [Google Scholar]
- Peng, A.P.; Li, L.; Zhang, Z. Study on the meso-mechanical behavior of California bearing ratio of graded gravel with discrete element method. J. Railw. Sci. Eng. 2019, 16, 2467–2474. [Google Scholar] [CrossRef]
- Jaing, Y.J.; Li, S.W.; Chen, Z.J.; Fang, J. Biaxial Numerical Simulation on Graded Broken Stone and Its Influence Factors. J. Tongji Univ. Nat. Sci. Ed. 2015, 43, 1045–1050. [Google Scholar]
- Jiang, Y.-J.; Ni, C.-Y.; Zhang, Y.; Yi, Y. Numerical investigation of the plastic deformation behaviour of graded crushed stone. PLoS ONE 2021, 16, e0258113. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.J.; Wang, X.M.; Yu, Q.D.; Hua, W.J.; Chen, X.B. Discrete Element Modeling of Shear Strength Evolution Characteristics of Unbound Permeable Aggregate Base Materials. J. China Highw. Eng. 2022, 1–23. Available online: http://kns.cnki.net/kcms/detail/61.1313.U.20220414.1050.002.html (accessed on 15 April 2022).
- Cao, M.M.; Tan, Q.Q.; Liu, J.L.; Huang, W. Methods to improve the use performance of graded gravel base. East Road 2019, 1, 109–114. [Google Scholar]
- Zhang, H.L.; Chen, G.B.; Zhang, Z.X. Simulations on the Triaxial Repeated Load Tests of Graded Crushed Stones. In International Workshop on Energy and Environment in the Development of Sustainable Asphalt Pavements; Highway School, Chang’an University: Xi’an, China; China Railway Engineering Consultants Group Co., Ltd.: Zhengzhou, China, 2010. [Google Scholar]
- Liu, J.L. Analysis of Structural Behavior of Inverted Base Asphalt Pavement. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Yuan, J.; Shao, M.H.; Huang, X.M. Grade selection of graded aggregates. Highway 2005, 4, 40–45. [Google Scholar]
- GB/T 50123-2019; Standard for Soil Method. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China; Standards Press of China: Beijing, China, 2019.
- Wang, L.; Xie, X.G.; Li, C.J. Comparative vibration and compaction molding tests on the performance of graded aggregates. China J. Highw. Transp. 2007, 6, 19–24. [Google Scholar]
- Zhou, W.F.; Li, Y.W.; Zhang, X.L.; Ma, B. Road performance and design criteria of graded aggregates based on vibration forming. J. Chongqing Jiaotong Univ. Nat. Sci. 2009, 28, 559–564. [Google Scholar]
- Liu, H.T.; Cheng, X.H. Discrete element analysis of the size effect of coarse-grained soils. Rock Soil Mech. 2009, 30, 287–292. [Google Scholar]
- JTG/T F20-2015[S]; Technical Guidelines for Construction of Highway Roadbases. Ministry of Transport of the People’s Republic of China: Beijing, China; China Communications Press: Beijing, China, 2015.
- Xu, G.H.; Gao, H.; Wang, Z.R. Analysis of continuous dynamic monitoring of vibratory compaction process of graded aggregates. Chin. J. Geotech. Eng. 2005, 11, 35–37. [Google Scholar]
- Jiang, Y.J.; Li, S.C.; Wang, T.L. Numerical simulation method for dynamic triaxial test of graded aggregates. J. Southeast Univ. Nat. Sci. Ed. 2013, 43, 604–609. [Google Scholar]
- Li, S.C. Numerical Simulation of Granular Flow for the Shakedown Behavior of Graded Aggregates. Master’s thesis, Chang’an University, Xi’an, China, 2013. [Google Scholar]



| Gradation Types | Mass Percentage (%) Passing Through the Following Square Mesh Sieve (mm) | |||||
|---|---|---|---|---|---|---|
| 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | |
| Gradation one | 100 | 82 | 70 | 60 | 40 | 0 |
| Gradation two | 100 | 75 | 63 | 52 | 34 | 0 |
| Gradation three | 100 | 70 | 57 | 44 | 27 | 0 |
| Sphere | Wall | |
|---|---|---|
| Normal stiffness (N/m) | 2 × 105/2 × 106/2 × 107/2 × 108 | 1 × 1010 |
| Tangential stiffness (N/m) | 2 × 105/2 × 106/2 × 107/2 × 108 | 1 × 1010 |
| Friction coefficient | 0.5 | 0.7 |
| Sphere | Wall | |||||
|---|---|---|---|---|---|---|
| Aggregate Size (mm) | 4.75 | 9.5 | 13.2 | 16 | 19 | All |
| Normal stiffness (N/m) | 0.88 × 107 | 0.98 × 107 | 1.10 × 107 | 1.25 × 107 | 2.05 × 107 | 1 × 1010 |
| Tangential stiffness (N/m) | 0.88 × 107 | 0.98 × 107 | 1.10 × 107 | 1.25 × 107 | 2.05 × 107 | 1 × 1010 |
| Friction coefficient | 0.5 | 0.7 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Liu, H.; Zhang, W.; Hei, T.; Ding, X.; Dong, Z. Evaluation of CBR of Graded Crushed Stone of Flexible Base Structural Layer Based on Discrete Element Model. Materials 2023, 16, 363. https://doi.org/10.3390/ma16010363
Hu Z, Liu H, Zhang W, Hei T, Ding X, Dong Z. Evaluation of CBR of Graded Crushed Stone of Flexible Base Structural Layer Based on Discrete Element Model. Materials. 2023; 16(1):363. https://doi.org/10.3390/ma16010363
Chicago/Turabian StyleHu, Zhaoguang, Heng Liu, Weiguang Zhang, Tianqing Hei, Xunhao Ding, and Zezhen Dong. 2023. "Evaluation of CBR of Graded Crushed Stone of Flexible Base Structural Layer Based on Discrete Element Model" Materials 16, no. 1: 363. https://doi.org/10.3390/ma16010363
APA StyleHu, Z., Liu, H., Zhang, W., Hei, T., Ding, X., & Dong, Z. (2023). Evaluation of CBR of Graded Crushed Stone of Flexible Base Structural Layer Based on Discrete Element Model. Materials, 16(1), 363. https://doi.org/10.3390/ma16010363






