High-Sensitivity Sensing in All-Dielectric Metasurface Driven by Quasi-Bound States in the Continuum
Abstract
:1. Introduction
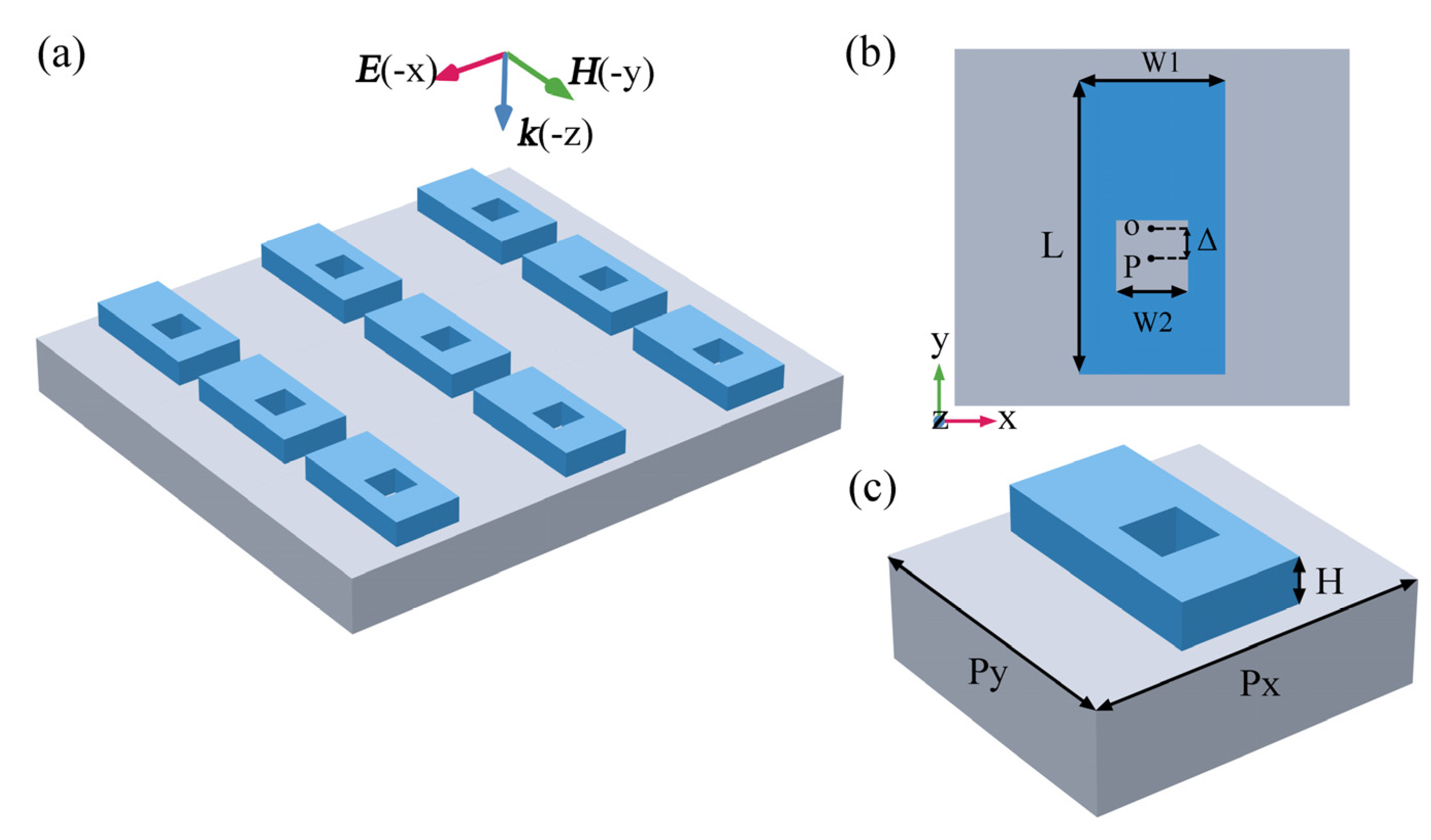
2. Structural Design
3. Results and Discussion
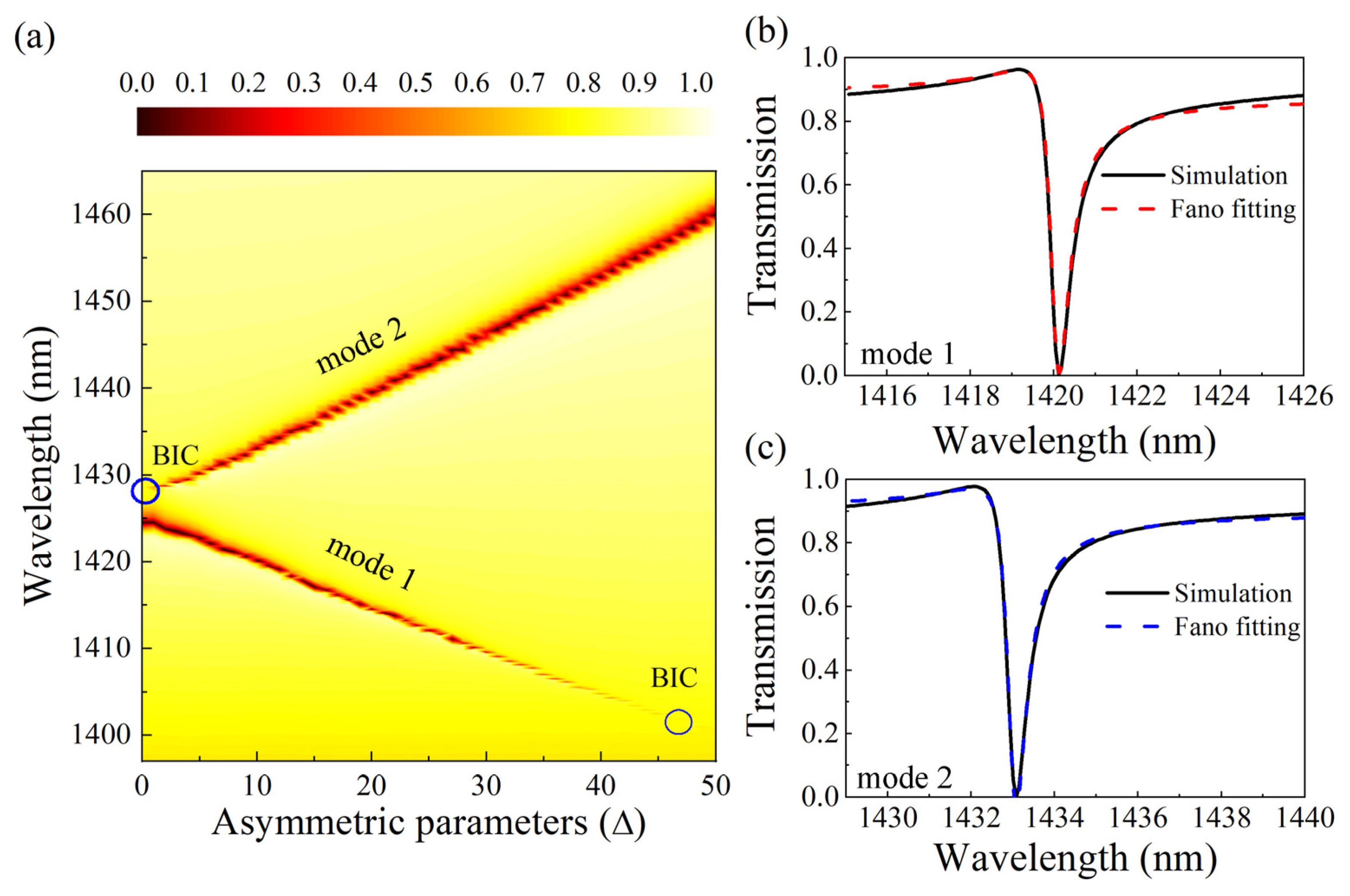
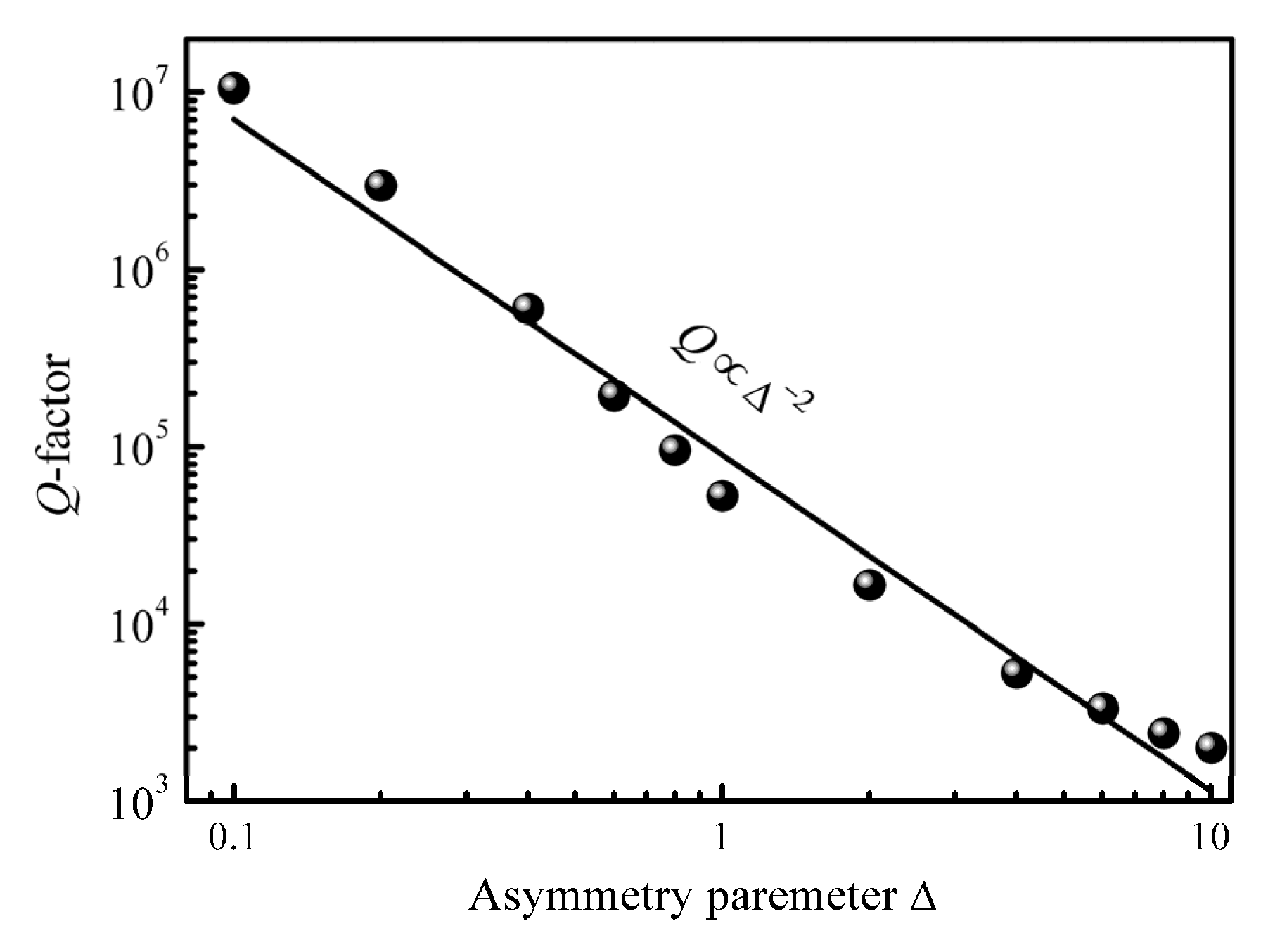
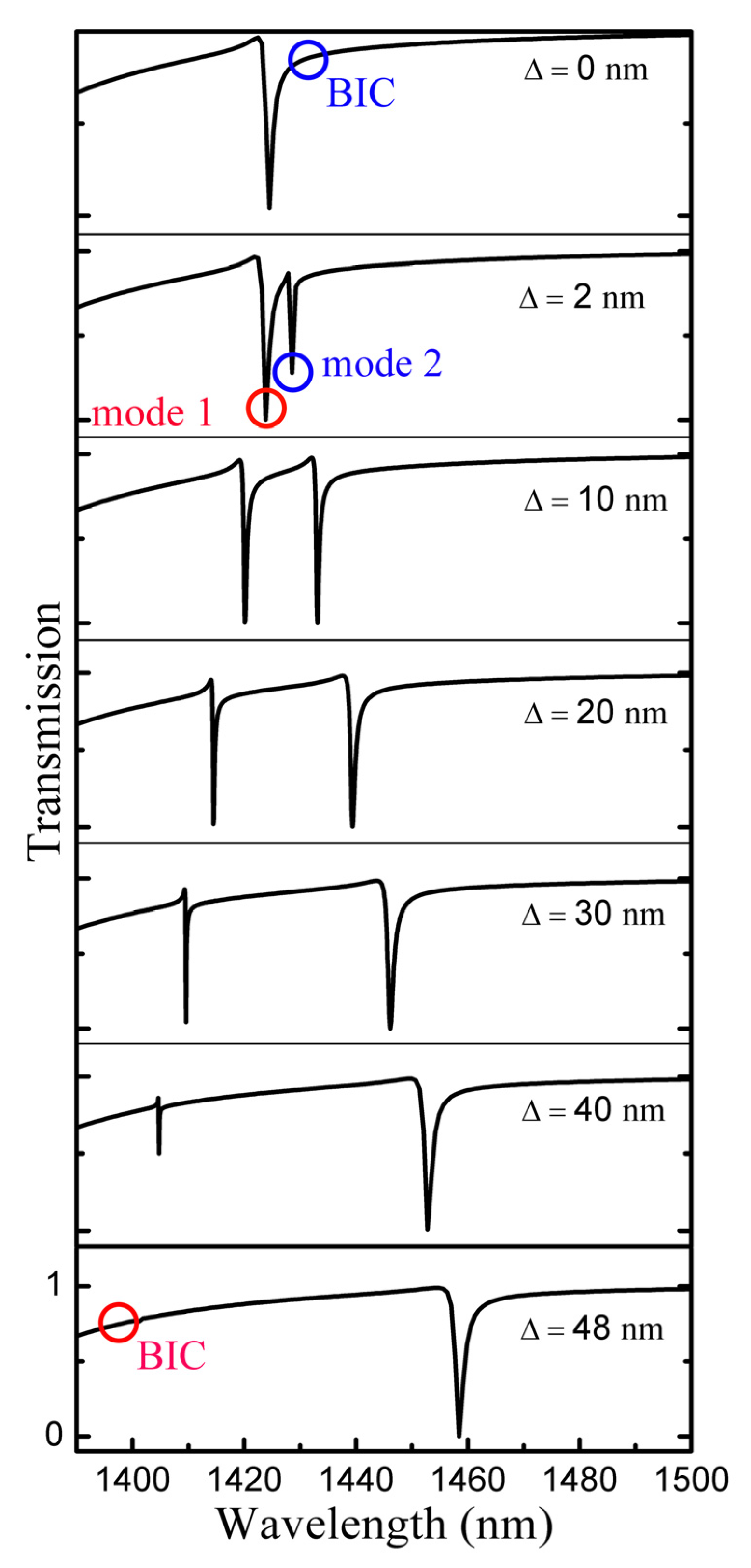
3.1. Resonance Performance Analysis
3.2. Influence of Structural Parameters on Transmission Performance
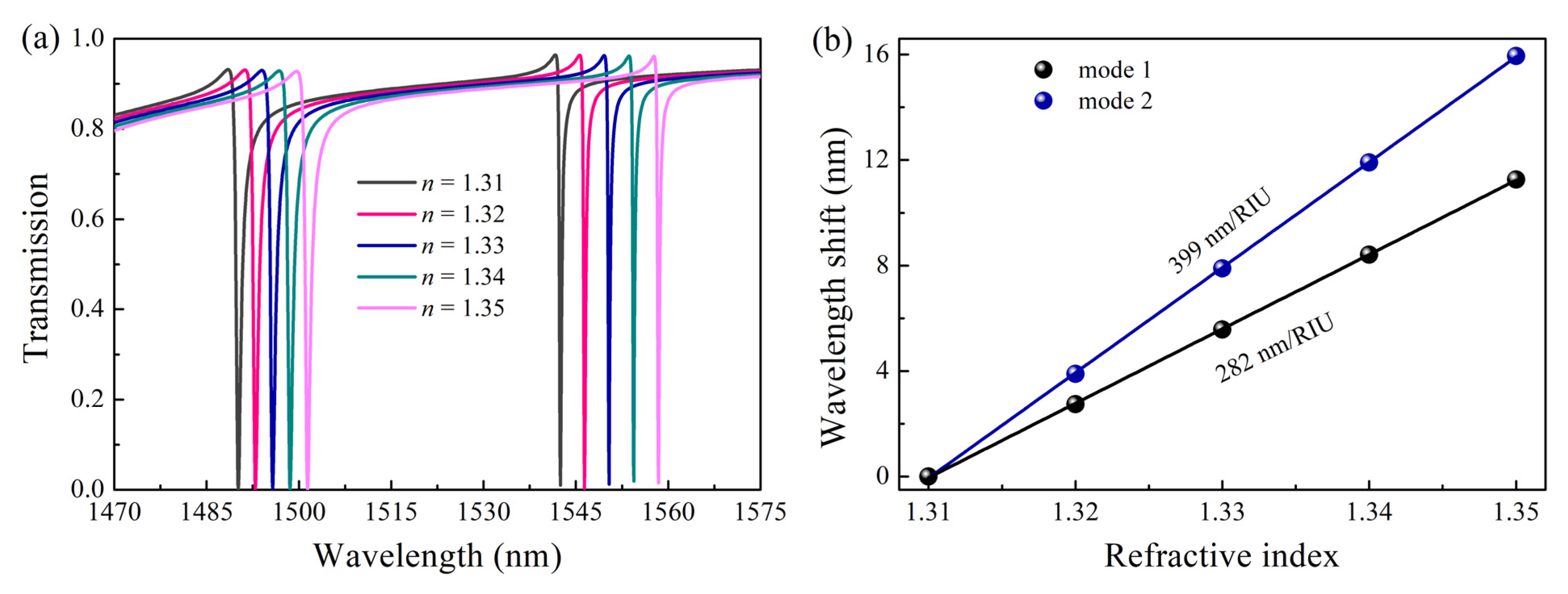
3.3. Analysis of Refractive Index Sensing Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinsey, N.; DeVault, C.; Boltasseva, A.; Shalaev, V.M. Near-zero-index materials for photonics. Nat. Rev. Mater. 2019, 4, 742–760. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Guo, X.; Zhang, J.; Zhang, X.; Li, S.; Yang, C. Asymmetric metasurface structures for light absorption enhancement in thin film silicon solar cell. J. Opt. 2019, 21, 045901. [Google Scholar] [CrossRef]
- Chen, T.; Li, S.; Sun, H. Metamaterials application in sensing. Sensors 2012, 12, 2742. [Google Scholar] [CrossRef] [Green Version]
- Neira, A.D.; Wurtz, G.A.; Ginzburg, P.; Zayats, A.V. Ultrafast all-optical modulation with hyperbolic metamaterial integrated in Si photonic circuitry. Opt. Express 2014, 22, 10987–10994. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Ding, C.; Jiang, L.; Wu, L.; Gao, R.; Xu, D.; Zhang, G.; Yao, J. Dual-band ultrasensitive THz sensing utilizing high quality Fano and quadrupole resonances in metamaterials. Opt. Commun. 2015, 350, 103–107. [Google Scholar] [CrossRef]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef]
- Bi, K.; Wang, Q.; Xu, J.; Chen, L.; Lan, C.; Lei, M. All-dielectric metamaterial fabrication techniques. Adv. Opt. Mater. 2021, 9, 2001474. [Google Scholar] [CrossRef]
- Cen, W.; Lang, T.; Wang, J.; Xiao, M. High-Q Fano Terahertz resonance based on bound states in the continuum in All-dielectric metasurface. Appl. Surf. Sci. 2022, 575, 151723. [Google Scholar] [CrossRef]
- Jeong, J.; Goldflam, M.D.; Campione, S.; Briscoe, J.L.; Vabishchevich, P.P.; Nogan, J.; Sinclair, M.B.; Luk, T.S.; Brener, I. High Quality Factor Toroidal Resonances in Dielectric Metasurfaces. ACS Photonics 2020, 7, 1699–1707. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, Z.; Meng, D.; Qin, Z.; Fan, Y.; Shi, X.; Smith, D.R.; Hou, E. All-dielectric refractive index sensor based on Fano resonance with high sensitivity in the mid-infrared region. Results Phys. 2021, 24, 104129. [Google Scholar] [CrossRef]
- Song, S.; Yu, S.; Li, H.; Zhao, T. Ultra-high Q-factor toroidal dipole resonance and magnetic dipole quasi-bound state in the continuum in an all-dielectric hollow metasurface. Laser Phys. 2022, 32, 025403. [Google Scholar] [CrossRef]
- Marinica, D.; Borisov, A.; Shabanov, S. Bound states in the continuum in photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Koshelev, K.; Zhang, F.; Lin, H.; Lin, S.; Wu, J.; Jia, B.; Kivshar, Y. Bound States in the Continuum in Anisotropic Plasmonic Metasurfaces. Nano Lett. 2020, 20, 6351–6356. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, H.; Lin, S.; Wu, J.; Li, W.; Meng, F.; Yang, Y.; Huang, X.; Jia, B.; Kivshar, Y. Hybrid anisotropic plasmonic metasurfaces with multiple resonances of focused light beams. Nano Lett. 2021, 21, 8917–8923. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, C.; Huo, Y.; Cui, P.; Song, M.; Liu, T.; Zhao, C.; Liao, Z.; Zhang, Z.; Xie, Y. Efficient Excitation and Tuning of Multi-Fano Resonances with High Q-Factor in All-Dielectric Metasurfaces. Nanomaterials 2022, 12, 2292. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, L.; Jin, R.; Xu, L.; Li, G.; Rahmani, M.; Chen, X.; Lu, W.; Miroshnichenko, A.E. Bound States in the Continuum in Asymmetric Dielectric Metasurfaces. Laser Photonics Rev. 2022, 2200564. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photonics 2019, 1, 016001. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Cong, L.; Srivastava, Y.K.; Qiang, B.; Rybin, M.V.; Kumar, A.; Jain, R.; Lim, W.X.; Achanta, V.G.; Prabhu, S.S. All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum. Adv. Mater. 2019, 31, 1901921. [Google Scholar] [CrossRef]
- Kyaw, C.; Yahiaoui, R.; Burrow, J.A.; Tran, V.; Keelen, K.; Sims, W.; Red, E.C.; Rockward, W.S.; Thomas, M.A.; Sarangan, A. Polarization-selective modulation of supercavity resonances originating from bound states in the continuum. Commun. Phys. 2020, 3, 212. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Liu, T.; Xiao, S. Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces. Phys. Rev. A 2019, 100, 063803. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-protected dual bound states in the continuum in metamaterials. Adv. Opt. Mater. 2019, 7, 1900383. [Google Scholar] [CrossRef]
- Fang, C.; Yang, Q.; Yuan, Q.; Gan, X.; Zhao, J.; Shao, Y.; Liu, Y.; Han, G.; Hao, Y. High-Q resonances governed by the quasi-bound states in the continuum in all-dielectric metasurfaces. Opto-Electron. Adv. 2021, 4, 06200030. [Google Scholar] [CrossRef]
- Hu, P.; Wang, J.; Jiang, Q.; Wang, J.; Shi, L.; Han, D.; Zhang, Z.-Q.; Chan, C.T.; Zi, J. Global phase diagram of bound states in the continuum. Optica 2022, 9, 1353–1361. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, L.; Xiong, L.; Qi, J.; Li, B. High Q-factor multiple Fano resonances for high-sensitivity sensing in all-dielectric metamaterials. OSA Contin. 2019, 2, 2818–2825. [Google Scholar] [CrossRef]
- Long, X.; Zhang, M.; Xie, Z.; Tang, M.; Li, L. Sharp Fano resonance induced by all-dielectric asymmetric metasurface. Opt. Commun. 2020, 459, 124942. [Google Scholar] [CrossRef]
- Peng, C.; Feng, C.; Xia, J.; Yap, C.; Zhou, G. Near-infrared Fano resonance in asymmetric silicon metagratings. J. Opt. 2020, 22, 095102. [Google Scholar] [CrossRef]
- Kupriianov, A.S.; Xu, Y.; Sayanskiy, A.; Dmitriev, V.; Kivshar, Y.S.; Tuz, V.R. Metasurface Engineering through Bound States in the Continuum. Phys. Rev. Appl. 2019, 12, 014024. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Han, Z.; Du, Y.; Qin, J. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 2021, 10, 1295–1307. [Google Scholar] [CrossRef]
- Campione, S.; Liu, S.; Basilio, L.I.; Warne, L.K.; Langston, W.L.; Luk, T.S.; Wendt, J.R.; Reno, J.L.; Keeler, G.A.; Brener, I. Broken symmetry dielectric resonators for high quality-factor Fano metasurfaces. Acs Photonics 2016, 3, 2362–2367. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Zhou, C.; Yuan, S.; Qiu, X.; Zhu, L.; Wang, Y.; Li, Y.; Song, J.; Huang, Q.; Wang, Y. Multiple Fano Resonances in Symmetry-Breaking Silicon Metasurface for Manipulating Light Emission. Acs Photonics 2018, 5, 4074–4080. [Google Scholar] [CrossRef]
- Lopez, G.; Estevez, M.C.; Soler, M.; Lechuga, L. Recent advances in nanoplasmonic biosensors: Applications and lab-on-a-chip integration. Nanophotonics 2016, 6, 123–136. [Google Scholar] [CrossRef]
- Smalley, J.S.T.; Ren, X.; Lee, J.Y.; Ko, W.; Joo, W.-J.; Park, H.; Yang, S.; Wang, Y.; Lee, C.S.; Choo, H.; et al. Subwavelength pixelated CMOS color sensors based on anti-Hermitian metasurface. Nat. Commun. 2020, 11, 3916. [Google Scholar] [CrossRef]
- Zhong, J.; Ghosh, P.; Li, Q. All-Dielectric Metasurface Refractive Index Sensor with Microfluidics. J. Phys. Conf. Ser. 2021, 1838, 012001. [Google Scholar] [CrossRef]
- Lim, W.X.; Manjappa, M.; Pitchappa, P.; Singh, R. Shaping High-Q Planar Fano Resonant Metamaterials toward Futuristic Technologies. Adv. Opt. Mater. 2018, 6, 1800502. [Google Scholar] [CrossRef]
- Yang, L.; Yu, S.; Li, H.; Zhao, T. Multiple Fano resonances excitation on all-dielectric nanohole arrays metasurfaces. Opt. Express 2021, 29, 14907–14916. [Google Scholar] [CrossRef] [PubMed]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An electromagnetic multipole expansion beyond the long-wavelength approximation. Opt. Commun. 2018, 407, 17–21. [Google Scholar] [CrossRef] [Green Version]
- Song, D.; Wang, H.; Deng, M.; Wang, Y. Toroidal dipole Fano resonances supported by latticeperturbed dielectric nanohole arrays in the nearinfrared region. Appl. Opt. 2021, 60, 3458–3463. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Xue, T.; Zhang, J.; Liu, L.; Xie, J.; Wang, G.; Yao, J.; Zhu, W.; Ye, X. Terahertz toroidal metasurface biosensor for sensitive distinction of lung cancer cells. Nanophotonics 2022, 11, 101–109. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, G.; Ban, G.; Li, S.; Huang, Q.; Xia, J.; Wang, Y.; Zhan, M. Tunable Fano resonator using multilayer graphene in the near-infrared region. Appl. Phys. Lett. 2018, 112, 101904. [Google Scholar] [CrossRef]
- Zhong, Y.; Du, L.; Liu, Q.; Zhu, L.G.; Zhang, B. All-Silicon Terahertz Metasurface With Sharp Fano Resonance and Its Sensing Applications. IEEE Photonics J. 2021, 13, 4600210. [Google Scholar] [CrossRef]
- Maksimov, D.N.; Gerasimov, V.S.; Romano, S.; Polyutov, S.P. Refractive index sensing with optical bound states in the continuum. Opt. Express 2020, 28, 38907–38916. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, C.; Li, H.; Gong, Q.; Chen, J. Self-reference plasmonic sensors based on double Fano resonances. Nanoscale 2017, 9, 11085–11092. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, X.-S.; Shi, Y.-W. An Optical Fiber Refractive Index Sensor Based on the Hybrid Mode of Tamm and Surface Plasmon Polaritons. Sensors 2018, 18, 2129. [Google Scholar] [CrossRef] [Green Version]
- Yildirim, D.U.; Ghobadi, A.; Soydan, M.C.; Gokbayrak, M.; Toprak, A.; Butun, B.; Ozbay, E. Colorimetric and Near-Absolute Polarization-Insensitive Refractive-Index Sensing in All-Dielectric Guided-Mode Resonance Based Metasurface. J. Phys. Chem. C 2019, 123, 19125–19134. [Google Scholar] [CrossRef]
- Yao, J.; Ou, J.-Y.; Savinov, V.; Chen, M.K.; Kuo, H.Y.; Zheludev, N.I.; Tsai, D.P. Plasmonic anapole metamaterial for refractive index sensing. PhotoniX 2022, 3, 23. [Google Scholar] [CrossRef]



| Reference Year | Material | Structure | Sensitivity (nm/RIU) | FOM (RIU−1) |
|---|---|---|---|---|
| [48] 2017 (Exprement) | Au | grating | 470 | 31 |
| [49] 2018 (Simulation) | TiO2/SiO2/Ag | Fiber | 2610 | 168 |
| [50] 2019 (Simulation) | Si3N4, SiO2 | Grating-waveguide | 110 | 190 |
| [13] 2020 (Exprement) | SiO2 | hollow cuboids | 161 | 80 |
| [14] 2021 (Simulation) | Si | Lucky knot | 986 | 32.7 |
| [51] 2022 (Simulation) | Au | Split ring-dumbbell | 445 | 1.5 |
| This work (Simulation) | Si | Square hole | 399 | 1281 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Z.; Jiaxian, W.; Lizhen, G.; Weibin, Q. High-Sensitivity Sensing in All-Dielectric Metasurface Driven by Quasi-Bound States in the Continuum. Nanomaterials 2023, 13, 505. https://doi.org/10.3390/nano13030505
Jing Z, Jiaxian W, Lizhen G, Weibin Q. High-Sensitivity Sensing in All-Dielectric Metasurface Driven by Quasi-Bound States in the Continuum. Nanomaterials. 2023; 13(3):505. https://doi.org/10.3390/nano13030505
Chicago/Turabian StyleJing, Zhao, Wang Jiaxian, Gao Lizhen, and Qiu Weibin. 2023. "High-Sensitivity Sensing in All-Dielectric Metasurface Driven by Quasi-Bound States in the Continuum" Nanomaterials 13, no. 3: 505. https://doi.org/10.3390/nano13030505
APA StyleJing, Z., Jiaxian, W., Lizhen, G., & Weibin, Q. (2023). High-Sensitivity Sensing in All-Dielectric Metasurface Driven by Quasi-Bound States in the Continuum. Nanomaterials, 13(3), 505. https://doi.org/10.3390/nano13030505








