Scheduling by NSGA-II: Review and Bibliometric Analysis

Abstract

NSGA-II is an evolutionary multi-objective optimization algorithm that has been applied to a wide variety of search and optimization problems since its publication in 2000. This study presents a review and bibliometric analysis of numerous NSGA-II adaptations in addressing scheduling problems. This paper is divided into two parts. The first part discusses the main ideas of scheduling and different evolutionary computation methods for scheduling and provides a review of different scheduling problems, such as production and personnel scheduling. Moreover, a brief comparison of different evolutionary multi-objective optimization algorithms is provided, followed by a summary of state-of-the-art works on the application of NSGA-II in scheduling. The next part presents a detailed bibliometric analysis focusing on NSGA-II for scheduling applications obtained from the Scopus and Web of Science (WoS) databases based on keyword and network analyses that were conducted to identify the most interesting subject fields. Additionally, several criteria are recognized which may advise scholars to find key gaps in the field and develop new approaches in future works. The final sections present a summary and aims for future studies, along with conclusions and a discussion.

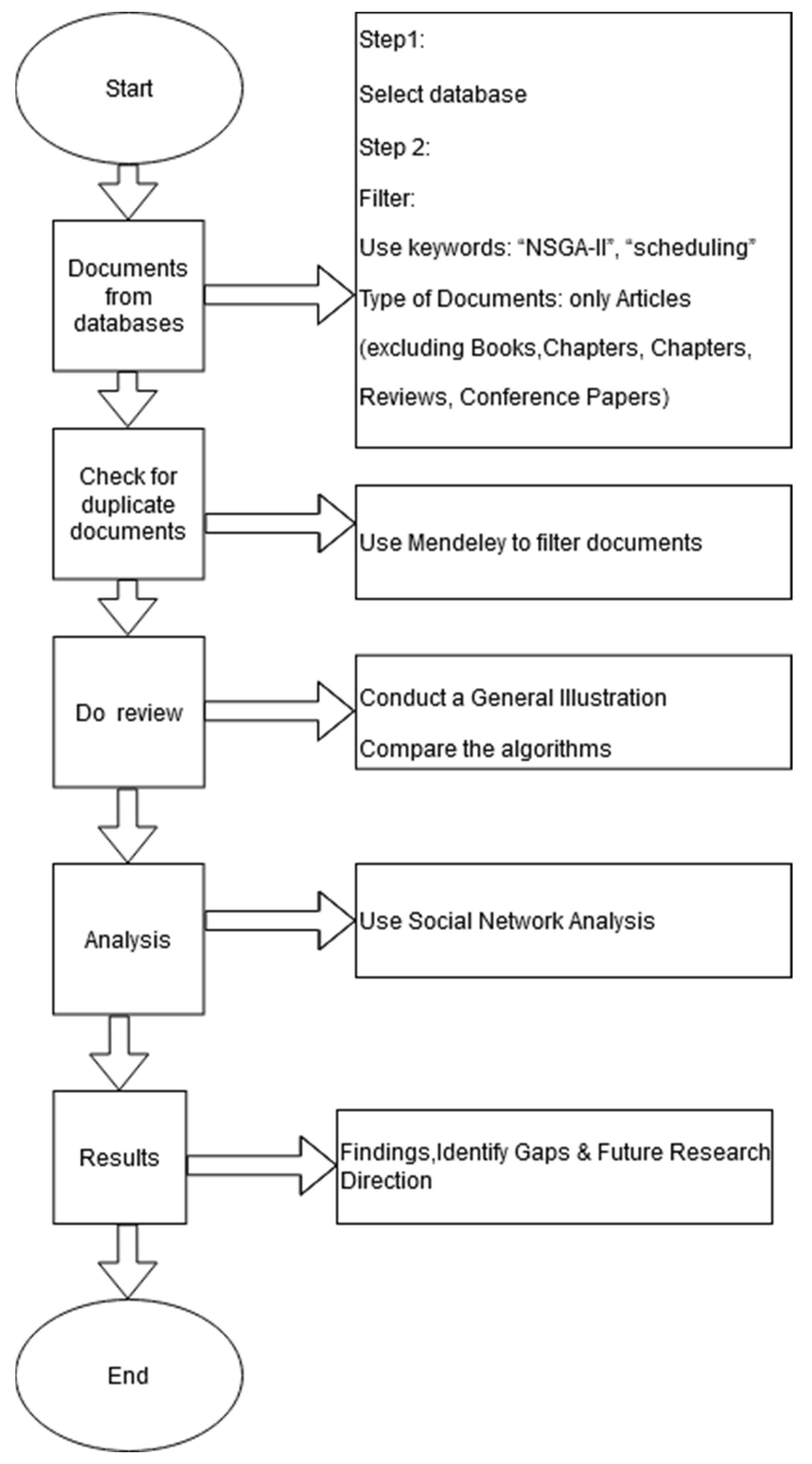
1. Introduction

Non-Dominated Sorting Genetic Algorithm II (NSGA-II) [1] has been proposed as a powerful decision space exploration engine based on a genetic algorithm for solving multi-objective optimization problems. The NSGA-II algorithm has been applied to a wide variety of search and optimization problems since its publication in 2000.

Scheduling problems are dedicated to allocating tasks to resources. Two major schools of thought in relation to schedule generation are algorithmic and knowledge-based approaches [2]. The first approach is based on a mathematical formulation that includes objective function(s) and constraints, while the second approach is not easy to explain in an analytical format and is often used in cases where a feasible solution is sufficient. In addition, scheduling problems are generally known to be complex, large-scale, challenging, NP-hard, and involve several constraints [3,4].

Therefore, discovering efficient and low-cost procedures for use of the scheduling systems is significantly essential. Although numerous techniques have been proposed to solve the optimization problem mentioned above, there is still a crucial need for more suitable techniques. A viable method to manage these issues is to employ global optimization algorithms, including exact optimization methods (e.g., branch-and-bound and branch-and-cut) and, in some cases, evolutionary computation (EC) techniques [5,6,7,8,9]. EC techniques have been employed for large, complex real-world problems that cannot be solved using classical methods [10,11,12].

Another serious problem is that numerous objectives could be identified to optimize systems simultaneously. Hence, several objectives must usually be identified for optimizing a real-world scheduling problem. Furthermore, multi-objective optimization problems arise naturally in most disciplines, and solving them has been a challenging issue for researchers. Although a variety of techniques have been developed in operations research and other fields to address these problems, alternative approaches are urgently needed because of the complexities of their solutions [13,14,15]. Since EC methods are identified as the more effective methods to handle this limitation, they are suitable for solving multi-objective optimization problems (MOOPs) [12,16]. EC approaches repeatedly modify a population of individual solutions to find the optimal set of solutions to a problem. Additionally, multi-objective evolutionary algorithms are able to find a set of non-dominated solutions, known as Pareto solutions, in a single run within an ideal time [12,17,18]. Among the EC approaches, genetic algorithm (GA)-based solution methods are quickly gaining popularity due to their dependence on the population and, therefore, are suitable for solving MOOPs.

Non-dominated sorting is a technique used to assign solutions in a population to different Pareto fronts according to their dominance relationships. Because individuals of the population in the first front have the maximum fitness value, they can obtain more copies [1,12,19]. The NGA-II [1,20] is a well-known evolutionary computation technique that has been used widely by researchers, with more than 40,000 citations as of April 2021. Owing to its lower computational complexity, elitism, and parameterless nature [20,21,22,23], it has been applied to a wide variety of search and optimization problems since its introduction. The NSGA-II algorithm creates a population of individuals, ranks and sorts each individual based on the nondomination level, and then performs crowding distance sorting to keep the population diverse [1]. This paper presents a review of the application of NSGA-II in scheduling problems.

To better understand the research field in this study and provide new insights from publications, the information provided in this work attempts to answer the following questions:

• What is the basic concept of scheduling, and why is NSGA-II important (Section 2)?
• What is the contribution of NSGA-II in scheduling (Section 3.2)?
• What are the different types of scheduling? Which fields of scheduling are the most important (Section 2)?
• What are the most important problems in scheduling, how do researchers tackle them, and what do researchers find from their experiments (Section 2 and Section 3.2)?
• What are the main topics and keywords regarding NSGA-II and scheduling problems (Section 4)?
• Which journals have the most contributions in the field? Who are the best researchers in the area, and what are their respective countries of origin (Section 4)?
• What are the current gaps and future trajectories in scheduling (Section 5 and Section 6)?

After a brief introduction of different scheduling problems, scheduling algorithms are introduced. A comparison of algorithms in both single-objective and multi-objective scheduling problems is addressed, followed by introducing the application of NSGA-II in scheduling problems. Moreover, scientometric analysis is conducted in the field. The last section provides a summary and future studies.

The research procedure in this work was divided into five stages (Figure 1). In the first stage, documents were gathered from the Scopus (https://www.scopus.com/ 31 December 2020) and WoS (https://clarivate.com/products/web-of-science/ 31 December 2020) databases. Before initiating the search in the databases, special keywords, namely “NSGA-II” AND “scheduling”, were searched for in titles, abstracts, and keywords to identify related articles. First, the authors filtered the documents with the special keywords to find the results, such as the type of objective function, problem statement, and solution approaches. Second, in some special cases where the research methodology using the title, abstract, and keywords did not help, the content of the papers was reviewed.

It is worthy to note that this work reviewed only the research article type, excluding books, book chapters, reviews, conference papers, and short letters, and 683 and 875 published articles (between 2000 and 2020) were extracted from WOS (Supplementary Material A) and Scopus (Supplementary Material B), respectively. Since some of the articles were duplicates, they were identified and removed from the library in stage 2 using Mendeley as a powerful reference manager. In addition, some research questions for this study were designed in stage 2. A comprehensive review was initiated in stage 3 with a general illustration of the basic concepts of scheduling and comparison of the algorithms. In stage 4, social network analysis was performed to provide a scientometric analysis of the documents using VOSviewer 1.6.17 and CitNetExplorer 1.0.0 [24,25], which have been identified as powerful tools for scientometric analysis. Stage 4 required several steps, including co-occurrence, co-authorship, citation, bibliographic coupling, and citation network analyses. In the last stage, the results were obtained to formulate a discussion to answer the proposed research questions. In stage 5, the findings were prepared, important gaps were identified, and future research directions were determined.

The remainder of the paper is organized as follows. Section 2 gives an overview of the scheduling. Section 3 discusses the scheduling algorithms, the solution methods based on the genetic algorithm in scheduling, and state-of-the-art works on the application of NSGA-II in scheduling. Section 4 presents a detailed scientometric analysis in the field. Finally, a summary and suggested future studies are given in Section 5, followed by concluding remarks and a discussion in Section 6.

2. Overview of Scheduling

The following subsections provide an overview of the different aspects of scheduling in manufacturing and services.

2.1. Scheduling

Scheduling and sequencing are the processes of arranging and optimizing the manufacturing and service activities that play an important role in industries [3,26]. Firms use backward and forward scheduling to allocate plants and resources, plan production processes, and purchase materials [27,28,29]. In addition, the benefits of production scheduling include the following: inventory reduction, leveling [30,31,32], increased production efficiency [33,34,35], accurate delivery date quotes [36,37,38], and real-time information [39,40,41,42,43]. “Manufacturing model” specifies the machine(s) or resource configuration used in the production process. Classification of scheduling in manufacturing was built over the last few decades, and it is proven and applied in defining the complexity of a scheduling problem. Since the mathematical model is related to the machine configuration, the system uses the machine configuration instead of the industry type for categorizing problems [44,45].

Table 1. Classification of different scheduling models.

Manufacturing Model	Model Type
Single	Linear Programing
Parallel Machines	Mixed-Integer Programming
Job-Shop	Mixed-Integer Quadratic Programming
Flow- or Open-Shop	Mixed-Integer Non-Linear Programming
Flexible Manufacturing	Queuing Techniques and Simulation
Lot Scheduling System
Project Scheduling
Objective Function	Constraints
Economic-Related Objective	Economic-Related Constraints
Minimize Makespan	Makespan Equation
Minimize or Maximize Tardiness	Makespan Value Limitation
Minimize Electricity Cost	Tardiness Equation
Minimize Labor Cost	Tardiness Value Limitation
Minimize Inventory Cost, etc.	Amount of Demand
Environment-Related Objective	Total Energy Cost
Minimize Total Energy Consumption	Energy Cost in Specific Mode
Minimize Peak Power	Electricity Price
Minimize Carbon Emissions	Revenue from Power Sold
Minimize Squatted Deviation	Labor Cost Equation, etc.
Maximize Utilization	Environment-Related Constraints
Minimize Water Consumption	Power’s Peak Constraint
Maximize Total Availability System, etc.	Total Energy Consumption
Social-Related Objective	Energy Consumption in Specific Mode
Minimize Noise Level	Total Power Supply
	Capacity Limitation
	Duration of Initiatives
	Carbon Emissions Value Limitation
	Carbon Emissions Equation
	Amount of Water
	Water Quality Class Function
	Cleaning Cost
	Amount of Water Discharge
	Amount of Contaminant
	Waste Water and Effluent Limitation, etc.
	Social-Related Constraints
	Recovery Time Ergonomic Time Value Limitation, etc.

presents a classification of different models.

2.1.1. Scheduling in Manufacturing

In industry, each order should be converted into a list of operations that the organization must carry out. These operations should be handled by different machines and are based on certain sequences. It is pertinent to note that the provided schedule of the organizations helps to optimize the strategic usage of resources, forecasting of demands, and resource requirements. Single-machine scheduling or single-resource scheduling is an optimization problem in computer science and operations research. We are given n jobs of varying processing times, which need to be scheduled on a single machine in a way that optimizes a certain objective. Parallel machine scheduling (PMS) is for scheduling jobs processed on a series of machines with the same function with the optimized objective.

In a general job scheduling problem, we are given n jobs of varying processing times, which need to be scheduled on m machines with varying processing power, while trying to minimize the makespan (i.e., the total length of the schedule). Flow-shop scheduling is a special case of job-shop scheduling where there is a strict order of all operations to be performed on all jobs. Flow-shop scheduling may apply to production facilities for computing designs as well.

Machine Scheduling

This type of scheduling includes single-machine, parallel-machine, multi-stage flow-shop, multi-stage flexible (hybrid) flow-shop, multi-stage assembly flow-shop, job-shop, flexible job-shop, or open-shop flow-shop, job-shop, and open-shop [46,47,48,49,50]. For example, there are several objectives pertaining to job-shop scheduling problems, including maximizing completion time ($C_{max}$), total flow time ($C_{total}$), machine workload ($W_{max}$), total machine workload ($W_{total}$), and minimizing earliness or tardiness (E/T).

Flexible Manufacturing

A flexible manufacturing system (FMS) is a production approach which is designed to easily adjust to changes in the type and quantity of the product being produced. As a result, flexible manufacturing can be an important element of a make-to-order strategy that allows customers to customize the products [51,52,53,54].

Lot Scheduling System

This type of scheduling is suitable for tactical and strategic processes. Unlike the previous three classes, the production and demand processes are continuous. The objective functions of lot scheduling include minimizing inventory and cost [55,56,57].

2.1.2. Personnel Scheduling

In personnel scheduling, a good schedule should satisfy management and increase the time an employee stays with an employer [1]. All problems are originally divided into static and dynamic categories. Static scheduling has a structure that does not change over time. An example could be a 3-month flight schedule chart at an airport. Dynamic scheduling often has a variable schedule structure. There are several scheduling classifications in the literature. As an example, Figure 2 presents a classification of personnel scheduling in service system scheduling. An example is given in the resource schedules [58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101].

3. Scheduling Algorithms

This section and the following subsections aim to justify the importance of NSGA-II and compare it with other evolutionary algorithms statistically and briefly.

Several optimization methods have been addressed in the literature to solve scheduling problems in addition to different classifications for solving optimization problems, namely the exact and approximate approaches (Figure 3). Exact methods include the efficient rule approach [49], mathematical programming approach [102], and branch-and-bound method [103,104]. Approximate methods pertain to constructive methods [105,106,107], artificial intelligence methods [108], local search methods [109], and metaheuristic approaches [110,111]. While exact methods are typically expensive in terms of computing time and often result in poor quality solutions, metaheuristic approaches produce alternative optimal solutions in a single run [112]. Most exact solution approaches convert MOOPs into a single optimization problem, while metaheuristic methods solve MOO problems without this conversion. Some metaheuristics incorporate certain mathematical methods [113], and others are suitable for solving global optimization problems [114].

For example, the authors of [115] proposed an idea and scheduling for a flexible job-shop (FJS) based on a hierarchical approach considering multiple performance objectives. A genetic algorithm for generating robust solutions for flexible job-shop schedules was introduced in [116].

The authors of [117] presented a two-job-shop scheduling problem with unrelated machines and solved it using the classical geometric approach. A hybrid algorithm based on swarm optimization and simulated annealing for solving multi-objective flexible job-shop scheduling problems was introduced in [118]. The authors of [119] presented a mixed-integer nonlinear program for solving common cycle economic lot scheduling in flexible job-shops. The latter study considered a combination of job-shops and parallel machines, and the authors suggested an efficient enumeration method for solving the mentioned problem. An integer linear programming model for flexible job-shop scheduling for the jobs that were on a make-to-order basis was proposed in [120]. The authors of [121] used a genetic algorithm approach for solving FJS scheduling under resource constraints. A Tabu search approach for flexible job-shop scheduling by minimizing $C_{max}$ was proposed in [122]. The authors of [123] established evolving dispatching rules for solving FJS scheduling using applied genetic programming. In total, more than 29,688 articles have been published in the area of optimization of scheduling problems (since 2000). Among the published articles, the genetic algorithm owns the most contributions (just above 26%) for solving scheduling problems, followed by particle swarm optimization (just above 9%), simulated annealing (6.4%), ant colony optimization (4.09%), and then tau search (4.47%) (Figure 4).

3.1. Genetic Algorithm (GA)-Based Solution Methods

Since genetic algorithms are based on the population, they are suitable for solving MOO problems. The most famous MOO algorithms based on genetic algorithms are as follows:

• VEGA (Vector-Evaluated Genetic Algorithm) [124]
• MOGA (Multi-Objective Genetic Algorithm) [125]
• WBGA (Weighted Based Genetic Algorithm) [126]
• RWGA (Random Weighted Genetic Algorithm) [127]
• NSGA (Non-Dominated Sorted Genetic Algorithm) [128]
• NSGA-II (Fast Non-Dominated Sorted Genetic Algorithm) [20]
• RDGA (Rank Density-Based Genetic Algorithm) [129]
• NPGA (Niched Pareto Genetic Algorithm) [130,131]
• DMOEA (Dynamic Multi-Objective Evolutionary Algorithm) [132]

Table 2. Comparison of different GA-based solution methods.

Algorithm	Fitness Function	Diversity	Elitism	Strengths	Weakness
VEGA [133,134,135,136]	Select subpopulation using an objective function	No	No	Easy to code	Fast convergence to an objective function
MOGA [137,138,139]	Pareto ranking	Using fitness function	No	Extension of single objective	Slow convergence and dependency on niche size parameter
WBGA [140]	Average normalized weighted objective function	Identifying weights	No	Extension of single objective	Difficulty in nonconvex space
RWGA [141,142]	Average normalized weighted objective function	Assign weight randomly	Yes	Easy to code	Difficulty in nonconvex space
RDGA [143]	Ranking based and reducing problem	Non-concentration based on cells	Yes	Updated cells	Difficulty in run
NPGA [144,145,146,147,148]	No	Niche count	No	Easy tournament selection	Dependency on niche size parameter
DMOEA [149]	Ranking based on cells	Adjusting density of cells	Yes	Updated cells	Difficulty in run
NSGA [150,151,152,153,154]	Ranking based on non-dominated solutions	Using fitness function	No	Fast convergence	Dependency on niche size parameter
NSGA-II [22,155,156,157,158,159]	Ranking based on non-dominated solutions	Crowding distance	Yes	Uses non-dominated sorting, crowding distance, and elitist techniques	Crowding distance performs only in objective functions

presents a comparison of the above-mentioned genetic algorithms based on three criteria: elitism, diversity, and fitness function.

3.2. NSGA-II

Most evolutionary multi-objective optimization (EMO) algorithms possess the following difficulties:

• Computational cost in non-dominated sorting increases significantly when the population increases;
• Lack of elitism reduces the algorithm’s performance and inhibits individuals with good fitness values in different generations;
• Difficulty in the parameter settings largely affects the performance of the majority of evolutionary algorithms.

To alleviate these difficulties, NSGA-II was proposed in 2000 [19] and has become one of the most popular EMO algorithms in use to date, along with multi-objective particle swarm optimization (MOPSO) and multi-objective ant colony optimization (MOACO). Figure 5 shows the trend of published articles considering the contributions of these algorithms. Since 2014, NSGA-II has been the most studied algorithm in scheduling, followed by MOPSO then MOACO.

The authors of [20] proposed NSGA-II as a revised version of the NSGA [128] that has lower computational complexity, is parameterless, and possesses elitism [20]. NSGA-II has been applied in many different fields of study by numerous researchers [22,160,161,162,163,164]. Figure 6 presents the total citations of original NSGA-II papers over the years and indicates that NSGA-II has been considered by numerous researchers.

Table 3. Summary of the literature review on NSGA-II applications in different fields, along with methodology and results.

Source	Problem	Objective	Methodology	Results and Findings
[165]	Weapon selection and planning problem	Optimizing net present value (NPV) and effectiveness	An MOEA based on NSGA-II is employed	The proposed measures are able to adapt to dynamic changes.
[166]	Allocation problem	Integrating MOMO process and Monte Carlo simulation technique.	Integrating MOMO, NSGA-II, and Tabu search	The MOMO technique possesses a better performance of seeking global optimum than other proposed methods.
[167]	Satellite scheduling problem	Proposing a multi-objective optimization method to solve the mentioned problem	Designing a decomposition method. Expressing a multi-objective integer-programming model. Designing multi-objective genetic algorithm NSGA-II.	The applicability of the proposed method under different situations has been proven.
[168]	High-dose rate brachytherapy planning	Determining an appropriate schedule of a radiation source	Four different MOEAs have been employed	Results present that MO-RV-GOMEA is the best performing MOEA.
[169]	FJS problem under mixed work calendars	Proposing two key technologies, namely time reckoning and sequential scheduling	Designing NSGA-II with an elite strategy	The suggested technique can gain an effective Pareto set within an acceptable time.

,

Table 4. Summary of the literature review on NSGA-II applications in different fields, along with methodology and results.

Source	Problem	Objective	Methodology	Results and Findings
[170]	Reliability in Cyber-Physical Systems (CPS) components	Designing and verifying CPS using multi-objective evolutionary optimization.	Using three scheduling methods: fixed priority, earliest deadline first, and deadline monotonic.	The results show that the proposed approach can be used to design and validate CPS for performance and verify timing guarantees.
[171]	Job-shop scheduling problem	Minimizing the mean weighted completion time and the sum of the weighted tardiness costs.	Proposing a new integer linear programming. Modifying PSO and comparing with NSGA-II.	The results depict that the proposed PSO outperforms NSGA-II.
[172]	Multi-objective unreliable unbalanced production lines	Maximizes the throughput rate and minimizes the total buffer capacities and cost.	Proposing DOE and RSM along with NRGA and NSGA-II.	The proposed system could be applied to a large-scale production line.

,

Table 5. Summary of the literature review on NSGA-II applications in different fields, along with methodology and results.

Source	Problem	Objective	Methodology	Results and Findings
[173]	Multi-objective traveling salesman problem	Improving a GA-based algorithm, namely Physarum-inspired computational model (PCM).	Using the hill-climbing algorithm to improve the proposed method.	Findings show that the proposed method has a better performance compared with the other MOTSP.
[174]	Project scheduling problem	Proposing a robust project scheduling.	Two-stage multi-objective buffer allocation approach.	The results indicate that the obtained buffered schedule reduces the cost of disruptions.
[175]	Process planning and FJS scheduling.	Makespan, critical machine workload, and machine total workload.	Integration of WGA and NSGA-II.	The proposed algorithm outperforms the exact solutions.

,

Table 6. Summary of the literature review on NSGA-II application in different fields, along with methodology and results.

Source	Problem	Objective	Methodology	Results and Findings
[176]	Generator scheduling considering environmental and economic issues.	Optimal generation scheduling.	Two-phase approach (hourly and 24-h scheduling)	Effectiveness of the proposed approach has been approved.
[177]	Multi-objective spatial forest planning.	Maximizing timber volume and minimizing sediment level.	Spatial NSGA-II approach	The results show that the proposed method has better performance for both constrained and unconstrained problems.
[178]	Resource allocation problem in a hospital.	Daily scheduling for residents or patients in a hospital.	Using variable neighborhood search, scatter search, and NSGA-II	Able to find efficient solutions.
[59]	Nurse scheduling problem considering human factors.	Minimizing the total cost of staffing as well as the sum of incompatibility and maximizing the satisfaction.	Keshtel algorithm, NSGA-II, and Tabu search.	Effectiveness of the proposed methods is approved.

,

Table 7. Summary of the literature review on NSGA-II applications in different fields, along with methodology and results.

Source	Problem	Objective	Methodology	Results and Findings
[179]	Process planning and scheduling	Optimizing the makespan, machine workload, and the total workload of machines.	Multi-objective memetic algorithm.	The results compared with NSGA-II show that the proposed algorithm has better performance.
[180]	Scheduling of locks and transshipment problem	Optimizing water–land transshipment co-scheduling.	Hybrid heuristic method using binary NSGA-II.	The feasibility and the superiority of the model have been verified.
[181]	Integration of process planning and scheduling	Minimizing of makespan, machining cost, and idle time.	Improved version of NSGA-II.	Results provide optimal and robust solutions.
[182]	Sudden drinking water contamination incident	Minimizing the volume of contaminated water and the operational costs.	Integration of NSGA-II and EPANET simulation model.	The validity of the model has been approved by two water distribution networks.

and

Table 8. Summary of the literature review on NSGA-II applications in different fields, along with methodology and results.

Source	Problem	Objective	Methodology	Results and Findings
[183]	Single machine scheduling with controllable processing times.	Developing a new multi-objective discrete backtracking search algorithm.	Through adaptive selection scheme and total cost reduction strategy.	The performance of the proposed method compared with other algorithms was validated.
[184]	Reentrant hybrid flow-shop scheduling.	Optimizing of makespan and total tardiness.	Genetic algorithms with Minkowski distance-based crossover operator.	The results show that NSGA-II outperformed in terms of convergence, diversity, and the dominance of solution.
[185]	Sustainable ship routing and scheduling.	Estimating the total fuel consumed and carbon emission from each vessel as well as improving the service level of the port.	Mixed-integer nonlinear programming using NSGA-II and MOPSO.	The robustness of the model has been approved by experimental results and comparative, and sensitive analysis.

present a summary of the literature review in the scheduling field, where the predominant areas include scheduling problems for job-shop scheduling, routing, satellites, projects, weapon selection, forest planning, and machinery. It is noteworthy to mention that some studies have compared NSGA-II with other well-known evolutionary algorithms, such as MOPSO, Tabu search, and the memetic algorithm. In addition, some authors have tried to improve the original version of NSGA-II and expand it for a specific problem. Optimizing the makespan, machining cost, and idle time are among the top objective functions in the published documents. Multi-objective constrained optimization was also found to be an interesting area for researchers.

Less than 10% (9.51%) of the papers published on NSGA-II in scheduling have addressed uncertainty. Among the above-mentioned papers, the power system owns the most contributions in the field at 32%, followed by project scheduling (13%), resource allocation (8%), and then job-shop scheduling (8%) (shown in Figure 7).

4. Scientometric Analysis

Scientometric analysis is the field of study that scientifically measures and analyzes the literature [186]. Bibliometrics is the most famous field of scientometrics that uses statistics to analyze and measure the impacts of books, research articles, conference papers, etc. [187]. Recently, this field of analysis has attracted much attention from researchers and has been used in various literature review fields [4,188,189,190,191,192]. To achieve this aim, VOSviewer 1.6.17 [24] and CitNetExplorer 1.0.0 [25] were employed in this work. The following subsections provide new insights into scientometric analysis in the field of scheduling.

4.1. Statistics Based on Document Types

Among the document types, including articles, proceedings papers, reviews, and other items indexed by WoS, a total of 683 publications on scheduling and NSGA-II were found (

Table 9. Citation analysis based on document type.

Document type	TP	%	AU	APP	TC2020	CPP2020
Article	462	67.64	1282	2.77	8766	18.97
Proceedings paper	231	33.82	652	2.82	1126	4.87
Review	5	0.73	15	3.0	155	31
Other items	15	2.19	154	10.26	269	17.93

). From the search, articles were the most popular document type with a total of 462 (67.64% of 683 documents) and 2.77 authors per publication (APP). Additionally, reviews as a document type had the highest CPP 2020 of 31, followed by articles (18.97). Moreover, there was a significant difference between the TC 2020 article and that of the proceedings paper. Figure 8 presents the distribution of documents based on different types, according to WoS. It is clear from the figure that proceedings papers had the greatest contributions before 2010, followed by articles. However, since 2010, articles had the most contributions in the field.

TP, AU, APP, TC2020, and CPP2020 refer to the total number of articles, total number of authors, total number of authors for each publication, total citations from WoS since the publication year to the end of 2020, and total citations for each paper, respectively. Other items include early access and letters.

4.2. Keyword Analysis

Figure 9 presents the total citations per year for the published documents (NSGA-II in scheduling). As an overall trend, it is clear that the sum of the number of times articles were cited increased gradually until the end of 2012, and then the trend increased sharply up to 2020. Figure 10 presents a treemap visualization of the different categories found by WoS. Accordingly, computer science artificial intelligence (#86), operation research management science (#86), computer science interdiscipline applications (#82), industrial engineering (#71), and manufacturing engineering (#65) were among the top categories, while computer science information systems (#28), computer science theory methods (#29), and automation control systems (#33) contributed the least in the field.

4.3. Network Visualization

The keywords indicate the basic parts of a certain field of research and can offer insight into the organization and knowledge provided in the articles. Figure 10 and Figure 11 depict the overlay visualization co-occurrence analyses via a network map based on the Scopus and WoS databases, respectively. In Figure 11, “scheduling”, “optimization”, “NSGA-II”, “multi-objective optimization”, “multi-objective genetic algorithm”, “Pareto-optimal”, “makespan”, and “stochastic models” were identified as the top keywords in Scopus. Figure 12 reveals that “genetic algorithm”, “algorithm”, “multi-objective genetic algorithm”, “design”, “cost”, “parallel machines”, “task analysis”, and “operations” were the most important keywords in WoS. The color of each circle represents the identified cluster, and the size of each circle illustrates the importance of the keywords; in other words, the keywords with larger circles were used more than others. The green and yellow colors show the keywords that were used recently, while the dark blue color indicates those that were used earlier (around 2012).

Table 10. The top 10 keywords of 1-word, 2-word, and 3-word lengths (WoS https://clarivate.com December 31, 2020).

1-Word		2-Word		3-Word
Keyword	Frequency	Keyword	Frequency	Keyword	Frequency
NSGA-II	76	Multi-objective optimization	86	Multi-objective genetic algorithm	9
Scheduling	38	Multi-objective	19	Particle swarm optimization	6
Makespan	22	Genetic algorithms	17	Unrelated parallel machine	3
Optimization	10	Energy consumption	13	Differential evolution algorithm	3
Reliability	9	Production scheduling	10	Single machine scheduling	3
Uncertainty	8	Cloud computing	9	Flexible job-shop	3
Microgrid	6	Project scheduling	8	Grey wolf optimizer	3
Metaheuristics	5	Preventive maintenance	8	Job-shop scheduling	3
Tardiness	4	Memetic algorithm	7	Just-in-time	3
Heuristic	3	Dynamic scheduling	6	Charge-discharge scheduling	1

and

Table 11. The top 10 keywords of 1-word, 2-word, and 3-word lengths (Scopus www.scopus.com December 31, 2020).

1-Word		2-Word		3-Word
Keyword	Frequency	Keyword	Frequency	Keyword	Frequency
NSGA-II	100	Preventive maintenance	10	Multi-objective evolutionary algorithm	13
Scheduling	54	NSGA-II algorithm	10	Particle swarm optimization	7
Multi-objective	32	Project scheduling	10	Non-dominated sorting	7
Makespan	28	Evolutionary algorithm	9	Ant colony optimization	6
Reliability	9	Multi-objective scheduling	8	Variable neighborhood search	6
Optimization	9	Optimal scheduling	7	Energy efficient scheduling	6
Microgrid	9	Task scheduling	7	Hybrid flow-shop	4
Metaheuristics	7	Memetic algorithm	6	Controllable processing times	4
Rescheduling	7	Generation scheduling	5	Demand side management	3
Uncertainty	6	Demand response	5	Single-machine scheduling	3

present the top 10 keywords of 1-word, 2-word, and 3-word lengths extracted from WoS and Scopus, respectively. NSGA-II, scheduling, and makespan were the top three one-word-long keywords for both WoS and Scopus. Multi-objective optimization, genetic algorithm, and multi-objective were the top three two-word-long keywords in WoS, while preventive maintenance, NSGA-II algorithm, and project scheduling were the top three two-word-long keywords in Scopus. In WoS, multi-objective genetic algorithm and particle swarm optimization were the top two three-word-long keywords, while EMO algorithm and non-dominated sorting were the top two three-word-long keywords in Scopus.

4.4. Bibliographic Coupling

When two documents reference other common documents, bibliographic coupling occurs [147,193]. Figure 13a–d shows the bibliographic coupling in documents from the WOS database. Specifically, Figure 13a,b presents the network visualization and overlay bibliographic visualization coupling, revealing that most bibliographic coupling [194,195,196,197] occurred prior to 2016 (dark blue), while the yellow color represents recent studies [198,199,200,201]. Figure 13c,d displays the network and overlay visualization bibliographic coupling organization over the studied time period, revealing that the Islamic Azad University (Iran), Capital University of Economics and Business (China), and Hong Kong University of Science and Technology (Hong Kong) were the three top universities in 2016, 2018, and 2020, respectively. Figure 14 shows the density visualization of bibliographic coupling based on item density sources. It is apparent that Computers & Industrial Engineering, International Journal of Advanced Manufacturing Technology, and Applied Soft Computing were three major sources, while Science of the Total Environment, Advanced Science Letters, and the IEEE Internet of Things Journal were three minor sources.

4.5. Publication Statistics Based on the Journal

Table 12. The top 10 productive Scopus categories.

	Scopus	ISSN	Number of Documents
1	Lecture Notes in Computer Science	1611-3349	30
2	Computers and Industrial Engineering	0360-8352	20
3	Robotics and Computer-Integrated Manufacturing	0736-5845	20
4	International Journal of Advanced Manufacturing Technology	1433-3015	19
5	Applied Soft Computing Journal	1568-4946	18
6	International Journal of Production Research	0020-7543	15
7	Advances in Intelligent Systems and Computing	2194-5365	13
8	IEEE Access	2169-3536	13
9	China Mechanical Engineering	2192-8258	13
10	Computers and Operations Research	0305-0548	11

presents the top 10 journals that published the greatest number of related papers based on Scopus. Accordingly, Lecture Notes in Computer Science (#30), Computers and Industrial Engineering (#20), and Computer Integrated Manufacturing Systems (#20) predominated in the field of optimization and evolutionary computations.

A total of 683 articles were published in 432 journals, which were classified among the 46 WoS categories in Sci-Expanded.

Table 13. The top 10 productive WoS categories.

	Web of Science Category	TP	AU	APP	TC 2020	CPP 2020
1	Computer Science Artificial Intelligence	175	523	2.98	2023	11.56
2	Computer Science Theory Methods	49	159	3.24	290	5.91
3	Engineering Electrical Electronic	40	125	3.12	541	13.52
4	Computer Science Interdisciplinary Applications	37	118	3.18	664	17.94
5	Operations Research Management Science	24	82	3.41	418	17.41
6	Automation Control Systems	16	44	2.75	201	12.56
7	Computer Science Information Systems	15	55	3.66	46	3.60
8	Engineering Manufacturing	9	31	3.44	167	18.55
9	Robotics	8	25	3.12	14	1.75
10	Computer Science Cybernetics	7	19	2.71	197	28.14

TP, AU, APP, TC 2020, and CPP 2020 present the total number of articles, total number of authors, total number of authors for each publication, total citations from WoS from the publication year to the end of 2020, and total citations for each paper, respectively. Other items: early access and letters.

lists the 10 most productive WoS categories. A total of 175 articles (25.62% of 683 articles) were published in the first category (computer science artificial intelligence), followed by computer science theory methods (7.17%) and engineering electrical electronic (5.85%). When comparing the top 10 categories, the highest CPP 2020 of articles published in the computer science cybernetics category was 28.14, followed by engineering manufacturing (18.55). The highest APP for articles published in the computer science information systems category was 3.66.

4.6. Statistics Based on Authors

Figure 15 shows the top authors with the most publications according to Scopus. Reza Tavakkoli-Moghaddam from the University of Tehran (Tehran, Iran), Farouk Yalaoui from Université de Technologie de Troyes (Troyes, France), and Mostafa Zabdieh from Shahid Beheshti University (Tehran, Iran) were the top 3 authors in the field, as indexed by Scopus, with 22, 18, and 14 publications, respectively.

4.7. Publication Statistics by Country

Figure 16 presents the distribution of documents by the most active countries in the database (Scopus). It is apparent that China, Iran, and India were the top three most active countries in the field. Additionally, it can be seen that there was a significant difference between the first rank (China) and second rank (Iran) based on the number of publications indexed by Scopus. Although Iran was identified as the second-ranked country in the field, when comparing the populations of China and Iran, it is noteworthy to mention that Iran performed well in this area.

Figure 17 displays the growth rate of the top five active countries. While China, Iran, and France had smooth trends between 2000 and 2020, India and the United States showed some fluctuations. Between 2009 and 2015, the US presented the highest growth rate (positive and negative rate), and then the trend continued smoothly until the end of 2020.

5. Summary

This paper presents a comprehensive review of NSGA-II applied to different scheduling problems. In the first part of the paper, the main idea of scheduling was defined, and the second part described the scientometric analysis in the field in detail.

It is noteworthy to mention that the European Journal of Operational Research owns the most contributions (19%) of published documents in scheduling, which is in the area of operations research.

This paper also reviewed different aspects of scheduling, namely production scheduling and personnel scheduling. It should be noted that about 9.51% of the published articles in the field considered uncertainty, while the majority of the mentioned articles addressed scheduling in power systems (32%), followed by project scheduling (13%), resource allocation (8%), and job-shop scheduling (8%). Among the different objective functions pertaining to job-shop scheduling, maximum completion time ($C_{max}$) possessed the most contributions (32%), followed by maximum machine workload (19%).

Although there are several optimization algorithms, metaheuristics are among the top solution approaches that have been used by researchers. Since genetic algorithms are based on populations, researchers have widely used genetic algorithms for scheduling problems (about 26%), followed by simulated annealing (6.4%), ant colony optimization (4.09%), and tau search (4.47%). The other GA-based solution methods in the field include VEGA, MOGA, WBGA, RWGA, NSGA, NSGA-II, RDGA, NPGA, and DMOEA. While most of the evolutionary algorithms possess difficulties, such as high computational cost, lack of elitism, and difficulty in parameter settings, NSGA-II, proposed in 2002, has attempted to alleviate all of the above difficulties.

Furthermore, the scientometric analysis indicated that computer science artificial intelligence (#86), operation research management science (#86), and computer science interdicipline applications (#82) were among the top categories. In addition, network visualization identified that scheduling, optimization, NSGA-II, multi-objective optimization, multi-objective genetic algorithm, Pareto-optimal, makespan, stochastic models, design, cost, parallel machines, task analysis, and operations were the top keywords. Moreover, the authors of this paper found that NSGA-II, scheduling, and makespan were the top three one-word-long keywords for both WoS and Scopus. Additionally, two-word- and three-word-long keywords were identified. Additional analyses, namely citation network, bibliographic coupling, and journal mapping, were conducted in this work.

Future Studies

In this paper, we discussed the benefits of NSGA-II and its application in different fields of study. Since NSGA-II was specifically designed to solve two- and three-objective problems, less than 1% of NSGA-II articles have considered many-objective scheduling problems (with more than three objectives) [202]. NSGA-III [203,204], its successor, was designed to solve problems with more than three objectives. Hence, it is suggested to review the application of NSGA-III in the field while considering many-objective scheduling problems. Furthermore, the majority of the studies used deterministic approaches, and there is an urgent need to provide more robust approaches for tackling uncertainties in scheduling problems. Additionally, a comprehensive review in other fields of solution methods applied to scheduling problems is encouraged for future studies. As the authors presented in the paper, MOPSO and MOACO are two other famous EMO algorithms, and thus, a comprehensive review in the area using the above-mentioned solution approaches is suggested. Moreover, the application of scheduling for energy conservation is an interesting area for research.

6. Conclusions and Discussions

Since exact methods are expensive in terms of computing time and often possess poor-quality solutions, researchers have become more interested in applying metaheuristics in scheduling problems, which can produce alternative optimal solutions in a single run. This study reviewed the most important scheduling problems that have been solved by the NSGA-II method and provides a bibliometric analysis of the published literature. In terms of MOO problems, most of the exact solution approaches convert MOO problems into a single optimization problem, while metaheuristic methods obtain solutions without this conversion.

This study addressed the most important subject fields based on keywords and network analysis. Moreover, a detailed scientometric analysis was employed as an influential tool in the bibliometric analyses and reviews.

According to the analyses performed in the work, several key arguments that are worthy of further discussion are offered below:

• In terms of keyword analysis, scheduling, optimization, NSGA-II, makespan, design, cost, genetic algorithm, and decision making are the most prevalent keywords for scholars;
• Among the current scheduling problems, machine scheduling (specifically job-shop scheduling), routing, satellite scheduling, project scheduling, weapon selection, and forest planning are most predominant in the reviewed articles;
• Among the proposed solution methods for solving scheduling problems, the genetic algorithm possessed the greatest contribution of (26%), followed by PSO (9%), SA (6.4%), ACO (4.09%), and then tabu search (4.47%);
• Since 2014, NSGA-II has been the most studied algorithm, followed by MOPSO and then MOACO;
• Despite the increasing complexity of scheduling problems, metaheuristic algorithms (specifically NSGA-II) are more suitable for finding efficient solutions or near-optimal solutions.