Influence of Moulding Pressure on the Burst Pressure of Reverse-Acting Rupture Discs
Abstract
:1. Introduction
2. Preparation for Experimental Study
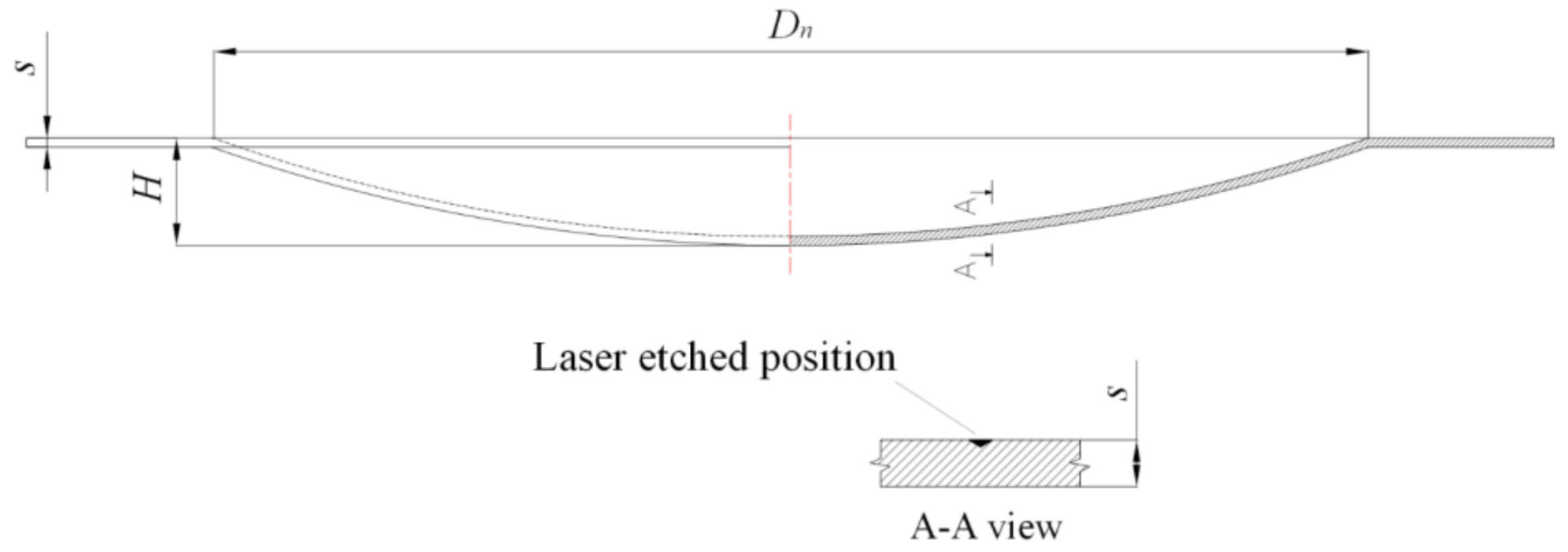
2.1. Selection of Design Parameters for Rupture Disc Production
2.2. Tests for the Mechanical Performance of the Base Material
3. Experimental Studies of Moulding Methods and Burst Pressure
3.1. Moulding Method and Sample Preparation
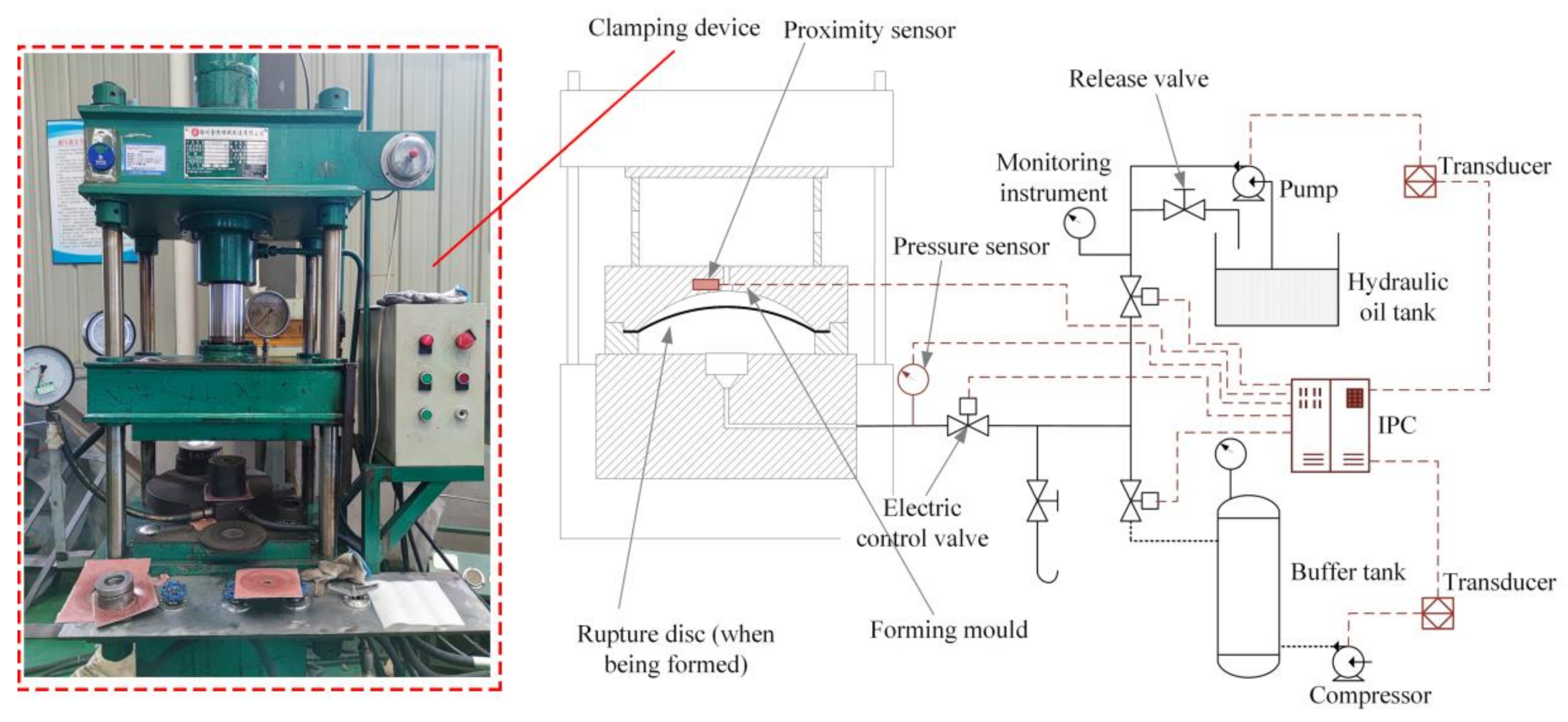
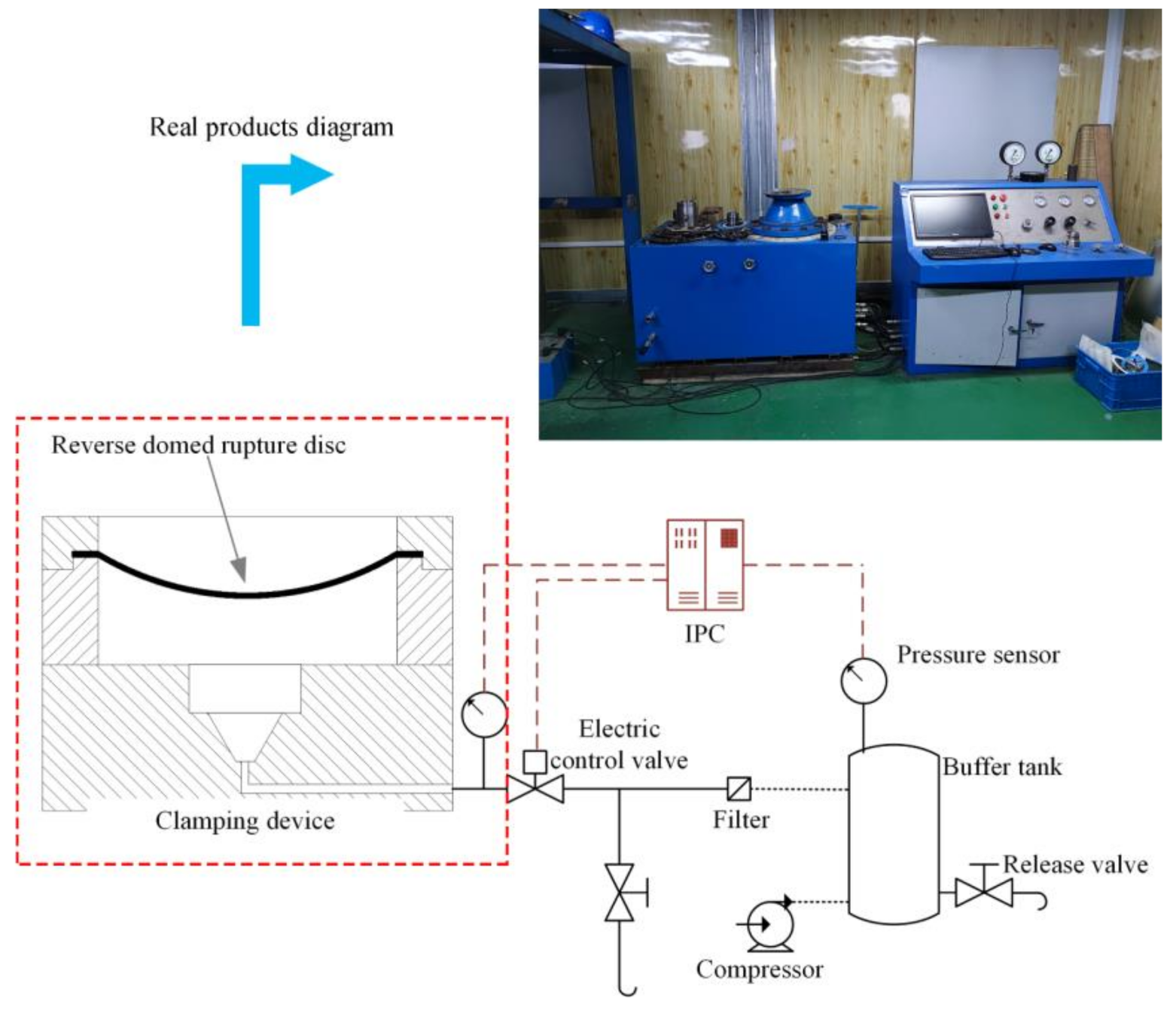
3.2. Forming Equipment and Pressure Loading Method
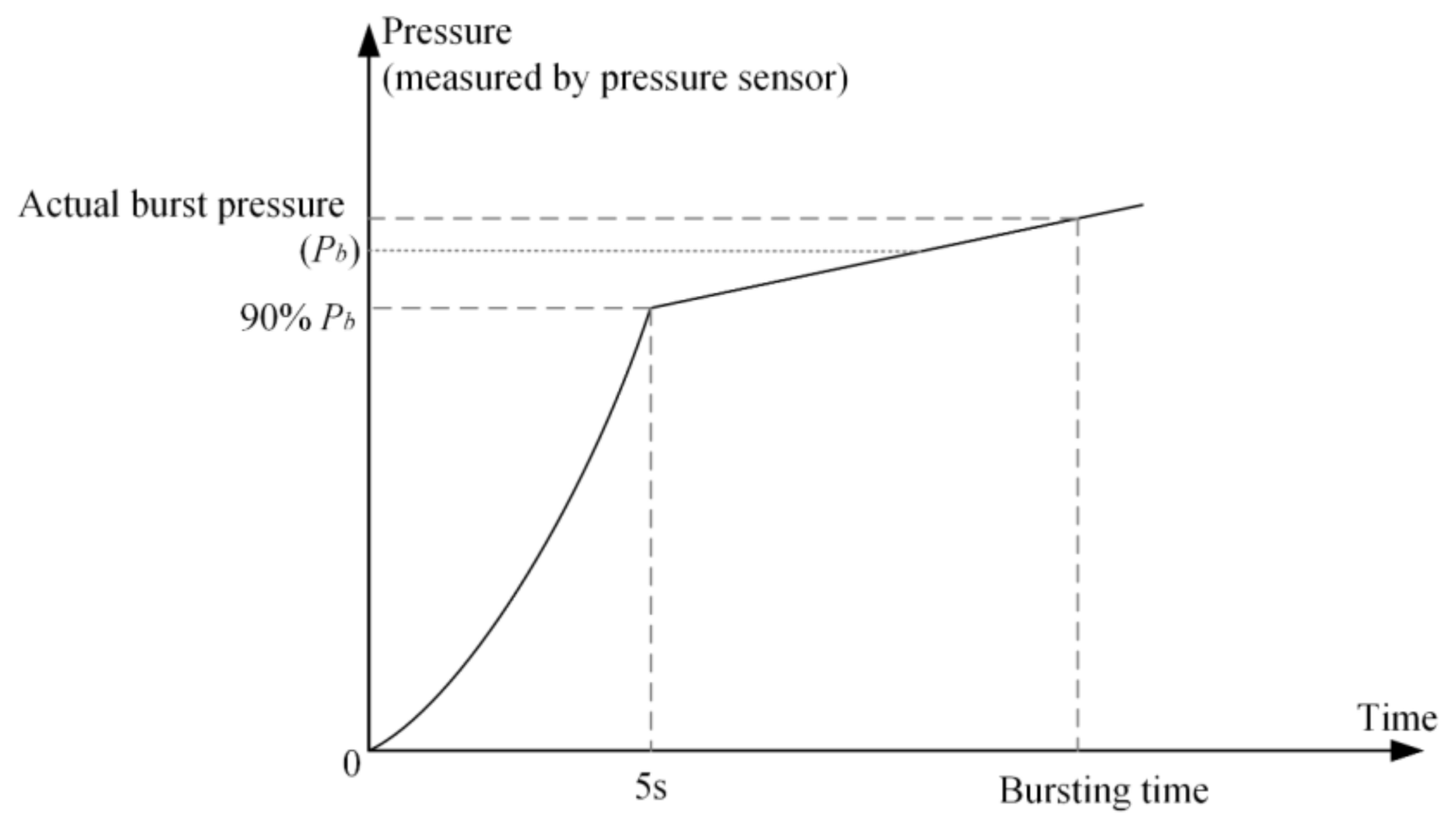
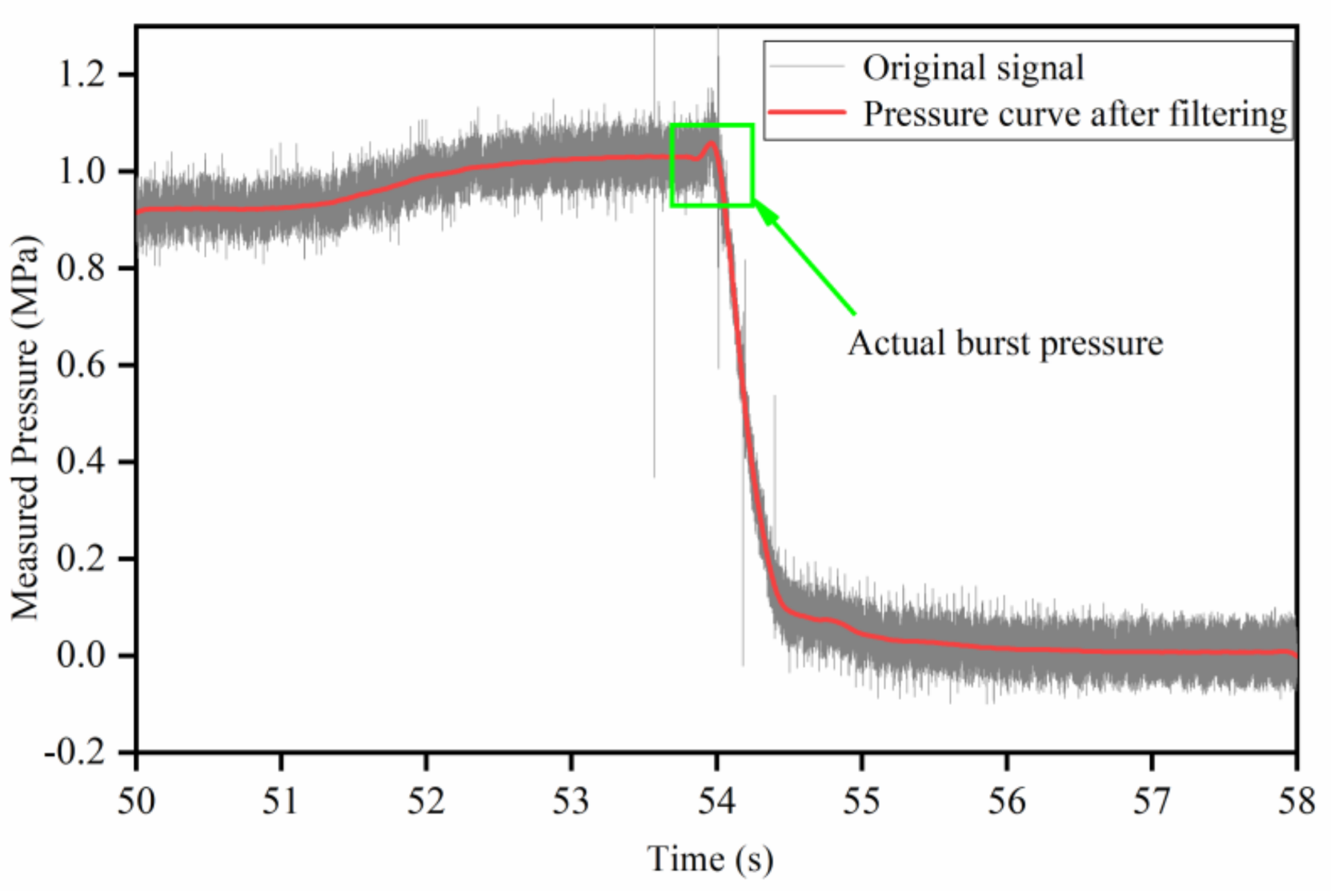
3.3. Experimental Equipment and Process
4. Analysis of Experimental Results
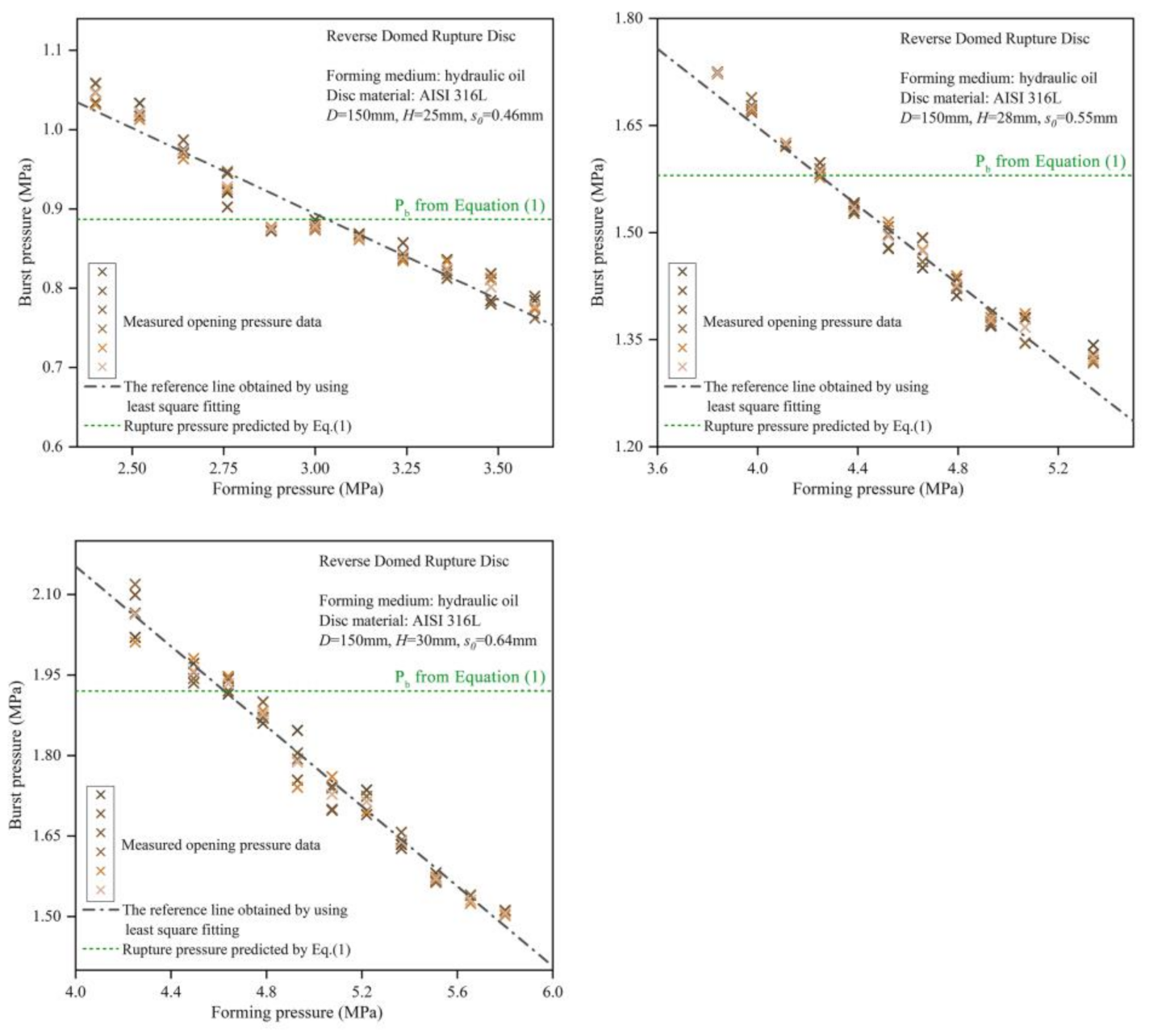
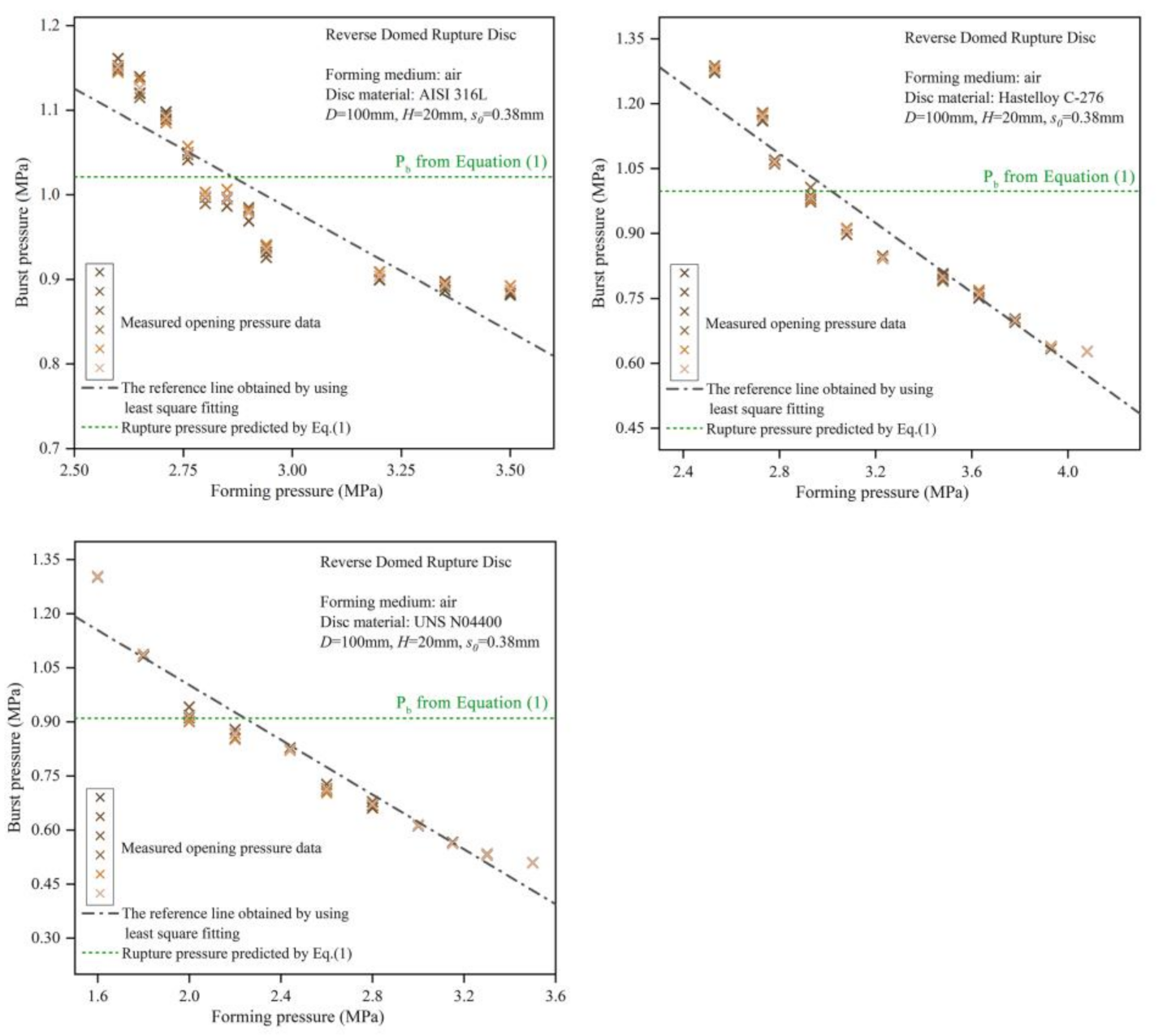
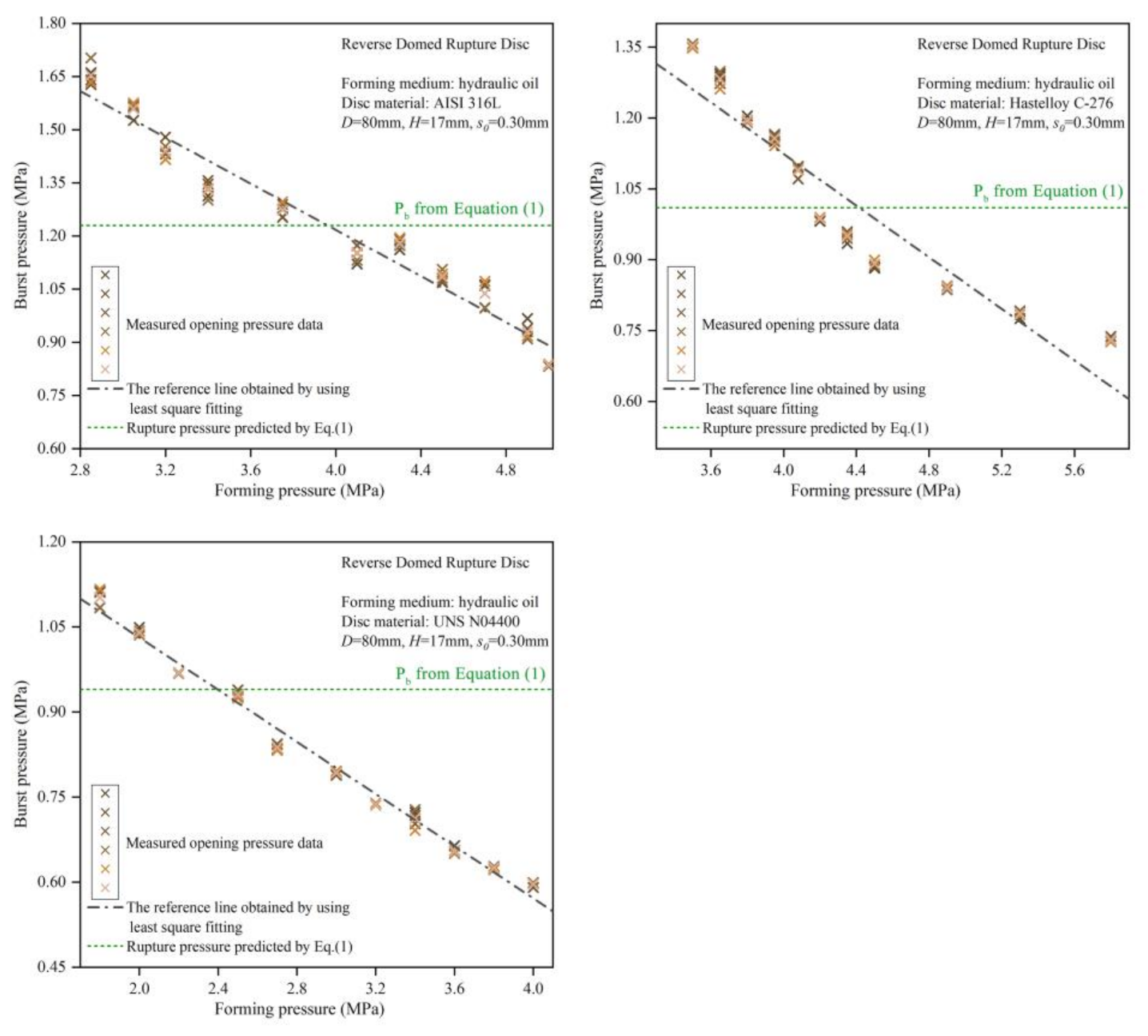
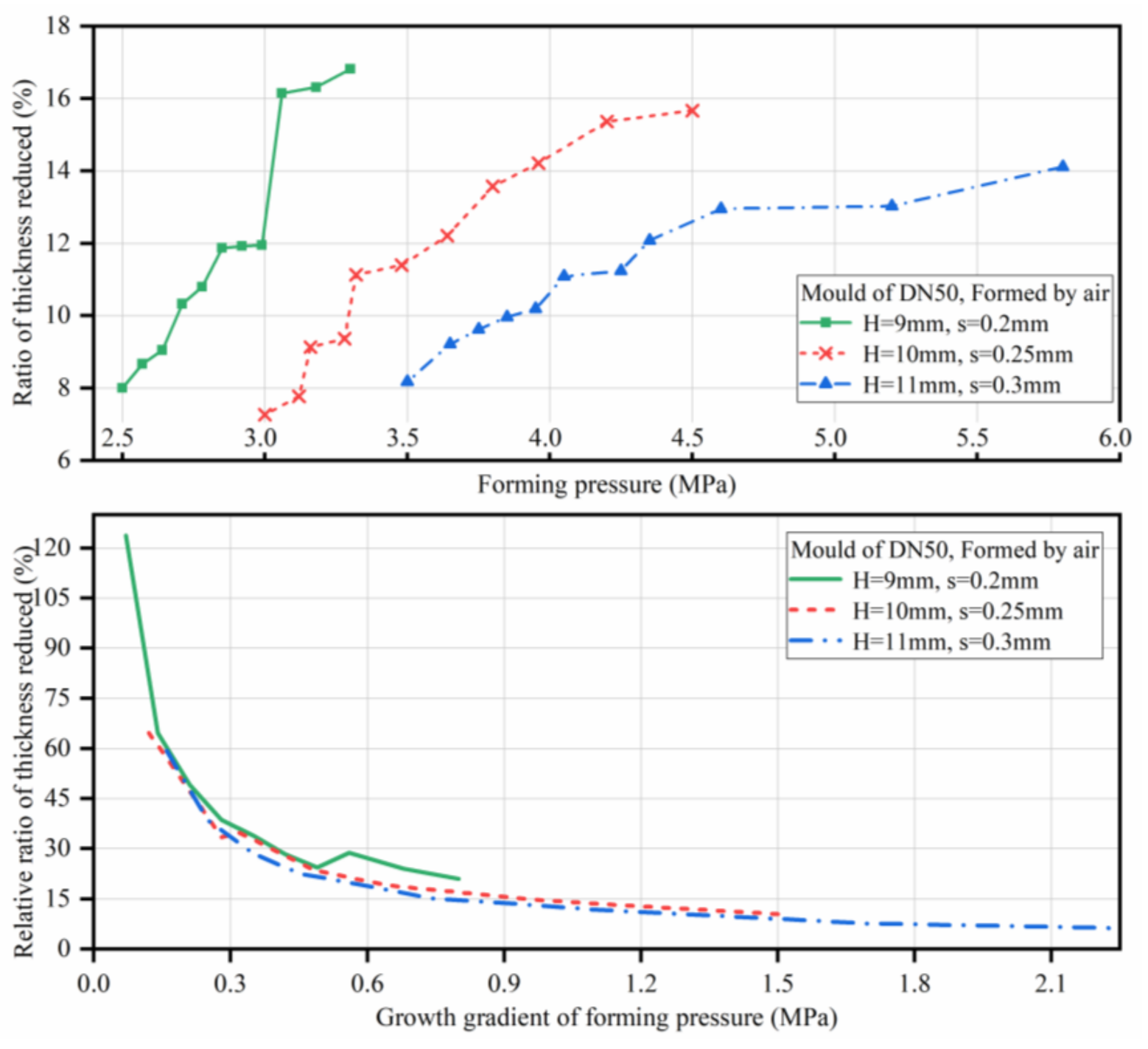
4.1. Analysis of the Burst Pressure Trends
4.2. Analysis of the Effect of Forming Pressure on Burst Pressure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lefebvre, D.; Leveneur, S. Special Issue on “Thermal Safety of Chemical Processes”. Processes 2021, 9, 1054. [Google Scholar] [CrossRef]
- Fu, G.; Zhao, Z. The accident path of coal mine gas explosion based on 24Model: A case study of the ruizhiyuan gas explosion accident. Processes 2019, 7, 73. [Google Scholar] [CrossRef] [Green Version]
- Looney, C.P.; Hagan, Z.M. Modelling the test methods used to determine material compatibility for hydrogen pressure vessel service. Int. J. Fatigue 2019, 132, 105339. [Google Scholar] [CrossRef]
- Salamonowicz, Z.; Krauze, A. Numerical Reconstruction of Hazardous Zones after the Release of Flammable Gases during Industrial Processes. Processes 2021, 9, 307. [Google Scholar] [CrossRef]
- Guojin, Z.; Yonghang, C.; Wenjing, Z.; Min, D. Research on evaluation and inspection of pressure relief valve. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Xi’an, China, 8–11 October 2020; Volume 1043, p. 42017. [Google Scholar]
- Lee, H.S.; Yun, H.C. A study on the rupture disk design and application at the two phase flow by runaway reaction at batch reactor. J. Korean Inst. Gas 2017, 21, 1–8. [Google Scholar]
- Kim, J.D.; Kwon, K.S.; Rhim, J.G.; Yang, W.B. A Study on Flow Analysis according to the Cause of Gas Leakage in the Specialty Gas Supply Device for Semiconductors. J. Korean Inst. Gas 2021, 25, 42–51. [Google Scholar]
- Zhao, G. An easy method to design gas/vapor relief system with rupture disk. J. Loss Prev. Process. Ind. 2015, 35, 321–328. [Google Scholar] [CrossRef]
- Truckenbrodt, E. Elementare Strömungsvorgänge Dichteveränderlicher Fluide; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Coker, A.K. Process Safety and Pressure-Relieving Devices. In Ludwig’s Applied Process Design for Chemical and Petrochemical Plants, 4th ed.; Gulf Professional Publishing: Houston, TX, USA, 2007; pp. 575–770. [Google Scholar]
- Shannak, B. Experimental and theoretical investigation of gas–liquid flow pressure drop across rupture discs. Nucl. Eng. Des. 2010, 240, 1458–1467. [Google Scholar] [CrossRef]
- Mutegi, M.K.; Schmidt, J. Challenges in sizing rupture disk vent line systems especially for compressible two-phase flow. Chem. Eng. Trans. 2016, 48, 631–636. [Google Scholar]
- Schmidt, J.; Claramunt, S. Sizing of rupture disks for two-phase gas/liquid flow according to HNE-CSE-model. J. Loss Prev. Process. Ind. 2016, 41, 419–432. [Google Scholar] [CrossRef]
- Kitabayashi, N.; Wada, Y. Experimental study on high pressure hydrogen jets coming out of tubes of 0.1–4.2 m in length. Int. J. Hydrogen Energy 2013, 38, 8100–8107. [Google Scholar] [CrossRef]
- Golovastov, S.; Bocharnikov, V. The influence of diaphragm rupture rate on spontaneous self-ignition of pressurized hydrogen: Experimental investigation. Int. J. Hydrogen Energy 2012, 37, 10956–10962. [Google Scholar] [CrossRef]
- Kim, Y.R.; Lee, H.J. A flow visualization study on self-ignition of high pressure hydrogen gas released into a tube. Proc. Combust. Inst. 2013, 34, 2057–2064. [Google Scholar] [CrossRef]
- Grune, J.; Sempert, K. Experimental investigation of flame and pressure dynamics after spontaneous ignition in tube geometry. Int. J. Hydrogen Energy 2014, 39, 20396–20403. [Google Scholar] [CrossRef]
- Kaneko, W.; Ishii, K. An experimental study on the mechanism of self-ignition of high-pressure hydrogen. Int. J. Hydrogen Energy 2017, 42, 7374–7379. [Google Scholar] [CrossRef]
- Devasenapathy, V.; Pathanjali, G.A. Laser technique in diaphragm cum rupture disc for defence oriented silver oxide zinc reserve batteries. Mater. Manuf. Process. 2018, 34, 1–8. [Google Scholar] [CrossRef]
- Gong, L.; Duan, Q. Effect of burst disk parameters on the release of high-pressure hydrogen. Fuel 2019, 235, 485–494. [Google Scholar] [CrossRef]
- Schrank, M. Investigation on the degradation and opening behavior of knife blade burst disks. J. Loss Prev. Process. Ind. 2014, 32, 161–164. [Google Scholar] [CrossRef]
- Zhu, H.B.; Xu, W.P.; Luo, Z.P. Finite Element Analysis on the Temperature- Dependent Burst Behavior of Domed 316L Austenitic Stainless Steel Rupture Disc. Met. Open Access Metall. J. 2020, 10, 232. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J.Y.; Lee, J. A study on the grooving process of a cross-scored rupture disc. Int. J. Precis. Eng. Manuf. 2012, 13, 219–227. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, J.; Li, X.; Jin, Z.; Zhong, H.; Zhan, Y.; Han, F. Experimental and finite element optimization analysis on hydroforming process of rupture disc. Procedia Manuf. 2018, 15, 892–898. [Google Scholar] [CrossRef]
- Chung, P.W.H.; Yang, S.H. Conceptual design of pressure relief systems. J. Loss Prev. Process. Ind. 2000, 13, 519–526. [Google Scholar] [CrossRef]
- Xu, W.P.; Liu, Y.T. Study on Conventional Domed Bursting Disc Material and Burst Pressure Test. Adv. Mater. Res. 2013, 690-693, 2371–2378. [Google Scholar] [CrossRef]
- Lee, D.W.; Park, J.M. Effect of rupture disc curvature on the compression waves in S/R valve. J. Mech. Sci. Technol. 2008, 22, 755–760. [Google Scholar] [CrossRef]
- Luo, G.M.; Hsu, Y.C. Nonlinear buckling strength of out-of-roundness pressure hull. Thin Walled Struct. 2018, 130, 424–434. [Google Scholar] [CrossRef]
- Jeong, J.Y.; Jo, W. Structural analysis on the superficial grooving stainless-steel thin-plate rupture discs. Int. J. Precis. Eng. Manuf. 2014, 15, 1035–1040. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Ren, X. Flow stress prediction of Hastelloy C-276 alloy using modified Zerilli− Armstrong, Johnson− Cook and Arrhenius-type constitutive models. Trans. Nonferrous Met. Soc. China 2020, 30, 3031–3042. [Google Scholar] [CrossRef]
- Li, L.; Li, N. Experimental study on heat transfer process in boilers to predict thermal strain/stress distribution and deformation risk of membrane walls. Process. Saf. Environ. Prot. 2020, 138, 186–198. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Research on large deflection deformation reconstruction of elastic thin plate based on strain monitoring. Measurement 2020, 149, 107000. [Google Scholar] [CrossRef]
- Li, H.W. Whole-process modeling of titanium disc forming for gradient distributions of temperature and deformation. Chin. J. Aeronaut. 2020, 33, 3550–3563. [Google Scholar] [CrossRef]
- Zhou, H.; Geng, T. Deformation simulation of the panel mold in the pressing process. Eng. Anal. Bound. Elem. 2005, 29, 894–902. [Google Scholar] [CrossRef]
- Bukhvostova, A.; Russo, E. Comparison of DNS of compressible and incompressible turbulent droplet-laden heated channel flow with phase transition. Int. J. Multiph. flow 2014, 63, 68–81. [Google Scholar] [CrossRef] [Green Version]
- Godderidge, B.; Turnock, S. The effect of fluid compressibility on the simulation of sloshing impacts. Ocean. Eng. 2009, 36, 578–587. [Google Scholar] [CrossRef]
- Sudha, C.; Parameswaran, P. Microstructure and deformation mode of a stainless steel rupture disc exposed to sodium–water reaction. Mater. Charact. 2008, 59, 1088–1095. [Google Scholar] [CrossRef]
- Nurick, G.N.; Shave, G.C. The deformation and tearing of thin square plates subjected to impulsive loads—An experimental study. Int. J. Impact Eng. 1996, 18, 99–116. [Google Scholar] [CrossRef]
- Mutegi, M.K.; Schmidt, J. Sizing rupture disk vent line systems for high-velocity gas flows. J. Loss Prev. Process. Ind. 2019, 62, 103950. [Google Scholar] [CrossRef]
- Meshalkin, V.P.; Belyakov, A.V. Methods Used for the Compaction and Molding of Ceramic Matrix Composites Reinforced with Carbon Nanotubes. Processes 2020, 8, 1004. [Google Scholar] [CrossRef]
- Gearing, D.; Mevissen, D. Hydroforming systems, equipment, controls and tooling—ScienceDirect. Hydroforming Adv. Manuf. 2008, 5, 33–51. [Google Scholar]
- Kumar, A.; Chanda, A.K.; Angra, S. Analysis of effects of varying face sheet thickness on different properties of composite sandwich Structure. Mater. Today Proc. 2021, 38, 116–121. [Google Scholar] [CrossRef]
- Lin, Y.; Zhong, C. Experimental Study on the Flexural Behavior of Concrete-Filled Steel Box Slabs. Processes 2021, 9, 649. [Google Scholar] [CrossRef]
- Ma, Q.; Zhu, Y. Buckling and strength of an externally pressurized spherical shell with reinforced opening. Int. J. Press. Vessel. Pip. 2018, 165, 11–19. [Google Scholar] [CrossRef]
- Alexandrov, S.; Lyamina, E. Plastic Bending at Large Strain: A Review. Processes 2021, 9, 406. [Google Scholar] [CrossRef]
- Nazarov, S.A.; Sweers, G.H. The flexural rigidity of a thin plate reinforced with periodic systems of separated rods. J. Appl. Math. Mech. 2010, 74, 313–322. [Google Scholar] [CrossRef]



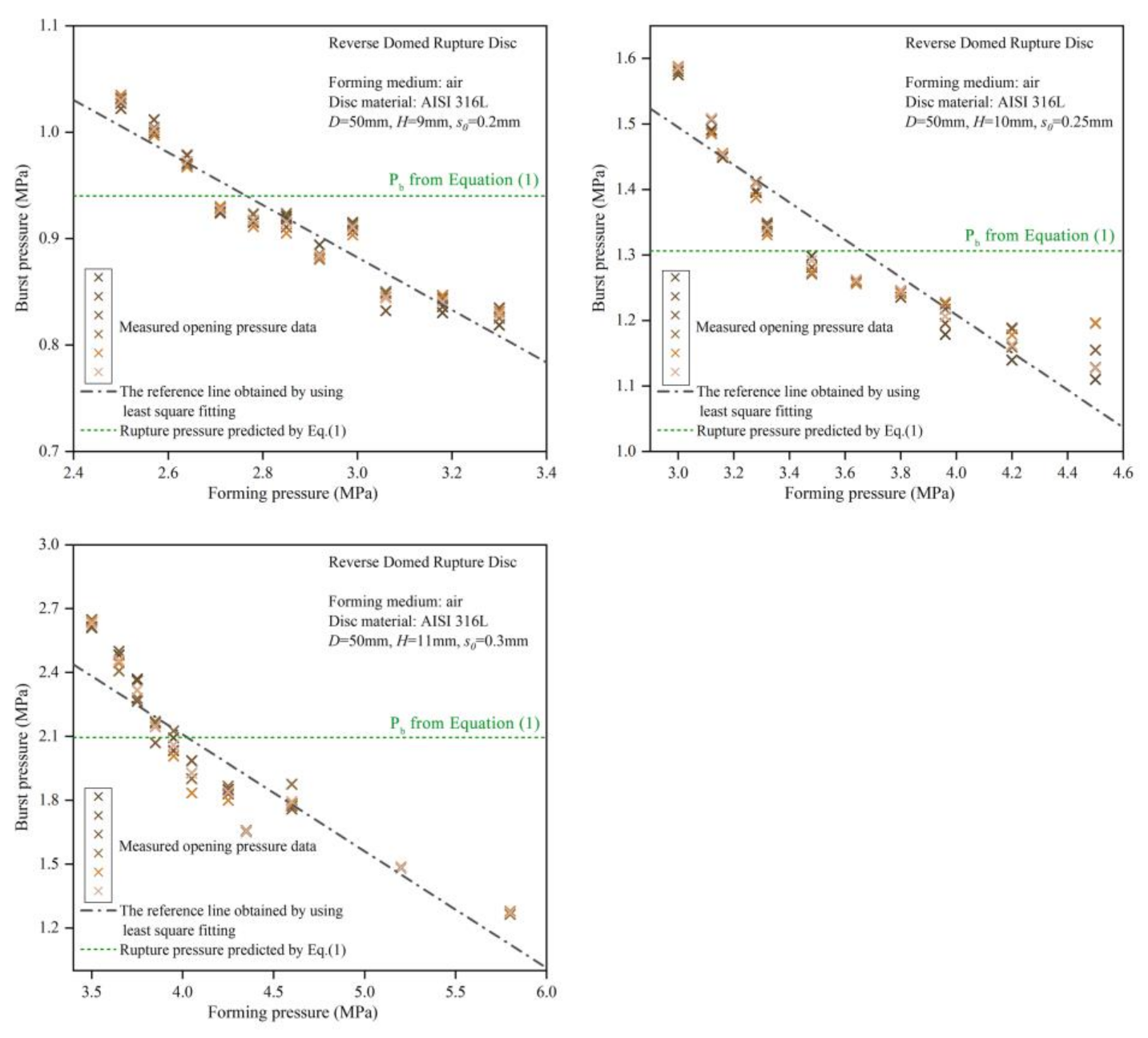
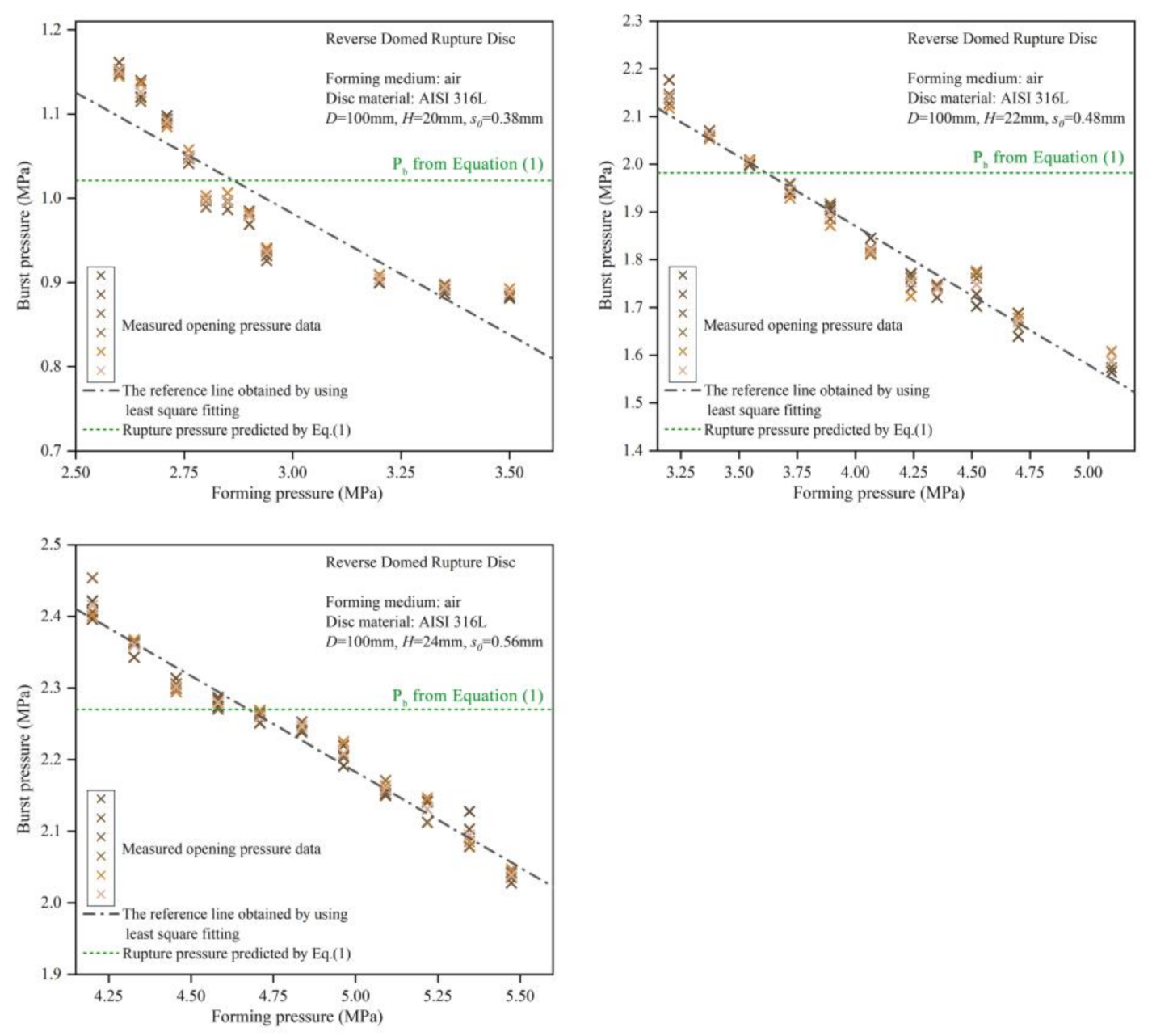
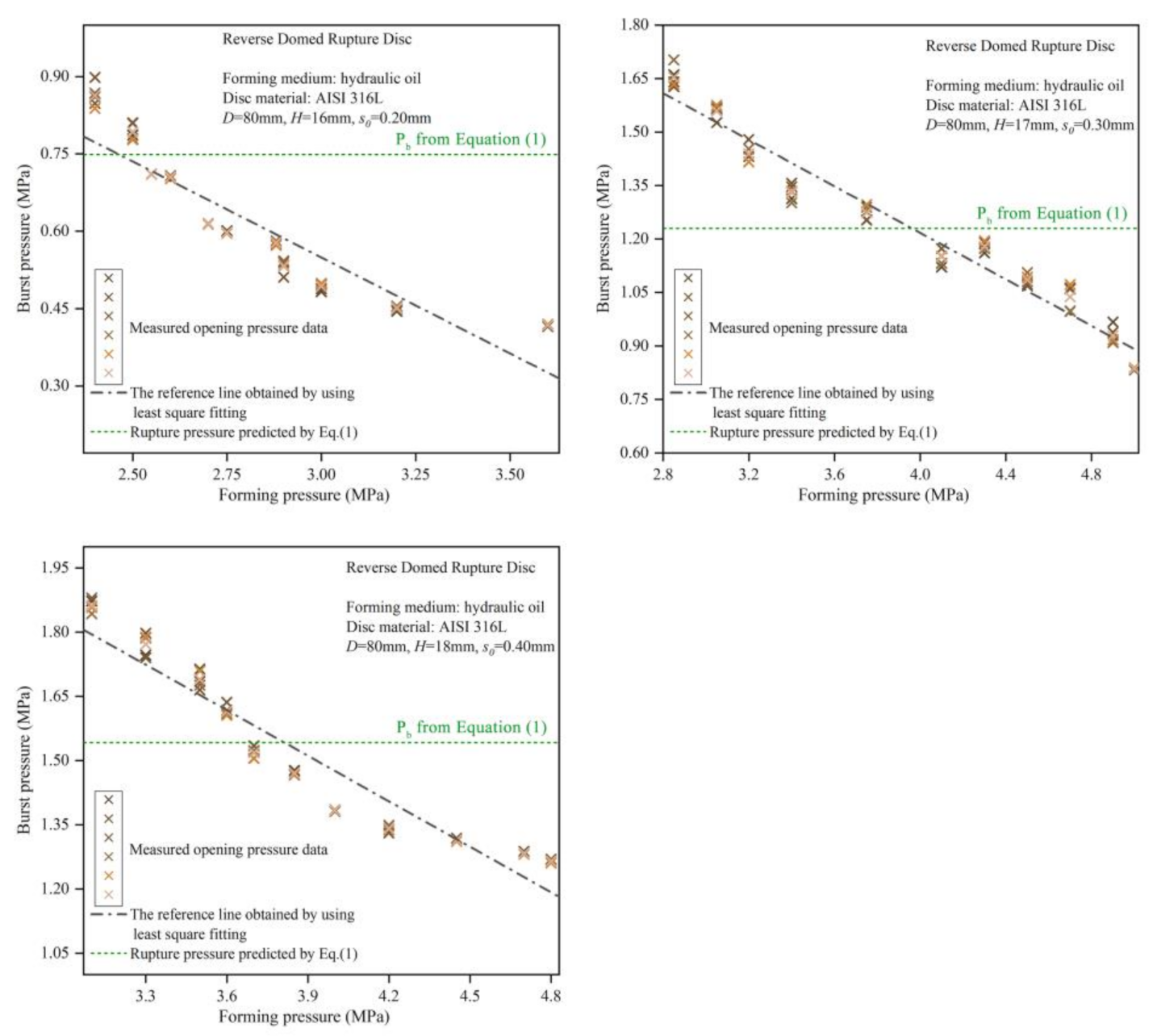
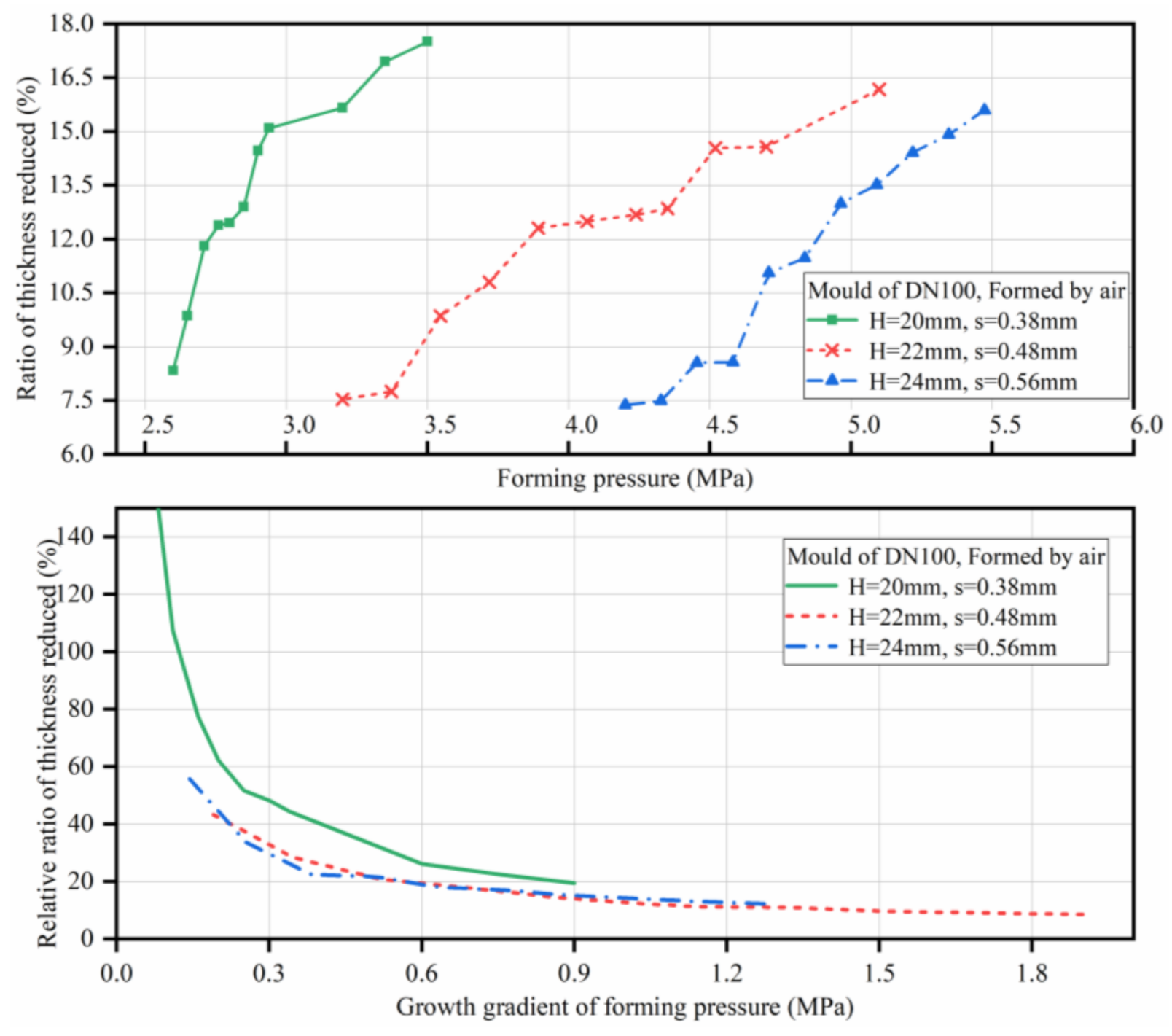
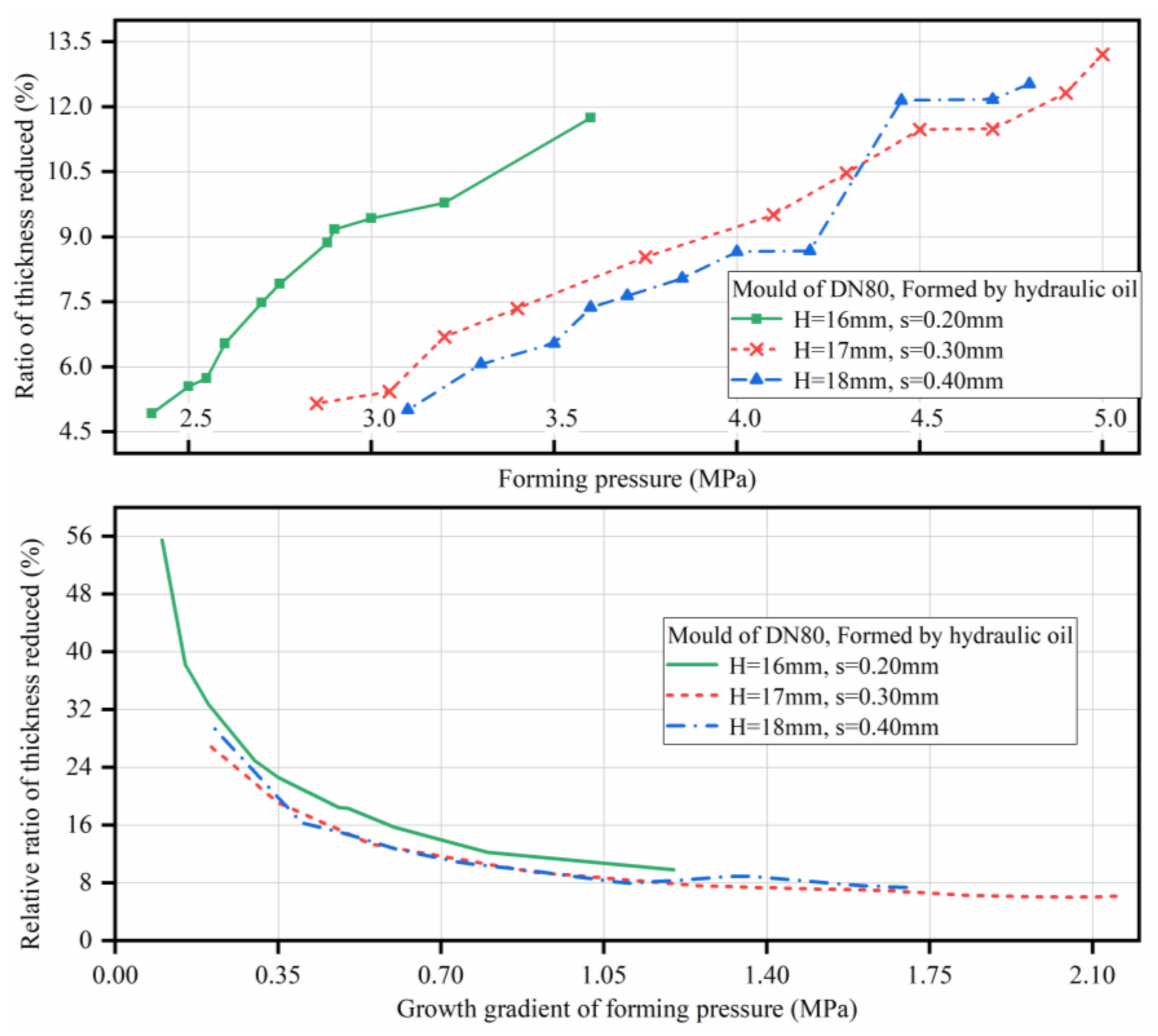

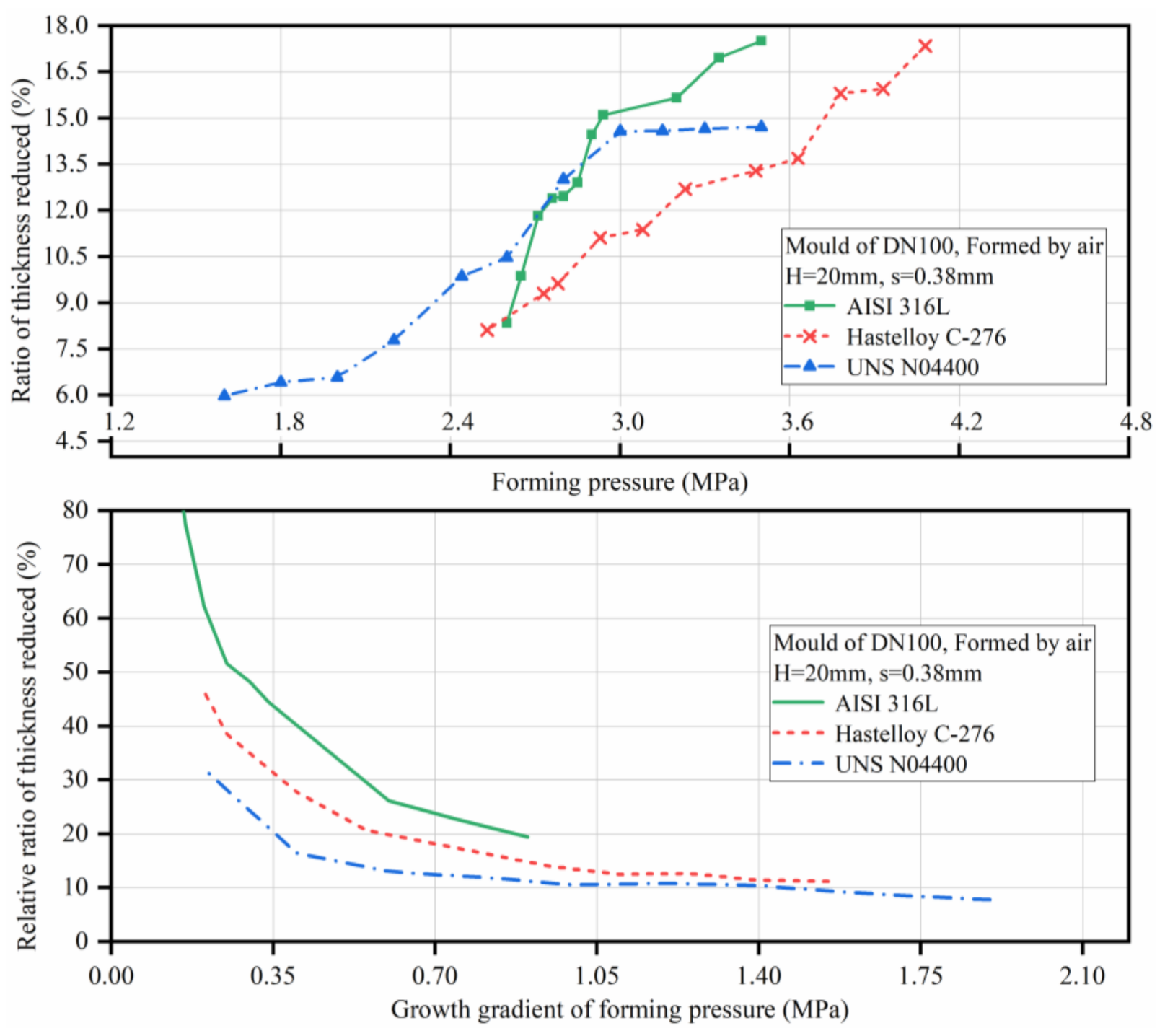
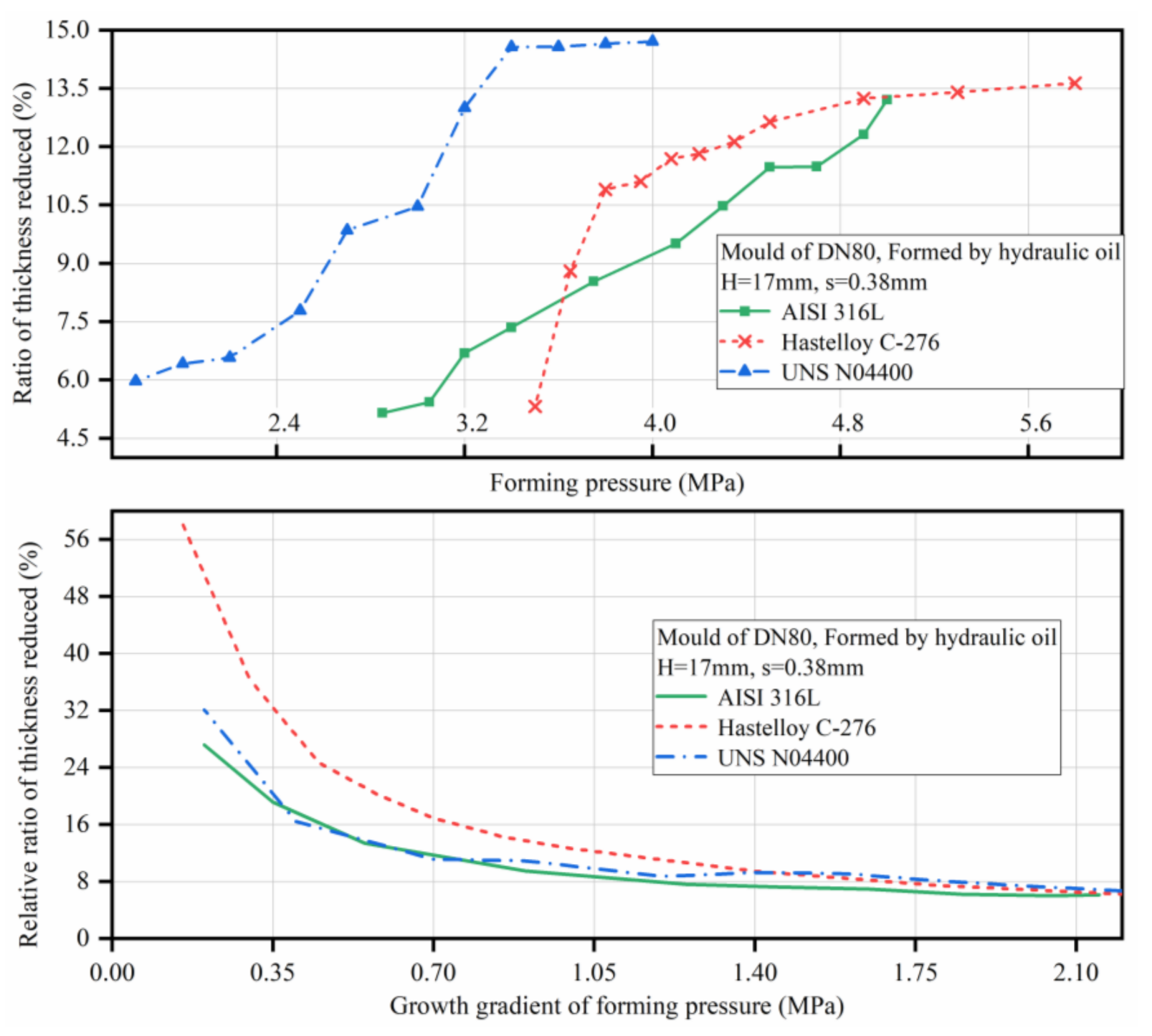
| Type of Mould | Height of Arch Top (H) | Plate Thickness (s) | Plate Materials | Theoretical Forming Pressure (Pb) | Compression Forming Medium |
|---|---|---|---|---|---|
| Dn50mm | 9 mm | 0.2 mm | AISI 316L | 2.52 MPa | Air |
| 10 mm | 0.25 mm | 3.17 MPa | |||
| 11 mm | 0.3 mm | 3.72 MPa | |||
| Dn80mm | 16 mm | 0.2 mm | AISI 316L | 2.63 MPa | Hydraulic oil |
| 17 mm | 0.3 mm | 3.01 MPa | |||
| 18 mm | 0.4 mm | 3.32 MPa | |||
| 17 mm | 0.3 mm | UNS N04400 | 2.55 MPa | ||
| 17 mm | 0.3 mm | Hastelloy C-276 | 3.28 MPa | ||
| Dn100mm | 20 mm | 0.38 mm | AISI 316L | 2.66 MPa | Air |
| 22 mm | 0.46 mm | 3.81 MPa | |||
| 24 mm | 0.56 mm | 4.27 MPa | |||
| 20 mm | 0.38 mm | UNS N04400 | 2.33 MPa | ||
| 20 mm | 0.38 mm | Hastelloy C-276 | 2.58 MPa | ||
| Dn150mm | 25 mm | 0.46 mm | AISI 316L | 2.72 MPa | Hydraulic oil |
| 28 mm | 0.55 mm | 3.89 MPa | |||
| 30 mm | 0.64 mm | 4.45 MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Yuan, C.; Li, W.; Li, B.; Liu, X. Influence of Moulding Pressure on the Burst Pressure of Reverse-Acting Rupture Discs. Processes 2021, 9, 1775. https://doi.org/10.3390/pr9101775
Liu L, Yuan C, Li W, Li B, Liu X. Influence of Moulding Pressure on the Burst Pressure of Reverse-Acting Rupture Discs. Processes. 2021; 9(10):1775. https://doi.org/10.3390/pr9101775
Chicago/Turabian StyleLiu, Lili, Chenxing Yuan, Wei Li, Beibei Li, and Xiumei Liu. 2021. "Influence of Moulding Pressure on the Burst Pressure of Reverse-Acting Rupture Discs" Processes 9, no. 10: 1775. https://doi.org/10.3390/pr9101775
APA StyleLiu, L., Yuan, C., Li, W., Li, B., & Liu, X. (2021). Influence of Moulding Pressure on the Burst Pressure of Reverse-Acting Rupture Discs. Processes, 9(10), 1775. https://doi.org/10.3390/pr9101775







