Inverse Kinematic Control of a Delta Robot Using Neural Networks in Real-Time
Abstract
:1. Introduction
- Development of a neural network model that learns the kinematics of a delta robot;
- Demonstration of the effect of updating the parameters of neural networks in inverse kinematics control of a delta robot with consideration of joint backlash.
2. Related Work
3. Material and Methods
3.1. Delta Robot Kinematics Estimation Using Neural Networks
- Number of hidden layers: [1, 2, 3];
- Number of neurons in each layer: ;
- Activation functions: {Sigmoid, Hyperbolic tangent, Softmax, Linear}.
3.2. Structure of Control System
| Algorithm 1: Overview of the algorithm for the neural network online training |
 |
4. Simulation and Experimental Results
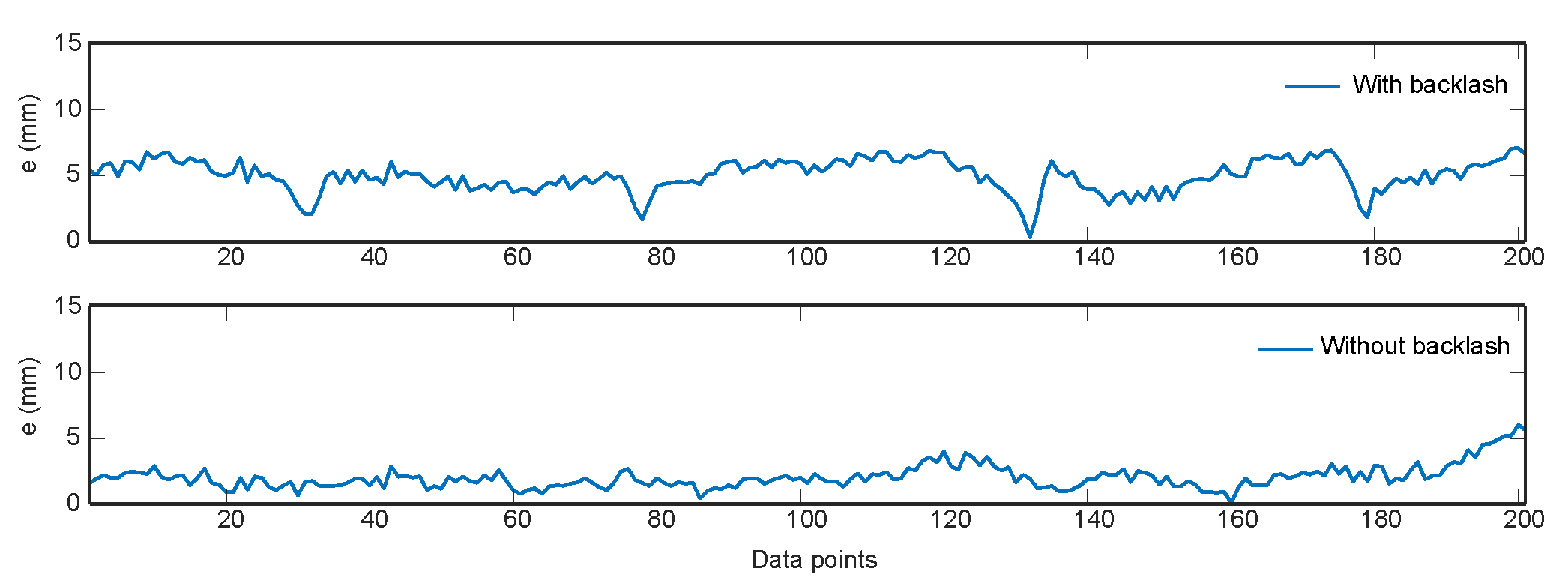
4.1. Joint Backlash and Kinematics Estimation Performance
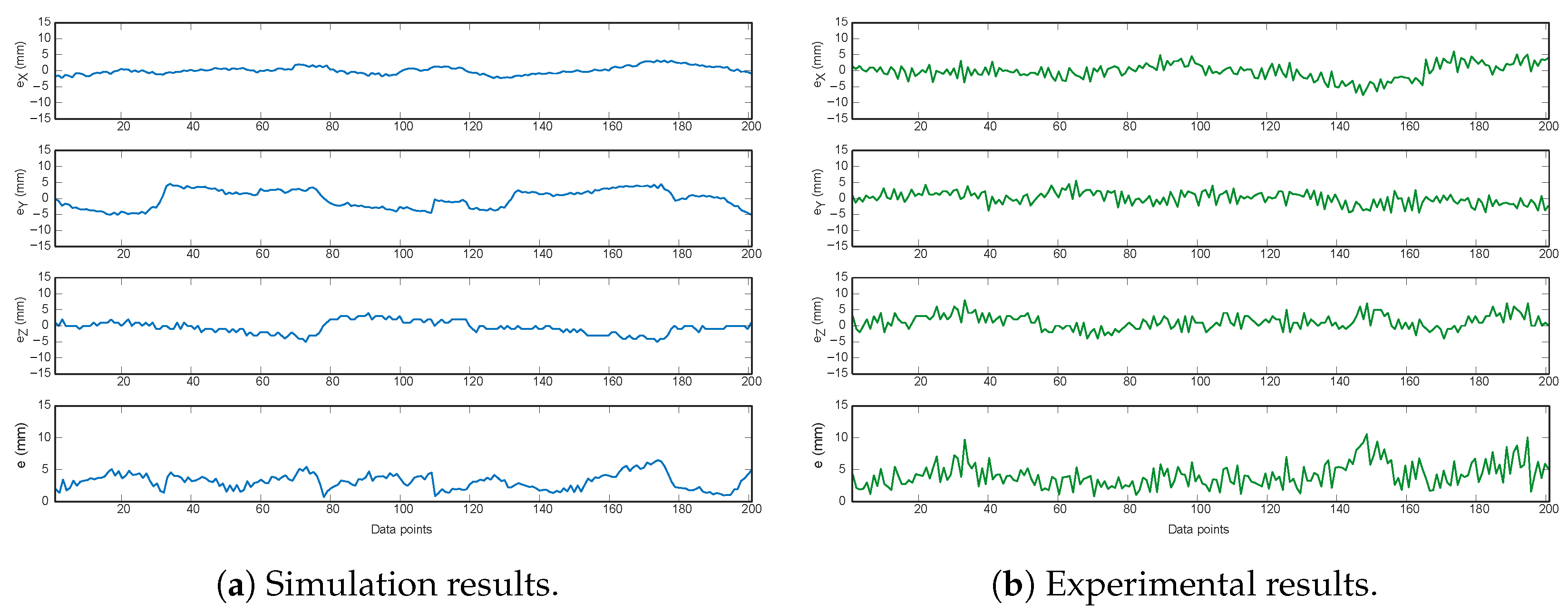
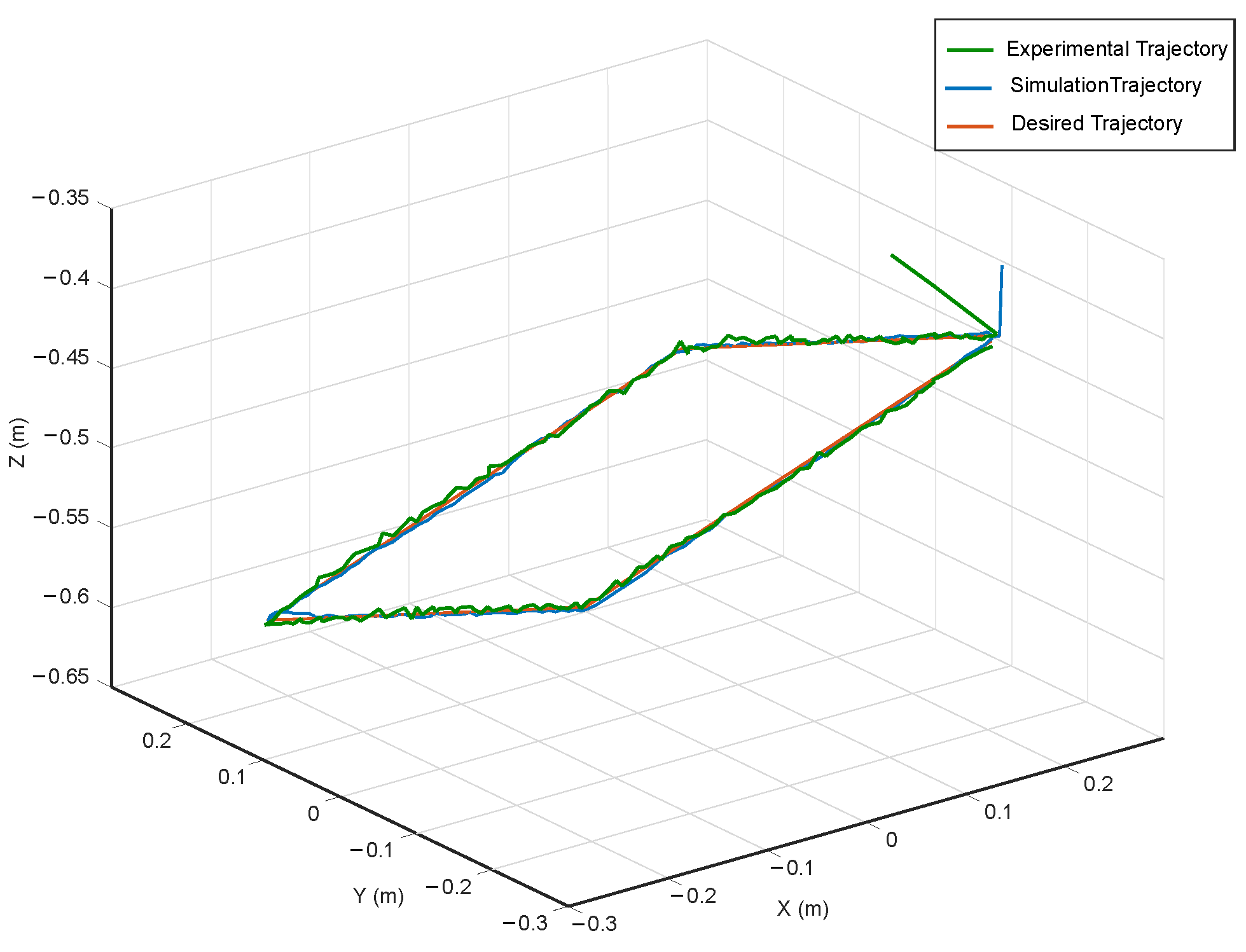
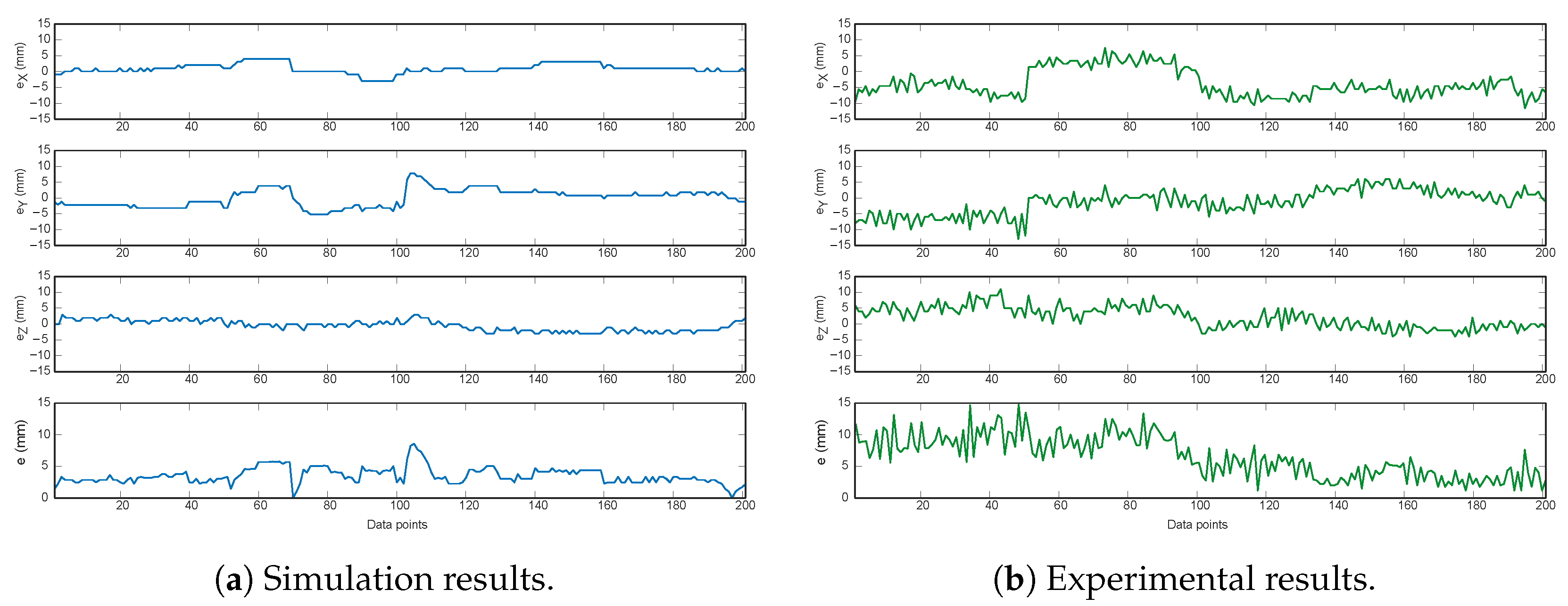
4.2. Tracking Performance
4.3. Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bingul, Z.; Karahan, O. Dynamic Modeling and Simulation of Stewart Platform. In Serial and Parallel Robot Manipulators; Kucuk, S., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 2. [Google Scholar]
- Ren, H.; Ben-Tzvi, P. Learning inverse kinematics and dynamics of a robotic manipulator using generative adversarial networks. Robot. Auton. Syst. 2020, 124, 103386. [Google Scholar] [CrossRef]
- Laribi, M.A.; Romdhane, L.; Zeghloul, S. Analysis and dimensional synthesis of the DELTA robot for a prescribed workspace. Mech. Mach. Theory 2007, 42, 859–870. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, C.; Na, J.; Li, G.; Li, Y.; Zhong, J. A Brief Review of Neural Networks Based Learning and Control and Their Applications for Robots. Complexity 2017, 2017, 1895897. [Google Scholar] [CrossRef]
- Sánchez-Sánchez, C.; Izzo, D. Real-time optimal control via Deep Neural Networks: Study on landing problems. arXiv 2016, arXiv:1610.08668. [Google Scholar] [CrossRef] [Green Version]
- Toquica, J.S.; Oliveira, P.S.; Souza, W.S.; Motta, J.M.S.; Borges, D.L. An analytical and a Deep Learning model for solving the inverse kinematic problem of an industrial parallel robot. Comput. Ind. Eng. 2021, 151, 106682. [Google Scholar] [CrossRef]
- Duka, A.V. Neural Network based Inverse Kinematics Solution for Trajectory Tracking of a Robotic Arm. Procedia Technol. 2014, 12, 20–27. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Peng, G.; Wang, Y.; Zhang, H. A New Solution for Inverse Kinematics of 7-DOF Manipulator Based on Neural Network. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 1958–1962. [Google Scholar]
- Zhou, X.; Sun, X.; Zhang, W.; Liang, S.; Wei, Y. Deep Kinematic Pose Regression. In Computer Vision—ECCV 2016 Workshops; Hua, G., Jégou, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 186–201. [Google Scholar]
- Brinker, J.; Corves, B.; Takeda, Y. Kinematic and Dynamic Dimensional Synthesis of Extended Delta Parallel Robots. In Robotics and Mechatronics; Springer International Publishing: Cham, Switzerland, 2019; pp. 131–143. [Google Scholar]
- Nguyen, V.L.; Lin, C.Y.; Kuo, C.H. Gravity compensation design of Delta parallel robots using gear-spring modules. Mech. Mach. Theory 2020, 154, 104046. [Google Scholar] [CrossRef]
- Lopez, M.; del Castillo, E.; García, G.R.; Bashir, A. Delta robot: Inverse, direct, and intermediate Jacobians. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 103–109. [Google Scholar] [CrossRef] [Green Version]
- Brinker, J.; Corves, B. A Survey on Parallel Robots with Delta-like Architecture. In Proceedings of the 14th IFToMM World Congress, Taipei, Taiwan, 25–30 October 2015. [Google Scholar]
- Mottola, G.; Gosselin, C.; Carricato, M. Dynamically feasible motions of a class of purely-translational cable-suspended parallel robots. Mech. Mach. Theory 2019, 132, 193–206. [Google Scholar] [CrossRef]
- Tang, L.; Shi, P.; Wu, L.; Wu, X.; Tang, X. Singularity Analysis on a Special Class of Cable-Suspended Parallel Mechanisms With Pairwise Cable Arrangement and Actuation Redundancy. J. Mech. Des. 2019, 142, 024501. [Google Scholar] [CrossRef]
- Le, T.D.; Kang, H.J. An adaptive tracking controller for parallel robotic manipulators based on fully tuned radial basic function networks. Neurocomputing 2014, 137, 12–23. [Google Scholar] [CrossRef]
- Escorcia-Hernández, J.M.; Aguilar-Sierra, H.; Aguilar-Mejía, O.; Chemori, A.; Arroyo-Núñez, J.H. An Intelligent Compensation Through B-Spline Neural Network for a Delta Parallel Robot. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 361–366. [Google Scholar]
- Xu, Q.; Li, Y. A 3-PRS Parallel Manipulator Control Based on Neural Network. In Advances in Neural Networks—ISNN 2007; Liu, D., Fei, S., Hou, Z.G., Zhang, H., Sun, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 757–766. [Google Scholar]
- Uzunovic, T.; Golubovic, E.; Baran, E.A.; Sabanovic, A. Configuration space control of a parallel Delta robot with a neural network based inverse kinematics. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 8–30 November 2013; pp. 497–501. [Google Scholar]
- Mohammed, A.M.; Li, S. Dynamic Neural Networks for Kinematic Redundancy Resolution of Parallel Stewart Platforms. IEEE Trans. Cybern. 2016, 46, 1538–1550. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lian, C.; Gao, R.; Shi, L. 3-Degree-of-Freedom Parallel Robot Control Based Fuzzy Theory. In Proceedings of the 2010 Second International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanjing, China, 26–28 August 2010; Volume 1, pp. 221–224. [Google Scholar]
- On-line regression algorithms for learning mechanical models of robots: A survey. Robot. Auton. Syst. 2011, 59, 1115–1129. [CrossRef] [Green Version]
- Aggarwal, L.; Aggarwal, K.; Urbanic, R.J. Use of Artificial Neural Networks for the Development of an Inverse Kinematic Solution and Visual Identification of Singularity Zone(s). Procedia CIRP 2014, 17, 812–817. [Google Scholar] [CrossRef] [Green Version]
- Hasan, A.T.; Ismail, N.; Hamouda, A.M.; Aris, I.; Marhaban, M.H.; Al-Assadi, H.M. Artificial neural network-based kinematics Jacobian solution for serial manipulator passing through singular configurations. Adv. Eng. Softw. 2010, 41, 359–367. [Google Scholar] [CrossRef] [Green Version]
- Almusawi, A.R.J.; Dülger, L.C.; Kapucu, S. A New Artificial Neural Network Approach in Solving Inverse Kinematics of Robotic Arm (Denso VP6242). Comput. Intell. Neurosci. 2016, 2016, 5720163. [Google Scholar] [CrossRef] [Green Version]
- Zubizarreta, A.; Larrea, M.; Irigoyen, E.; Cabanes, I.; Portillo, E. Real time direct kinematic problem computation of the 3PRS robot using neural networks. Neurocomputing 2018, 271, 104–114. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Yu, J.; He, J. Robot manipulator control using neural networks: A survey. Neurocomputing 2018, 285, 23–34. [Google Scholar] [CrossRef]
- Doukim, C.A.; Dargham, J.A.; Chekima, A. Finding the number of hidden neurons for an MLP neural network using coarse to fine search technique. In Proceedings of the 10th International Conference on Information Science, Signal Processing and their Applications (ISSPA 2010), Kuala Lumpur, Malaysia, 10–13 May 2010; pp. 606–609. [Google Scholar]
- Toshani, H.; Farrokhi, M. Real-time inverse kinematics of redundant manipulators using neural networks and quadratic programming: A Lyapunov-based approach. Robot. Auton. Syst. 2014, 62, 766–781. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, Z.; Li, S.; Wu, H.; Cheng, T.; Lv, X. RNN Based Adaptive Compliance Control for Robots with Model Uncertainties. In AI Based Robot Safe Learning and Control; Springer: Singapore, 2020; pp. 39–61. [Google Scholar]
- Li, S.; Shao, Z.; Guan, Y. A Dynamic Neural Network Approach for Efficient Control of Manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 932–941. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Rafique, M.U. A Novel Recurrent Neural Network for Manipulator Control With Improved Noise Tolerance. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1908–1918. [Google Scholar] [CrossRef] [PubMed]
- Mirza, M.A.; Li, S.; Jin, L. Simultaneous learning and control of parallel Stewart platforms with unknown parameters. Neurocomputing 2017, 266, 114–122. [Google Scholar] [CrossRef]
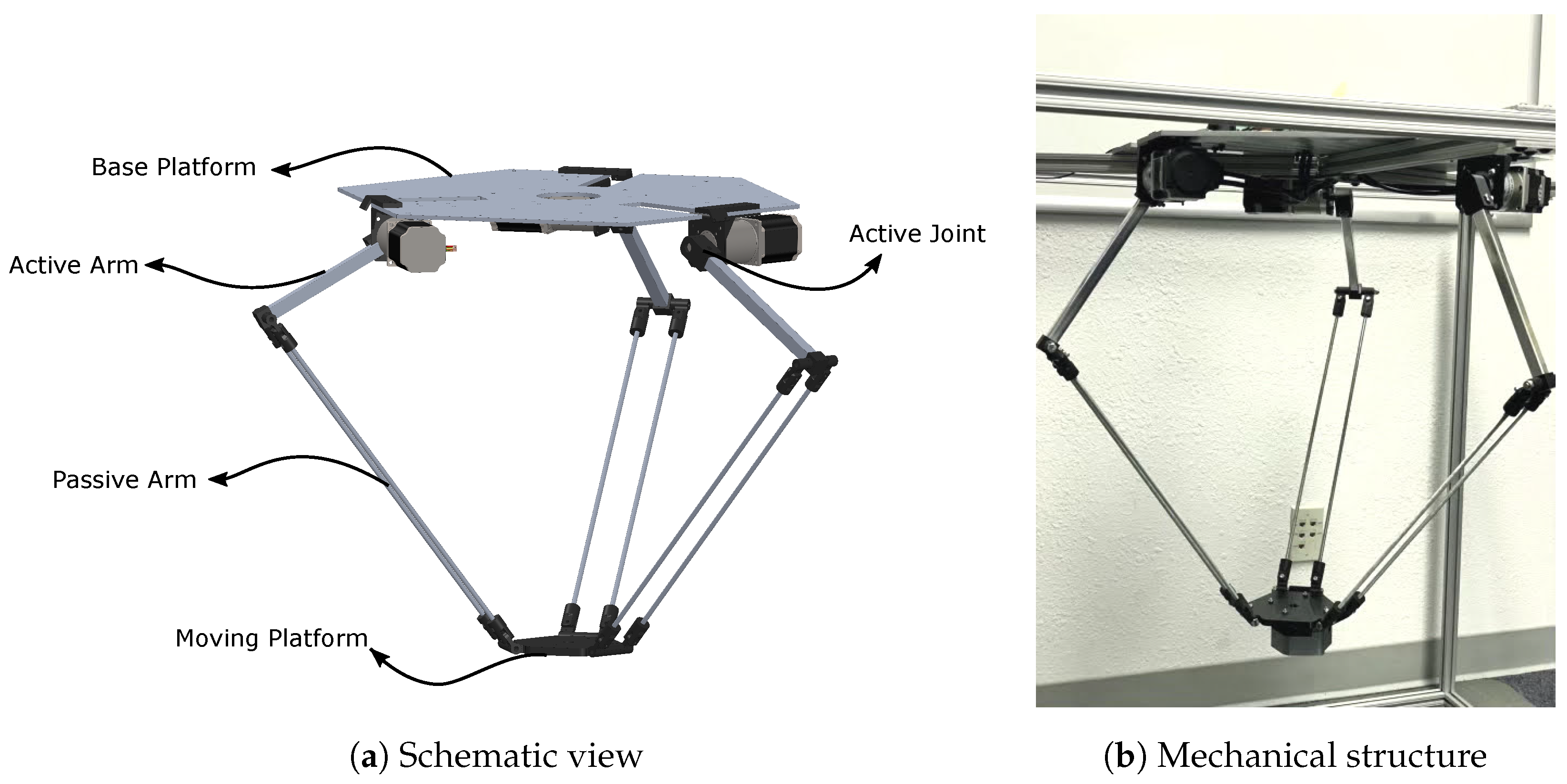





| Link | Dimension (m) |
|---|---|
| Active arm length | |
| Passive arm length | |
| Base platform radius | |
| Moving platform radius |
| Spiral path | Without backlash | ||||
| With backlash | |||||
| With backlash and NN update (simulation) | |||||
| With backlash and NN update (experiment) | |||||
| Square path | Without backlash | ||||
| With backlash | |||||
| With backlash and NN update (simulation) | |||||
| With backlash and NN update (experiment) |
| This Paper | [30] | [31] | [32] | [33] | |
|---|---|---|---|---|---|
| Model information | No | Yes | No | Yes | No |
| Handling model uncertainty | Yes | Yes | Yes | No | Yes |
| Handling system change | Yes | Yes | - | No | No |
| Handling noise | Yes | - | Yes | Yes | Yes |
| Number of adjustable parameters | L | M | L | H | M |
| Complexity | L | M | M | M | L |
| Level of solving problem | P | F | V | V | V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, A.; Homayouni, T.; Ehsani, R.; Sun, J.-Q. Inverse Kinematic Control of a Delta Robot Using Neural Networks in Real-Time. Robotics 2021, 10, 115. https://doi.org/10.3390/robotics10040115
Gholami A, Homayouni T, Ehsani R, Sun J-Q. Inverse Kinematic Control of a Delta Robot Using Neural Networks in Real-Time. Robotics. 2021; 10(4):115. https://doi.org/10.3390/robotics10040115
Chicago/Turabian StyleGholami, Akram, Taymaz Homayouni, Reza Ehsani, and Jian-Qiao Sun. 2021. "Inverse Kinematic Control of a Delta Robot Using Neural Networks in Real-Time" Robotics 10, no. 4: 115. https://doi.org/10.3390/robotics10040115
APA StyleGholami, A., Homayouni, T., Ehsani, R., & Sun, J.-Q. (2021). Inverse Kinematic Control of a Delta Robot Using Neural Networks in Real-Time. Robotics, 10(4), 115. https://doi.org/10.3390/robotics10040115





