Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids
Abstract
:1. Introduction
- It is noted that the number of simple and complex ML algorithms/models in the literature has grown exponentially, thus making it almost impossible to compare all available models [3].
- There are many contradictory conclusions regarding the best performing algorithm(s) mainly due to the lack of proper statistical significance analyses of many output results. For example, the authors in [5,6] claim that statistical techniques (i.e., regression-based approaches) perform better than simple ML methods, whereas the findings in [7,8,9] suggest that ML methods typically outperform statistical techniques. Thus, such contradictory reports exist in the literature.
- Some authors can be prejudiced toward publishing only those metrics that demonstrate how well their approach may have outperformed other methods, while failing to report other relevant metrics of concern [3]. Such practices can distort the findings of such studies in favor of the suggested method(s) over existing ones, which should not be the case.
- Furthermore, many research works neglect to perform proper hyperparameter tuning exercises of the various algorithms under consideration before conducting comparison assessments. In other cases, crucial information about the source of the training and testing data is omitted, as is the proportion of the training and test split, making it difficult to replicate previously published results [3]. Note that the difference between a hyperparameter and hyperparameter tuning is that a hyperparameter is a parameter whose value is used to control the learning process and to determine the values of the model parameters of a learning algorithm, whereas hyperparameter tuning is the problem of selecting the optimal set of hyperparameters for a learning algorithm [10].
- 1.
- We conducted a comparative performance analyses of six well-known ML algorithms, namely the artificial neural network (ANN), Gaussian regression (GR), k-nearest neighbor (k-NN), linear regression (LR), random forest (RF), and the support vector machine (SVM).
- 2.
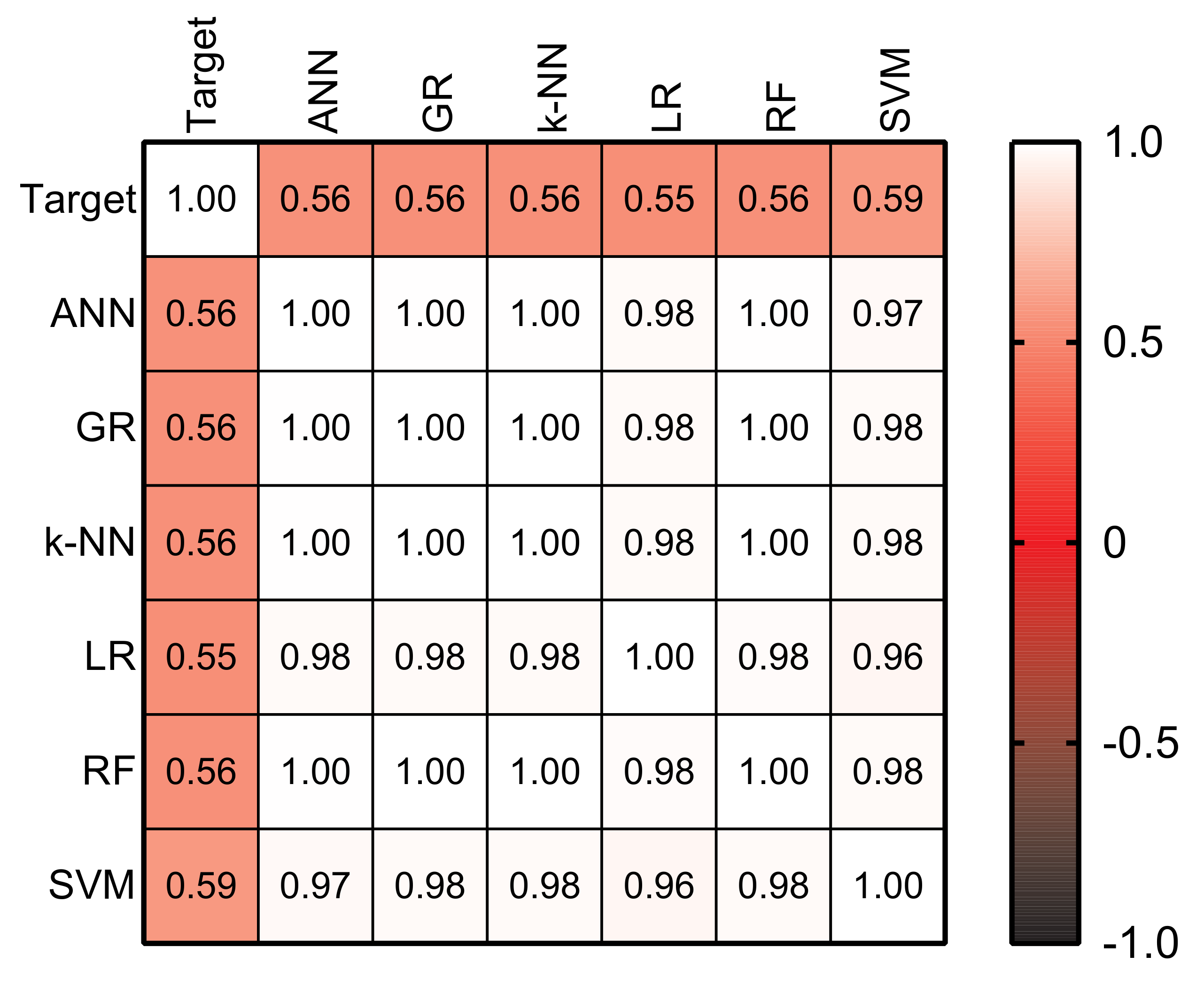
- We examined three different data sources spanning across the system hourly demand, photovoltaic, and wind generation datasets from the Eskom database. We observed that the different ML algorithms considered herein performed poorly, particularly on the wind power generation dataset, which we attributed to the highly stochastic nature of the wind source.
- 3.
- A thorough statistical significance analysis of the different methods revealed that within the confines of the datasets used in this study, there was little/no significant difference in the performance of the different ML algorithms. Thus, this early observation suggests that any of the simple ML algorithms considered here can be used for demand/supply forecasting, albeit after a thorough hyperparameter tuning exercise is conducted.
2. Related Work
3. Methodology
3.1. Machine Learning Algorithms
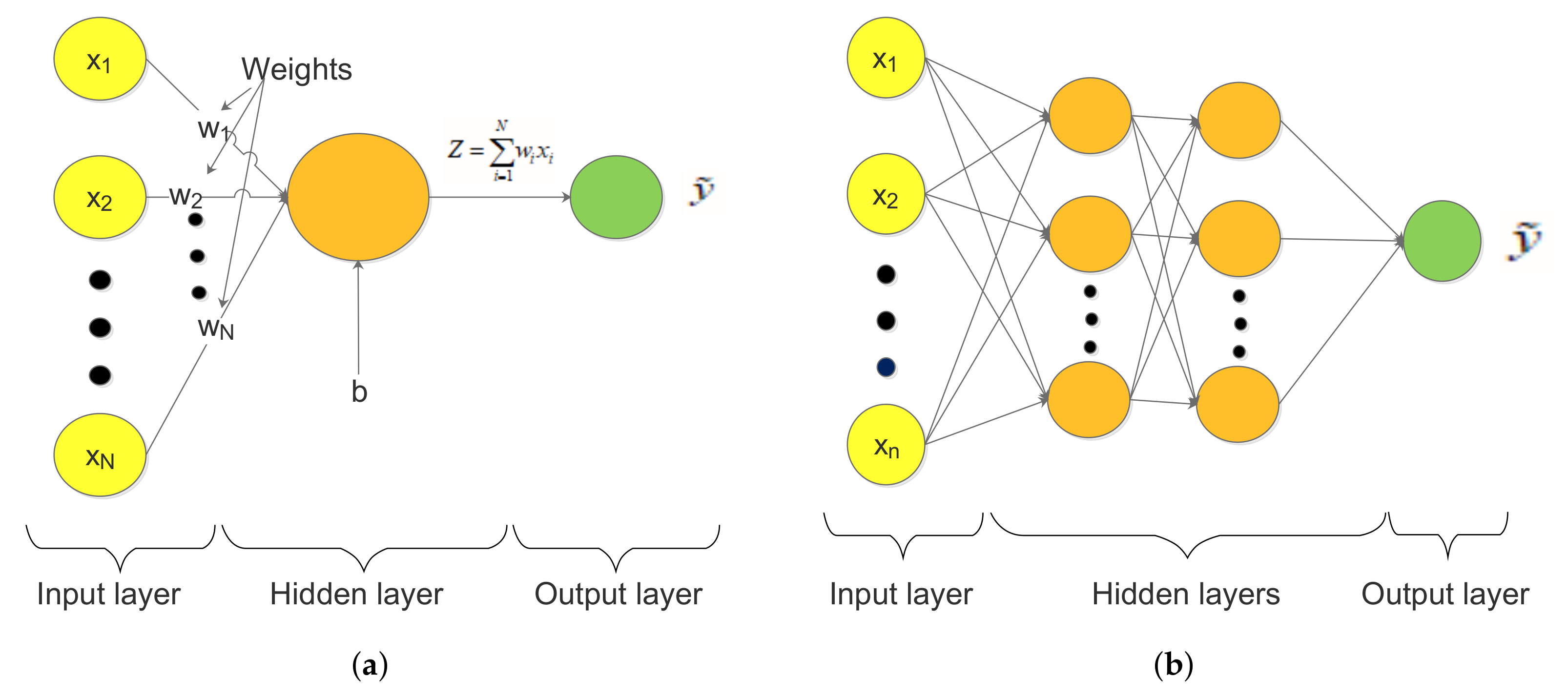
3.1.1. Artificial Neural Network
- 1.
- The dot product between the inputs and weights is computed. This involves multiplying each input by its corresponding weight and then summing them up along with a bias term b. This is obtained as
- 2.
- The summation of the dot products is passed through an activation function. The activation function bounds the input values between 0 and 1, and a popular function, which we used in our study, is the sigmoid activation function, stated mathematically asThe sigmoid function returns values close to 1 when the input is a large positive value, returns 0 for large negative values, and returns 0.5 when the input is zero. It is best suited for predicting the output as a probability, which ranges between 0 and 1, which makes it the right choice for our forecasting problem. The result of the activation function is essentially the predicted output for the input features.
- 3.
- Backpropagation is conducted by first calculating the cost via the cost function, which can simply be the mean square error (MSE) given aswhere is the target output value, is the predicted output value, and N is the number of observations (also called instances). Then, the cost function is minimized, where the weights and the bias are fine tuned to ensure that the function returns the smallest value possible. The smaller the cost, the more accurate the predictions. Minimization is conducted via the gradient descent algorithm, which can be mathematically represented aswhere is the new weight, is the old weight, a is the learning rate, and is the derivative of the error with respect to the weight, where is the cost function. The learning rate determines how fast the algorithm learns. The gradient descent algorithm iterates repeatedly (called the number of epochs) until the cost is minimized. Consequently, the steps followed can be summarized as follows:
- (a)
- Define the inputs (i.e., features) and output variables.
- (b)
- Define the hyperparameters.
- (c)
- Define the activation function and its derivatives.
- (d)
- Train the model and make predictions.
3.1.2. Linear and Gaussian Regression
3.1.3. k-Nearest Neighbour
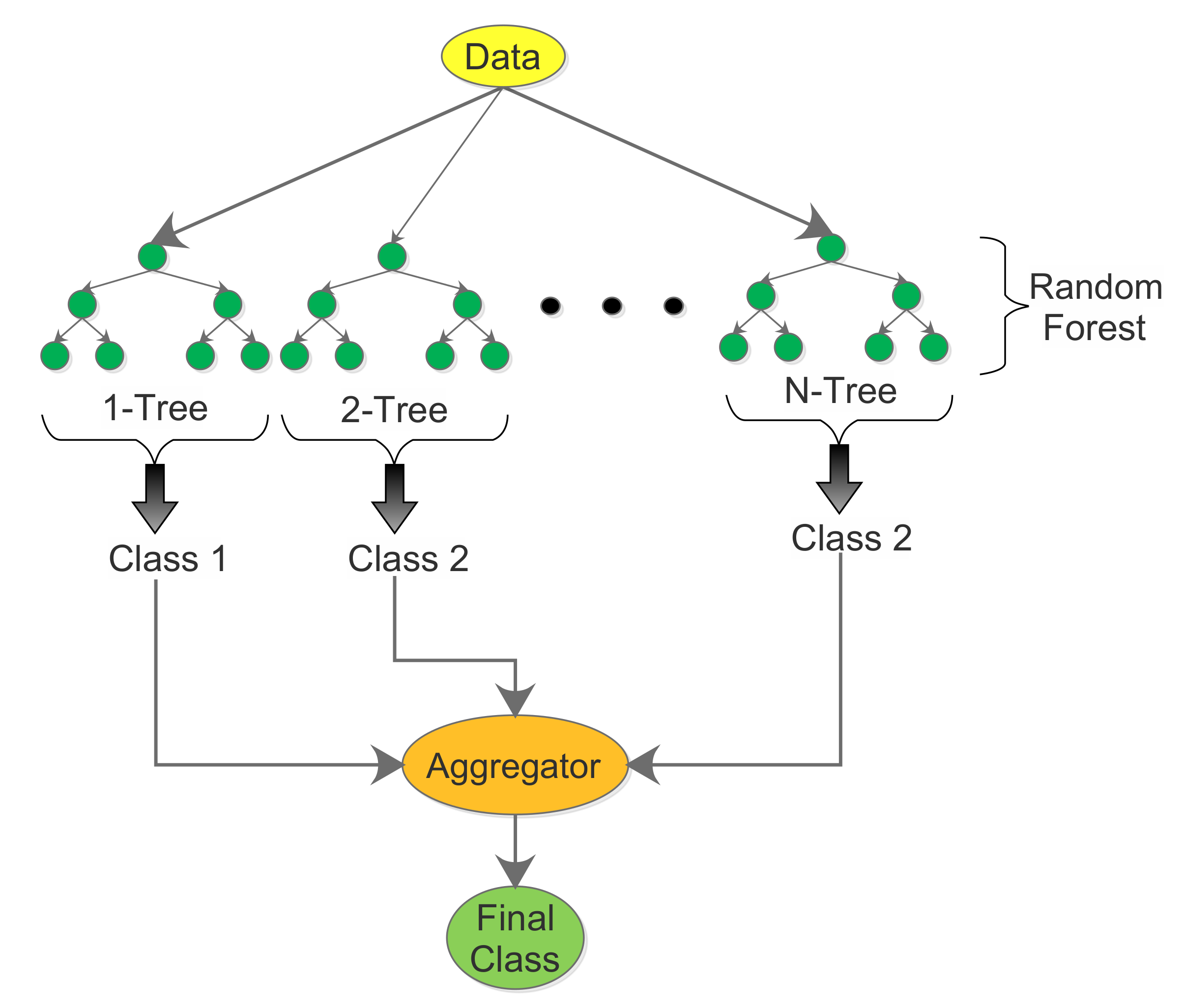
3.1.4. Random Forest
3.1.5. Support Vector Machine
3.2. Dataset
- 1.
- System hourly demand: This dataset presents the hourly power demand measured from 5 to 18 October 2021 (https://www.eskom.co.za/dataportal/demand-side/system-hourly-actual-and-forecasted-demand/, accessed on 1 October 2021). It is classed into the residual and the Republic of South Africa (RSA) contracted demand. However, we considered only the residual demand data in our study, which suffices to compare the different algorithms. The entire dataset comprised 528 data points, with the residual demand data comprising 336 data points collated from 5 to 10 October 2021, and 192 data points from the residual forecast dataset provided from 11 to 18 October 2021. In this case, a training to testing split ratio of 65% to 35% was used, respectively.
- 2.
- Hourly renewable generation: This dataset presents the hourly renewable generation per resource type, namely, from photovoltaic (PV) and wind sources (https://www.eskom.co.za/dataportal/renewables-performance/hourly-renewable-generation/, accessed on 1 October 2021). These datasets reflect only renewable sources owned by Eskom or that Eskom has contracts with. The PV and wind datasets comprised 960 data points in total, each measured per hour from 1 September 2021 to 10 October 2021. For both the PV and wind use cases, we used 80% of the dataset for training and 20% for testing. This implies that 770 data points from 1 September 2021 to 2 October 2021 were used to train each model, whereas 190 data points from 3 to 10 October 2021 were used for testing purposes. It should be noted that the term “target” used henceforth in this article refers to the actual data against which the different models are compared with during the testing phase.
3.3. Performance Metrics
3.3.1. Correlation Coefficient
3.3.2. Relative Absolute Error
3.3.3. Root Relative Square Error
3.3.4. Mean Absolute Error
3.3.5. Root Mean Square Error
4. Results and Discussion
4.1. Hyper-Parameter Optimization
4.1.1. Artificial Neural Network
- 1.
- The model’s performance typically decreases under an increased learning rate and momentum values, irrespective of the number of hidden layers used. This implies that a low learning rate and momentum values are best suitable for an ANN model, with the values of 0.1 and 0.1 yielding the lowest error rates, respectively. This can be easily explained noting that low learning rate values imply smaller step sizes and thus higher resolutions, which leads to improved convergence to better approximations.
- 2.
- A model with two hidden layers with 12 nodes per layer yielded the lowest error rates under a low learning rate and momentum values. Although this configuration cannot be generalized for all ANN models, it yielded the lowest error rate for the present use case. Furthermore, we note that increasing the number of nodes above 12 produced no improvement in model performance.
- 3.
- Generally, under the same low learning rate and momentum values, we observed that the double-layered model performed marginally better than the single layer configuration. For example, considering in Table 2 the best model of (12,12) hidden layer configuration, and learning rate and momentum of 0.1 each, we obtained a decrease in the error rate when using the double-layered model instead of the single-layered model of same number of nodes.
- 4.
- Since there is no single fixed global configuration or model for all possible use cases, it becomes vital to ensure that a model’s hyperparameters are accurately fine tuned. For example, by fine tuning our model, we achieved a error reduction rate in using a double-layer model with 12 nodes per layer (learning rate = 0.1, momentum = 0.1) over a single-layer model with 9 nodes (learning rate = 0.3, momentum = 0.2).
4.1.2. Gaussian Regression
- 1.
- A combination of the poly kernel and standardization of the training data led to the best model, which yielded the lowest RAE and RRSE values of 44.7277% and 45.5645%, respectively.
- 2.
- Hyperparameter tuning of the GR algorithm can achieve as much as and error reduction rate in the RAE and RRSE, respectively, thus emphasizing the importance of hyperparameter tuning.
- 3.
- With and RRSE differences of 3.121% and 3.645%, respectively, there exists little/no significant advantage in using either the normalization or standardization of the training data as it pertains to the poly kernel. Consequently, the most important parameter is simply the choice of the kernel to be used.
- 4.
- We presume that the RBF kernel may have performed poorly owing to the large size of the training dataset, which is a well-known limitation of the RBF. Nevertheless, it is noted that performance improvement can yet be achieved by standardizing the training data.
4.1.3. k-Nearest Neighbor
4.1.4. Linear Regression
4.1.5. Random Forest
4.1.6. Support Vector Machine
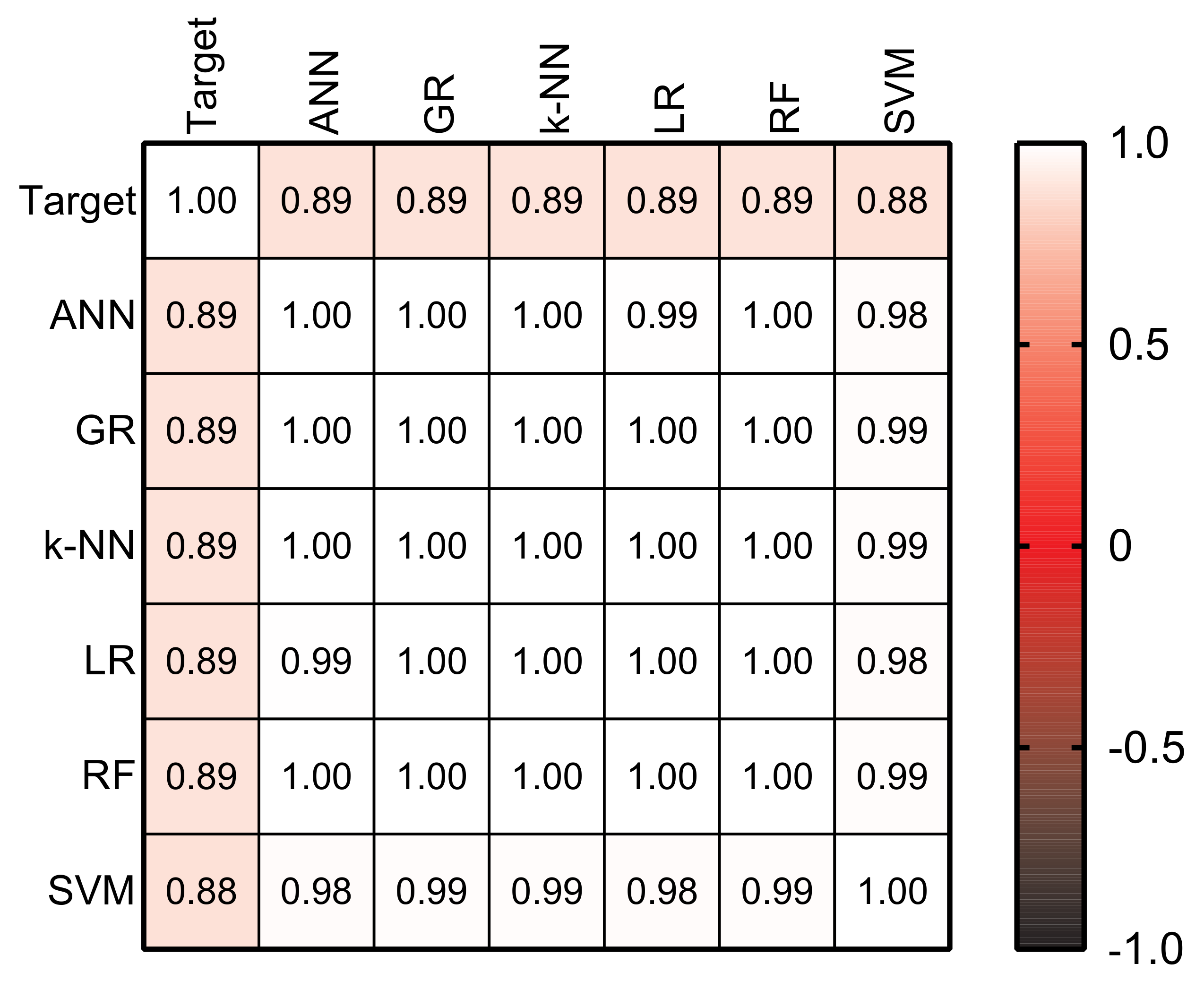
4.1.7. Comparison of the Different Methods
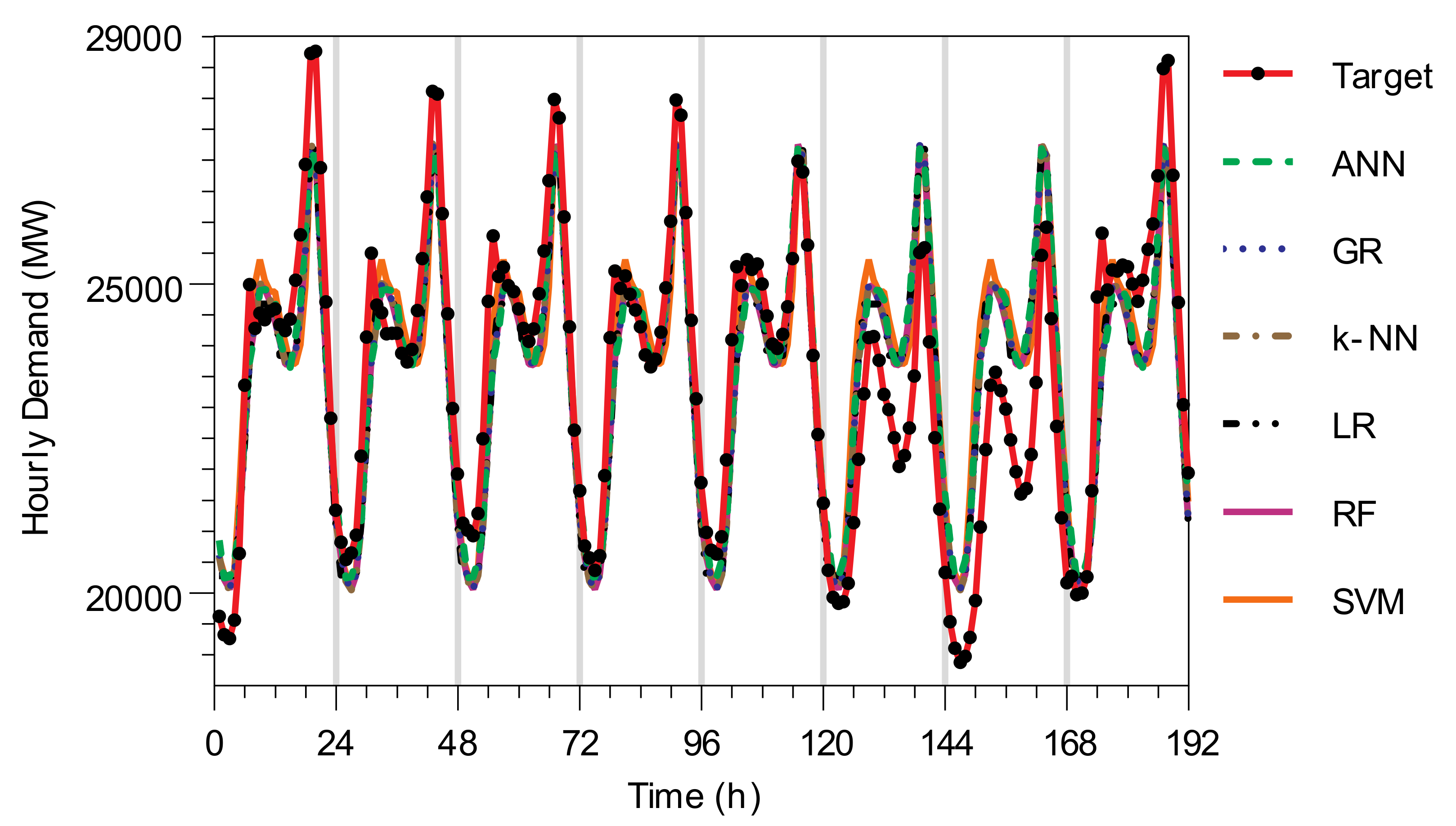
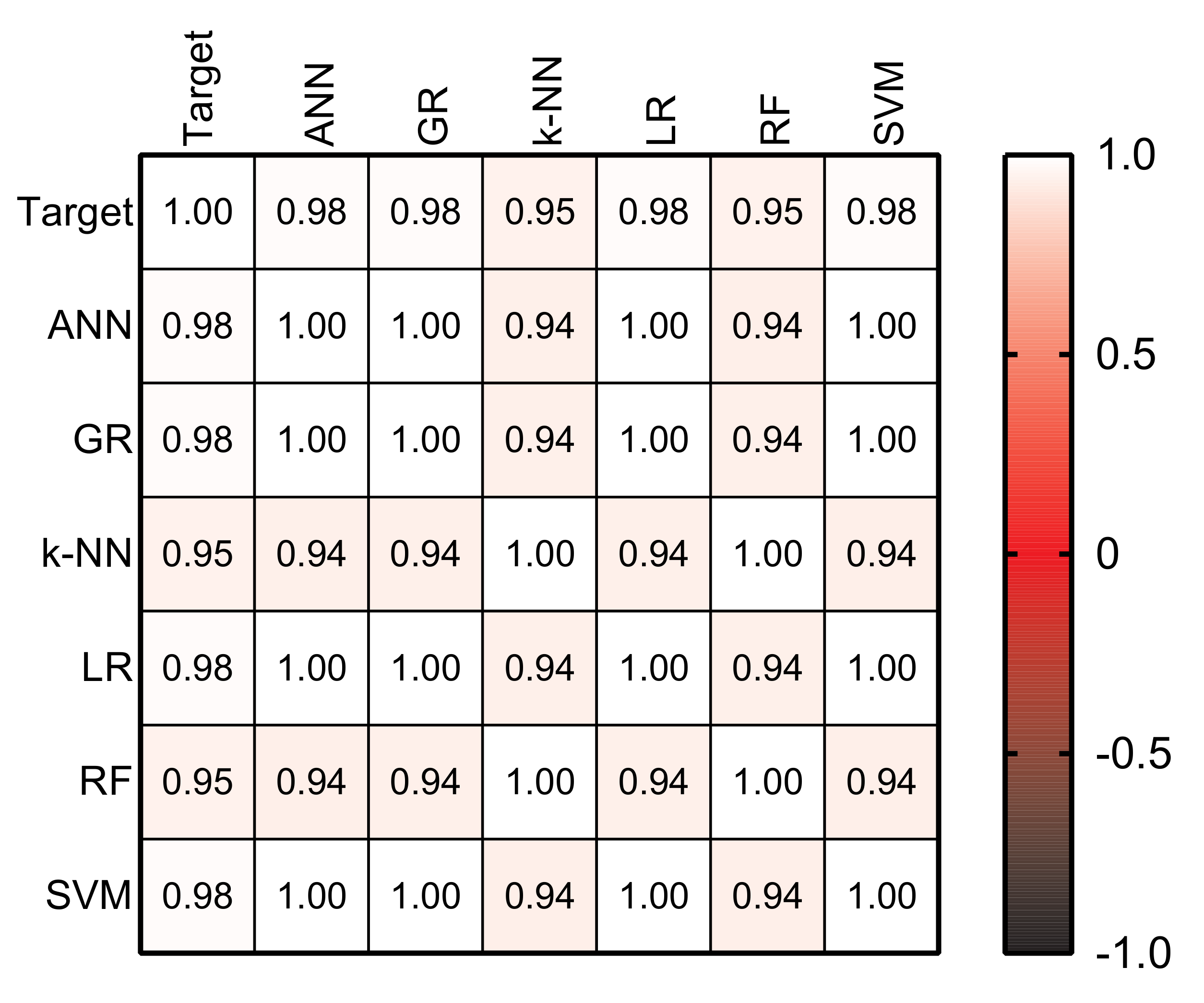
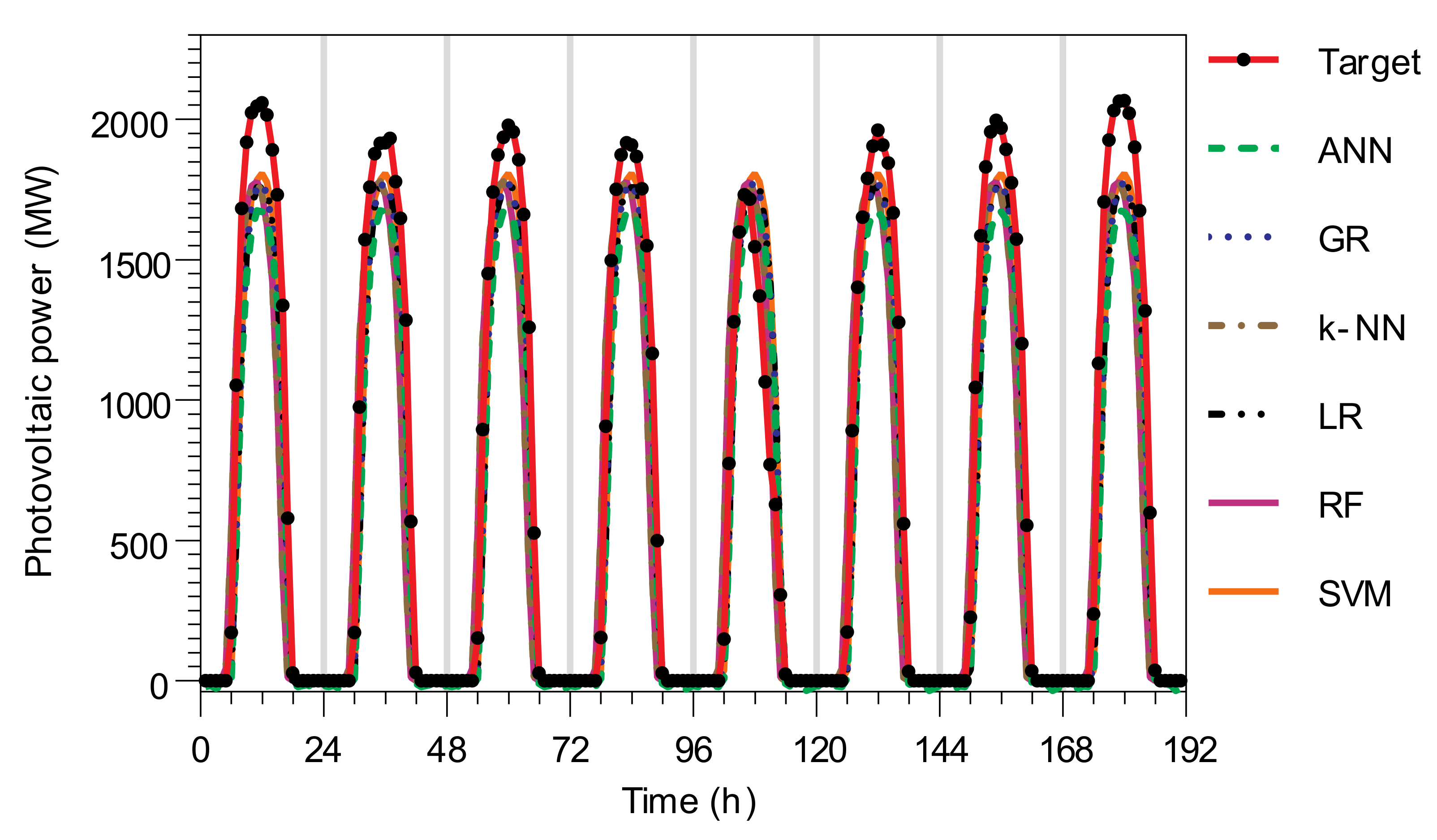
4.1.8. Visual Assessment of Predicted Values of the Different Methods
4.2. Hourly Renewable Generation
4.2.1. Photovoltaic Generation
4.2.2. Wind Generation
4.2.3. Runtime Performance of the Different Algorithms
- 1.
- The same datasets (i.e., PV and wind data) were used to evaluate each algorithm.
- 2.
- Both the training and testing runtime performance was measured and reported.
- 3.
- To ensure that no extra processing time was incurred by the PC, only the simulation software was kept running as the foreground process during each simulation period. This was accomplished by closing all other foreground processes in the PC’s task manager.
- 4.
- Finally, the timing results shown in Table 15 were obtained by averaging the results of 50 independent runs of each algorithm.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| CC | Correlation coefficient |
| ELM | Extreme learning machine |
| EPN | Ensemble prediction network |
| FFANN | Feed-forward artificial neural network |
| GR | Gaussian regression |
| KELM | Kernel-based extreme learning machine |
| k-NN | k-nearest neighbor |
| LR | Linear regression |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MSE | Mean square error |
| MVR | Multi-variable regression |
| PV | Photovoltaic |
| RAE | Relative absolute error |
| RBF | Radial basis function |
| RF | Random forest |
| RMSE | Root mean square error |
| RRSE | Root relative square error |
| RSA | Republic of South Africa |
| RSS | Residual sum of squares |
| SA | Simulated annealing |
| SVM | Support vector machine |
| WT | Wavelet transform |
| Brackets | |
| Parentheses | |
| Square root | |
| dy/dx | Derivative |
| Euclidean norm | |
| ∑ | Summation |
| Absolute value |
References
- Danish, M.S.S.; Senjyu, T.; Funabashia, T.; Ahmadi, M.; Ibrahimi, A.M.; Ohta, R.; Howlader, H.O.R.; Zaheb, H.; Sabory, N.R.; Sediqi, M.M. A sustainable microgrid: A sustainability and management-oriented approach. Energy Procedia 2019, 159, 160–167. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Pretto, S.; Gavazzeni, M.; Vigani, S.; Paccanelli, F. Electrical Load Forecast by Means of LSTM: The Impact of Data Quality. Forecasting 2021, 3, 91–101. [Google Scholar] [CrossRef]
- Lago, J.; Marcjasz, G.; Schutter, B.D.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy 2021, 293, 1–21. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy Forecasting: A Review and Outlook. IEEE Open Access J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Uniejewski, B.; Weron, R.; Ziel, F. Variance Stabilizing Transformations for Electricity Spot Price Forecasting. IEEE Trans. Power Syst. 2018, 33, 2219–2229. [Google Scholar] [CrossRef] [Green Version]
- Marcjasz, G.; Uniejewski, B.; Weron, R. On the importance of the long-term seasonal component in day-ahead electricity price forecasting with NARX neural networks. Int. J. Forecast. 2019, 35, 1520–1532. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Chen, J. Short-Term Electricity Price Forecasting with Stacked Denoising Autoencoders. IEEE Trans. Power Syst. 2017, 32, 2673–2681. [Google Scholar] [CrossRef]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity Price Forecasting Using Recurrent Neural Networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Wang, Y.; Ma, J.; Jin, Q. BRIM: An Accurate Electricity Spot Price Prediction Scheme-Based Bidirectional Recurrent Neural Network and Integrated Market. Energies 2019, 12, 2241. [Google Scholar] [CrossRef] [Green Version]
- Rijn, J.N.; Hutter, F. Hyperparameter Importance Across Datasets. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2367–2376. [Google Scholar] [CrossRef] [Green Version]
- Bhotto, M.Z.A.; Jones, R.; Makonin, S.; Bajic, I.V. Short-Term Demand Prediction Using an Ensemble of Linearly-Constrained Estimators. IEEE Trans. Power Syst. 2021, 36, 3163–3175. [Google Scholar] [CrossRef]
- Muni, S.P.; Sharma, R. Short-term electricity price prediction using kernel-based machine learning techniques. In Proceedings of the 2021 1st Odisha International Conference on Electrical Power Engineering, Communication and Computing Technology (ODICON), Bhubaneswar, India, 8–9 January 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Yang, Z. Optimal Scheduling of Isolated Microgrids Using Automated Reinforcement Learning-Based Multi-Period Forecasting. IEEE Trans. Sustain. Energy 2022, 13, 159–169. [Google Scholar] [CrossRef]
- Shi, Z.B.; Li, Y.; Yu, T. Short-Term Load Forecasting Based on LS-SVM Optimized by Bacterial Colony Chemotaxis Algorithm. In Proceedings of the 2009 International Conference on Information and Multimedia Technology, Beijing, China, 16–18 December 2009; pp. 306–309. [Google Scholar] [CrossRef]
- Sabzehgar, R.; Amirhosseini, D.Z.; Rasouli, M. Solar power forecast for a residential smart microgrid based on numerical weather predictions using artificial intelligence methods. J. Build. Eng. 2020, 32, 101629. [Google Scholar] [CrossRef]
- Scolari, E.; Sossan, F.; Paolone, M. Irradiance prediction intervals for PV stochastic generation in microgrid applications. Sol. Energy 2016, 139, 116–129. [Google Scholar] [CrossRef]
- Mohamed, M.; Chandra, A.; Abd, M.A.; Singh, B. Application of machine learning for prediction of solar microgrid system. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Onumanyi, A.J.; Isaac, S.J.; Kruger, C.P.; Abu-Mahfouz, A.M. Transactive Energy: State-of-the-Art in Control Strategies, Architectures, and Simulators. IEEE Access 2021, 9, 131552–131573. [Google Scholar] [CrossRef]
- Viel, F.; Silva, L.A.; Leithardt, V.R.Q.; Santana, J.F.D.P.; Teive, R.C.G.; Zeferino, C.A. An Efficient Interface for the Integration of IoT Devices with Smart Grids. Sensors 2020, 20, 2849. [Google Scholar] [CrossRef]
- Helfer, G.A.; Barbosa, J.L.V.; Alves, D.; da Costa, A.B.; Beko, M.; Leithardt, V.R.Q. Multispectral Cameras and Machine Learning Integrated into Portable Devices as Clay Prediction Technology. J. Sens. Actuator Netw. 2021, 10, 40. [Google Scholar] [CrossRef]
- Dalai, I.; Mudali, P.; Pattanayak, A.S.; Pattnaik, B.S. Hourly prediction of load using edge intelligence over IoT. In Proceedings of the 2019 11th International Conference on Advanced Computing (ICoAC), Chennai, India, 18–20 December 2019; pp. 117–121. [Google Scholar] [CrossRef]
- Ma, Y.J.; Zhai, M.Y. Day-Ahead Prediction of Microgrid Electricity Demand Using a Hybrid Artificial Intelligence Model. Processes 2019, 7, 320. [Google Scholar] [CrossRef] [Green Version]
- Dridi, A.; Moungla, H.; Afifi, H.; Badosa, J.; Ossart, F.; Kamal, A.E. Machine Learning Application to Priority Scheduling in Smart Microgrids. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1695–1700. [Google Scholar] [CrossRef]
- Tian, W.; Lei, C.; Tian, M. Dynamic prediction of building HVAC energy consumption by ensemble learning approach. In Proceedings of the 2018 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 12–14 December 2018; Volume 8, pp. 254–257. [Google Scholar] [CrossRef]
- Hajjaji, I.; Alami, H.E.; El-Fenni, M.R.; Dahmouni, H. Evaluation of Artificial Intelligence Algorithms for Predicting Power Consumption in University Campus Microgrid. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; pp. 2121–2126. [Google Scholar] [CrossRef]
- Kubat, M. Artificial Neural Networks. In An Introduction to Machine Learning; Springer International Publishing: New York, NY, USA, 2021; pp. 117–143. [Google Scholar] [CrossRef]
- Graupe, D. Principles of Artificial Neural Networks, 3rd ed.; Advanced Series in Circuits and Systems; World Scientific Publishers: Singapore, 2013; Volume 7, pp. 1–382. [Google Scholar] [CrossRef]
- Hajian, A.; Styles, P. Artificial Neural Networks. In Application of Soft Computing and Intelligent Methods in Geophysics; Springer International Publishing: New York, NY, USA, 2018; pp. 3–69. [Google Scholar] [CrossRef]
- Principe, J. Artificial Neural Networks. In Electrical Engineering Handbook; CRC Press: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Pirjatullah; Kartini, D.; Nugrahadi, D.T.; Muliadi; Farmadi, A. Hyperparameter Tuning using GridsearchCV on The Comparison of The Activation Function of The ELM Method to The Classification of Pneumonia in Toddlers. In Proceedings of the 2021 4th International Conference of Computer and Informatics Engineering (IC2IE), Jakarta, Indonesia, 22–24 October 2021; pp. 390–395. [Google Scholar] [CrossRef]
- Fontenla-Romero, O.; Erdogmus, D.; Principe, J.C.; Alonso-Betanzos, A.; Castillo, E. Linear Least-Squares Based Methods for Neural Networks Learning. In Artificial Neural Networks and Neural Information Processing—ICANN/ICONIP 2003; Springer: Istanbul, Turkey, 2003; pp. 84–91. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Banerjee, A.; Dunson, D.B.; Tokdar, S.T. Efficient Gaussian process regression for large datasets. Biometrika 2013, 100, 75–89. [Google Scholar] [CrossRef]
- Gramacy, R.B. Gaussian Process Regression. In Surrogates; Chapman and Hall/CRC: London, UK, 2020; pp. 143–221. [Google Scholar] [CrossRef]
- Cunningham, P.; Delany, S.J. k-Nearest Neighbour Classifiers - A Tutorial. ACM Comput. Surv. 2021, 54, 1–25. [Google Scholar] [CrossRef]
- Ali, N.; Neagu, D.; Trundle, P. Evaluation of k-nearest neighbour classifier performance for heterogeneous data sets. SN Appl. Sci. 2019, 1, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Biau, G.; Scornet, E. A random forest guided tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Probst, P.; Boulesteix, A.L. To tune or not to tune the number of trees in random forest? J. Mach. Learn. Res. 2017, 18, 1–18. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S. Support vector machine and regression. Chapter Support vector machine and regression. In Introduction to Algorithms for Data Mining and Machine Learning; Yang, X.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 129–138. [Google Scholar] [CrossRef]
- Pisner, D.A.; Schnyer, D.M. Support vector machine. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–121. [Google Scholar] [CrossRef]
- Suthaharan, S. Support Vector Machine. In Machine Learning Models and Algorithms for Big Data Classification; Springer: New York, NY, USA, 2016; pp. 207–235. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Mondi, L. Eskom: Electricity and technopolitics in South Africa by Syvly Jaglin, Alain Dubresson. Transform. Crit. Perspect. South. Afr. 2017, 93, 176–185. [Google Scholar] [CrossRef]
- Roy-Aikins, J. Challenges in Meeting the Electricity Needs of South Africa. In Proceedings of the ASME 2016 Power Conference, Charlotte, NC, USA, 26–30 June 2016. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D.K. What is the proper way to apply the multiple comparison test? Korean J. Anesthesiol. 2018, 71, 353–360. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Ref. | Year | Methods Compared | Metrics of Comparison | Was Statistical Significance Analysis Performed? | Was Processing Time Measured? | Findings |
|---|---|---|---|---|---|---|
| [11] | 2021 | EPN, LSTM, ANN | RMSE, MAPE | No | Yes: EPN was fastest | EPN outperformed LSTM, MLP, SVR and ETR in terms of RMSE over a wide variety of data |
| [12] | 2021 | ELM Kernel-based technique | MAE, MAPE, RMSE | No | No | Kernel based methods performed better than ELM; Gaussian kernel performed better than other kernel methods. |
| [15] | 2020 | ANN, MVR, SVM | MAPE, MSE | No | No | The developed neural network model outperformed the MVR and SVM |
| [17] | 2020 | Regression, ANN | MSE, RMSE, R-squared Chi-squared | No | No | Regression approach has a better performance than some state-of-the-art method such as feed forward neural network. |
| [21] | 2019 | LR, ANN, SMO regression, SVM | MAE, RMSE, CC | No | Yes, but only for SVM | SVM performed better than other algorithms compared with. |
| [22] | 2019 | FFANN, WT, SA | MAPE, RMSE, NMAE | No | No | FFANN performed better than BP-, GA-, and PSO-FFANN schemes |
| [23] | 2020 | LSTM | RMSE, MAE | No | No | No comparison |
| [24] | 2018 | MLR, decision tree, RF, Gradient boosted trees | ARE | No | No | Gradient boosted trees performed better than others. |
| [25] | 2021 | ARIMA, SARIMA, SVM, XGBoost, RNN, LSTM, LSTM-RNN | MAE, MAPE, MSE, R-squared | No | No | Deep learning approaches such as RNN, LSTM achieved better results than time series and machine learning. While hybrid of RNN-LSTM achieved the best accuracy |
| Present Article | 2022 | ANN, GR, k-NN, LR, RF, SVM | CC, RAE, RRSE, MAE, RMSE | Yes | Yes | There was no statistical significant difference in the performance of the different methods |
| Hidden Layer | Learning Rate | Momentum | CC | RAE (%) | RRSE (%) |
|---|---|---|---|---|---|
| 6 | 0.1 | 0.4 | 0.8909 | 44.6982 | 45.9884 |
| 6 | 0.3 | 0.2 | 0.8897 | 48.2524 | 49.068 |
| 6,6 | 0.1 | 0.1 | 0.8895 | 44.1209 | 45.73 |
| 6,6 | 0.5 | 0.4 | 0.8795 | 47.2956 | 49.1213 |
| 9 | 0.1 | 0.4 | 0.8909 | 44.7817 | 46.0154 |
| 9 | 0.3 | 0.2 | 0.8884 | 48.9404 | 49.2918 |
| 9,9 | 0.1 | 0.1 | 0.8894 | 44.0081 | 45.7508 |
| 9,9 | 0.5 | 0.4 | 0.8844 | 47.4725 | 51.764 |
| 12 | 0.1 | 0.4 | 0.8909 | 44.8448 | 46.0465 |
| 12 | 0.3 | 0.2 | 0.888 | 48.7637 | 49.0518 |
| 12,12 | 0.1 | 0.1 | 0.8894 | 43.8782 | 45.764 |
| 12,12 | 0.5 | 0.4 | 0.8851 | 46.897 | 51.3911 |
| Kernel | Filter Type | CC | RAE (%) | RRSE (%) |
|---|---|---|---|---|
| Poly kernel | Normalized training data | 0.8905 | 46.1688 | 47.2879 |
| Poly kernel | Standardize training data | 0.8905 | 44.7277 | 45.5645 |
| RBF | Normalized training data | 0.8905 | 92.0074 | 91.6804 |
| RBF | Standardize training data | 0.8905 | 52.0316 | 52.7159 |
| Normalized Poly Kernel | Normalized training data | 0.8905 | 46.1688 | 47.2879 |
| Normalized Poly Kernel | Standardize training data | 0.8905 | 46.045 | 47.1676 |
| K | Neighbour Search Algorithm | CC | RAE (%) | RRSE (%) |
|---|---|---|---|---|
| 1 | Euclidean (LNNSearch) | 0.8905 | 44.7124 | 45.5615 |
| 3 | Euclidean (LNNSearch) | 0.8905 | 44.7124 | 45.5615 |
| 5 | Euclidean (LNNSearch) | 0.8905 | 44.7124 | 45.5615 |
| 10 | Euclidean (LNNSearch) | 0 | 100 | 100 |
| Attribute Selection Method | CC | RAE (%) | RRSE (%) |
|---|---|---|---|
| No attribute selection | 0.8905 | 44.7124 | 45.5615 |
| M5 method | 0.89 | 44.3709 | 45.657 |
| Greedy methods | 0.89 | 44.3709 | 45.657 |
| Max. Depth | Iterations | CC | RAE (%) | RRSE (%) |
|---|---|---|---|---|
| 0 | 100 | 0.8901 | 44.909 | 45.7124 |
| 10 | 200 | 0.8904 | 44.8519 | 45.6262 |
| 20 | 500 | 0.8907 | 44.7255 | 45.5394 |
| Kernel | Filter Type | CC | RAE (%) | RRSE (%) |
|---|---|---|---|---|
| Poly kernel | Normalized training data | 0.8836 | 44.2875 | 47.1576 |
| Poly kernel | Standardize training data | 0.8835 | 44.2983 | 47.1763 |
| RBF | Normalized training data | 0.8654 | 71.6087 | 73.5864 |
| RBF | Standardize training data | 0.8703 | 46.9236 | 50.3859 |
| Normalize Poly Kernel | Normalized training data | 0.8836 | 44.2875 | 47.1576 |
| Normalize Poly Kernel | Standardize training data | 0.8835 | 44.3023 | 47.1848 |
| Methods | CC | RAE (%) | RRSE (%) | MAE | RMSE |
|---|---|---|---|---|---|
| ANN | 0.8894 | 43.8782 | 45.764 | 833.8811 | 1046.1255 |
| GR | 0.8905 | 44.7277 | 45.5645 | 850.8696 | 1040.5409 |
| k-NN | 0.8905 | 44.7124 | 45.5615 | 850.5788 | 1040.4722 |
| LR | 0.89 | 44.3709 | 45.657 | 844.0817 | 1042.6523 |
| RF | 0.8907 | 44.7255 | 45.5394 | 850.5656 | 1039.2409 |
| SVM | 0.8836 | 44.2875 | 47.1576 | 842.4953 | 1076.9213 |
| Comparison | Mean Diff. | 95.00% CI of Diff. | Below Threshold? | Summary | Adjusted p Value |
|---|---|---|---|---|---|
| Target vs. ANN | −48.69 | −669.1 to 571.7 | No | ns | >0.9999 |
| Target vs. GR | 58.07 | −562.3 to 678.5 | No | ns | >0.9999 |
| Target vs. k-NN | 58.07 | −562.3 to 678.5 | No | ns | >0.9999 |
| Target vs. LR | 58.07 | −562.3 to 678.5 | No | ns | >0.9999 |
| Target vs. RF | 63.45 | −556.9 to 683.8 | No | ns | >0.9999 |
| Target vs. SVM | −125.1 | −745.5 to 495.3 | No | ns | 0.997 |
| ANN vs. GR | 106.8 | −513.6 to 727.2 | No | ns | 0.9987 |
| ANN vs. k-NN | 106.8 | −513.6 to 727.2 | No | ns | 0.9987 |
| ANN vs. LR | 106.8 | −513.6 to 727.2 | No | ns | 0.9987 |
| ANN vs. RF | 112.1 | −508.2 to 732.5 | No | ns | 0.9983 |
| ANN vs. SVM | −76.37 | −696.8 to 544.0 | No | ns | 0.9998 |
| GR vs. k-NN | −0.00167 | −620.4 to 620.4 | No | ns | >0.9999 |
| GR vs. LR | 0.00125 | −620.4 to 620.4 | No | ns | >0.9999 |
| GR vs. RF | 5.383 | −615.0 to 625.8 | No | ns | >0.9999 |
| GR vs. SVM | −183.1 | −803.5 to 437.3 | No | ns | 0.9767 |
| k-NN vs. LR | 0.002917 | −620.4 to 620.4 | No | ns | >0.9999 |
| k-NN vs. RF | 5.385 | −615.0 to 625.8 | No | ns | >0.9999 |
| k-NN vs. SVM | −183.1 | −803.5 to 437.3 | No | ns | 0.9767 |
| LR vs. RF | 5.382 | −615.0 to 625.8 | No | ns | >0.9999 |
| LR vs. SVM | −183.1 | −803.5 to 437.3 | No | ns | 0.9767 |
| RF vs. SVM | −188.5 | −808.9 to 431.9 | No | ns | 0.973 |
| Symbol | Range | Interpretation |
|---|---|---|
| ns | p > 0.05 | not significant |
| * | p ≤ 0.05 | weakly significant |
| ** | p ≤ 0.01 | significant |
| *** | p ≤ 0.001 | very significant |
| **** | p ≤ 0.0001 | extremely significant |
| Methods | CC | RAE (%) | RRSE (%) | MAE | RMSE |
|---|---|---|---|---|---|
| ANN | 0.9833 | 21.7619 | 27.9011 | 163.8525 | 231.0859 |
| GR | 0.9835 | 16.292 | 23.1943 | 122.6677 | 192.1026 |
| k-NN | 0.9460 | 16.212 | 23.1527 | 122.0658 | 191.7581 |
| LR | 0.9834 | 16.333 | 23.1825 | 122.9761 | 192.0049 |
| RF | 0.9460 | 16.2378 | 23.1726 | 122.2594 | 191.9225 |
| SVM | 0.9824 | 15.3522 | 22.3847 | 115.5917 | 185.3969 |
| Comparison | Mean Diff. | 95.00% CI of Diff. | Below Threshold? | Summary | Adjusted p Value |
|---|---|---|---|---|---|
| Target vs. ANN | 144.9 | −81.66 to 371.4 | No | ns | 0.4884 |
| Target vs. GR | 97.92 | −128.6 to 324.4 | No | ns | 0.8628 |
| Target vs. k-NN | 97.91 | −128.6 to 324.4 | No | ns | 0.8628 |
| Target vs. LR | 97.92 | −128.6 to 324.4 | No | ns | 0.8628 |
| Target vs. RF | 98.13 | −128.4 to 324.7 | No | ns | 0.8616 |
| Target vs. SVM | 87.07 | −139.4 to 313.6 | No | ns | 0.9173 |
| ANN vs. GR | −46.94 | −273.5 to 179.6 | No | ns | 0.9965 |
| ANN vs. k-NN | −46.95 | −273.5 to 179.6 | No | ns | 0.9965 |
| ANN vs. LR | −46.94 | −273.5 to 179.6 | No | ns | 0.9965 |
| ANN vs. RF | −46.73 | −273.3 to 179.8 | No | ns | 0.9965 |
| ANN vs. SVM | −57.79 | −284.3 to 168.7 | No | ns | 0.9891 |
| GR vs. k-NN | −0.00628 | −226.5 to 226.5 | No | ns | >0.9999 |
| GR vs. LR | 0.00178 | −226.5 to 226.5 | No | ns | >0.9999 |
| GR vs. RF | 0.2102 | −226.3 to 226.7 | No | ns | >0.9999 |
| GR vs. SVM | −10.85 | −237.4 to 215.7 | No | ns | >0.9999 |
| k-NN vs. LR | 0.008063 | −226.5 to 226.5 | No | ns | >0.9999 |
| k-NN vs. RF | 0.2165 | −226.3 to 226.7 | No | ns | >0.9999 |
| k-NN vs. SVM | −10.84 | −237.4 to 215.7 | No | ns | >0.9999 |
| LR vs. RF | 0.2084 | −226.3 to 226.7 | No | ns | >0.9999 |
| LR vs. SVM | −10.85 | −237.4 to 215.7 | No | ns | >0.9999 |
| RF vs. SVM | −11.06 | −237.6 to 215.5 | No | ns | >0.9999 |
| Methods | CC | RAE (%) | RRSE (%) | MAE | RMSE |
|---|---|---|---|---|---|
| ANN | 0.558 | 98.7794 | 99.8968 | 279.4048 | 344.7094 |
| GR | 0.5559 | 80.9548 | 85.1445 | 228.9867 | 293.8042 |
| k-NN | 0.5559 | 80.9542 | 85.1432 | 228.9848 | 293.7998 |
| LR | 0.5486 | 81.229 | 85.609 | 229.7621 | 295.4071 |
| RF | 0.5565 | 80.7043 | 84.9551 | 228.2781 | 293.1508 |
| SVM | 0.5884 | 77.8575 | 81.5118 | 220.2257 | 281.269 |
| Comparison | Mean Diff. | 95.00% CI of Diff. | Below Threshold? | Summary | Adjusted p Value |
|---|---|---|---|---|---|
| Target vs. ANN | −213 | −274.4 to −151.6 | Yes | **** | <0.0001 |
| Target vs. GR | −112.4 | −173.8 to −50.96 | Yes | **** | <0.0001 |
| Target vs. k-NN | −112.4 | −173.8 to −50.96 | Yes | **** | <0.0001 |
| Target vs. LR | −112.7 | −174.1 to −51.27 | Yes | **** | <0.0001 |
| Target vs. RF | −111 | −172.4 to −49.56 | Yes | **** | <0.0001 |
| Target vs. SVM | −94.63 | −156.1 to −33.19 | Yes | *** | 0.0001 |
| ANN vs. GR | 100.6 | 39.16 to 162.0 | Yes | **** | <0.0001 |
| ANN vs. k-NN | 100.6 | 39.16 to 162.0 | Yes | **** | <0.0001 |
| ANN vs. LR | 100.3 | 38.86 to 161.7 | Yes | **** | <0.0001 |
| ANN vs. RF | 102 | 40.56 to 163.4 | Yes | **** | <0.0001 |
| ANN vs. SVM | 118.4 | 56.93 to 179.8 | Yes | **** | <0.0001 |
| GR vs. k-NN | −0.00093 | −61.44 to 61.43 | No | ns | >0.9999 |
| GR vs. LR | −0.3068 | −61.74 to 61.13 | No | ns | >0.9999 |
| GR vs. RF | 1.396 | −60.04 to 62.83 | No | ns | >0.9999 |
| GR vs. SVM | 17.77 | −43.67 to 79.21 | No | ns | 0.979 |
| k-NN vs. LR | −0.3059 | −61.74 to 61.13 | No | ns | >0.9999 |
| k-NN vs. RF | 1.397 | −60.04 to 62.83 | No | ns | >0.9999 |
| k-NN vs. SVM | 17.77 | −43.67 to 79.21 | No | ns | 0.979 |
| LR vs. RF | 1.703 | −59.73 to 63.14 | No | ns | >0.9999 |
| LR vs. SVM | 18.08 | −43.36 to 79.51 | No | ns | 0.9771 |
| RF vs. SVM | 16.37 | −45.06 to 77.81 | No | ns | 0.9862 |
| PV | Wind | |||
|---|---|---|---|---|
| Methods | Training Time (s) | Test Time (s) | Training Time (s) | Test Time (s) |
| ANN | 2.14 | 0.08 | 2.24 | 0.07 |
| GR | 0.63 | 0.26 | 0.55 | 0.28 |
| k-NN | - | 0.1 | - | 0.09 |
| LR | 0.04 | 0.09 | 0.02 | 0.07 |
| RF | 0.25 | 0.15 | 0.12 | 0.08 |
| SVM | 0.52 | 0.07 | 0.14 | 0.07 |
| Tukey’s Multiple Comparisons Test | Mean Diff. | 95.00% CI of Diff. | Below Threshold? | Summary | Adjusted p Value |
|---|---|---|---|---|---|
| ANN vs. GR | −0.195 | −0.2832 to −0.1068 | Yes | *** | 0.001 |
| ANN vs. k-NN | −0.02 | −0.1082 to 0.06825 | No | ns | 0.9326 |
| ANN vs. LR | −0.005 | −0.09325 to 0.08325 | No | ns | 0.9999 |
| ANN vs. RF | −0.04 | −0.1282 to 0.04825 | No | ns | 0.5242 |
| ANN vs. SVM | 0.005 | −0.08325 to 0.09325 | No | ns | 0.9999 |
| GR vs. k-NN | 0.175 | 0.08675 to 0.2632 | Yes | ** | 0.0017 |
| GR vs. LR | 0.19 | 0.1018 to 0.2782 | Yes | ** | 0.0011 |
| GR vs. RF | 0.155 | 0.06675 to 0.2432 | Yes | ** | 0.0033 |
| GR vs. SVM | 0.2 | 0.1118 to 0.2882 | Yes | *** | 0.0008 |
| k-NN vs. LR | 0.015 | −0.07325 to 0.1032 | No | ns | 0.9784 |
| k-NN vs. RF | −0.02 | −0.1082 to 0.06825 | No | ns | 0.9326 |
| k-NN vs. SVM | 0.025 | −0.06325 to 0.1132 | No | ns | 0.8545 |
| LR vs. RF | −0.035 | −0.1232 to 0.05325 | No | ns | 0.6371 |
| LR vs. SVM | 0.01 | −0.07825 to 0.09825 | No | ns | 0.9964 |
| RF vs. SVM | 0.045 | −0.04325 to 0.1332 | No | ns | 0.4217 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cebekhulu, E.; Onumanyi, A.J.; Isaac, S.J. Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids. Sustainability 2022, 14, 2546. https://doi.org/10.3390/su14052546
Cebekhulu E, Onumanyi AJ, Isaac SJ. Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids. Sustainability. 2022; 14(5):2546. https://doi.org/10.3390/su14052546
Chicago/Turabian StyleCebekhulu, Eric, Adeiza James Onumanyi, and Sherrin John Isaac. 2022. "Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids" Sustainability 14, no. 5: 2546. https://doi.org/10.3390/su14052546
APA StyleCebekhulu, E., Onumanyi, A. J., & Isaac, S. J. (2022). Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids. Sustainability, 14(5), 2546. https://doi.org/10.3390/su14052546







