1. Introduction
To reduce the waste of various resources and indirectly protect the environment, the proposal of the concept of the green mine requires a scientific mining process and efficient utilization of equipment resources. Standardized and intensive mining are the main mining modes of the future. Underground production equipment is gradually developing in a large-scale and intelligent direction. Therefore, effectively improving the mining efficiency and equipment utilization will become one of the key parameters for developing green mines and improving the economic benefits of mining enterprises. With the continuous development of information technology, big data, and artificial intelligence, intelligent mining theory and technology have come a long way, thereby providing basic support for the transformation of mining enterprises from extensive to refined. Optimal preparation of production plans and reasonable equipment scheduling are important aspects of green mines and intelligent mining. However, due to factors such as the mining environment, equipment performance, and personnel quality, abnormal conditions such as equipment breakdowns and safety accidents will inevitably occur during the production process. As a result, the original scheduling plan may not be completed, which in turn affects the overall production schedule of the mine and the economic benefits of the enterprise. Therefore, solving the problem of production equipment rescheduling under abnormal conditions and completing the original production plan to the greatest extent have become new research hot spots in the field of green mines and intelligent mining.
Regarding the research on the short-term plan of underground mines, some scholars conceptualize it as ore blending plan [
1], and the planning preparation model is constructed with the goal of maximizing profits, considering the technical and economic requirements and spatial sequence relationship in the mining process as constraints [
2]. Campeau and Gamache proposed an optimization model for short-term planning. The model considers all aspects of development and production, as well as specific restrictions on equipment and workers. Moreover, the model employs a preemptive mixed-integer program to prepare the best production planning in a short time frame [
3]. Based on the short-term production plan, in order to realize the compactness of underground mine production, it is necessary to schedule production equipment scientifically and efficiently, and the scheduling optimization model is constructed with the shortest total completion time as the goal [
4]. To reduce the ineffective travel time of haulage equipment, Yardimci and Karpuz proposed a shortest-path optimization method for underground mine haulage road design based on the evolutionary algorithm. This method considers kinematic constraints such as minimum turning radius and maximum slope to determine the optimal haulage path [
5]. For such instances, it is necessary to prepare high-quality operation planning for haulage equipment. Åstrand et al., proposed a constraint programming method that can automatically execute short-term scheduling plans, employ large-scale neighborhood search with neighborhood definitions in specific areas, and contribute to finding high-quality schedules faster [
6].
On the basis of the short-term operation plan and equipment scheduling plan, in order to conform to the actual production situation as much as possible and further improve the utilization rate of equipment, scholars from various countries consider equipment breakdowns as a precondition for the preparation of the scheduling plan, and reprepare the dispatching plan of equipment. Samatemba et al., used Rstudio software to develop an algorithm and evaluate sensitive inputs of the life cycle of mining equipment. Moreover, the algorithm was used to determine, analyze, and optimize the overall equipment efficiency [
7]. After the equipment performance of the haulage equipment was evaluated, the breakdown probability of the equipment was calculated by counting the number of breakdowns and constructing a random breakdown algorithm to simulate the moment of breakdown. Zandieh and Gholami investigated the mixed flow shop scheduling problem with sequence-related setup time and random machine breakdowns. The authors employed the expected completion time as the optimization goal [
8]. Al-Hinai and Elmekkawy solved the problem of flexible job shop scheduling with random breakdowns based on opportunity-constrained programming [
9]. Ai et al., comprehensively considered random factors such as unit breakdowns, line breakdowns, load forecast errors, and interruptible load defaults. Moreover, the authors took the minimum system operating cost as the objective function to construct an optimization model with interruptible loads [
10]. Based on the internal relationship between the scheduling scheme structure, machine breakdown probability, maintenance time, and scheduling robustness, Ba et al., proposed an alternative measurement method based on the propagation of process breakdown effects. The authors wanted to investigate the problem of measuring the robustness of job shop scheduling in a random machine breakdown environment [
11].
According to the existing research of scholars from various countries, the main equipment rescheduling research work can be carried out in three steps. First, the breakdown problem is considered [
12,
13,
14], and the original plan is reprogrammed [
15]. Second, the existing rescheduling model is employed to construct a new rescheduling model [
16], or corresponding rescheduling strategies [
17,
18,
19,
20,
21] and frameworks [
22] are proposed according to different breakdown problems. When proposing the rescheduling strategy, some researchers proposed that a method can be used to determine whether rescheduling is required [
23]. Finally, based on completing the construction of the rescheduling model, the corresponding optimization algorithm [
24,
25,
26,
27] is improved to solve the strategy model.
Existing research mostly involves the problem of assembly line production, which is very different from the actual production in mines. Based on the existing research, in order to ensure the completion of the original operation plan on time, the multi-equipment is rescheduled, and an optimization method for an underground mine haulage equipment rescheduling plan based on random breakdowns simulation is proposed, aimed at the scheduling problem in the case of the breakdown of the underground mining equipment. The main tasks of the method are:
Constructing a random breakdown algorithm, determining the time of breakdown occurrence and the maintenance end, and classifying and segmenting those times according to whether each breakdown time is intersected or not.
Constructing a rescheduling plan model during each equipment breakdown period. Here, the main goal of minimum ore grade deviation and the secondary goal of maximum completion rate of the planning during the rescheduling period are taken into consideration. Finally, the rescheduling plan model is solved via the improved wolf pack algorithm.
Comparing the solution results of the rescheduling plan optimization model with the traditional scheduling plan to verify its feasibility.
3. Optimization Algorithm
The wolf colony algorithm based on the intelligence of the wolf colony can quickly find the optimal solution, with a large probability, with a random probability search in multiple points simultaneously, thereby simulating the predatory behavior of the wolf colony and its prey distribution method. This method abstracts three intelligent behaviors: wandering, rushing, and sieging. The wolf generation rule of “the winner takes all,” as well as the wolf colony update mechanism of “only the strong survive,” are employed. This algorithm is characterized by high solution accuracy, fast convergence speed, few control parameters, and strong robustness. However, its disadvantage of falling into a local optimum requires enhancing the global search ability and increasing the diversity of the population to find the optimal solution in the global scope.
The wolf colony algorithm divides the population of an artificial wolf colony into three types of wolves: head wolves, detective wolves, and fierce wolves. In the solution space, the artificial wolf with the best fitness is the head wolf. The best section of artificial wolves (apart from the head wolf) in the solution space are regarded as detection wolves. The remaining population is designated as the fierce wolves. The head wolf is responsible for the command and maintenance of the entire wolf colony. The detective wolves hunt within the possible range of their prey, make independent decisions based on the scent left by the prey, and always search in the direction with the strongest smell. The fierce wolves are responsible for sieging the prey when the detective wolves find it on the trail.
3.1. Algorithm Performance Testing
The performance of the wolf colony algorithm is compared with the particle swarm optimization (PSO), the genetic algorithm (GA), and the gravitational search algorithm (GSA). The method is to optimize and solve Formula (11), the range of variable is [–10, 10], and the theoretical minimum value is 0. The optimal fitness value of each generation will deviate in every algorithm due to the randomness of the initial population. The fitness value can be ignored when analyzing the performance of each algorithm. Compared with other algorithms, the wolf colony algorithm converges faster in the early stage, and after the convergence, the variation of the curve is relatively smooth (
Figure 2).
3.2. Algorithm Design and Improvement
3.2.1. Population Initialization
The equipment rescheduling plan problem is a typical non-deterministic polynomial (NP) problem. When solving this type of problem, the chromosome encoding method in the genetic algorithm is preferred for describing the solution of the problem. Therefore, the chromosome encoding method is employed to initialize the wolf colony. The combination of multiple chromosomes represents a feasible solution to the problem. The chromosome length is determined according to the problem scale and can be adjusted.
Lowercase letters are used for stopes, while capital letters are used for ore passes. For example, represents the operating route of a scraper. Multiple chromosomes form a single individual in the wolf colony, thereby indicating the current location of an artificial wolf. The position of the head wolf represents the position of the prey. For equipment rescheduling planning problems, the operation route of the scraper can be coded in periods. Each chromosome represents the operation route of the scraper in a specific period. After determining the chromosome coding method, the initial population is randomly generated according to the constraint conditions.
3.2.2. Rules for Determining the Head Wolf
First, the calculation method of individual fitness value is determined. The optimization model for equipment rescheduling planning is to minimize the objective function. Therefore, the reciprocal of the objective function is taken as the fitness of the individual. In addition, multiple objective functions correspond to multiple fitness values:
Since the objective function is not unique, and primary as well as secondary goals exist, the first fitness value of each artificial wolf in the solution space is compared against the head wolf rules. If there are multiple artificial wolves with the optimal first fitness values, the second fitness value is compared. If multiple equal second fitness values are present, one artificial wolf is randomly selected as the head wolf among all artificial wolves with equal first and second fitness values. The head wolf does not execute three intelligent behaviors. Moreover, it directly enters the next iteration.
3.2.3. Wandering Behavior
The wandering behavior of detective wolves determines the global search ability of the wolf colony algorithm. With an increase in the number of detective wolves, the chance of finding the global optimal solution is also increased. All artificial wolves in the solution space are first sorted. Then, better artificial wolves with half the population size (apart from the head wolf) are considered as detective wolves. First, prey concentration at the current position of the i-th detective wolf is calculated. If is higher than the prey concentration perceived by the head wolf, then . The i-th detective wolf initiates the call by replacing the wolf. If , then the i-th detective wolf takes one step forward in h directions and records the perceived prey concentration after each step before returning to the original position.
The detective wolf can advance in h directions by randomly selecting h gene positions in all chromosomes of the individual detective wolf. The step length is set as two. In other words, each time detective wolves wander a single step forward, the number of genes that are exchanged between each side of the selected gene position is increased by one.
For example, the position update method of wandering forward in the
h-th direction for two steps (
Figure 3) is:
To prevent the algorithm from falling into a local solution, when detective wolves wander in h directions and are still in place after reaching the predetermined number of wandering, the detective wolves choose to move to a certain position in h directions via the roulette method. Only fitness1 is selected in the roulette method.
3.2.4. Rushing Behavior
When detective wolves initiate a call, or the detective wolves fail to update the head wolf during the maximum number of wandering, the head wolf initiates a call. Once a call is initiated, all fierce wolves begin to rush towards the position of the head wolf. During that time, if the prey concentration perceived by the i-th fierce wolf is greater than , then . After all fierce wolves have completed rushing, the fierce wolf will transform into the head wolf and re-initiate a call. The rushing number is not calculated repeatedly. If , the i-th fierce wolf continues to rush. When the maximum number of rushing is reached or the distance between the fierce wolf and the head wolf is less than d, the sieging behavior is initiated.
The rushing method of the fierce wolves is as follows. First, the rushing step length is set as two. Then, the gene exchange position j of each chromosome of the i-th fierce wolf is randomly selected, and a single gene on each side of the gene position j is exchanged with some position of the head wolf. The number of exchanged genes increases with the number of rushing.
The location update method for the second rushing of the
i-th fierce wolf (
Figure 4) can be expressed as:
The distance
between the fierce wolves and the head wolf can be calculated as:
3.2.5. Sieging Behavior
When the fierce wolves get closer to the prey, they should unite with the detective wolf to conduct a close sieging on the prey and capture it. The position of the head wolf is regarded as the moving position of the prey.
The sieging method of artificial wolves is as follows. The sieging step is set to two. When each artificial wolf in the wolf colony participates in the sieging behavior, a gene position is first randomly determined. Then, the position of the artificial wolf is updated according to the location update method of the rushing behavior.
3.2.6. “The Winner Takes All” Wolf Generation Rules
The prey is distributed according to the principle of “from strong to weak” resulting in weak wolves being eliminated. To maintain the population diversity of the wolf colony, 40% of the artificial wolves with poor fitness are eliminated. Lastly, new artificial wolves are regenerated.
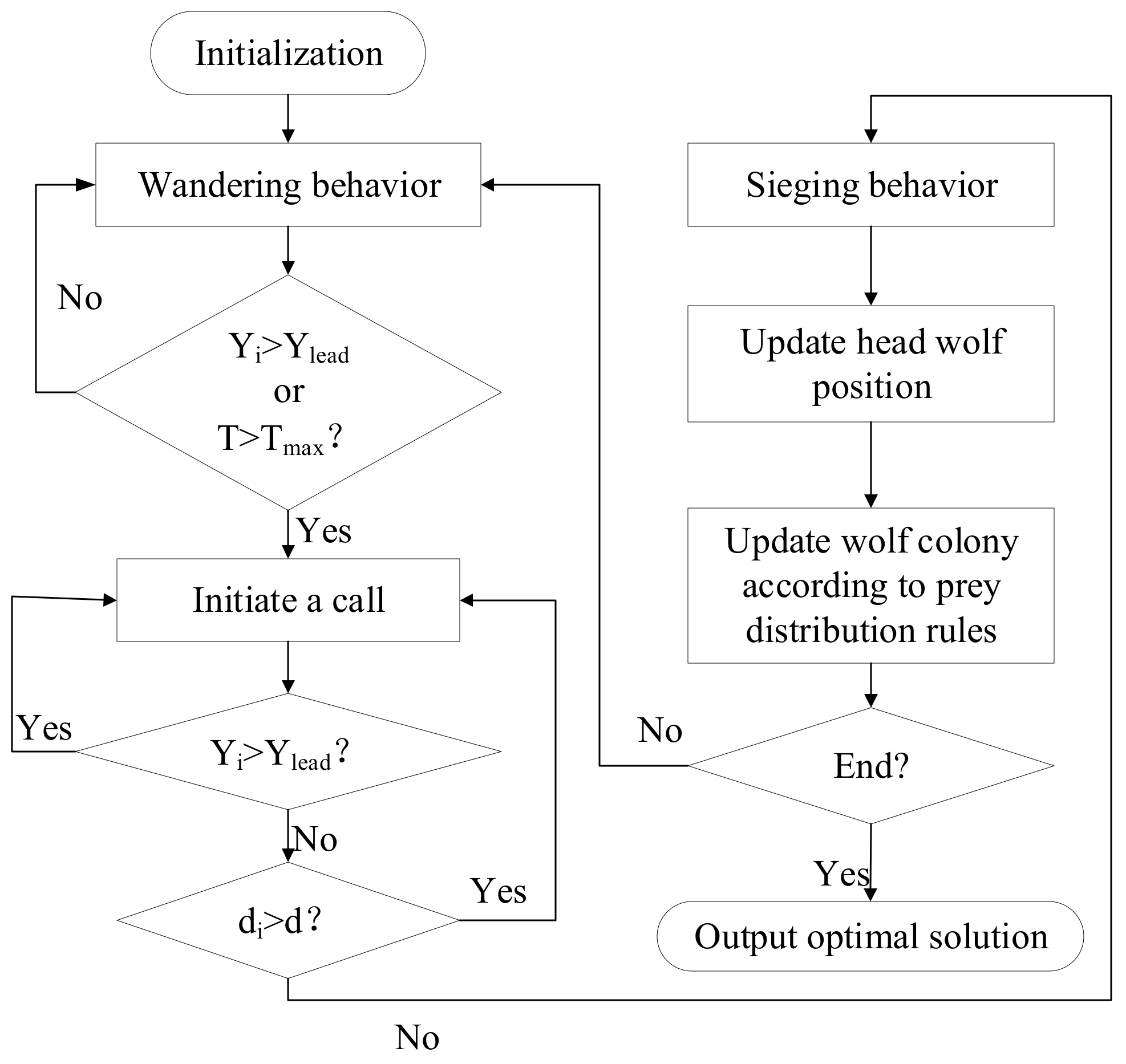
3.3. Algorithm Flow
The specific operation flow of the algorithm is shown in
Figure 5.
5. Discussion
Compared with other algorithms, WCA can find the optimal solution relatively quickly due to its ability to search at multiple points simultaneously. However, WCA is mostly used to solve the problem with continuous variables. The coding method of GA can intuitively display the scheduling decision scheme. Through performance testing, it is found that its solving ability is weak in that of WCA. In order to solve the problem of discrete coding, it is necessary to redefine the various behaviors of the individual artificial wolves.
To successfully prepare the rescheduling plan and simplify the problem, several assumptions are made in this paper. The mathematical model constructed in this study can be used in actual production. When the amount of haulage equipment is not increased, the model can be used to obtain a multi-equipment rescheduling plan, which can guide mining production. It can be considered to improve the model when spare equipment is involved. In addition, the construction method of this model can also be used for the rescheduling of other types of equipment, and the objective functions and constraints in the model may be slightly different. However, due to many factors affecting the operation of mining equipment, it is relatively difficult to predict its breakdowns. Therefore, accurately predicting the breakdown time of equipment will become one of the key aspects for the accurate preparation of a rescheduling plan, as well as one of the important research directions in the future. In addition to the breakdown time prediction, the preparation of the equipment rescheduling plan conducted in this paper is a type of static preparation method. This type belongs to the category of short-term planning and can be used as preparation for subsequent research. However, the actual equipment operation plan is dynamic, i.e., it can be adjusted in real-time. Therefore, converting a static rescheduling plan into dynamic real-time breakdown dispatching also represents an important research direction. In addition, when carrying out the dynamic real-time breakdown dispatching of equipment, resources and environmental costs can be optimized as the targets. The aforementioned can be done to reduce environmental pollution and the loss of natural resources, as well as to promote green mine production and construction.