1. Introduction
Cardiovascular disease has become the leading cause of death globally [
1,
2]. Electrocardiogram (ECG) monitoring is widely used for the screening and follow-up management of cardiovascular diseases. However, the interpretation of ECGs is a professional and time-consuming task. The rapid increase in ECG data has led to shortages in qualified physician resources. Consequently, the technology required for automatic ECG analysis and abnormality detection is in demand to cope with the rapid growth in ECG monitoring data [
3]. Considering the diversity of cardiac conditions and the complex correlations between them, the automatic detection of ECG abnormalities can be formed as a multi-label classification (MLC) problem, i.e., multiple different kinds of abnormalities may coexist in a single ECG recording. An ideal ECG classifier, therefore, should identify all of the abnormalities existing in a recording.
The problem of multi-label ECG classification is challenging for several reasons. First, the number of label combinations that are possibly present in an ECG recording is very large. As there are more than 100 ECG labels, the label combinations amount to over 2100. Such an enormous number of combinations makes the learning task difficult to solve. Second, the categories needing to be classified are extremely imbalanced. In a realistic dataset, the samples of one category (e.g., sinus tachycardia) may be many orders of magnitude more than that of another category (e.g., Brugada syndrome). Furthermore, the problem regarding multi-label ECG classification is cost-sensitive, which means that the costs of misclassification between different pairs of categories can be different. The cost here refers mainly to the impact of the diagnosis on the patient’s prognosis: a diagnosis that may make a patient more unwell is costlier than one that may improve patient outcomes. For example, the cost of classifying an ECG recording of atrial fibrillation (AF) as atrial flutter (AFL) should be less than the cost of classifying an AF recording as normal sinus rhythm (NSR). As AFL is closer to AF than NSR in terms of outcomes and treatments, a prediction of AFL, although not accurate, may encourage doctors to further diagnose and treat patients to improve their condition, while a prediction of NSR would hide the disease and may lead to missing the optimum treatment time and exacerbating the disease.
MLC methods can be categorized into two groups: problem transformation methods and algorithm adaptation methods [
4]. The concept of problem transformation methods is to transform the problem of multi-label classification into well-studied learning problems, such as binary classification and multi-class classification. Thus, the well-established methods used for the transformed problems can be used to solve the original problem. The most representative problem transformation methods include binary relevance [
5], which decomposes MLC into a series of binary classification problems, and random k-label sets [
6], which transforms MLC into a number of multi-class classification problems. Algorithm adaptation methods aim to adapt existing learning algorithms to tackle the MLC problem. Many traditional learning algorithms have been adapted for MLC along these lines, such as multi-label k-nearest neighbor (ML-kNN) [
7], multi-label decision tree (ML-DT) [
8], ranking-based support vector machine (rank-SVM) [
9], and collective multi-label classifier (CML) [
10]. Recently, deep learning algorithms have been widely adopted for MLC [
11,
12,
13]. In particular, the method of binary relevance can be easily combined with deep learning models in a multi-task framework, where the detection of each label is regarded as a binary classification task, and a deep neural network (DNN) for representation learning is shared cross all binary classifiers [
14]. As the representation learning is optimized for multiple tasks, the correlations among labels will be implicitly manifested in the intermediate representations, which can make up for a well-known drawback of binary relevance, i.e., the ignorance of label correlations. Due to its simplicity and efficiency, this method has been adopted in many studies for multi-label ECG classification [
15,
16,
17]. However, the transformation to binary classifications further worsens the category imbalance, as the positive samples are generally much less than the negative samples for each binary classifier.
To address the category imbalance problem, a series of methods have been proposed generally following one of three approaches: data resampling, algorithm adaption, and ensemble learning. The data resampling techniques tackle the problem by removing instances of the most frequent classes (or majority classes) (i.e., undersampling) [
18], or augmenting instances of the less frequent classes (or minority classes) (i.e., oversampling) [
19]. Unlike traditional datasets where each sample has only one label, a sample in multi-label datasets may be associated with majority classes and minority classes simultaneously, which is known as concurrence among imbalanced labels [
20]. If a dataset has a high concurrence between the majority and minority classes, the effectiveness of resampling would be reduced. The algorithm adaptation approach, on the other hand, adjusts the learning algorithms to make them suitable for the category imbalance problem. For example, the effect of category imbalance on the learning model can be alleviated by assigning different weights to the positive and negative samples of each label in loss calculation with methods such as weighted focal loss [
21] and asymmetric loss [
22]. The algorithm adaptation methods are usually tightly coupled with the adjusted algorithms, so their versatility will be reduced. The approach of ensemble learning is also commonly used to address the class imbalance problem in MLC. The basic idea is that the ensemble of multiple classifiers, each with a bias to different labels, will improve the model performance in learning imbalanced datasets. A series of ensemble techniques have been proposed in this approach, such as inverse random undersampling for the ensemble of binary classifiers [
23] and the heterogeneous ensemble of multi-label classifiers [
24]. Compared with previous methods, the ensemble learning approach is usually more computationally expensive, as multiple classifiers need to be trained and executed for prediction. The high computation complexity will hinder the algorithm from being embedded in platforms with limited computation resources, such as mobile ECG monitors.
The cost-sensitive property of multi-label ECG classification also has an important impact on the model performance, but has usually been ignored in previous studies. In a general sense, the methods for cost-sensitive learning can be classified into two categories: direct approaches and meta-learning approaches. The direct approaches adjust the learning algorithms by introducing cost information about misclassifications into the model training procedure, such as cost-sensitive decision trees [
25] and cost-sensitive SVM [
26]. By contrast, the meta-learning approaches do not adjust the learning algorithms, but modify the training data (pre-processing) or the model’s outputs (post-processing) to make the predictions cost-sensitive. One of the most representative pre-processing meta-learning methods is MetaCost, which relabels the training data according to pre-defined cost information. The post-processing methods are usually conducted by rescaling the model’s prediction or moving the thresholds based on the cost information [
27]. One of the advantages of the post-processing methods is that the model predictions can be adjusted flexibly when the cost definitions are changed, while other methods must retrain the models to adapt to the changes of classification costs. However, the number of thresholds that need to be tuned is usually no less than the number of considered labels (perhaps several dozen or even hundreds), which results in the choice of proper thresholds being a challenging task in MLC. For example, if the number of thresholds is 20, and 10 candidate values are assessed for each threshold, the number of considered threshold combinations will be 10
20, thus making a brute-force search infeasible.
In this study, we aim to develop a cost-sensitive learning framework for multi-label ECG classification. The developed framework is in the form of multi-task learning, where the stem part for representation learning is constructed with a deep residual network (ResNet) and class-wise attention (CWA), and the branches are multiple binary classifiers, with one for each category. In response to the challenges stated above, we propose a category imbalance and cost-sensitive thresholding (CICST) method to efficiently compute the thresholds for the binary classifiers according to predefined misclassification costs. The definition of “misclassification costs” considers not only the similarity of outcomes or treatments between categories, but also the category imbalance of the dataset. Furthermore, as the thresholding method is in a post-processing manner, the classification model can be adjusted flexibly to different cost definitions without retraining the model. This property allows our model to better adapt to application scenarios with different evaluation criteria.
2. Materials and Methods
In this section, we first introduce the datasets that were used for model training and evaluation in our study. We then present our method to address the problem of multi-label ECG classification. Our method consists of three parts, namely the pre-processing for data cleaning, the learning model based on a deep neural network (DNN), and the thresholding mechanism (i.e., CICST) to address the challenges of category imbalance and cost-sensitive learning.
2.1. Datasets
Several realistic datasets from the PhysioNet/CinC challenge 2021 named “
Will Two Do? Varying Dimensions in Electrocardiography” [
28] were used for model training and testing in this study. The dataset information is shown in
Table 1. One of the data sources was the China Physiological Signal Challenge (CPSC) [
29], which provided two datasets, namely CPSC and CPSC-Extra, in the list. The Physikalisch Technische Bundesanstalt (PTB) provided another two datasets, namely PTB and PTB-XL [
30]. The dataset named G12EC was from the Georgia 12-lead ECG challenge. The last two datasets, namely Chapman-Shaoxing and Ningbo, were provided by the Chapman University and the Shaoxing People’s Hospital [
31,
32].
From the statistics of the datasets, we found some differences among these datasets. First, the number of recordings and label kinds are different from dataset to dataset. Furthermore, the number of label kinds in a dataset not proportional to the number of its recordings. For example, the dataset CPSC containing 6877 recordings involves nine kinds of labels in the annotations, while the dataset CPSC-Extra containing only 3453 recordings involves 72 kinds of labels (much more than that of CPSC). This indicates that the data distributions are quite different among these datasets, which may be attributed to the different data filtering or annotating rules among them. One example of the different data filtering rules is that each kind of label in CPSC have a relatively large sample size (≥236), while some labels in other datasets have very small sample sizes (as small as one). As for the annotating rules, the label granularity may be different from dataset to dataset. For example, incomplete right bundle branch block and complete right bundle branch block seem to be annotated as their supertype (i.e., right bundle branch block) in CPSC, while they are annotated distinctively in some other datasets. In addition, the recording lengths are different in some datasets, such as CPSC, CPSC-Extra, and PTB. In addition, the length ranges are also different among these datasets. Furthermore, the ECG recorder type and configurations may be different from dataset to dataset. For example, the device used by PTB is a non-commercial, PTB prototype recorder, while the device used by PTB-XL is from Schiller AG [
30]. A consequence of this inconsistency is the diversity of sampling rate, ranging from 250 Hz to 1000 Hz. All these differences should be considered in the development of machine learning models.
2.2. Pre-Processing
Pre-processing is the first step in our learning framework. The purposes of pre-processing are to clean and normalize the ECG data. As the data are from different data sources, the sampling frequency and signal quality may be different from recording to recording. First, we resample the ECG signals to 250 Hz. The signals are then processed to remove baseline wanders and other kinds of noise. The baseline wander in signals is estimated by a moving the average filter in a window of one second (i.e., 250 sampling points). The estimated baseline is then subtracted from the original signals for baseline wander removal. The signals are further processed by a band-passing filter, with a passing band of 0.1~50 Hz, to suppress other kinds of noise, such as power-line interference, muscle noise, and respiration noise. Next, the signals are normalized to have mean zero and variance one. The difference in record lengths is another problem that should be addressed in the pre-processing stage. The DNN models are usually trained in mini-batches, where the records in a mini-batch should have the same signal length. For convenience in the model training, we convert the records in the training set to the same length by truncating (for longer records) or padding with zeros (for shorter records) from the end of the signals. The target length is set to 20 s in this work, as most of the records in the datasets are no longer than 20 s.
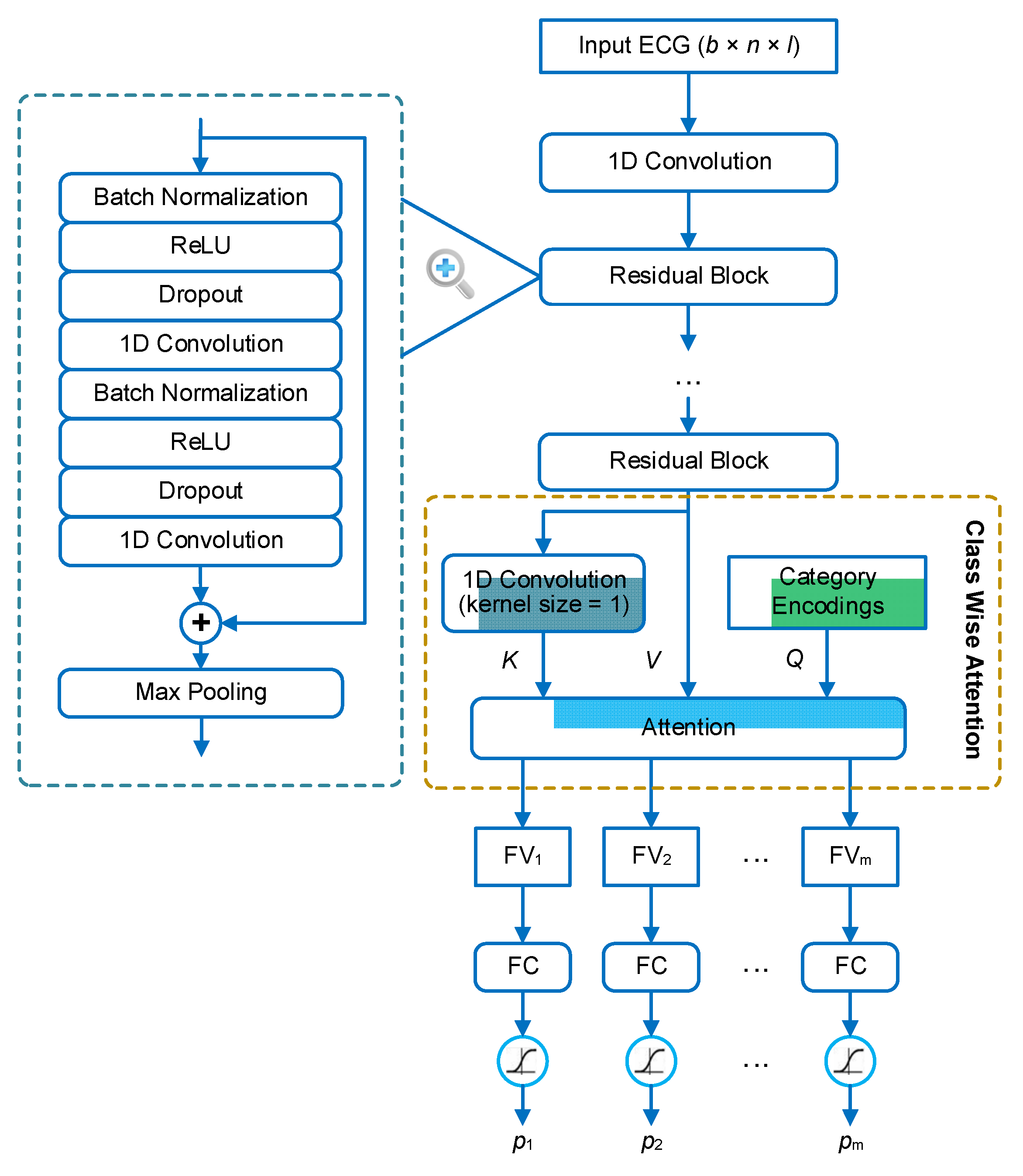
2.3. Structure of the Neural Network
We address the problem of multi-label ECG classification based on the methodology of deep learning. The architecture of the neural network is shown in
Figure 1. The backbone of the network is a 1D residual neural network (1D ResNet), which consists of several residual blocks. The structure of each residual block is in a full pre-activation manner [
33], where the first two layers in the block are batch normalization [
34] and ReLU activation [
35], respectively. In the residual block, the input is added to the output of the last convolutional layer through a short-cut connection. Thus, the main part of the block is aimed to learn a residual function between the output and the input. This structure has been demonstrated to be effective in facilitating the training of extreme deep neural networks [
33,
36]. The sum of the input and the residual is finally processed by a max-pooling layer for down-sampling. In our framework, the ResNet is used to extract features, or rather feature maps, from the ECG signals. The extracted feature map is a 3D tensor in the shape of
b ×
t ×
f, where
b is the batch size,
t is the length in the time dimension, and
f is the number of feature types.
In order to make classifications based on the extracted features, the feature maps are further aggregated to several feature vectors, one for each category. This aggregation is based on a mechanism, named class-wise attention (CWA), that was proposed in our previous study [
21]. The idea behind CWA is that different categories may be associated with different time regions of the signal. For example, if premature atrial beats (PAB) and premature ventricular beats (PVB) coexist in an ECG recording, they are generally distributed in different heartbeats. Therefore, during the feature aggregation, the detector of PAB expects the features of the PABs to be present in the feature vector, while the detector of PVB expects the features of the PVBs to be present in the feature vector. If all detectors use the same feature vector, there will be a competition between the features of different categories, and the features of some categories (i.e., categories with subtle features or small sample sizes) may be at a disadvantage. To address this problem, CWA tries to search relevant features for each detector based on the attention mechanism, and aggregate the feature maps according to the degrees of relevance. In CWA, the inner attention layer has three inputs: the query vectors (
Q), the key vectors (
K), and the value vectors (
V).
Q includes the encodings (one-hot encoding in our implementation) of the categories.
K is transformed from the feature maps based on a convolutional layer with the kernel size equal to 1 and the filter number equal to the category number.
V contains just the feature maps. The output of CWA contains the feature vector with respect to each query vector (or category). Finally, each feature vector is input into a dedicated fully connected (FC) layer to predict the probability that the corresponding category is present in the recording.
2.4. Class Imbalance and Cost-Sensitive Thresholding
The outputs of the model on a sample are a list of scalar values in the range of 0–1 that specify the confidence that the sample belongs to each considered category. To generate categorical predictions, a threshold is generally applied on the scalar values. The choice of threshold will affect the trade-offs between positive and negative errors. Raising the threshold will reduce the chance that a sample is classified as positive, as the criteria for positive is more stringent. By contrast, the increased threshold will lead to more samples to be predicted as negative, as the number of negative predictions and the number of positive predictions are negatively related. As the ECG classification is cost-sensitive, the choice of thresholds should minimize the expected classification costs on the test set. The mechanism of CICST consists of two parts: one is the method for obtaining the cost information of different kinds of misclassification, and the other is the method for calculating the threshold for each binary classifier based on the cost information.
2.4.1. Obtaining the Cost Matrix
The cost of misclassifying one category for another can be assessed in different ways. In this study, we consider the misclassification cost from two perspectives. The first is the similarity of outcomes and treatments between categories. In other words, if two categories of ECG have similar clinical risks or should be treated similarly, the cost of misclassification between them would be relatively small. The other perspective is the ratio of frequencies between categories in the training dataset. It has been demonstrated that the frequency ratio between categories can affect the distribution of classifiers’ outputs [
27]. In our learning framework, the categories (positive or negative) faced by most binary classifiers are extremely imbalanced, where there are much less positives samples than negative samples. As a consequence, the learning algorithm tends to classify a large proportion of positive samples into the negative category. From the application point of view, the positive class is actually the focus of the classification problem. The cost of a false positive detection would be conducting additional tests, while the cost of a false negative detection would be the severity of an illness. Therefore, the property of category imbalance and the significance of the positive categories should also be taken into account in the definition of classification costs. Furthermore, the classification costs need to be quantified for comparison and calculation purposes. Ideally, the cost of misclassification between each pair of categories should be specified. The costs are generally organized in a cost matrix, denoted by
. The entry
specifies the cost of classifying a sample as category
i when the true category is
j.
The measurement of classification costs is a highly skilled and delicate task. Thanks to the organizers of the PhysioNet/CinC challenge 2020/2021 [
28,
37], a benefit matrix judged by the cardiologists of the challenge is now available. The benefit matrix, denoted by
, contains information on the relationships of the 26 ECG categories. The entry
specifies the benefit of classifying a sample belonging to category
j as a category
i. A high value of
indicates that categories
i and
j have similar outcomes or treatments, and vice versa.
reaches its maximum value (i.e., 1) when
i is equal to
j. The details of this benefit matrix are available at
https://github.com/physionetchallenges/evaluation-2021 (accessed on 30 September 2021). The benefit matrix can be regarded as the opposite of the cost matrix; thus we can derive a cost matrix from the benefit matrix with the formula:
.
As the multi-label classification is converted to multiple binary classification problems, we need the cost information of false negatives and false positives to calculate the threshold for detecting each category. To address this problem, we define the false negative cost for each category to be 1, and calculate the false positive costs, denoted by
, based on the cost matrix
and the label distribution in the training set. The algorithm for converting the cost matrix
to the false positive cost of each category is shown in Algorithm 1. The input of the algorithm include the cost matrix
and the label matrix
of the training set. The entry
, if and only if the sample
i is annotated with label
j. In this algorithm,
is first normalized to
by dividing each entry by the annotated label number of its corresponding sample. To avoid dividing by zero, the entries of samples with no labels are divided by 1. The misclassification cost of each label on each sample is then calculated by the dot product between the normalized label matrix and the cost matrix. The resulting entries with positive labels are multiplied by zero, as the cost of a right prediction is zero. Finally, the false positive costs for each category are averaged over all samples to obtain the representative false positive costs, denoted by
.
| Algorithm 1 The pseudo-code of the algorithm to convert the cost matrix to multi-label classification cost. C′ denotes the cost matrix specifying the misclassification cost between each pair of categories. Y is the label matrix of the training dataset. c′ contains the derived false positive costs for each category |
| = computeFalsePositiveCosts (,) |
# Normalize the training set labels to for i 1 to N do # Calculate the label number of samples i max(sum(), 1) # Normalize the training set labels endfor # Calculate the misclassification cost of each label on each sample matrix_multiply (, ) # Mask out the entries with positive labels # Calculate the mean false positive costs of each label in the training set for i 1 to m do endfor Return
|
The false positive cost vector
does not reflect the property of class imbalance. Therefore, we designed a method to merge the cost information from both a prior cost definition and the imbalance ratios (IRs). The IR is defined as the ratio of the negative sample number to the positive sample number in the training set. The false positive cost of label
i is then defined as follows:
where
is a modulating factor. When
,
ignoring the effects of category imbalance on the model performance. When
,
ignoring the effects of predefined misclassification costs with respect to the category similarities. Therefore, to ensure that the final cost definition involves both kinds of information, the value of
should be between 0 and 1. In the results section, we will evaluate the influence of different choices of
on the model performance.
2.4.2. Calculation of Thresholds
With the cost information obtained, we need to compute the threshold for each binary classifier in our framework. The method to calculate the threshold for a binary classifier based on the cost information has been proposed in previous studies [
27]. With the same method, we can derive the thresholds from the estimated costs as follows:
where
and
denote the cost of true negative and true positive predictions for category
i, respectively. They are all zero in our definition of the costs.
denotes the cost of a false positive prediction for category
i, thus
. Analogously,
denotes the cost of a false negative prediction for category
i, which is 1 in our definition. If the model prediction for category
i on a sample is larger than the threshold
, category
i will be added to the predicted label set of the sample.
2.5. Experimental Setup
The learning framework is implemented with the TensorFlow framework. To better evaluate the effects of the thresholding methods, we use binary cross-entropy without sample or category weighting as the loss function for model training. The Adaptive Moment Estimation (Adam) method (with β1 = 0.9 and β2 = 0.999) is used to update the model parameters during the model training. The initial learning rate is 0.001, then it is scheduled with the exponential decay method with the decay factor equal to 0.9.
We train and evaluate the learning framework in a 5-fold cross-validation manner. The original datasets are first shuffled randomly, and then evenly split into 5 subsets. In each fold, 4 subsets (including about 70,500 recordings) are used as the training set, and the rest (including about 17,600 recordings) is used as the validation set. We evaluate the model performance on the validation set of each fold.
2.6. Metrics
In view of the cost-sensitive characteristic of multi-label ECG classification, we adopt a scoring metric recently proposed by the PhysioNet/CinC challenge [
28] to measure the model performance. We name this metric cost-weighted accuracy (
CWAcc) as it is derived by introducing cost-based weights to the traditional accuracy metric. To calculate
CWAcc, the prediction results on the validation set should be organized in a multi-class confusion matrix, denoted by
, where
is the number of recordings of category
j classified to category
i. The score is computed by weighted averaging the matrix
A:
where
is the entry of the benefit matrix
B that measures the similarity between each pair of categories in terms of outcomes and treatments. Furthermore,
CWAcc is normalized so that a score of 1 is obtained when the classifier always outputs the right labels, and a score of 0 is obtained when the classifier always outputs the normal class.
We also calculate some other commonly used metrics in clinical scenarios to evaluate the performance of our method, including accuracy (
Acc), sensitivity (
Se), and specificity (
Sp). The
Acc is defined as the proportion of samples that are correctly classified for each of the considered labels:
where
N denotes the number of test recordings,
denotes the annotated labels of recording
i, and
denotes the predicted labels of recording
i.
is the indicator function, which is one if the predicted labels for recording
i are same as the annotated labels, and zero otherwise. To calculate the
Se and
Sp, we first calculate the overall true positives (
TP), false positives (
FP), true negatives (
TN), and false negatives (
FN) by summing the corresponding category-wise statistics over all considered categories:
,
,
,
, where
m is the number of categories. The
Se and
Sp are then calculated as follows:
4. Discussion
This work proposes an approach to achieving cost-sensitive multi-label ECG classification using a thresholding method, namely CICST. It has been found that medical diagnosis is a cost-sensitive problem [
26]. However, this property has been widely ignored in previous studies on ECG classification methods. Most of the previous studies have focused on designing novel methods to improve the accuracy of the classifier. Some studies have tried to strike a balance between sensitivity and specificity, particularly in cases of category imbalance [
15,
21]. As we cannot achieve a perfect algorithm that makes correct predictions in every instance, the domain-related classification costs help us to find a reasonable balance when optimizing the algorithm. If the cost-sensitive property is not considered, the optimization goal of the algorithm would be mismatched with the actual demand.
The experimental results demonstrate the effectiveness of CICST in addressing the problem of multi-label ECG classification. Although all of the tested thresholding methods share the sample classification model, different choices of thresholds have substantial impacts on the model performance. In particular, the fixed threshold of 0.5 is used as the default threshold for a wide spectrum of classifiers. However, due to the category imbalance, this default thresholding strategy suffers a severe performance slump. By contrast, CICST is effective in finding proper thresholds to address the challenge of extreme category imbalance. Moreover, the performance of fixed thresholding with the threshold of 0.2 is close to that of CICST. However, a proper fixed threshold value should be tuned on the validation set, while CICST computes the threshold directly from the cost definition and the imbalance ratios.
As CICST is a post-processing method, it can be applied to a series of existing classification algorithms without the need to modify the original algorithms. Furthermore, as demonstrated in the experiments, CICST is flexible to adapt to changes in the definition of classification costs. This ability has important practical implications. It makes it easy to customize a classifier with a particular purpose. For example, by changing the definition of the cost or benefit matrix and then applying the CICST method, we can increase the sensitivity of the classifier to some categories, while increasing the specificity to other categories without retraining the model.
This work also has some limitations. First, the cost information in the cost matrix is converted to the costs for binary classification, which may lead to a certain loss of cost information. Second, the category relationships are explored implicitly in a multi-task learning framework. However, this cannot avoid the presence of unreasonable predictions, e.g., normal sinus rhythm and some kinds of arrhythmias may be predicted to coexist in a recording. Third, the possible differences in annotation rules among different datasets are not addressed in this study. Furthermore, the lack of interpretability of deep learning models may be a hindrance to clinical application. How to improve the model’s interpretability is an open question with significant implications. Therefore, more sophisticated methods for utilizing the cost information should be explored in further research, and new mechanisms should also be studied to explicitly utilize the label relationships, handle the diversity of the annotation rules, and improve the interpretability of the predictions.