Design and Experiment of a Clamping-Drive Alternating Operation Piezoelectric Actuator
Abstract
:1. Introduction
2. Structure and Principle
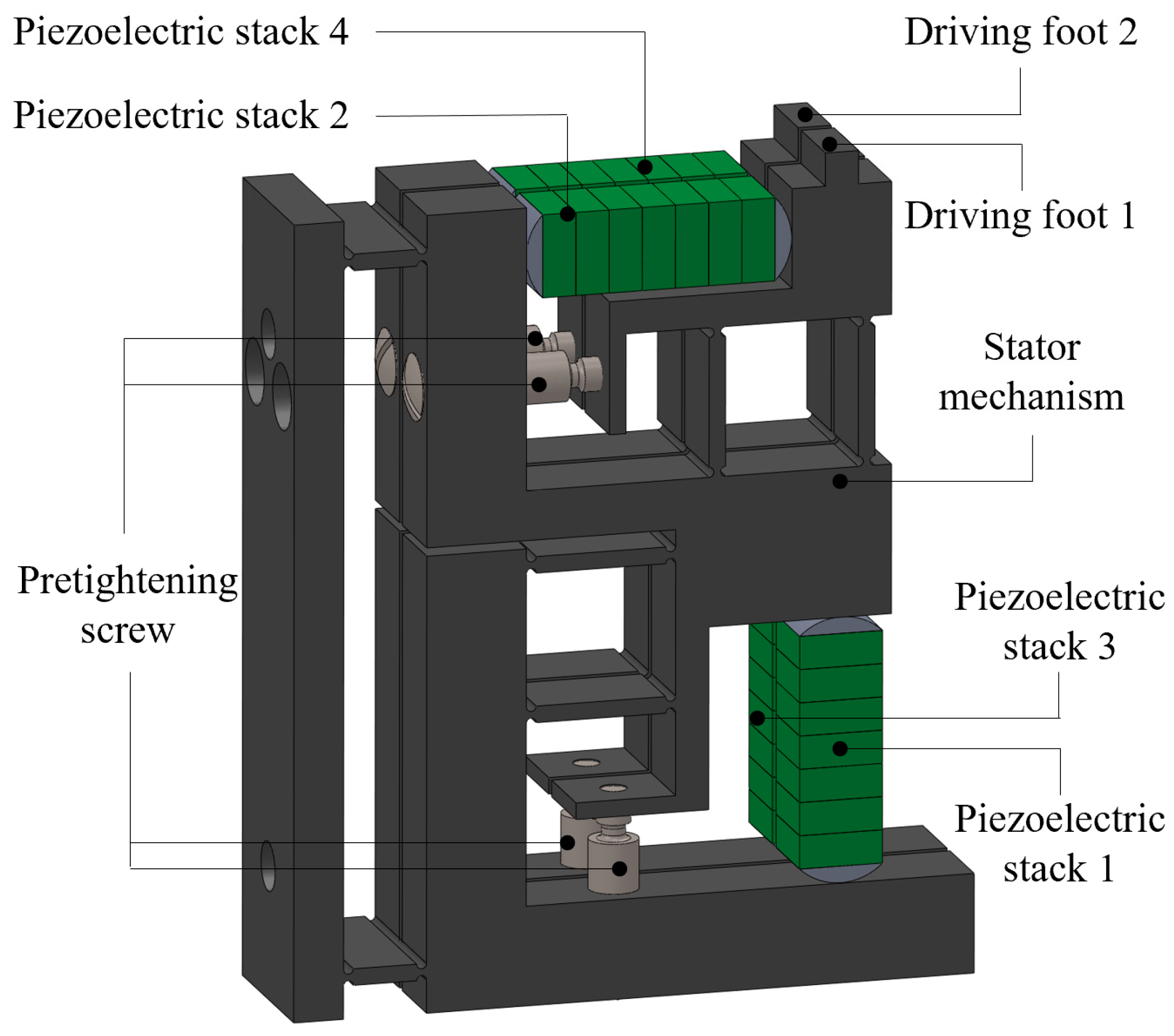
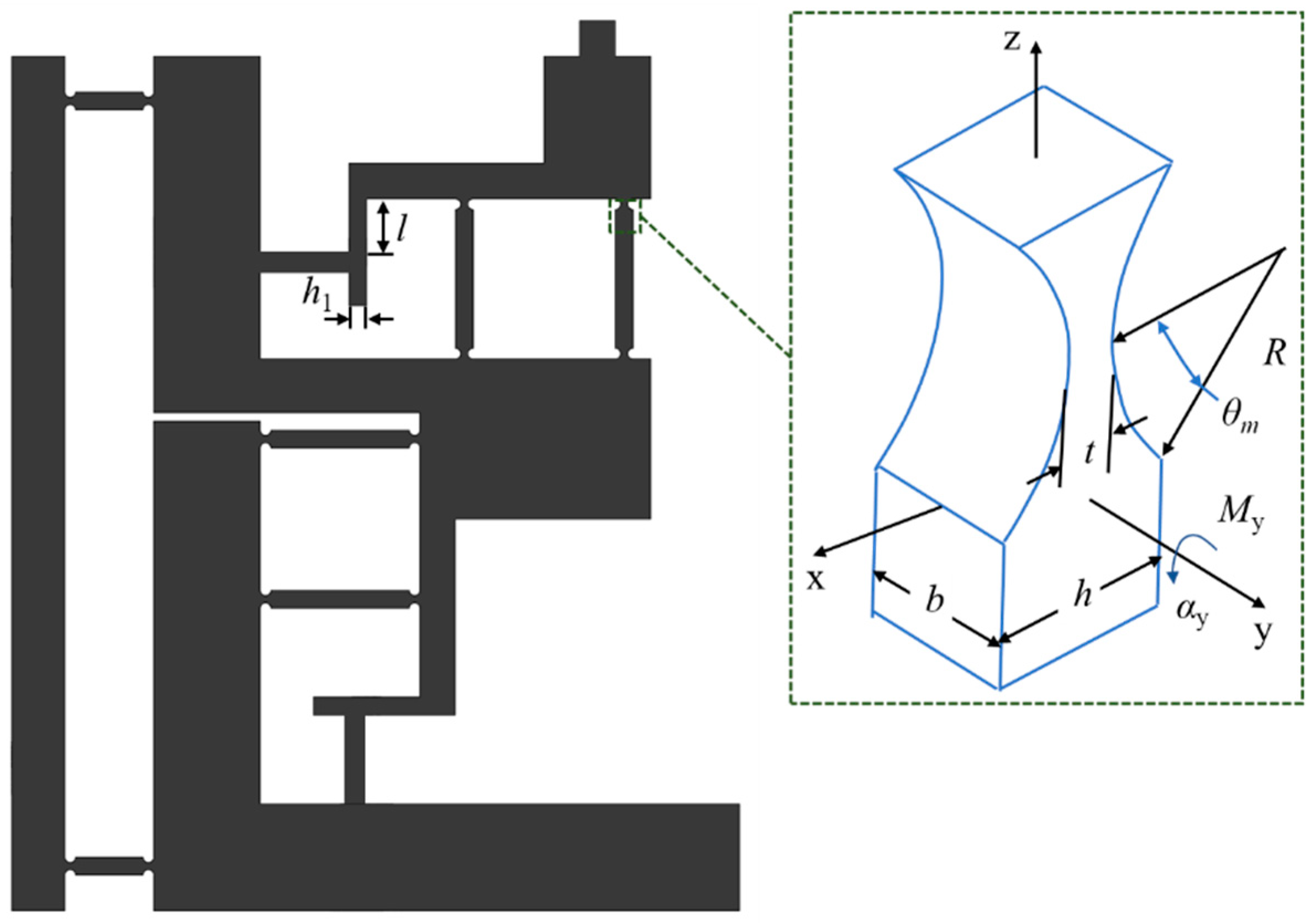
2.1. Integral Actuator and Stator Structure
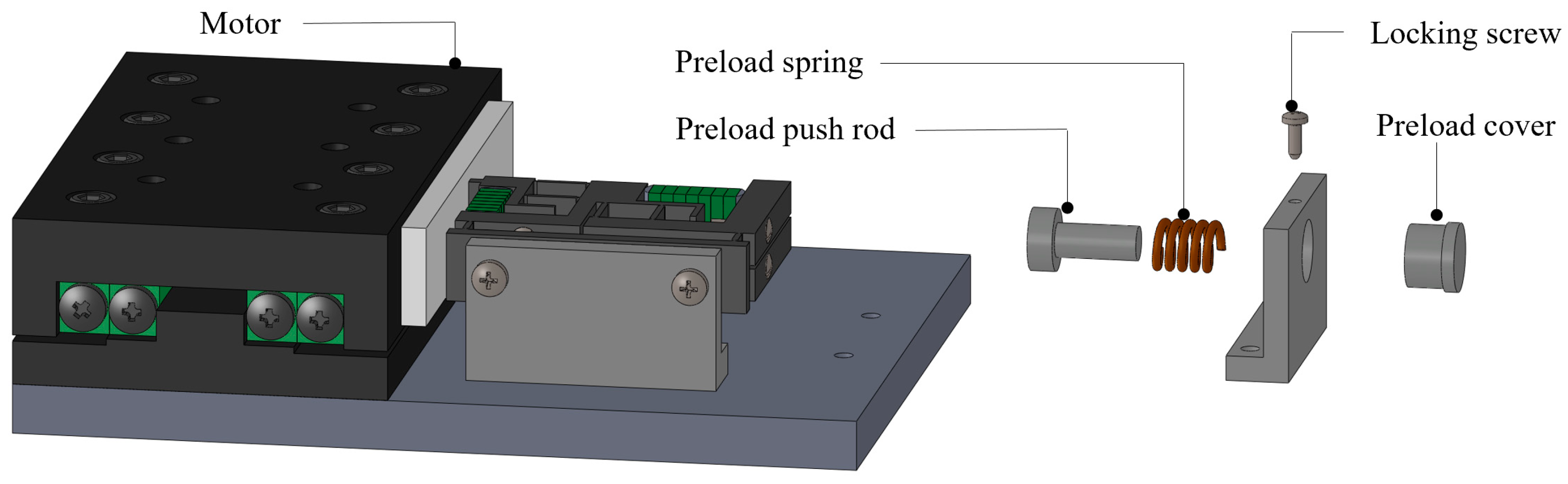
2.2. Preload Mechanism
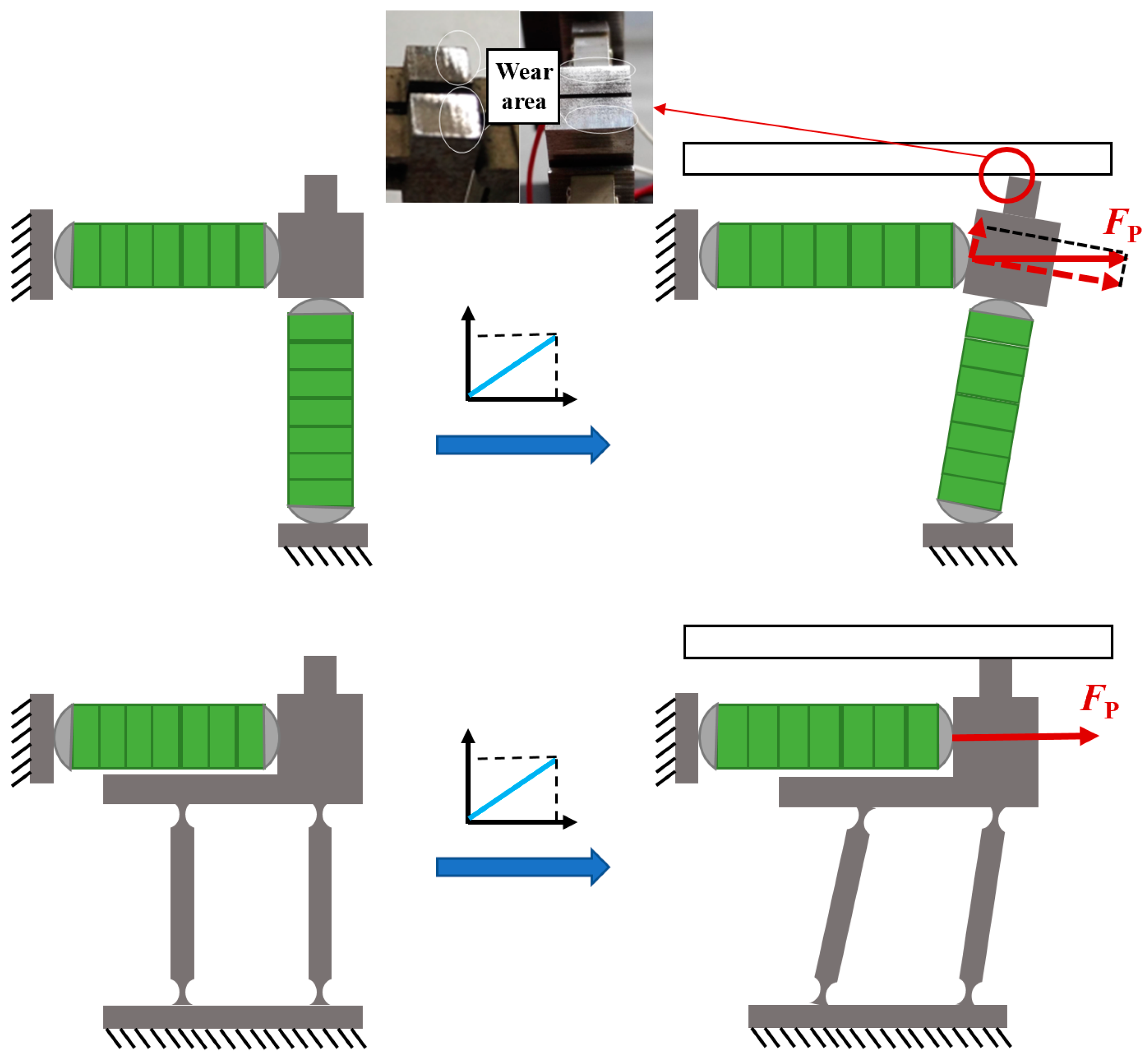
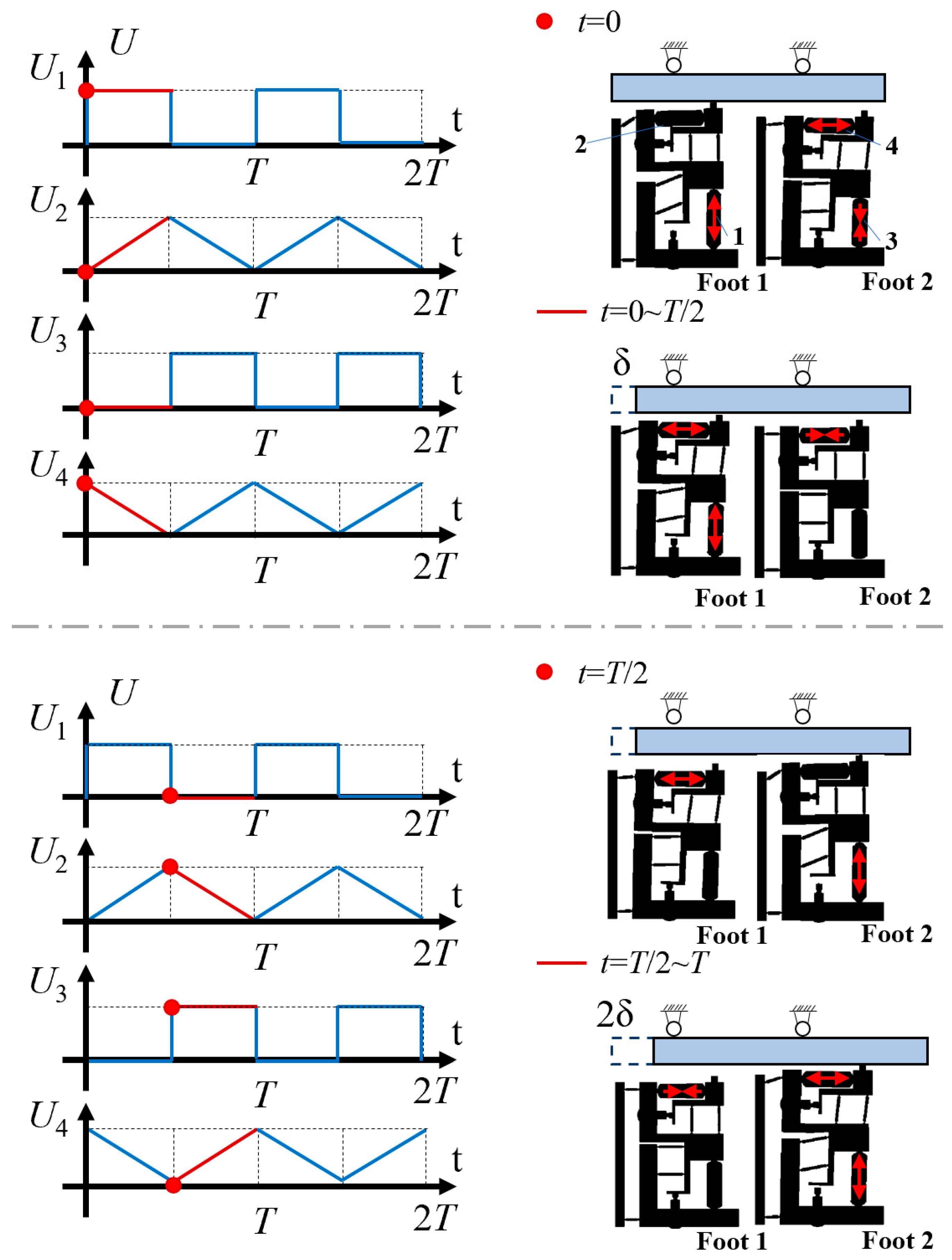
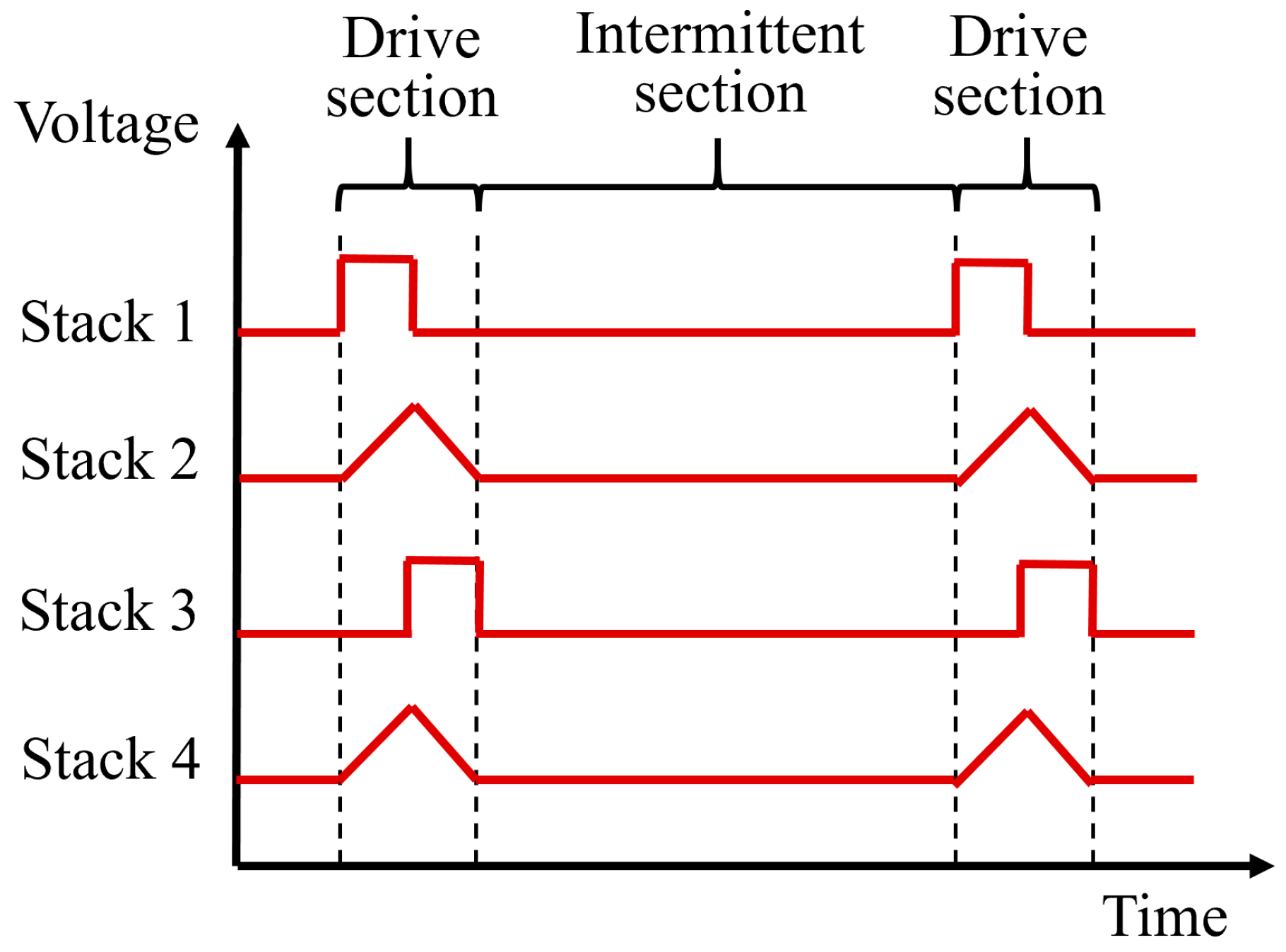
2.3. Principle of Actuator
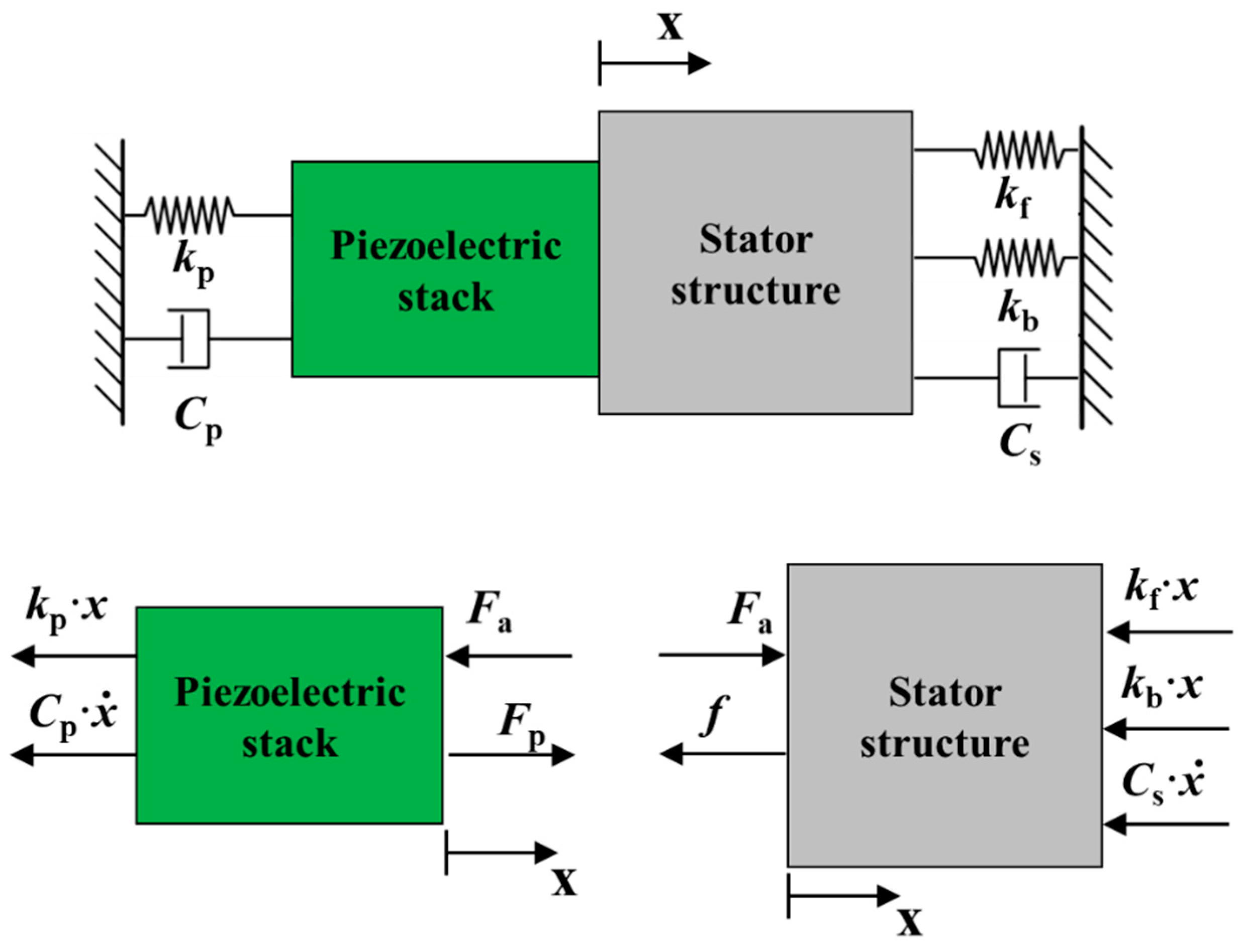
3. Theoretical Analysis
4. Experimental Research
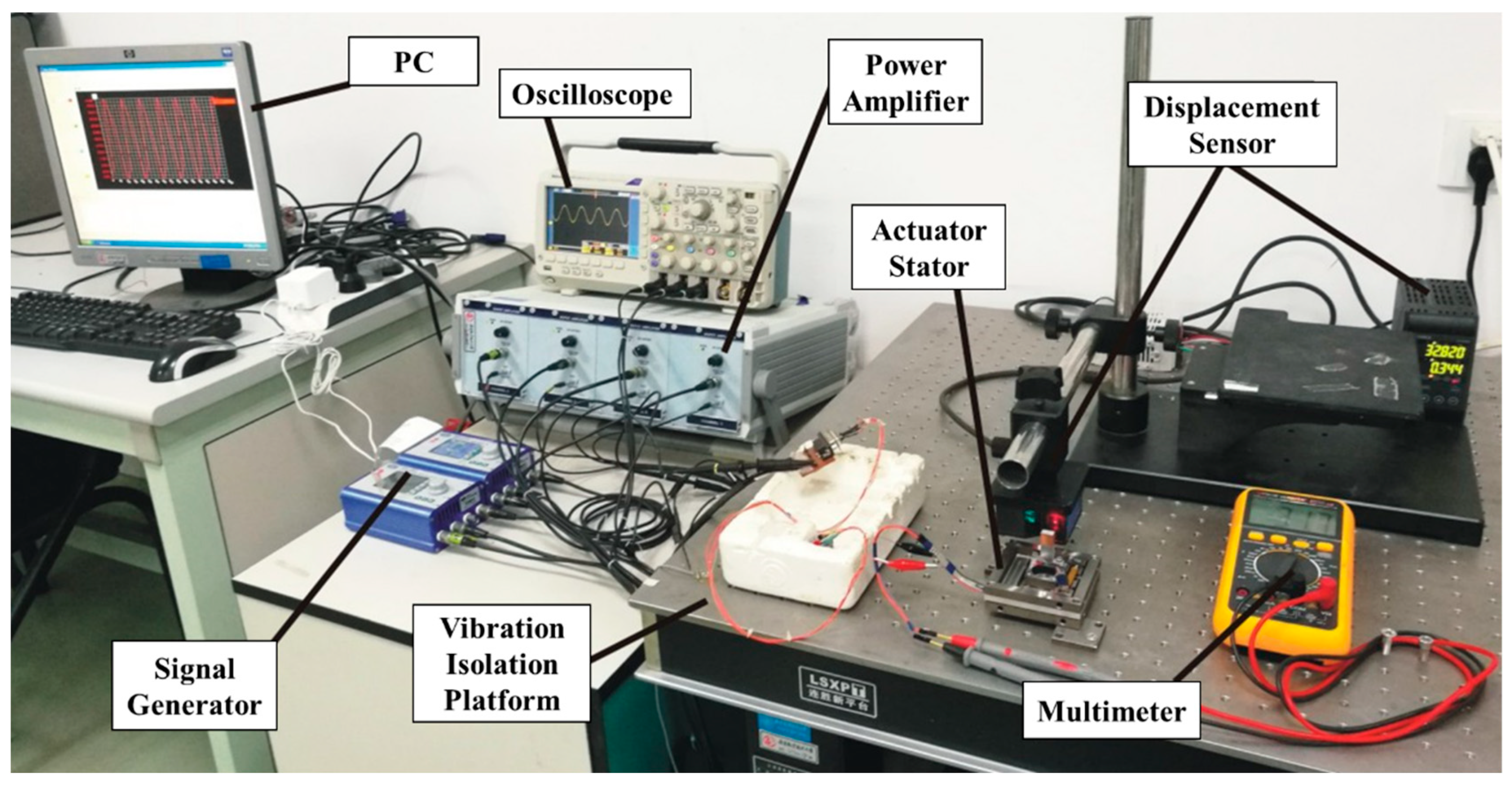
4.1. Prototype and Experimental Environment
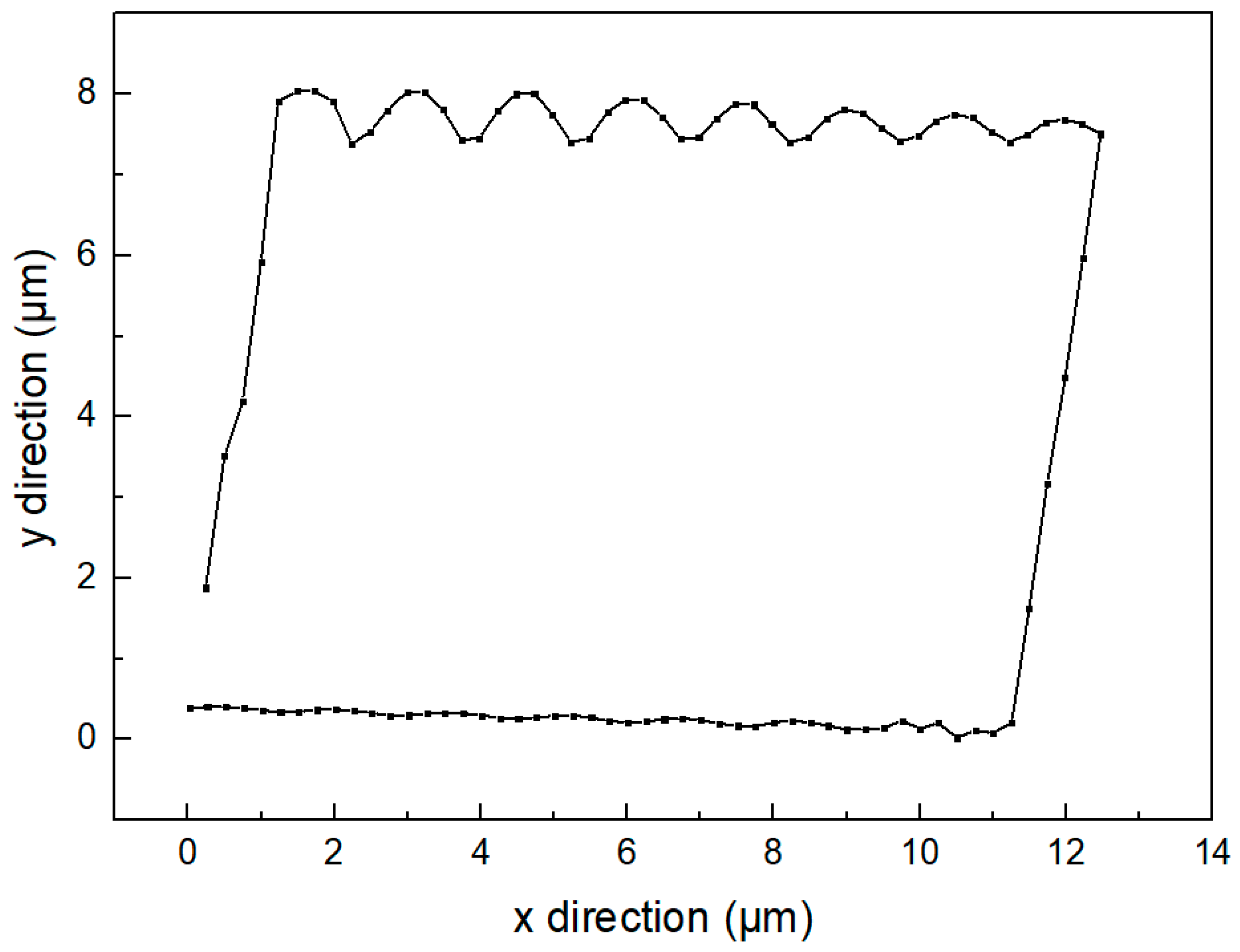
4.2. Amplitude Test
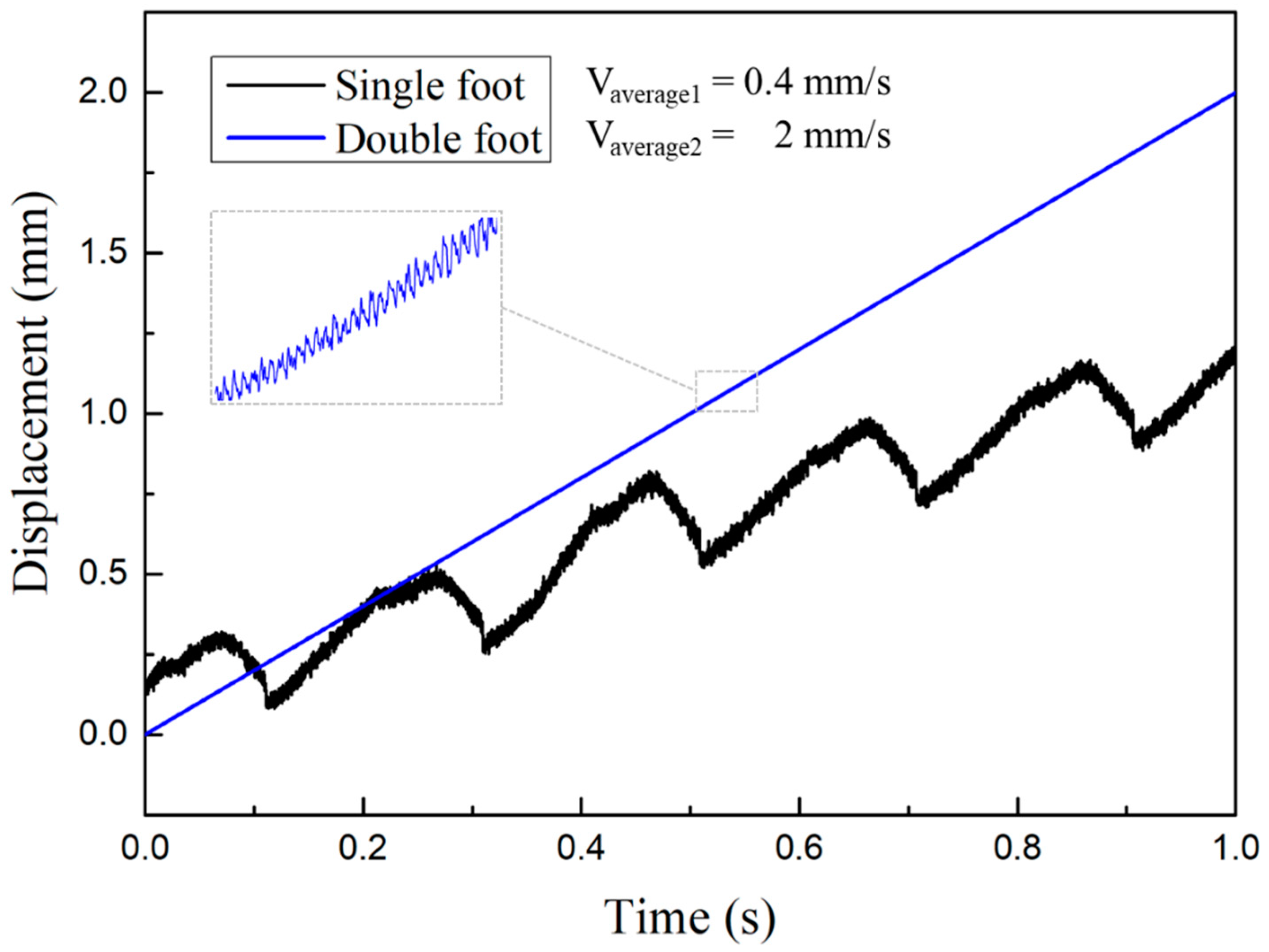
4.3. Double-Foot Alternating Motion Mode
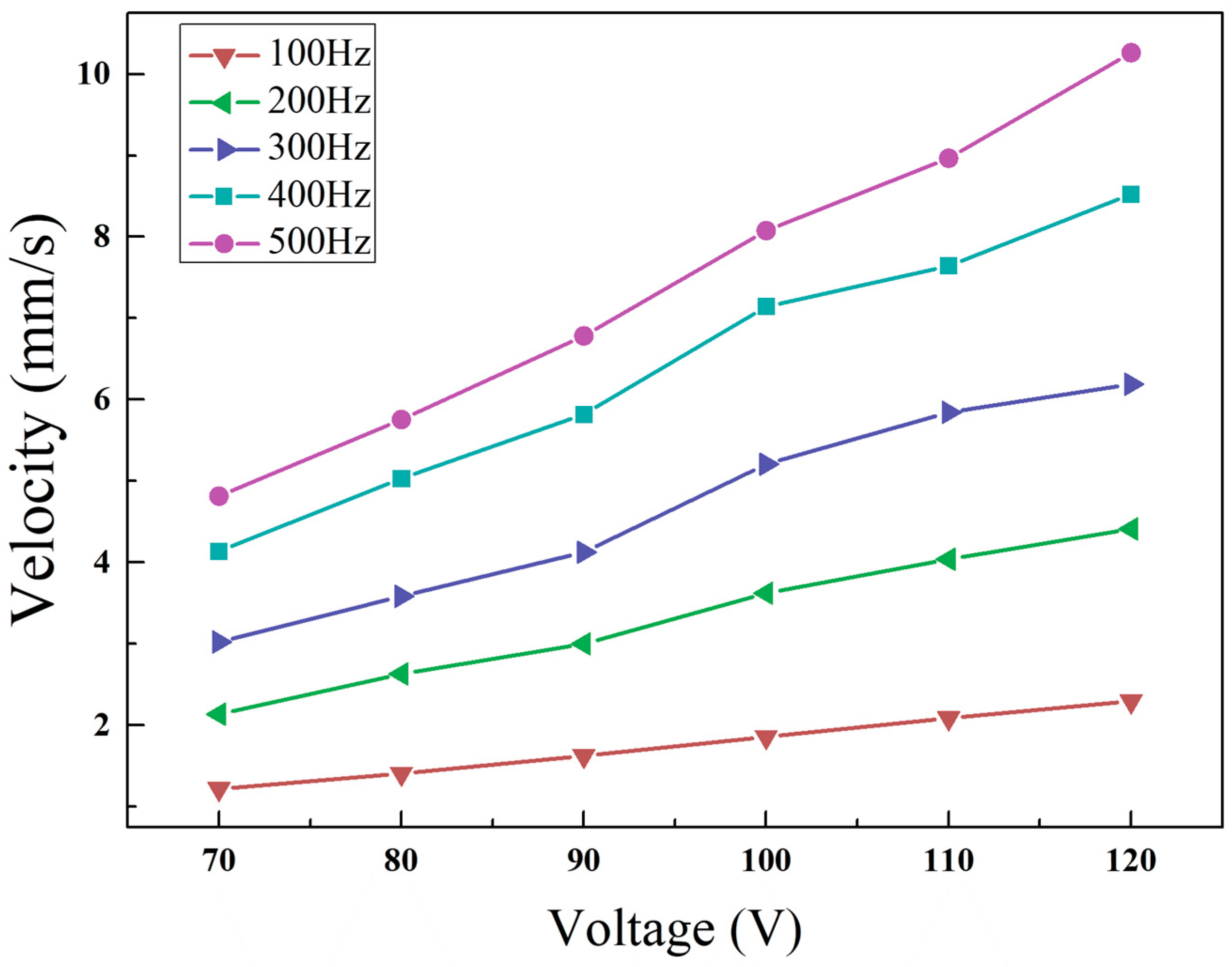
4.4. Single Step Actuation Mode
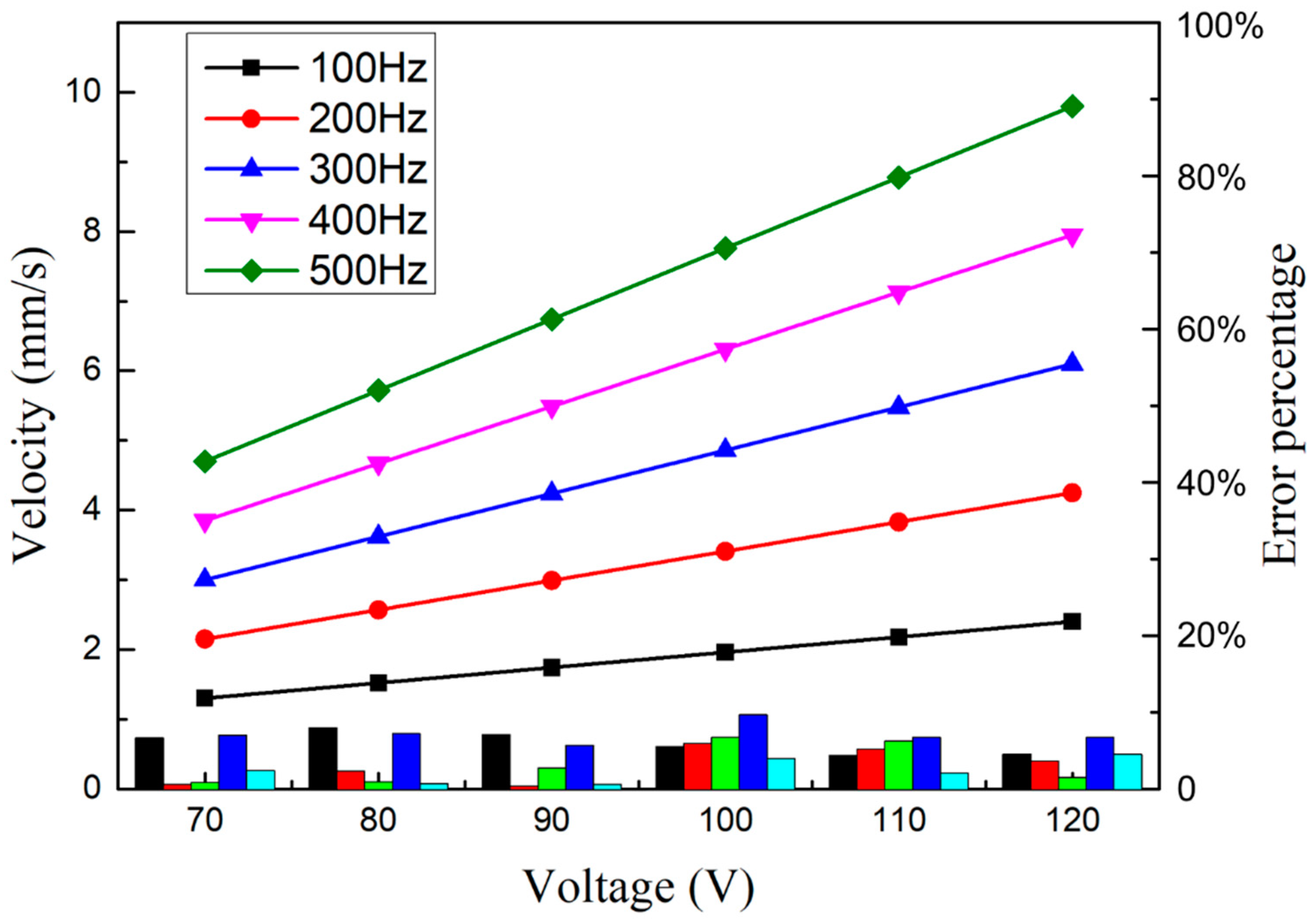
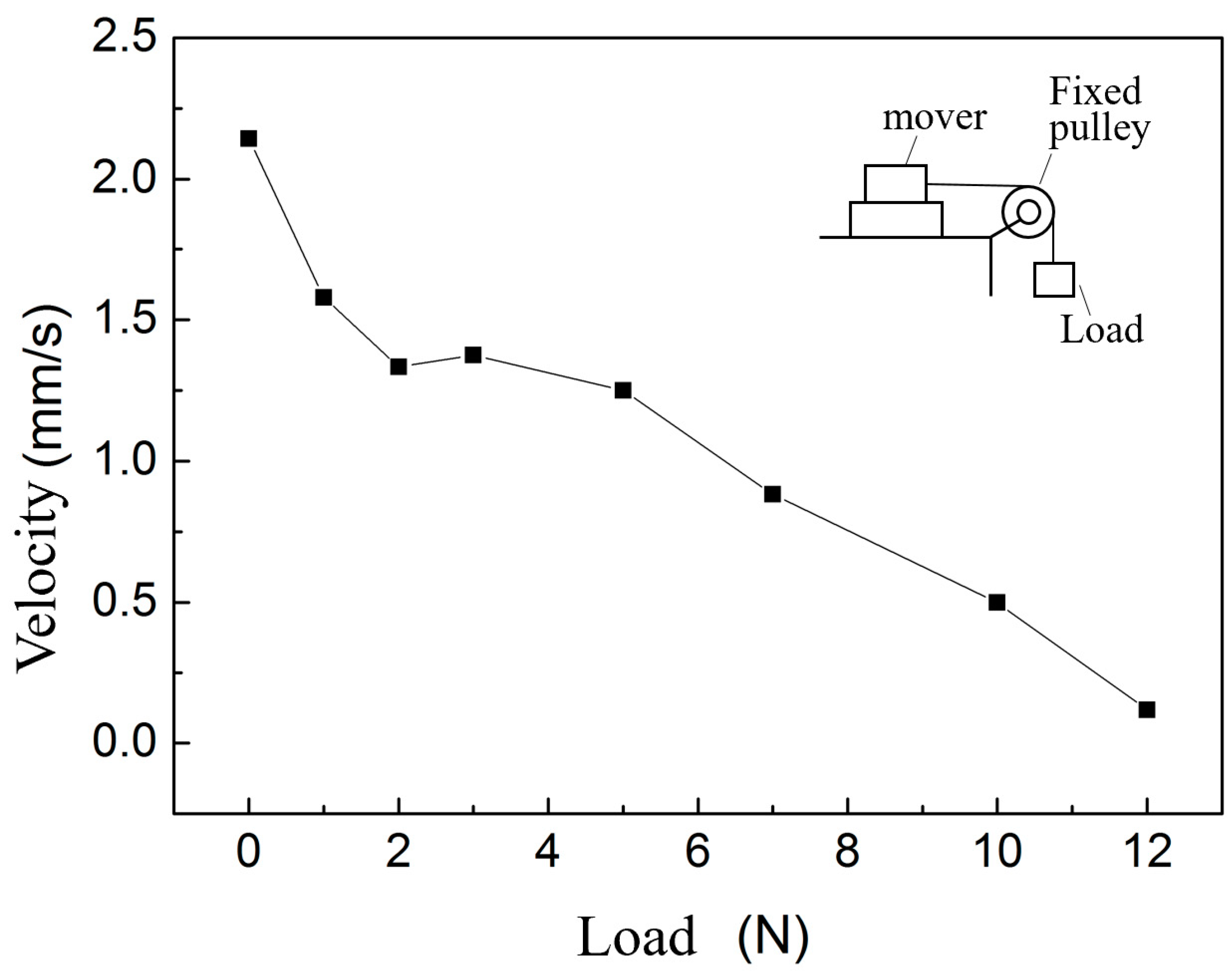
4.5. Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Thickness of the flexure hinge |
| t | Width of the beam connecting flexure hinge |
| R | Diameter of the semi-circle flexure hinge |
| h | Width of the flexure hinge |
| h1 | Width of the beam |
| E | Elastic modulus |
| Kp | Stiffness of the piezoelectric stack |
| Cp | Damping coefficients of the piezoelectric stack |
| Cs | Damping coefficients of the piezoelectric stack |
| Fa | Internal force of piezoelectric stack and stator structure |
| Fp | Output force of the piezoelectric stack |
| f | Friction force |
| mp | Mass of the piezoelectric stack |
| ms | Mass of the stator structure |
| U0(s) | Initial voltage |
| ka | Amplification ratio of input voltage for the piezoelectric stack |
| Rc | Resistance of the driving circuit |
| C | Capacitance of the piezoelectric stack |
| X(s) | Lateral output displacement |
| n | Number of layers of piezoelectric stack |
| d33 | Piezoelectric coefficient of the piezoelectric stack |
| β | Structural stiffness coefficient |
| Uc | Maximum voltage on transverse piezoelectric stack |
| da | Step distance |
| UD | Maximum voltage on longitudinal piezoelectric stack |
| P | Preload force |
| M | Mass of the mover |
References
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Ba Hashwan, S.S.; Junaid, M.M. A Review of Actuation and Sensing Mechanisms in MEMS-Based Sensor Devices. Nanoscale Res. Lett. 2021, 16, 16. [Google Scholar] [CrossRef]
- Srinivasa Rao, K.; Hamza, M.; Ashok Kumar, P.; Girija Sravani, K. Design and optimization of MEMS based piezoelectric actuator for drug delivery systems. Microsyst. Technol. Sens. Actuators Syst. Integr. 2020, 26, 1671–1679. [Google Scholar] [CrossRef]
- Toledo, J.; Ruiz-Díez, V.; Hernando-García, J.; Sánchez-Rojas, J.L. Piezoelectric Actuators for Tactile and Elasticity Sensing. Actuators 2020, 9, 21. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Deng, J.; Liu, Y.; Wang, Y. Piezoelectric hybrid actuation mode to improve speeds in cross-scale micromanipulations. Int. J. Mech. Sci. 2023, 240, 107943. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. Smart Mater. Struct. 2020, 29, 53001. [Google Scholar] [CrossRef]
- Chen, J.; Lu, M.; Lin, J.; Zhou, J.; Fu, X.; Zhou, X. Non-resonant 3D Elliptical Vibration Cutting Induced Submicron Grating Coloring. Int. J. Precis. Eng. Man. 2021, 22, 659–669. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 13002. [Google Scholar] [CrossRef]
- Hou, Y.; He, L.; Hu, D.; Zhang, L.; Yu, B.; Cheng, G. Recent trends in structures and applications of valveless piezoelectric pump—A review. J. Micromech. Microeng. 2022, 32, 53002. [Google Scholar] [CrossRef]
- Jin, H.; Gao, X.; Ren, K.; Liu, J.; Qiao, L.; Liu, M.; Chen, W.; He, Y.; Dong, S.; Xu, Z.; et al. Review on piezoelectric actuators based on high performance piezoelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A. Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Liu, R.; Zhao, H.; Wang, L.; Jin, J.; Lai, D.; Chen, Y. A novel structural–functional integration piezoelectric thruster for miniature unmanned underwater vehicles. Smart Mater. Struct. 2022, 32, 015016. [Google Scholar] [CrossRef]
- Ryndzionek, R.; Sienkiewicz, L. A review of recent advances in the single- and multi-degree-of-freedom ultrasonic piezoelectric motors. Ultrasonics 2021, 116, 106471. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Piao, S.; Chen, H.; Wu, J.; Nakamura, K. A Linear Piezoelectric Actuator Using “A-Shaped” Structure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1382–1391. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, J.; Xu, Z.; Qin, F.; Wang, Z.; Zhu, H.; Zhao, H. Analysis and comparison of the effect of different drive feet on the output performance of stick-slip piezoelectric actuators. Mech. Syst. Signal Process. 2023, 186, 109752. [Google Scholar] [CrossRef]
- Lu, X.; Gao, Q.; Li, Y.; Yu, Y.; Zhang, X.; Qiao, G.; Cheng, T. A Linear Piezoelectric Stick-Slip Actuator via Triangular Displacement Amplification Mechanism. IEEE Access 2020, 8, 6515–6522. [Google Scholar] [CrossRef]
- Shi, Y.; Lou, C.; Zhang, J. Investigation on a Linear Piezoelectric Actuator Based on Stick-Slip/Scan Excitation. Actuators 2021, 10, 39. [Google Scholar] [CrossRef]
- Zhao, B.; Fang, R.; Shi, W. Modeling of Motion Characteristics and Performance Analysis of an Ultra-Precision Piezoelectric Inchworm Motor. Materials 2020, 13, 3976. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Wang, Y.; Fan, W. Long Stroke Design of Piezoelectric Walking Actuator for Wafer Probe Station. Micromachines 2022, 13, 412. [Google Scholar] [CrossRef] [PubMed]
- Tahmasebipour, M.; Sangchap, M. A novel high performance integrated two-axis inchworm piezoelectric motor. Smart Mater. Struct. 2019, 29, 15034. [Google Scholar] [CrossRef]
- Kiong Tan, K.; Liang, W.; Huang, S.; Pham, L.P.; Chen, S.; Wee Gan, C.; Yee Lim, H. Precision control of piezoelectric ultrasonic motor for myringotomy with tube insertion. J. Dyn. Syst. Meas. Control 2015, 137, 064504. [Google Scholar] [CrossRef]
- Makarem, S.; Delibas, B.; Koc, B. Data-Driven Tuning of PID Controlled Piezoelectric Ultrasonic Motor. Actuators 2021, 10, 148. [Google Scholar] [CrossRef]
- Wan, H.; Peng, H.; Tang, X.; Chen, W. A small piezoelectric stack motor designed for vacuum and micro-dust environment. Smart Mater. Struct. 2022, 32, 015009. [Google Scholar] [CrossRef]
- Ozaki, T.; Ohta, N.; Fujiyoshi, M. Highly Linear and Wide Non-Resonant Two-Degree-of-Freedom Piezoelectric Laser Scanner. Sensors 2022, 22, 4215. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Xu, Z.; Wang, K.; Li, X.; Tang, J.; Yang, Z.; Huang, H. An Impact Inertial Piezoelectric Actuator Designed by Means of the Asymmetric Friction. IEEE Trans. Ind. Electron. 2023, 70, 699–708. [Google Scholar] [CrossRef]
- Pinskier, J.; Shirinzadeh, B.; Al-Jodah, A. Design and evaluation of a dual-stage, compensated stick-slip actuator for long-range, precision compliant mechanisms. Sens. Actuators A Phys. 2021, 331, 113007. [Google Scholar] [CrossRef]
- Ling, J.; Chen, L.; Feng, Z.; Zhu, Y. Development and test of a high speed pusher-type inchworm piezoelectric actuator with asymmetric driving and clamping configuration. Mech. Mach. Theory 2022, 176, 104997. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Y.; Deng, J.; Gao, X.; Cheng, J. A compact inchworm piezoelectric actuator with high speed: Design, modeling, and experimental evaluation. Mech. Syst. Signal Process. 2023, 184, 109704. [Google Scholar] [CrossRef]
- Park, M.; Chong, H.; Lee, B.; Jeong, S.; Park, T. Study on the new type of piezoelectric actuator utilizing smooth impact drive mechanism. Ferroelectrics 2016, 500, 218–228. [Google Scholar] [CrossRef]
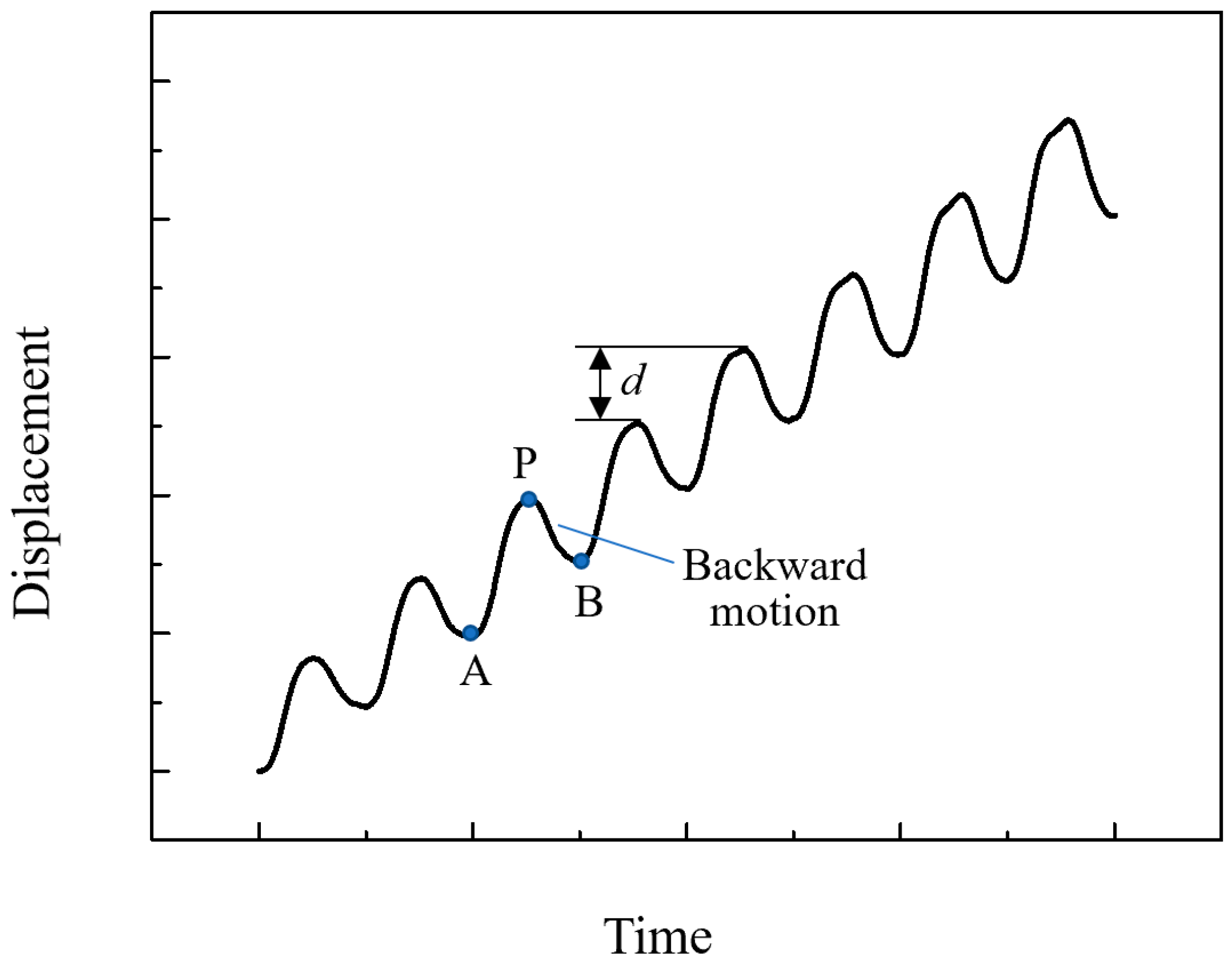
- Hu, Y.; Lin, S.; Ma, J.; Zhang, Y.; Li, J.; Wen, J. Piezoelectric inertial rotary actuator operating in two-step motion mode for eliminating backward motion. Appl. Phys. Lett. 2020, 117, 31902. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, X.; Huang, H.; Dong, J.; Fan, Z.; Zhao, H. On the Suppression of the Backward Motion of a Piezo-Driven Precision Positioning Platform Designed by the Parasitic Motion Principle. IEEE Trans. Ind. Electron. 2020, 67, 3870–3878. [Google Scholar] [CrossRef]
- Fan, H.; Tang, J.; Li, T.; Yang, X.; Liu, J.; Guo, W.; Huang, H. Active suppression of the backward motion in a parasitic motion principle (PMP) piezoelectric actuator. Smart Mater. Struct. 2019, 28, 125006. [Google Scholar] [CrossRef]
- Qin, F.; Tian, L.; Huang, H.; Wang, J.; Liang, T.; Zu, X.; Zhao, H. Actively controlling the contact force of a stick-slip piezoelectric linear actuator by a composite flexible hinge. Sens. Actuators A Phys. 2019, 299, 111606. [Google Scholar] [CrossRef]
- Ding, M.; Ma, J.; Hu, Y.; Li, J.; Wen, J. An inertial piezoelectric rotary actuator characterized by the motion without rollback. Smart Mater. Struct. 2020, 29, 95015. [Google Scholar] [CrossRef]
- Jia, B.; Wang, L.; Wang, R.; Jin, J.; Wu, D. Theoretical modeling and experimental investigation on a novel screwed-type piezoelectric focusing mechanism for space cameras. Mech. Syst. Signal Process. 2022, 171, 108844. [Google Scholar] [CrossRef]
- Koc, B.; Delibas, B. Impact Force Analysis in Inertia-Type Piezoelectric Motors. Actuators 2023, 12, 52. [Google Scholar] [CrossRef]







| Parameter | Size (mm × mm × mm) | Free Stroke, Max (μm) | Piezoelectric Constant, d33 (10−12 C/N) | Capacitance (nF) | Stiffness (N/μm) |
|---|---|---|---|---|---|
| Value | 5 × 5 × 14 | 19.8 | 443 | 1080 | 118 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Cao, Z.; Zheng, L. Design and Experiment of a Clamping-Drive Alternating Operation Piezoelectric Actuator. Micromachines 2023, 14, 525. https://doi.org/10.3390/mi14030525
Sun M, Cao Z, Zheng L. Design and Experiment of a Clamping-Drive Alternating Operation Piezoelectric Actuator. Micromachines. 2023; 14(3):525. https://doi.org/10.3390/mi14030525
Chicago/Turabian StyleSun, Mengxin, Zhenwei Cao, and Lukai Zheng. 2023. "Design and Experiment of a Clamping-Drive Alternating Operation Piezoelectric Actuator" Micromachines 14, no. 3: 525. https://doi.org/10.3390/mi14030525
APA StyleSun, M., Cao, Z., & Zheng, L. (2023). Design and Experiment of a Clamping-Drive Alternating Operation Piezoelectric Actuator. Micromachines, 14(3), 525. https://doi.org/10.3390/mi14030525






