Review of Fundamental Active Current Extraction Techniques for SAPF
Abstract
:1. Introduction
2. Harmonic Extraction Algorithms
2.1. Instantaneous Reactive Power Theory
2.2. Cross-Vector Theory
2.3. Rotating PQR Theory
2.4. Unity Power Vector
2.5. Perfect Harmonic Cancellation
2.6. Synchronous Reference Frame
2.7. Synchronous Detection Method
2.8. Cross-Correlation Technique
2.9. Sine-Multiplication Theorem
2.10. Vectorial Formulation
2.11. Conservative Power Theory
2.12. Fourier Transform
2.13. Recursive DFT
2.14. Wavelet Transform
2.15. Hilbert Transform
2.16. Kalman Filter
2.17. Extended Kalman Filter
2.18. Unscented Kalman Filte
2.19. Adaptive Linear Neuron
2.20. Adaptive Neuro-Fuzzy Inference System
2.21. Least Mean Squares Algorithm
2.22. Recursive Least Squares
2.23. Notch LMS Algorithm
2.24. Notch RLS Algorithm
2.25. Conclusions of Harmonic Extraction Algorithms
3. Synchronisation Techniques
3.1. Zero-Cross Detection
3.2. Space Vector
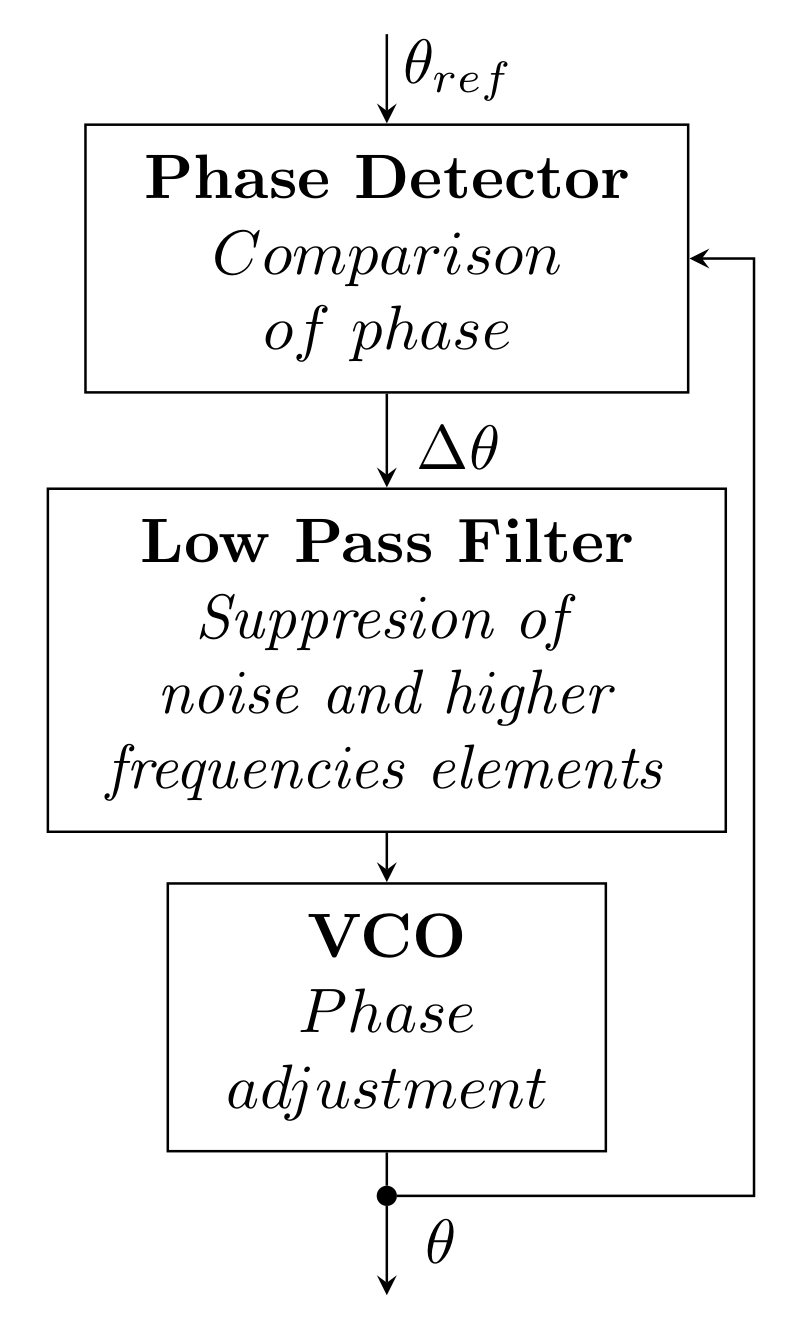
3.3. Phase-Locked Loop
3.3.1. Synchronous Reference Frame PLL
3.3.2. Self-Tuning Filter PLL
3.3.3. Enhanced PLL
3.3.4. Sinusoidal Signal Integrator PLL
3.3.5. Decoupled Double SRF PLL
3.4. Conclusions of Synchronisation Techniques
4. Further Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| DCC | Direct Current Control |
| DFT | Discrete Fourier Transform |
| DSP | Digital Signal Processor |
| FCE | Fundamental Component Extraction |
| FFT | Fast Fourier Transformation |
| FIR | Finite Impulse Response |
| FIS | Fuzzy Inference System |
| FPGA | Field Programmable Gate Array |
| GD | Gradient Descent |
| GTO | Gate turn-off |
| HPF | High-Pass Filter |
| ICC | Indirect Current Control |
| IGBT | Insulated Gate Bipolar transistors |
| IGCT | Integrated gate commutated |
| IIR | Infinite Impulse Response |
| LF | Loop Filter |
| LMS | Least Mean Squares |
| LPF | Low-Pass Filter |
| MMSE | Minimum Mean Square Error |
| MNN | Multilayer Neural Network |
| PCC | Point of Common Coupling |
| PD | Phase Detector |
| PLL | Phase-Locked Loop |
| PWM | Pulse-Width Modulation |
| RDFT | Recursive Discrete Fourier Transform |
| RLS | Recursive Least Squares |
| SAPF | Shunt-Active Power Filter |
| SCG | Scale Conjugate Gradient |
| SNR | Signal to Noise Ratio |
| SVPWM | Space Vector PWM |
| THD | Total Harmonic Distortion |
| VCO | Voltage-Controlled Oscillator |
| ZCD | Zero-Cross Detection |
References
- Thakur, P. Load Distribution and VFD Topology Selection for Harmonic Mitigation in an Optimal Way. IEEE Trans. Ind. Appl. 2020, 56, 48–56. [Google Scholar] [CrossRef]
- Xu, Y.; Xiao, X.; Liu, H.; Wang, H. Parallel Operation of Hybrid Active Power Filter with Passive Power Filter or Capacitors. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 18 August 2005; pp. 1–6. [Google Scholar] [CrossRef]
- Arritt, R.F.; Dugan, R.C. Distributed Generation Interconnection Transformer and Grounding Selection. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Baghzouz, Y.; Gong, X. Analysis of Three-Phase Transformer No-Load Characteristics. IEEE Trans. Power Syst. 1995, 10, 18–26. [Google Scholar] [CrossRef]
- Sanjay, J.S.; Misra, B. Power Quality Improvement for Non Linear Load Applications Using Passive Filters. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 10–11 October 2019; pp. 585–589. [Google Scholar] [CrossRef]
- Phannil, N.; Jettanasen, C.; Ngaopitakkul, A. Harmonics and Reduction of Energy Consumption in Lighting Systems by Using LED Lamps. Energies 2018, 11, 3169. [Google Scholar] [CrossRef] [Green Version]
- Goschler, C. (Ed.) Compensation in Practice: The Foundation ‘Remembrance, Responsibility and Future’ and the Legacy of Forced Labour during the Third Reich, 1st ed.; Berghahn Books: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Hansen, S.; Nielsen, P.; Blaabjerg, F. Harmonic Cancellation by Mixing Nonlinear Single-Phase and Three-Phase Loads. IEEE Trans. Ind. Appl. 2000, 36, 152–159. [Google Scholar] [CrossRef]
- Rastogi, M.; Mohan, N.; Edris, A.A. Hybrid-Active Filtering of Harmonic Currents in Power Systems. IEEE Trans. Power Deliv. 1995, 10, 1994–2000. [Google Scholar] [CrossRef]
- Akagi, H. Active Harmonic Filters. Proc. IEEE 2005, 93, 2128–2141. [Google Scholar] [CrossRef]
- Duda, T. Robust Algorithms for Control of Dynamic Systems. Ph.D. Thesis, Vysoká Škola Báňská-Technická Univerzita Ostrava, Ostrava, Czech Republic, 2015. [Google Scholar]
- Chamrád, P. Optimalization of Parameters of MRAS Observer for Sensorless Control of Asynchronal Motor. Ph.D. Thesis, Vysoká Škola Báňská-Technická Univerzita Ostrava, Ostrava, Czech Republic, 2019. [Google Scholar]
- Massoud, A.; Finney, S.; Williams, B. Review of Harmonic Current Extraction Techniques for an Active Power Filter. In Proceedings of the 2004 11th International Conference on Harmonics and Quality of Power (IEEE Cat. No.04EX951), Lake Placid, NY, USA, 12–15 September 2004; pp. 154–159. [Google Scholar] [CrossRef]
- Abu Hasim, A.S.; Talib, M.H.N.; Ibrahim, Z. Comparative Study of Different PWM Control Scheme for Three-Phase Three-Wire Shunt Active Power Filter. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June 2012; pp. 119–123. [Google Scholar] [CrossRef]
- Kim, H.; Blaabjerg, F.; Bak-Jensen, B.; Choi, J. Instantaneous Power Compensation in Three-Phase Systems by Using p-q-r Theory. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference (IEEE Cat. No. 01CH37230), Vancouver, BC, Canada, 17–21 June 2001; Volume 2, pp. 478–485. [Google Scholar] [CrossRef]
- Montero, M.I.M.; Cadaval, E.R.; Gonzalez, F.B. Comparison of Control Strategies for Shunt Active Power Filters in Three-Phase Four-Wire Systems. IEEE Trans. Power Electron. 2007, 22, 229–236. [Google Scholar] [CrossRef]
- Herrera, R.S.; Salmerón, P.; Kim, H. Instantaneous Reactive Power Theory Applied to Active Power Filter Compensation: Different Approaches, Assessment, and Experimental Results. IEEE Trans. Ind. Electron. 2008, 55, 184–196. [Google Scholar] [CrossRef]
- Benhabib, M.; Saadate, S. New Control Approach for Four-Wire Active Power Filter Based on the Use of Synchronous Reference Frame. Electr. Power Syst. Res. 2005, 73, 353–362. [Google Scholar] [CrossRef]
- Revuelta, P.S.; Herrera, R.S. Application of the Instantaneous Power Theories in Load Compensation with Active Power Filters. In Proceedings of the 10th European Conference on Power Electronics and Applications, Toulouse, France, 2–4 September 2003; pp. 2–4. [Google Scholar]
- Salam, Z.; Tan, P.C.; Jusoh, A. Harmonics Mitigation Using Active Power Filter: A Technological Review. Elektr. J. Electr. Eng. 2006, 8, 17–26. [Google Scholar]
- Dolen, M.; Lorenz, R. An Industrially Useful Means for Decomposition and Differentiation of Harmonic Components of Periodic Waveforms. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy (Cat. No.00CH37129), Rome, Italy, 8–12 October 2000; Volume 2, pp. 1016–1023. [Google Scholar] [CrossRef]
- Mortezaei, A.; Lute, C.; Simoes, M.G.; Marafao, F.P.; Boglia, A. PQ, DQ and CPT Control Methods for Shunt Active Compensators—A Comparative Study. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 2994–3001. [Google Scholar] [CrossRef]
- Qasim, M.; Khadkikar, V. Application of Artificial Neural Networks for Shunt Active Power Filter Control. IEEE Trans. Ind. Inform. 2014, 10, 1765–1774. [Google Scholar] [CrossRef]
- Routhu, B.; Arun, N. PI, FUZZY and ANFIS Control of 3-Phase Shunt Active Power Filter. Int. J. Eng. Technol. (IJET) 2013. [Google Scholar]
- Tamboli, D.A.; Chile, R.H. Reference Signal Generation for Shunt Active Power Filter Using Adaptive Filtering Approach. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 766–770. [Google Scholar] [CrossRef]
- Abdeslam, D.O.; Wira, P.; Merckle, J.; Flieller, D.; Chapuis, Y.A. A Unified Artificial Neural Network Architecture for Active Power Filters. IEEE Trans. Ind. Electron. 2007, 54, 61–76. [Google Scholar] [CrossRef]
- Abdusalam, M.; Poure, P.; Karimi, S.; Saadate, S. New Digital Reference Current Generation for Shunt Active Power Filter under Distorted Voltage Conditions. Electr. Power Syst. Res. 2009, 79, 759–765. [Google Scholar] [CrossRef]
- Bacon, V.D.; de Souza, V.; Padim, E.T.; da Silva, S.A.O. Influence of the PLL Phase-Angle Quality on the Static and Dynamic Performance of Grid-Connected Systems. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Bhattacharya, A.; Chakraborty, C. A Shunt Active Power Filter With Enhanced Performance Using ANN-Based Predictive and Adaptive Controllers. IEEE Trans. Ind. Electron. 2011, 58, 421–428. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, S.A.O.; Bacon, V.D.; Campanhol, L.B.G.; Angélico, B.A. An Adaptive Phase-Locked Loop Algorithm for Single-Phase Utility Connected System. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Djazia, K.; Krim, F.; Chaoui, A.; Sarra, M. Active Power Filtering Using the ZDPC Method under Unbalanced and Distorted Grid Voltage Conditions. Energies 2015, 8, 1584–1605. [Google Scholar] [CrossRef]
- Elangovan, S.; Thanushkodi, K.; Neelakantan, P.N. A Two Level Shunt Active Power Filter without Pll for Industrial Loads. Aust. J. Basic Appl. Sci 2014, 8, 71–77. [Google Scholar]
- Golestan, S.; Monfared, M.; Freijedo, F.D. Design-Oriented Study of Advanced Synchronous Reference Frame Phase-Locked Loops. IEEE Trans. Power Electron. 2013, 28, 765–778. [Google Scholar] [CrossRef]
- Han, Y.; Xu, L.; Khan, M.M.; Yao, G.; Zhou, L.D.; Chen, C. A Novel Synchronization Scheme for Grid-Connected Converters by Using Adaptive Linear Optimal Filter Based PLL (ALOF–PLL). Simul. Model. Pract. Theory 2009, 17, 1299–1345. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Operation of Three-Level Inverter-Based Shunt Active Power Filter Under Nonideal Grid Voltage Conditions With Dual Fundamental Component Extraction. IEEE Trans. Power Electron. 2018, 33, 7558–7570. [Google Scholar] [CrossRef]
- Jaalam, N.; Rahim, N.; Bakar, A.; Tan, C.; Haidar, A.M. A Comprehensive Review of Synchronization Methods for Grid-Connected Converters of Renewable Energy Source. Renew. Sustain. Energy Rev. 2016, 59, 1471–1481. [Google Scholar] [CrossRef] [Green Version]
- McGrath, B.; Holmes, D.; Galloway Galloway, J. Power Converter Line Synchronization Using a Discrete Fourier Transform (DFT) Based on a Variable Sample Rate. IEEE Trans. Power Electron. 2005, 20, 877–884. [Google Scholar] [CrossRef]
- Mohd Zainuri, M.; Mohd Radzi, M.; Che Soh, A.; Mariun, N.; Abd Rahim, N.; Hajighorbani, S. Fundamental Active Current Adaptive Linear Neural Networks for Photovoltaic Shunt Active Power Filters. Energies 2016, 9, 397. [Google Scholar] [CrossRef] [Green Version]
- Oliveira da Silva, S.A.; Garcia Campanhol, L.B.; Goedtel, A. Application of Shunt Active Power Filter for Harmonic Reduction and Reactive Power Compensation in Three-Phase Four-Wire Systems. IET Power Electron. 2014, 7, 2825–2836. [Google Scholar] [CrossRef]
- Özerdem, Ö.C.; Khadem, S.K.; Biricik, S.; Basu, M.; Redif, S. Real-Time Control of Shunt Active Power Filter under Distorted Grid Voltage and Unbalanced Load Condition Using Self-Tuning Filter. IET Power Electron. 2014, 7, 1895–1905. [Google Scholar] [CrossRef] [Green Version]
- Radzi, M.; Rahim, N. Neural Network and Bandless Hysteresis Approach to Control Switched Capacitor Active Power Filter for Reduction of Harmonics. IEEE Trans. Ind. Electron. 2009, 56, 1477–1484. [Google Scholar] [CrossRef]
- Rahman, N.F.A.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Dual Function of Unified Adaptive Linear Neurons Based Fundamental Component Extraction Algorithm for Shunt Active Power Filter Operation. Int. Rev. Electr. Eng. 2015, 10, 544–552. [Google Scholar]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled Double Synchronous Reference Frame PLL for Power Converters Control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Shah, M.C.; Chauhan, S.K.; Tekwani, P.N.; Tiwari, R.R. Analysis, Design and Digital Implementation of a Shunt Active Power Filter with Different Schemes of Reference Current Generation. IET Power Electron. 2014, 7, 627–639. [Google Scholar] [CrossRef]
- Shinnaka, S. A New Characteristics-Variable Two-Input/Output Filter in D-Module-Designs, Realizations, and Equivalence. IEEE Trans. Ind. Appl. 2002, 38, 1290–1296. [Google Scholar] [CrossRef]
- Timbus, A.; Liserre, M.; Teodorescu, R.; Blaabjerg, F. Synchronization Methods for Three Phase Distributed Power Generation Systems. An Overview and Evaluation. In Proceedings of the IEEE 36th Conference on Power Electronics Specialists, Aachen, Germany, 16 June 2005; pp. 2474–2481. [Google Scholar] [CrossRef]
- Vainio, O.; Ovaska, S.; Polla, M. Adaptive Filtering Using Multiplicative General Parameters for Zero-Crossing Detection. IEEE Trans. Ind. Electron. 2003, 50, 1340–1342. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd Radzi, M.A.; Hassan, M.K.; Mailah, N.F. A Self-Tuning Filter-Based Adaptive Linear Neuron Approach for Operation of Three-Level Inverter-Based Shunt Active Power Filters under Non-Ideal Source Voltage Conditions. Energies 2017, 10, 667. [Google Scholar] [CrossRef]
- Zainuri, M.; Radzi, M.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Simplified Adaptive Linear Neuron Harmonics Extraction Algorithm for Dynamic Performance of Shunt Active Power Filter. Int. Rev. Model. Simul. 2016, 9, 144–154. [Google Scholar]
- Girgis, A.; Chang, W.; Makram, E. A Digital Recursive Measurement Scheme for Online Tracking of Power System Harmonics. IEEE Trans. Power Deliv. 1991, 6, 1153–1160. [Google Scholar] [CrossRef]
- Ribeiro, R.L.A.; Rocha, T.O.A.; de Sousa, R.M.; dos Santos, E.C.; Lima, A.M.N. A Robust DC-Link Voltage Control Strategy to Enhance the Performance of Shunt Active Power Filters Without Harmonic Detection Schemes. IEEE Trans. Ind. Electron. 2015, 62, 803–813. [Google Scholar] [CrossRef]
- Kumar, S.J.; Sangeetha, P.; Charan, C.R. Shunt Active Power Filter Control by Instantaneous Reactive Power Compensation. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016; pp. 2012–2016. [Google Scholar] [CrossRef]
- Geetha, K.; Sangeetha, B. Performance Evaluation of Conventional and Intelligent Controller Based Shunt Active Filter. In Proceedings of the Third International Conference on Computational Intelligence and Information Technology (CIIT 2013), Mumbai, India, 18–19 October 2013; pp. 564–569. [Google Scholar] [CrossRef]
- Patjoshi, R.K.; Mahapatra, K.K. Performance Comparison of Direct and Indirect Current Control Techniques Applied to a Sliding Mode Based Shunt Active Power Filter. In Proceedings of the 2013 Annual IEEE India Conference (INDICON), Mumbai, India, 13–15 December 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Rahman, N.A.; Nasir, N.M.; Baharom, R. Comparative Study of Direct and Indirect Current Control Algorithms for Shunt Active Power Filter. In Proceedings of the 2019 International Conference on Electrical Engineering and Informatics (ICEEI), Bandung, Indonesia, 18 July 2019; pp. 324–329. [Google Scholar] [CrossRef]
- Imad, A.; Hani, S.E.; Mediouni, H.; Echchaachouai, A. Comparative Analysis on Current Control Methods of Shunt Active Power Filter for the Improvement of Grid Energy Quality. In Proceedings of the 2017 International Conference on Electrical and Information Technologies (ICEIT), Rabat, Morocco, 15–18 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.S. Generalized Instantaneous Reactive Power Theory for Three-Phase Power Systems. IEEE Trans. Instrum. Meas. 1996, 45, 293–297. [Google Scholar] [CrossRef] [Green Version]
- Nabae, A.; Tanaka, T. A New Definition of Instantaneous Active-Reactive Current and Power Based on Instantaneous Space Vectors on Polar Coordinates in Three-Phase Circuits. IEEE Trans. Power Deliv. 1996, 11, 1238–1243. [Google Scholar] [CrossRef]
- Fujita, H.; Akagi, H. The Unified Power Quality Conditioner: The Integration of Series-and Shunt-Active Filters. IEEE Trans. Power Electron. 1998, 13, 315–322. [Google Scholar] [CrossRef] [Green Version]
- Peng, F.Z.; Ott, G.W.; Adams, D.J. Harmonic and Reactive Power Compensation Based on the Generalized Instantaneous Reactive Power Theory for Three-Phase Four-Wire Systems. IEEE Trans. Power Electron. 1998, 13, 1174–1181. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, A. A New Approach to Load Balancing and Power Factor Correction in Power Distribution System. IEEE Trans. Power Deliv. 2000, 15, 417–422. [Google Scholar] [CrossRef]
- Boussaid, A.; Nemmour, A.L.; Louze, L.; Khezzar, A. A Novel Strategy for Shunt Active Filter Control. Electr. Power Syst. Res. 2015, 123, 154–163. [Google Scholar] [CrossRef]
- Büyük, M.; İnci, M.; Tan, A.; Tümay, M. Improved Instantaneous Power Theory Based Current Harmonic Extraction for Unbalanced Electrical Grid Conditions. Electr. Power Syst. Res. 2019, 177, 106014. [Google Scholar] [CrossRef]
- Kim, H.; Akagi, H. The Instantaneous Power Theory on the Rotating P-q-r Reference Frames. In Proceedings of the IEEE 1999 International Conference on Power Electronics and Drive Systems. PEDS’99 (Cat. No. 99TH8475), Hong Kong, China, 27–29 July 1999; Volume 1, pp. 422–427. [Google Scholar] [CrossRef]
- Chebabhi, A.; Fellah, M.K.; Benkhoris, M.F. Application of PQR Theory for Control of a 3-Phase 4-Wire 4-Legs Shunt Active Power Filter in the αβo-Axes Using 3d-SVM Technique. Leonardo J. Sci. 2015, 14, 17–28. [Google Scholar]
- Rafiei, S.R.; Toliyat, H.; Ghazi, R.; Gopalarathnam, T. An Optimal and Flexible Control Strategy for Active Filtering and Power Factor Correction under Non-Sinusoidal Line Voltages. IEEE Trans. Power Deliv. 2001, 16, 297–305. [Google Scholar] [CrossRef]
- Zhao, H.J.; Pang, Y.F.; Qiu, Z.M.; Chen, M. Study on UPF Harmonic Current Detection Method Based on DSP. J. Phys. Conf. Ser. 2006, 48, 1327. [Google Scholar] [CrossRef] [Green Version]
- Eid, A.; Abdel-Salam, M.; El-Kishky, H.; El-Mohandes, T. Active Power Filters for Harmonic Cancellation in Conventional and Advanced Aircraft Electric Power Systems. Electr. Power Syst. Res. 2009, 79, 80–88. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Frank, T.M.; Divan, D.M.; Banerjee, B. Active Filter System Implementation. IEEE Ind. Appl. Mag. 1998, 4, 47–63. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Divan, D. Synchronous Frame Based Controller Implementation for a Hybrid Series Active Filter System. In Proceedings of the In IAS’95. Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995; Volume 3, pp. 2531–2540. [Google Scholar] [CrossRef]
- Da Silva, C.H.; Pereira, R.R.; da Silva, L.E.B.; Lambert-Torres, G.; Bose, B.K.; Ahn, S.U. A Digital PLL Scheme for Three-Phase System Using Modified Synchronous Reference Frame. IEEE Trans. Ind. Electron. 2010, 57, 3814–3821. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Three-Phase Three-Level Shunt Active Power Filter with Simplified Synchronous Reference Frame. In Proceedings of the 2016 IEEE Industrial Electronics and Applications Conference (IEACon), Kota Kinabalu, Malaysia, 20–22 November 2016; pp. 1–6. [Google Scholar]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F.; Wahab, N.I.A. A Simplified Synchronous Reference Frame for Indirect Current Controlled Three-Level Inverter-Based Shunt Active Power Filters. J. Power Electron. 2016, 16, 1964–1980. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Bansal, H.O. Real-Time Implementation of Adaptive PV-Integrated SAPF to Enhance Power Quality. Int. Trans. Electr. Energy Syst. 2019, 29, e12004. [Google Scholar] [CrossRef]
- Msigwa, C.J.; Kundy, B.J.; Mwinyiwiwa, B.M. Control Algorithm for Shunt Active Power Filter Using Synchronous Reference Frame Theory. World Acad. Sci. Eng. Technol. 2009, 58, 1828–1834. [Google Scholar]
- Musa, S.; Radzi, M.A.M.; Hizam, H.; Wahab, N.I.A.; Hoon, Y.; Zainuri, M.A.A.M. Modified Synchronous Reference Frame Based Shunt Active Power Filter with Fuzzy Logic Control Pulse Width Modulation Inverter. Energies 2017, 10, 758. [Google Scholar] [CrossRef] [Green Version]
- Pigazo, A.; Moreno, V.M.; Estebanez, E.J. A Recursive Park Transformation to Improve the Performance of Synchronous Reference Frame Controllers in Shunt Active Power Filters. IEEE Trans. Power Electron. 2009, 24, 2065–2075. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Dai, N.Y.; Chio, U.F.; Wong, M.C.; Wong, C.K.; Sin, S.W.; Seng-Pan, U.; Martins, R.P. FPGA-Based Decoupled Double Synchronous Reference Frame PLL for Active Power Filters. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 2145–2150. [Google Scholar]
- Sundaram, E.; Venugopal, M. On Design and Implementation of Three Phase Three Level Shunt Active Power Filter for Harmonic Reduction Using Synchronous Reference Frame Theory. Int. J. Electr. Power Energy Syst. 2016, 81, 40–47. [Google Scholar] [CrossRef]
- Mattavelli, P. Synchronous-Frame Harmonic Control for High-Performance AC Power Supplies. IEEE Trans. Ind. Appl. 2001, 37, 864–872. [Google Scholar] [CrossRef]
- Escobar, G.; Stankovic, A.M.; Mattavelli, P. An Adaptive Controller in Stationary Reference Frame for D-Statcom in Unbalanced Operation. IEEE Trans. Ind. Electron. 2004, 51, 401–409. [Google Scholar] [CrossRef]
- Marmouh, S.; Boutoubat, M.; Mokrani, L. Performance and Power Quality Improvement Based on DC-Bus Voltage Regulation of a Stand-Alone Hybrid Energy System. Electr. Power Syst. Res. 2018, 163, 73–84. [Google Scholar] [CrossRef]
- De Lacerda de Oliveira, L.; da Silva, L.; da Silva, V.; Torres, G.; Pinto, J. Improving the Dynamic Response of Active Power Filters Based on the Synchronous Reference Frame Method. In Proceedings of the APEC, Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No. 02CH37335), Dallas, TX, USA, 10–14 March 2002; Volume 2, pp. 742–748. [Google Scholar] [CrossRef]
- Kabir, M.A.; Mahbub, U. Synchronous Detection and Digital Control of Shunt Active Power Filter in Power Quality Improvement. In Proceedings of the 2011 IEEE Power and Energy Conference at Illinois, Urbana, IL, USA, 25–26 February 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Bajaj, M.; Rautela, S.; Sharma, A. A Comparative Analysis of Control Techniques of SAPF under Source Side Disturbance. In Proceedings of the In 2016 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Nagercoil, India, 18–19 March 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Narongrit, T.; Santiprapan, P.; Janpong, S. A Synchronous Detection with Fourier Analysis for Single-Phase Shunt Active Power Filters. In Proceedings of the 2018 5th International Conference on Electric Power and Energy Conversion Systems (EPECS), Kitakyushu, Japan, 23–25 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Tali, M.; Essadki, A.; Nasser, T. Harmonic Detection Methods of Shunt Active Power Filter under Unbalanced Loads. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 14–17 November 2016; pp. 1017–1023. [Google Scholar] [CrossRef]
- Sujatha, C.H.; Kusam, S.; Shekar, K.C. Shunt Active Filter Algorithms for a Three Phase System Fed to Adjustable Speed Drive. Int. J. Eng. Sci. Technol. 2011, 3, 7577–7586. [Google Scholar]
- Tanaka, T.; Okamoto, M.; Hiraki, E. Control Strategies of Active Power Line Conditioners in Single-Phase Circuits. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 1813–1820. [Google Scholar] [CrossRef]
- Dongre, G.A.; Choudhari, V.V.; Diwan, S.P. A Comparison and Analysis of Control Algorithms for Shunt Active Power Filter. In Proceedings of the 2015 International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Melmaruvathur, Chennai, India, 22–23 April 2015; pp. 129–133. [Google Scholar] [CrossRef]
- Jou, H.L. New Single-Phase Active Power Filter. IEE Proc.-Electr. Power Appl. 1994, 141, 129. [Google Scholar] [CrossRef]
- Hsu, C.; Wu, H. A New Single-Phase Active Power Filter with Reduced Energy-Storage Capacity. IEE Proc.-Electr. Power Appl. 1996, 143, 25. [Google Scholar] [CrossRef]
- Bains, B.K.; Dhingra, A. A Review of Current Control Techniques for Active Power Filter Applications. J. Eng. Econ. Dev. 2018, 4, 18–22. [Google Scholar]
- Tenti, P.; Mattavelli, P.; Morales Paredes, H.K. Conservative Power Theory, Sequence Components and Accountability in Smart Grids. In Proceedings of the 2010 International School on Nonsinusoidal Currents and Compensation, Lagow, Poland, 15–18 June 2010; pp. 37–45. [Google Scholar] [CrossRef]
- Rosa, R.B.; Vahedi, H.; Godoy, R.B.; Pinto, J.O.P.; Al-Haddad, K. Conservative Power Theory Used in NPC-Based Shunt Active Power Filter to Eliminate Electric Metro System Harmonics. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Haugan, T.S.; Tedeschi, E. Reactive and Harmonic Compensation Using the Conservative Power Theory. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Taher, S.A.; Alaee, M.H.; Dehghani Arani, Z. Model Predictive Control of PV-Based Shunt Active Power Filter in Single Phase Low Voltage Grid Using Conservative Power Theory. In Proceedings of the 2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017; pp. 253–258. [Google Scholar] [CrossRef]
- Bitoleanu, A.; Popescu, M. Shunt Active Power Filter Overview on the Reference Current Methods Calculation and Their Implementation. In Proceedings of the 2013 4th International Symposium on Electrical and Electronics Engineering (ISEEE), Galati, Romania, 11–13 October 2013; pp. 1–12. [Google Scholar] [CrossRef]
- Paredes, H.K.M.; Brandao, D.I.; Terrazas, T.M.; Marafao, F.P. Shunt Active Compensation Based on the Conservative Power Theory Current’s Decomposition. In Proceedings of the XI Brazilian Power Electronics Conference, Natal, Brazil, 11–15 September 2011; pp. 788–794. [Google Scholar] [CrossRef]
- Suru, C.V.; Patrascu, A.; Linca, M. Conservative Power Theory Implementation in Shunt Active Power Filtering. In Proceedings of the International School on Nonsinusoidal Currents and Compensation 2013 (ISNCC 2013), Zielona Góra, Poland, 20–21 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Karbasforooshan, M.S.; Monfared, M. An Adaptive Recursive Discrete Fourier Transform Technique for the Reference Current Generation of Single-Phase Shunt Active Power Filters. In Proceedings of the 2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 16–18 February 2016; pp. 253–259. [Google Scholar] [CrossRef]
- Borisov, K.; Ginn, H.; Chen, G. A Computationally Efficient RDFT-Based Reference Signal Generator for Active Compensators. IEEE Trans. Power Deliv. 2009, 24, 2396–2404. [Google Scholar] [CrossRef]
- Reza, M.S.; Ciobotaru, M.; Agelidis, V.G. A Recursive DFT Based Technique for Accurate Estimation of Grid Voltage Frequency. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 6420–6425. [Google Scholar] [CrossRef]
- Asiminoael, L.; Blaabjerg, F.; Hansen, S. Detection Is Key—Harmonic Detection Methods for Active Power Filter Applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. [Google Scholar] [CrossRef]
- Ginn, H.L.; Chen, G. Digital Control Method for Grid-Connected Converters Supplied With Nonideal Voltage. IEEE Trans. Ind. Inform. 2014, 10, 127–136. [Google Scholar] [CrossRef]
- Kumar, R.; Bansal, H.O. Hardware in the Loop Implementation of Wavelet Based Strategy in Shunt Active Power Filter to Mitigate Power Quality Issues. Electr. Power Syst. Res. 2019, 169, 92–104. [Google Scholar] [CrossRef]
- Firouzjah, K.G.; Sheikholeslami, A.; Karami-Mollaei, M.R.; Khaleghi, M. A New Harmonic Detection Method for Shunt Active Filter Based on Wavelet Transform. J. Appl. Sci. Res. 2008, 4, 1561–1568. [Google Scholar]
- Driesen, J.; Belmans, R. Active Power Filter Control Algorithms Using Wavelet-Based Power Definitions. In Proceedings of the 10th International Conference on Harmonics and Quality of Power. Proceedings (Cat. No. 02EX630), Rio de Janeiro, Brazil, 6–9 October 2002; Volume 2, pp. 466–471. [Google Scholar] [CrossRef]
- Aghazadeh, A.; Niazazari, I.; Khodabakhshi, N.; Hosseinian, S.H.; Abyaneh, H.A. A New Method of Single-Phase Active Power Filter for AC Electric Railway System Based on Hilbert Transform. In Proceedings of the 2013 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 28–30 August 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Swarnkar, N.K.; Mahela, O.P.; Lalwani, M. Evaluation of Power Quality in Distribution System with High Penetration of Wind Power Generation. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 27–29 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Panigrahi, R.; Subudhi, B. Performance Enhancement of Shunt Active Power Filter Using a Kalman Filter-Based H∞ Control Strategy. IEEE Trans. Power Electron. 2017, 32, 2622–2630. [Google Scholar] [CrossRef]
- Panigrahi, R.; Panda, P.C.; Subudhi, B.D. New Strategy for Generation of Reference Current in Active Power Filters with Distortion in Line Voltage. In Proceedings of the 2012 IEEE 7th International Conference on Industrial and Information Systems (ICIIS), Chennai, India, 6–9 August 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Hasim, A.S.B.A.; Dardin, S.M.F.B.S.M.; Ibrahim, Z.B. Kalman Filters for Reference Current Generation in Shunt Active Power Filter (APF). In Kalman Filters—Theory for Advanced Applications; Serra, G.L., Ed.; InTech: London, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Prince, S.K.; Panda, K.P.; Kumar, V.N.; Panda, G. Power Quality Enhancement in a Distribution Network Using PSO Assisted Kalman Filter—Based Shunt Active Power Filter. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hoffmann, N.; Fuchs, F.W. Minimal Invasive Equivalent Grid Impedance Estimation in Inductive—Resistive Power Networks Using Extended Kalman Filter. IEEE Trans. Power Electron. 2014, 29, 631–641. [Google Scholar] [CrossRef]
- Panigrahi, R.; Subudhi, B.; Panda, P.C. Model Predictive-based Shunt Active Power Filter with a New Reference Current Estimation Strategy. IET Power Electron. 2015, 8, 221–233. [Google Scholar] [CrossRef]
- Panigrahi, R.; Patjoshi, R.K. Robust Extended Complex Kalman Filter Based LQR Control Strategy of Shunt Active Power Filter. Int. J. Electr. Eng. Inform. 2020, 12, 278–295. [Google Scholar] [CrossRef]
- Prince, S.K.; Panda, K.P.; Patowary, M.; Panda, G. FPA Tuned Extended Kalman Filter for Power Quality Enhancement in PV Integrated Shunt Active Power Filter. In Proceedings of the 2019 International Conference on Computing, Power and Communication Technologies (GUCON), New Delhi, India, 27–28 September 2019; pp. 257–262. [Google Scholar]
- Regulski, P.; Terzija, V. Estimation of Frequency and Fundamental Power Components Using an Unscented Kalman Filter. IEEE Trans. Instrum. Meas. 2012, 61, 952–962. [Google Scholar] [CrossRef]
- Anderson, J.A.; Rosenfeld, E. Talking Nets: An Oral History of Neural Networks; MiT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Dash, P.; Swain, D.; Liew, A.; Rahman, S. An Adaptive Linear Combiner for On-Line Tracking of Power System Harmonics. IEEE Trans. Power Syst. 1996, 11, 1730–1735. [Google Scholar] [CrossRef]
- Hammer, M.; Janda, O.; Ertl, J. Selected Soft-Computing Methods in Power Oil Transformer Diagnostics—Part 1. J. Elektrorevue 2012, 1–13. [Google Scholar]
- Martinek, R.; Žídek, J. Refining the Diagnostic Quality of the Abdominal Fetal Electrocardiogram Using the Techniques of Artificial Intelligence. Prz. Elektrotech. 2012, 88, 155–160. [Google Scholar]
- Shukla, A.; Tiwari, R.; Kala, R. Towards Hybrid and Adaptive Computing; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; Volume 307. [Google Scholar] [CrossRef]
- Karthikeyan, V.V.; Kalpana, M. Power Quality Enhancement Using Shunt Active Filter with ANFIS Controller. Int. J. Adv. Inf. Sci. Technol. 2013, 2. [Google Scholar] [CrossRef]
- Martinek, R.; Manas, J.; Zidek, J.; Bilik, P. Power Quality Improvement by Shunt Active Performance Filters Emulated by Artificial Intelligence Techniques. In Proceedings of the 2nd International Conference on Advances in Computer Science and Engineering, Los Angeles, CA, USA, 1–2 July 2013; Atlantis Press: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef] [Green Version]
- Terriche, Y.; Guerrero, J.M.; Vasquez, J.C. Performance Improvement of Shunt Active Power Filter Based on Non-Linear Least-Square Approach. Electr. Power Syst. Res. 2018, 160, 44–55. [Google Scholar] [CrossRef]
- Martinek, R.; Zidek, J.; Bilik, P.; Manas, J.; Koziorek, J.; Teng, Z.; Wen, H. The Use of LMS and RLS Adaptive Algorithms for an Adaptive Control Method of Active Power Filter. Energy Power Eng. 2013, 5, 1126–1133. [Google Scholar] [CrossRef]
- Clarkson, P.M. Optimal and Adaptive Signal Processing; Routledge: London, UK, 2017. [Google Scholar]
- Martinek, R.; Rzidky, J.; Jaros, R.; Bilik, P.; Ladrova, M. Least Mean Squares and Recursive Least Squares Algorithms for Total Harmonic Distortion Reduction Using Shunt Active Power Filter Control. Energies 2019, 12, 1545. [Google Scholar] [CrossRef]
- Douglas, S. A Family of Normalized LMS Algorithms. IEEE Signal Process. Lett. 1994, 1, 49–51. [Google Scholar] [CrossRef]
- Trilochan, P.; Mrutyunjaya, M.; Kumar, P.A.; Kumar, S.S. Sparse LMS Control Algorithm for Fuel Cell Based SAPF. In Proceedings of the 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON), Varanasi, India, 9–11 December 2016; pp. 72–77. [Google Scholar] [CrossRef]
- Martinek, R.; Bilik, P.; Baros, J.; Brablik, J.; Kahankova, R.; Jaros, R.; Danys, L.; Rzidky, J.; Wen, H. Design of a Measuring System for Electricity Quality Monitoring within the SMART Street Lighting Test Polygon: Pilot Study on Adaptive Current Control Strategy for Three-Phase Shunt Active Power Filters. Sensors 2020, 20, 1718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pereira, R.R.; da Silva, C.H.; da Silva, L.E.B.; Lambert-Torres, G.; Pinto, J.O.P. Improving the Convergence Time of Adaptive Notch Filters to Harmonic Detection. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 521–525. [Google Scholar] [CrossRef]
- Brenna, M.; Lazaroiu, G.; Superti-Furga, G.; Tironi, E. Bidirectional Front End Converter for DG With Disturbance Insensitivity and Islanding-Detection Capability. IEEE Trans. Power Deliv. 2008, 23, 907–914. [Google Scholar] [CrossRef]
- Choi, J.W.; Kim, Y.K.; Kim, H.G. Digital PLL Control for Single-Phase Photovoltaic System. IEE Proc.-Electr. Power Appl. 2006, 153, 40. [Google Scholar] [CrossRef]
- Svensson, J. Synchronisation Methods for Grid-Connected Voltage Source Converters. IEE Proc.-Gener. Transm. Distrib. 2001, 148, 229. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.R. PLL-Based Battery Charge Circuit Topology. IEEE Trans. Ind. Electron. 2004, 51, 1344–1346. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M. A Nonlinear Adaptive Filter for Online Signal Analysis in Power Systems: Applications. IEEE Trans. Power Deliv. 2002, 17, 617–622. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M. A Signal Processing Module for Power System Applications. IEEE Trans. Power Deliv. 2003, 18, 1118–1126. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M. A Method for Synchronization of Power Electronic Converters in Polluted and Variable-Frequency Environments. IEEE Trans. Power Syst. 2004, 19, 1263–1270. [Google Scholar] [CrossRef]
- Bojoi, R.; Griva, G.; Bostan, V.; Guerriero, M.; Farina, F.; Profumo, F. Current Control Strategy for Power Conditioners Using Sinusoidal Signal Integrators in Synchronous Reference Frame. IEEE Trans. Power Electron. 2005, 20, 1402–1412. [Google Scholar] [CrossRef]
- Yuan, X.; Allmeling, J.; Merk, W.; Stemmler, H. Stationary Frame Generalized Integrators for Current Control of Active Power Filters with Zero Steady State Error for Current Harmonics of Concern under Unbalanced and Distorted Operation Conditions. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference, Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy (Cat. No. 00CH37129), Rome, Italy, 8–12 October 2000; Volume 4, pp. 2143–2150. [Google Scholar] [CrossRef]
- Baros, J.; Martinek, R.; Jaros, R.; Danys, L.; Soustek, L. Development of Application for Control of SMART Parking Lot. IFAC-PapersOnLine 2019, 52, 19–26. [Google Scholar] [CrossRef]
- Kuncicky, R.; Kolarik, J.; Soustek, L.; Kuncicky, L.; Martinek, R. IoT Approach to Street Lighting Control Using MQTT Protocol. In AETA 2018—Recent Advances in Electrical Engineering and Related Sciences: Theory and Application; Zelinka, I., Brandstetter, P., Trong Dao, T., Hoang Duy, V., Kim, S.B., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 554, pp. 429–438. [Google Scholar] [CrossRef]
- Baros, J.; Danys, L.; Jaros, R.; Martinek, R. Wireless Power Quality Analyser Based on Virtual Instrumentation. IFAC-PapersOnLine 2019, 52, 465–472. [Google Scholar] [CrossRef]
- Danys, L.; Martinek, R.; Jaros, R.; Baros, J.; Bilik, P. Visible Light Communication System Based on Virtual Instrumentation. IFAC-PapersOnLine 2019, 52, 311–316. [Google Scholar] [CrossRef]
- Martinek, R.; Danys, L.; Jaros, R. Adaptive Software Defined Equalization Techniques for Indoor Visible Light Communication. Sensors 2020, 20, 1618. [Google Scholar] [CrossRef] [Green Version]
- Martinek, R.; Danys, L.; Jaros, R.; Mozny, D.; Siska, P.; Latal, J. VLC Channel Equalization Simulator Based on LMS Algorithm and Virtual Instrumentation. In Proceedings of the 2019 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rome, Italy, 27–29 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Danys, L.; Martinek, R.; Jaros, R.; Baros, J.; Bilik, P. OFDM VLC System Based on Virtual Instrumentation and SDR. IFAC-PapersOnLine 2019, 52, 453–458. [Google Scholar] [CrossRef]
- Soustek, L.; Martinek, R.; Kuncicky, R.; Danys, L.; Baros, J. Possibilities of Intelligent Camera System Based on Virtual Instrumentation: Technology of Broadband LIGHT for “Smart City” Concept. IFAC-PapersOnLine 2019, 52, 170–174. [Google Scholar] [CrossRef]
























| Algorithm | One-Phase | Three-Phase | Distorted Conditions | Only Current Meas. | No Need to Set Parameters | Implementation Complexity (1–5) | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|---|
| iPQ | x | ✓ | x | x | ✓ | 1 | Easy to implement and correct functionality with balanced and sinusoidal voltage. | Necessary to measure three voltages and currents. Impaired function in case of unbalanced and non-sinusoidal voltages. |
| CVT | x | ✓ | x | x | ✓ | 1 | Easy to implement and correct functionality with balanced and sinusoidal voltage. Eliminates neutral current in all cases. | Same as iPQ. |
| PQR | x | ✓ | x | x | ✓ | 2 | Easy to implement and correct functionality with balanced and sinusoidal voltage. Eliminates neutral current in all cases. | Two transformations are needed. |
| UPC | x | ✓ | x | x | ✓ | 1 | The power factor always has a value of 1, so the instantaneous reactive power is eliminated. | Method does not meet IEEE 1459 standard, and the current waveforms correspond to voltage, thus it may not correspond to IEEE 519 standard. |
| PHC | x | ✓ | ✓ | x | ✓ | 1 | Method is insensitive to external negative conditions such as distorted or imbalanced main voltage. Eliminates neutral current in all cases. | Necessary to measure three voltages and currents. The power factor does not take the value of 1. |
| SRF | x | ✓ | ✓ | ✓ | ✓ | 2 | It is not necessary to measure voltage. This method is simple to implement and often used. | Cannot be used for single-phase system. |
| SDM | x | ✓ | ✓ | x | ✓ | 2 | Works effectively in both balanced and unbalanced systems. Eliminates neutral current in all cases. | Significantly slower than iPQ. It is necessary to measure three voltages and currents. |
| CCT | ✓ | ✓ | ✓ | x | ✓ | 2 | Method does not require any transformation, and all calculations are performed in a-b-c coordinate system. | Necessary to measure three voltages and currents. |
| SMT | ✓ | ✓ | ✓ | x | ✓ | 2 | Works effectively in both balanced and unbalanced system. Eliminates neutral current in all cases. | Necessary to measure three voltages and currents. |
| VF | x | ✓ | ✓ | x | ✓ | 2 | Method is insensitive to external negative conditions such as distorted or imbalanced main voltage. Eliminates neutral current in all cases. | Necessary to measure three voltages and currents. |
| CPT | ✓ | ✓ | ✓ | x | ✓ | 2 | Method does not require any transformation and all calculations are performed in a-b-c coordinate system. . | Necessary to measure three voltages and currents. Computationally demanding. |
| FFT & DFT | ✓ | ✓ | ✓ | ✓ | x | 2 | Easy to implement. | Necessary to measure a whole period for correct estimation of the reference current. FFT and DFT are sensitive to incomplete periods. |
| RDFT | ✓ | ✓ | ✓ | ✓ | x | 3 | Method calculates the reference current from N samples and does not require whole period. Suitable for real-time applications. Less computationally demanding than FFT and DFT. | Necessary to measure a whole period for correct estimation of the reference current. RDFT is sensitive to incomplete periods. |
| WT | ✓ | ✓ | ✓ | ✓ | x | 3 | Easy to implement. | Necessary to measure at least one whole measuring window . |
| HT | ✓ | ✓ | ✓ | ✓ | ✓ | 2 | Easy to implement. Better than FFT in case of noisy signals. | Not able to determine short-time and weak disturbances. |
| KF | ✓ | ✓ | ✓ | ✓ | x | 3 | Easy to implement and computationally undemanding. | Method assumes that the system and observation models are linear, which does not correspond to real systems. |
| EKF | ✓ | ✓ | ✓ | ✓ | x | 3 | Easy to implement and computationally undemanding. Can be used in nonlinear systems. | Filter parameters dependent on measured input data. |
| ADALINE | ✓ | ✓ | ✓ | ✓ | x | 5 | The results of filtration are independent of external conditions and the method manages to filter even dynamically changing types of distortion. | High computational complexity. Sensitive to bad settings. Strongly heuristic. |
| ANFIS | ✓ | ✓ | ✓ | ✓ | x | 5 | The results of filtration are independent of external conditions and the method manages to filter even dynamically changing types of distortion. | High computational complexity. Sensitive to bad settings. Strongly heuristic. |
| LMS | ✓ | ✓ | ✓ | ✓ | x | 3 | Easy to implement. | Necessary to choose correct settings of the adaptive filter. Time of convergence is longer than RLS. |
| RLS | ✓ | ✓ | ✓ | ✓ | x | 4 | Easier setup of the adaptive algorithm than LMS. Time of convergence is shorter than LMS. | More complex implementation than LMS. |
| Notch LMS | x | ✓ | ✓ | ✓ | x | 4 | The filter is used only as second order, so the delay is one sample. Suitable for FPGA implementation. | Strongly dependent on the setting of the parameter. |
| Notch RLS | x | ✓ | ✓ | ✓ | x | 4 | The filter is used only as second order, so the delay is one sample. Suitable for FPGA implementation. | More complex implementation than Notch LMS. |
| Technique | One-Phase | Three-Phase | Non-Ideal Voltage Conditions | Heuristic Setting | Implementation Complexity (1–5) | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| ZCD | ✓ | ✓ | x | x | 1 | Easy to control. | HW circuit, noise sensitive, slow response to dynamic changes, poor results under distorted network conditions. |
| SV | x | ✓ | x | x | 3 | Robust and not sensitive to disturbances. If configured properly, it provides highly distortion-free estimation. | Sensitivity to the input frequency variation and imbalance. |
| EPLL | x | ✓ | ✓ | x | 3 | Good robustness. Insensitivity to inferences from the input signal. Used to synchronize grid-interfaced converters. Provides additional information regarding amplitude and phase angle due to introduction of PD. | Requires correct setting of the K parameter. |
| SSI-PLL | ✓ | ✓ | ✓ | ✓ | 4 | Immunity to voltage distortion and imbalance. Adaptable. | Requires correct setting of the filtering response and bandwidth parameters. |
| SRF-PLL | ✓ | ✓ | x | ✓ | 2 | Easy to implement, accurate synchronization under ideal network conditions, one of the most commonly used methods. | The PI controller must be optimally set, and it cannot work under distorted network conditions. |
| STF-PLL | ✓ | ✓ | ✓ | ✓ | 3 | Suitable for implementation under distorted or asymmetric conditions. | PI controller must be optimally set, STF gain must be chosen carefully, STF integration makes control more complicated. |
| DDSRF-PLL | x | ✓ | ✓ | ✓ | 3 | Suitable for implementation under distorted or asymmetric conditions. | The PI controller must be optimally set, and the extra SRF loop increases the computational complexity of the method. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baros, J.; Sotola, V.; Bilik, P.; Martinek, R.; Jaros, R.; Danys, L.; Simonik, P. Review of Fundamental Active Current Extraction Techniques for SAPF. Sensors 2022, 22, 7985. https://doi.org/10.3390/s22207985
Baros J, Sotola V, Bilik P, Martinek R, Jaros R, Danys L, Simonik P. Review of Fundamental Active Current Extraction Techniques for SAPF. Sensors. 2022; 22(20):7985. https://doi.org/10.3390/s22207985
Chicago/Turabian StyleBaros, Jan, Vojtech Sotola, Petr Bilik, Radek Martinek, Rene Jaros, Lukas Danys, and Petr Simonik. 2022. "Review of Fundamental Active Current Extraction Techniques for SAPF" Sensors 22, no. 20: 7985. https://doi.org/10.3390/s22207985
APA StyleBaros, J., Sotola, V., Bilik, P., Martinek, R., Jaros, R., Danys, L., & Simonik, P. (2022). Review of Fundamental Active Current Extraction Techniques for SAPF. Sensors, 22(20), 7985. https://doi.org/10.3390/s22207985







