Contributions of Support Point Number to Mirror Assembly Thermal Sensitivity Control
Abstract
:1. Introduction
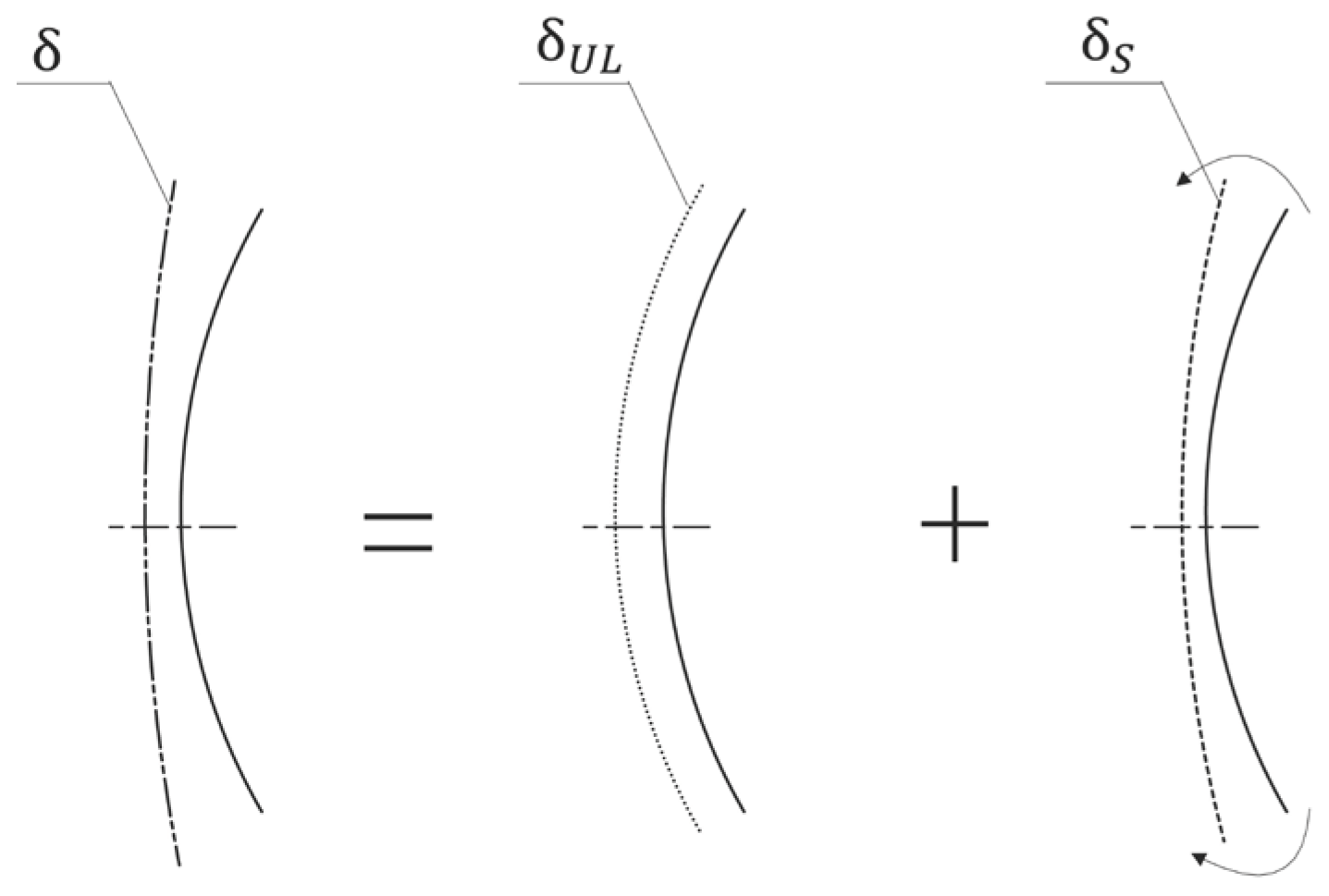
2. Aspects of Surface Thermal Deformation
3. The TCML at the Mirror Support Point and Sensitivity Control
3.1. Thermal Coupled Mechanical Load
3.2. Summary of TCML Sensitivity Control
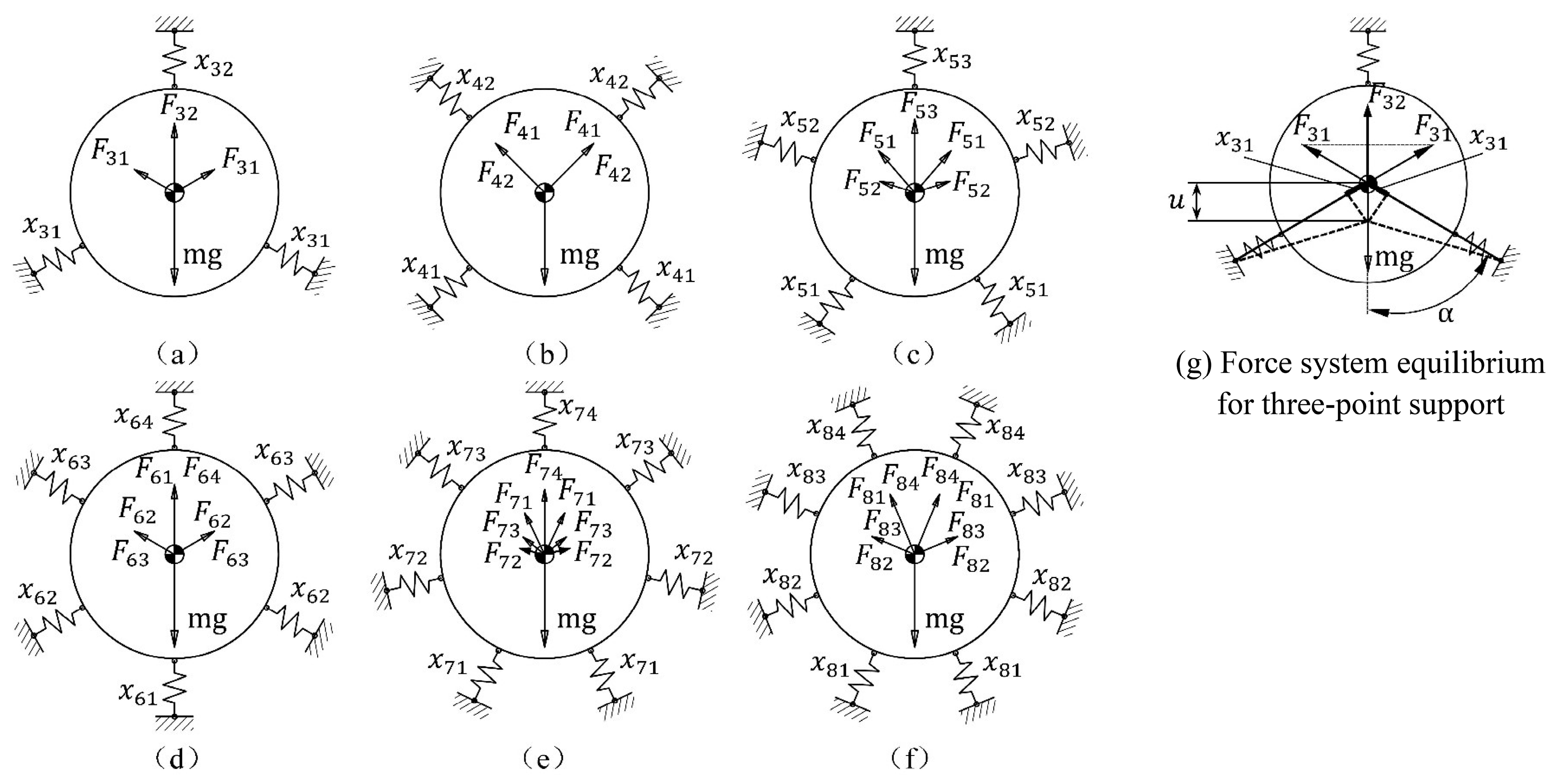
4. Contributions of the Support Point Number
4.1. Contribution to Connecting Stiffness Reduction
4.2. Contribution to Surface Deformation Sensitivity
- (a)
- Ideally, the radial support stiffness that balances with the mirror displacement due to gravity is inversely proportional to the support point number. Even though only the radial support stiffness is considered, the TCML-induced surface deformation sensitivity reduces dramatically with the increase in the support point number.
- (b)
- Under the given mirror displacement constraints resulting from gravity, tangential stiffness at each support point contributes to the further reduction in radial support stiffness. For the same support point number configuration, TCML induced surface deformation sensitivity can be further reduced with increases in the tangential stiffness at each support point.
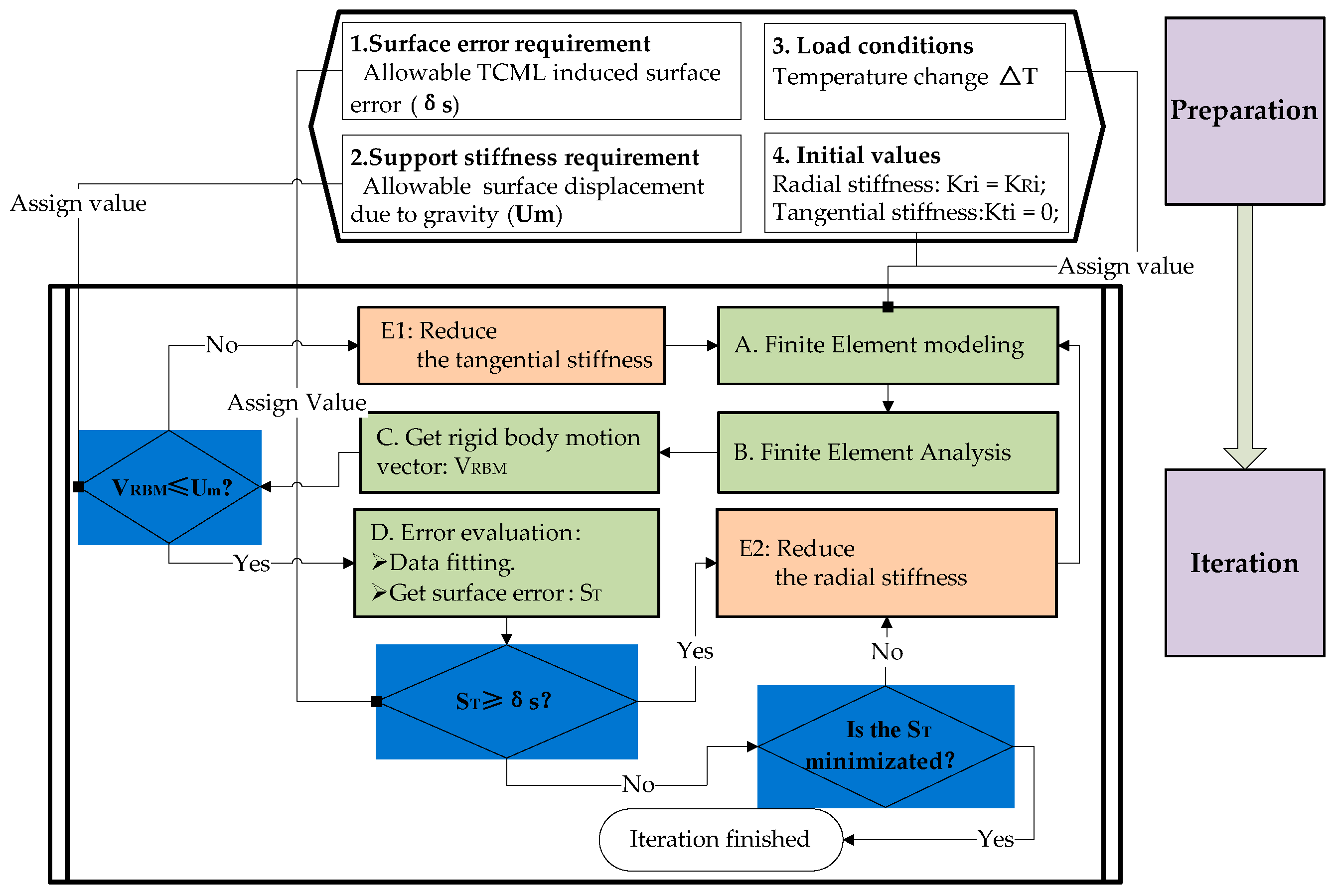
5. Theoretical Design of the Mirror Mount System
5.1. Design Process
- (a)
- Obtain an initially optimized mirror profile.Thickness of the mirror blank can be determined according to the material configuration and the allocated geometric design space. For large temperature variation suitability, a relatively thicker mirror blank is recommended. The distribution of the support points can be optimized under the constraint that the surface deformation error due to gravity along the axial direction is minimized.
- (b)
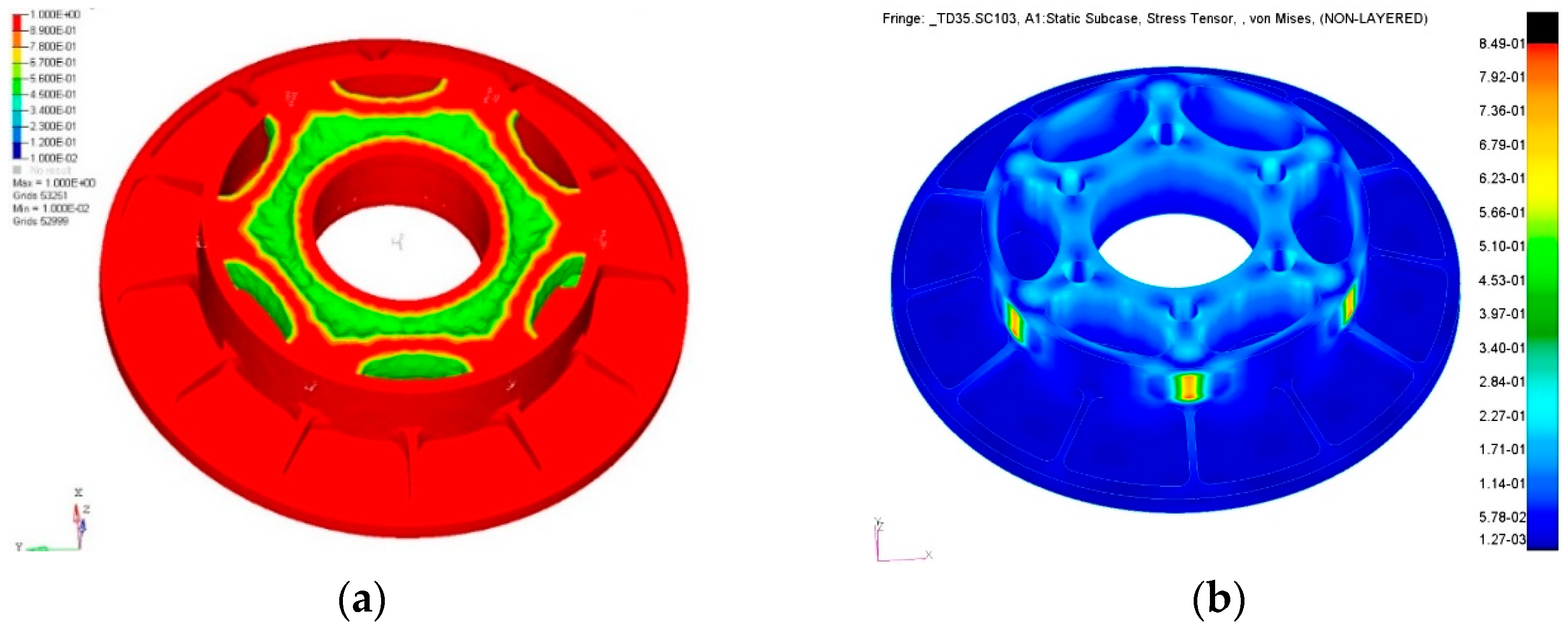
- Determine the maximum allowable compressive force at the mirror support point.Based on the initially optimized mirror profile, the maximum allowable compressive force can be evaluated by the FEA on the simplified mirror assembly model (see Section 4.2).

- (c)
- Calculate the thermally induced interface displacement mismatch.The radius of the support point distribution circle (see the in Equation (5)), the CTE mismatch between the mirror and the mount structure (see the in Equation (5), and the considered temperature change (see the in Equation (5)), are required for this calculation.
- (d)
- Obtain an initial radial stiffness that equals the required lateral support stiffness.The required lateral support stiffness (see the in Equation (10)) equals the mirror gravity divided by the allowable surface lateral displacement. The required radial stiffness (exemplified by the in Equation (10)) equals to the required lateral support stiffness can be calculated by using the simplified model, as described in Section 4.1.
- (e)
- Calculate components of the optimized stiffness vector at the mirror support point.Generally, the stiffness vector at each support point consists of an axial component, a radial component, and a tangential component (see Figure 6). For the mirror assembly that has high axis-symmetric properties, the axial component of the stiffness vector at support point can be solved in a relative independent manner. To simplify the illustration, consider the simplified two-element stiffness vector that consists of the radial component and the tangential component under high symmetric load conditions in-plane. Because only one equilibrium equation exists, a fixed solution to the stiffness vector that contains multiple components does not exist. Optimization is needed to calculate the stiffness vector.

5.2. Optimization of the Stiffness Vector at Mirror Support Point
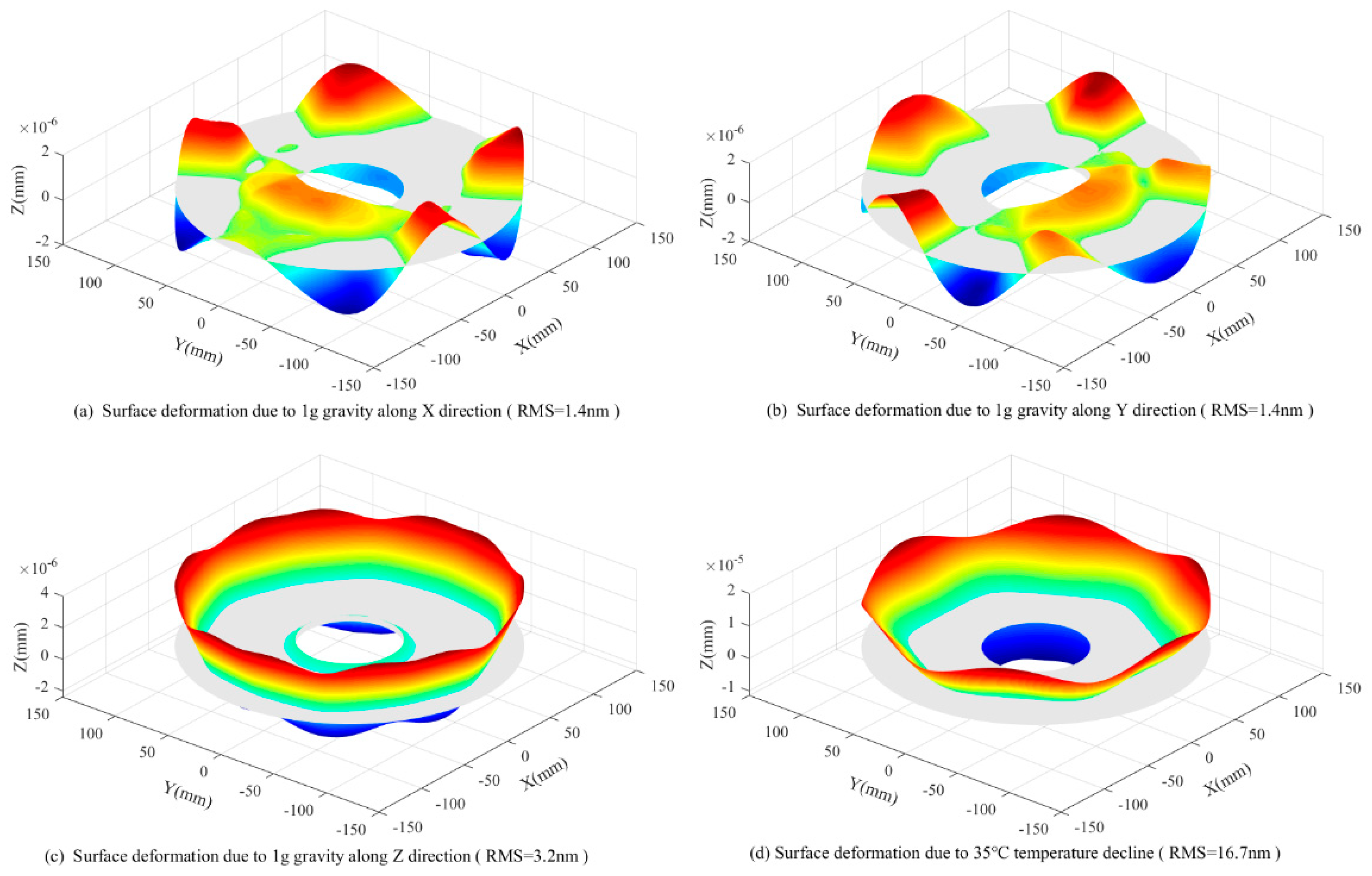
6. Demonstration
6.1. Requirements
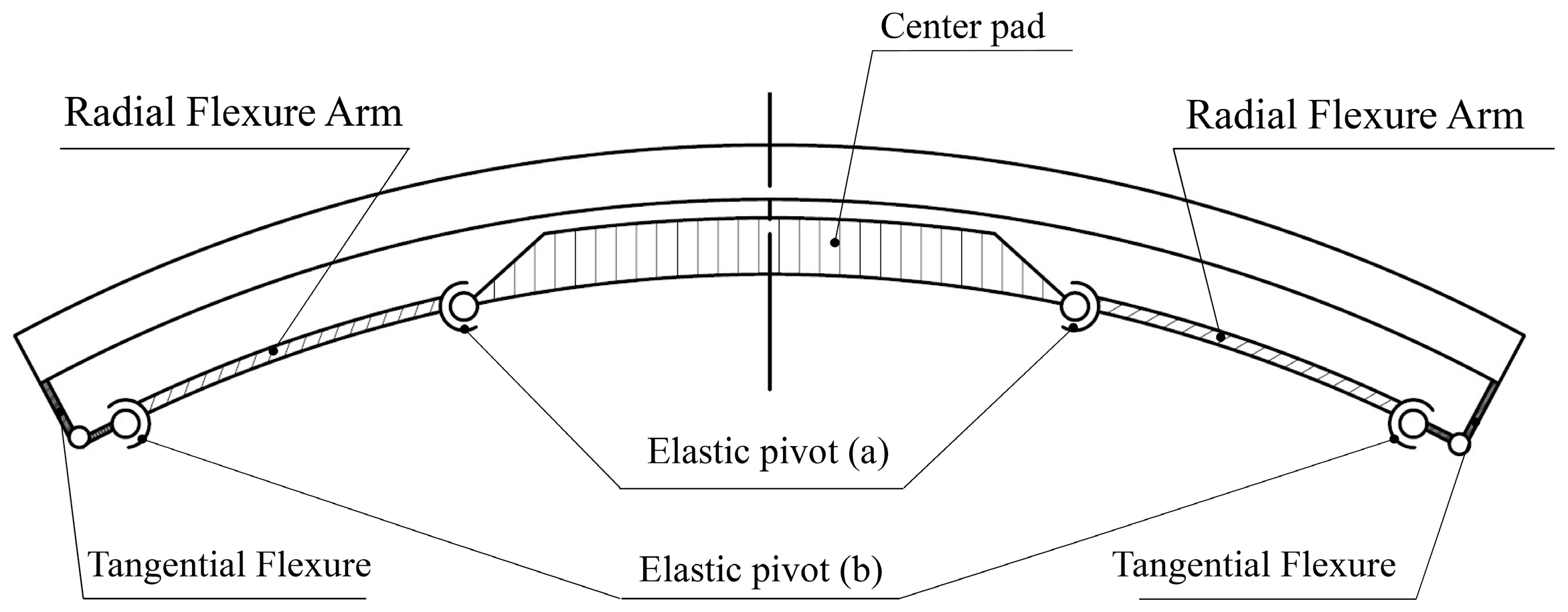
6.2. Proposed Support System
6.3. Discussions
6.3.1. Mirror Topological Optimization
6.3.2. Ultra-Low Radial Stiffness MF
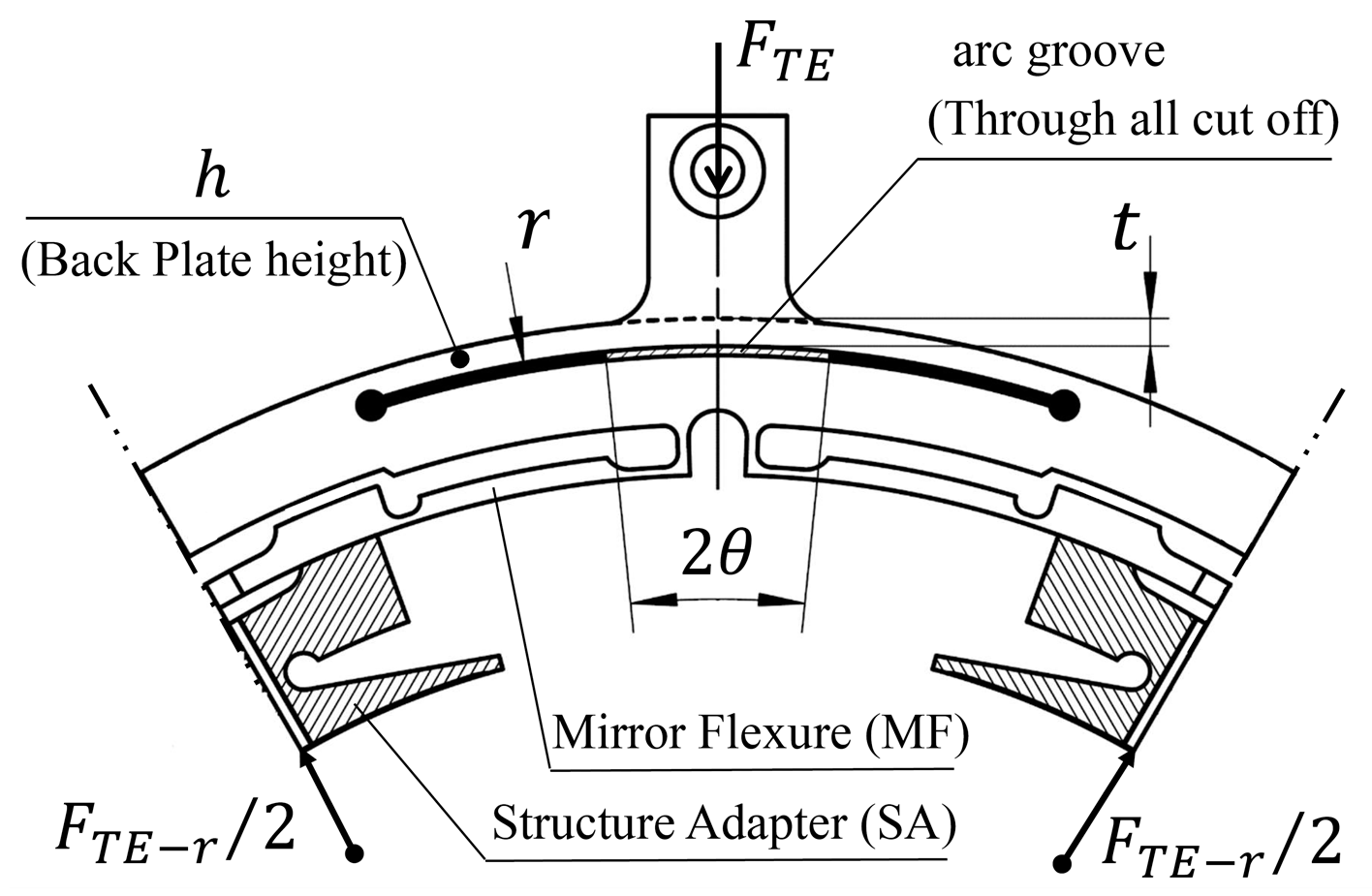
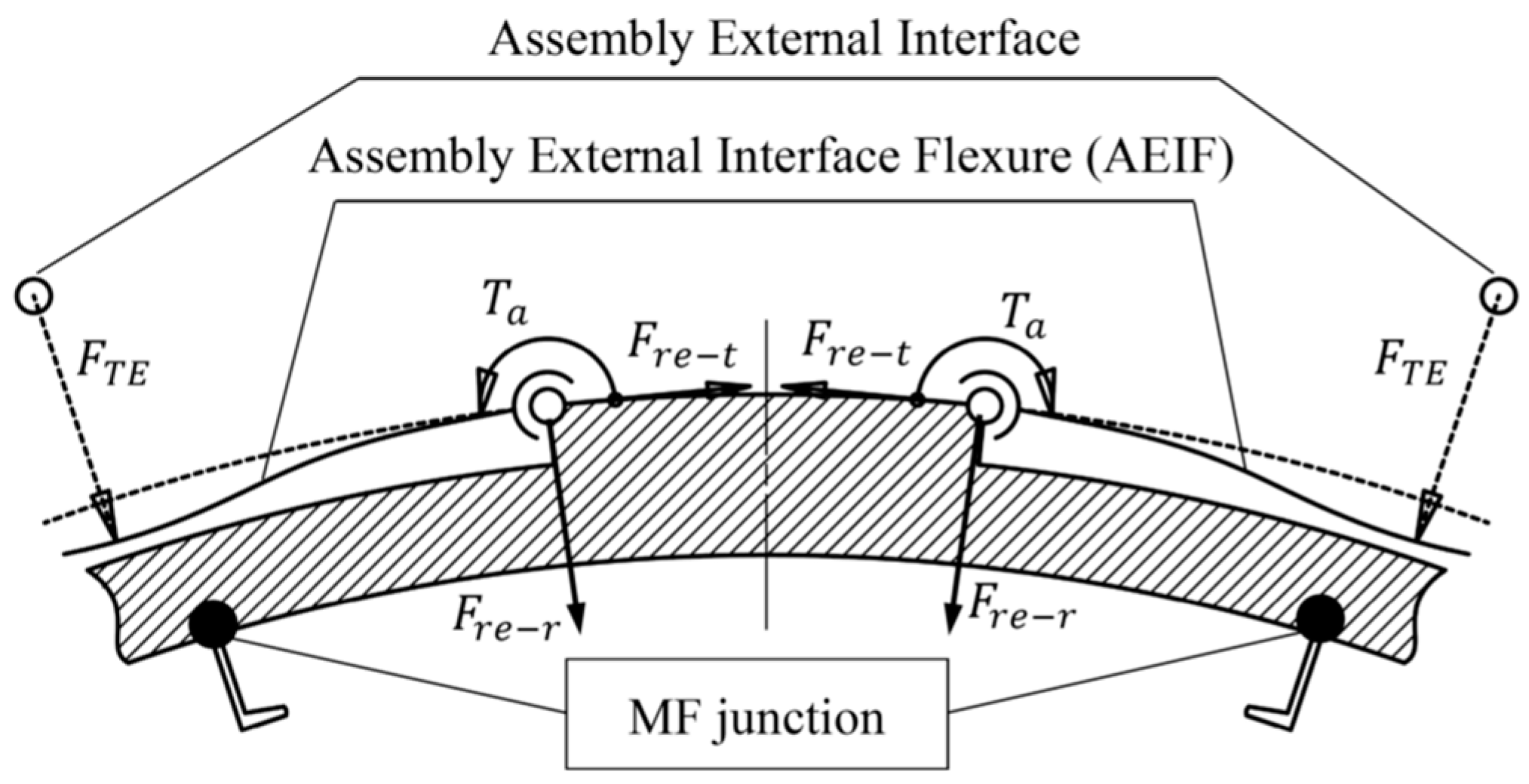
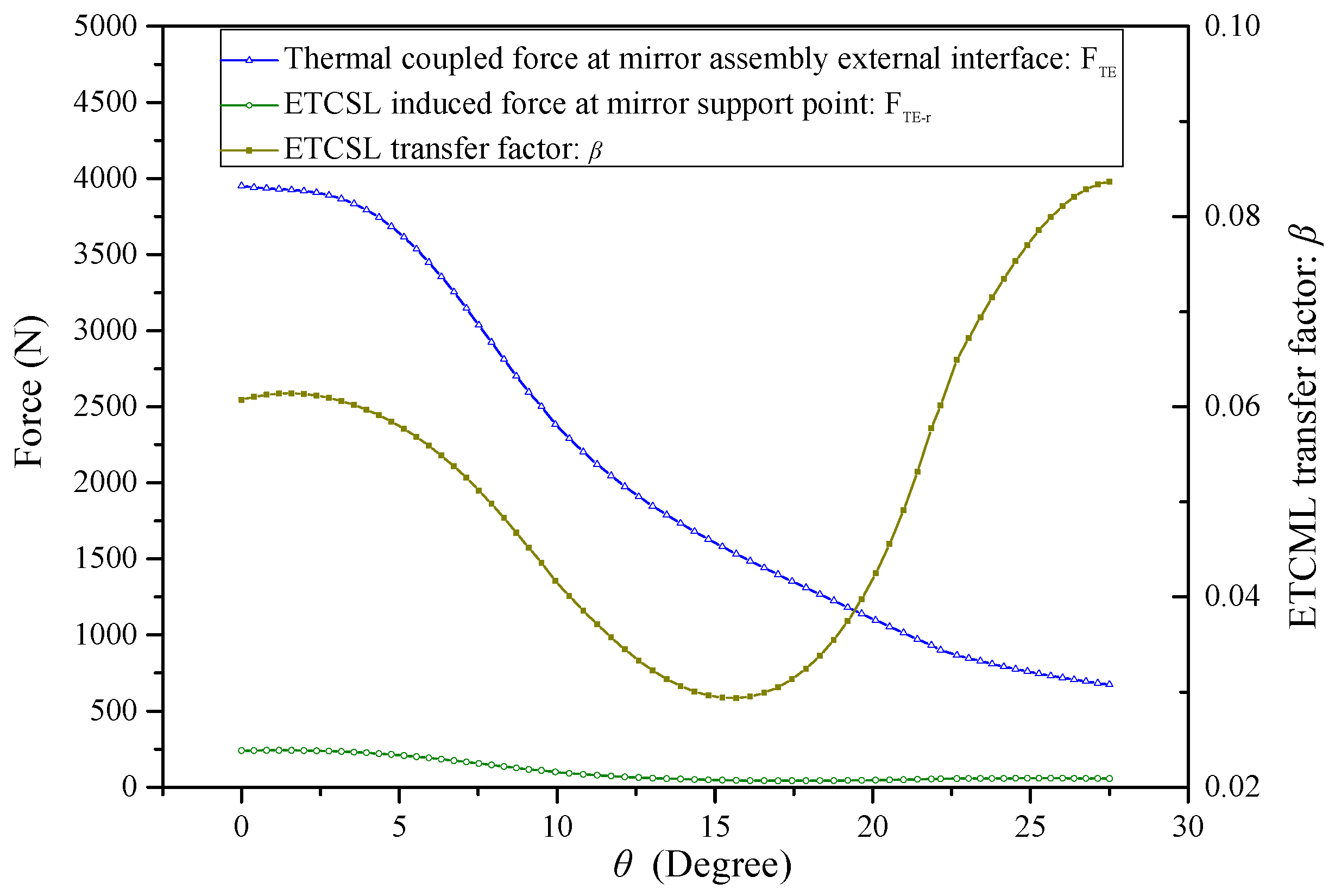
6.3.3. Effects of AEIF on ETCML Control
- (a)
- The ETCML equivalent radial force that compresses (or stretches) the BP middle layer along the radial direction decreases, according to the cosine law of the groove semi-arc angle.
- (b)
- The increase in the load path length due to the groove semi-arc angle increase simultaneously causes the BP compressive stiffness reduction.
- (c)
6.4. Performance Evaluation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Paul, R.; Yoder, Jr. Environmental Influences. In Opto-Mechanical Systems Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2005; pp. 39–42. [Google Scholar]
- Koper, H.F.; Murray, T.J. Design considerations for long focal length reconnaissance systems from an applications point of view. Proc. SPIE 1980, 0242, 52–56. [Google Scholar]
- Sementelli, R.G. EO/IR dual-band reconnaissance system DB-110. Proc. SPIE 1995, 2555, 222–231. [Google Scholar]
- Liu, F.; Cheng, Z.; Jia, P.; Zhang, B.; Liu, X.; Hu, R. Impact of Thermal Control Measures on the Imaging Quality of an Aerial Optoelectronic Sensor. Sensors 2019, 19, 2753. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Sun, L.; Liu, F.; Liu, X.; Li, L.; Li, Q.; Hu, R.; Liu, L. Engineering Design of an Active–Passive Combined Thermal Control Technology for an Aerial Optoelectronic Platform. Sensors 2019, 19, 5241. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Ding, Y.; Wu, Q.; Jia, J.; Guo, L.; Wang, L. Thermal analysis and design of the aerial camera’s primary optical system components. Appl. Therm. Eng. 2012, 38, 40–47. [Google Scholar] [CrossRef]
- Liu, W.; Ge, M.; Xu, Y.; Xu, Y.; Cheng, Z.; Huang, M. Design of a thermal control device suitable for airborne remote sensors. Appl. Therm. Eng. 2014, 73, 894–898. [Google Scholar]
- Chin, D. Optical Mirror-Mount Design and Philosophy. App. Opt. 1964, 3, 895–901. [Google Scholar] [CrossRef]
- Li, H.; Ding, Y.; Zhang, H. Support system study of rectangular mirror. Acta Optica Sinica 2015, 35, 523002. [Google Scholar]
- Onaka, T.; Kaneda, H.; Enya, K.; Nakagawa, T.; Matsuhara, H.; Kataza, H. Development of large aperture cooled telescopes for the Space Infrared Telescope for Cosmology and Astrophysics (SPICA) mission. Proc. SPIE 2005, 59621, 59621J. [Google Scholar]
- Jiang, P.; Zhou, P. Optimization of a lightweight mirror with reduced sensitivity to the mount location. Appl. Opt. 2020, 59, 3799–3805. [Google Scholar] [CrossRef]
- Zhang, M.; Lu, Q.; Tian, H.; Wang, D.; Chen, C.; Wang, X. Design and optimization for mounting primary mirror with reduced sensitivity to temperature change in an aerial optoelectronic sensor. Sensors 2021, 21, 7993. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Zhang, F.; Zhao, H.; Zhao, Y.; Zheng, X. Design and optimization of integrated flexure mounts for unloading lateral gravity of a lightweight mirror for space application. Appl. Opt. 2021, 60, 417–426. [Google Scholar] [CrossRef]
- Woods, M.J.; Schnal, D.; Weingrod, I.; Kvamme, T.; Connolly, P.; Feinstein, K.; Holmes, B.; Lee, S.; Peters, B. A catalog approach to mounting optics for space applications. Proc. SPIE 2020, 11487, 11487Y. [Google Scholar]
- Kihm, H.; Yang, H.; Moon, I.; Yeon, J.; Lee, S.; Lee, Y. Adjustable bipod flexures for mounting mirrors in a space telescope. Appl. Opt. 2012, 51, 7776–7783. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Huang, B.-K.; You, Z.-T.; Chan, C.-Y.; Huang, T.-M. Optimization of lightweight structure and supporting bipod flexure for a space mirror. Appl. Opt. 2016, 55, 10382–10391. [Google Scholar] [CrossRef]
- Weingrod, I.; Chou, C.Y.; Holmes, B.; Hom, C.; Irwin, J.W.; Lindstrom, O.; Lopez, F.; Stubbs, D.M.; Wüelser, J.-P. Design of bipod flexure mounts for the IRIS spectrometer. Proc. SPIE 2013, 88360, 88360Q. [Google Scholar]
- Yang, Y.; Yan, Z.; Shen, J.; Kuang, Y.; Wan, W.; Jia, J.; Liu, C.; Chen, J.; Wang, B.; Bao, T.; et al. Design and material selection of optomechanical systems for the extreme environment on Mars. J. Astron. Telesc. Instrum. Syst. 2021, 7, 034003. [Google Scholar] [CrossRef]
- Nam, J.R.; Yoo, J.; Kim, Y.H.; Kim, Y. Athermal performance of a dual-band LOROP sensor with an all-SiC Telescope. J. Korean Phys. Soc. 2020, 76, 458–462. [Google Scholar] [CrossRef]
- Bae, J.; Lee, H.; Kim, J.; Kim, M. Design of All-SiC Lightweight Secondary and Tertiary Mirrors for Use in Spaceborne Telescopes. Curr. Opt. Photonics 2022, 6, 60–68. [Google Scholar]
- Li, Z.; Chen, B.; Song, K.; Wang, X.; Liu, S.; Yang, L.; Hu, Q.; Qiao, K.; Zhang, L.; Wu, G.; et al. Opto-mechanisms design of extreme-ultraviolet camera onboard Chang E lunar lander. Opt. Expr. 2014, 22, 15932–15940. [Google Scholar] [CrossRef]
- Mimovich, M.E.; Griffee, J.C.; Goodding, J.C. Optical mounts for harsh environments. Proc. SPIE 2009, 7424, 74240B. [Google Scholar]
- Grant, J.; Wood, T.; Bhatti, I.; Cañas, A.; Reddick, P.; van Wyk, P.; Bharadia, S.; Storey, T.; Potterton, T.; Rits, W.; et al. Cryogenic optical mounting for shortwave infrared spectrometers. Proc. SPIE 2014, 91513, 91513Z. [Google Scholar]
- Fitzsimmons, J.; Hill, A. Design and analysis of a large-diameter precision optical mount for NFIRAOS. Proc. SPIE 2014, 9147, 2842–2851. [Google Scholar]
- Sun, Y.; Luo, S.; Bai, J.; Liu, Z.; Tang, S. Design and Optimization of the Flexible Support Structure for Space Mirror. In Aerospace Mechatronics and Control Technology; Ding, H., Ed.; Springer Nature Singapore Pte Ltd.: Singapore, Singapore, 2022; pp. 119–128. [Google Scholar]
- Jiang, P.; Xue, C.; Wang, K.; Wang, X.; Zhou, P. Design and optimization of the tripod flexure for a 2m lightweight mirror for space application. Appl. Opt. 2023, 62, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Liu, S.; Li, Q. Topology-optimization-based design method of flexures for mounting the primary mirror of a large-aperture space telescope. Appl. Opt. 2017, 56, 4551–4560. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Z.; Jin, L.; Chen, J. Finite element calculation for surface shape optimization of a polished synchrotron radiation thin mirror based on Bessel-point supporting. Nucl. Instr. Meth. Phys. Res. Sect. A 2022, 1042, 167458. [Google Scholar] [CrossRef]
- Ruthven, G.P.; Crout, R.R.; Krim, M.H.; Nonnenmacher, A.L.; Stier, M.T. Design and analysis of a 1-meter cryogenic mirror. Proc. SPIE 1993, 1765, 11–28. [Google Scholar]
- Doyle, K.B.; Genberg, V.L.; Michels, G.J. Integrated Optomechanical Analysis, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2012. [Google Scholar]
- Sepehripour, F.; van Beurden, M.C.; de Hon, B.P. Direct Computation of the PEC Body of Revolution Modal Green Function for the Electric Field Integral Equation. IEEE J. Multiscale Multiphysics Comput. Tech. 2022, 7, 186–194. [Google Scholar] [CrossRef]
- Shao, M.; Zhang, L.; Jia, X. Optomechanical integrated optimization of a lightweight mirror for space cameras. Appl. Opt. 2021, 60, 539–546. [Google Scholar] [CrossRef]
- Li, C.; Ding, Y.; Lin, C.; Wei, Y.; Zheng, Y.; Zhang, L. Optomechanical design and simulation of a cryogenic infrared spectrometer. Appl. Opt. 2020, 59, 4642–4649. [Google Scholar] [CrossRef]
- Xue, Z.-P.; Wang, C.-X.; Yu, Y.; Wang, P.-P.; Zhang, H.-Y.; Sui, Y.-Y.; Li, M.; Luo, Z.-Y. Integrated optomechanical analyses and experimental verification for a thermal system of an aerial camera. Appl. Opt. 2019, 58, 6996–7005. [Google Scholar] [CrossRef]
- Kihm, H.; Yang, H.S. Design optimization of a 1-m lightweight mirror for a space telescope. Opt. Eng. 2013, 52, 091806. [Google Scholar] [CrossRef]




| Multiplier |
| Parameters | Value | |
|---|---|---|
| Aperture size | Outer diameter | 260 mm |
| Central perforation diameter | 80 mm | |
| Surface displacement due to gravity | ≤1 micron | |
| Surface deformation RMS due to 35 °C temperature variation | ≤ | |
| Material | Density ρ (g/cm3) | CTE α (×10−6) | Young’s Modulus E (GPa) | Poisson’s Ratio ν |
|---|---|---|---|---|
| Zerodur | 2.53 | 0 ± 0.05 | 90.6 | 0.24 |
| Ti-6Al-4V | 4.44 | 8.9 | 114 | 0.34 |
| Invar | 8.13 | 0.31 | 148 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, H.; Ding, Y.; Zhang, J.; Cai, Y. Contributions of Support Point Number to Mirror Assembly Thermal Sensitivity Control. Sensors 2023, 23, 1951. https://doi.org/10.3390/s23041951
Li H, Zhang H, Ding Y, Zhang J, Cai Y. Contributions of Support Point Number to Mirror Assembly Thermal Sensitivity Control. Sensors. 2023; 23(4):1951. https://doi.org/10.3390/s23041951
Chicago/Turabian StyleLi, Haixing, Hongwen Zhang, Yalin Ding, Jichao Zhang, and Yuqi Cai. 2023. "Contributions of Support Point Number to Mirror Assembly Thermal Sensitivity Control" Sensors 23, no. 4: 1951. https://doi.org/10.3390/s23041951
APA StyleLi, H., Zhang, H., Ding, Y., Zhang, J., & Cai, Y. (2023). Contributions of Support Point Number to Mirror Assembly Thermal Sensitivity Control. Sensors, 23(4), 1951. https://doi.org/10.3390/s23041951





