Method for Diagnosing Bearing Faults in Electromechanical Equipment Based on Improved Prototypical Networks
Abstract
:1. Introduction
- (1)
- The prototypical network, which performs well on small-sample classification tasks, was improved by calculating the differences between the influence of the support sample distributions in order to achieve the prototypical calculation. The change in sample influence was calculated using the Kullback–Leibler divergence of the sample distribution. The influence change of a specific sample can be measured by assessing how much the distribution changes in the absence of that sample.
- (2)
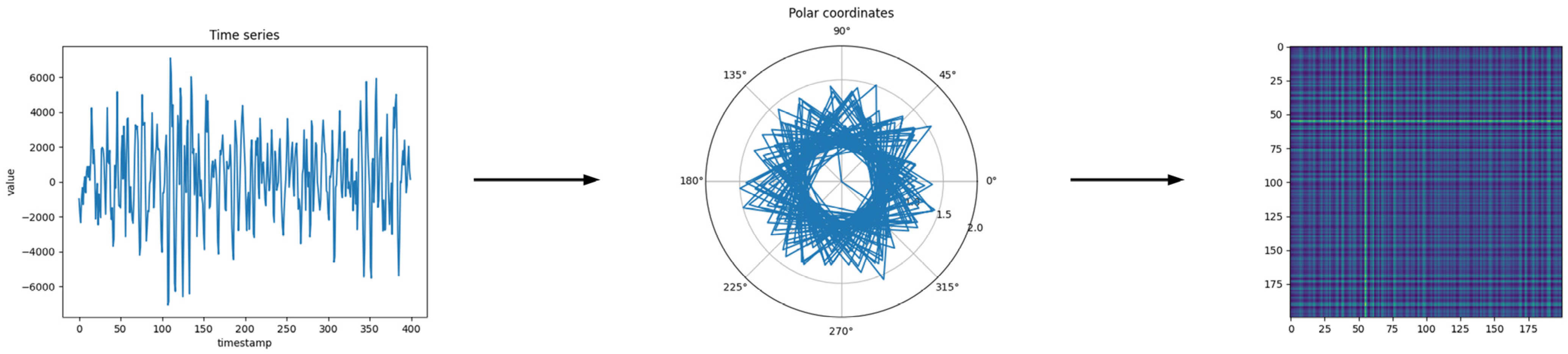
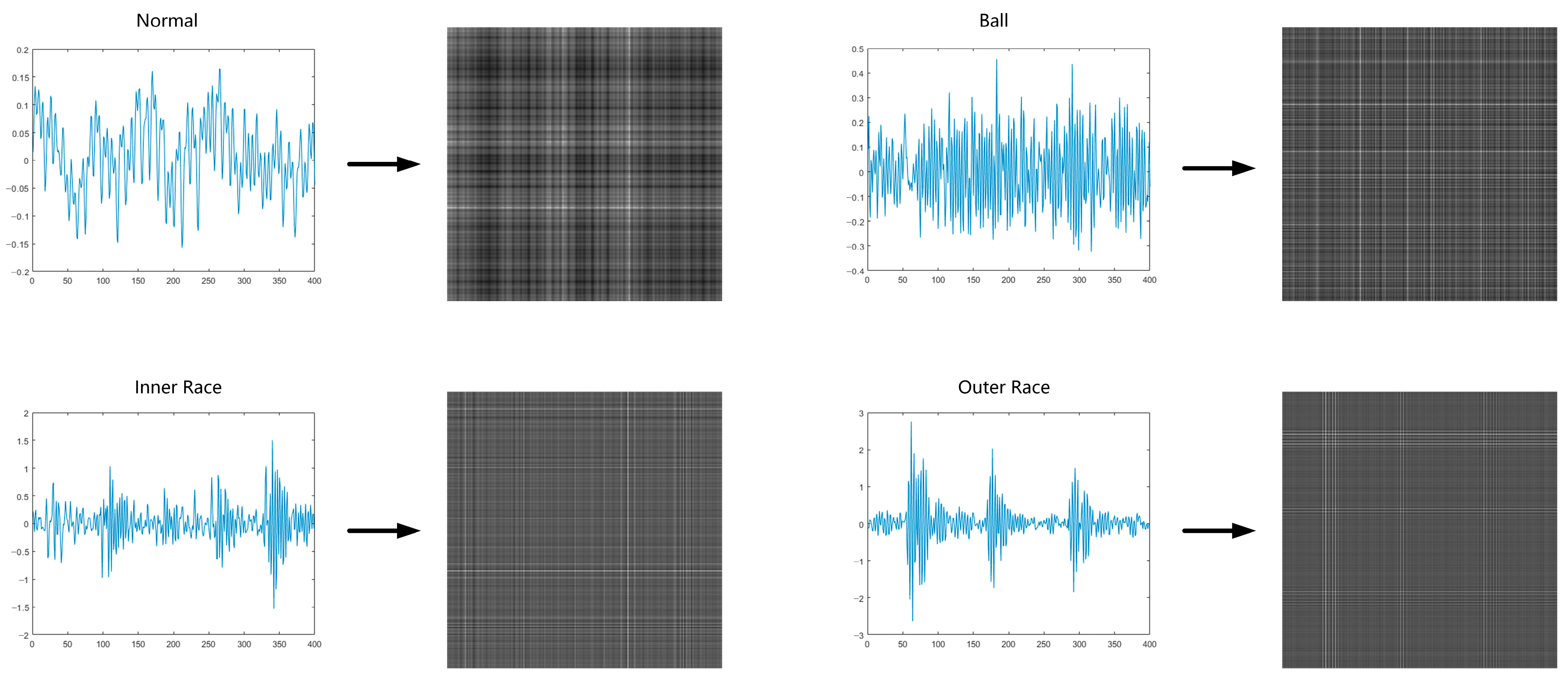
- The Gramian Angular Field algorithm was used to transform a one-dimensional time series into two-dimensional vibration images, thus greatly improving the application effect of the 2D convolutional neural network.
2. Preliminary Knowledge
2.1. Meta Learning and Prototypical Networks
2.2. Gramian Angular Field Transformation
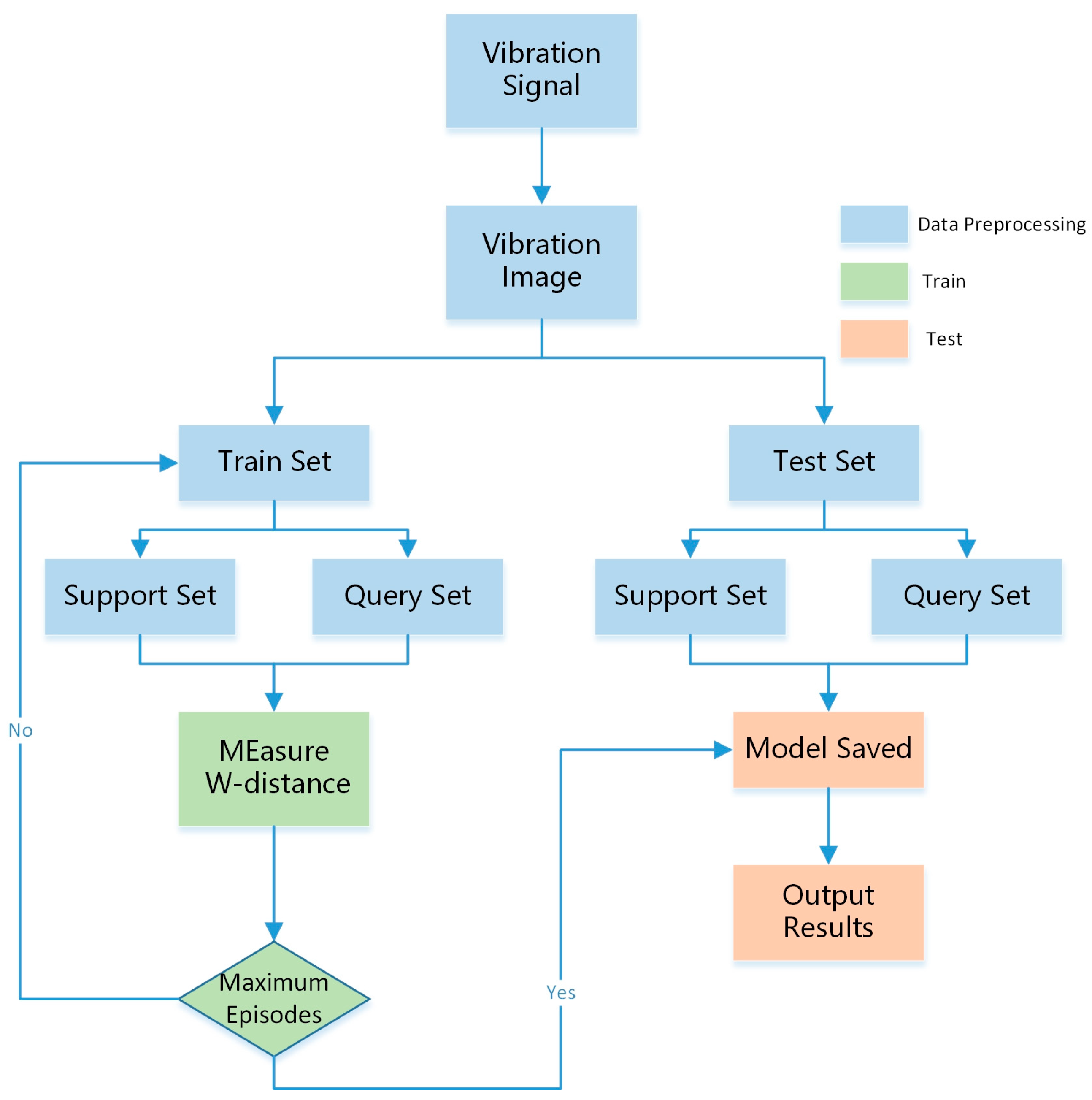
3. Fault Diagnosis Method Based on WproNet
3.1. Improved Model Architecture
3.2. Encoder Layer
3.3. Distribution–Prototypical Layer
3.3.1. K–L Divergence
3.3.2. Distribution–Prototypical Layer Design
3.4. Fault Diagnosis Process
3.4.1. Dataset
3.4.2. Data Preprocessing
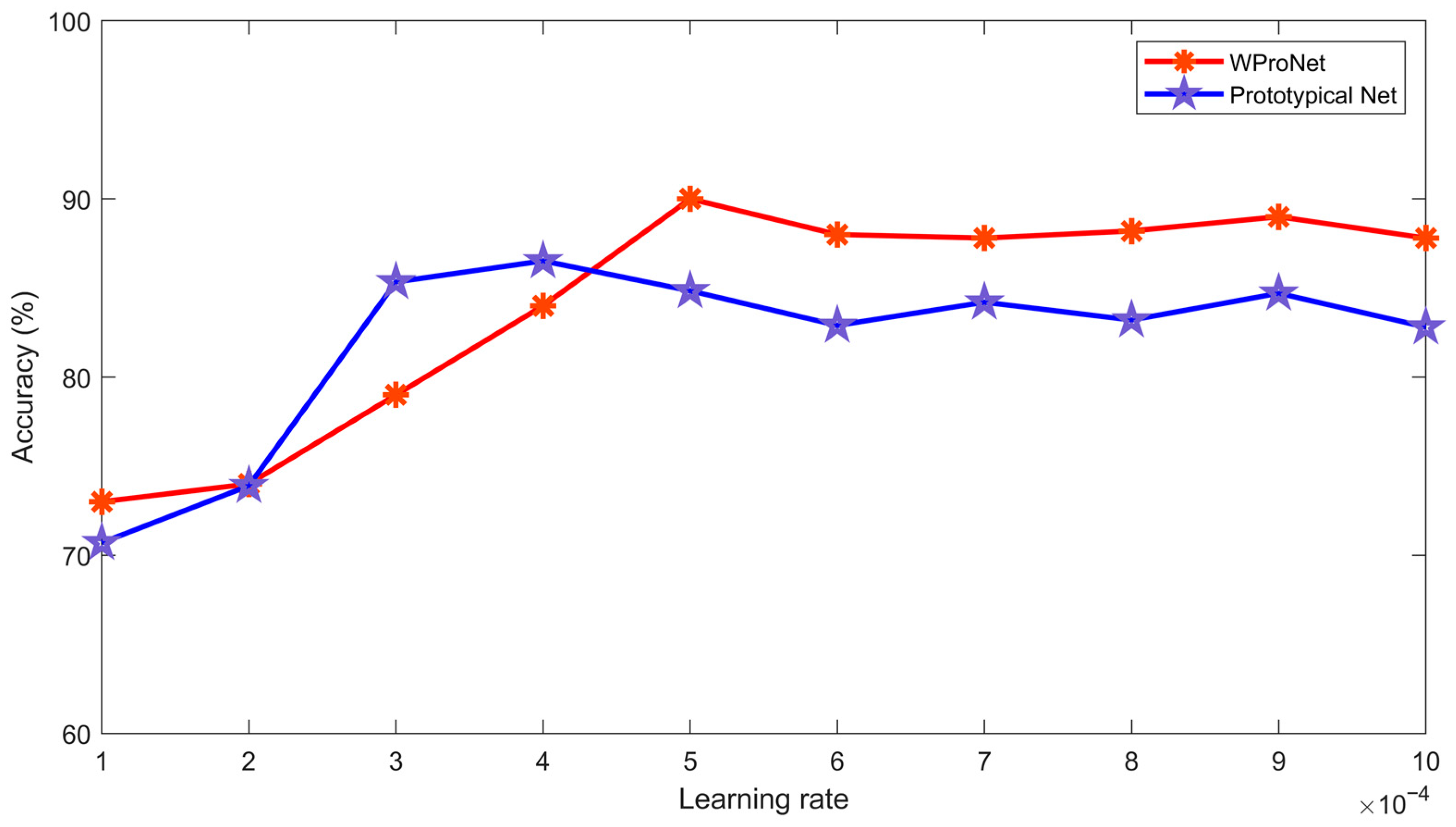
3.4.3. Training and Testing of Models
- 1.
- The model parameters and various prototypes were trained using support and query set data. During the training process, the stochastic gradient descent (SGD) method was used to optimize and adjust parameters until a better performance was achieved. The training process of the WproNet is shown in Algorithm 1.
| Algorithm 1 Training process of the WproNet |
| Input: Training Dataset Output: The trained network parameter Begin: 1: For in do: 2: 3: End For 4: For epoch to set value, do: 5: For epoch to set value, do: 6: For in do: 7: Randomly take samples from as the support set 8: Randomly take samples from as the query set 9: For in do: 10: Compute distribution changes of the samples: 11: Normalization as weight: 12: Compute prototypical of the samples: 13: End For 14: End For 15: 16: For indo: 17: For in do: 18: Update loss: 19: Update the parameter via the SGD method 20: End For 21: End For 22: End For 23: End For |
- 2.
4. Results
4.1. Comparative Experiments
- SVM [9]: The Support Vector Machine is a supervised learning algorithm for classification and regression analysis. It is a binary classification model that finds the optimal hyperplane to achieve classification. SVM can handle non-linear classification problems well;
- WDCNN [22]: Deep Convolutional Neural Networks with Wide First-layer Kernels is a traditional machine learning model based on deep convolutional neural networks (DCNNs). Its main feature is that it uses wide convolutional kernels to increase the number of features and reduce network depth. It requires a large number of samples for training;
- Matching Networks [33]: Matching Networks is a meta-learning method that uses an attention-based approach to compare input samples with samples in the support set, thus enabling rapid model adaptation.
- Prototypical network [28];
- DSN—Conv4 [38]: Discriminative Deep Subspace Networks, the backbone of which is composed of Conv4;
- PNMD [39]: Prototypical network based on the Manhattan distance.
4.1.1. Ablation Experiment
4.1.2. Training Time Analysis
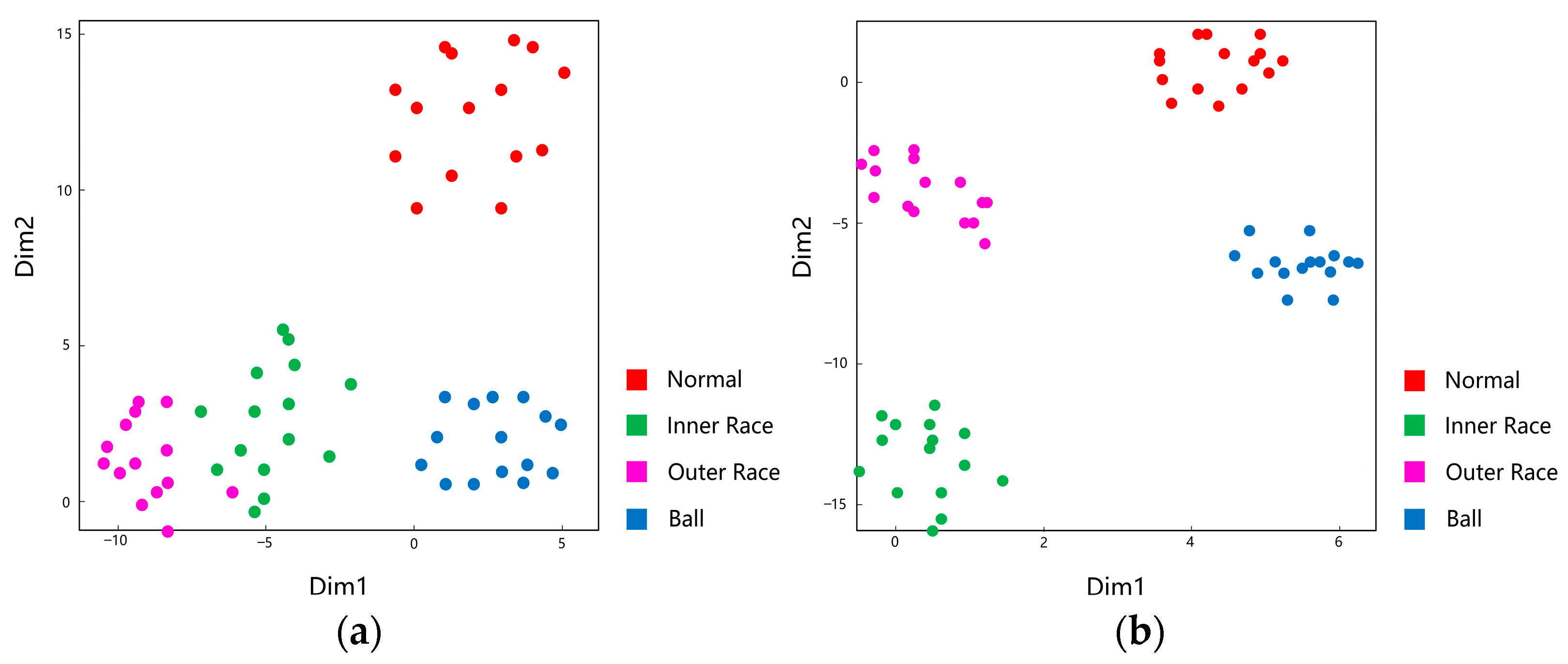
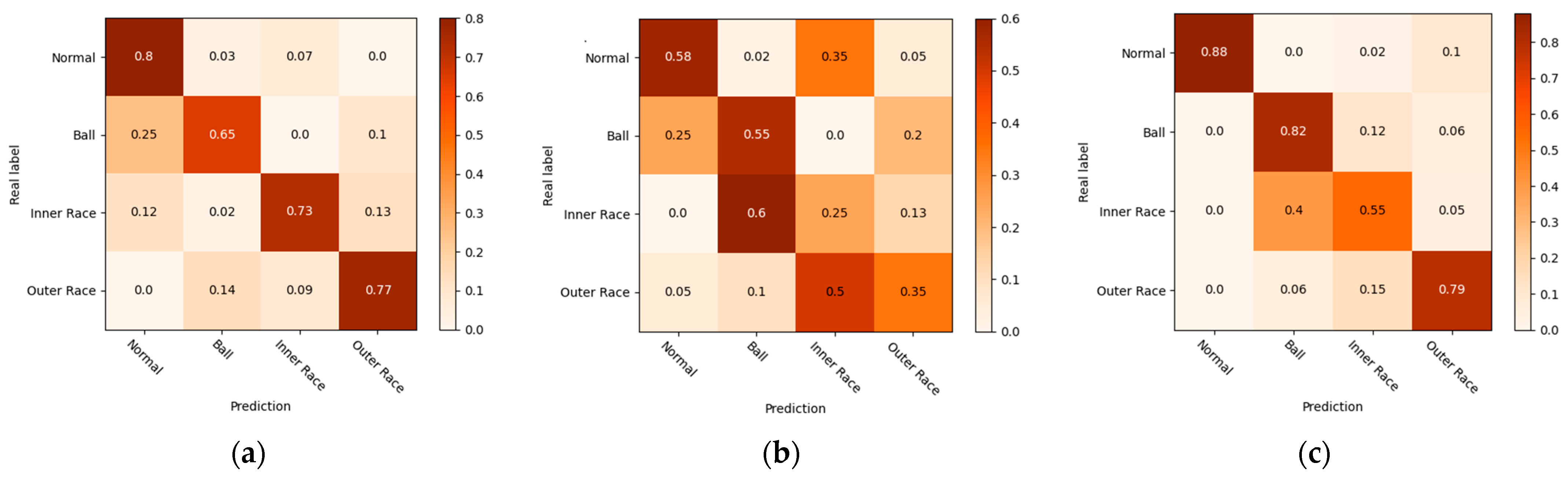
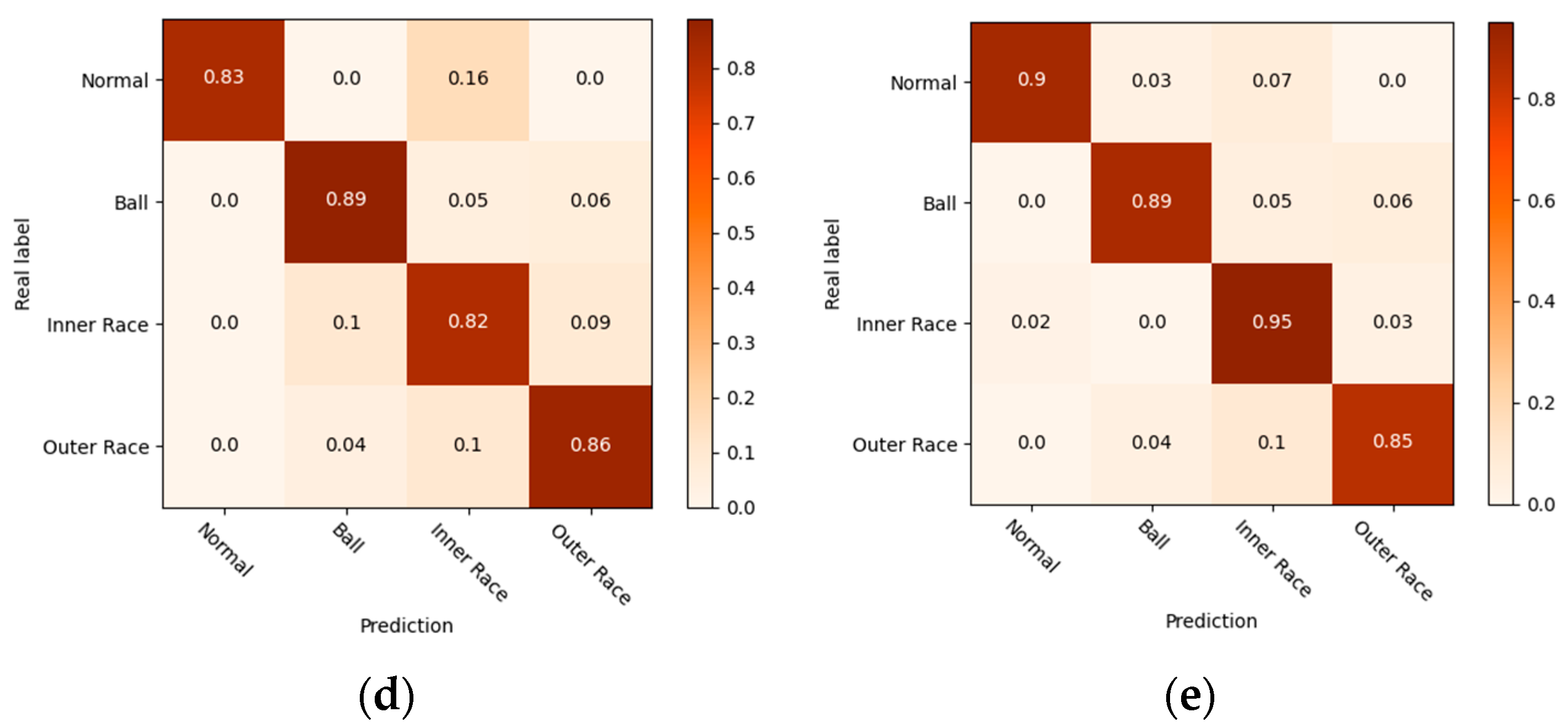
4.1.3. Visualization Analysis
4.1.4. Comparison of WProNet with Several Other Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pecht, M.G. Prognostics and Health Management of Electronics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mishra, S.; Pecht, M.; Goodman, D.L. In-situ sensors for product reliability monitoring. In Design, Test, Integration, and Packaging of MEMS/MOEMS 2002; SPIE: New York, NY, USA, 2002; Volume 4755, pp. 10–19. [Google Scholar]
- Kelkar, N.; Dasgupta, A.; Pecht, M.; Knowles, I.; Hawley, M.; Jennings, D. ‘Smart’electronic Systems for Condition-Based Health Management. Qual. Reliab. Eng. Int. 1997, 13, 3–8. [Google Scholar] [CrossRef]
- Engel, S.J.; Gilmartin, B.J.; Bongort, K.; Hess, A. Prognostics, the real issues involved with predicting life remaining. In Proceedings of the 2000 IEEE Aerospace Conference, (Cat. No. 00TH8484), Big Sky, MT, USA, 25 March 2000; Volume 6, pp. 457–469. [Google Scholar]
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: Shallow and deep learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef]
- Kirubarajan, T. Physically based diagnosis and prognosis of cracked rotor shafts. Proceedings of SPIE—The International Society for Optical Engineering; SPIE: New York, NY, USA, 2002; p. 4733. [Google Scholar]
- Shen, H.; Li, Z.; Qi, L.; Qiao, L. A method for gear fatigue life prediction considering the internal flow field of the gear pump. Mech. Syst. Signal Process. 2018, 99, 921–929. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.; Wang, L. Research on Root Strain Response Characteristics of Inner Ring of Planetary Gear Transmission System with Crack Fault. Sensors 2023, 23, 253. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Hou, J. Recent advances on SVM based fault diagnosis and process monitoring in complicated industrial processes. Neurocomputing 2016, 174, 643–650. [Google Scholar] [CrossRef]
- Zhao, W.; Shi, T.; Wang, L. Fault diagnosis and prognosis of bearing based on hidden Markov model with multi-features. Appl. Math. Nonlinear Sci. 2020, 5, 71–84. [Google Scholar] [CrossRef]
- Zhang, D.; Li, W.; Wu, X.; Lv, X. Application of simulated annealing genetic algorithm-optimized back propagation (BP) neural network in fault diagnosis. Int. J. Model. Simul. Sci. Comput. 2019, 10, 1950024. [Google Scholar] [CrossRef]
- Graves, G.; Wayne, M.; Reynolds, T.; Harley, I.; Danihelka, A.; Wayne, M.; Reynolds, T.; Harley, I.; Danihelka, A.; Grabska-Barwińska, A.P. Badia, Hybrid computing using a neural network with dynamic external memory. Nature 2016, 538, 471. [Google Scholar]
- Zbontar, J.; LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Anderson, M.A.; Burda, J.E.; Ren, Y.; Ao, Y.; O’Shea, T.M.; Kawaguchi, R.; Sofroniew, M.V. Astrocyte scar formation aids central nervous system axon regeneration. Nature 2016, 532, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Seixas, A.I.; Azevedo, M.M.; de Faria, J.P.; Fernandes, D.; Pinto, I.M.; Relvas, J.B. Evolvability of the actin cytoskeleton in oligodendrocytes during central nervous system development and aging. Cell Mol. Life Sci. 2019, 76, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Eren, L.; Ince, T.; Kiranyaz, S. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Zhou, J.; Luo, M.; Pu, S.; Yang, X. An Imbalanced Fault Diagnosis Method Based on TFFO and CNN for Rotating Machinery. Sensors 2022, 22, 8749. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Kan, J.; Luo, H. Rolling bearing fault diagnosis based on Markov transition field and residual network. Sensors 2022, 22, 3936. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef]
- Gao, Y.; Kim, C.H.; Kim, J.M. A novel hybrid deep learning method for fault diagnosis of rotating machinery based on extended WDCNN and long short-term memory. Sensors 2021, 21, 6614. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Wu, J.; Deng, C.; Jiang, W. Wide Residual Relation Network-Based Intelligent Fault Diagnosis of Rotating Machines with Small Samples. Sensors 2022, 22, 4161. [Google Scholar] [CrossRef]
- Xiao, D.; Huang, Y.; Zhao, L.; Qin, C. Domain adaptive motor fault diagnosis using deep transfer learning. IEEE Access 2019, 7, 80937–80949. [Google Scholar] [CrossRef]
- Wang, C.; Qiao, Z.; Huang, Z.; Xu, J.; Fang, S.; Zhang, C.; Liu, J.; Zhu, R.; Lai, Z. Research on a Bearing Fault Enhancement Diagnosis Method with Convolutional Neural Network Based on Adaptive Stochastic Resonance. Sensors 2022, 22, 8730. [Google Scholar] [CrossRef] [PubMed]
- Yue, K.; Li, J.; Chen, J.; Huang, R.; Li, W. Multiscale Wavelet Prototypical Network for Cross-Component Few-Shot Intelligent Fault Diagnosis. IEEE Trans. Instrum. Meas. 2022, 72, 1–11. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Zhang, A.; He, Q.; Liao, Z.; Hu, J. Meta-learning for few-shot bearing fault diagnosis under complex working conditions. Neurocomputing 2021, 439, 197–211. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical Networks for Few-shot Learning. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 4077–4087. [Google Scholar]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Nichol, A.; Achiam, J.; Schulman, J. On first-order meta-learning algorithms. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; p. 29. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.S.; Hospedales, T.H. Learning to compare: Relation network for few-shot learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1199–1208. [Google Scholar]
- Wang, Z.; Oates, T. Imaging time-series to improve classification and imputation. arXiv 2015, arXiv:1506.00327. [Google Scholar]
- Case Western Reserve University. Bearing Data Center Web-Site: Bearing Data Center Seeded Fault Test Data. Available online: https://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 27 November 2007).
- Machinery Fault Database. Available online: http://www02.smt.ufrj.br/~offshore/mfs/page_01.html (accessed on 25 May 2021).
- Simon, C.; Koniusz, P.; Nock, R.; Harandi, M. Adaptive Subspaces for Few-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 4136–4145. [Google Scholar]
- Yu, Z.; Wang, K.; Xie, S.; Zhong, Y.; Lv, Z. Prototypical Network Based on Manhattan Distance. Cmes-Comput. Model. Eng. Sci. 2022, 131, 655–675. [Google Scholar] [CrossRef]
- Maaten, L.V.D.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]



| Name | Channels | Kernel Size | Stride | Input Size | Output Size | Activation Function |
|---|---|---|---|---|---|---|
| convolutional block1 | 64 | 3 × 3 | 1 × 1 | 80 × 80 × 64 | 40 × 40 × 64 | Relu |
| convolutional block2 | 64 | 3 × 3 | 1 × 1 | 40 × 40 × 64 | 20 × 20 × 64 | Relu |
| convolutional block3 | 64 | 3 × 3 | 1 × 1 | 20 × 20 × 64 | 10 × 10 × 64 | Relu |
| convolutional block4 | 64 | 3 × 3 | 1 × 1 | 10 × 10 × 64 | 5 × 5 × 64 | Relu |
| Distribution-Prototypical Layer | / | / | / | 1600 | 1600 | Softmax |
| Parameter Type | Parameter Value |
|---|---|
| Optimizer | SGD |
| Initial learning rate | 0.0005 |
| Learning rate decay period | 2000 episodes |
| Model | 2-Way | 4-Way | ||||
|---|---|---|---|---|---|---|
| 10-Shot | 20-Shot | 50-Shot | 10-Shot | 20-Shot | 50-Shot | |
| SVM | 74.78 ± 1.59 | 77.89 ± 1.41 | 82.85 ± 1.03 | 50.67 ± 2.62 | 58.21 ± 2.87 | 74.06 ± 1.53 |
| WDCNN | 42.35 ± 2.32 | 47.12 ± 2.17 | 59.64 ± 1.52 | 33.42 ± 2.89 | 38.80 ± 2.21 | 43.71 ± 1.98 |
| Match Networks | 72.93 ± 1.39 | 74.86 ± 1.31 | 80.31 ± 0.92 | 48.56 ± 2.28 | 57.78 ± 2.49 | 77.21 ± 1.67 |
| Prototypical Networks | 85.14 ± 1.13 | 85.68 ± 0.96 | 91.87 ± 0.70 | 59.77 ± 1.71 | 67.67 ± 1.82 | 85.02 ± 1.33 |
| DSN- Conv4 | 88.39 ± 0.66 | 89.61 ± 0.53 | 95.52 ± 0.34 | 71.08 ± 0.70 | 72.36 ± 0.54 | 88.67 ± 0.30 |
| PNMD | 85.54 ± 1.61 | 85.80 ± 1.13 | 92.27 ± 0.69 | 61.37 ± 1.85 | 68.19 ± 1.35 | 87.05 ± 0.92 |
| WProNet(ours) | 90.37 ± 0.83 | 91.42 ± 0.77 | 96.24 ± 0.75 | 71.79 ± 0.91 | 78.14 ± 1.14 | 89.68 ± 0.96 |
| Model | 2-Way | 4-Way | ||||
|---|---|---|---|---|---|---|
| 10-Shot | 20-Shot | 50-Shot | 10-Shot | 20-Shot | 50-Shot | |
| SVM | 76.49 ± 1.64 | 80.16 ± 1.32 | 83.37 ± 0.88 | 51.67 ± 2.47 | 59.04 ± 2.20 | 77.43 ± 1.43 |
| WDCNN | 44.61 ± 2.09 | 46.12 ± 2.19 | 61.36 ± 1.87 | 34.12 ± 3.05 | 41.06 ± 2.51 | 47.26 ± 2.14 |
| Match Networks | 75.80 ± 1.40 | 78.20 ± 1.41 | 83.32 ± 0.85 | 50.61 ± 2.09 | 61.88 ± 1.89 | 82.64 ± 1.55 |
| Prototypical Networks | 86.02 ± 1.09 | 88.64 ± 1.05 | 93.50 ± 0.65 | 62.28 ± 1.38 | 70.07 ± 2.06 | 88.16 ± 0.83 |
| DSN- Conv4 | 89.03 ± 0.51 | 91.15 ± 0.60 | 94.76 ± 0.38 | 70.84 ± 0.40 | 77.76 ± 0.45 | 90.33 ± 0.41 |
| PNMD | 85.79 ± 0.86 | 88.31 ± 0.96 | 93.97 ± 0.59 | 62.16 ± 1.66 | 70.19 ± 1.39 | 89.25 ± 0.86 |
| WProNet(ours) | 91.70 ± 0.85 | 93.71 ± 0.70 | 96.45 ± 0.69 | 75.35 ± 1.32 | 80.73 ± 1.16 | 91.93 ± 0.94 |
| Model | 2-Way | 4-Way | ||||
|---|---|---|---|---|---|---|
| 10-Shot | 20-Shot | 50-Shot | 10-Shot | 20-Shot | 50-Shot | |
| ProNet | 85.14 ± 1.13 | 85.68 ± 0.96 | 91.87 ± 0.70 | 59.77 ± 1.71 | 67.67 ± 1.82 | 85.02 ± 1.33 |
| W+ProNet | 90.37 ± 0.83 | 91.42 ± 0.77 | 96.24 ± 0.75 | 71.79 ± 0.91 | 78.14 ± 1.14 | 89.68 ± 0.96 |
| Model | 2-Way | 4-Way | ||||
|---|---|---|---|---|---|---|
| 10-Shot | 20-Shot | 50-Shot | 10-Shot | 20-Shot | 50-Shot | |
| ProNet | 86.02 ± 1.09 | 88.64 ± 1.05 | 93.50 ± 0.65 | 62.28 ± 1.38 | 70.07 ± 2.06 | 88.16 ± 0.83 |
| W+ProNet | 91.70 ± 0.85 | 93.71 ± 0.70 | 96.45 ± 0.69 | 75.35 ± 1.32 | 80.73 ± 1.16 | 91.93 ± 0.94 |
| Model | Training Tasks | 2-Way | 4-Way | ||||
|---|---|---|---|---|---|---|---|
| 10-Shot | 20-Shot | 50-Shot | 10-Shot | 20-Shot | 50-Shot | ||
| SVM | 100,000 | 0.5 h | 0.8 h | 1.2 h | 1.3 h | 1.8 h | 2.3 h |
| WDCNN | 100,000 | 1 h | 1.3 h | 2 h | 2.6 h | 3 h | 4.3 h |
| Match Networks | 100,000 | 1.7 h | 2 h | 2.2 h | 2.5 h | 4 h | 6 h |
| Prototypical Networks | 100,000 | 1.5 h | 1.8 h | 2.4 h | 2.5 h | 3.8 h | 5 h |
| DSN-Conv4 | 100,000 | 8 h | 13 h | 19 h | 15 h | 21 h | 35 h |
| PNMD | 100,000 | 1 h | 1.2 h | 2 h | 1.5 h | 1.7 h | 2.5 h |
| WProNet(ours) | 100,000 | 2 h | 2.3 h | 3.5 h | 2.4 h | 3.3 h | 4.4 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Shen, H.; Xiong, W.; Zhang, X.; Hou, J. Method for Diagnosing Bearing Faults in Electromechanical Equipment Based on Improved Prototypical Networks. Sensors 2023, 23, 4485. https://doi.org/10.3390/s23094485
Wang Z, Shen H, Xiong W, Zhang X, Hou J. Method for Diagnosing Bearing Faults in Electromechanical Equipment Based on Improved Prototypical Networks. Sensors. 2023; 23(9):4485. https://doi.org/10.3390/s23094485
Chicago/Turabian StyleWang, Zilong, Honghai Shen, Wenzhuo Xiong, Xueming Zhang, and Jinghua Hou. 2023. "Method for Diagnosing Bearing Faults in Electromechanical Equipment Based on Improved Prototypical Networks" Sensors 23, no. 9: 4485. https://doi.org/10.3390/s23094485






