Deformed Generalization of the Semiclassical Entropy
Abstract
:1. Introduction
2. Semiclassical distribution in phase-space





3. q-deformed coherent states





 is one of the so-called Jackson’s q-exponentials introduced in 1909 [24] such that limq→1 Eq[(1 − q)x] = ex. Since Nq(|z|2) is equal to Eq[(1 − q)q|z|2] (a well defined function in 0 < q < 1), the new states are normalizable on the whole complex plane. On the other hand, the states |z〉q are always continuous in z. Finally, for the resolution of unity one needs
is one of the so-called Jackson’s q-exponentials introduced in 1909 [24] such that limq→1 Eq[(1 − q)x] = ex. Since Nq(|z|2) is equal to Eq[(1 − q)q|z|2] (a well defined function in 0 < q < 1), the new states are normalizable on the whole complex plane. On the other hand, the states |z〉q are always continuous in z. Finally, for the resolution of unity one needs


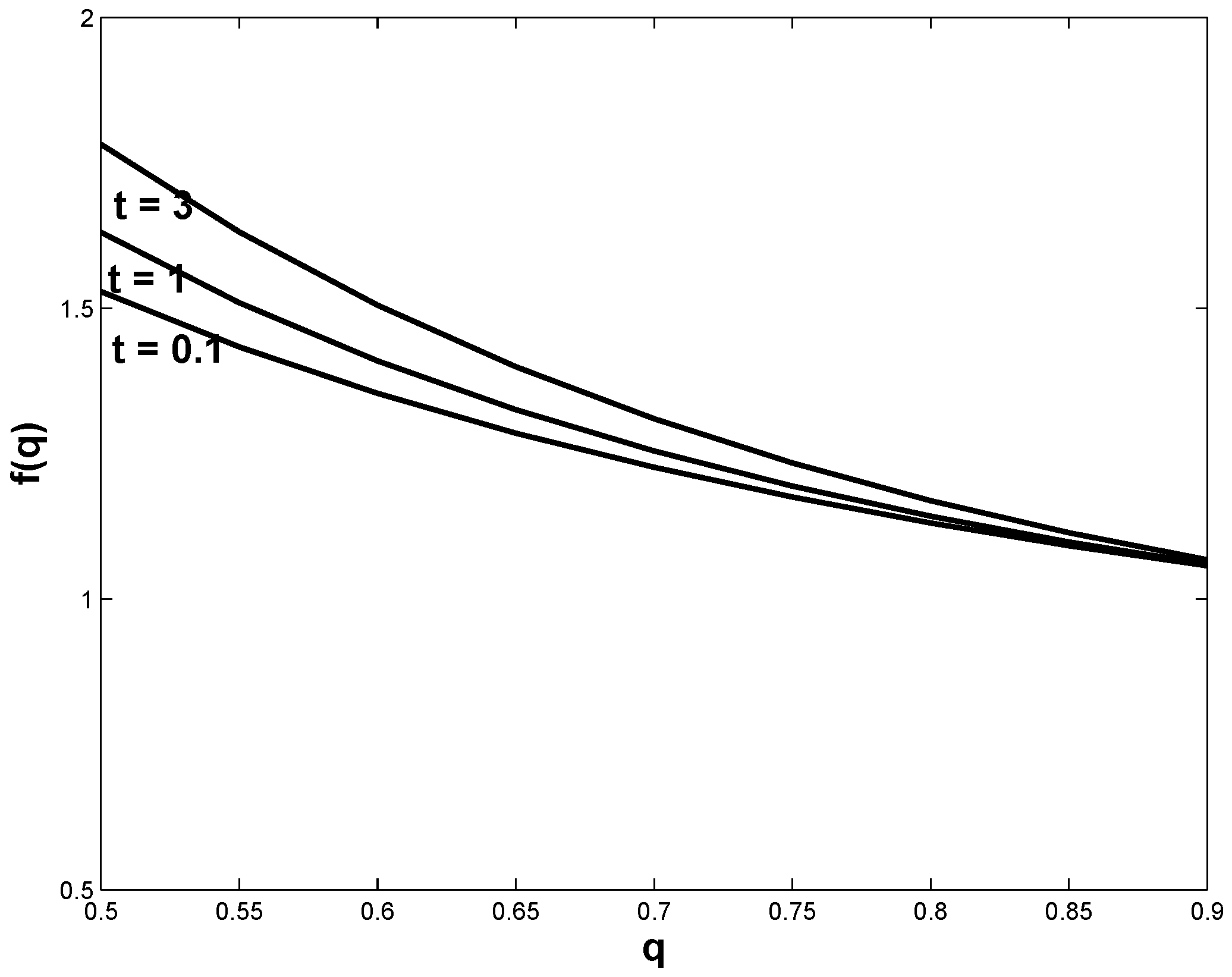
4. The q-Husimi distribution for 0 < q < 1



5. Deformed Wehrl entropies


6. q-Wehrl entropy bounds




7. Conclusions
- we have advanced a q-generalization of the Husimi distribution µq(z), which arises from the family of q-coherent states and found that the q-deformation does not change the HD’s property of being legitimate probability distributions.
- the above leads to a concomitant generalization, that we call the q-Wehrl one, Wq(µq), whose lower bound coincides with the well-known Lieb one. These semiclassical q-entropy approach the standard one when q tends to unity.
- Although in general deformed (or Tsallis’) entropies are quite different objects as compared with Shannon’s one, save for q close to unity, such is not the case for q-Wehrl entropies, which differ from the orthodox ones in just an additive quantity.
8. Acknowledgments
References
- Dimassi, M.; Sjoestrand, J. Spectral Asymptotics in the Semi-Classical Limit; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Brack, M.; Bhaduri, R. K. Semiclassical Physics; Addison-Wesle: Reading, MA, 1997. [Google Scholar]
- Gell-Mann, M.; Tsallis, C. (Eds.) Nonextensive Entropy: Interdisciplinary applications; Oxford University Press: Oxford, UK, 2004; (and references therein).
- Borges, E. P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Physica A: Stat. Mech. App. 2004, 340, 95–101. [Google Scholar] [CrossRef]
- Biedenharn, L. The quantum group SUq(2) and a q-analogue of the boson operators. J. Phys. A: Math. Gen. 1989, 22, L873–L878. [Google Scholar] [CrossRef]
- Macfarlane, A. A model of electron propagation in Zwanziger’s formulation of quantum electrodynamics. J. Phys. A: Math. Gen. 1989, 22, 4589–4598. [Google Scholar]
- Gruver, J. L. q-deformed dynamics of q-deformed oscillators. Phys. Lett. A 1999, 254, 1–6. [Google Scholar] [CrossRef]
- Boon, J. P.; Tsallis, C. Nonextensive Statistical Mechanics: New Trends, new perspectives. Europhys. News 2005, 36, 183–231. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistic. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Havrda, J.; Charvát, F. Quantification method of classification processes. Concept of structural a-entropy. Kybernetika (Prague) 1967, 3, 30–35. [Google Scholar]
- Vajda, I. Igor Axioms for a-entropy of a generalized probability scheme. Kybernetika (Prague) 1968, 4, 105. [Google Scholar]
- Daróczy, Z. Generalized information functions. Information and Control 1979, 16, 36–51. [Google Scholar] [CrossRef]
- Abe, S.; Okamoto, Y. (Eds.) Nonextensive statistical mechanics and its applications; Springer Verlag: Berlin, Germany, 2001.
- (a) Arik, M.; Coon, D. D. Hilbert spaces of analytic functions and generalized coherent states. J. Math. Phys. 1976, 17, 524–527. [Google Scholar] [CrossRef] (b) Solomon, A. I. A characteristic functional for deformed photon phenomenology. Phys. Lett. A 1994, 196, 29–34. [Google Scholar] [CrossRef] (c) Katriel, J.; Solomon, A.I. Nonideal Lasers, Nonclassical Light and Deformed Photon States. Phys. Rev. A 1994, 49, 5149–5151. [Google Scholar] [CrossRef] [PubMed] (d) Quesne, C. New q-deformed coherent states with an explicitly known resolution of unity. J. Phys. A 2002, 35, 9213–9226. [Google Scholar] [CrossRef]
- Klauder, J. R.; Skagerstam, B.-S. Coherent States, Applications in Physics and Mathematical Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Deumens, E.; Diz, A.; Longo, R.; Oehrn, Y. Time-dependent theoretical treatments of the dynamics of electrons and nuclei in molecular systems. Rev. Mod. Phys. 1994, 66, 917–983. [Google Scholar] [CrossRef]
- Davis, K. B.; Mewes, M. O.; Andrews, M. R.; van Druten, N. J.; Durfee, D. S.; Kurn, D. M.; Ketterle, W. Bose-Einstein Condensation in a Gas of Sodium Atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C. C.; Sackett, C. A.; Hulet, R. G. Bose-Einstein Condensation of Lithium: Observation of Limited Condensate Number. Phys. Rev. Lett. 1997, 78, 985–989. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Glauber, R. J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Anderson, A.; Halliwell, J. J. Information-theoretic measure of uncertainty due to quantum and thermal fluctuations. Phys. Rev. D 1993, 48, 2753–2765. [Google Scholar] [CrossRef]
- Husimi, K. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264.
- Lieb, E. H. Proof of an Entropy Conjecture of Wehrl. Commun. Math. Phys. 1978, 62, 35–41. [Google Scholar] [CrossRef]
- Jackson, F. H. On q-definite integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
© 2008 by the authors licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ferri, G.; Olivares, F.; Pennini, F.; Plastino, A.; Plastino, A.R.; Casas, M. Deformed Generalization of the Semiclassical Entropy. Entropy 2008, 10, 240-247. https://doi.org/10.3390/e10030240
Ferri G, Olivares F, Pennini F, Plastino A, Plastino AR, Casas M. Deformed Generalization of the Semiclassical Entropy. Entropy. 2008; 10(3):240-247. https://doi.org/10.3390/e10030240
Chicago/Turabian StyleFerri, Gustavo, Fernando Olivares, Flavia Pennini, Angel Plastino, Anel R. Plastino, and Montserrat Casas. 2008. "Deformed Generalization of the Semiclassical Entropy" Entropy 10, no. 3: 240-247. https://doi.org/10.3390/e10030240
APA StyleFerri, G., Olivares, F., Pennini, F., Plastino, A., Plastino, A. R., & Casas, M. (2008). Deformed Generalization of the Semiclassical Entropy. Entropy, 10(3), 240-247. https://doi.org/10.3390/e10030240


