Wavelet-Based Analysis on the Complexity of Hydrologic Series Data under Multi-Temporal Scales
Abstract
:1. Introduction
2. Methods
2.1. Wavelet Analysis
2.2. Entropy Measures
3. Results and Discussion
3.1. Data
| Type | Abbreviation | Length | Measured Place | Climatic Condition |
|---|---|---|---|---|
| Runoff | RS1 | 276 months (1978–2000) | Dashankou in the northwest of China | Inland climate |
| Runoff | RS2 | 648 months (1950–2003) | Lijin in the north of China | Temperate east-Asian monsoon climate |
| Precipitation | RS3 | 492 months (1961–2001) | Nanjing in the mid-east of China | subtropical monsoon climate |
| Temperature | RS4 | 492 months (1961–2001) | Nanjing in the mid-east of China | subtropical monsoon climate |
| Mine discharge | RS5 | 125 days (June 1 to October 3 in 2003) | Hanqiao in the mid-east of China | subtropical monsoon climate |
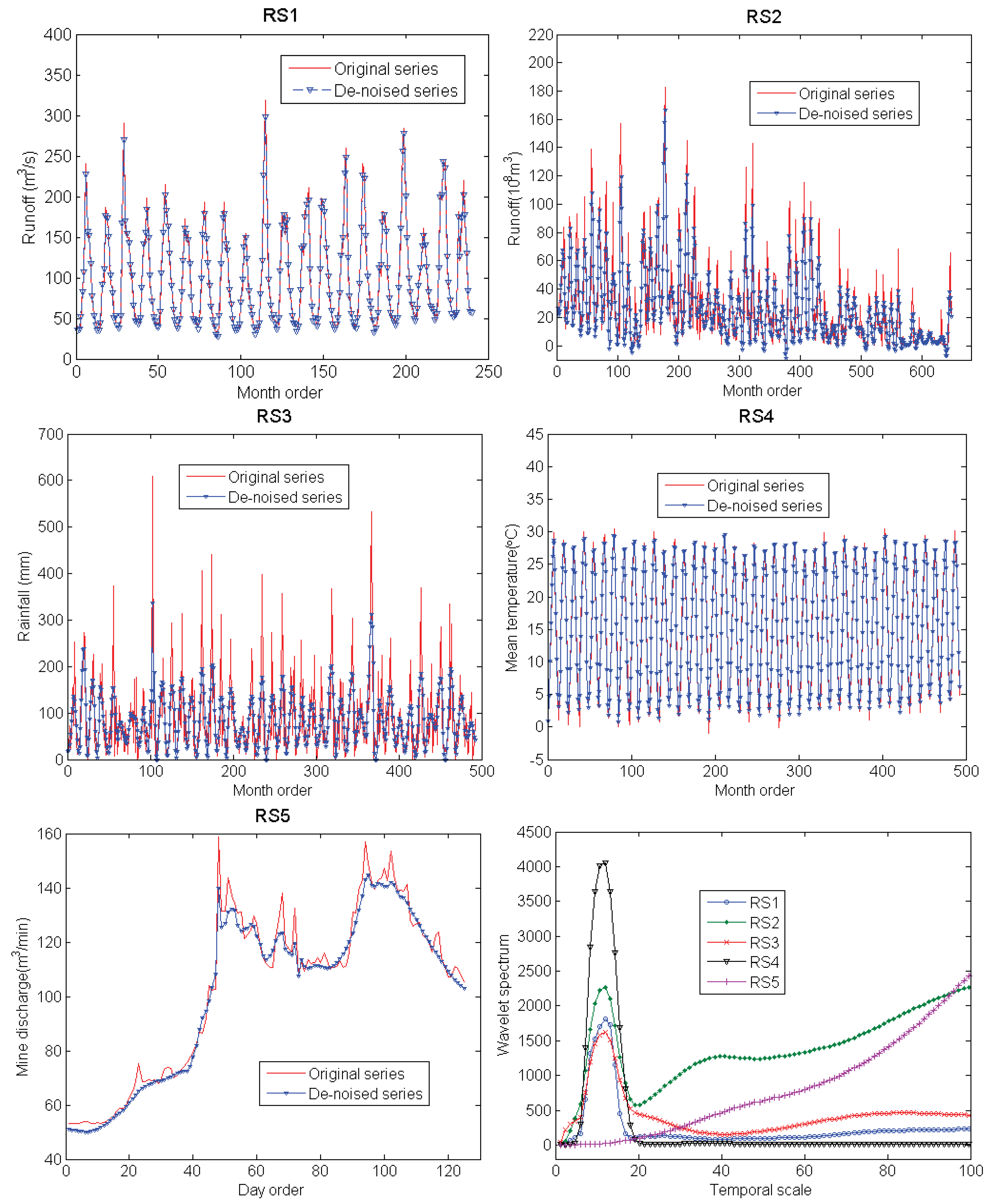
| Series | Statistical Characters* | SNR | Wavelet Used | |||
|---|---|---|---|---|---|---|
| Cv | Cs | R1 | ||||
| RS1 | 107.46 | 0.63 | 1.29 | 0.75 | 26.77 | dmey |
| RS2 | 27.05 | 1.08 | 1.91 | 0.74 | 14.80 | coif4 |
| RS3 | 86.95 | 0.93 | 2.21 | 0.29 | −0.59 | db10 |
| RS4 | 15.45 | 0.59 | −0.07 | 0.85 | 42.02 | db10 |
| RS5 | 103.50 | 0.30 | −0.32 | 0.96 | 32.84 | sym5 |
3.2. Analysis of Influence of Wavelets

3.3. Analysis of Influence of Noise
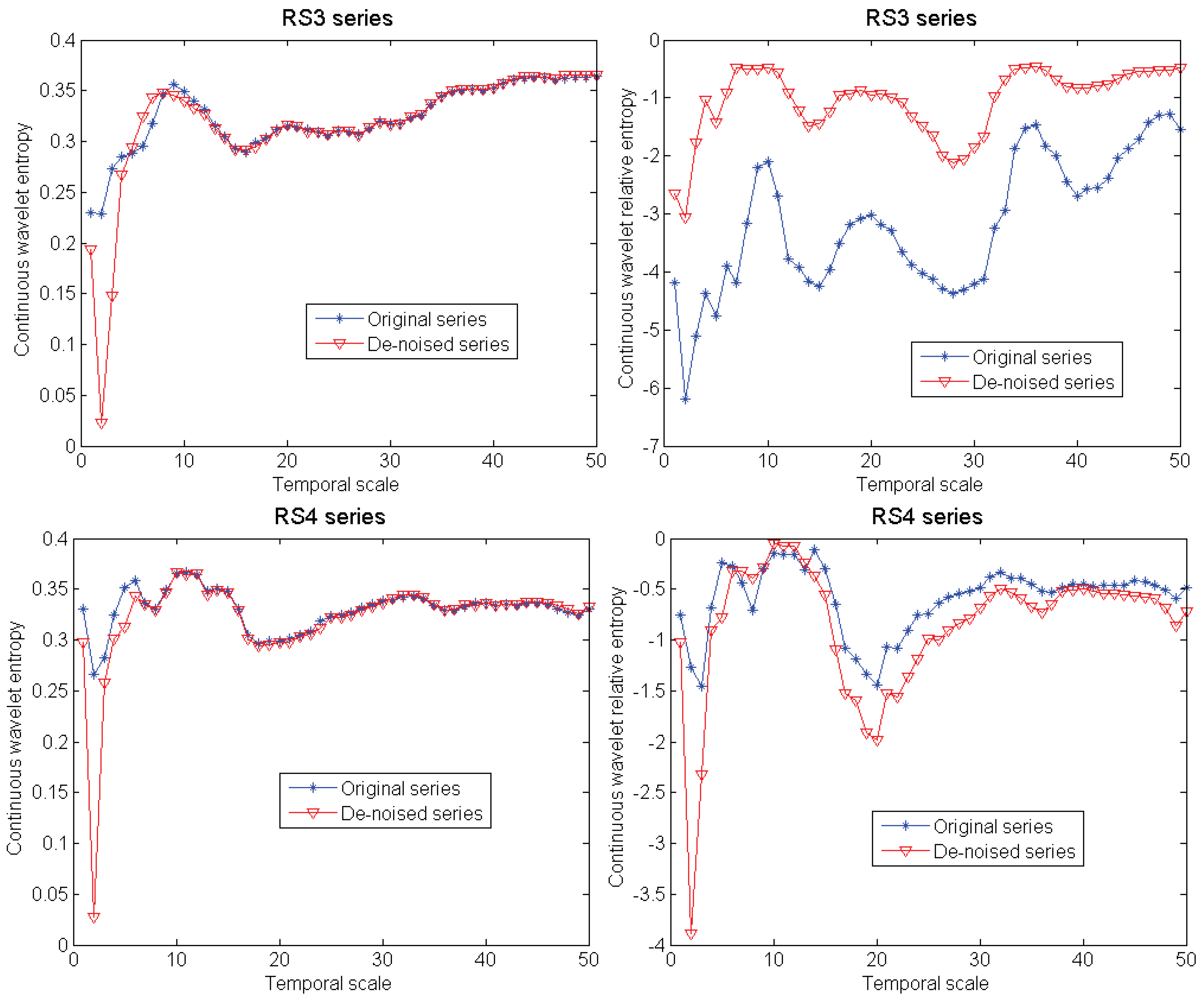
3.4. Analysis of Influence of pdf

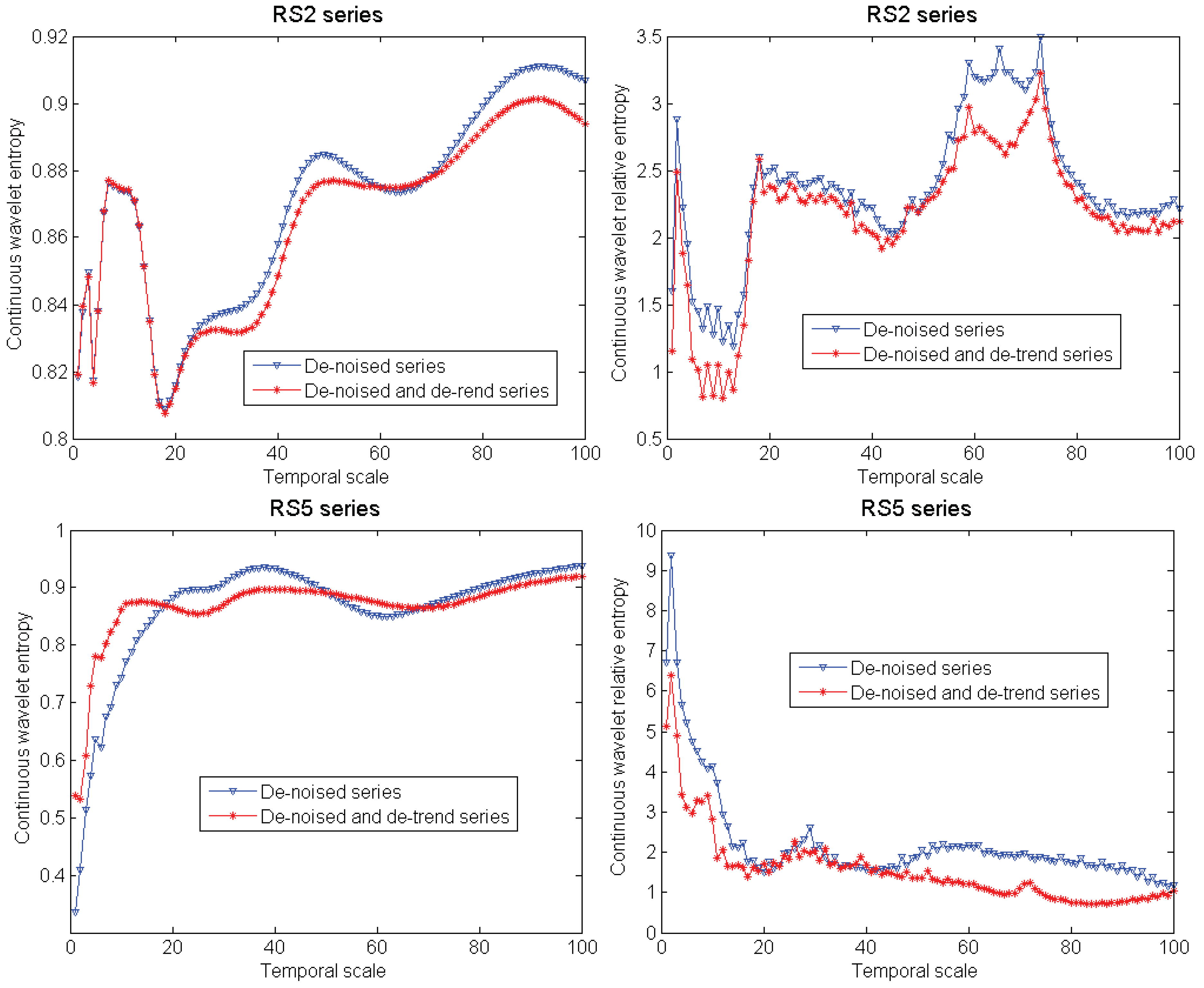
3.5. Analysis of Influence of Series’ Trend
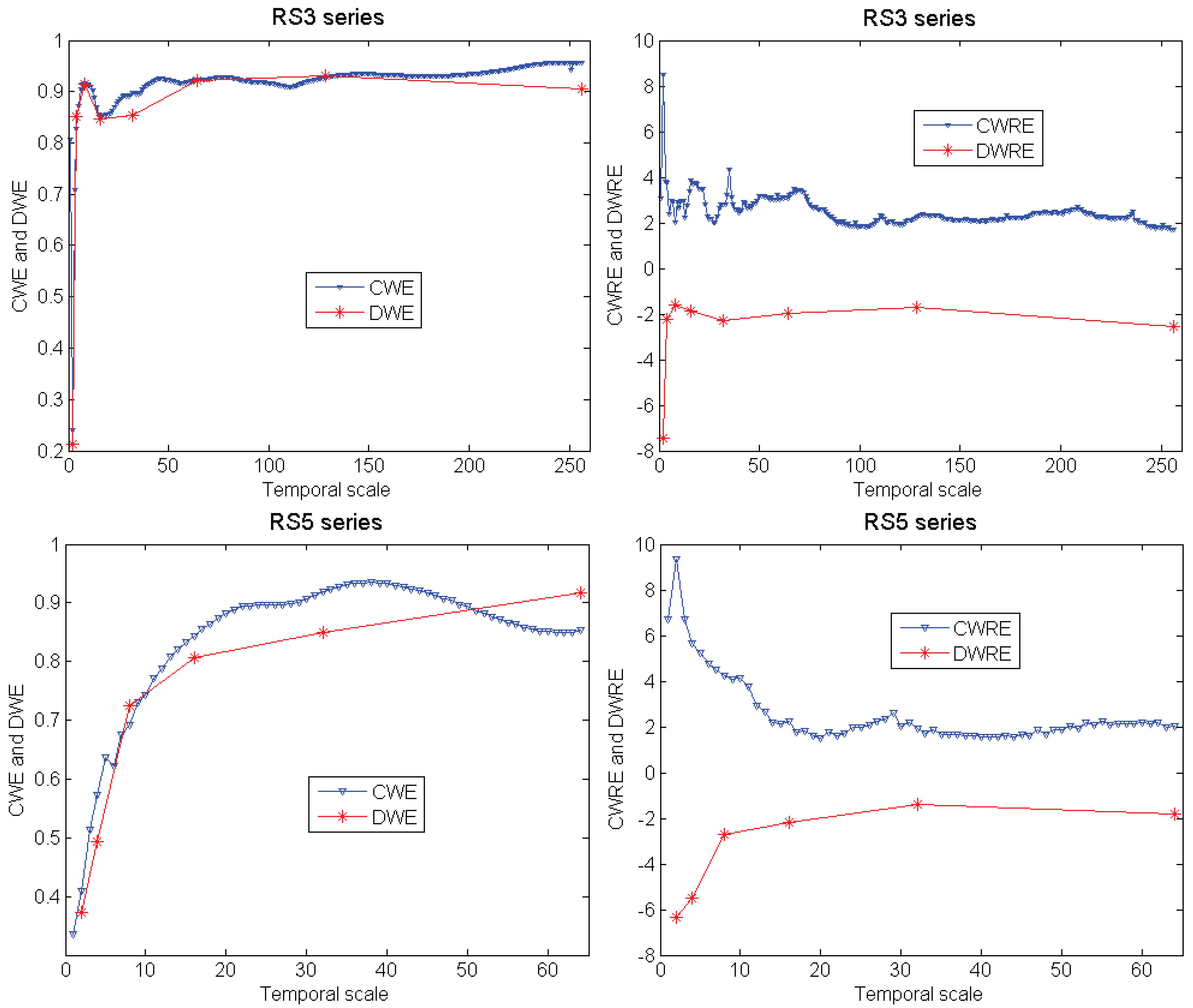
3.6. Comparison of Various Entropy Measures
4. Conclusions
- (1) Both the wavelet choice and noise have great influence on the quantification of hydrologic series’ complexity. It is suggested that the method of choosing wavelet in [26] be used in practice, because by using it both the appropriate wavelet and reliable de-noising results of hydrologic series data can be obtained.
- (2) The estimation of probability density function is a key issue influencing the calculation of entropy values. Comparatively, the Type-II pdf is recommended, because it is based on the energy distribution of series data, and by using it the complexity of hydrologic series data under multi-temporal scales can be quantified more accurately and reasonably.
- (3) The trend of hydrologic series also influences the calculation of entropy values. Therefore in the analytic process of hydrologic series’ complexity, the composition of series data, especially the trend, should be carefully taken into consideration.
- (4) Analytic results of complexity of hydrologic series data vary with the entropy measures used. It is suggested that the wavelet-based relative entropy (CWRE and DWRE) be used in practice, because it can not only subtly quantify the complexity but also reveal the characteristics and composition of hydrologic series data.
Acknowledgements
References
- Wagener, T.; Gupta, H.V. Model identification for hydrological forecasting under uncertainty. Stoch. Environ. Res. Risk Assess. 2005, 19, 378–387. [Google Scholar] [CrossRef]
- Ravines, R.R.; Schmidt, A.M.; Migon, H.S.; Renno, C.D. A joint model for rainfall-runoff: The case of Rio Grande Basin. J. Hydrol. 2008, 35, 189–200. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, D.; Wu, J.C.; Zhu, Q.P.; Wang, L. The relation between periods’ identification and noises in hydrologic series data. J. Hydrol. 2009, 368, 165–177. [Google Scholar] [CrossRef]
- Hanson, R.T.; Newhouse, M.W.; Dettinger, M.D. A methodology to assess relations between climatic variability and variations in hydrologic time series in the southwestern United States. J. Hydrol. 2004, 287, 252–269. [Google Scholar] [CrossRef]
- Boyer, C.; Chaumont, D.; Chartier, I.; Roy, A.G. Impact of climate change on the hydrology of St. Lawrence tributaries. J. Hydrol. 2010, 384, 65–83. [Google Scholar] [CrossRef]
- Jones, R.N.; Chiew, F.H.S.; Boughton, W.C.; Zhang, L. Estimating the sensitivity of mean annual runoff to climate change using selected hydrological models. Adv. Water Resour. 2006, 29, 1419–1429. [Google Scholar] [CrossRef]
- Carsten, M.; Morton, C.; Ralf, K.; Gunter, M.; Harry, V.; Frank, W. Modeling the water balance of a mesoscale catchment basin using remotely sensed land cover data. J. Hydrol. 2008, 353, 322–334. [Google Scholar]
- Labat, D. Recent advances in wavelet analyses: Part 1. A review of concepts. J. Hydrol. 2005, 314, 275–288. [Google Scholar] [CrossRef]
- Li, Z.W.; Zhang, Y.K. Multi-scale entropy analysis of Mississippi river flow. Stoch. Environ. Res. Risk Assess. 2008, 22, 507–512. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics. 1. Marginal distributional properties of hydrological processes and state scaling. Hydrol. Sci. J. 2005, 50, 381–404. [Google Scholar]
- Brunsell, N.A. A multiscale information theory approach to assess spatial-temporal variability of daily precipitation. J. Hydrol. 2010, 385, 165–172. [Google Scholar] [CrossRef]
- Wang, D.; Singh, V.P.; Zhu, Y.S. Hybrid fuzzy and optimal modeling for water quality evaluation. Water Resour. Res. 2007, 43, W05415. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Elsner, J.; Tsonis, A. Complexity and predictability of hourly precipitation. J. Atmos. Sci. 1993, 50, 400–405. [Google Scholar] [CrossRef]
- Padmanabhan, G.; Rao, A.R. Maximum entropy spectral analysis of hydrologic data. Water Resour. Res. 1988, 24, 1519–1533. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy-based Parameter Estimation in Hydrology; Kluwer Academic Publishers: Boston, MA, USA/London, UK, 1998. [Google Scholar]
- Zhang, Y.C. Complexity and 1/f noise: A phase space approach. J. Phys. I France 1991, 1, 971–977. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Amer. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Zunino, L.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. Wavelet entropy of stochastic processes. Phys. A 2007, 379, 503–512. [Google Scholar] [CrossRef]
- Emre Cek, M.; Ozgoren, M.; Acar Savaci, F. Continuous time wavelet entropy of auditory evoked potentials. Comput. Bio. Med. 2010, 40, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Molini, A.; Barbera, P.L.; Lanza, L.G. Correlation patterns and information flows in rainfall fields. J. Hydrol. 2006, 322, 89–104. [Google Scholar] [CrossRef]
- Abramov, R.; Majda, A.; Kleeman, R. Information theory and predictability for low-frequency variability. J. Atmos. Sci. 2005, 62, 65–87. [Google Scholar] [CrossRef]
- Chui, C.K. Wavelet Analysis and Its Applications. In An Introduction to Wavelets; Academic Press: Boston, MA, USA, 1992; Volume 1. [Google Scholar]
- Sang, Y.F.; Wang, D.; Wu, J.C.; Zhu, Q.P.; Wang, L. Entropy-based wavelet de-noising method for time series analysis. Entropy 2009, 11, 1123–1147. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, D.; Wu, J.C. Entropy-Based Method of Choosing the Decomposition Level in Wavelet Threshold De-noising. Entropy 2010, 6, 1499–1513. [Google Scholar] [CrossRef]
- Donoho, D.H. De-noising by soft-thresholding. IEEE Trans. Inform. Theory 1995, 41, 613–617. [Google Scholar] [CrossRef]
- Jansen, M. Minimum risk thresholds for data with heavy noise. IEEE Signal Process. Lett. 2006, 13, 296–299. [Google Scholar] [CrossRef]
- Chen, X.D.; Cao, S.L.; Wang, G.A.; Zhang, M.Q. Yellow River Hydrology; (in Chinese). The Publisher of Water Conservancy of the Yellow River: Zhengzhou, China, 1996. [Google Scholar]
- Schaefli, B.; Maraun, D.; Holschneider, M. What drives high flow events in the Swiss Alps? Recent developments in wavelet spectral analysis and their application to hydrology. Adv. Water Resour. 2007, 30, 2511–2525. [Google Scholar] [CrossRef]
- Alexander, M.E.; Baumgartner, R.; Summers, A.R.; Windischberger, C.; Klarhoefer, M.; Moser, E.; Somorjai, R.L. A wavelet-based method for improving signal-to-noise ratio and contrast in MR images. Magn. Reson. Imag. 2000, 18, 169–180. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Soulsby, C.; Tetzlaff, D.; Dawson, J.J.C.; Dunn, S.M.; Malcolm, I.A. Using long-term data sets to understand transit times in contrasting headwater catchments. J. Hydrol. 2009, 367, 237–248. [Google Scholar] [CrossRef]
- Khan, T.; Ramuhalli, P.; Zhang, W.G.; Raveendra, S.T. De-noising and regularization in generalized NAH for turbomachinery acoustic noise source reconstruction. Noise Contr. Eng. J. 2010, 58, 93–103. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, D.; Wu, J.C. Probabilistic forecast and uncertainty assessment of hydrologic design values using Bayesian theories. Hum. Ecol. Risk Assess. 2010, 16, 1184–1207. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sang, Y.-F.; Wang, D.; Wu, J.-C.; Zhu, Q.-P.; Wang, L. Wavelet-Based Analysis on the Complexity of Hydrologic Series Data under Multi-Temporal Scales. Entropy 2011, 13, 195-210. https://doi.org/10.3390/e13010195
Sang Y-F, Wang D, Wu J-C, Zhu Q-P, Wang L. Wavelet-Based Analysis on the Complexity of Hydrologic Series Data under Multi-Temporal Scales. Entropy. 2011; 13(1):195-210. https://doi.org/10.3390/e13010195
Chicago/Turabian StyleSang, Yan-Fang, Dong Wang, Ji-Chun Wu, Qing-Ping Zhu, and Ling Wang. 2011. "Wavelet-Based Analysis on the Complexity of Hydrologic Series Data under Multi-Temporal Scales" Entropy 13, no. 1: 195-210. https://doi.org/10.3390/e13010195






