Analysis of the Magnetic Field Effect on Entropy Generation at Thermosolutal Convection in a Square Cavity

Abstract

Thermosolutal convection in a square cavity filled with air and submitted to an inclined magnetic field is investigated numerically. The cavity is heated and cooled along the active walls with a mass gradient whereas the two other walls of the cavity are adiabatic and insulated. Entropy generation due to heat and mass transfer, fluid friction and magnetic effect has been determined in transient state for laminar flow by solving numerically the continuity, momentum energy and mass balance equations, using a Control Volume Finite—Element Method. The structure of the studied flows depends on four dimensionless parameters which are the Grashof number, the buoyancy ratio, the Hartman number and the inclination angle. The results show that the magnetic field parameter has a retarding effect on the flow in the cavity and this lead to a decrease of entropy generation, Temperature and concentration decrease with increasing value of the magnetic field parameter.

1. Introduction

The analysis of natural convection in enclosures has received increasing attention due to everyday practices and applications extending from the double paned windows in buildings to the cooling of electronic systems. Double-diffusion natural convection also occurs in a wide range of scientific fields such as oceanography, astrophysics, geology, biology, chemical vapor transformation processes and other fields where temperature and concentration differences are combined. Most studies on this topic are concerned with double diffusive convection in a vertical cavity, for which the flows induced by the buoyancy forces result from the imposition of both thermal and solutal boundary conditions on the vertical walls. Garandet et al. [1] proposed an analytical solution of the equations of magneto hydrodynamics that can be used to model the effect of a transverse magnetic field on buoyancy driven convection in a two-dimensional cavity. They observed that when the Hartmann number (Ha) gets high, velocity and temperature follow a Ha⁻² power law. DeVahl Davis [2] studied the two-dimensional natural convection in a square cavity with differentially heated side walls and has suggested a bench mark solution. Valencia and Frederick [3] investigated the natural convection of air in square cavities with half-active and half-insulated vertical walls numerically for various Rayleigh numbers. They observed that the heat transfer rates could be controlled, to a certain extent, by varying the relative positions of the hot and cold elements. Saravanan and Kandaswamy [4] analyzed the convection in a low Prandtl number fluid driven by the combined mechanism of buoyancy and surface tension in the presence of a uniform vertical magnetic field. They showed that the heat transfer across the cavity from the hot wall to cold wall becomes poor for a decrease in thermal conductivity in the presence of a vertical magnetic field. Deng et al. [5] studied numerically a two-dimensional, steady and laminar natural convection in a rectangular enclosure with discrete heat sources on walls. They remarked that the heat source on the floor increases the thermal instability and acts as a proportional effect on convection, while the heat source on the side wall increases the thermal stability and acts as a reverse effect on convection. Nithyadevi et al. [6] investigated the effect of aspect ratio on the natural convection of a fluid contained in a rectangular cavity with partially thermally active side walls. They found that heat transfer rate increases with increase in the aspect ratio and when the cooling location is at the top of the enclosure.

Kandaswamy et al. [7] studied the natural convection in a square cavity filled with an electrically conducting fluid with partially thermally active vertical walls, for nine different combinations of active locations in the presence of external magnetic field parallel to gravity. They found that the heat transfer rate is enhanced in the middle thermally active locations, while it is poor for the top-bottom case. The average Nusselt number increases with increase of Grashof number, but decreases with increase in Hartmann number. As the strength of the magnetic field increases (Ha = 100), convection is completely suppressed and the heat transfer in the cavity is mostly due to conduction mode. The rate of flow also decreases for increase in Hartmann number in all different active positions. Increase in Prandtl number leads to increase in the average Nusselt number. Hossain et al. [8] numerically investigated buoyancy and thermo capillary driven convection of an electrically conducting fluid in an enclosure with internal heat generation. They found that the increase in the value of heat generation causes the development of more cells inside the cavity. A numerical study of unsteady two dimensional natural convection of an electrically conducting fluid in a laterally and volumetrically heated square cavity under the influence of a magnetic field is investigated by Sarris and al. [9]. They showed that the heat transfer is enhanced with increasing internal heat generation parameter, but no significant effect of the magnetic field is observed due to the small range of the Hartmann number. Chenoweth and Paolucci. [10], Vierendeels et al. [11], Sivasankaran and Ho [12] and Nishimura et al. [13] studied this topic. Chamkha, Al-Naser and Sathiyamoorthy [14,15,16,17] numerically studied the hydromagnetic double-diffusive convection in a rectangular enclosure with opposing temperature and concentration gradients. A magnetic field and heat generation are imposed. Results showed that the magnetic field reduces the heat transfer and fluid circulation within the enclosure. Also, they concluded that the average Nusselt number increases owing to the presence of a heat sink while it decreases when a heat source is present. They reported that the periodic oscillatory behavior in the stream function inherent in the problem was decayed by the presence of the magnetic field. This decay in the transient oscillatory behavior was speeded up by the presence of a heat source. They found that the heat and mass transfer mechanisms and the flow characteristics inside the enclosure depended strongly on the strength of the magnetic field and heat generation or absorption effects. The effect of the magnetic field was found to reduce the heat transfer and fluid circulation within the enclosure. In addition, they concluded that the average Nusselt number was increased owing to the presence of a heat sink while it was decreased when a heat source was present. For the case of linearly heated left wall with cooled right wall, a two-cell (one primary and one secondary) feature was predicted. In general, the application of the magnetic field reduces the convective heat transfer rate in the cavity for any inclined angle. In addition, the local Nusselt number at the bottom wall of the cavity exhibited oscillatory behavior along the horizontal distance for the case of linearly heated side walls whereas it increased continuously for the case of linearly heated left wall and cooled right wall with the exception of large Hartmann numbers for a vertically-applied magnetic field. A numerical investigation of the steady of magneto-hydrodynamics free convection in a rectangular cavity has been studied by Grosan et al. [18] and Ralph and Ulrich [19]. They observed that the effect of the magnetic field is to reduce the convective heat transfer inside the cavity, the convection modes within the cavity were found to depend upon both the strength and the inclination of the magnetic field. The applied magnetic field in the horizontal direction was found to be most effective in suppressing the convection flow for a stronger magnetic field in comparison with the vertical direction. The flat isotherms in the core region indicated that there is negligible lateral heat conduction and the equal spacing of the streamlines implies a uniform vertical velocity in this region, and the magnetic field has a negligible effect on the heat transfer mechanism for small values of the inclination angle and Hartmann number (Ha) widely superior than unity. This is true since pure conduction becomes dominant when the magnetic field is applied in the horizontal direction. However, for Ra = 10⁵ the parabolic profile is destroyed. For Rayleigh number, Ra = 10³, and small Hartmann numbers, the flow and heat transfer are characterized by a parallel flow structure in the central region of the cavity. The conduction is the dominant mode of heat transfer and vertical velocity profiles and temperatures are almost parabolic. The number of convection rolls depends on the Rayleigh and the Hartmann numbers. The resulting Lorentz forces and their braking effect explain the seemingly strange shape of the velocity profiles with excessive intensities in regions near the corners. Unsteady double-diffusive magneto convection of water in an enclosure with Soret and Dufour effects around the density maximum has been numerically investigated by Nithyadevi and Yang [20]. They observed that the density inversion leaves strong effects on fluid flow, heat and mass transfer due to the formation of bi-cellular structure. The formation of dual cell structure and strength of each cell is always dependent on the density inversion parameter, thermal Rayleigh and Hartmann numbers. The heat and mass transfer rates decrease with an increase of Hartmann number. The heat and mass transfer rates are found to increase with increasing thermal Rayleigh number. The heat transfer rate increases and mass transfer rate decreases when the density inversion parameter increases in the presence of Soret and the absence of Dufour parameters. Hakan et al. [21] found in their numerical analysis that heat transfer increases with increasing amplitude of sinusoidal function and decreases with increasing of Hartmann number. However, heat transfer also increases with the increasing of Rayleigh number. Hartmann number can be a control parameter for heat transfer and flow field.

The irreversibility phenomena which are expressed by entropy generation are of important interest during the design of any thermodynamic system. Many studies concerning entropy generation have been carried out. However, the entropy generation during the double diffusive convection in enclosed cavities submitted to a magnetic field has not received much attention. Numerical analyses of entropy generation in rectangular cavities were done by Rejane et al. [22], Gamze et al. [23] and Achintya [24]. The total entropy generation in steady state linearly increases in both cases, the aspect ratio and the irreversibility coefficient, and exponentially with the Rayleigh number. The influence of the aspect ratio on Bejan number is proportional to Rayleigh number and inversely proportional to the irreversibility coefficient for the same aspect ratio. Entropy generation due to viscous effects increases with the Rayleigh number and, for a certain Rayleigh number, entropy generation due to viscous effects also increases with the aspect ratio. Entropy generation in rectangular cavities with the same area but for different aspect ratios is numerically investigated. It was found that heat transfer and fluid friction irreversibilities varied considerably with aspect ratio. For cavities with low values of Rayleigh number (i.e., Ra = 10²) and irreversibility coefficient (i.e., φ = 10⁻⁴), the heat transfer irreversibility is strongly dominant and the total entropy generation increases with the increase of the aspect ratio. For cavities with high Ra values (i.e., Ra = 10⁵) and φ = 10⁻⁴, fluid friction irreversibility is dominant and total entropy generation increases with the aspect ratio, reaches a maximum, then decreases. A peak point for the maximum total entropy generation exists. For irreversibility coefficient, φ = 10⁻², the magnitudes of fluid friction irreversibilities are considerably greater than for those for φ = 10⁻⁴. Hence, the fluid friction entropy generation for a cavity with φ = 10⁻² is more dominant compared to that for φ = 10⁻⁴. Similar peak points for the total entropy generation are also observed for a cavity with φ = 10⁻². The average Bejan number is a proper criterion to predict the domination of heat transfer or fluid friction irreversibilities for the entire domain. The total entropy generation in a cavity increases with Rayleigh number, however, the rate of increase depends on the aspect ratio. For the same Rayleigh number, the total entropy generation for a tall cavity may be less than that for a shorter one. The dominant contribution to entropy generation came from heat transfer irreversibilities, with fluid friction accounting for only a small fraction of the total entropy generation. Entropy generation in convective heat and mass transfer through an inclined enclosure is numerically investigated by Magherbi et al. [25]. They showed that entropy generation increases with the thermal Grashof number and the buoyancy ratio for moderate Lewis number. At local level, irreversibility due to heat and mass transfer are nearly identical and are localized in the bottom heated and the top cooled walls of the enclosure. The inclination angle of the cavity has more effect on entropy generation for thermal Grashof number Gr_t ≥ 10⁴. In this case, irreversibility increases towards a maximum value obtained for α = 45°, then decreases and tends towards unity value for inclination angle α ≈ 180°. The influence of an oriented magnetic field on entropy generation in natural convection flow for air and liquid gallium is numerically studied by Eljery et al. [26], they showed that transient entropy generation exhibits oscillatory behavior for air when Gr_t ≥ 10⁴ at small values of Hartmann number. Asymptotic behavior is obtained for considerable values of Hartmann number. A transient irreversibility always exhibits asymptotic behavior for liquid gallium. They also showed that heat transfer rate is always described by pure conduction mode for liquid gallium, whereas it presents oscillatory behavior for air Gr_t ≥ 10⁴. Local irreversibility is strongly dependent on magnetic field direction, magnitude of irreversibility lines increases up to 30°, and then gradually decreases.

Recent studies on entropy generation analysis [27,28,29,30,31,32,33,34,35] reveal new methods for reducing computational cost and in which entropy generation due heat/mass transfer is analyzed. Chen et al. [27] introduced a simple lattice Boltzmann model to investigate convectional phenomena at higher Rayleigh number up to 10⁷.They obtained that the flow is primarily dominated by thermal buoyancy effects, whereas for N > 1, the flow is mainly dominated by compositional buoyancy effects. The average Nusselt number Nu and the average Sherwood number Sh at the inner wall both are monotonic increasing functions of aspect ratio for N > 1. Compositional convection in a rotating annulus with opposing temperature and concentration gradients is investigated by [28]. Results show that the flow will keep steady even with very high frequency rotation. But for Ra_T = 10⁶, the flow will become unsteady either when the ratio of buoyancy forces approaches to unity or when rotation frequency increases. A new LB-based entropy generation analysis algorithm is developed for complex systems [29,30]. Firstly, important features of entropy generation in a vertically concentric annular space are revealed: when Pr and curvature ratio are equal to unity, the time-averaged total entropy generation number is a monotonic increasing function of Ra, and there is an approximate linear relationship between the logarithm of S_total and Ra. But the time-volume-averaged Bejan number has an inverse trend. The entropy intensely generates within two layers along the vertical walls. The differences between these two layers become being erased with curvature ratio increasing and they are point symmetric with respect to the geometric center of the cavity when this parameter is sufficiently big. The variations of total entropy generation and time-volume-averaged Bejan numbers with curvature ratio are slight, and they approach asymptotically to the values of their planar counterparts. The maximum of entropy generation number will jump from the inner wall to the outer wall with Ra and curvature ratio increasing. The total entropy generation number and average Bejan number both increase monotonously with Pr. Entropy generation inside disk driven rotating convectional flow is secondly investigated. The situation becomes complex when the influences of rotating of the disk and the buoyancy force both should be considered. The variations of the total entropy generation number and Bejan number depend on the detailed combination of Reynolds and Grashof numbers. Entropy generation due to heat/mass transfer of turbulent natural convection due to internal heat generation in a cavity is studied by [31]. It was found that the time-volume averaged Bejan number almost equals one and then decreases quickly against Ra increasing. Though the maximum of entropy generation number increases quickly with Ra, the time-averaged total entropy generation number changes in the opposite trend.

Results showed that for increasing Rayleigh number viscous irreversibility begins to dominate heat transfer irreversibility. Entropy generation is spread over the whole domain at small Rayleigh numbers, but is confined to the neighborhood of the boundaries at high Rayleigh numbers. The numerical results also showed the time-volume-averaged Bejan number, the time-averaged total entropy generation number and the maximum of entropy generation number decrease quickly against Pr increasing. In [32,33], entropy generation in multi-components flow with combustion are analyzed. Entropy generation in counter-flow premixed

Hydrogen-air flames confined by planar opposing jets are investigated for the first time. Results revealed that the contribution of viscous effect on entropy generation cannot be ignored, while the contribution of mass transfer is negligible; the relative total entropy generation rates are nearly insensitive to the change of equivalence ratio; the order of the relative total entropy generation rates changes significantly depending on the inlet Reynolds number. As Re < 60 entropy generation due to chemical reaction is predominant. However, when Re > 100 the largest share of entropy generation comes from fluid friction. The whole domain can be divided into two parts according to predominant irreversibilities: Zone I and II. Zone I is dominated by irreversibility due to chemical reaction, heat transfer and mass transfer while in Zone II it is predominated by irreversibility due to mass transfer and fluid friction. The relationship among the total entropy generation number S_total, the inlet Reynolds number Re and the equivalence ratio can be approximated as a linear increasing function. For the second time, entropy generation in hydrogen-enriched ultra-lean counter-flow methane-air non-premixed combustion confined is analyzed. Entropy generation in this kind of combustion is different from that reported in previous case: despite the fact that the whole domain can be divided into two parts similar to premixed case, the area of Zone I is expanded with equivalence ratio increasing, which is contrary to its premixed counterpart. In this kind of combustion, with more fuel mixture being injected into the combustion, the share of irreversibility due to mixing is reduced while that due to heat transfer increases, which is fully contrary to its premixed counterpart. However, with more H₂ being added into the fuel blends of this kind of non-premixed combustion, the share of irreversibility due to heat transfer is reduced while that, due to mixing increases, which is consistent with its premixed counterpart and is quite different from the co-flow non-premixed combustion.

Entropy generation due to heat/mass transfer during transient state in micro-systems is discussed for the micro-Couette flow by [34]. Results show that the total entropy generation has a maximum value at the onset of transient state, which is a monotonically decreasing function of Knudsen number but depends non-monotonously on Prandtl and Eckert numbers. The same scene emerges for the volume-averaged Bejan number. The maximum appears when the front of the disturbance induced by the top moving wall arrives at the bottom wall. The entropy generation at the bottom usually is higher than that at the top wall. In steady state, the location where the extremum of the volumetric entropy generation number emerges depends on Prandtl and Eckert numbers. The Bejan number is mainly dominated by Eckert number. Less entropy generates within more rarefied flow. Chen and Du [35] investigated the entropy generation of turbulent double-diffusive natural convection in a rectangle cavity. They obtained that The total entropy generation number (S_total) increases with Ra, and the relative total entropy generation rates are nearly insensitive to Ra when Ra ≤ 10⁹; Since N > 1, S_total increases quickly and linearly with N and the relative total entropy generation rate due to diffusive irreversibility becomes the dominant irreversibility; S_total increases nearly linearly with aspect ratio. The relative total entropy generation rate due to diffusive and thermal irreversibilities both are monotonic decreasing functions against aspect ratio while that due to viscous irreversibility is a monotonic increasing function with aspect ratio.

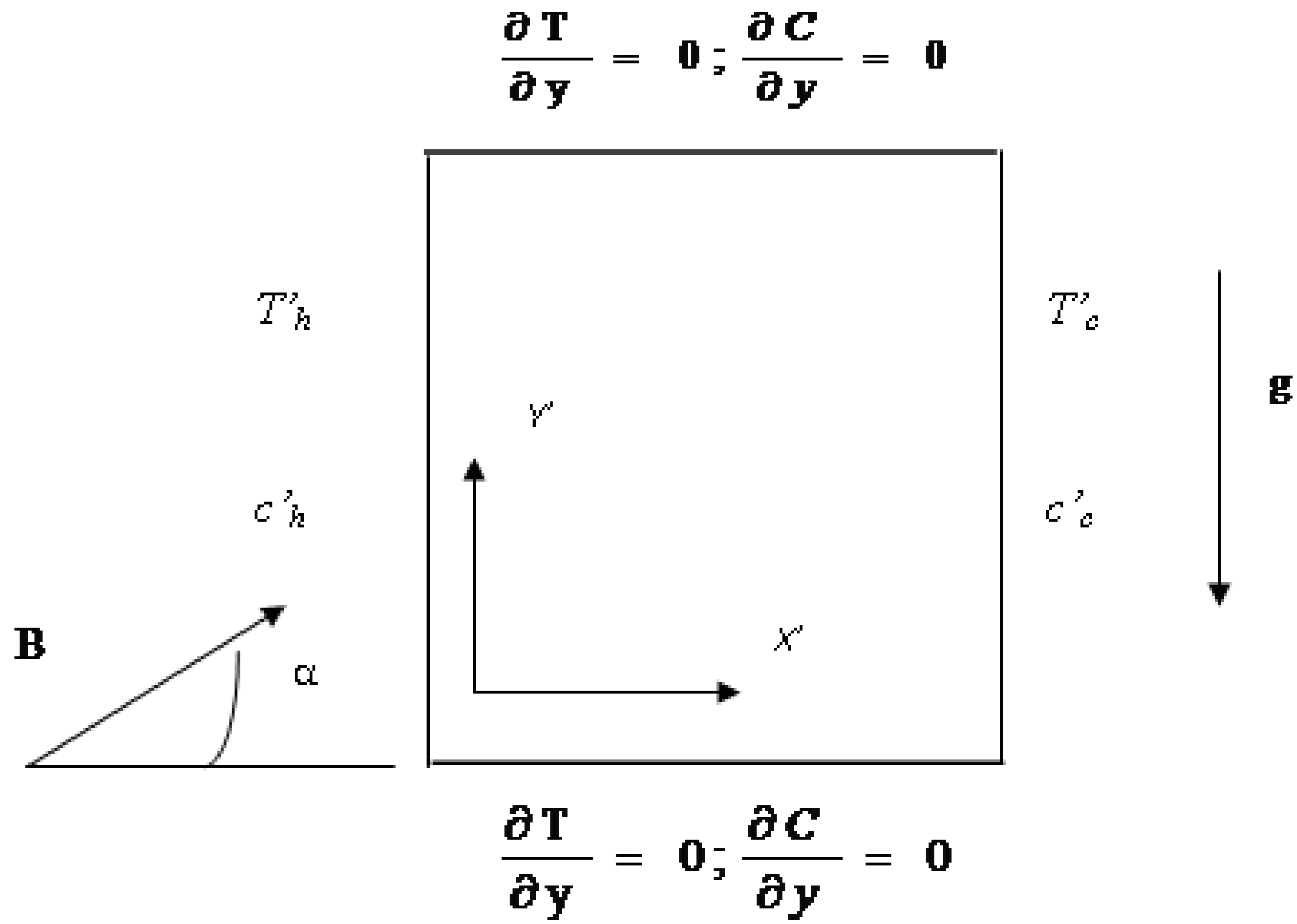
The aim of the present study is to examine the influence of a magnetic field on entropy generation in convective heat and mass transfer for the case of a binary gas mixture with a single diffusive species in a square cavity. The numerical resolution is based on control volume finite-element method for resolving the governing equations in 2D approximation. Entropy generation in double diffusive convection in presence of an oriented magnetic field is firstly derived. Local and total irreversibilities are then studied by using four dimensionless independent variables which are: The Grashof number, the buoyancy ratio, the Hartmann number and the inclination angle of the magnetic field.

2. Governing Equations

Let us consider a 2D square cavity submitted to an oriented magnetic field, $\overrightarrow{\text{B}}$ with an inclination angle, α as shown in Figure 1.

Figure 1. Schematic view of the physical model.

Figure 1. Schematic view of the physical model.

The two active left and right walls are at different but uniform temperatures and concentrations (T’_h, C’_h) and (T’_c, C’_c), respectively while the two other walls are insulated and adiabatic. The fluid, is considered mixture (air and a gas diffusing species) as a Newtonian, Boussinesq incompressible fluid, their properties are described by its kinematic viscosity ν, its thermal and solutal diffusivities, α_T and D, respectively and its thermal and solutal volumetric expansion coefficients β_T and β_c respectively. The mass density of the fluid is considered to vary linearly with temperature and concentration such as:

ρ = ρ_o [1 − β_T (T − T_o) − β_c (C − C_o)]

(1)

where:

$${\beta }_T=-\frac{1}{{\rho }_o}{\left(\frac{\partial \rho }{\partial T}\right)}_P$$

(2)

$${\beta }_C=-\frac{1}{{\rho }_o}{\left(\frac{\partial \rho }{\partial C}\right)}_P$$

(3)

The set of the dimensionless governing equations is, given by:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(4)

$$\frac{\partial u}{\partial t}+div{J}_u=-\frac{\partial P}{\partial x}+\mathrm{Pr}\cdot H{a}^2(v\cos \alpha -u\sin \alpha )\sin \alpha$$

(5)

$$\frac{\partial v}{\partial t}+div{J}_v=-\frac{\partial P}{\partial y}+Gr(T+NC)+\mathrm{Pr}\cdot H{a}^2(u\sin \alpha -v\cos \alpha )\cos \alpha$$

(6)

$$\frac{\partial T}{\partial t}+div{J}_T=0$$

(7)

$$\frac{\partial C}{\partial t}+div{J}_C=0$$

(8)

with:

$$\begin{gathered} J_u=u\cdot V-\mathrm{Pr}gradu \\ {J}_T=T\cdot V-gradT \\ {J}_C=C\cdot V-(\frac{1}{Le})gradC \end{gathered}$$

(9)

where the dimensionless variables are defined by:

$$\begin{gathered} x=\frac{x^{\prime }}{L};y=\frac{y^{\prime }}{L};u=\frac{u^{\prime }}{U^{\ast }};v=\frac{v^{\prime }}{U^{\ast }};t=\frac{t^{\prime }{U}^{*}}{L};p=\frac{p^{\prime }}{{\rho }_0{U}^{{*}^2}};T=\frac{T^{\prime }-T^{\prime }0}{\Delta T};C=\frac{C^{\prime }-C^{\prime }0}{\Delta C} \\ {U}^{\ast }=\frac{\alpha }{L};\mathrm{Pr}=\frac{\nu }{\alpha }; \Delta \mathrm{T’} ={\mathrm{T’}}_{\text{h}}-{\mathrm{T’}}_{\text{c}}; \Delta \mathrm{C’} ={\mathrm{C’}}_{\text{h}}-{\mathrm{C’}}_{\text{c}} \\ \begin{array}{l}G{r}_t=\frac{g{\beta }_T\cdot \Delta T\cdot L^3}{\nu ²};G{r}_c=\frac{g{\beta }_C\cdot \Delta C\cdot L^3}{\nu ²},N=\frac{G{r}_c}{G{r}_t};\lambda =\rho {\alpha }_{T}Cp\\ Ha²=\frac{{\sigma }_{e}B²L²}{\mu };\mathrm{Pr}=\frac{v}{{\alpha }_T};Le=\frac{{\alpha }_T}{D}\end{array} \end{gathered}$$

(10)

The appropriate initial and boundary conditions to the laminar flow within the cavity are:

at, t = 0 for whole space:

u = v = 0; P = 0; C = 0.5 − x and T = 0.5 − x

(11)

Adiabatic walls:

$$\frac{\partial \phi }{\partial y}=0 \text{at y}=0 \text{and y}=1$$

(12)

Active walls:

$$\begin{array}{c}\phi =0.5 \text{at x}=0\\ \phi =-0.5 \text{at x}=1\end{array}$$

(13)

where $\phi$ is a physical parameter representing temperature or concentration

3. Formulation

The existence of thermal and diffusive gradients between the active walls of the cavity, in addition to magnetic field effects, set the fluid in a non-equilibrium state which causes entropy generation in the system. According to local thermodynamic equilibrium with linear transport theory, the local entropy generation is given by [38]:

$${\dot{S}}_{gen}=\frac{\lambda {\left(gradT\prime \right)}^2}{T{\prime }^2}-\frac{1}{T\prime }{\displaystyle \sum _i{J}_{\alpha \prime i}grad{\mu }_i}+\frac{\overline{\overline{\tau }}:\overline{\overline{grad}}V}{T\prime }+{\frac{{\sigma }_e\left|V\times B\right|}{T\prime }}^2$$

(14)

$J_{\alpha \prime i}$ and ${\mu }_i$ are mass diffusion flux of species i in phase α’ and its chemical potential, respectively. As it can be seen from Equation (14), the right hand side this equation represents four terms which are: Irreversibility due to heat transfer, the second is due to mass transfer, the third is due to fluid friction and the fourth is due to magnetic force.

For a two dimensional flow and by assuming bulk concentration (C’₀) and temperature (T’₀) in the denominator of Equation (14) with a single diffusing species, Equation (14) can therefore be written as follows:

$$\begin{array}{l}{\dot{S}}_{gen}=\frac{\lambda }{{T_0}^{\prime 2}}{(gradT\prime )}^2+\frac{RD}{C_0^{\prime }}{(gradC\prime )}^2+\frac{RD}{{{\mathrm{{\rm T}}}^{\prime }}_o}\left[\left(gradC\prime \right)\cdot \left(gradT\prime \right)\right]\\ +\frac{\mu }{T_0\prime }\left[2{\left(\frac{\partial u\prime }{\partial x\prime }\right)}^2+2{\left(\frac{\partial v\prime }{\partial y\prime }\right)}^2+{\left(\frac{\partial u\prime }{\partial y\prime }+\frac{\partial v\prime }{\partial x\prime }\right)}^2\right]+\frac{{\sigma }_e{B}^2}{T_0\prime }{\left(u\sin \phi -v\cos \phi \right)}^2\end{array}$$

(15)

The local entropy generation can be putted in a dimensionless form by using the dimensionless variables listed in Equation (10) in the following way:

$${\mathrm{{\rm N}}}_{s,\ell }={\mathrm{{\rm N}}}_h+{\mathrm{{\rm N}}}_f+{\mathrm{{\rm N}}}_d^{C.C}+{\mathrm{{\rm N}}}_d^{T.C}+{\mathrm{{\rm N}}}_B$$

(16)

where:

$${\mathrm{{\rm N}}}_h=\left[{\left(\frac{\partial \mathrm{{\rm T}}}{\partial x}\right)}^2+{\left(\frac{\partial \mathrm{{\rm T}}}{\partial y}\right)}^2\right]$$

(17)

$${\mathrm{{\rm N}}}_f={\lambda }_1\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}^2\right]$$

(18)

$${\mathrm{{\rm N}}}_d^{C.C}={\lambda }_2\left[{\left(\frac{\partial C}{\partial x}\right)}^2+{\left(\frac{\partial C}{\partial y}\right)}^2\right]$$

(19)

$${\mathrm{{\rm N}}}_d^{T.C}={\lambda }_3\left[\left(\frac{\partial \mathrm{{\rm T}}}{\partial x}\right)\left(\frac{\partial C}{\partial x}\right)+\left(\frac{\partial \mathrm{{\rm T}}}{\partial y}\right)\left(\frac{\partial C}{\partial y}\right)\right]$$

(20)

$${\mathrm{{\rm N}}}_{\mathrm{{\rm B}}}={\lambda }_4\cdot {\left(u\sin \varphi -v\cos \varphi \right)}^2$$

(21)

with:

$$\begin{gathered} {\lambda }_1=\frac{\mu }{\lambda }{T}_0^{\prime }{\left(\frac{{\alpha }_T}{L\Delta \mathrm{{\rm T}}}\right)}^2;{\lambda }_2=\frac{RD{\mathrm{{\rm T}}}_o^{\prime }}{\lambda \cdot S_o^{\prime }}{\left(\frac{\Delta C}{\Delta \mathrm{{\rm T}}}\right)}^2 \\ {\lambda }_3=\frac{RD{T}_0^{\prime }}{\lambda }\left(\frac{\Delta C}{\Delta \mathrm{{\rm T}}}\right);{\lambda }_4=\frac{{\sigma }_e{T}_0^{\prime }}{\lambda }{\left(\frac{\mathrm{{\rm B}}\alpha }{\Delta \mathrm{{\rm T}}}\right)}^2 \end{gathered}$$

(22)

where ${\mathrm{{\rm N}}}_h$ ,${\mathrm{{\rm N}}}_f$, ${\mathrm{{\rm N}}}_d^{C.C}$, ${\mathrm{{\rm N}}}_d^{T.C}$ and ${\mathrm{{\rm N}}}_B$ are defined as local dimensionless entropy generation due to heat transfer (S_th), fluid friction (S_vis), mass transfer (S_diff) by pure concentrations gradients, mass transfer by mixed product of concentration and thermal gradients and magnetic field (S_mag), respectively.

${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ and ${\lambda }_4$ are irreversibility distribution ratios related to velocity gradients, concentrations gradients, mixed product of concentration and thermal gradients and magnetic field, respectively.

Total dimensionless entropy generation is obtained by a numerical integration of dimensionless local entropy generation through the entire volume of the cavity, Ω. That is:

$$S={\int }_{\Omega }\cdot {\mathrm{{\rm N}}}_{S.l}\cdot d\Omega$$

(23)

The temperature and concentration gradients are computed through the heat wall of the cavity, and then used to calculate the average Nusselt and Sherwood numbers, they are given respectively by:

$$\overline{\mathrm{{\rm N}}u}={\displaystyle \underset{0}{\overset{1}{\int }}(-\frac{\partial T}{\partial y})\cdot }dx$$

(24)

and:

$$\overline{Sh}={\displaystyle \underset{0}{\overset{1}{\int }}(-\frac{\partial C}{\partial y})\cdot }dx$$

(25)

4. Numerical Procedure

Governing Equations (4)–(8) could be solved for the determination of the temperature, the concentration and the velocity scalar fields which depend on the choice of the numerical support of resolution. In this study, a Control Volume Finite-Element Method (CVFEM) of Saabas and Baliga [36] is used. A standard grid at which diagonals are added to form triangular elements around each node where velocity components are calculated is considered. For pressure, temperature and concentration scalar field a staggered grid is used. Pressure and the other scalar field are calculated at different points to avoid the problem of oscillations.

The system of the governing equations is resolved by applying the SIMPLE algorithm of Patankar [37]. The SIMPLER algorithm and the SIMPLEC approximation of Van Doormal and Raithby are used in conjunction with an Alternating Direction Implicit (ADI) Scheme for performing the time evolution. The used numerical Code written in FORTRAN language was described and validated in details in Abbassi et al. [39, 40]

5. Results and Discussion

The used numerical code to solve the governing equations was validated by an important physical parameter which is Nusselt number by comparison with results found in literature. As it can be seen from Table 1, numerical results are in good agreements with those given in literature. The thermal Grashof number, the irreversibility distribution ratios and the inclination angle of the magnetic field are in the following ranges: 10³ ≤ Gr_t ≤ 10⁵, 10⁻⁷ ≤ ${\lambda }_1$ ≤ 10⁻⁴, 10⁻¹ ≤ ${\lambda }_2$ ≤ 0.5, 10⁻⁵ ≤ ${\lambda }_3$ ≤ 10⁻² and 0° ≤ α ≤ 180°. ${\lambda }_2$ and ${\lambda }_3$ are equal to 0 in natural convection. Grids of sizes of 31 × 31, 41 × 41 and 51 × 51 nodal points are used for Grt = 103, 104 and 105, respectively. A step time, Δt = 10⁻⁴ for is used for all the studied thermal Grashof numbers.

Table 1. Comparison of average Nusselt number for different values of Rayleigh number in a square cavity with Pr = 0.71, N = 0, Ha = 0.

Ra = Gr × Pr	Davis [2]	Nithyadevi et al. [6]	Present Study
103	1.118	1.123	1.099
104	2.243	2.304	2.295
105	4.519	4.899	4.664

Table 1. Comparison of average Nusselt number for different values of Rayleigh number in a square cavity with Pr = 0.71, N = 0, Ha = 0.

Ra = Gr × Pr	Davis [2]	Nithyadevi et al. [6]	Present Study
103	1.118	1.123	1.099
104	2.243	2.304	2.295
105	4.519	4.899	4.664

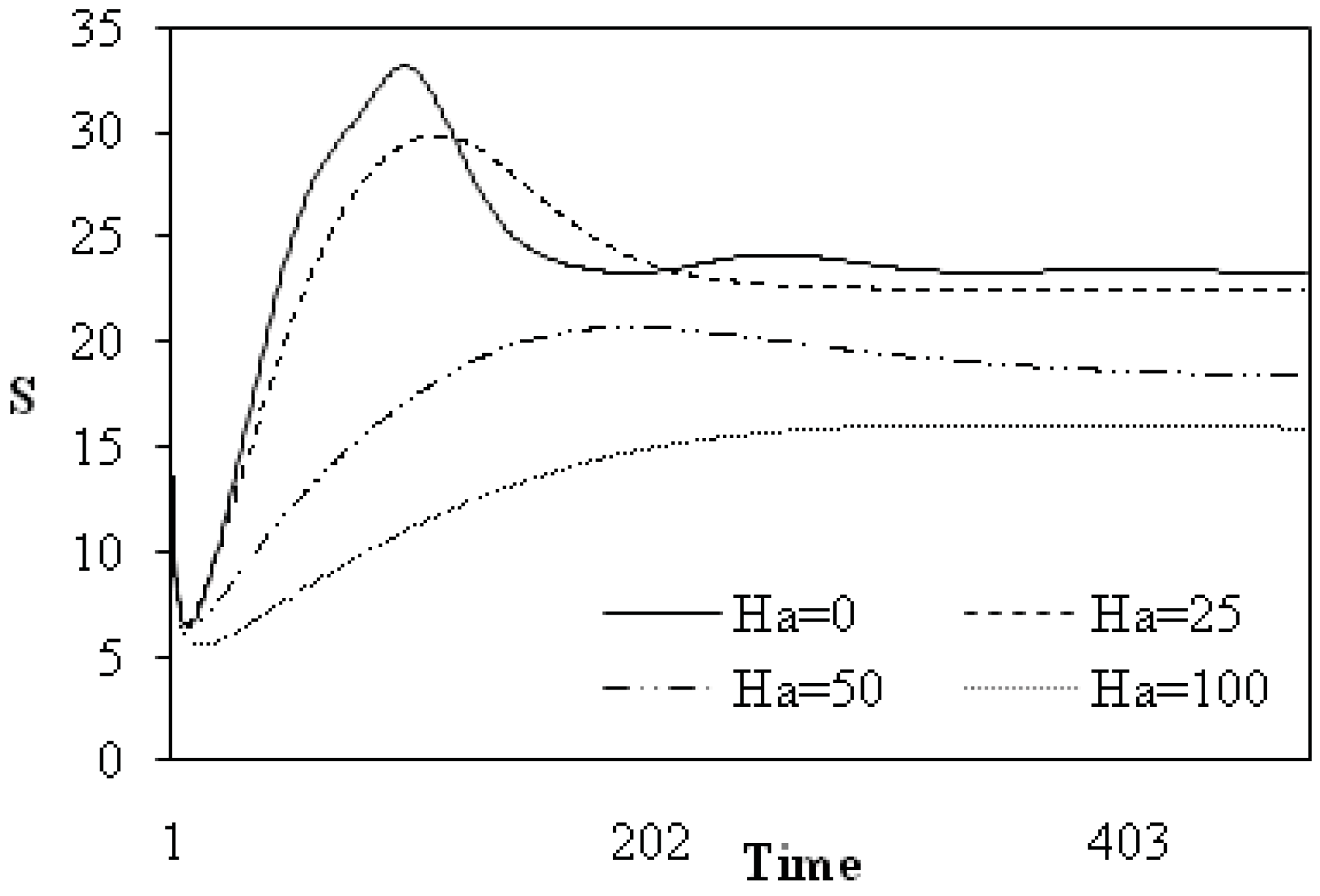
Figure 2 shows the influence of the magnetic field on the transient entropy generation for the case of natural convection (i.e., N = 0) and for relatively high value of thermal Grashof number (Gr_t = 10⁵). In absence of the magnetic field (i.e., Ha = 0), entropy generation quickly passes from a minimum value at the very beginning of the transient state towards a maximum value, then exhibits an oscillatory behaviour before reaching a constant value in steady state.

Figure 2. Dimensionless total entropy generation versus time for: N = 0; β = 90°; α = 0°; Ra = 10⁵.

Figure 2. Dimensionless total entropy generation versus time for: N = 0; β = 90°; α = 0°; Ra = 10⁵.

On increasing Hartmann number (i.e., 0 < Ha ≤ 50), a similar situation is also observed but with more flattened maximum entropy generation value and a decreased of both oscillations of transient entropy generation and its magnitude. For higher Hartmann number value (i.e., Ha ≥ 100), entropy generation slowly increases at the beginning of the transient state without oscillations towards a constant value at steady state.

As an important conclusion, the presence of a magnetic field tends to reduce entropy generation where the system passes from an oscillatory behavior describing non linear branch of irreversible process towards an asymptotic behaviour showing the linear branch of thermodynamics for irreversible processes.

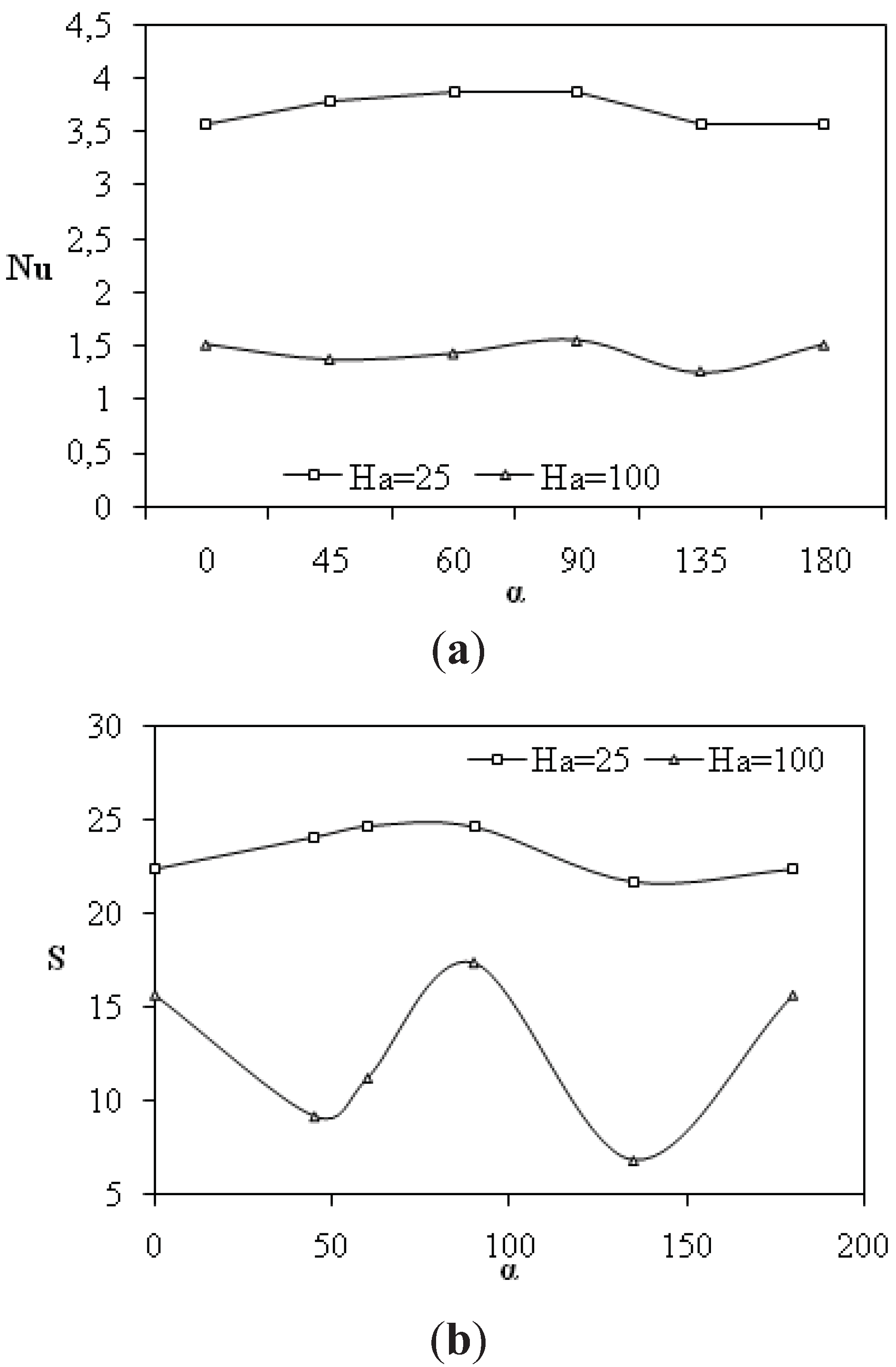
Figures 3 illustrates the effect of inclination angle on average Nusselt number and total entropy generation at different values of Hartmann number and thermal Rayleigh number (10⁵). Maximum value of Nusselt number is obtained at about α = 90° for which entropy generation is also maximum for both studied Hartmann number values (see Figure 3b). This is due to the increased value of thermal and velocity gradients at this point. Increasing Hartmann number induces the decrease of heat transfer and consequently the dissipated energy expressed by entropy generation. It is important to notice that minimum of entropy generation is obtained for α ≈ 140°.

Figure 3. (a) Average Nusselt number and (b) Dimensionless total entropy generation versus inclination angle for different Hartmann numbers: Ra = 10⁵; β = 90°; N = 0.

Figure 3. (a) Average Nusselt number and (b) Dimensionless total entropy generation versus inclination angle for different Hartmann numbers: Ra = 10⁵; β = 90°; N = 0.

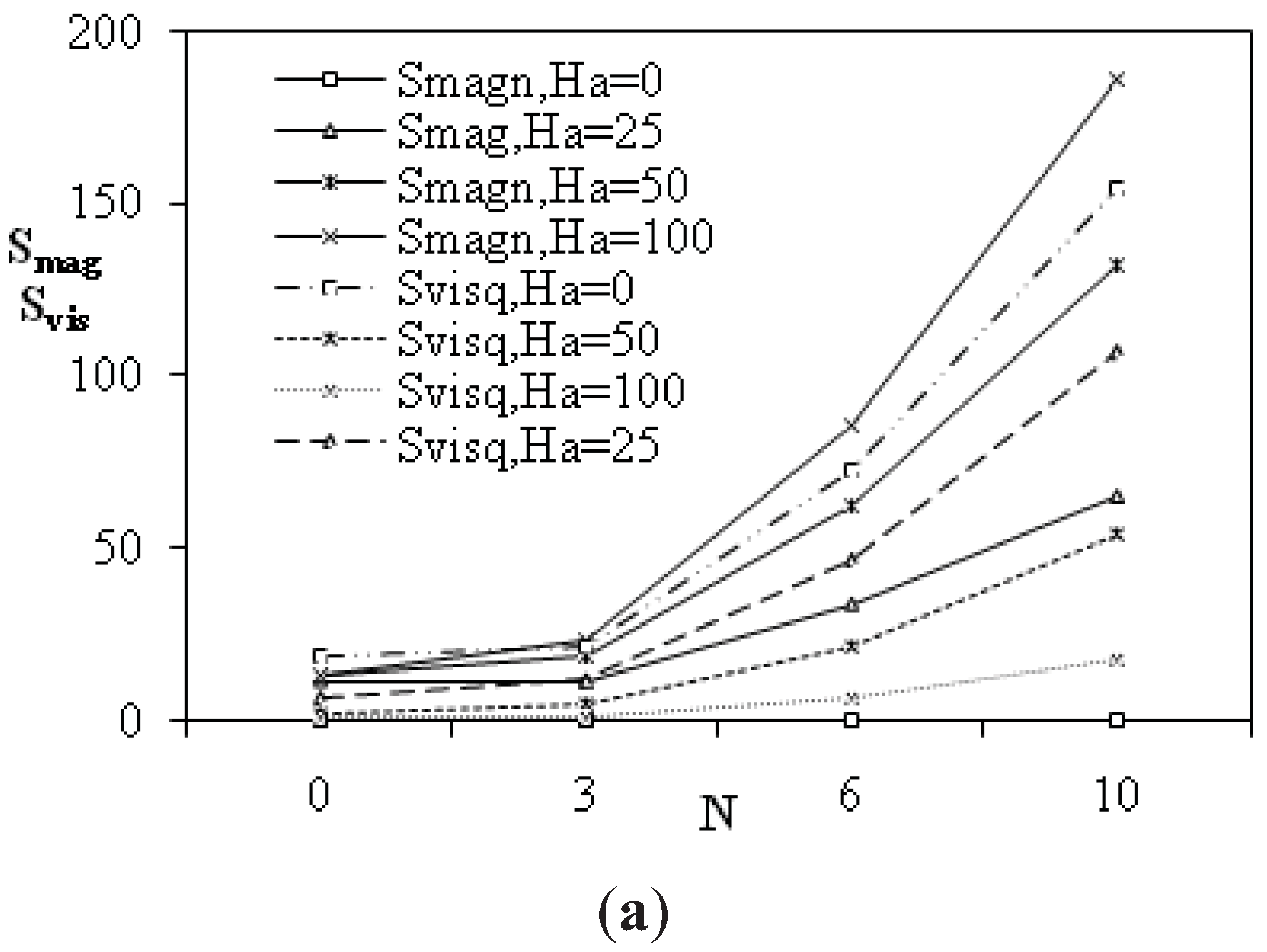
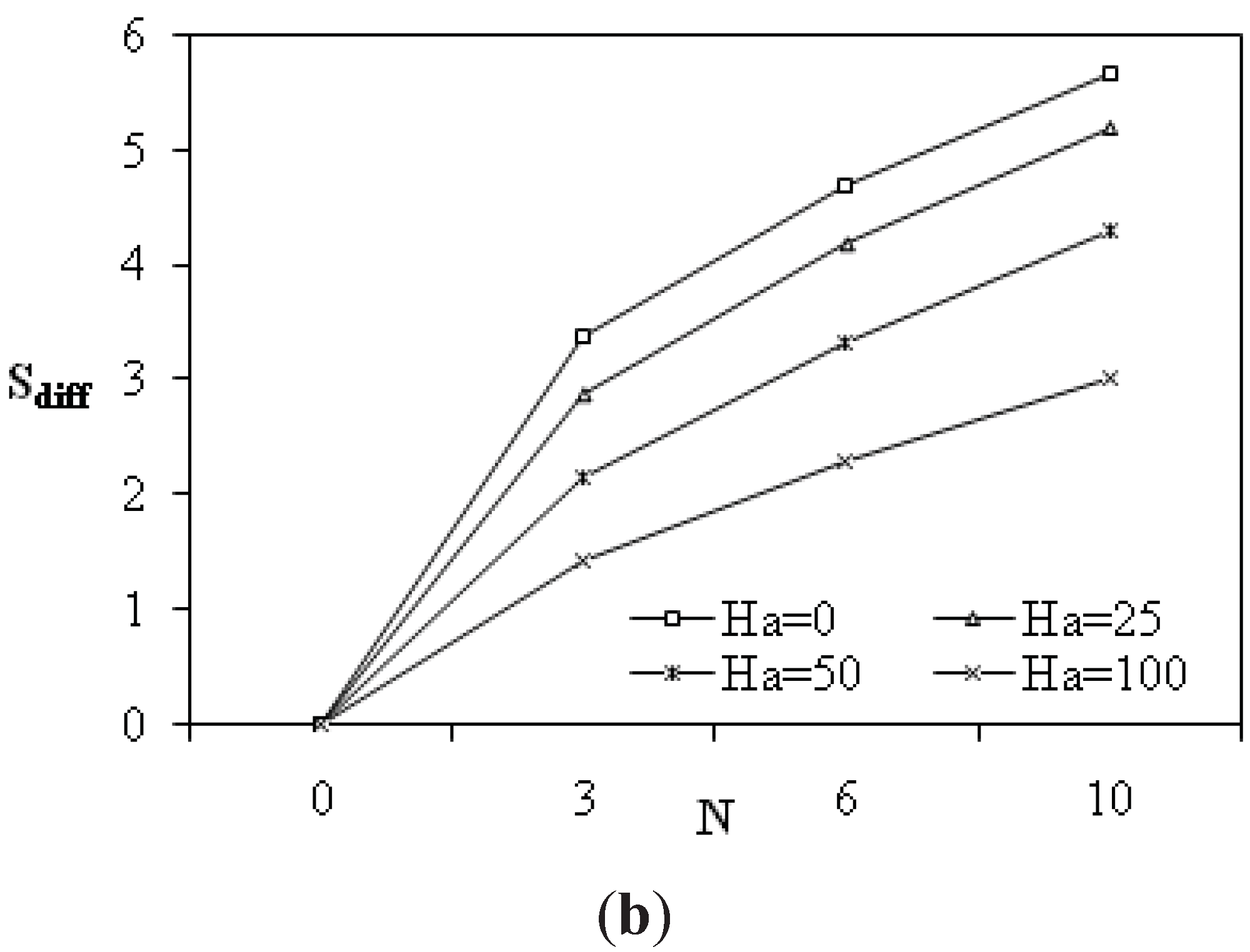
The increase of Hartmann number for both cooperating and opposite double-diffusive induces a decrease of entropy generation value and of average Nusselt and Sherwood numbers as can be seen in Figure 4, Figure 5. Profiles of different origins of irreversibility were plotted, the main irreversibility was due to viscous effect in the absence of magnetic effect (Ha = 0) and to magnetic term in the presence of a magnetic field (Ha = 25).

Figure 4. (a) Dimensionless total entropy generation versus Hartmann number for different buoyancy ratios and (b) Thermal entropy generation versus buoyancy ratio for different Hartmann numbers: Ra = 10⁵; β = 90°; α = 0°.

Figure 4. (a) Dimensionless total entropy generation versus Hartmann number for different buoyancy ratios and (b) Thermal entropy generation versus buoyancy ratio for different Hartmann numbers: Ra = 10⁵; β = 90°; α = 0°.

Figure 5. (a) Magnetic and Viscous entropy generation and (b) Diffusion entropy generation versus buoyancy ratio: Ra = 10⁵; β = 90°; α = 0°.

Figure 5. (a) Magnetic and Viscous entropy generation and (b) Diffusion entropy generation versus buoyancy ratio: Ra = 10⁵; β = 90°; α = 0°.

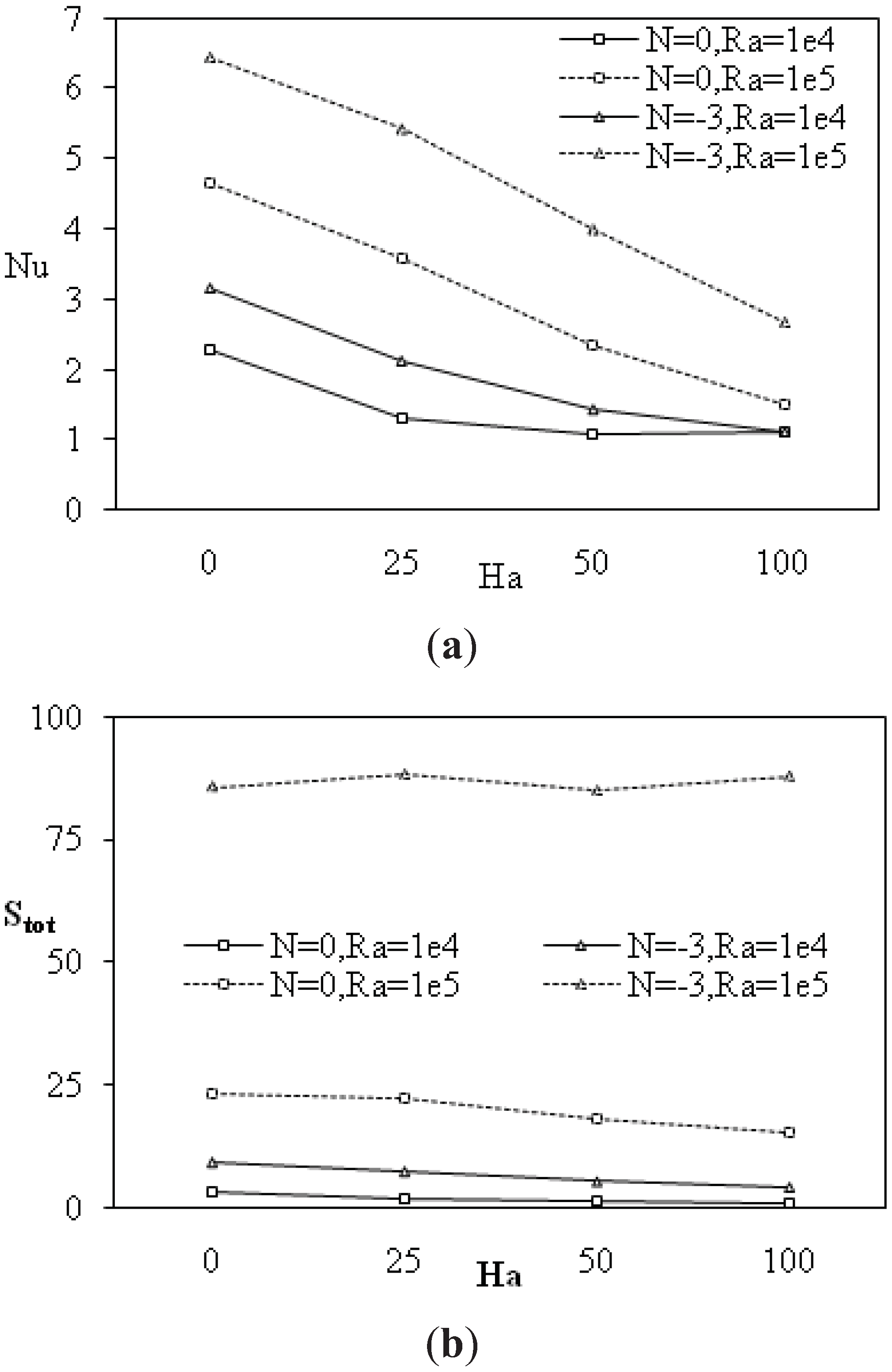
It was remarked from these figures the existence of minimum values in Nu and Sh for a critical buoyancy ratio N_cr. Both Nu and Sh tend to decrease with increasing values of N for N < N_cr and to increase with increasing values of N for N > N_cr. Both average Nu and Sh increase and decrease when the buoyancy forces assist or oppose, respectively those from thermal origin. The profiles of Nu and Sh with N tended to be symmetric about the value of N_cr. For a horizontal magnetic field, results show that average Nu and Sh increase in the beginning, reach maximums values and then decrease towards the pure conduction regime.

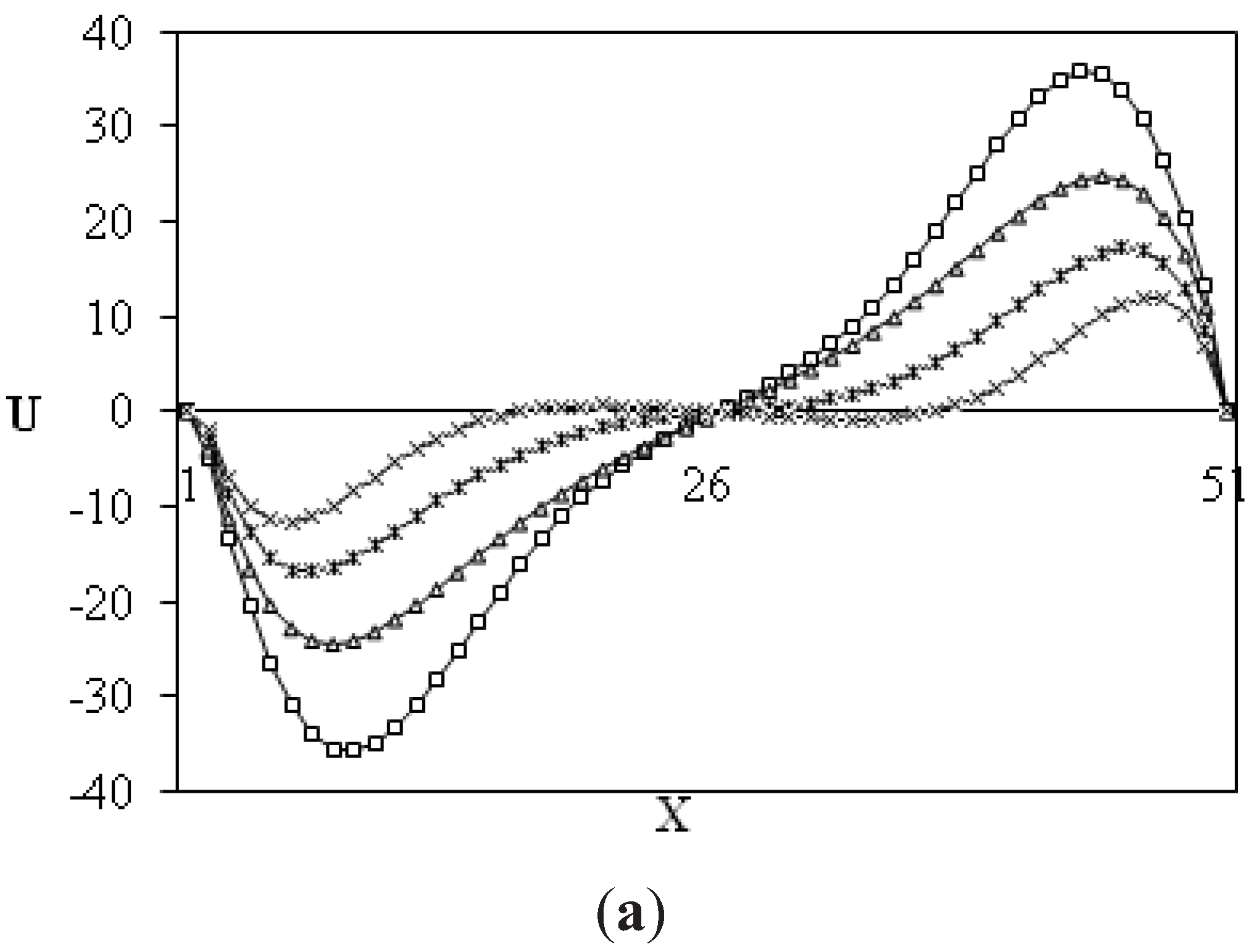
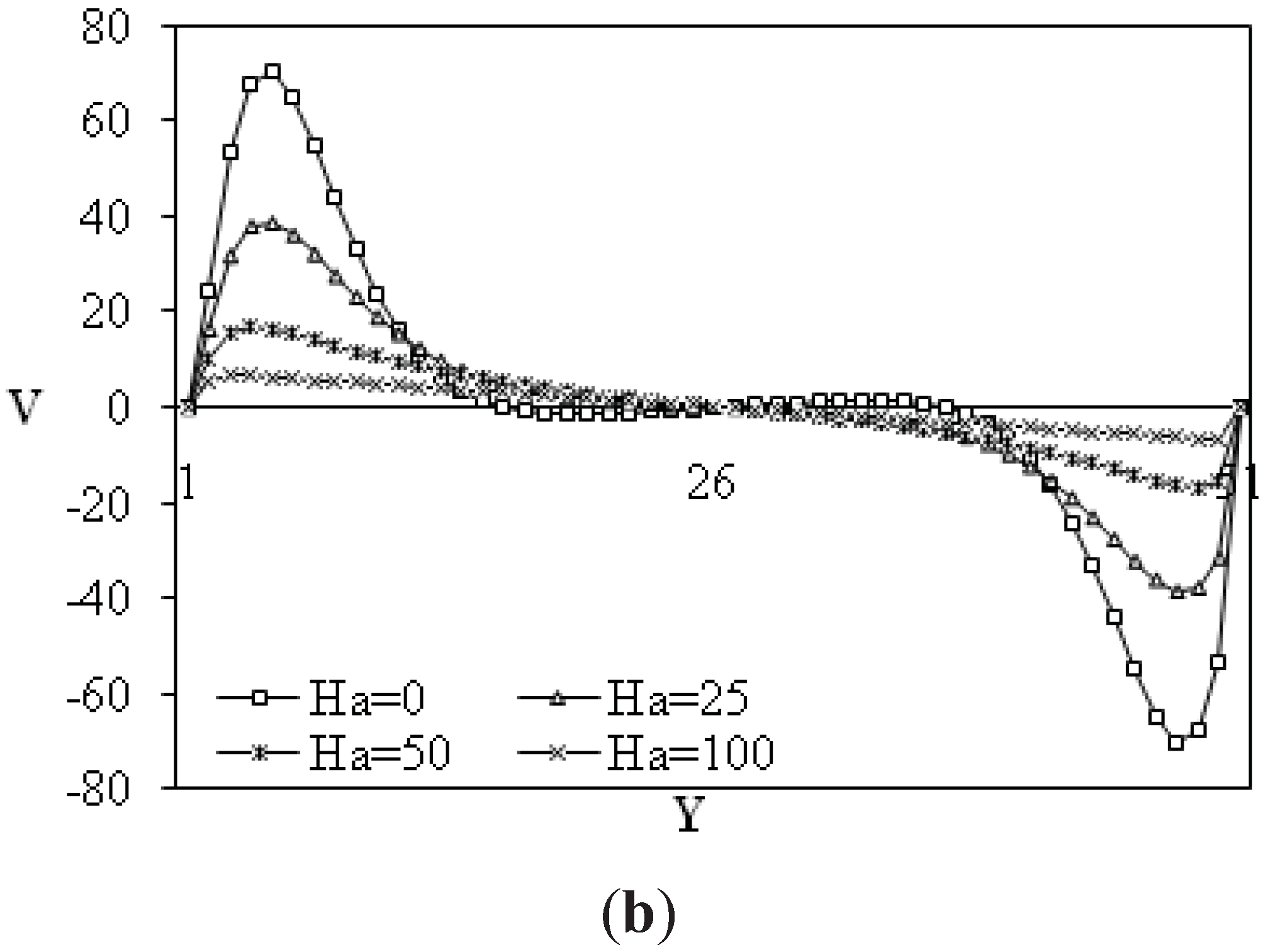
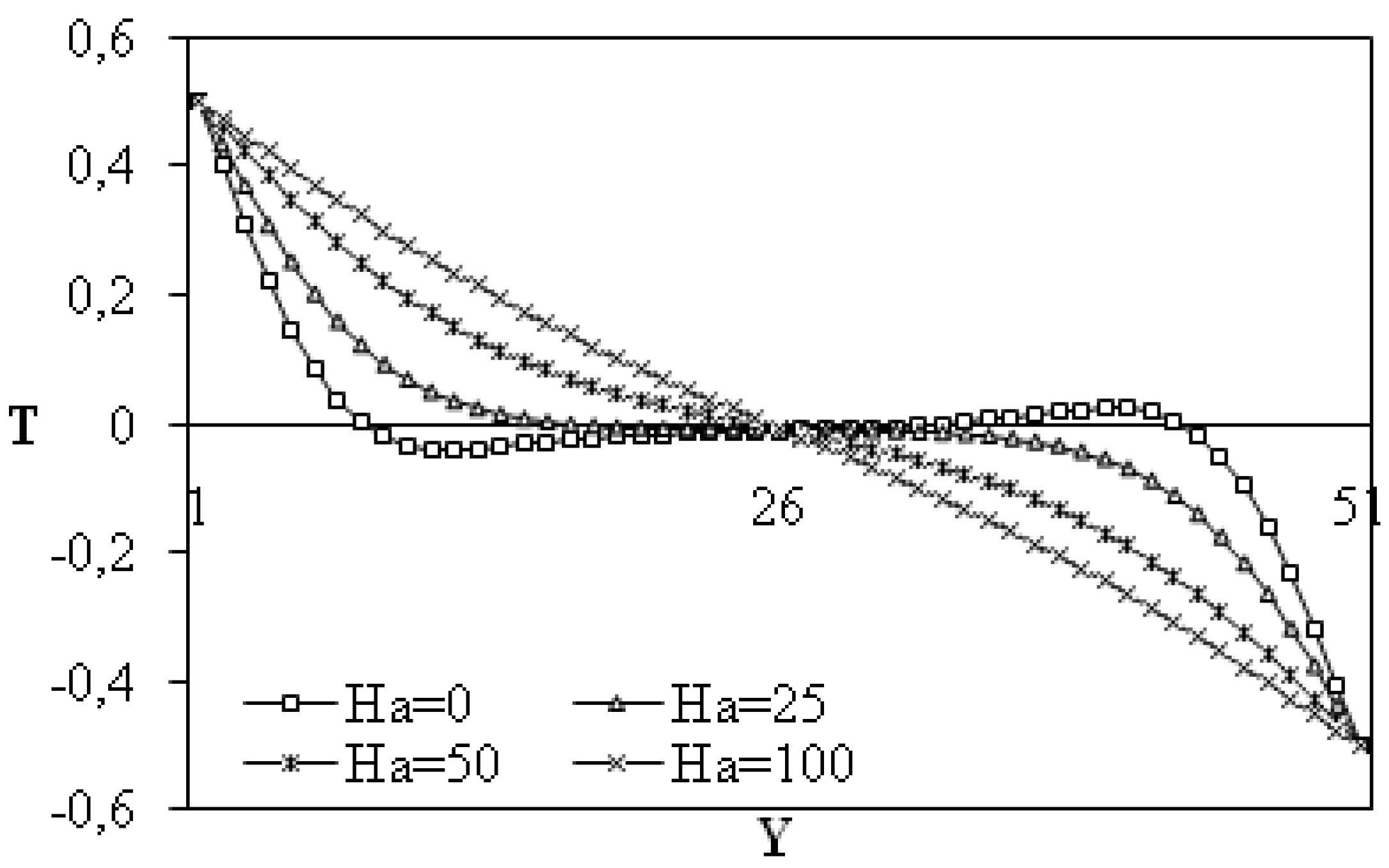
To explain these results, Figure 6, Figure 7, Figure 8 and Figure 9 illustrate the behaviors of midsection velocity components, temperature and concentration profiles in both cases of natural and thermosolutal convection. These profiles show a non symmetric trend about the mid horizontal direction of the enclosure. The magnitude of the net velocity tends to decrease as the strength of the magnetic field increases. The left vertical wall temperature and concentration tend to decrease as the Hartmann number increases. The influence of the magnetic field combined with thermosolutal effect was illustrated in Figure 8, Figure 9 on the temperature and concentration profiles. The effect of the magnetic field was found to reduce the overall heat transfer and fluid circulation within the enclosure.

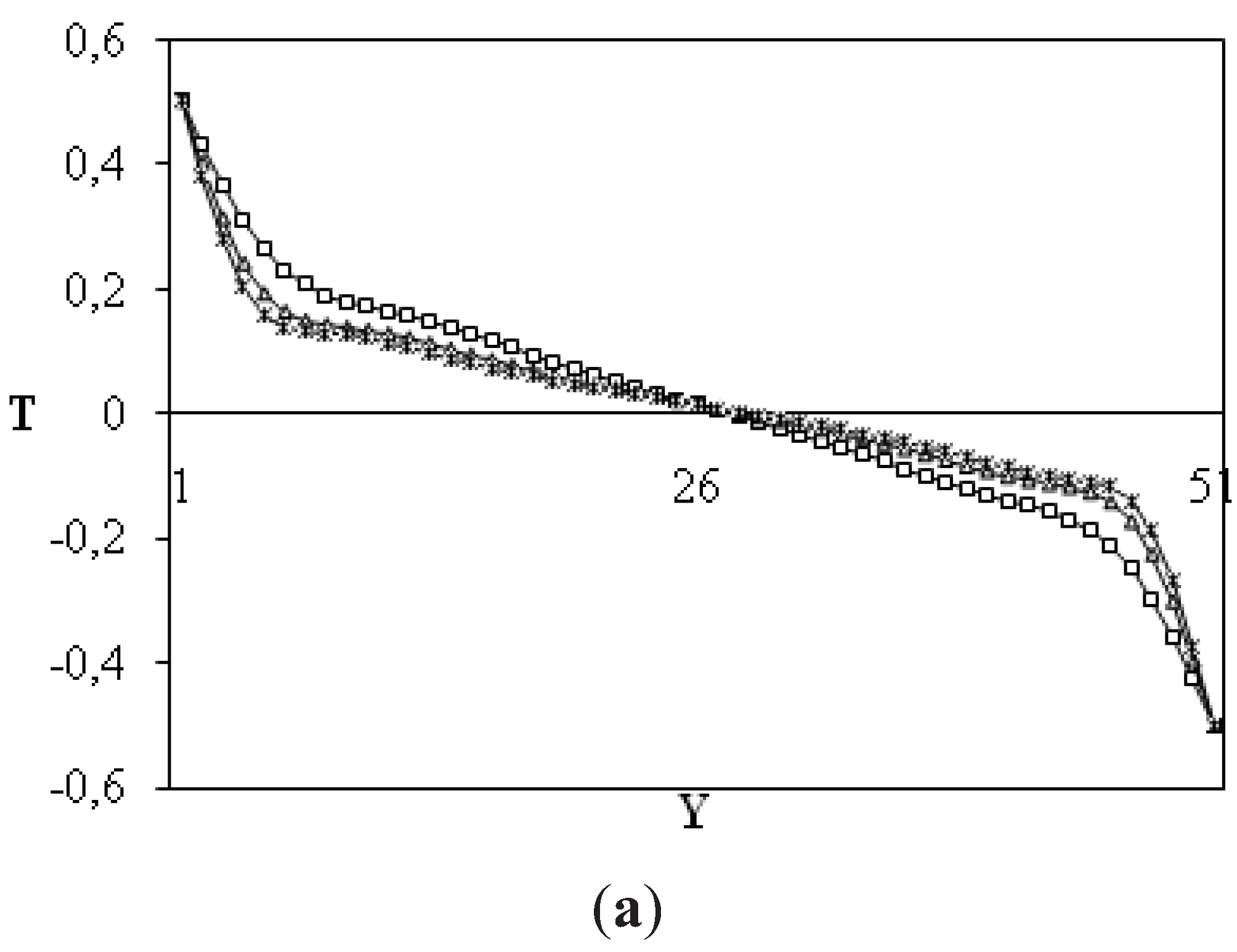
Figure 6. (a) Midsection x-component velocity at y = 0.5 and (b) midsection y-component velocity at x = 0.5 for different Hartmann numbers: Ra = 10⁵; β = 90°; α = 0°; N = 0.

Figure 6. (a) Midsection x-component velocity at y = 0.5 and (b) midsection y-component velocity at x = 0.5 for different Hartmann numbers: Ra = 10⁵; β = 90°; α = 0°; N = 0.

Figure 7. Midsection y-component temperature at y = 0.5 for different Hartmann numbers: Ra = 10⁵; β = 90°; α = 0°; N = 0.

Figure 7. Midsection y-component temperature at y = 0.5 for different Hartmann numbers: Ra = 10⁵; β = 90°; α = 0°; N = 0.

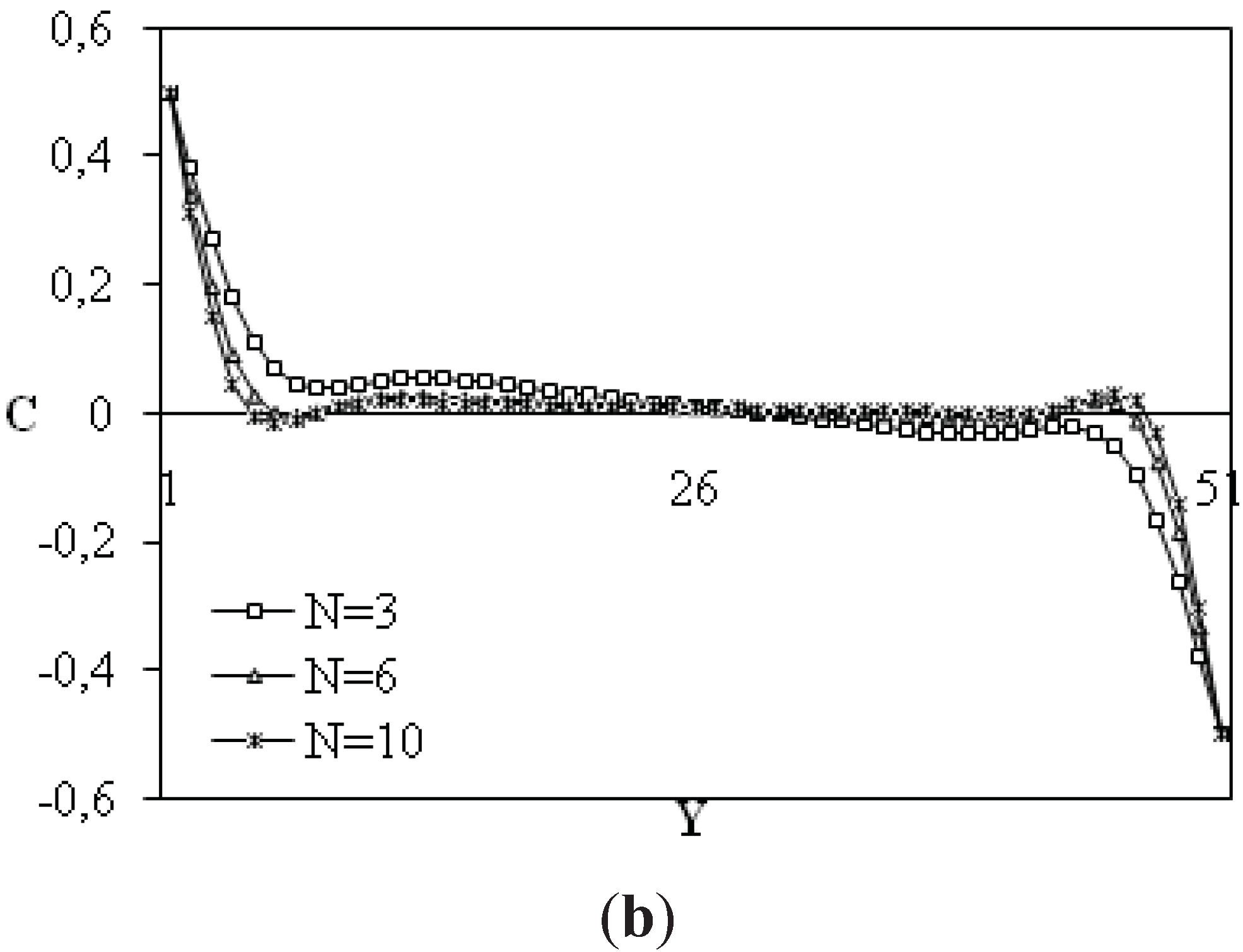
Figure 8. Midsection y-component temperature (a) and concentration (b) at y = 0.5 for different buoyancy ratios Ra = 10⁵; Ha = 25; β = 90°; α = 0°.

Figure 8. Midsection y-component temperature (a) and concentration (b) at y = 0.5 for different buoyancy ratios Ra = 10⁵; Ha = 25; β = 90°; α = 0°.

Figure 9. Average Nusselt number (a) and Total entropy generation (b) versus Hartmann number for different buoyancy ratios and Rayleigh numbers, β = 90°; α = 0°.

Figure 9. Average Nusselt number (a) and Total entropy generation (b) versus Hartmann number for different buoyancy ratios and Rayleigh numbers, β = 90°; α = 0°.

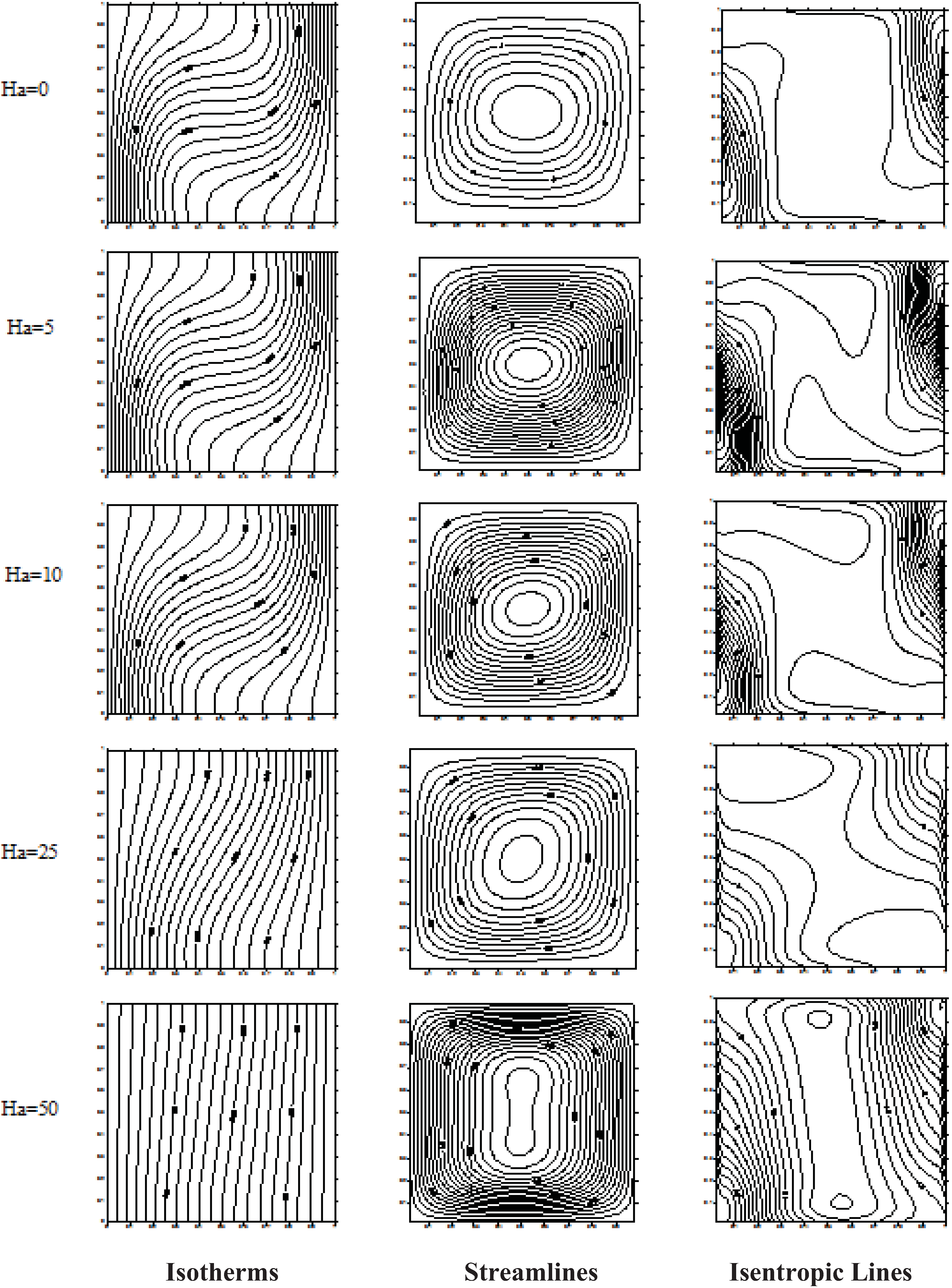
At local level, Maximum values of entropy generation are illustrated in Figure 10: isothermal, streamlines and isentropic lines for different values of Hartmann number at natural convection are then plotted. Entropy generation is localized on lower heated and upper cooled walls of the cavity. As Hartmann number increases, amplitudes of isentropic lines decreases due to the decrease of temperature and velocity gradients as plotted by isothermal and streamlines.

Figure 10. Isotherms, Streamlines and Isentropic lines for N = 0 with different values of Hartmann number for α = 0°; Gr = 10⁴.

Figure 10. Isotherms, Streamlines and Isentropic lines for N = 0 with different values of Hartmann number for α = 0°; Gr = 10⁴.

6. Conclusions

Entropy generation due to natural and thermosolutal convection in a square cavity is numerically calculated using the Control Volume Finite-Element Method (CVFEM). Results show that the total entropy generation increases for high thermal Grashof number and with the buoyancy ratio in cooperative case. The transient state study shows that entropy generation increases in the beginning of this regime, reaches a maximum, then decreases asymptotically at low thermal Grashof number and with oscillations at high thermal Grashof number towards a constant value at the steady state. Maximum entropy generation is obtained at around 90° for Gr_t = 10⁴. Contributions of thermal, diffusive, friction and magnetic terms on entropy generation are investigated. The more effect was due to heat transfer and then to mass transfer. Results showed that magnetic effect is more pronounced than friction one. The magnetic field parameter suppresses the flow in the cavity and this lead to a decrease of entropy generation, temperature and concentration decrease with increasing value of the magnetic field parameter. At local level, results show that entropy generation lines are localized on lower heated and upper cooled regions of the active walls.