The Michaelis-Menten-Stueckelberg Theorem
Abstract
:1. Introduction
1.1. Main Asymptotic Ideas in Chemical Kinetics
1.2. The Structure of the Paper
1.3. Main Results: One Asymptotic and Two Theorems
- The compounds are in fast equilibrium with the corresponding input reagents (QE);
- They exist in very small concentrations compared to other components (QSS).
- The activated complexes are in a quasi-equilibrium with the reactant molecules;
- Rates of the reactions are studied by studying the activated complexes at the saddle point of a potential energy surface.
2. QE and Preservation of Entropy Production
3. The Classics and the Classical Confusion
3.1. The Asymptotic of Fast Reactions
3.2. QSS and the Briggs-Haldane Asymptotic
- Enzymes (or catalysts, or radicals) participate in fast reactions and, hence, relax faster than substrates or stable components. This is obviously wrong for many QSS systems: For example, in the Michaelis-Menten system all reactions include enzyme together with substrate or product. There are no separate fast reactions for enzyme without substrate or product.
- Concentrations of intermediates are constant because in QSS we equate their time derivatives to zero. In general case, this is also wrong: We equate the kinetic expressions for some time derivatives to zero, indeed, but this just exploits the fact that the time derivatives of intermediates concentrations are small together with their values, but not obligatory zero. If we accept QSS then these derivatives are not zero as well: To prove this we can just differentiate the Michaelis-Menten formula (11) and find that [ES] in QSS is almost constant when , this is an additional condition, different from the Briggs-Haldane condition (for more details see [1,14,33] and a simple detailed case study [41]).
3.3. The Michaelis and Menten Asymptotic
4. Chemical Kinetics and QE Approximation
4.1. Stoichiometric Algebra and Kinetic Equations
4.2. Formalism of QE Approximation for Chemical Kinetics
4.2.1. QE Manifold
4.2.2. QE in Traditional MM System
4.2.3. Heterogeneous Catalytic Reaction
4.2.4. Discussion of the QE procedure for Chemical Kinetics
5. General Kinetics with Fast Intermediates Present in Small Amount
5.1. Stoichiometry of Complexes
5.2. Stoichiometry of Compounds
5.3. Energy, Entropy and Equilibria of Compounds
5.4. Markov Kinetics of Compounds
5.5. Thermodynamics and Kinetics of the Extended System
5.6. QE Elimination of Compounds and the Complex Balance Condition
5.7. The Big Michaelis-Menten-Stueckelberg Theorem
- Concentrations of the compounds are much smaller than the concentrations of the components : There is a small positive parameter , and do not depend on ε;
- Kinetics of transitions between compounds is linear (Markov) kinetics with reaction rate constants .
6. General Kinetics and Thermodynamics
6.1. General Formalism
- The energy of the Universe is constant.
- The entropy of the Universe tends to a maximum.
6.2. Accordance Between Kinetics and Thermodynamics
6.2.1. General Entropy Production Formula
6.2.2. Detailed Balance
6.2.3. Complex Balance
6.2.4. G-Inequality
7. Linear Deformation of Entropy
7.1. If Kinetics Does not Respect Thermodynamics then Deformation of Entropy May Help
7.2. Entropy Deformation for Restoration of Detailed Balance
7.3. Entropy Deformation for Restoration of Complex Balance
7.4. Existence of Points of Detailed and Complex Balance
7.5. The Detailed Balance is Needed More Often than the Complex Balance
8. Conclusions
- The detailed balance: The kinetic factors for mutually reverse reaction should coincide, . This identity is proven for systems with microreversibility (Section 7.5).
- The complex balance: The sum of the kinetic factors for all elementary reactions of the form is equal to the sum of the kinetic factors for all elementary reactions of the form (91). This identity is proven for all systems under the Michaelis-Menten-Stueckelberg assumptions about existence of intermediate compounds which are in fast equilibria with other components and are present in small amounts.
References
- Klonowski, W. Simplifying Principles for chemical and enzyme reaction kinetics. Biophys. Chem. 1983, 18, 73–87. [Google Scholar] [CrossRef]
- Gibbs, G.W. Elementary Principles in Statistical Mechanics; Yale University Press: New Haven, CT, USA, 1902. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. In Statistical Physics. Brandeis Lectures; Ford, K.W., Ed.; Benjamin: New York, NY, USA, 1963; pp. 160–185. [Google Scholar]
- Balian, R.; Alhassid, Y.; Reinhardt, H. Dissipation in many-body systems: A geometric approach based on information theory. Phys. Rep. 1986, 131, 1–146. [Google Scholar] [CrossRef]
- Gorban, A.N.; Karlin, I.V.; Ilg, P.; Öttinger, H.C. Corrections and enhancements of quasi–equilibrium states. J. Non-Newtonian Fluid Mech. 2001, 96, 203–219. [Google Scholar] [CrossRef]
- Gorban, A.N.; Karlin, I.V. Invariant Manifolds for Pphysical and Chemical Kinetics (Lecture Notes in Physics); Springer: Berlin, Germary, 2005. [Google Scholar]
- Bodenstein, M. Eine Theorie der Photochemischen Reaktionsgeschwindigkeiten. Z. Phys. Chem. 1913, 85, 329–397. [Google Scholar]
- Michaelis, L.; Menten, M. Die kinetik der intervintwirkung. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Semenov, N.N. On the kinetics of complex reactions. J. Chem. Phys. 1939, 7, 683–699. [Google Scholar] [CrossRef]
- Christiansen, J.A. The elucidation of reaction mechanisms by the method of intermediates in quasi-stationary concentrations. Adv. Catal. 1953, 5, 311–353. [Google Scholar]
- Helfferich, F.G. Systematic approach to elucidation of multistep reaction networks. J. Phys. Chem. 1989, 93, 6676–6681. [Google Scholar] [CrossRef]
- Briggs, G.E.; Haldane, J.B.S. A note on the kinetics of enzyme action. Biochem. J. 1925, 19, 338–339. [Google Scholar] [CrossRef] [PubMed]
- Aris, R. Introduction to the Analysis of Chemical Reactors; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1965. [Google Scholar]
- Segel, L.A.; Slemrod, M. The quasi-steady-state assumption: A case study in perturbation. SIAM Rev. 1989, 31, 446–477. [Google Scholar] [CrossRef]
- Wei, J.; Kuo, J.C. A lumping analysis in monomolecular reaction systems: Analysis of the exactly lumpable system. Ind. Eng. Chem. Fund. 1969, 8, 114–123. [Google Scholar] [CrossRef]
- Wei, J.; Prater, C. The structure and analysis of complex reaction systems. Adv. Catal. 1962, 13, 203–393. [Google Scholar]
- Kuo, J.C.; Wei, J. A lumping analysis in monomolecular reaction systems. Analysis of the approximately lumpable system. Ind. Eng. Chem. Fund. 1969, 8, 124–133. [Google Scholar] [CrossRef]
- Li, G.; Rabitz, H. A general analysis of exact lumping in chemical kinetics. Chem. Eng. Sci. 1989, 44, 1413–1430. [Google Scholar] [CrossRef]
- Toth, J.; Li, G.; Rabitz, H.; Tomlin, A.S. The effect of lumping and expanding on kinetic differential equations. SIAM J. Appl. Math. 1997, 57, 1531–1556. [Google Scholar]
- Coxson, P.G.; Bischoff, K.B. Lumping strategy. 2. System theoretic approach. Ind. Eng. Chem. Res. 1987, 26, 2151–2157. [Google Scholar] [CrossRef]
- Djouad, R.; Sportisse, B. Partitioning techniques and lumping computation for reducing chemical kinetics. APLA: An automatic partitioning and lumping algorithm. Appl. Numer. Math. 2002, 43, 383–398. [Google Scholar] [CrossRef]
- Lin, B.; Leibovici, C.F.; Jorgensen, S.B. Optimal component lumping: Problem formulation and solution techniques. Comput. Chem. Eng. 2008, 32, 1167–1172. [Google Scholar] [CrossRef]
- Gorban, A.N.; Radulescu, O. Dynamic and static limitation in reaction networks, revisited. Adv. Chem. Eng. 2008, 34, 103–173. [Google Scholar]
- Gorban, A.N.; Radulescu, O.; Zinovyev, A.Y. Asymptotology of chemical reaction networks. Chem. Eng. Sci. 2010, 65, 2310–2324. [Google Scholar] [CrossRef]
- Gorban, A.N. Equilibrium encircling. Equations of Chemical Kinetics and Their Thermodynamic Analysis; Nauka: Novosibirsk, USSR, 1984. [Google Scholar]
- Stueckelberg, E.C.G. Theoreme H et unitarite de S. Helv. Phys. Acta 1952, 25, 577–580. [Google Scholar]
- Boltzmann, L. Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen. Sitzungsber. keis. Akad. Wiss. 1872, 66, 275–370. [Google Scholar]
- Cercignani, C.; Lampis, M. On the H-theorem for polyatomic gases. J. Stat. Phys. 1981, 26, 795–801. [Google Scholar] [CrossRef]
- Heitler, W. Quantum Theory of Radiation; Oxford University Press: London, UK, 1944. [Google Scholar]
- Coester, F. Principle of detailed balance. Phys. Rev. 1951, 84, 1259. [Google Scholar] [CrossRef]
- Watanabe, S. Symmetry of physical laws. Part I. Symmetry in space-time and balance theorems. Rev. Mod. Phys. 1955, 27, 26–39. [Google Scholar] [CrossRef]
- Gorban, A.N.; Gorban, P.A.; Judge, G. Entropy: The Markov ordering approach. Entropy 2010, 12, 1145–1193. [Google Scholar] [CrossRef]
- Yablonskii, G.S.; Bykov, V.I.; Gorban, A.N.; Elokhin, V.I. Kinetic Models of Catalytic Reactions; Elsevier: Amsterdam, The Netherlands, 1991; Volume 32. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Method of invariant manifold for chemical kinetics. Chem. Eng. Sci. 2003, 58, 4751–4768. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. [Google Scholar] [CrossRef]
- Laidler, K.J. Tweedale, A. The current status of Eyring’s rate theory. In Advances in Chemical Physics: Chemical Dynamics: Papers in Honor of Henry Eyring; Hirschfelder, J.O., Henderson, D., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; Volume 21. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Quasi-equilibrium closure hierarchies for the Boltzmann equation. Physica A 2006, 360, 325–364. [Google Scholar] [CrossRef]
- Gorban, A.N.; Karlin, I.V. Uniqueness of thermodynamic projector and kinetic basis of molecular individualism. Physica A 2004, 336, 391–432. [Google Scholar] [CrossRef]
- Hangos, K.M. Engineering model reduction and entropy-based Lyapunov functions in chemical reaction kinetics. Entropy 2010, 12, 772–797. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Li, B. Quasi-steady-state laws in enzyme kinetics. J. Phys. Chem. A 2008, 112, 2311–2321. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A.N. Systems of differential equations containing small parameters multiplying some of the derivatives. Mat. Sb. 1952, 31, 575–586. [Google Scholar]
- Vasil’eva, A.B. Asymptotic behaviour of solutions to certain problems involving nonlinear differential equations containing a small parameter multiplying the highest derivatives. Russ. Math. Survey. 1963, 18, 13–84. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C. Singular perturbations on the infinite interval. Trans. Am. Math. Soc. 1966, 123, 521–535. [Google Scholar] [CrossRef]
- Battelu, F.; Lazzari, C. Singular perturbation theory for open enzyme reaction networks. IMA J. Math. Appl. Med. Biol. 1986, 3, 41–51. [Google Scholar] [CrossRef]
- Feinberg, M. On chemical kinetics of a certain class. Arch. Ration. Mech. Anal. 1972, 46, 1–41. [Google Scholar] [CrossRef]
- Lebiedz, D. Entropy-related extremum principles for model reduction of dissipative dynamical systems. Entropy 2010, 12, 706–719. [Google Scholar] [CrossRef]
- Ò Conaire, M.; Curran, H.J.; Simmie, J.M.; Pitz, W.J.; Westbrook, C.K. A comprehensive modeling study of hydrogen oxidation. Int. J. Chem. Kinet. 2004, 36, 603–622. [Google Scholar] [CrossRef]
- Yablonskii, G.S.; Lazman, M.Z. Non-linear steady-state kinetics of complex catalytic reactions: Theory and applications. Stud. Surf. Sci. Catal. 1997, 109, 371–378. [Google Scholar]
- Balescu, R. Equilibrium and Nonequilibrium Statistical Mechanics; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Horn, F.; Jackson, R. General mass action kinetics. Arch. Ration. Mech. Anal. 1972, 47, 81–116. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Themostatistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Bykov, V.I.; Gorban, A.N.; Yablonskii, G.S. Description of non-isothermal reactions in terms of Marcelin-De-Donder Kinetics and its generalizations. React. Kinet. Catal. Lett. 1982, 20, 261–265. [Google Scholar] [CrossRef]
- Clausius, R. Über vershiedene für die Anwendungen bequeme Formen der Hauptgleichungen der Wärmetheorie. Poggendorffs Annalen der Physic und Chemie 1865, 125, 353–400. [Google Scholar] [CrossRef]
- Orlov, N.N.; Rozonoer, L.I. The macrodynamics of open systems and the variational principle of the local potential, J. Franklin Inst-Eng. Appl. Math. 1984, 318, 283–341. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Nonlinear irreversible processes. Physica 1973, 67, 1–22. [Google Scholar] [CrossRef]
- Gorban, A.N.; Bykov, V.I.; Yablonskii, G.S. Essays on Chemical Relaxation; Nauka: Novosibirsk, USSR, 1986. [Google Scholar]
- Volpert, A.I.; Khudyaev, S.I. Analysis in Classes of Discontinuous Functions and Equations of Mathematical Physics; Nijoff: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Hangos, K.M.; Alonso, A.A.; Perkins, J.D.; Ydstie, B.E. Thermodynamic approach to the structural stability of process plants. AIChE J. 1999, 45, 802–816. [Google Scholar] [CrossRef]
- Wu, B.Y.; Chao, K.-M. Spanning Trees and Optimization Problems; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Feinberg, M. Complex balancing in general kinetic systems. Arch. Ration. Mech. Anal. 1972, 49, 187–194. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On Onsager’s principle of microscopic reversibility. Rev. Mod. Phys. 1945, 17, 343–350. [Google Scholar] [CrossRef]
- Grmela, M. Thermodynamics of driven systems. Phys. Rev. E 1993, 48, 919–930. [Google Scholar] [CrossRef]
- Gorban, A.N.; Karlin, I.V. Scattering rates versus moments: Alternative Grad equations. Phys. Rev. E 1996, 54, 3109–3112. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Temkin, O.N.; Zeigarnik, A.V.; Bonchev, D.G. Chemical Reaction Networks: A Graph-Theoretical Approach; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Morimoto, T. Markov processes and the H-theorem. J Phys. Soc. Jpn. 1963, 12, 328–331. [Google Scholar] [CrossRef]
- Meyn, S.R.; Tweedie, R.L. Markov Chains and Stochastic Stability; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
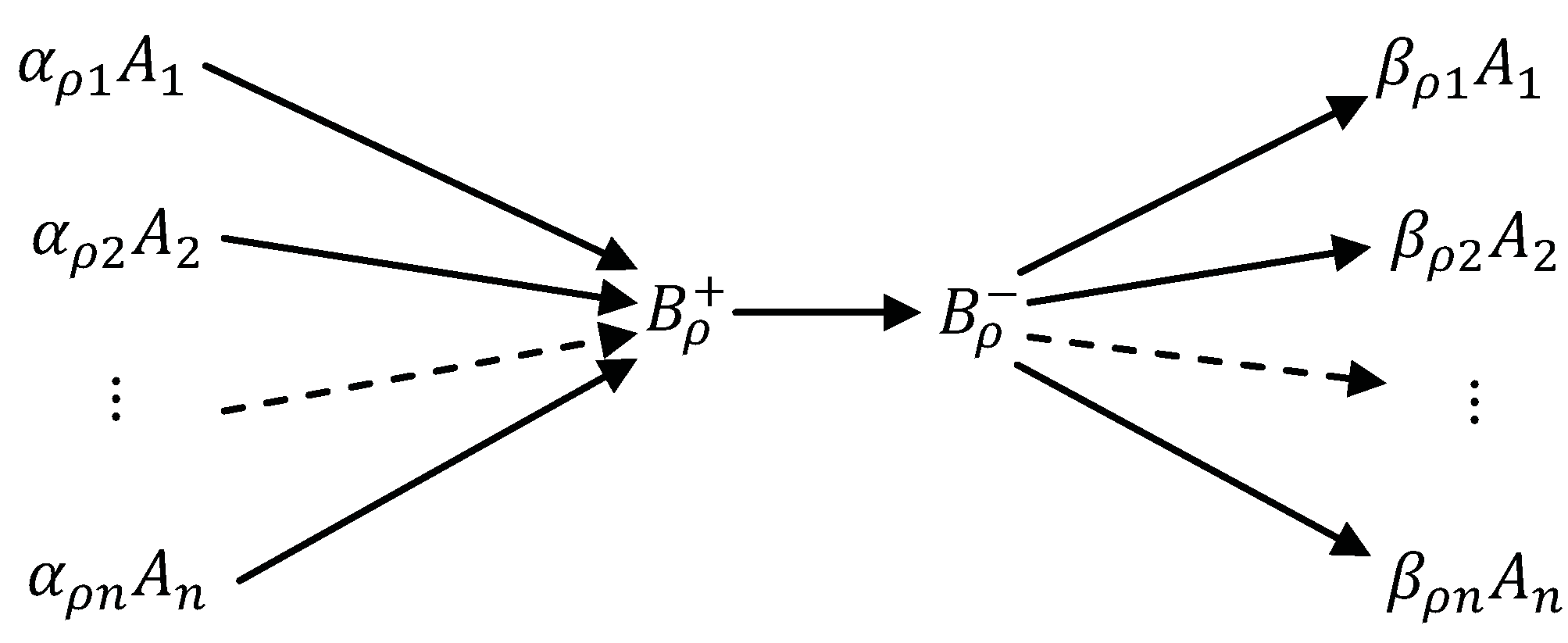
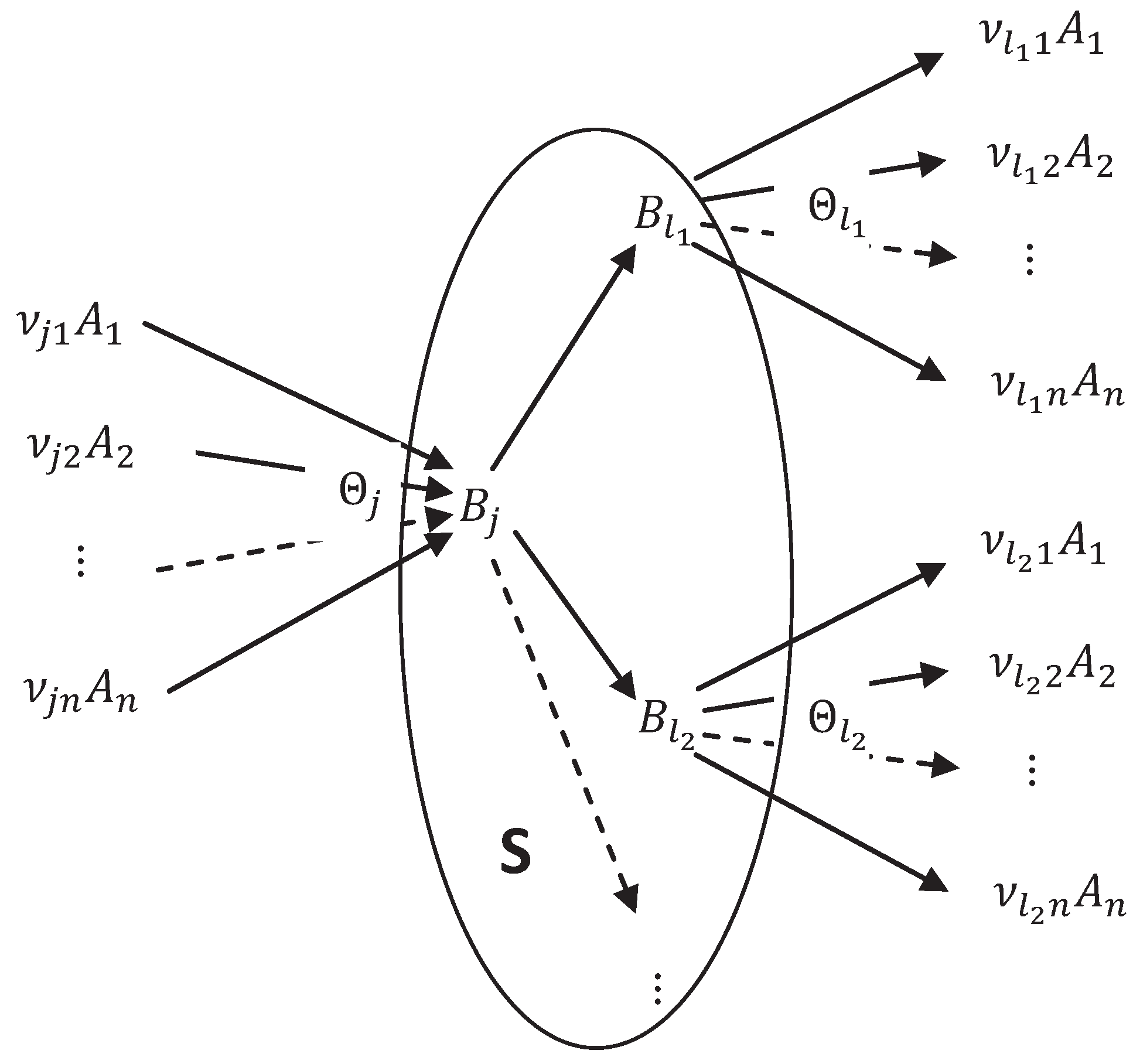
Appendix
1. Quasiequilibrium Approximation
1.1. Quasiequilibrium Manifold
1.2. Preservation of Entropy Production
2. First Order Kinetics and Markov Chains
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Gorban, A.N.; Shahzad, M. The Michaelis-Menten-Stueckelberg Theorem. Entropy 2011, 13, 966-1019. https://doi.org/10.3390/e13050966
Gorban AN, Shahzad M. The Michaelis-Menten-Stueckelberg Theorem. Entropy. 2011; 13(5):966-1019. https://doi.org/10.3390/e13050966
Chicago/Turabian StyleGorban, Alexander N., and Muhammad Shahzad. 2011. "The Michaelis-Menten-Stueckelberg Theorem" Entropy 13, no. 5: 966-1019. https://doi.org/10.3390/e13050966





