Maximum-Entropy Method for Evaluating the Slope Stability of Earth Dams
Abstract
:1. Introduction
2. Probabilistic Slope Stability Analysis
2.1. The Performance Function


2.2. Simplified Bishop Method

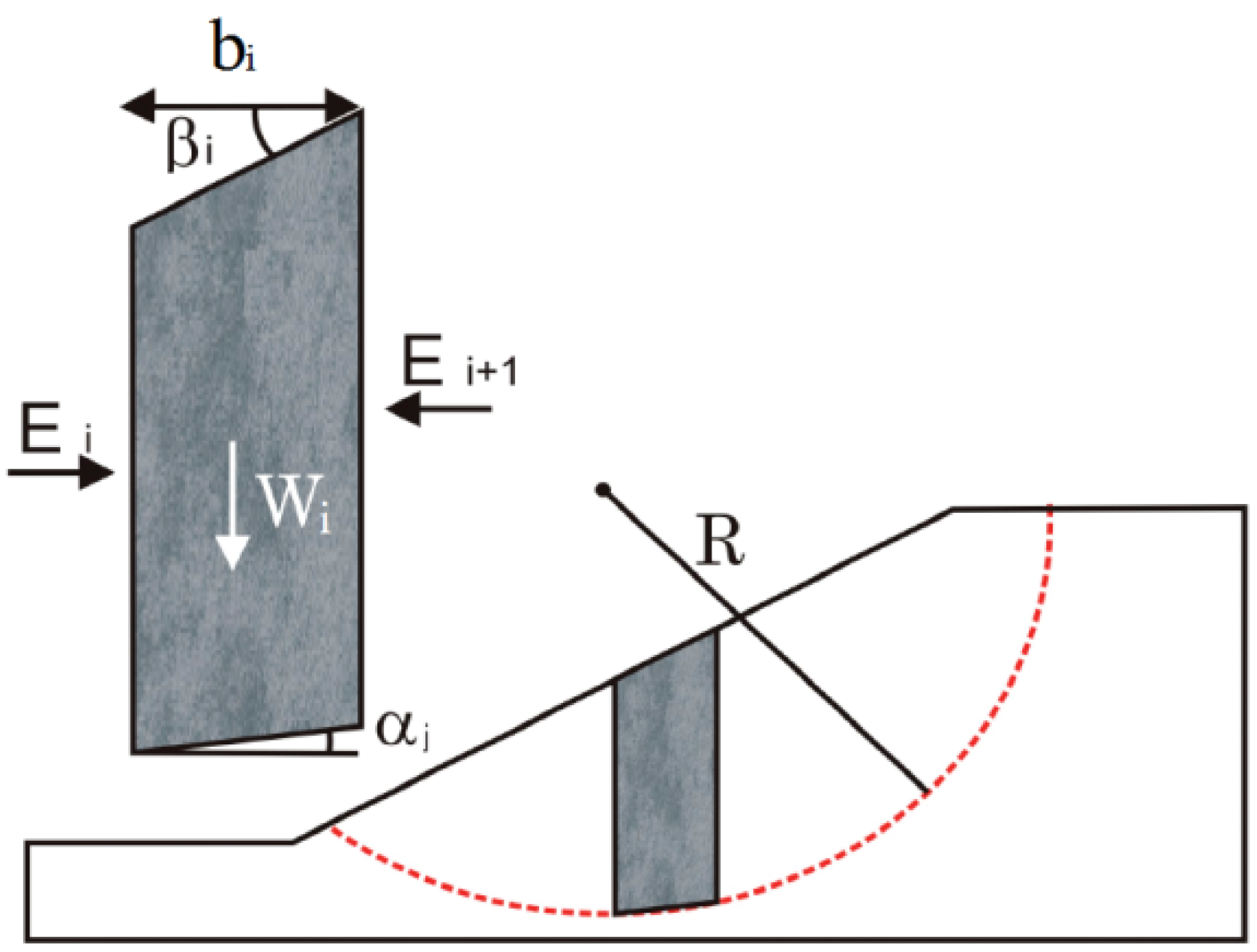
3. Estimation for Moments of the Performance Function
3.1. Calculation of Moments for Sample Variables



| Distribution type | Normal distribution | Lognormal distribution | Exponential distribution |
|---|---|---|---|
| Skewness coefficient CsX | 0 | 0.324 | 2 |
| Kurtosis coefficient CkX | 3 | 3.514 | 9 |
3.2. Estimation for Moments of the Performance Function

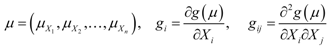

4. Maximum Entropy Method for Calculation of PDF

4.1. Optimization Formulation to Calculate PDF

















4.2. Calculation of Failure Probability of Slope
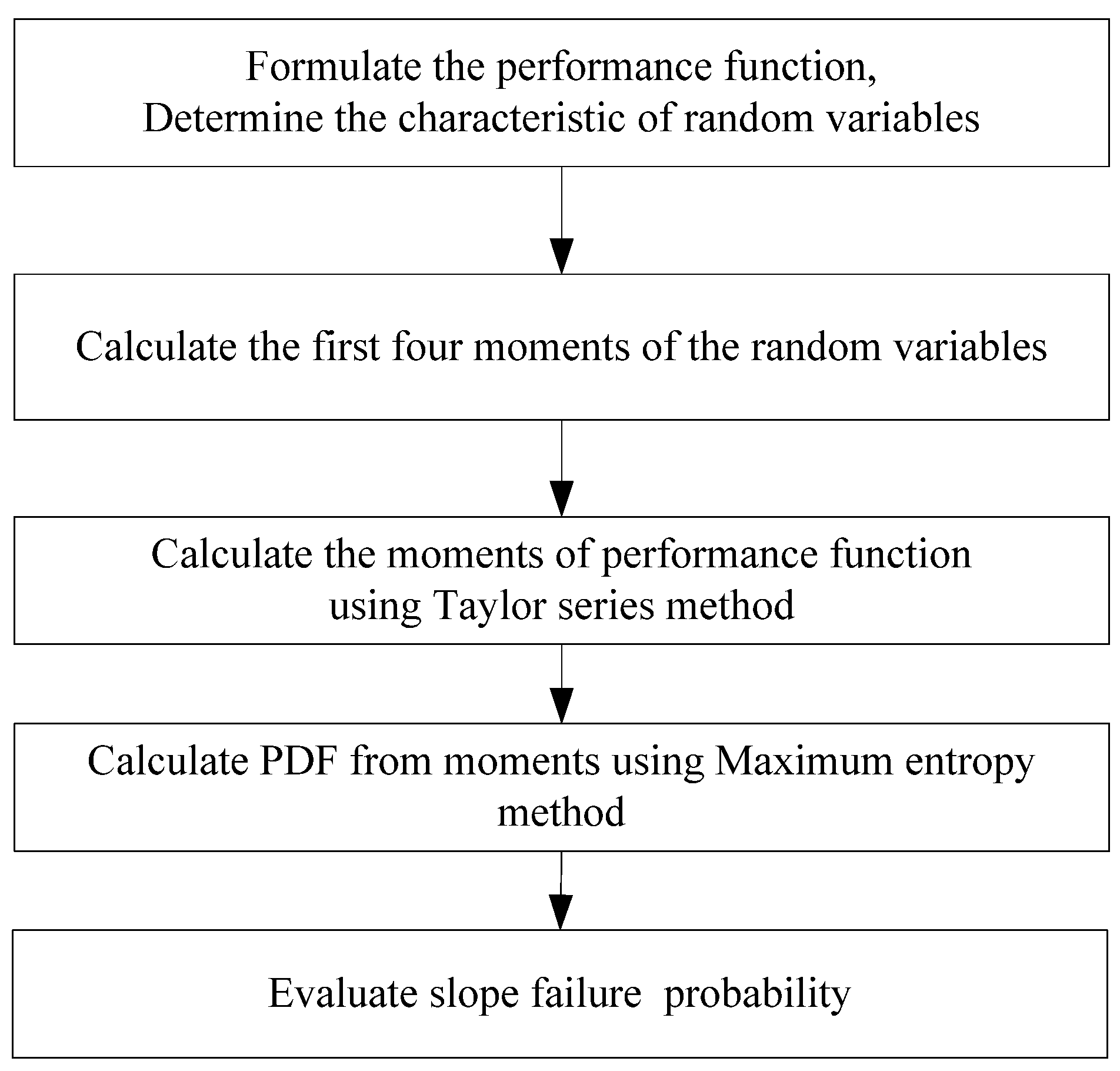
5. Numerical Example
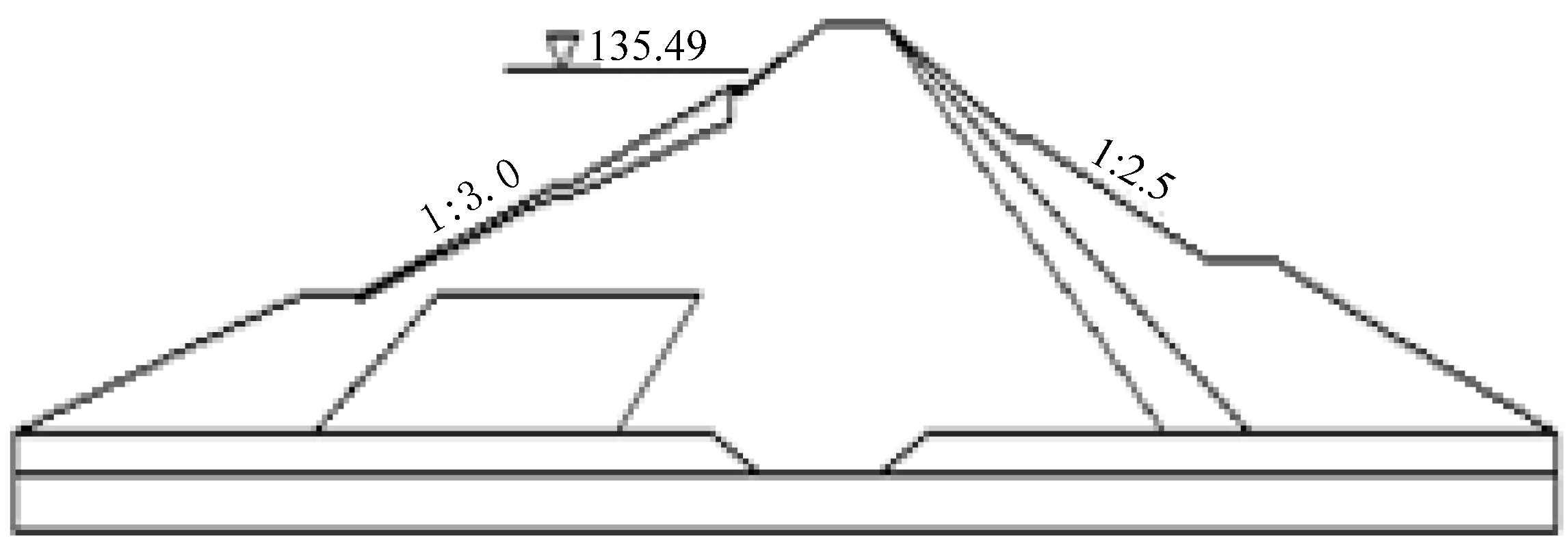
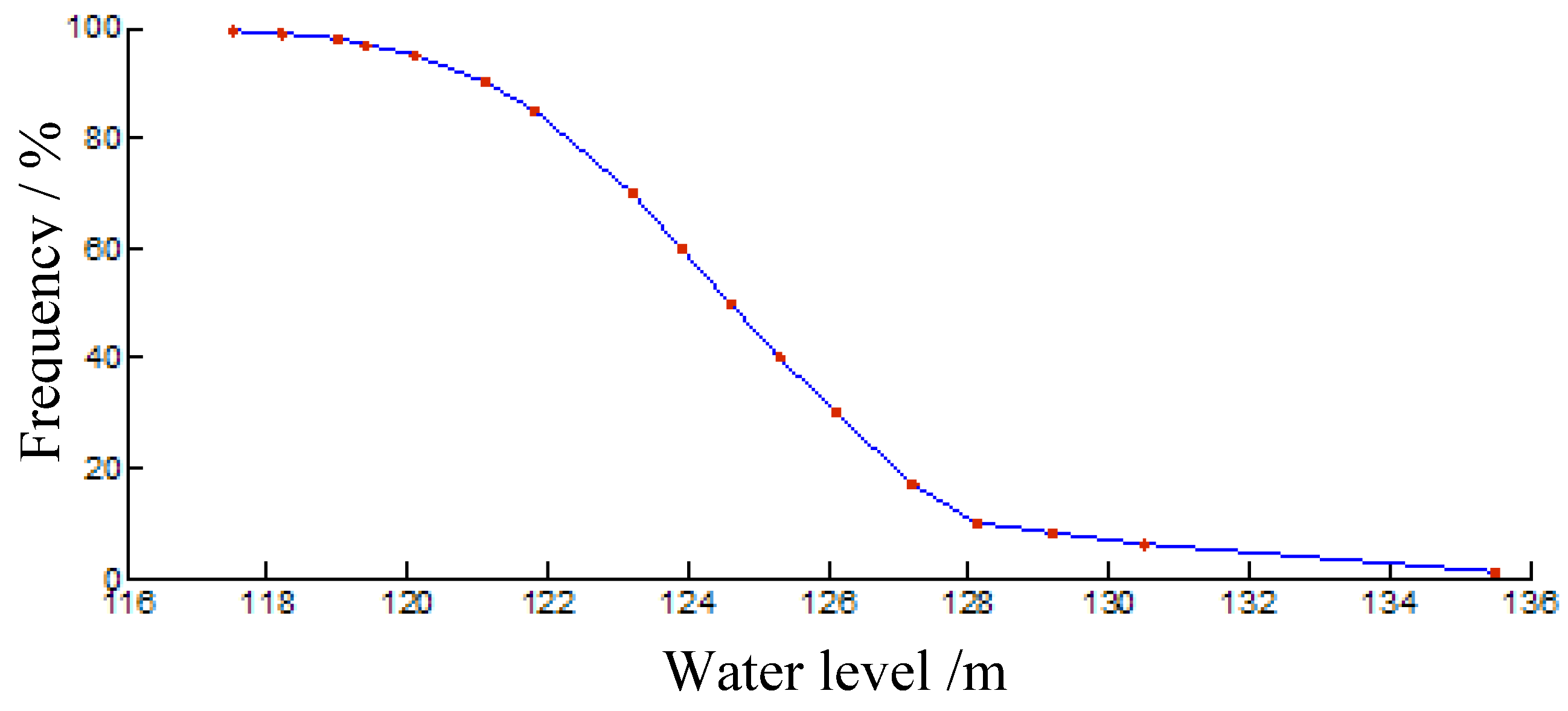
| Soil parameter | Distribution type | Mean value | Standard deviation |
|---|---|---|---|
| Cohesion, c (KN/m2) | Extreme type Ι | 12 | 2.1 |
| Internal friction coefficient , Tanφ | Lognormal | 0.325 | 0.059 |

| Moments | Soil parameter | Performance function /Z | Standardized form / X | |
|---|---|---|---|---|
| c | Tanφ | |||
| 0 | 1 | 1 | 1 | 1 |
| 1st | 0 | 0 | 0 | 0 |
| 2nd | 2.1 | 0.0594 | 4.819E+4 | 1 |
| 3rd | 0 | 0.0217 | 1.520E+07 | 1.437 |
| 4th | 0 | 0.0053 | 3.669E+09 | 1.580 |





| Water level/m | Minimum safety Factor | Reliability index | Failure probability/% | Risk level/10−8 |
|---|---|---|---|---|
| 117.5 | 1.672 | 3.892 | 0.0076 | |
| 118.2 | 1.563 | 3.753 | 0.0112 | 0.516 |
| 119.0 | 1.537 | 3.694 | 0.0126 | 1.096 |
| 119.4 | 1.531 | 3.688 | 0.0139 | 1.221 |
| 120.1 | 1.522 | 3.681 | 0.0144 | 2.608 |
| 121.1 | 1.511 | 3.668 | 0.0157 | 13.845 |
| 121.8 | 1.504 | 3.653 | 0.0162 | 14.690 |
| 123.2 | 1.488 | 3.642 | 0.0168 | 15.210 |
| 123.9 | 1.479 | 3.631 | 0.0175 | 15.795 |
| 124.6 | 1.466 | 3.623 | 0.0188 | 16.705 |
| 125.3 | 1.459 | 3.614 | 0.0199 | 17.810 |
| 126.1 | 1.452 | 3.598 | 0.0238 | 20.150 |
| 127.2 | 1.448 | 3.573 | 0.0251 | 11.278 |
| 128.1 | 1.443 | 3.545 | 0.0278 | 17.063 |
| 129.2 | 1.437 | 3.521 | 0.0327 | 13.943 |
| 130.5 | 1.434 | 3.503 | 0.0392 | 6.279 |
| 135.5 | 1.400 | 3.412 | 0.0429 | 17.875 |
| ∑ | 186.082 |
| Method | Failure probability |
|---|---|
| MCS | 3.85E−04 |
| AFOSM | 4.42E−04 |
| Proposed method | 4.29E−04 |
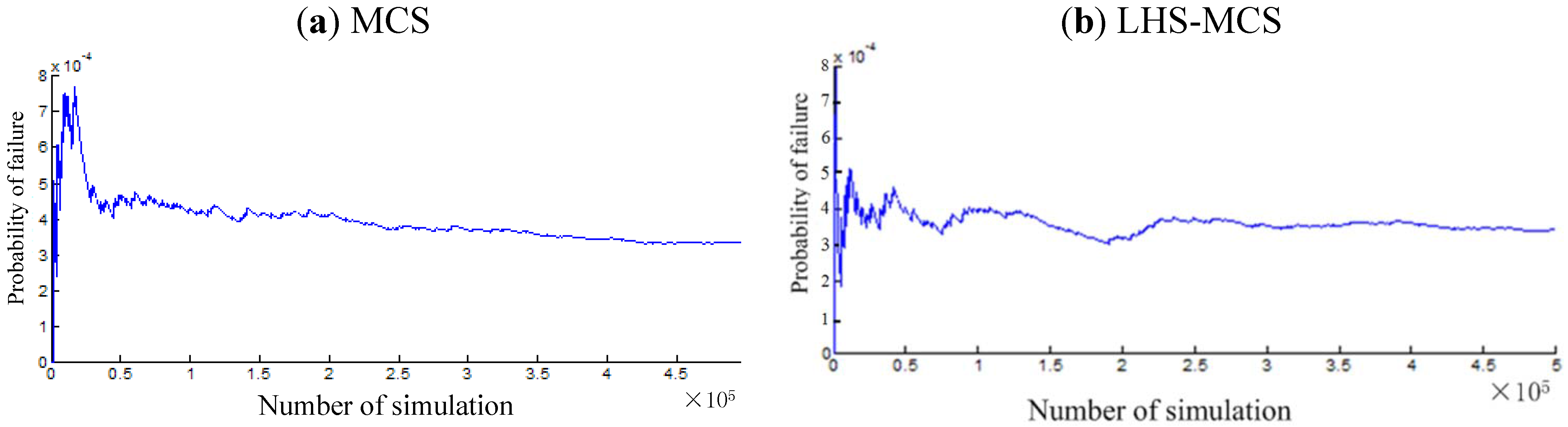
6. Conclusions
Acknowledgments
References
- Tang, W.H.; Yucemen, M.S.; Ang, A.H.-S. Probability based short term design of soil slopes. Can. Geotech. J. 1976, 13, 201–215. [Google Scholar] [CrossRef]
- Christian, J.T.; Ladd, C.C.; Baecher, G.B. Reliability applied to slope stability analysis. J. Geotech. Eng. 1994, 120, 2180–2207. [Google Scholar] [CrossRef]
- Hassan, A.M.; Wolff, T.F. Search algorithm for minimum reliability index of earth slopes. J. Geotech. Geoenviron. 1999, 125, 301–308. [Google Scholar] [CrossRef]
- Low, B.K.; Tang, W.H. Reliability analysis of reinforced embankments on soft ground. Can. Geotech. J. 1997, 34, 672–685. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Gollwitzer, S.; Kruse, W.; Rackwitz, R. New light on first- and second-order reliability methods. Struct. Saf. 1987, 4, 267–284. [Google Scholar] [CrossRef]
- Xu, B.; Low, B.K. Probabilistic stability analyses of embankments based on finite-element method. J. Geotech. Geoenviron. 2006, 132, 1444–1454. [Google Scholar] [CrossRef]
- Greco, V.R. Efficient Monte Carlo technique for locating critical slip surface. J. Geotech. Eng. 1996, 122, 517–525. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Lagaros, N.D. Reliability-based structural optimization using neural networks and Monte Carlo simulation. Comput. Method Appl. Mech. Eng. 2002, 191, 3491–3507. [Google Scholar] [CrossRef]
- Li, C.; Wang, S.; Wang, W. Overtopping risk analysis using LHS-MC method (in Chinese). J. Hydrol. Eng. 2012, 31, 5–9. [Google Scholar]
- Zhao, Y.G.; Ono, T. Moment method for structural reliability. Struct. Saf. 2001, 23, 47–75. [Google Scholar] [CrossRef]
- Lee, S.H.; Choi, H.S.; Kwak, B.M. Multilevel design of experiments for statistical moment and probability calculation. Struct. Multidiscip. Optim. 2008, 37, 57–70. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Dakessian, T. Multiple design points in first and second-order reliability. Struct. Saf. 1998, 20, 37–49. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. Nonnormal dependent vectors in structural reliability. J. Eng. Mech. Div. 1981, 107, 1127–1238. [Google Scholar]
- Seo, H.S.; Kwak, B.M. Efficient statistical tolerance analysis for general distributions using three-point information. Int. J. Prod. Res. 2002, 40, 931–944. [Google Scholar] [CrossRef]
- Kang, H.Y.; Kwak, B.M. Application of maximum entropy principle for reliability-based design optimization. Struct. Multidiscip. Optim. 2009, 38, 331–346. [Google Scholar] [CrossRef]
- Sobczyk, K.; Trebicki, J. Approximate probability distributions for stochastic systems: Maximum entropy method. Comput. Method Appl. Mech. Eng. 1999, 168, 91–111. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, W.; Bai, S. A method of maximum entropy density function for calculation of approximate failure probability (in Chinese). Chin. J. Rock Mech. Eng. 1995, 14, 119–129. [Google Scholar]
- Zheng, J.-J.; Xu, Z.-J.; Liu, Y. Reliability analysis for vertical bearing capacity of piles based on the maximum entropy principle (in Chinese). Chin. J. Geotech. Eng. 2010, 32, 1643–1647. [Google Scholar]
- Bishop, A.W. The use of the slip circle in the stability analysis of earth slopes. Geotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, G. Reliability analysis of structures based on maximum entropy theory (in Chinese). J. Dalian Univ. Technol. 1992, 32, 455–459. [Google Scholar]
- Jaynes, ET. Information theory and statistical mechanics. Phys Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, C.; Wang, W.; Wang, S. Maximum-Entropy Method for Evaluating the Slope Stability of Earth Dams. Entropy 2012, 14, 1864-1876. https://doi.org/10.3390/e14101864
Li C, Wang W, Wang S. Maximum-Entropy Method for Evaluating the Slope Stability of Earth Dams. Entropy. 2012; 14(10):1864-1876. https://doi.org/10.3390/e14101864
Chicago/Turabian StyleLi, Chuanqi, Wei Wang, and Shuai Wang. 2012. "Maximum-Entropy Method for Evaluating the Slope Stability of Earth Dams" Entropy 14, no. 10: 1864-1876. https://doi.org/10.3390/e14101864
APA StyleLi, C., Wang, W., & Wang, S. (2012). Maximum-Entropy Method for Evaluating the Slope Stability of Earth Dams. Entropy, 14(10), 1864-1876. https://doi.org/10.3390/e14101864




