Quantitative Comparison of Conformational Ensembles
Abstract
:1. Introduction
1.1. Terminology and Definitions
1.2. Established Measures of Conformational and Shape Similarity
2. Generating Conformational Ensembles
2.1. Invariance and Degeneracy
2.2. Conformational Boltzmann Distribution
2.3. Elastic Network Models
3. Similarity Measures for Conformational Ensembles
3.1. Difference
3.2. Kullback-Leibler Divergence
4. Numerical Examples and Comparison with RMSD
4.1. Example 1: Perturbed Protein Structure
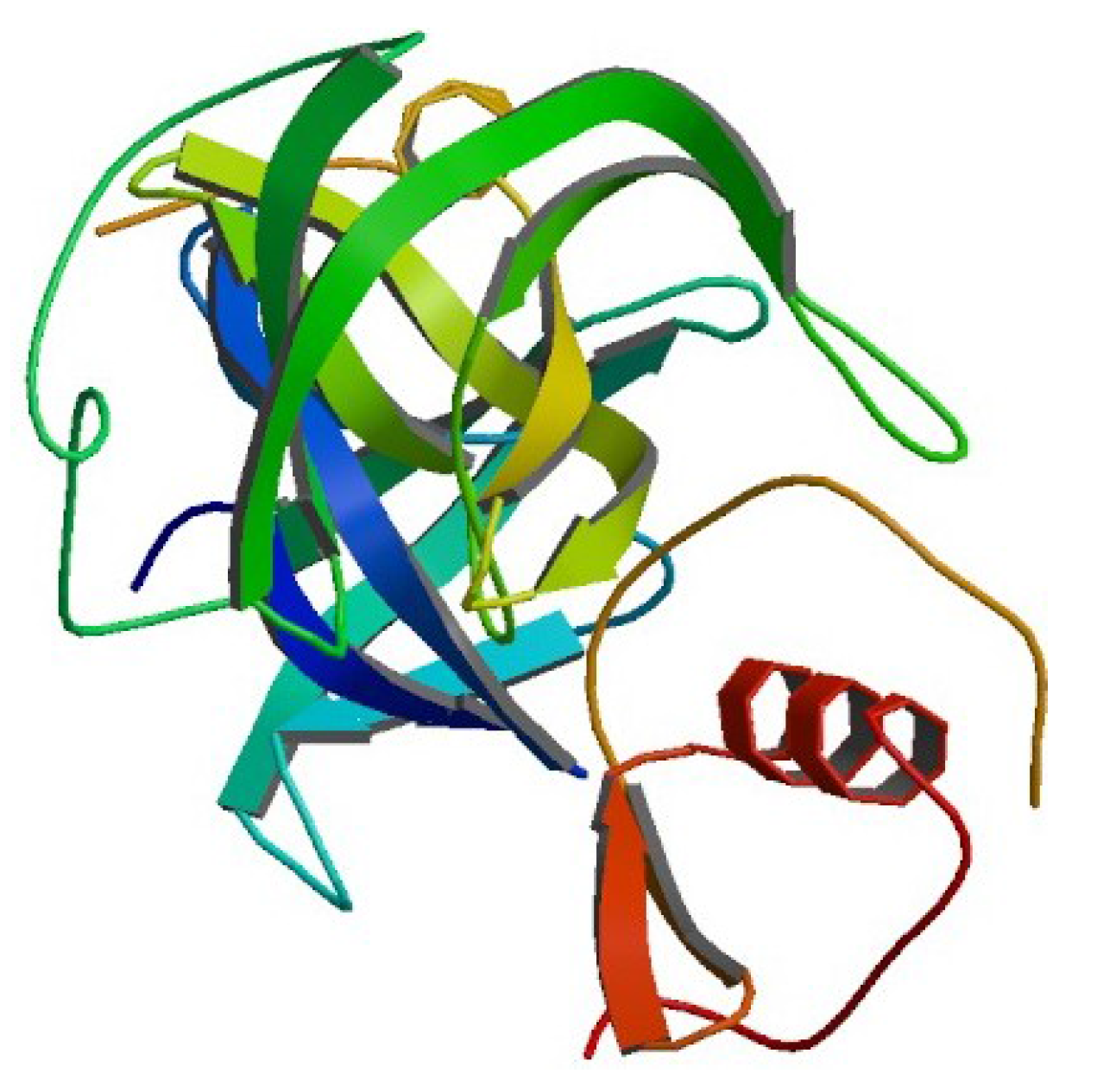
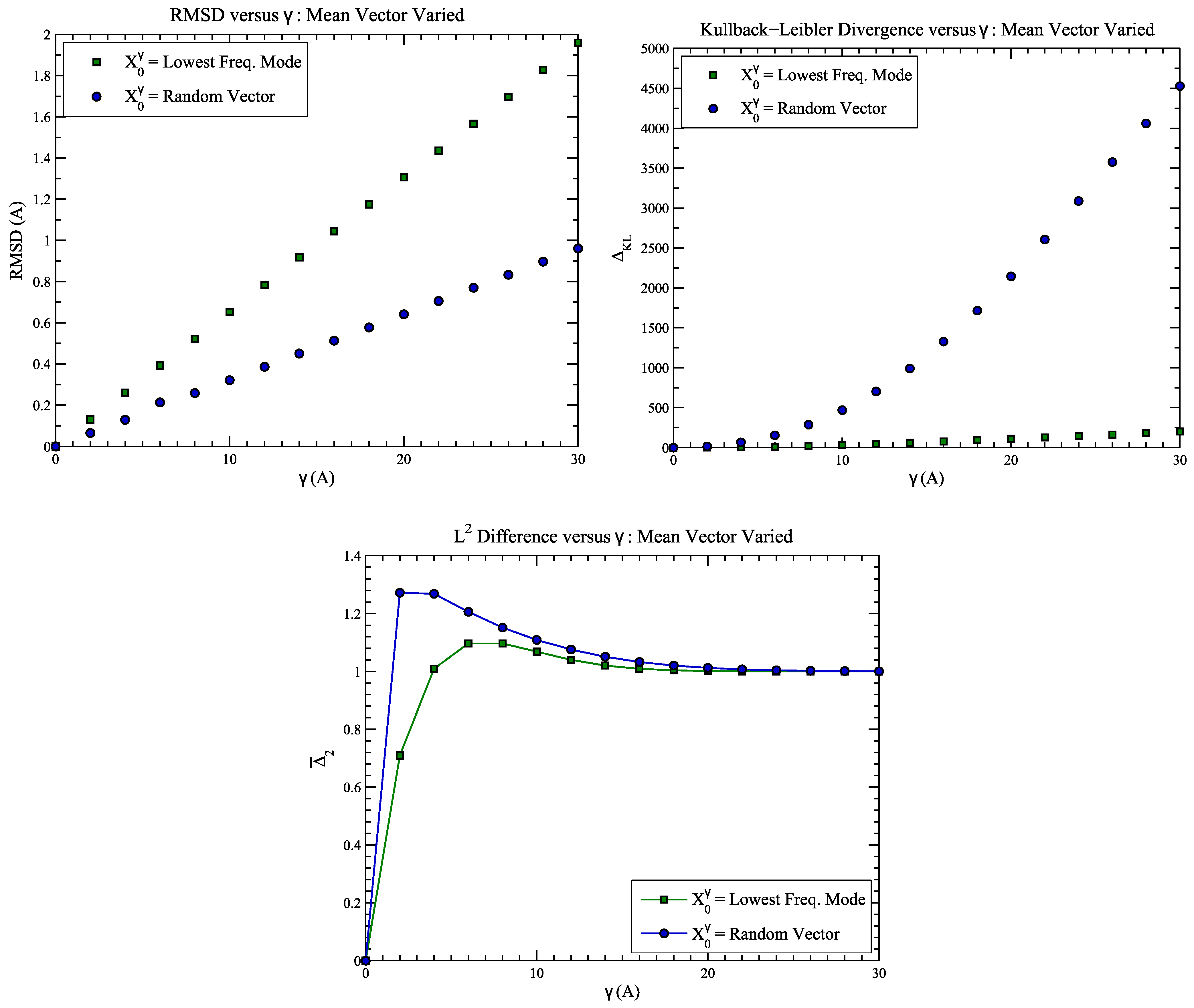
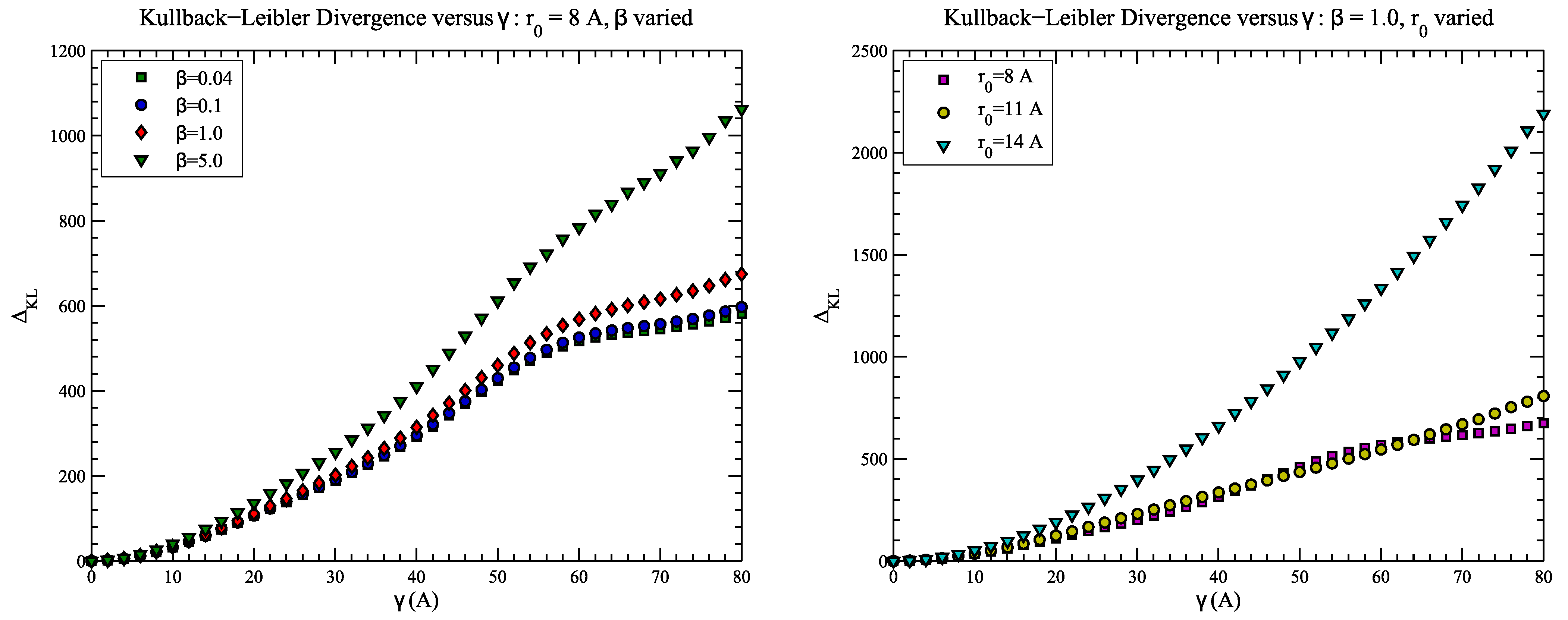
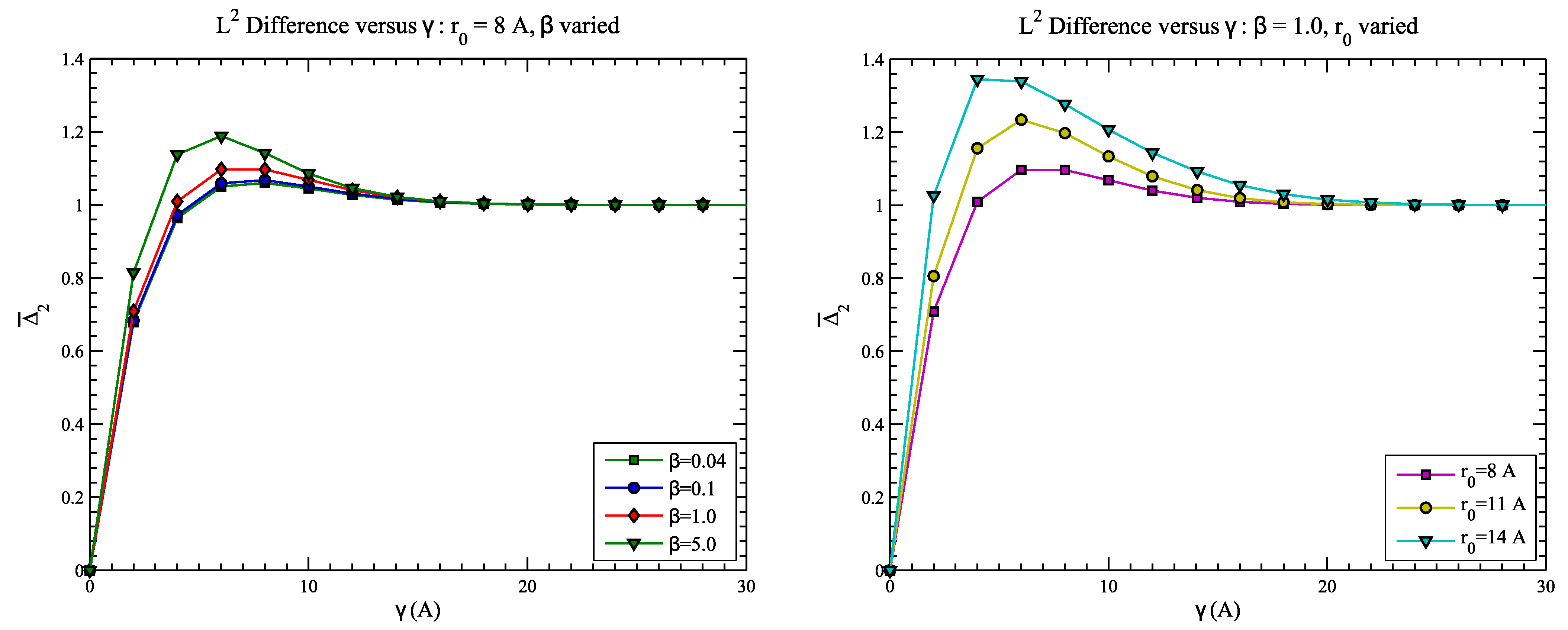
4.2. Example 2: CASP Predictions


5. Conclusions
Acknowledgements
References and Notes
- Holm, L.; Sander, C. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 1993, 233, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, E.M.; Artymiuk, P.J.; Rice, D.W.; Willett, P. Use of techniques derived from graph theory to compare secondary structure motifs in proteins. J. Mol. Biol. 1989, 212, 151–166. [Google Scholar] [CrossRef]
- Zemla, A.; Venclovas, C.; Moult, J.; Fidelis, K. Processing and analysis of CASP3 protein structure predictions. Protein. Struct. Funct. Bioinform. 1999, 37, 22–29. [Google Scholar] [CrossRef]
- Gong, H.P.; Rose, G.D. Does secondary structure determine tertiary structure in proteins? Protein. Struct. Funct. Bioinform. 2005, 61, 338–343. [Google Scholar] [CrossRef] [PubMed]
- Irving, J.A.; Whisstock, J.C.; Lesk, A.M. Protein structural alignments and functional genomics. Proteins 2001, 42, 378–382. [Google Scholar] [CrossRef]
- Jewett, A.I.; Huang, C.C.; Ferrin, T.E. MINRMS: An efficient algorithm for determining protein structure similarity using root-mean-squared-distance. Bioinformatics 2003, 19, 625–634. [Google Scholar] [CrossRef] [PubMed]
- Hilser, V.J.; Garcia-Moreno, E.B.; Oas, T. G; Kapp, G.; Whitten, S.T. A statistical thermodynamic model of the protein ensemble. Chem. Rev. 2006, 106, 1545–1558. [Google Scholar] [CrossRef] [PubMed]
- Hilser, V.J.; Dowdy, D.; Oas, T.G.; Freire, E. The structural distribution of cooperative interactions in proteins: Analysis of the native state ensemble. Proc. Nat. Acad. Sci. U. S. A. 1998, 95, 9903–9908. [Google Scholar] [CrossRef]
- Tyka, M.D.; Keedy, D.A.; Andre, I.; Dimaio, F.; Song, Y.; Richardson, D.C.; Richardson, J.S.; Baker, D. Alternate states of proteins revealed by detailed energy landscape mapping. J. Struct. Biol. 2011, 405, 607–618. [Google Scholar] [CrossRef] [PubMed]
- Burra, P.V.; Zhang, Y.; Godzik, A.; Stec, B. Global distribution of conformational states derived from redundant models in the PDB points to non-uniqueness of the protein structure. Proc. Nat. Acad. Sci. U. S. A. 2009, 106, 10505–10510. [Google Scholar] [CrossRef] [PubMed]
- Chirikjian, G.S. Modeling loop entropy. Methods Enzymol. 2011, 487, 99–132. [Google Scholar] [PubMed]
- Zhou, H.-X. Loops in proteins can be modeled as worm-like chains. J. Phys. Chem. B 2001, 105, 6763–6766. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, M.; Chen, R.; Wang, W.; Liang, J. Discrete state model and accurate estimation of loop entropy of RNA secondary structures. J. Chem. Phys. 2008, 128. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Clementi, C.; Kavraki, L.E. Modeling protein conformational ensembles: From missing loops to equilibrium fluctuations. Protein. Struct. Funct. Bioinform. 2006, 65, 164–179. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Kavraki, L.E.; Clementi, C. On the characterization of protein native state ensembles. Biophys. J. 2007, 92, 1503–1511. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Brooks, B.R. Toward canonical ensemble distribution from self-guided Langevin dynamics simulation. J. Chem. Phys. 2011, 134, 134108:1–134108:12. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; American Institute of Physics: New York, NY, USA, 1994. [Google Scholar]
- Jacobs, D.J.; Rader, A.J.; Kuhn, L.A.; Thorpe, M.F. Protein flexibility predictions using graph theory. Protein. Struct. Funct. Bioinform. 2001, 44, 150–165. [Google Scholar] [CrossRef] [PubMed]
- Damm, K.L.; Carlson, H.A. Gaussian-weighted RMSD superposition of proteins: A structural comparison for flexible proteins and predicted protein structures. Biophys. J. 2006, 90, 4558–4573. [Google Scholar] [CrossRef] [PubMed]
- Moult, J.; Pederson, J.T.; Judson, R.; Fidelis, K. A large-scale experiment to assess protein structure prediction methods. Protein. Struct. Funct. Genet. 1995, 23, ii–iv. [Google Scholar] [CrossRef] [PubMed]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Tramontano, A. Critical assessment of methods of protein structure prediction (CASP)—Round IX. Protein. Struct. Funct. Bioinform. 2011, 79, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Wodak, S.J. From the Mediterranean coast to the shores of Lake Ontario: CAPRI’s premiere on the American continent. Protein. Struct. Funct. Bioinform. 2007, 69, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Janin, J. Welcome to CAPRI: A critical assessment of predicted interactions. Protein. Struct. Funct. Bioinform. 2002, 47. [Google Scholar] [CrossRef]
- Here the word “similarity” is not used in the sense of basic geometry which involves rigid-body and scale transformations, but rather describes small differences in shape.
- Chiang, C.-J.; Chirikjian, G.S. Similarity metrics with applications in modular robot motion planning. Auton. Robot. 2001, 10, 91–106. [Google Scholar] [CrossRef]
- Pamecha, A.; Ebert-Uphoff, I.; Chirikjian, G.S. Useful metrics for modular robot motion planning. IEEE Trans. Robot. Autom. 1997, 13, 531–545. [Google Scholar] [CrossRef]
- The interpretation of the “action” · depends on the context. We can talk about the action on a function, g·ρ′, or on a vector, g·x, or other objects.
- Chennubhotla, C.; Rader, A.J.; Yang, L.-W.; Bahar, I. Elastic network models for understanding biomolecular machinery: From enzymes to supramolecular assemblies. Phys. Biol. 2005, 2, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K.; Chirikjian, G.S.; Jernigan, R.L. Elastic models of conformational transitions in macromolecules. J. Mol. Graph. Model. 2002, 21, 151–160. [Google Scholar] [CrossRef]
- Zheng, W.; Brooks, B.R.; Hummer, G. Protein conformational transitions explored by mixed elastic network models. Protein. Struct. Funct. Bioinform. 2007, 69, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Maragakis, P.; Karplus, M. Large amplitude conformational change in proteins explored with a plastic network model: Adenylate kinase. J. Mol. Biol. 2005, 352, 807–822. [Google Scholar] [CrossRef] [PubMed]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Bahar, I.; Atilgan, A.R.; Erman, B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Design 1997, 2, 173–181. [Google Scholar] [CrossRef]
- Doruker, P.; Jernigan, R.L.; Bahar, I. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem. 2002, 23, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Rader, A.J.; Bahar, I.; Jernigan, R.L. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 2004, 147, 302–314. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- CASP9. Protein Structure Prediction Center, University of California, Davis. 2010. Available online: http://predictioncenter.org/casp9/ (accessed on 25 January 2012).
- Read, R.J.; Fujinaga, M.; Sielecki, A.R.; James, M.N. Structure of the complex of Streptomyces griseus protease B and the third domain of the turkey ovomucoid inhibitor at 1.8-A resolution. Biochemistry 1983, 22, 4420–4433, PDB ID: 3GSB. [Google Scholar] [CrossRef] [PubMed]
- RCSB Protein Data Bank. Available online: http://www.pdb.org (accessed on 20 January 2012).
- Joint Center for Structural Genomics. Crystal structure of a TetR family transcriptional regulator (Caur_2714) from Chloroflexus aurantiacus J-10-FL at 2.56 A resolution. PDB ID: 3NRG.
Appendix
A. Restricting the Conformational Boltzmann Distribution and Applying a Rigid-Body Transformation
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wolfe, K.C.; Chirikjian, G.S. Quantitative Comparison of Conformational Ensembles. Entropy 2012, 14, 213-232. https://doi.org/10.3390/e14020213
Wolfe KC, Chirikjian GS. Quantitative Comparison of Conformational Ensembles. Entropy. 2012; 14(2):213-232. https://doi.org/10.3390/e14020213
Chicago/Turabian StyleWolfe, Kevin C., and Gregory S. Chirikjian. 2012. "Quantitative Comparison of Conformational Ensembles" Entropy 14, no. 2: 213-232. https://doi.org/10.3390/e14020213
APA StyleWolfe, K. C., & Chirikjian, G. S. (2012). Quantitative Comparison of Conformational Ensembles. Entropy, 14(2), 213-232. https://doi.org/10.3390/e14020213



