3.1. Introduction of a Multibaker Chain System and the Conventional Formalism
The multibaker chain consists of
N rectangular sites of width
and height
h. The length,
l, is the total length of the chain, determining the typical length for the sites to span in a given direction. At each time step, the
nth square site,
, is divided into three vertical columns numbered from
ω=0 (leftmost) to two (rightmost). That is why the map is called a triadic multibaker chain system. The
ωth strip of width
and height,
h, is to be mapped onto the
ωth horizontal strip of width
and height
on the
th site,
. The summation of
and
with respect to
ω are unity for the site,
. Such a map
T can be described as:
where (
n,
x,
y) denotes a position (
x,
y) on the
nth site; the map is defined in the range
and
. The origin is fixed at the lower left corner of each site, and the coordinates,
x and
y, are the horizontal and vertical direction, respectively.
The site
is partitioned by disjoint
horizontal cells, identified by
, where
= 0, 1 or 2. The partitioning is based on the fact that the SRB (Sinai-Ruelle-Bowen) measure [
1] is smooth in the unstable direction [
13,
24]. The quantity,
, can be regarded as a ternary number, and each cell of width
by height
forms a line in its numerical order from bottom to top. Then,
d, independent of
n, is interpreted as a trit number expressing the resolution of the partitioning. Hereafter, a partition identified by the number on the
nth site is denoted by
.
Now, let us introduce the following vertical position,
:
where:
The above-mentioned partitioning leads to a Markov partition [
21,
24] when the vertical range of the partition
is arranged to be
, where
denotes the ternary number obtained by the addition of one to the number
. Note that the height,
, of the partition can be expressed as:
Herein, appropriate boundary conditions are needed so that the site number
m=
in Equation (24) can be defined, even if the number is outside the range of
, described later.
The condition for a dissipative chain system to be consistent with non-equilibrium thermodynamics requires that
[
6,
7], and such a map is found to be invertible in the sense that it has a time-reversal operator
R, defined as
, such that
and the reversed map
can be described as
.
The definition (24) can be utilized to define a region
where
k is a positive integer and the region is a partition like the ones mentioned above if
. The region has the area of
, and the equation for the probability measure on the region can be expressed as:
where
denotes the probability measure at the
tth step in the region
, and
. This equation shows that
corresponds to the transition probability,
. If all of the
partitions in the
N sites are numbered and the
ith corresponding measure,
P, at the
tth step is denoted by
, then Equation (26) for
k=
d can be rewritten in the form of Equation (
1). Thus, we have the form of the balance Equations (11), (18) and (20) for local entropy density specific to this multibaker chain system.
Ishida [
10] and Vollmer
et al. [
6,
7,
8,
9] introduced a triadic multibaker chain system whose macroscopic measure (probability) density
ρ is governed by the one-dimensional Fokker-Planck equation, namely:
When
v and
D are uniform in the bulk system, the macroscopic density profile is microscopically realized by the following transition probability, which is independent of site number
n for
:
where
D(>0) denotes the diffusion coefficient,
v the drift velocity and
the time step. For the case of
, the bulk system becomes dissipative. The transfer rate has the property that
when
. This property of the triadic multibaker model is the key to realizing a convergent macroscopic density profile that is governed by the Fokker-Planck equation [
5,
7]. As described later, a different transfer rate is imposed on the boundary site
.
When the probability
η corresponding to the transition probability
is thus defined, it is straightforward to confirm that:
for the inversion of the drift,
i.e., the sign of the drift velocity,
v, where
and
are the expansion rate and transition probability for the inverted map, respectively. As a result, the symmetric and antisymmetric parts of the transition volume
are identified as Equation (
4).
Considering that the transition probability (28) can be rewritten as:
the condition that
should be positive yields:
where
and
is the so-called grid Péclet number [
25]. Therefore, the time step
τ must be greater than or equal to the order of
. In this study, the order is taken to be
, so that
β is constant [
10].
For comparison, let us consider here the formulation proposed by Gilbert, Dorfman and Gaspard [
5] in which the time change of the coarse-grained entropy,
, at a site,
, based on the partition,
, is divided into entropy flux
, entropy flow due to a thermostat,
, and internal entropy production,
. A similar formalism has also been utilized by Vollmer, Tél and Breymann [
6]. Applying the formulation to the present multibaker chain in which both
ν and
η depend on site
n, we obtain the following balance equation:
where:
Substituting Equation (26) into Equation (31), we can easily find its local, coarse-grained form, Equation (22), such that:
and so on. Herein,
means the sum of a quantity over the partitions included in the site,
, and the summation divided by
is in accord with the definition of the averaging, Equation (6), on a macroscopic small region,
. Vollmer, Tél and Breymann [
6] theoretically show that the averaged quantities have the following convergent properties:
as
, where:
The macroscopic quantities appearing on the RHS of Equation (33) should be evaluated at a macroscopic position,
, and at a macroscopic time,
. It should be stressed here that the property depends only on the transition probability in Equation (28), independent of boundary conditions.
As described in the previous section, the limiting value, Equation (33b), involves a flux term. In order to eliminate the contribution, Vollmer, Tél and Mátyás [
18] proposed another form,
, for the entropy flow due to a thermostat at a site
. For the case of uniform temperature,
becomes:
where
is the site-mean, macroscopic density at the
nth site, defined as:
In the subsequent sections, we will verify the quantity, Equation (34), of the flow to both the bulk system and the boundary. Note, however, the additional term in
cannot be written by the averaging of a coarse-grained term as
, Equation (22c), that communicates with incoming and outgoing partitions. Such a property inheres in the equations for local entropy balance, Equations (13), (15) and (22). That is why the form is not desirable when compared to the averaged form of
, Equation (15).
The remaining problem is the introduction of the boundary condition that leads to a non-equilibrium steady state. As the probability measure is dealt with in this study, however, the total measure included in N sites should be held constant at unity to construct a probability space. To this end, the following probability-measure-preserving map, called a circuit model, is introduced.
3.2. Circuit-Like Model on a Multibaker Chain
Hereafter, the height, h, is fixed at unity, and the N sites are in a circular form of , so that the site number, , in Equation (24) would be defined. A circuit-like, unidirectional property is set in by a thermostat placed on the boundary site , which mimics the action of a battery.
In this model, the transition probability
at site
is set to be:
where
in Equation (35) is defined in Equation (28). In the model, therefore, the local drift velocity,
v, and the diffusion coefficient,
D, are almost uniform in the
r direction, and the boundary site realizes the non-equilibrium steady state, even if
. The form inherently conserves the total probability measure. As described in
Section 3.1, the relation
is given for invertible, dissipative multibaker chains.
The determination of the transfer rate,
, on the boundary follows the model originally proposed by Vollmer, Tél and Mátyás (Model III in [
18]). The rate can be expressed as:
where a Péclet number,
, must be a constant with respect to the site width,
, so that a non-equilibrium (non-uniform) steady state can be realized in the continuous (macroscopic) limit,
[
18]. In order for the rate to be positive, its absolute value must be less than two. This condition, in conjunction with the condition (30), ensures that the density at each site is always positive. The property is essential for evaluating the macroscopic entropy source,
, Equation (7c). Actually, we also have a degree of freedom when setting
different from
β. As long as the ratio,
, is kept constant, however, we can easily show that the ratio,
i.e.,
, does not affect the macroscopic behavior described in the next section. The difference between this circuit model and Model III of Vollmer
et al. [
18] lies in the global Péclet number,
: in the present model, it is not necessarily zero, which would mimic an electric current induced by a battery. Rigorously speaking, heat sources should be distributed along the bulk system provided that such an electric current is induced by only a battery (Model IV in [
18]). In this respect, the current model needs further examination. However, it gives rise to a non-uniform contribution to the macroscopic entropy balance, Equation (7), even in the steady state, allowing us to evaluate averaged quantities under more complex situations.
3.3. Analytical Unsteady Solution of the Fokker-Planck Equation and the Slowest Decaying Mode
The last choice, Equation (36), of transition probability at the boundary site, , determines the unsteady behavior of the macroscopic (averaged) density ρ. Hereafter, we will obtain its analytical unsteady solution.
The circuit model macroscopically realizes a nonequilibrium steady state while the density
ρ evolves according to the Fokker-Planck equation, Equation (27) [
6,
7,
10]. If we choose the spatial mean density, the diffusion coefficient,
D, and the total length,
l, of the chain as three primary quantities, the equation is normalized into the following dimensionless form:
subject to the boundary conditions realized by Equation (36):
and the condition for the total measure:
where
,
and
are dimensionless density, position and time, respectively. The strength
determines the non-uniformity of the steady density distribution. In this study, the reference density
is set to be the spatial mean density 1/
l. Then, its normalized density
is unity, and as such, the normalized local entropy density can be simply expressed as
. Hereafter, the superscript, *, is omitted.
Equation (37) has the analytical solution of the form:
where:
and
is the steady solution of the form:
Here, a complex number,
, made from the sequence of positive real numbers,
, is a solution of the following equation:
and the coefficient,
,
, is determined by an initial probability density. The steady solution, Equation (38c), is responsible for the total measure in the sense that the second term of Equation (38a) is integrated to vanish on the whole space. In Equation (38a), the summand at
n=1 decays most slowly and provides the macroscopic time scale
λ towards the steady state, defined as:
Hereafter, this term is called the slowest decay mode.
Vollmer, Tél and Mátyás [
18] have shown that the summation of the entropy flow, Equation (34), due to a thermostat on and near the boundary site,
i.e.:
recovers the macroscopic entropy flux density into the thermostat on the boundary in the macroscopic limit provided
and
are sufficiently small. In the present model, we obtain:
in the limit for an arbitrary
, and an instant
t. Provided
is sufficiently small, we have that:
This is the extension of Equation (43) of Vollmer
et al. [
18].
Referring to the formulation described in
Section 2, we can define the following analog of
:
and this is the entropy flux density based on the form of Equation (15). In the next section, we will numerically find that
and
agree very well in the continuous limit.
3.4. Numerical Verification of the Decomposed Forms
Next, we shall numerically confirm the validity of the decomposed forms (18) and (20) and the law of order estimation (LOE) on the circuit model.
First, the initial probability measure,
, on each partition,
, is set to be:
where the quantity
R is a sample of a (0,1)-uniform random number generated by an M-sequence [
26], and the coefficient,
, is determined, such that:
Herein,
is an analytical solution expressed as:
where the coefficient,
, is set to be 95% of the maximum,
, such that
for
and
in Equation (38b) is zero. Note that the set is based on the slowest decay mode,
i.e., the typical macroscopic relaxation to the steady state. The global density, Equation (44), is utilized to evaluate each term of the following normalized entropy-density balance equation:
In the following numerical experiments, the trit number,
d, and the coefficient,
β, are fixed at three and 1/2, respectively, for almost all cases.
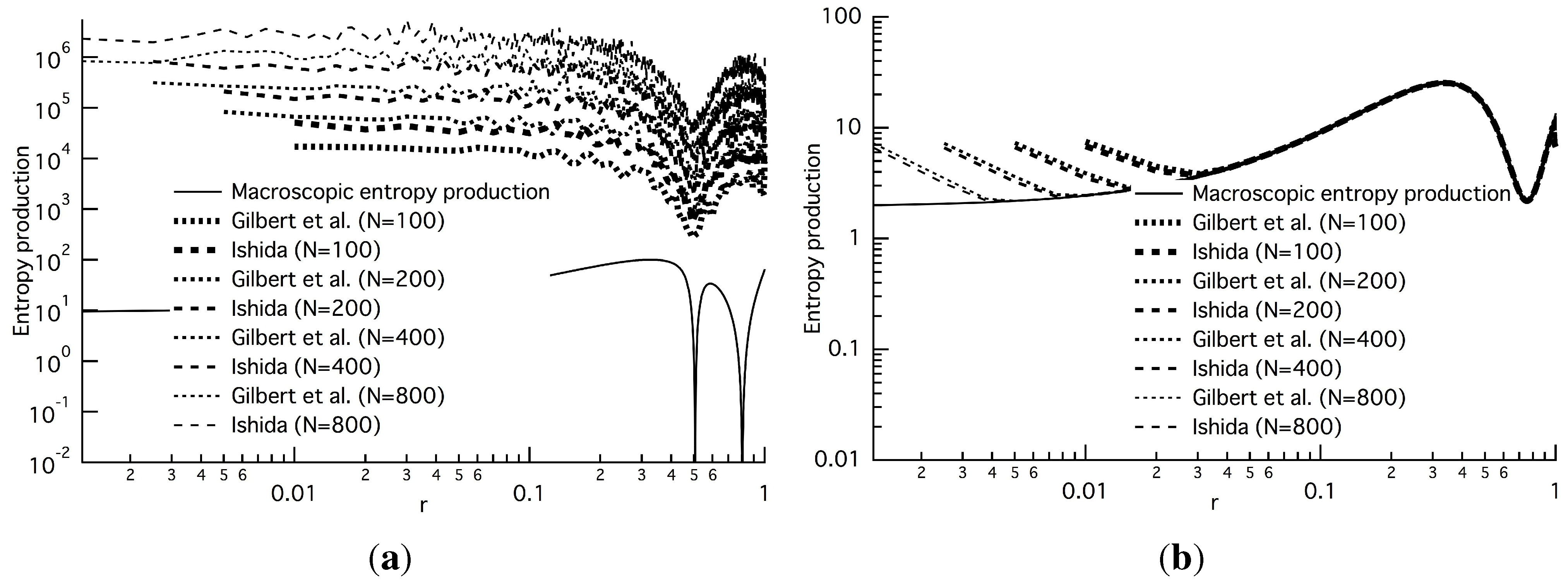
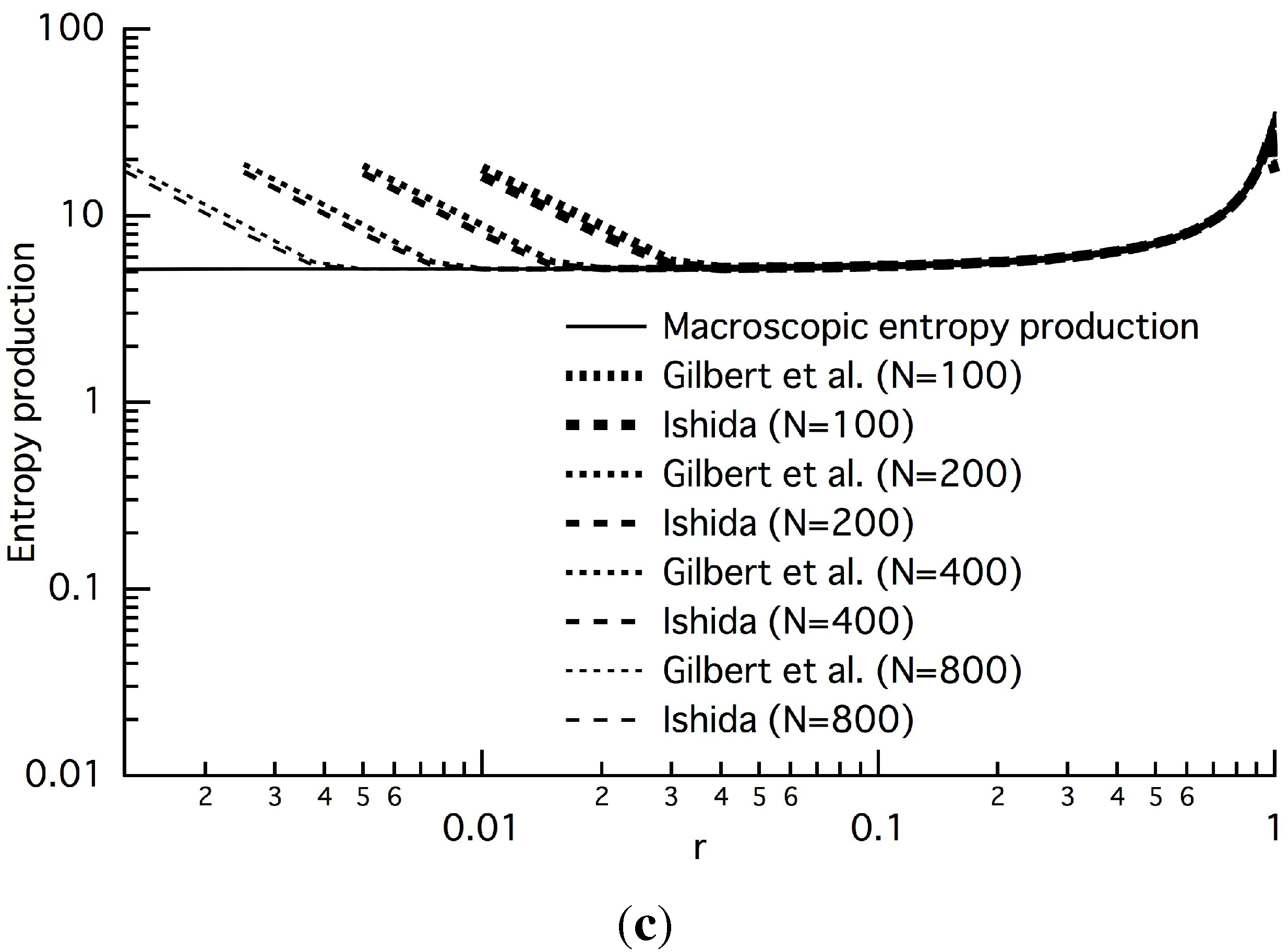
Figure 1 shows the distribution of the macroscopic entropy production,
, Equation (45), and the averaged quantities of
, Equation (20b), and
, Equation (22d), at
Pe=1.5. At the initial state, the three quantities do not coincide (
Figure 1(a)), because the averaged quantities depend on a sequence of random numbers. After
d time steps, however, the dependence vanishes, and we can numerically confirm that the bigger the number of sites
N, the more the two averaged quantities will approach the phenomenological expression,
, of non-equilibrium thermodynamics (
Figure 1(b) and
Figure 1(c)), except near both ends. As the transition probability
η is uniform for almost all sites in this model, the correspondence between
and
can be simply regarded as a numerical confirmation of Equation (33c), theoretically proven by Vollmer, Tél and Breymann [
6]. As shown in
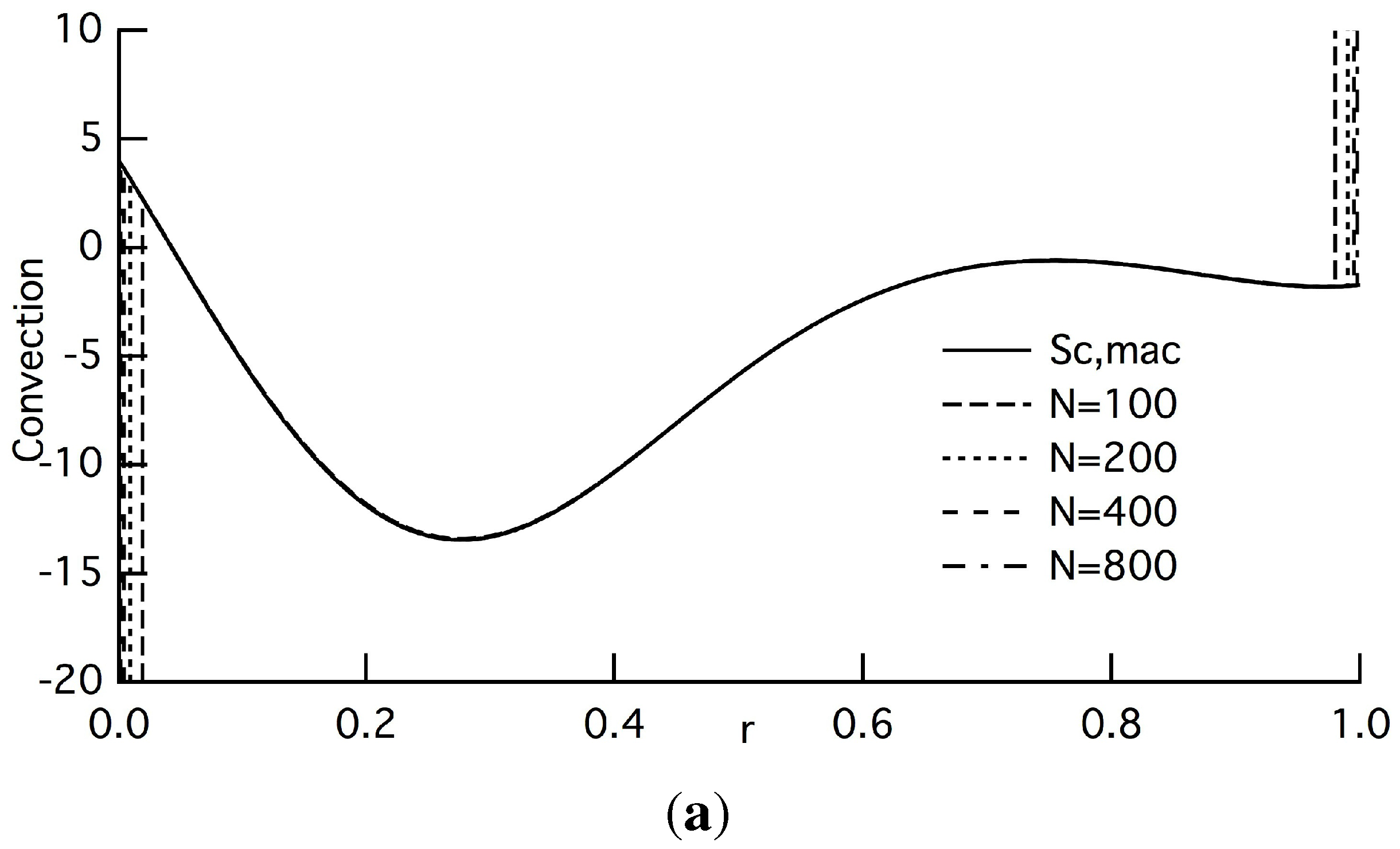
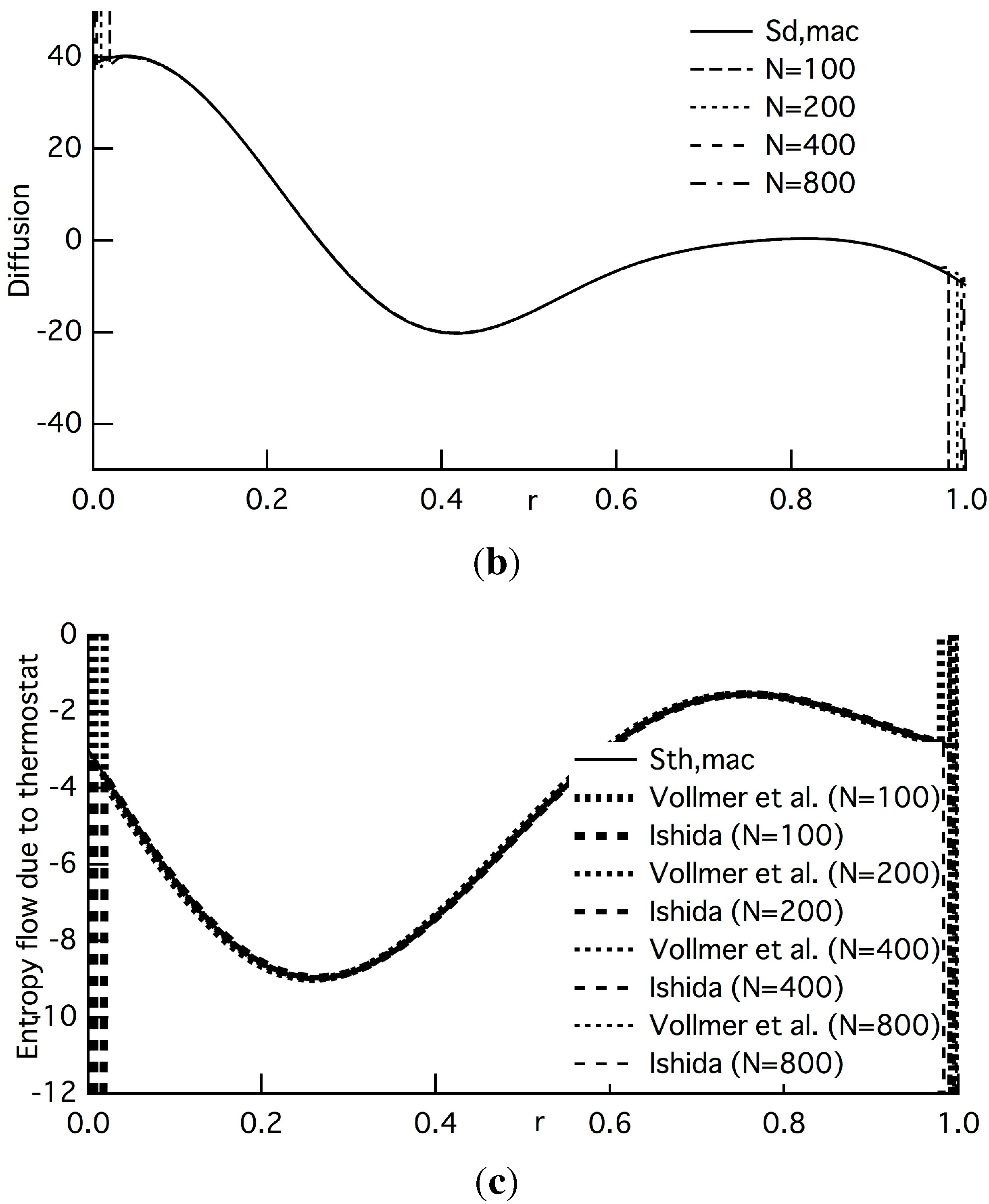
Figure 2, the coincidence in the macroscopic limit is also confirmed for the other terms of the entropy-density balance equation,
i.e.,
,
and
, defined in Equation (45). We can also confirm that the averaged quantity of
agrees very well with
, except near the boundaries (
Figure 2(c)). We can confirm this coincidence for other Péclet’s numbers. These results also validate the LOE, showing that the major terms in Equations (18) and (20) are averaged to be of
in the macroscopic limit. In these figures, we can observe that the macroscopic quantities take a local minimum near
r = 0.4. This is a result of the initial density profile
, Equation (44), having a local minimum near
r = 0.5 and vanishing towards the steady state.
Figure 1.
Entropy production at
,
and
: (
a)
; (
b)
(Equation (39)); (
c) steady state; In this case
,
,
and
in Equation (44) are 2.4873, 12.733,
and zero, respectively. The solid line denotes the macroscopic or phenomenological entropy production,
, Equation (45). The dotted and long-dashed lines are the averaged quantities of
, Equation (22d), introduced by Gilbert
et al. [
5], and the entropy production,
, Equation (20b), respectively. The two quantities are too close to be distinguished from each other.
Figure 1.
Entropy production at
,
and
: (
a)
; (
b)
(Equation (39)); (
c) steady state; In this case
,
,
and
in Equation (44) are 2.4873, 12.733,
and zero, respectively. The solid line denotes the macroscopic or phenomenological entropy production,
, Equation (45). The dotted and long-dashed lines are the averaged quantities of
, Equation (22d), introduced by Gilbert
et al. [
5], and the entropy production,
, Equation (20b), respectively. The two quantities are too close to be distinguished from each other.
Figure 2.
Leading terms except the entropy production at
and
: (
a) convection; (
b) diffusion; (
c) entropy flow due to a thermostat. The solid line denotes the macroscopic terms in the macroscopic balance equation for the entropy density, Equation (45): (a)
, (b)
, (c)
. In
Figure 2(a) and 2(b), the other lines denote corresponding averaged terms appearing in Equation (18): (a)
, Equation (18b), (b)
, Equation (18c). Short-dashed, pecked, long-dashed and dash-dotted lines denote the cases of
N=100, 200, 400 and 800, respectively. In
Figure 2(c), the dotted and long-dashed lines are
, Equation (34), introduced by Vollmer, Tél and Mátyás [
18], and the averaged quantity of entropy flow,
, Equation (20c), respectively. All of the lines agree very well, except near both ends.
Figure 2.
Leading terms except the entropy production at
and
: (
a) convection; (
b) diffusion; (
c) entropy flow due to a thermostat. The solid line denotes the macroscopic terms in the macroscopic balance equation for the entropy density, Equation (45): (a)
, (b)
, (c)
. In
Figure 2(a) and 2(b), the other lines denote corresponding averaged terms appearing in Equation (18): (a)
, Equation (18b), (b)
, Equation (18c). Short-dashed, pecked, long-dashed and dash-dotted lines denote the cases of
N=100, 200, 400 and 800, respectively. In
Figure 2(c), the dotted and long-dashed lines are
, Equation (34), introduced by Vollmer, Tél and Mátyás [
18], and the averaged quantity of entropy flow,
, Equation (20c), respectively. All of the lines agree very well, except near both ends.
Although the details are not given here, we can also numerically confirm Equations (33a) and (33b). Note that the present decomposition makes it possible to directly evaluate all the macroscopic terms in Equation (45) by averaging the corresponding local, coarse-grained terms.
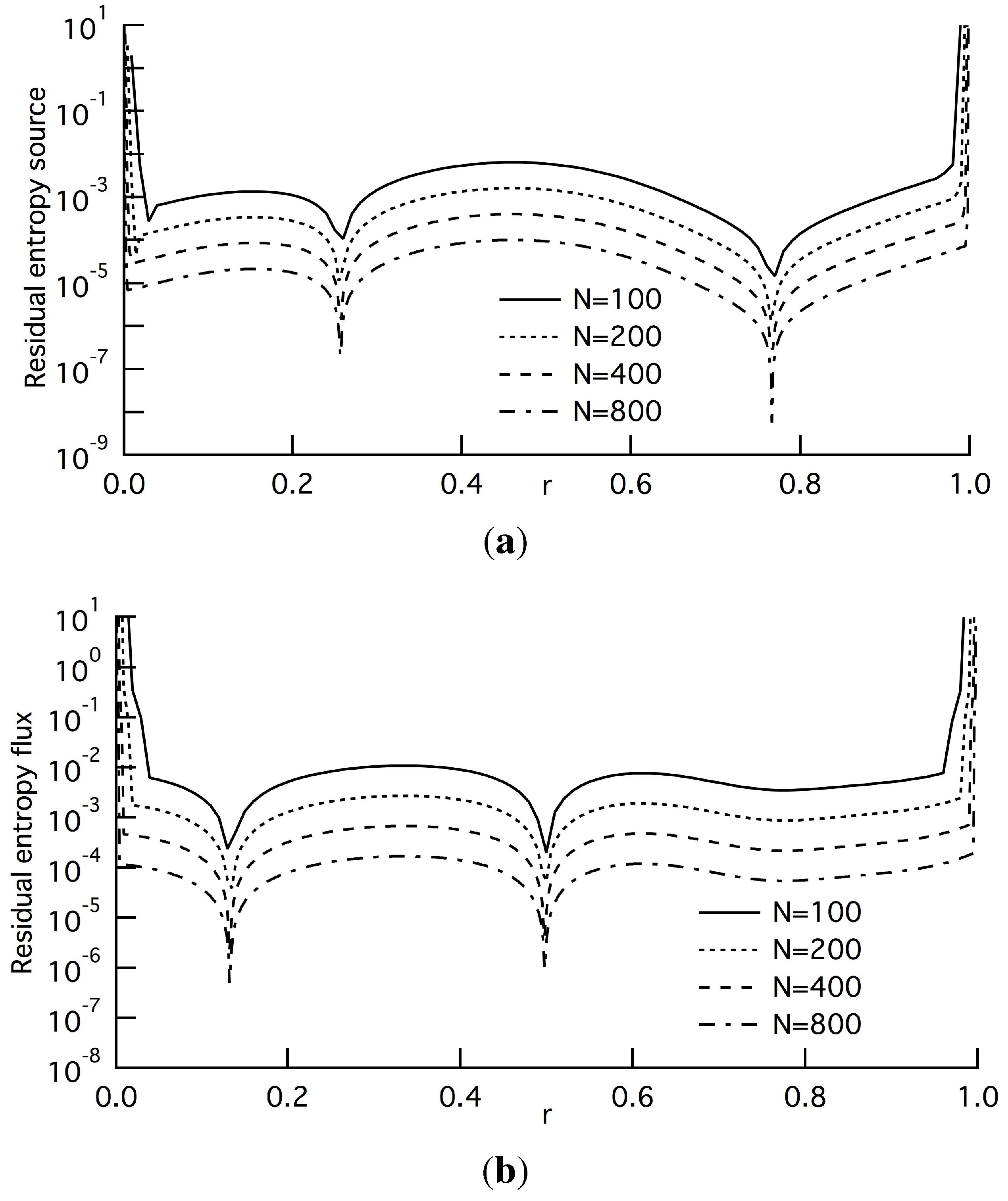
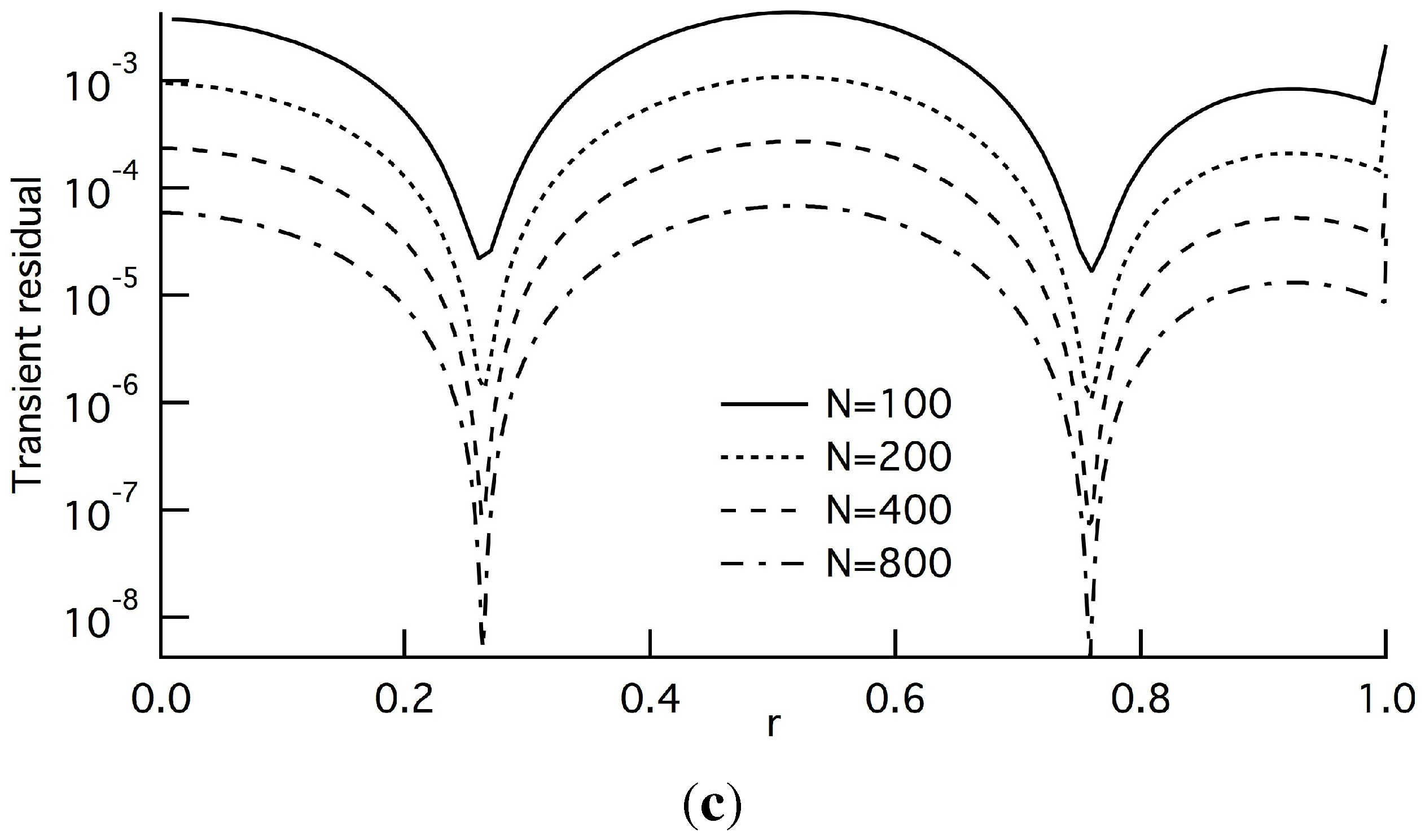
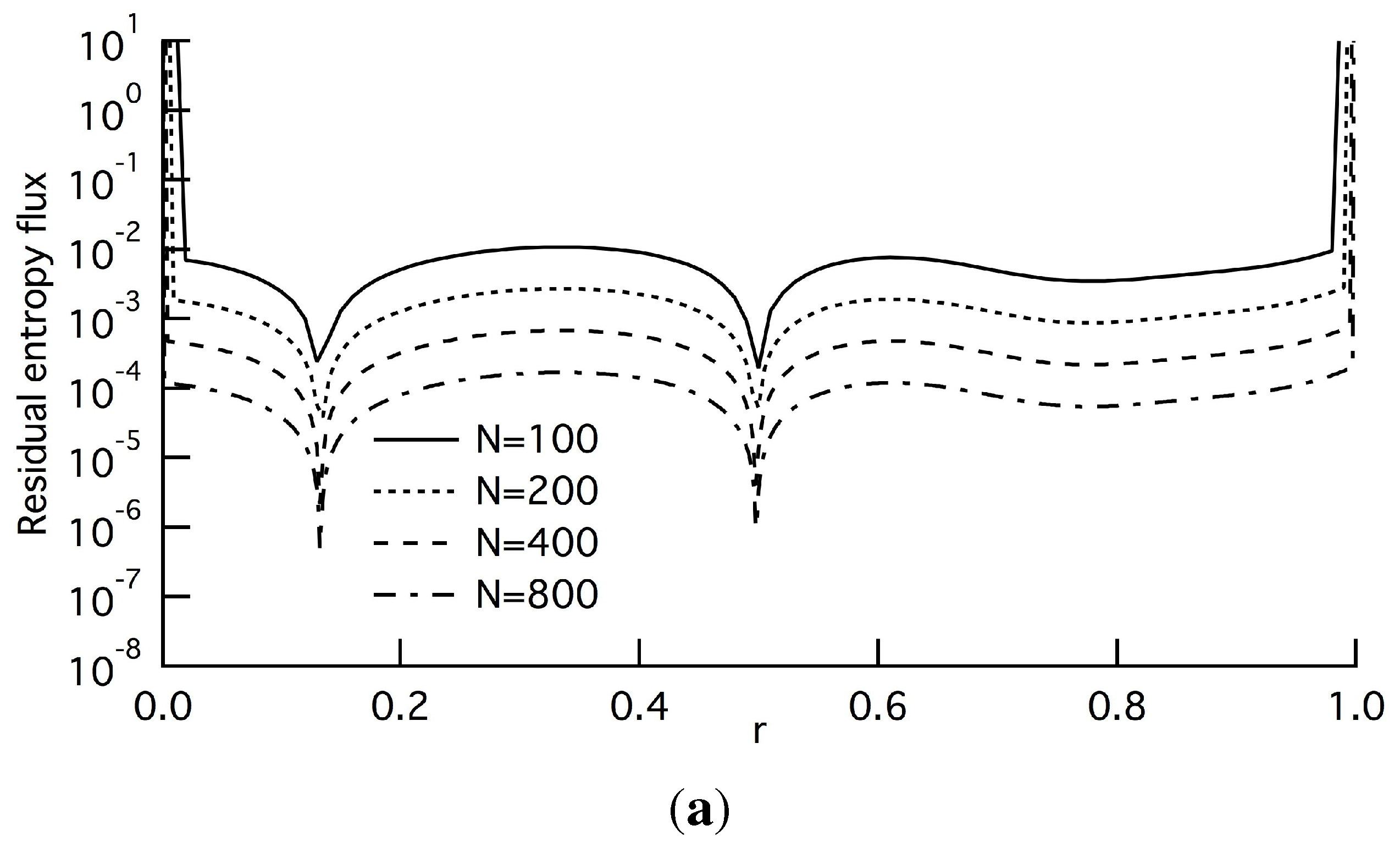
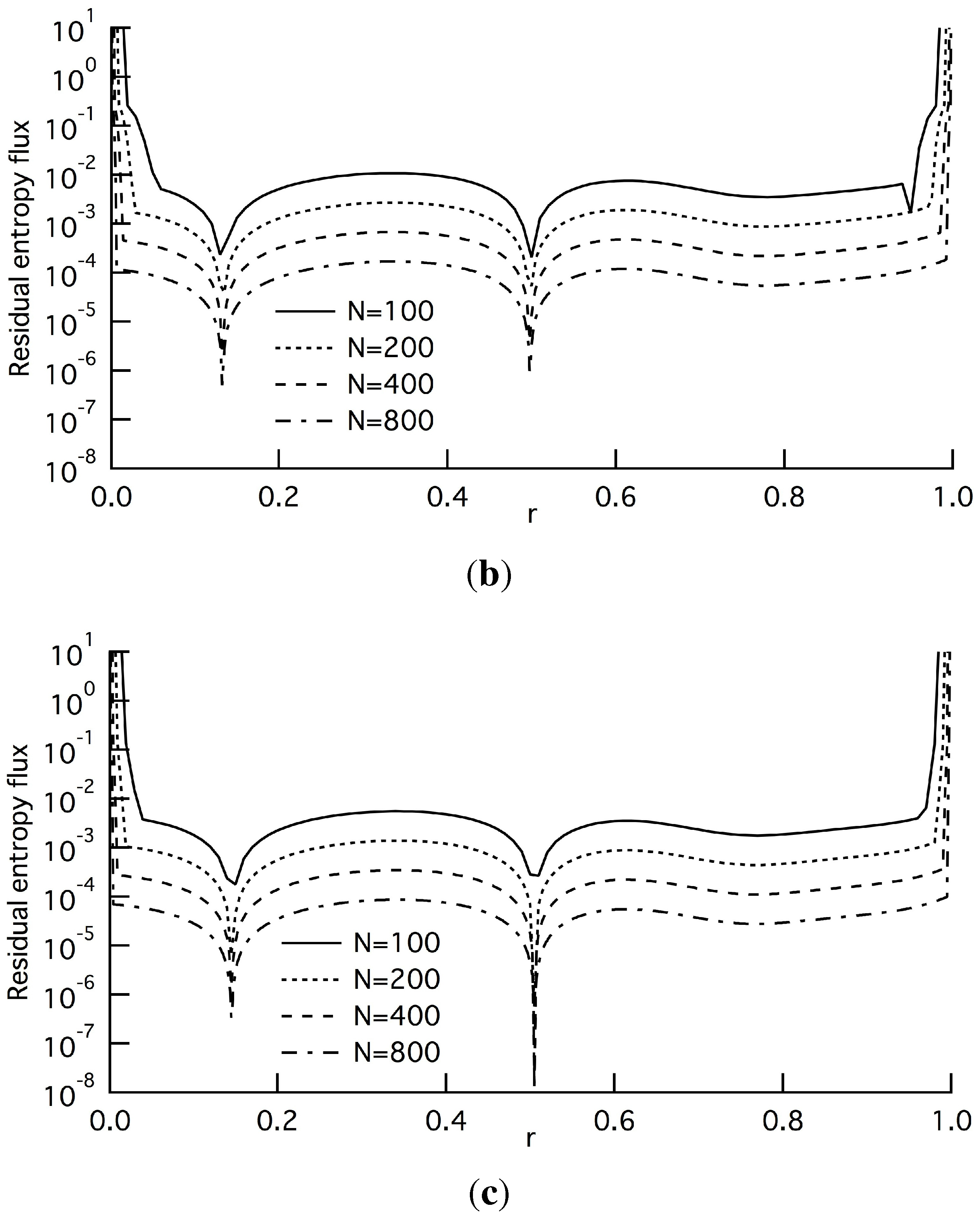
In contrast, as shown in
Figures 3(a) and 3(b), the averaged quantities of the residual entropy source and residual entropy flux,
and
, are vanishing in the macroscopic limit, and the four lines are equally spaced in the vertical direction for almost all regions of
r. This indicates that the two quantities behave according to
as
increases [
10], and
b is evaluated to be two from the width in accord with the LOE. This equally-spaced behavior is also confirmed in the averaged quantity of
(
Figure 3(c)) and the two minor terms,
and
(
Figure 4). It is surprising that all of the quantities behave according to
. As described in
Section 3.1, however, the order of the averaged quantity of
is not of
, but of
, and the agreement relies on the present setting of
,
i.e.,
. In
Figure 3 and
Figure 4, we can find several dips, which can be explained by the form of the leading terms of these averaged quantities: the prefactors of
, composed of higher-order derivatives, becomes small at these positions. At this time, however, they are unknown.
In the above-mentioned figures, we find a divergence in the evaluated values near both ends. This indicates that the LOE is not satisfied on the boundary. This is caused by the gap of both the global measure and the transition probability near the boundary site,
. For the entropy flow due to a thermostat, however, we can interpret the quantities as the heat transfer into the boundary.
Table 3 shows such a boundary effect. We can numerically confirm that
and
agree very well in spite of the disagreement of each component and that they approach the macroscopic entropy flux density,
, into the thermostat in the continuous limit. Because of the violation of the LOE at the boundary site, the averaged values of the residual
and the minor term,
, do not vanish in the continuous limit. The effectiveness of the fundamental form
, including the contribution of these terms, therefore, comes from the simplicity of deriving the term only on the basis of the symmetric and antisymmetric properties.
Figure 3.
Absolute value of the averaged residual terms at and : (a) residual entropy source , Equation (20f); (b) residual entropy flux , Equation (18d); (c) transient residual , Equation (9c). Solid, broken, long-dashed and dash-dotted lines denote the cases of N = 100, 200, 400 and 800, respectively. All of the lines are equally spaced in the vertical direction, and the width indicates that these averaged quantities are of .
Figure 3.
Absolute value of the averaged residual terms at and : (a) residual entropy source , Equation (20f); (b) residual entropy flux , Equation (18d); (c) transient residual , Equation (9c). Solid, broken, long-dashed and dash-dotted lines denote the cases of N = 100, 200, 400 and 800, respectively. All of the lines are equally spaced in the vertical direction, and the width indicates that these averaged quantities are of .
Figure 4.
Absolute value of the averaged minor terms at and : (a) minor entropy production , Equation (20d); (b) minor entropy flow due to a thermostat , Equation (20e). Solid, broken, long-dashed and dash-dotted lines denote the cases of N = 100, 200, 400 and 800, respectively. All of the lines are also equally spaced in the vertical direction, and the width indicates that these averaged quantities are also of .
Figure 4.
Absolute value of the averaged minor terms at and : (a) minor entropy production , Equation (20d); (b) minor entropy flow due to a thermostat , Equation (20e). Solid, broken, long-dashed and dash-dotted lines denote the cases of N = 100, 200, 400 and 800, respectively. All of the lines are also equally spaced in the vertical direction, and the width indicates that these averaged quantities are also of .
Table 3.
Entropy flux density into the boundary ().
Table 3.
Entropy flux density into the boundary ().
| | N | t | (Equation (40)) | (Equation (42)) | (Equation (41)) |
|---|
| 1.5 | 100 | λ | | | |
| 1.5 | 100 | ∞ | | | |
| 1.5 | 1.5 | 100 | λ | | | |
| 1.5 | 1.5 | 800 | λ | | | |
| 1.5 | 1.5 | 100 | ∞ | | | |
| 1.5 | 1.5 | 800 | ∞ | | | |
| 1.5 | 0.1 | 100 | λ | −20.0 | −19.8 | −15.5 |
| 1.5 | 0.1 | 800 | λ | | | |
| 10 | 1.5 | 100 | λ | | | |
| 10 | 1.5 | 800 | λ | | | |
On the other hand, we can numerically find that the way of partitioning,
i.e.,
β and
d, affects the averaged quantity of the residual and minor terms.
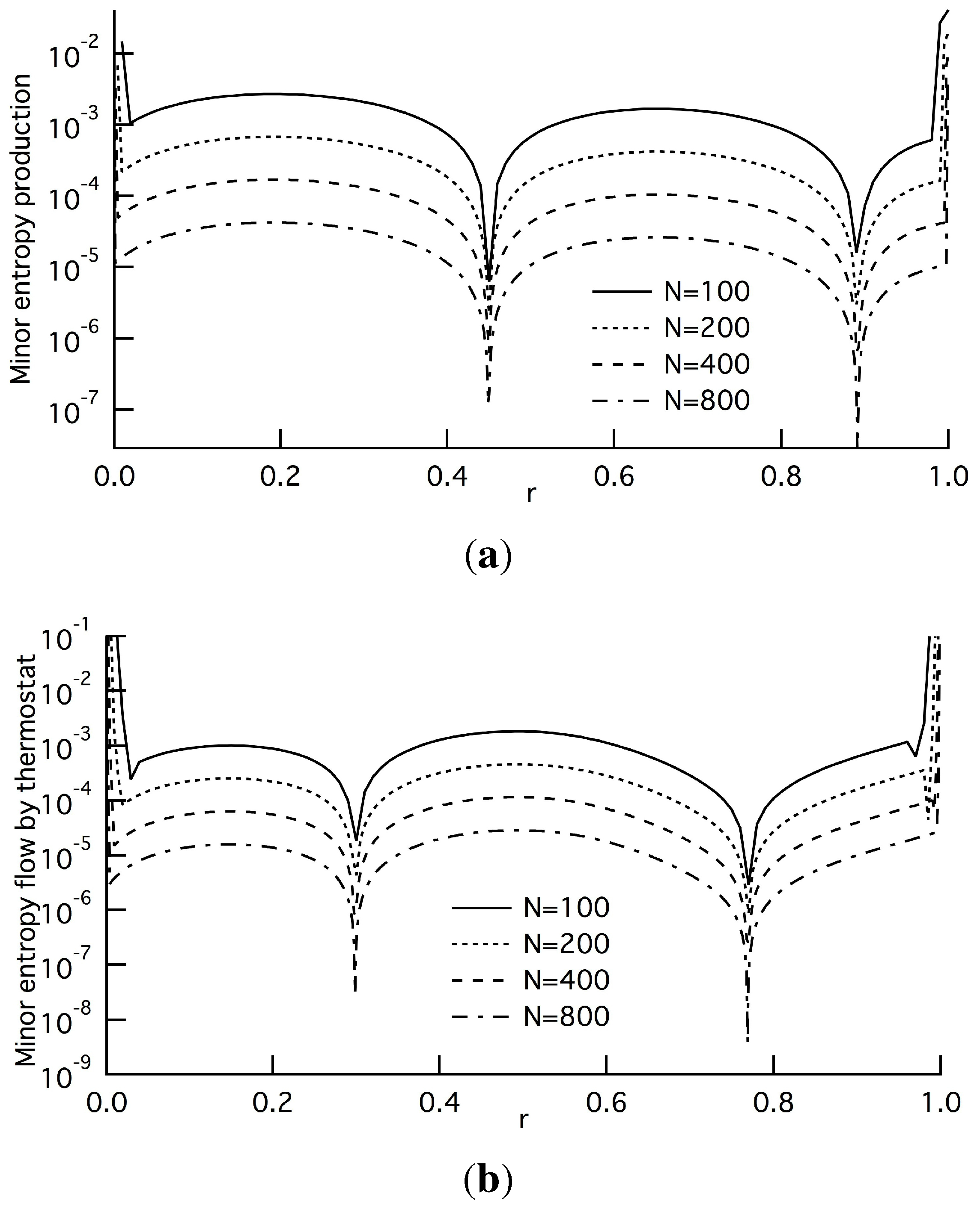
Figure 5 shows the distributions of the averaged residual entropy flux when
β and
d are changed at
t =
λ and
Pe = 1.5. We can ascertain that the partitioning does affect the quantity. However, the four lines are equally spaced, and the width is identical. That is to say, the order of
of the averaged residual, estimated from the LOE, is independent of the partitioning. This is the case for the other residual and minor terms, too.
Figure 5.
Partitioning effects on the absolute value of averaged residual entropy flux , Equation (18d), at : (a) ; (b) ; (c) . Solid, broken, long-dashed and dash-dotted lines denote the cases of N=100, 200, 400 and 800, respectively. The partitioning effects appear. However, all of the lines are equally spaced in the vertical direction, and the width, i.e., the order of these quantities of , is independent of the partitioning.
Figure 5.
Partitioning effects on the absolute value of averaged residual entropy flux , Equation (18d), at : (a) ; (b) ; (c) . Solid, broken, long-dashed and dash-dotted lines denote the cases of N=100, 200, 400 and 800, respectively. The partitioning effects appear. However, all of the lines are equally spaced in the vertical direction, and the width, i.e., the order of these quantities of , is independent of the partitioning.
Similarly, the averaged quantities of the leading terms,
i.e., the zeroth-order (
O(1)) terms, are quantitatively affected by higher order terms.
Figure 6 shows the averaged entropy production at
Pe = 1.5. As shown in the figure, the way of partitioning affects the quantity while
N is relatively small. However, we can confirm that the quantity comes to be independent of the partitioning when
N is sufficiently large. This indicates that the limiting value as
, as well as the order of
estimated from the law are also independent of the partitioning.
The fact that the averaged quantities and their orders are independent of the resolution parameter
d are consistent with the discussions by Gaspard, Gilbert and Barra
et al. [
5,
11,
12,
13,
14,
15,
16,
17,
21]. At the same time, we now confirm that the coarsest partitioning of
d=1 is fine enough to recover macroscopic quantities. This is in accordance with the discussion about “structural stability” by Vollmer, Breymann and Mátyás
et al. [
6,
7,
20]. Since the inverse mapping of a partition of
d=1 (level-1 partition) is a full site (level-0 partition), we cannot treat the past density distribution on a site. Thus, in order to recover the results of thermodynamics, it is sufficient for us to consider one-time mapping from an initial uniform density [
6,
7,
8,
9,
18,
19,
20,
22].
These properties are essential for the coarse-grained statistics [
7,
13]. However, the partitioning can affect averaged quantities not discussed in this study. This is an issue for us to deal with in the future.
Figure 6.
Partitioning effects on the entropy production at : (a) ; (b) ; (c) . The solid line denotes the macroscopic entropy production , Equation (45). The dotted and long-dashed lines are the averaged quantities of , Equation (22d), and the entropy production , Equation (20b), respectively. The two averaged quantities are too close to be distinguished from each other. The partitioning effects are also confirmed. As the site number N increases, however, the effects are weakened.
Figure 6.
Partitioning effects on the entropy production at : (a) ; (b) ; (c) . The solid line denotes the macroscopic entropy production , Equation (45). The dotted and long-dashed lines are the averaged quantities of , Equation (22d), and the entropy production , Equation (20b), respectively. The two averaged quantities are too close to be distinguished from each other. The partitioning effects are also confirmed. As the site number N increases, however, the effects are weakened.