Analysis of Entropy Generation Rate in an Unsteady Porous Channel Flow with Navier Slip and Convective Cooling
Abstract
:1. Introduction
2. Mathematical Model

3. Entropy Analysis
4. Numerical Solution
5. Results and Discussion
5.1. Transient and Steady Flow Profiles

5.2. Code Validation

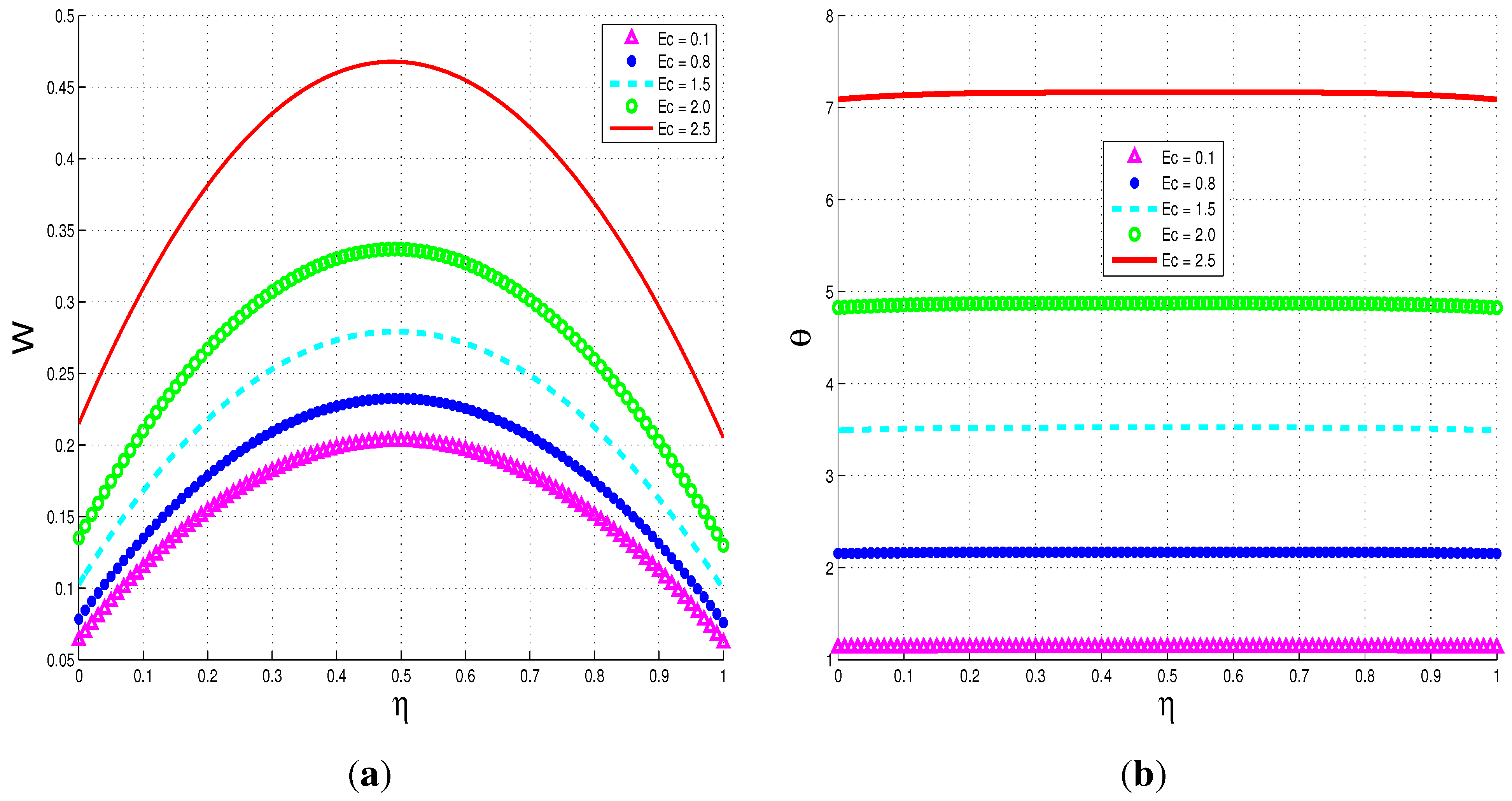
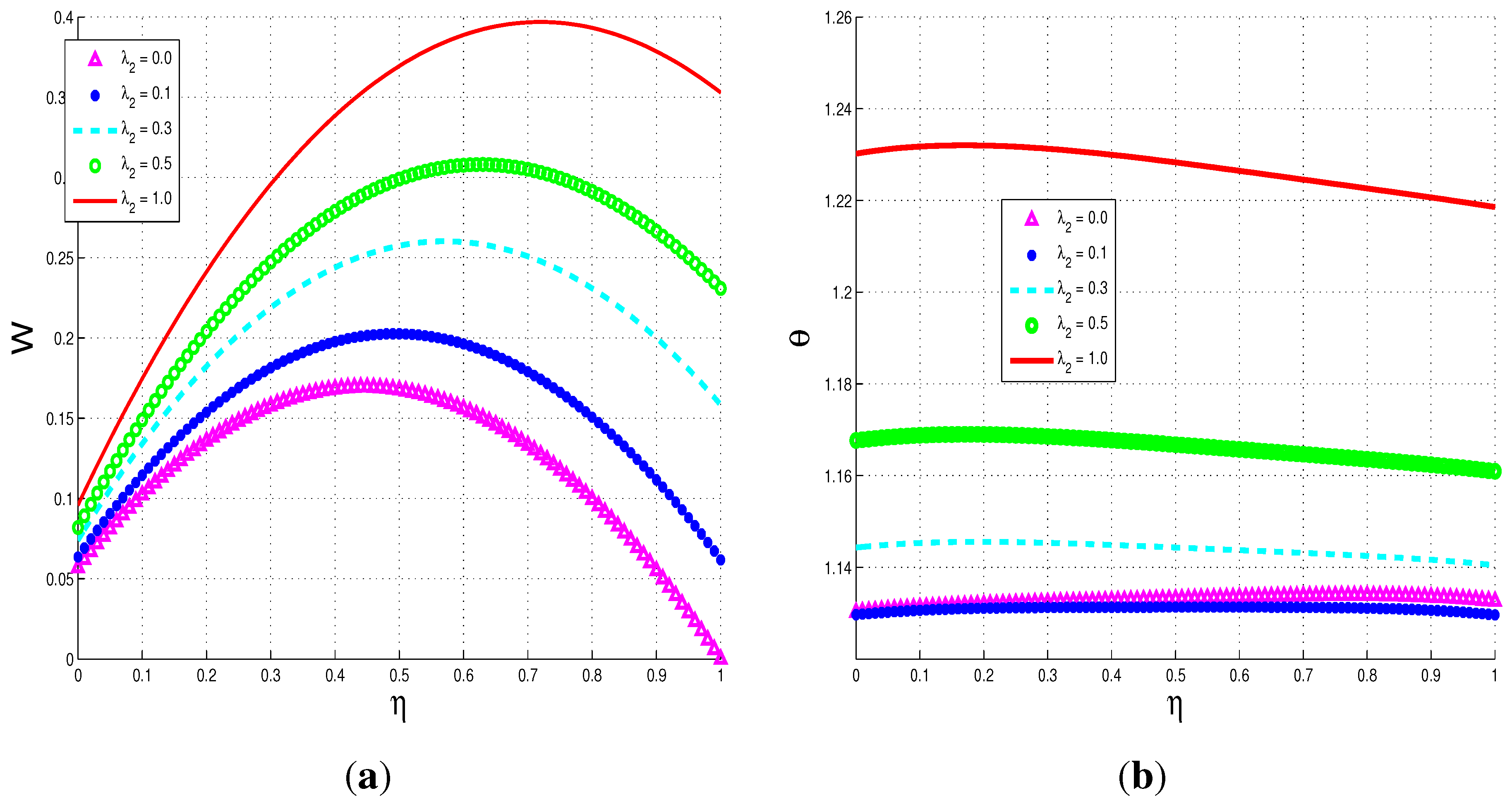
5.2.1. Parameter Dependence of Solutions
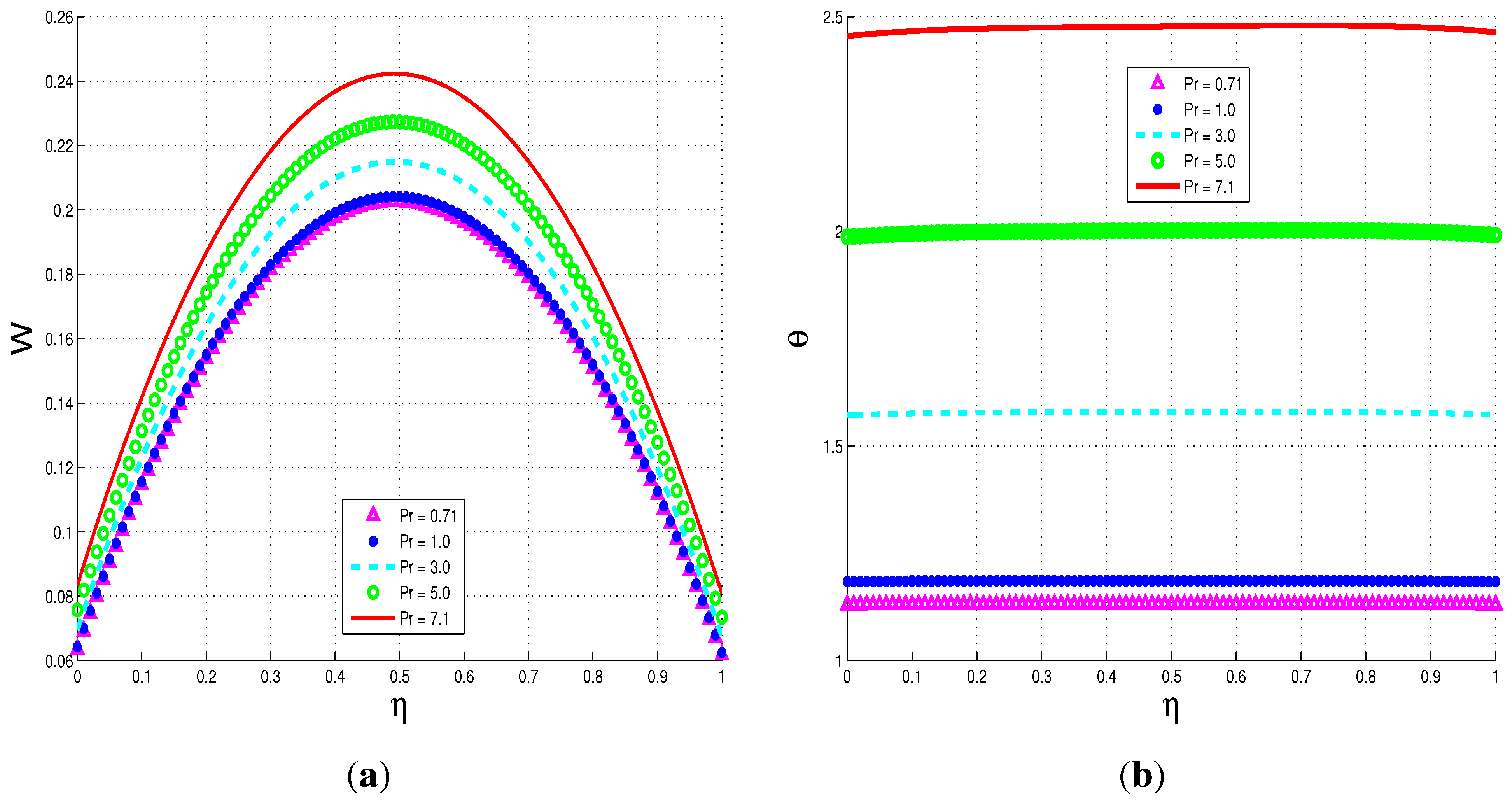
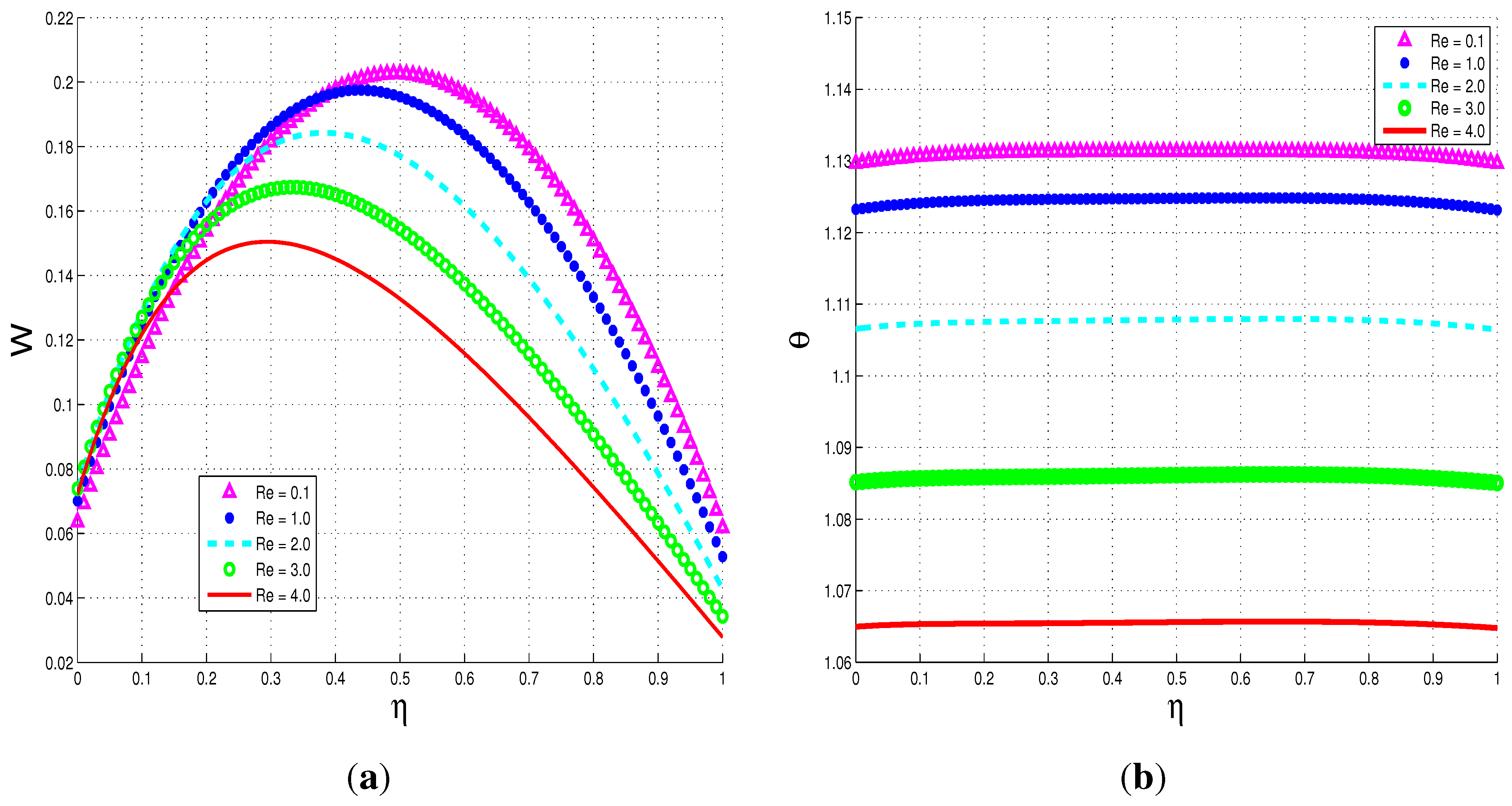
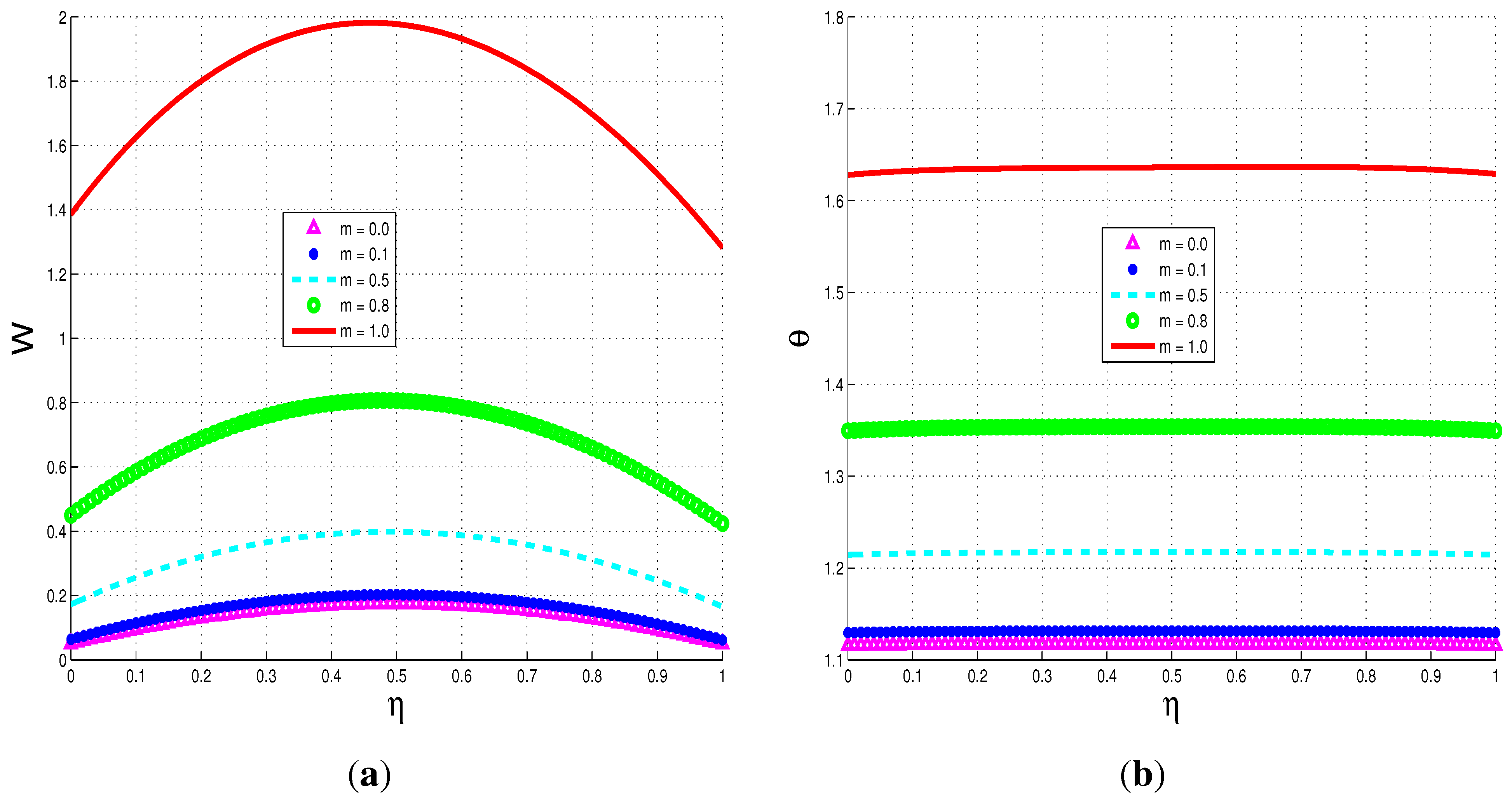

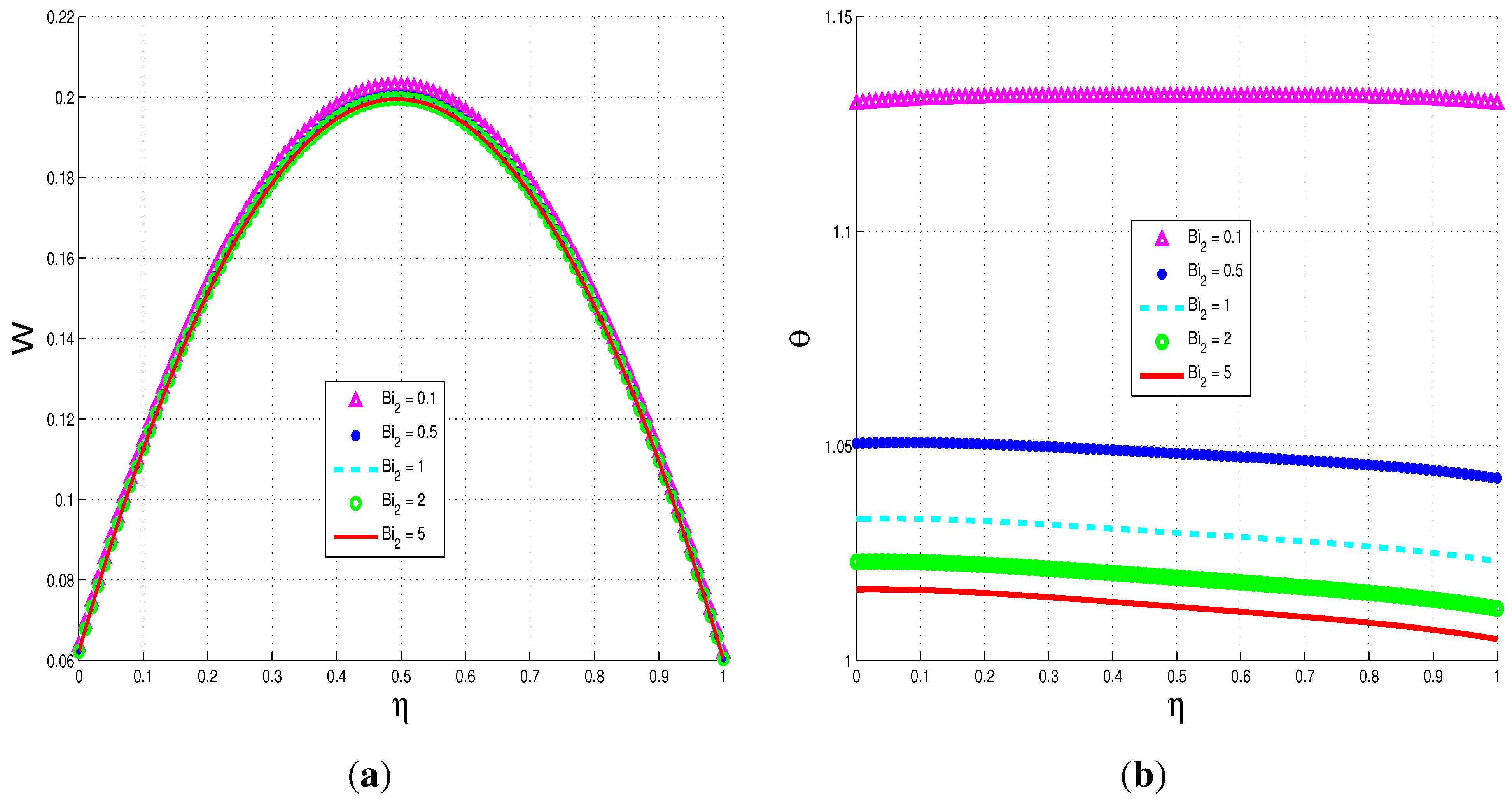

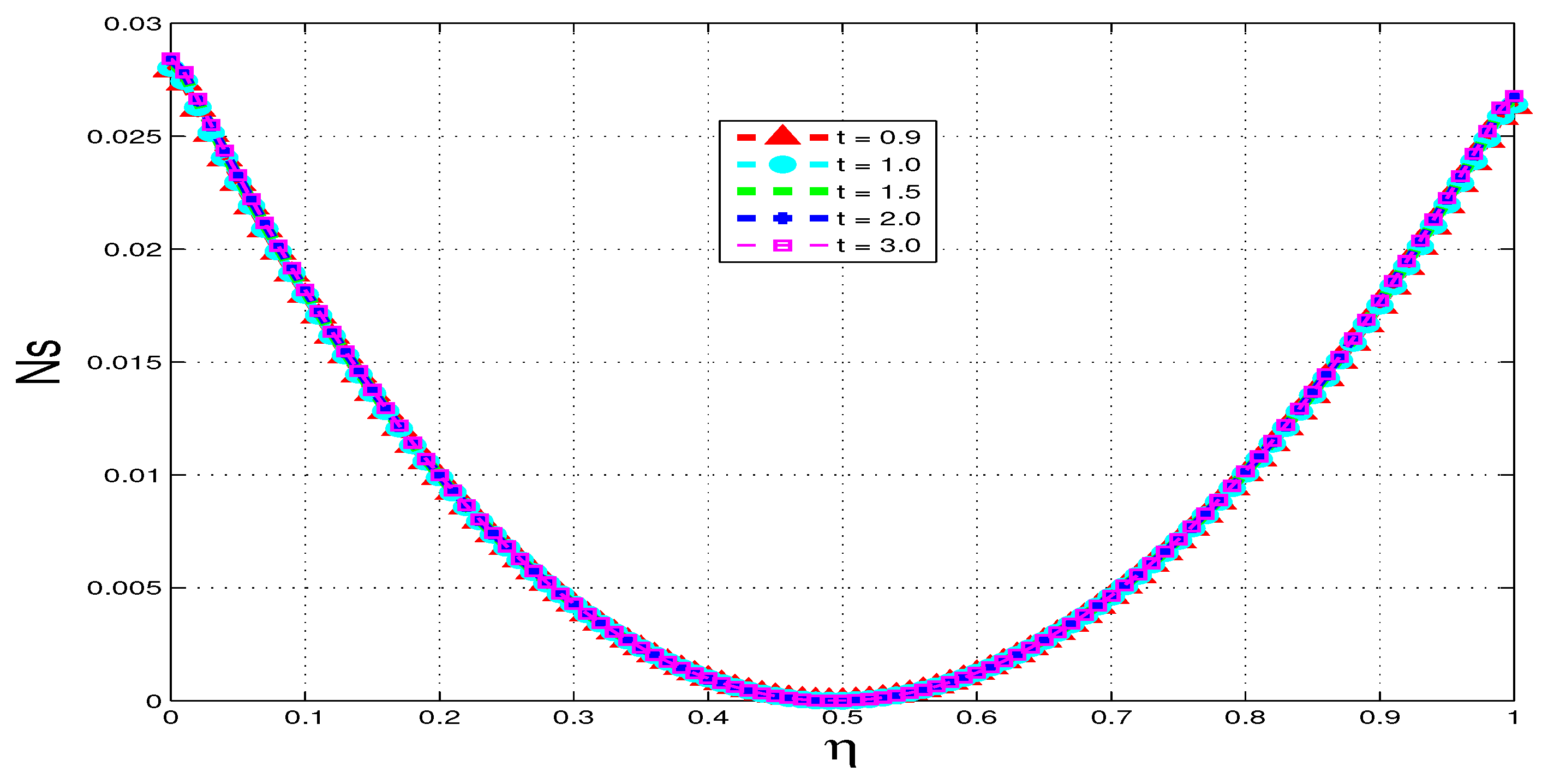
5.3. Entropy Generation
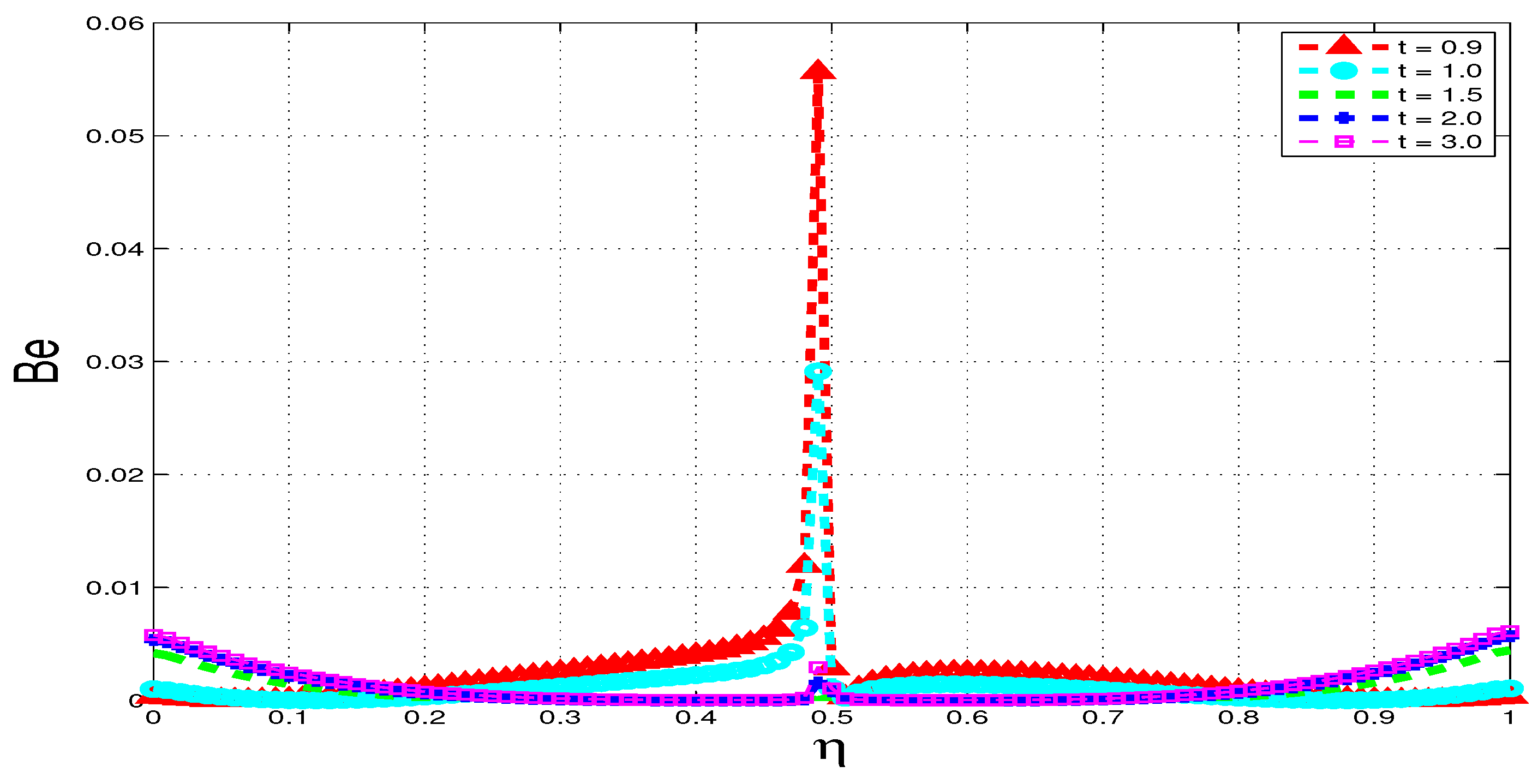
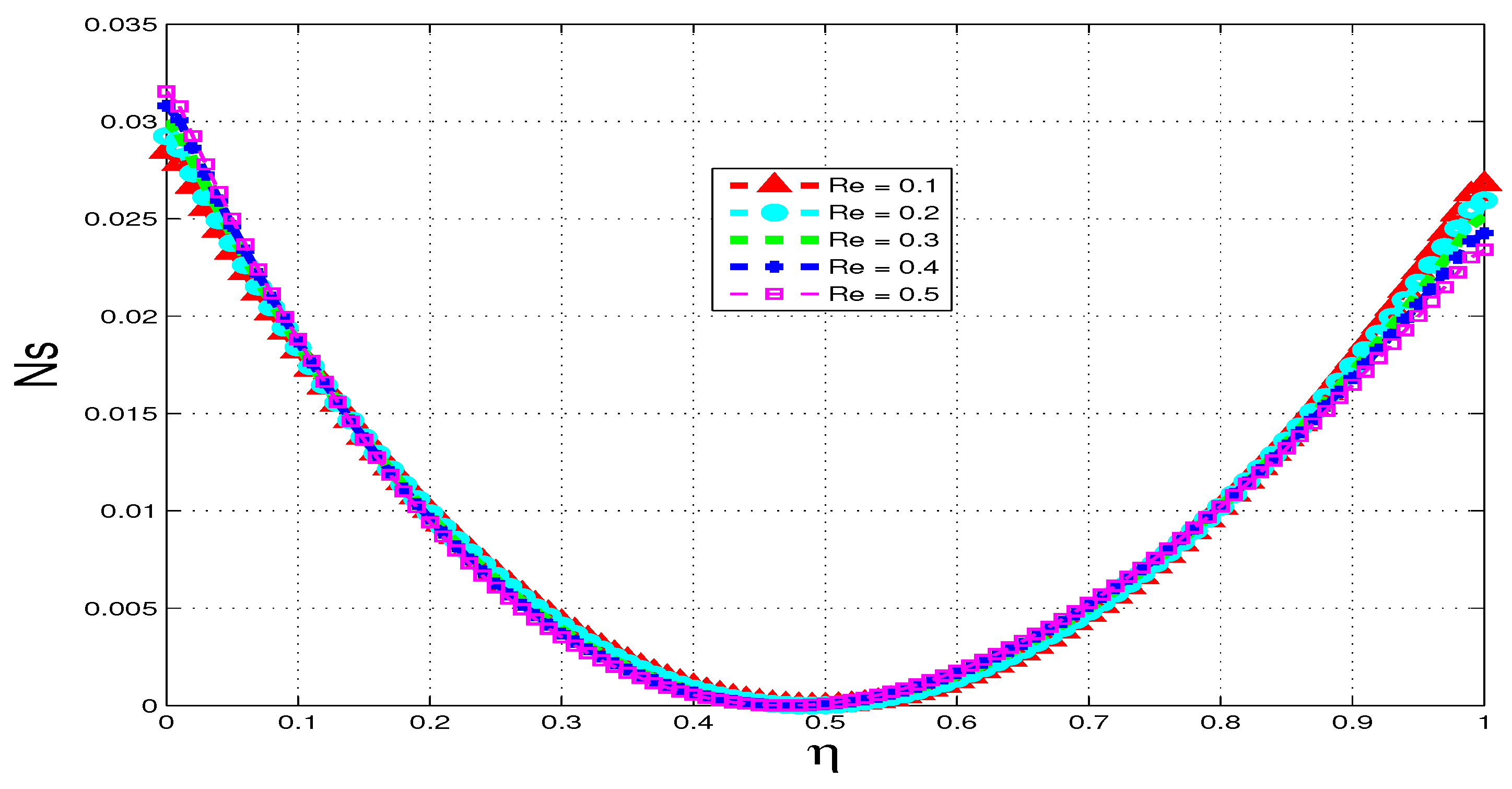
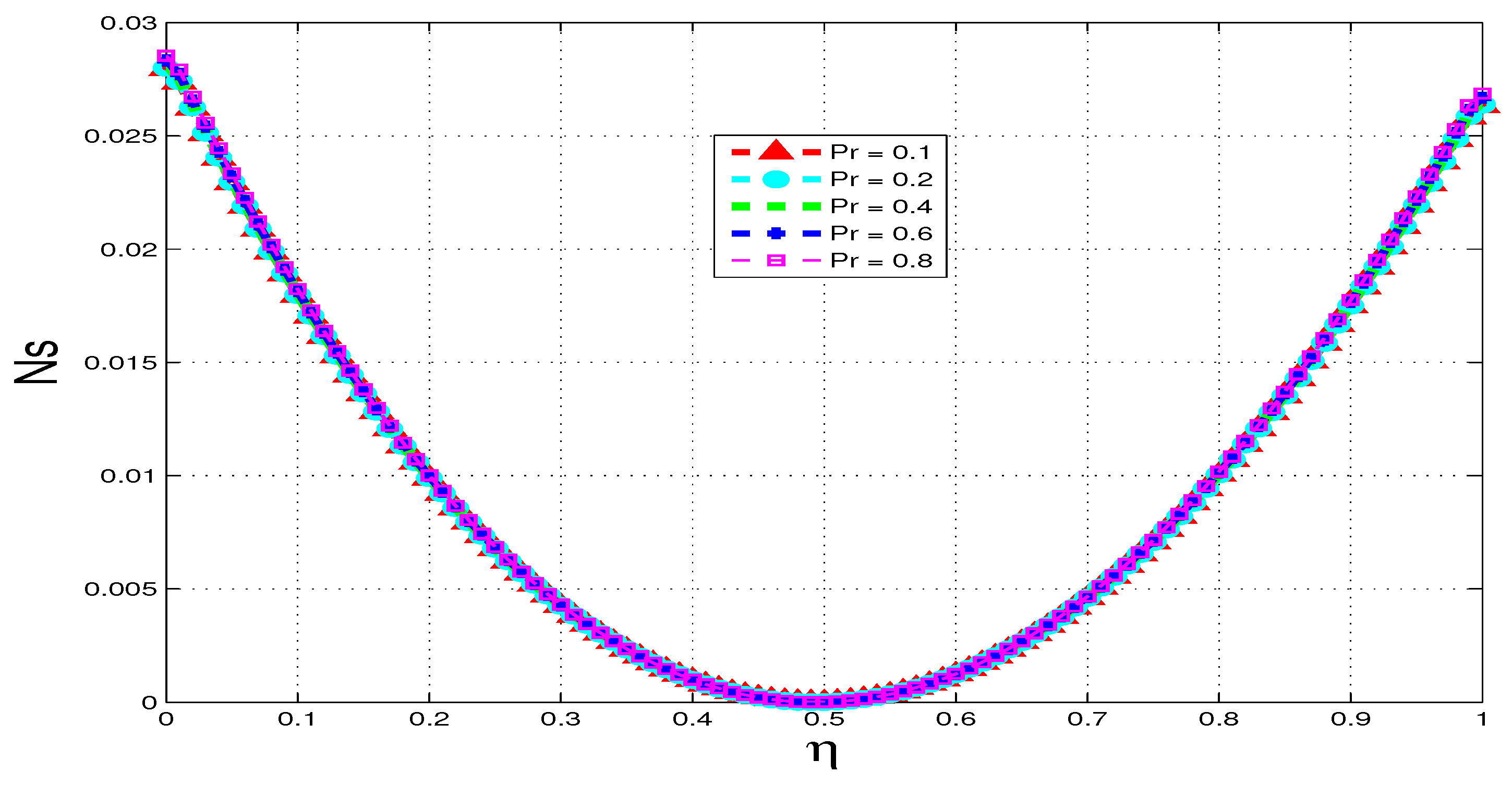
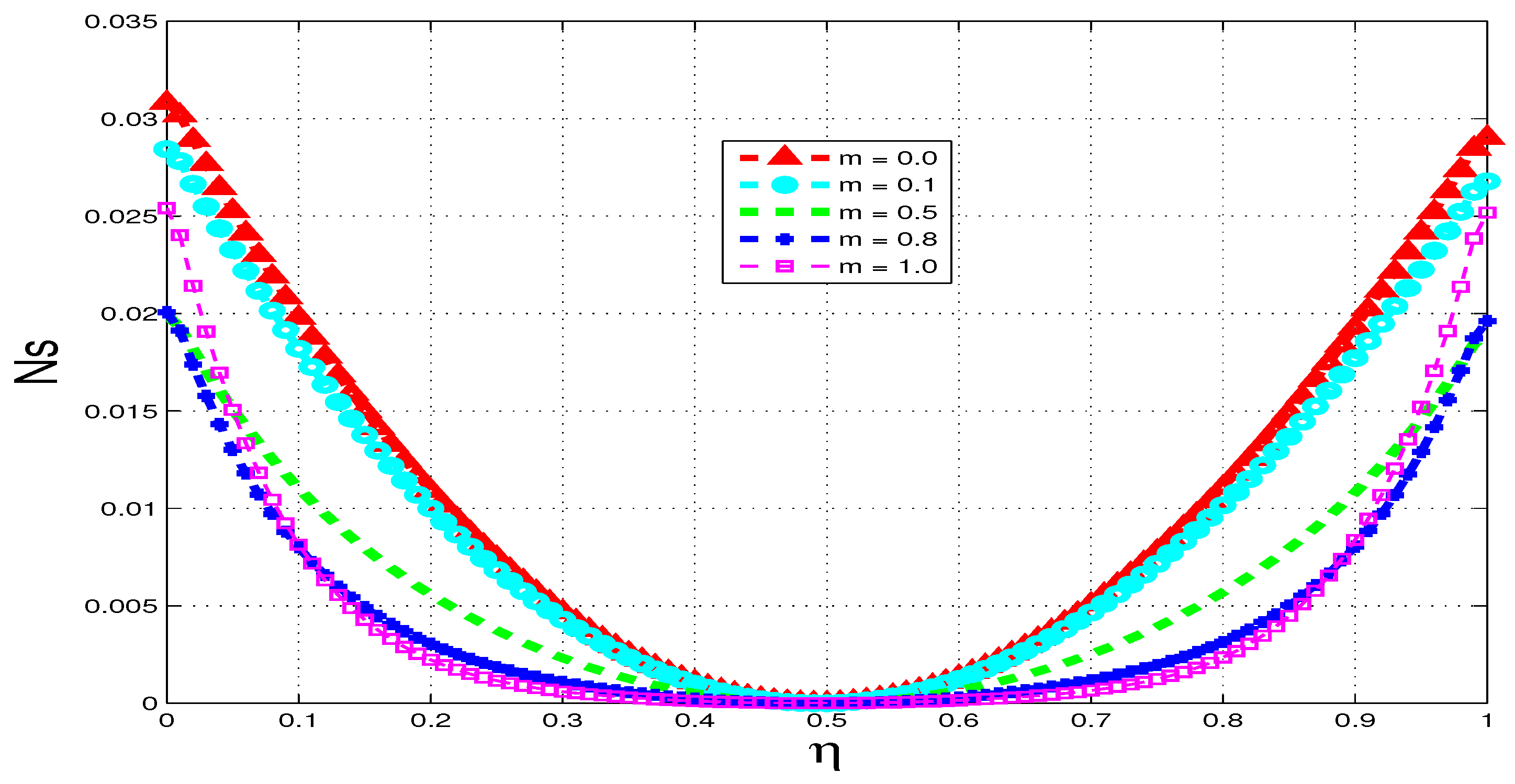
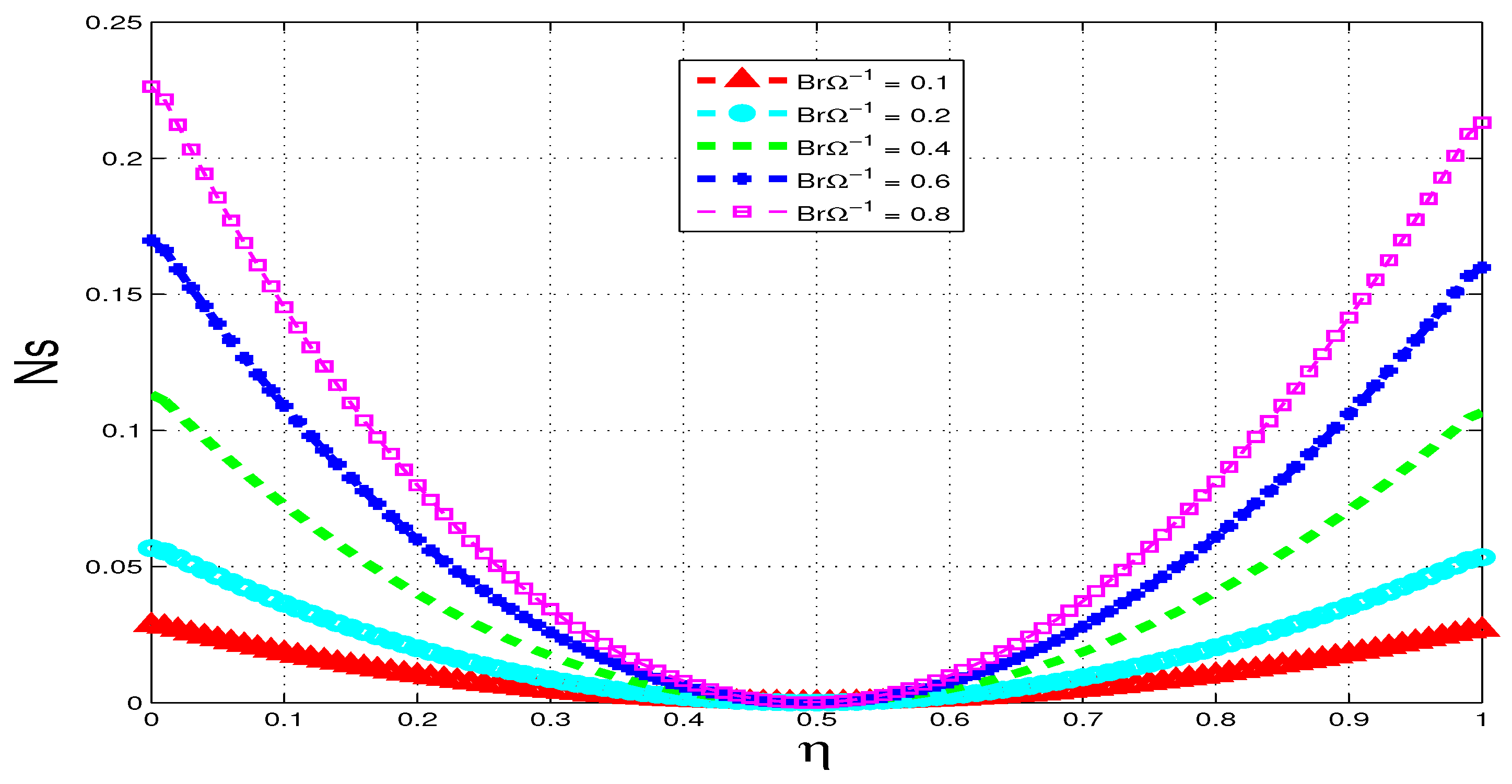
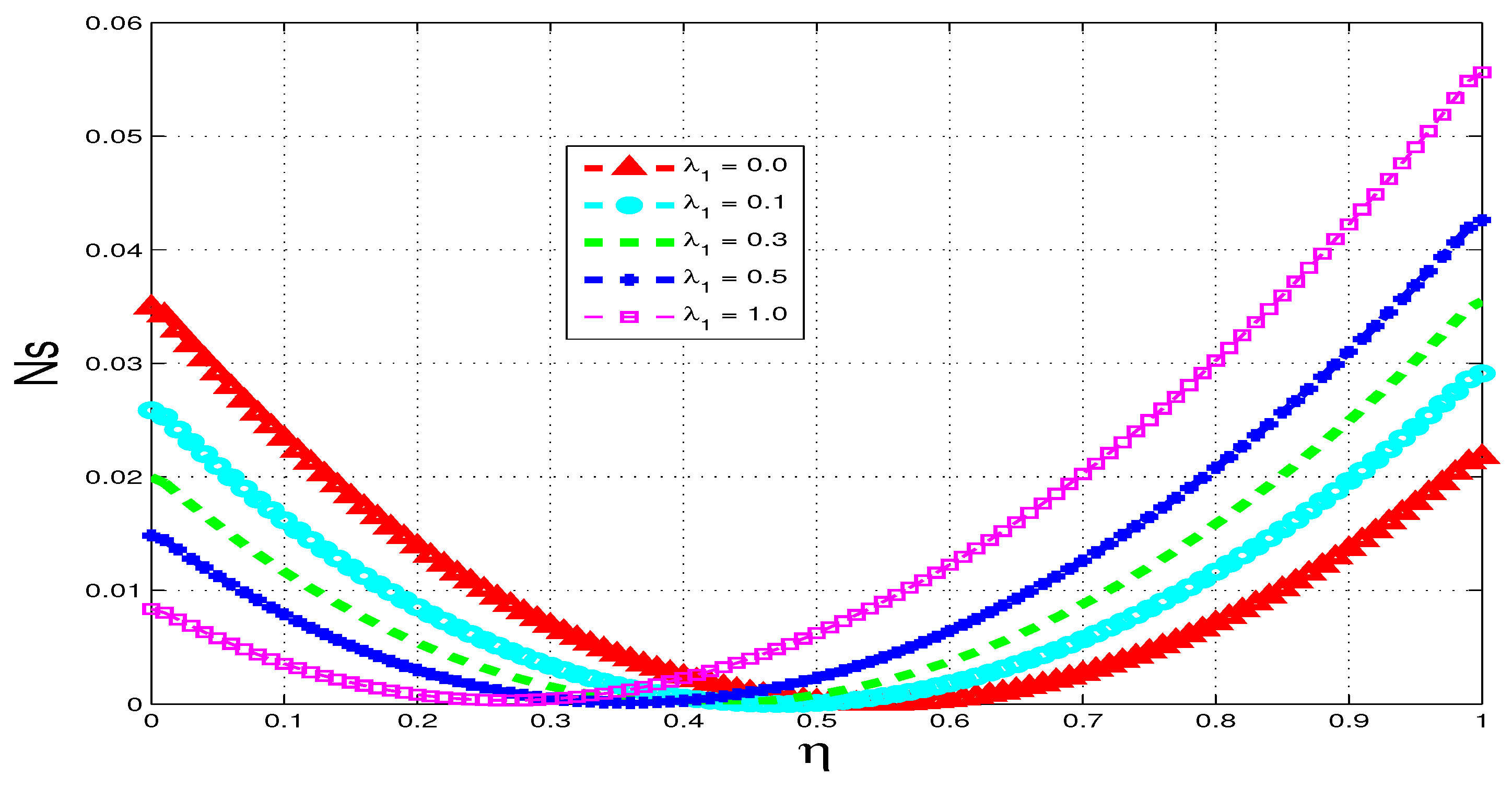
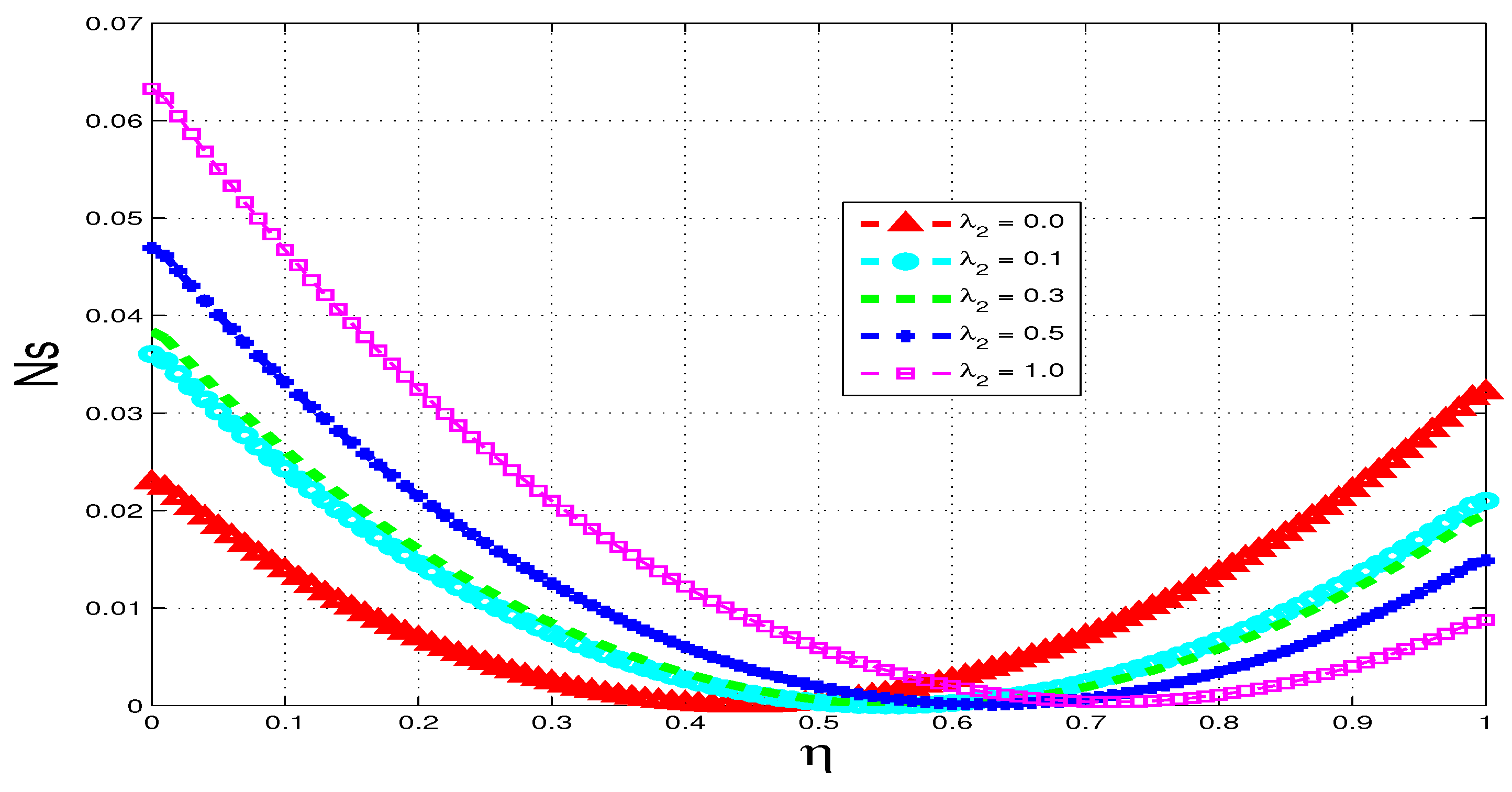

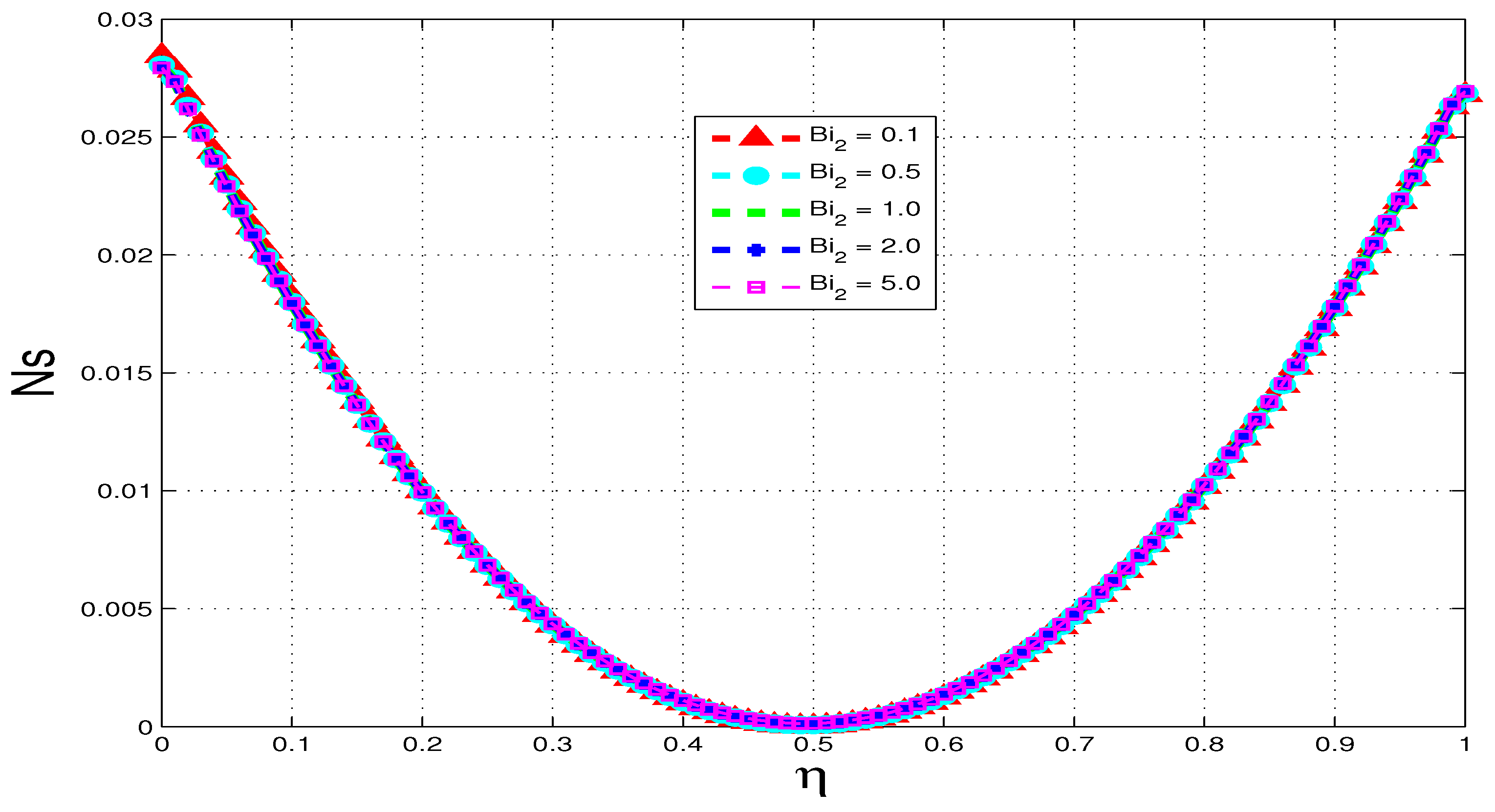
5.4. Bejan Number
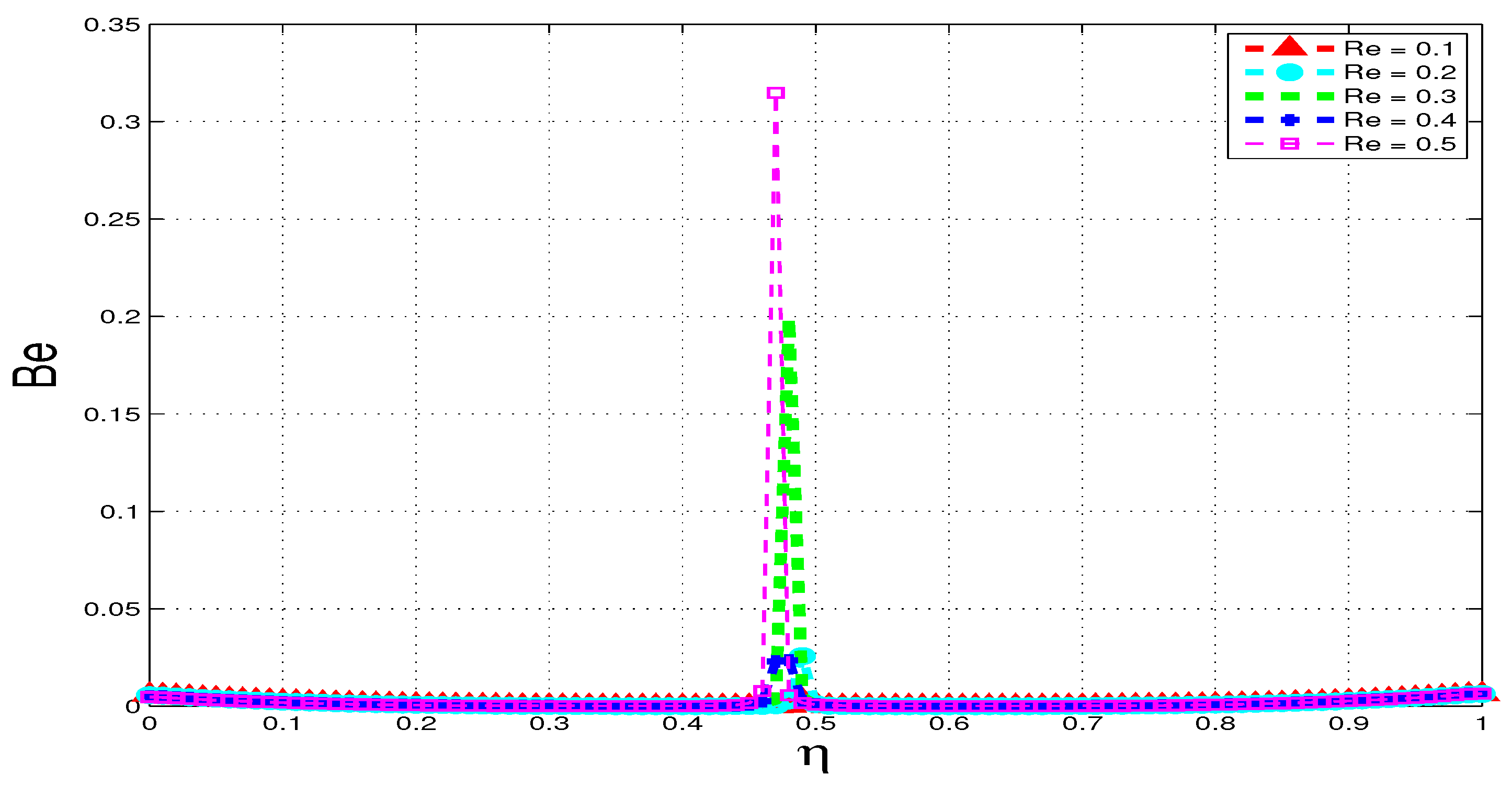
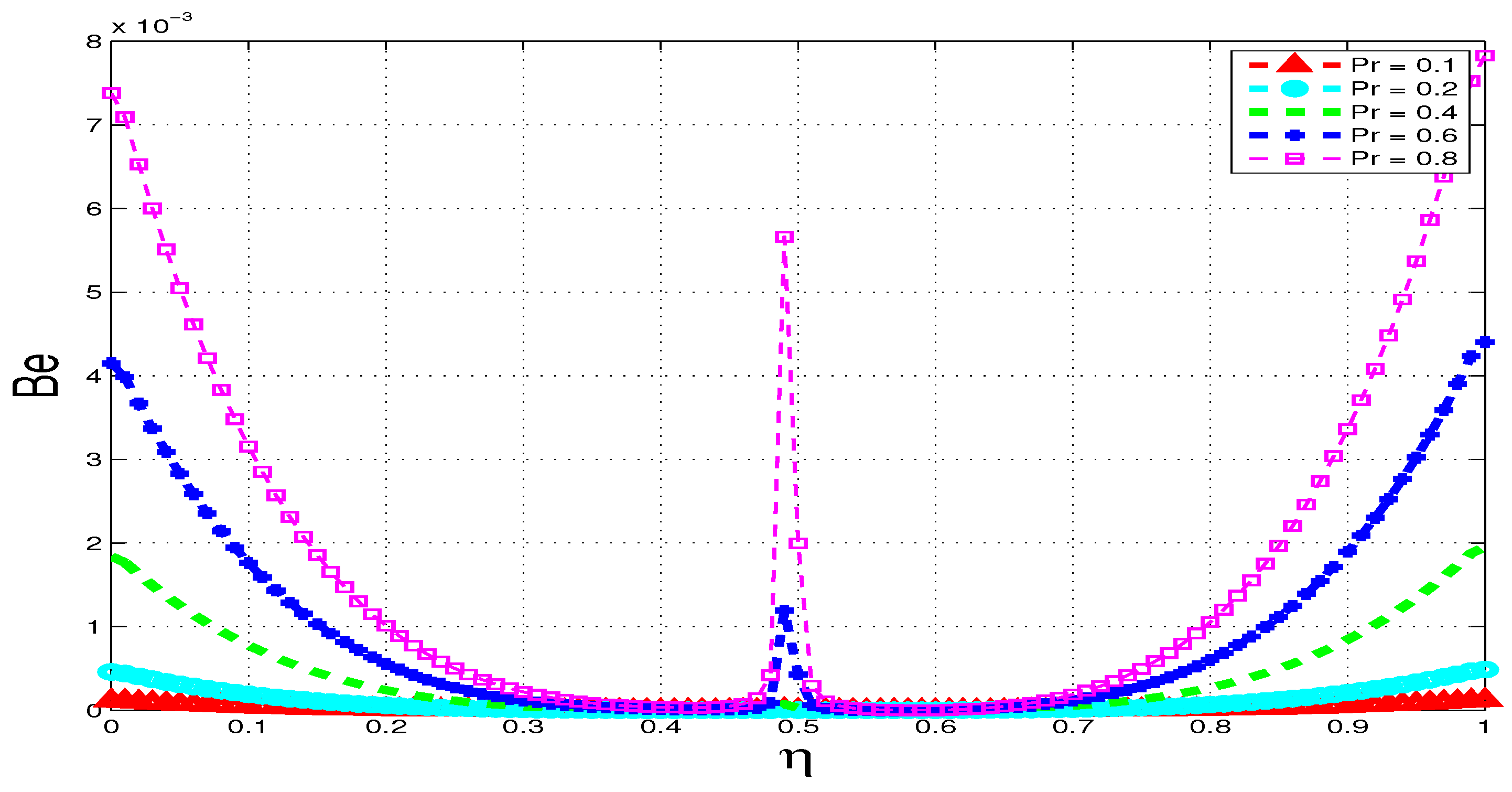
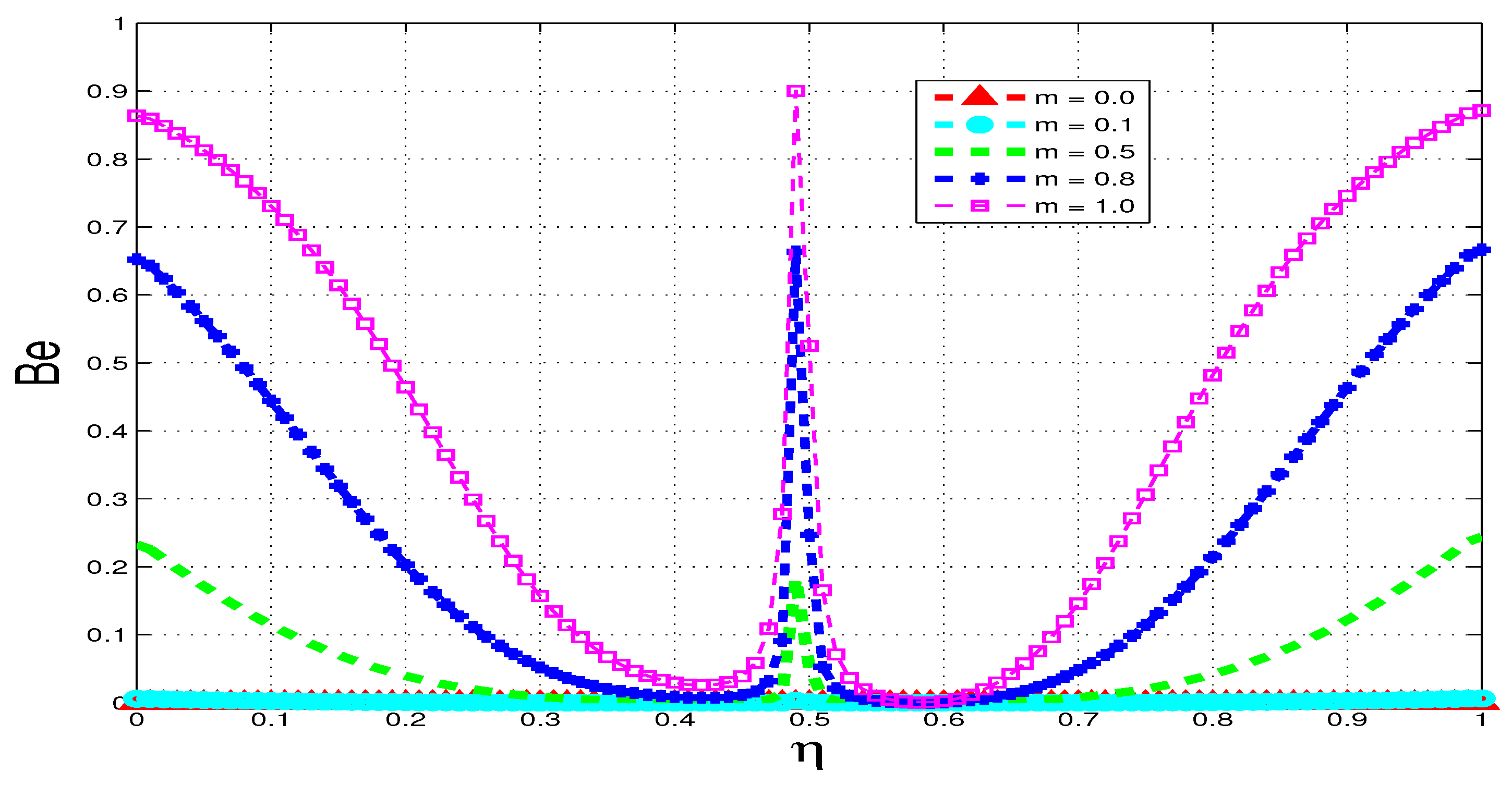
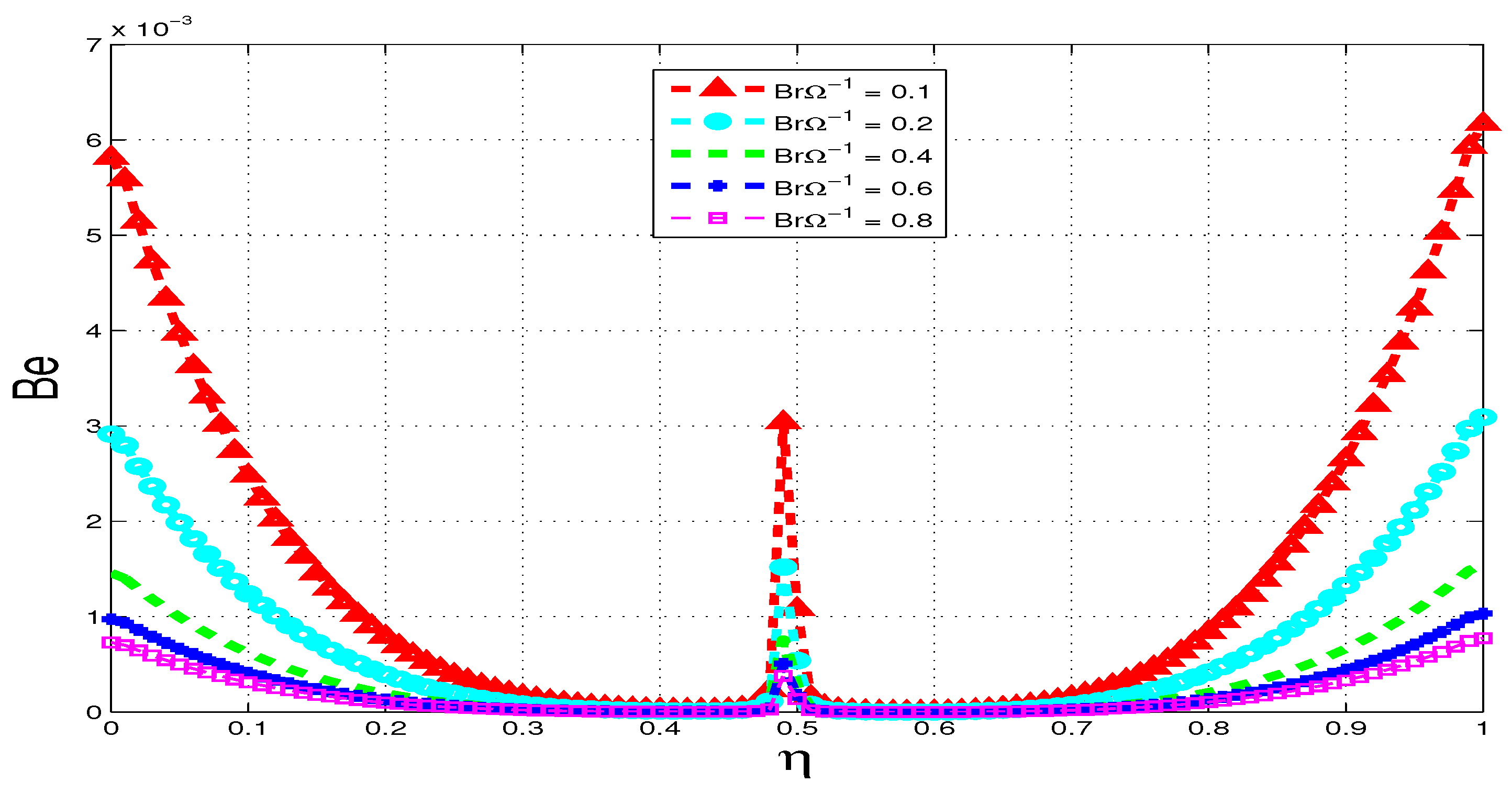
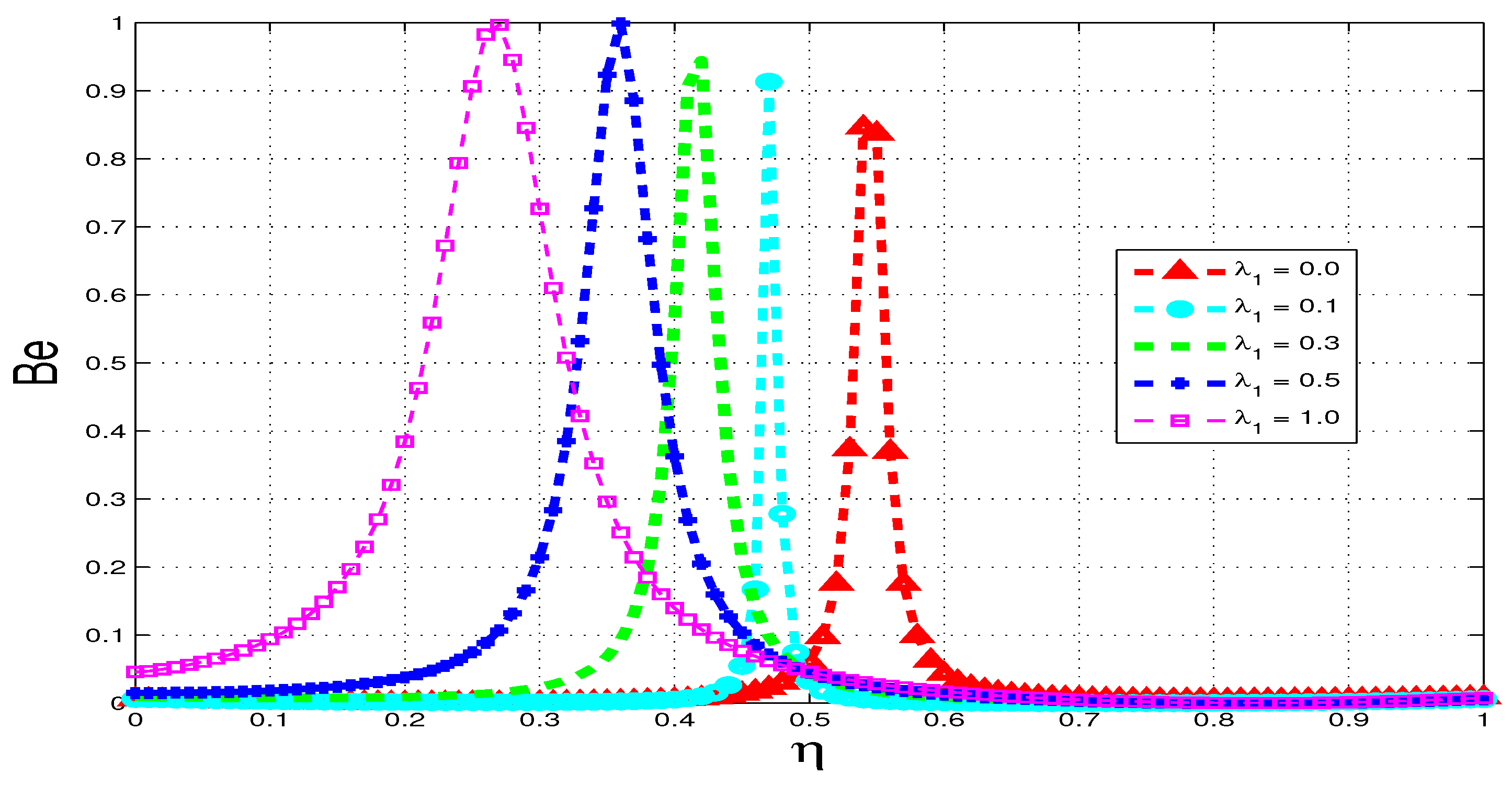
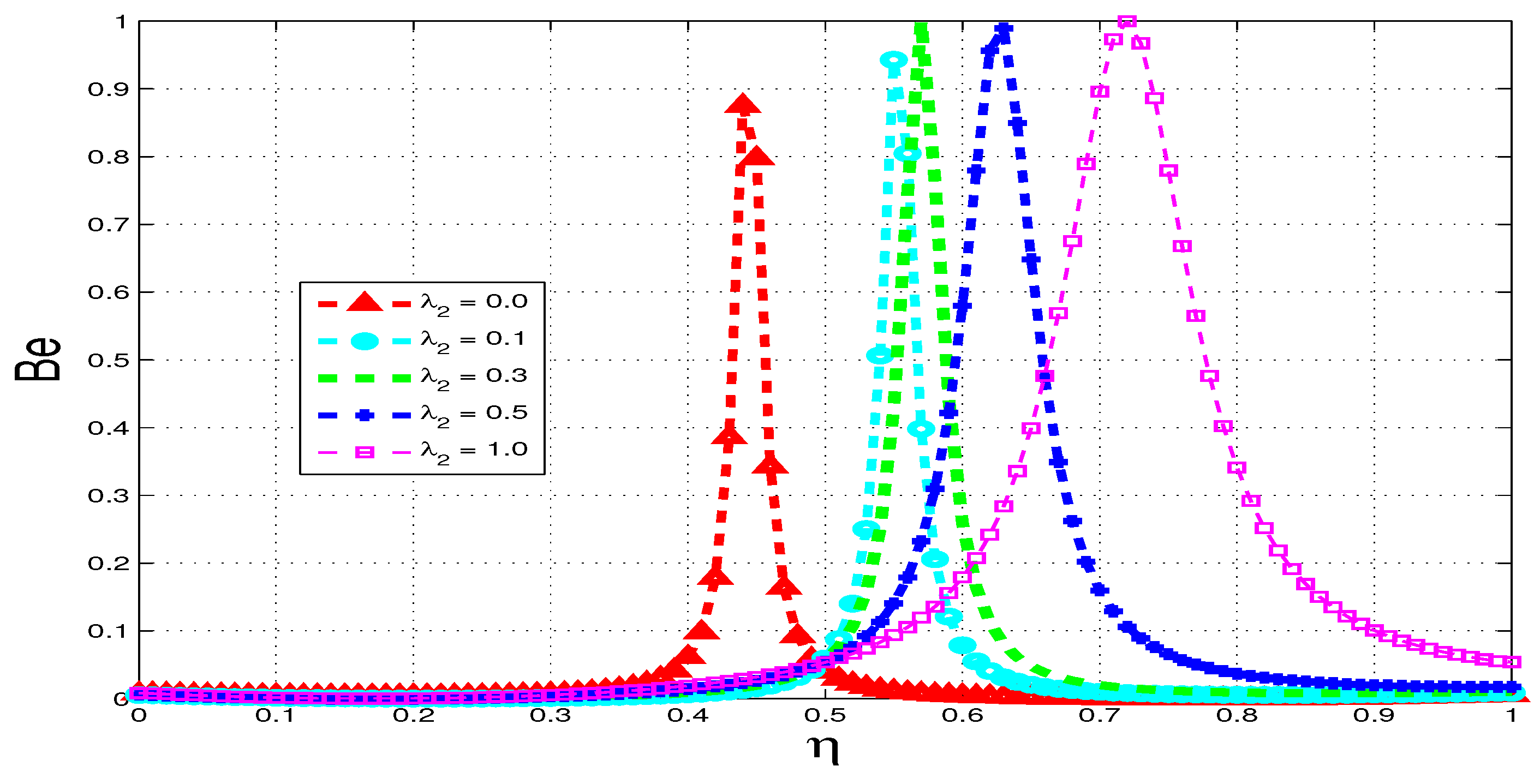
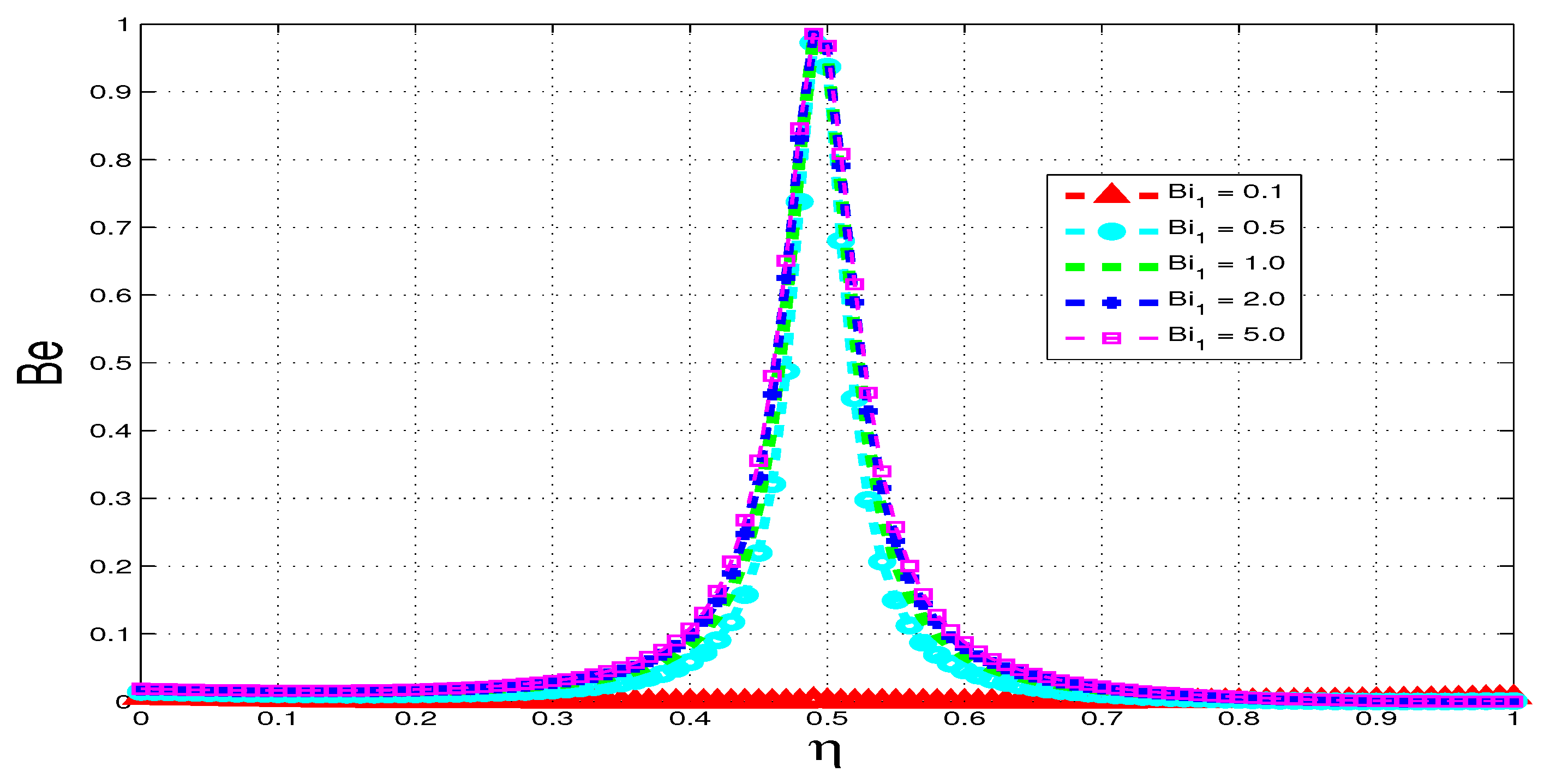
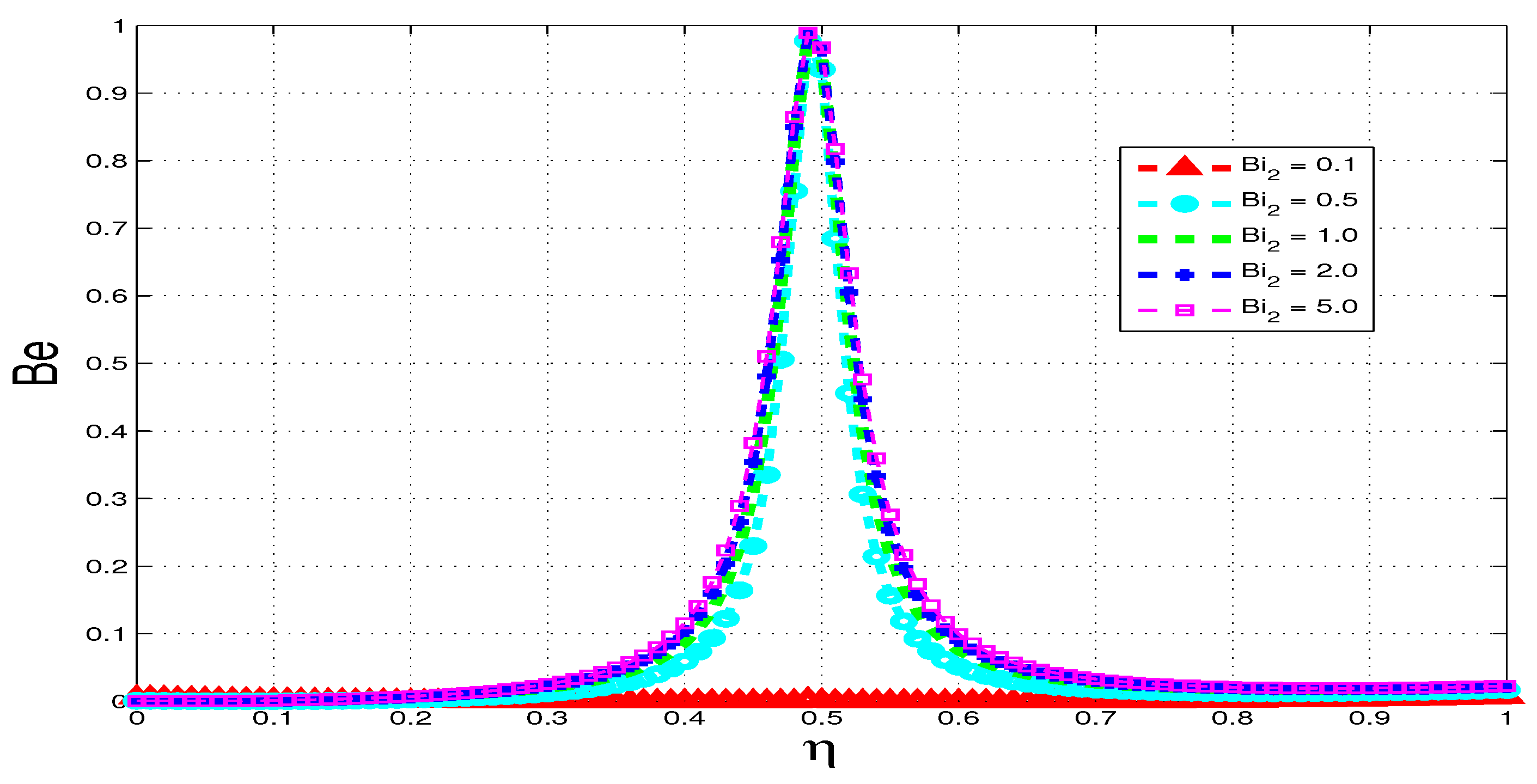
6. Conclusions
References
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar]
- Bejan, A. Entropy Genaration Minimization; CRC: Boca Raton, NY, USA, 1996. [Google Scholar]
- Bejan, A. Fundamentals of exergy analysis, entropy generation minimization, and the generation of flow architecture. Int. J. Energy Res. 2002, 26, 545–565. [Google Scholar] [CrossRef]
- Wood, L.C. Thermodynamics of Fluid Systems; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Sahin, A.Z. A second law comparison for optimum shape of duct subjected to constant wall temperature and laminar flow. Heat Mass Transf. 1998, 33, 425–430. [Google Scholar]
- Tasnim, S.H.; Mahmud, S. Entropy generation in a vertical concentric channel with temperature dependent viscosity. Int. Comm. Heat Mass Transf. 2002, 29, 907–918. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. Thermodynamic analysis of flow and heat transfer inside channel with two parallel plates. Energy 2002, 2, 140–146. [Google Scholar] [CrossRef]
- Chinyoka, T. Suction-injection control of shear banding in non-isothermal and exothermic channel flow of johnson-segalman liquids. Trans. ASME J. Fluids Eng. 2011, 133, 071205. [Google Scholar] [CrossRef]
- Ireka, I.E.; Chinyoka, T. Non-isothermal flow of a Johnson-Segalman liquid in a lubricated pipe with wall slip. J. Non-Newton. Fluid Mechan. 2013, 192, 20–28. [Google Scholar] [CrossRef]
- Aziz, A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1064–1068. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. MHD mixed convection from a vertical plate embedded in a porous medium with a convective boundary condition. Int. J. Therm. Sci. 2010, 49, 1813–1820. [Google Scholar] [CrossRef]
- Makinde, O.D. Thermal ignition in a reactive viscous flow through a channel filled with a porous medium. Trans. ASME J. Heat Transf. 2006, 128, 601–604. [Google Scholar] [CrossRef]
- Makinde, O.D. Thermal stability of a reactive viscous flow through a porous-saturated channel with convective boundary conditions. Appl. Therm. Eng. 2009, 29, 1773–1777. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Mahmood, R.; Ghori, Q.K. Thin film flow of a third grade fluid on a moving belt by He’s homotopy perturbation method. Int. J. Non-Linear Sci. Numer. Simul. 2006, 7, 1–8. [Google Scholar] [CrossRef]
- Massoudi, M.; Christe, I. Effects of variable viscosity and viscous dissipation on the flow of a third grade fluid in a pipe. Int. J. Non-Linear Mech. 1995, 30, 687–699. [Google Scholar]
- Yurusoy, M.; Pakdemirli, M. Approximate analytical solutions for the flow of a third grade fluid in a pipe. Int. J. Non-Linear Mech. 2002, 37, 187–195. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. Numerical investigation of transient heat transfer to hydromagnetic channel flow with radiative heat and convective cooling. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3919–3930. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. Transient analysis of pollutant dispersion in a cylindrical pipe with a nonlinear waste discharge concentration. Comput. Math. Appl. 2010, 60, 642–652. [Google Scholar] [CrossRef]
- Chinyoka, T. Computational dynamics of a thermally decomposable viscoelastic lubricant under shear. Trans. ASME J. Fluids Eng. 2008, 130, 121201. [Google Scholar] [CrossRef]
- Chinyoka, T. Poiseuille flow of reactive phan–thien–tanner liquids in 1D channel flow. Trans. ASME J. Heat Transf. 2010, 132, 111701. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chinyoka, T.; Makinde, O.D. Analysis of Entropy Generation Rate in an Unsteady Porous Channel Flow with Navier Slip and Convective Cooling. Entropy 2013, 15, 2081-2099. https://doi.org/10.3390/e15062081
Chinyoka T, Makinde OD. Analysis of Entropy Generation Rate in an Unsteady Porous Channel Flow with Navier Slip and Convective Cooling. Entropy. 2013; 15(6):2081-2099. https://doi.org/10.3390/e15062081
Chicago/Turabian StyleChinyoka, Tirivanhu, and Oluwole Daniel Makinde. 2013. "Analysis of Entropy Generation Rate in an Unsteady Porous Channel Flow with Navier Slip and Convective Cooling" Entropy 15, no. 6: 2081-2099. https://doi.org/10.3390/e15062081




