Quantum Thermodynamics: A Dynamical Viewpoint
Abstract
:1. Introduction
- The 0-law of thermodynamics deals with the partition of the system from the bath.
- I-law: The first law of thermodynamics is a statement of conservation of energy.
- II-law: The second law is a statement on the irreversibility of dynamics: the breakup of time reversal symmetry. An empirical definition: heat will flow spontaneously from a hot source to a cold sink. These statements are translated to quantum definitions of positive entropy generation.
- III-law: We will analyze two formulations. The first is that the entropy of any pure substance in thermodynamic equilibrium approaches zero as the temperature approaches absolute zero. The second formulation is a dynamical one, known as the unattainability principle: it is impossible by any procedure, no matter how idealized, to reduce any assembly to absolute zero temperature in a finite number of operations.
2. Quantum Open Systems
3. The 0-Law
3.1. System Bath Partition
3.2. Thermal Equilibrium
4. The I-Law
4.1. The Dynamical Generator in the Weak System-Bath Coupling Limit
4.2. Thermal Generators for Periodic Driving Fields
- (1)
- The system’s renormalized Hamiltonian is now periodic in time:The role of the constant Hamiltonian is played by an effective Hamiltonian defined by the spectrum of the periodic propagator:the are called “quasi-energies".
- (2)
- The Fourier decomposition (23) is replaced by a double Fourier decomposition:where and . The decomposition above follows from Floquet theory.
- (3)
- The generator in the interaction picture is the sum of its Fourier components:where:
4.3. Heat Flows and Power for Periodically Driven Open Systems
5. The II-Law
5.1. Entropy
5.2. Quantum Networks and Quantum Devices
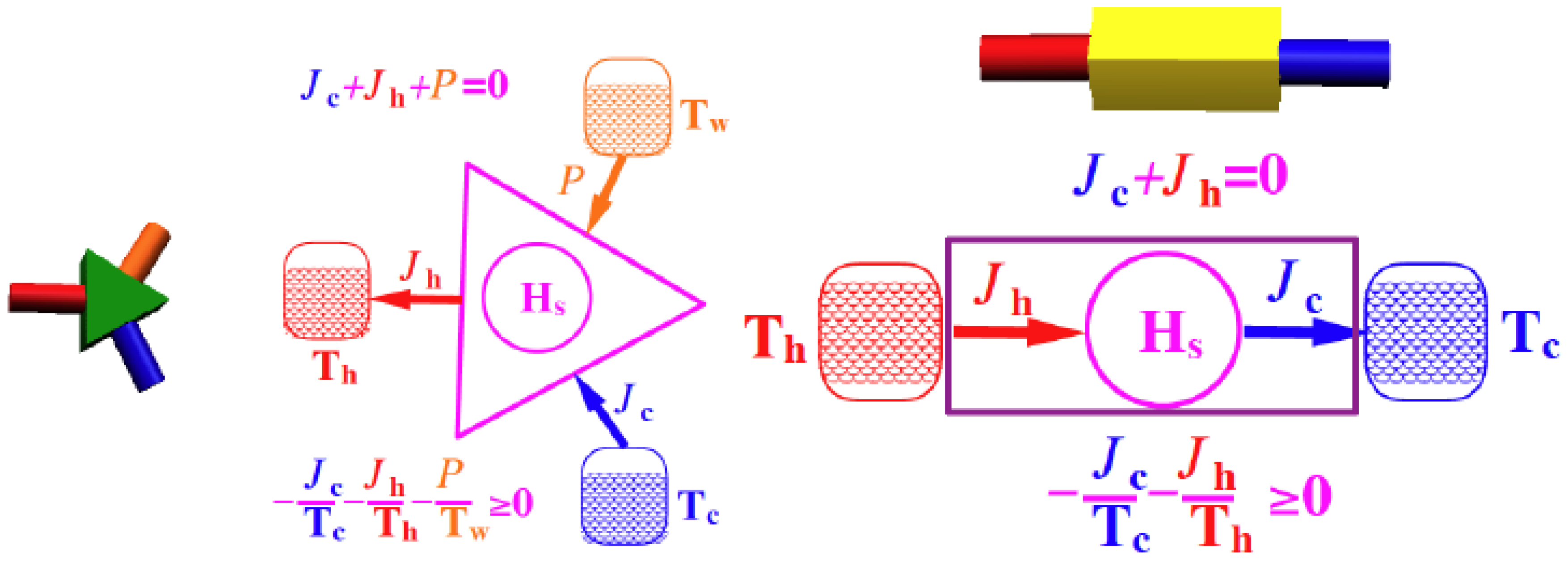

- No process is possible whose sole result is the transfer of heat from a body of lower temperature to a body of higher temperature.
5.3. Approach to Steady State: Limit Cycle
5.4. The Quantum and Thermodynamic Adiabatic Conditions and Quantum Friction
6. The III-Law
- The entropy of any pure substance in thermodynamic equilibrium approaches zero as the temperature approaches zero.
6.1. Harmonic Oscillator Cold Heat Bath
6.2. The Existence of a Ground State
6.3. Ideal Bose/Fermi Gas Cold Heat Bath

6.4. Thermoelectric Refrigerators
7. Conclusions
Acknowledgments
References
- Einstein, A. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (On a Heuristic Viewpoint Concerning the Production and Transformation of Light). Annalen der Physik 1905, 17, 132. [Google Scholar] [CrossRef]
- Scovil, H.E.; du Bois, E.O.S. Three-level masers as heat engines. Phys. Rev. Lett. 1959, 2, 262–263. [Google Scholar] [CrossRef]
- Geusic, J.; du Bois, E.O.S.; Grasse, R.D.; Scovil, H.E. Quantum equivalence of the carnot cycle. Phys. Rev. 1967, 156, 343–351. [Google Scholar] [CrossRef]
- Carnot, S. Réflections sur la Puissance Motrice du Feu et sur les Machines propres à Développer cette Puissance; Bachelier: Paris, France, 1824. [Google Scholar]
- Lindblad, G. On the generators of quantum dynamical semigroups. Comm. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Alicki, R. Quantum open systems as a model of a heat engine. J. Phys A: Math. Gen. 1979, 12, L103–L107. [Google Scholar] [CrossRef]
- Kosloff, R. A quantum mechanical open system as a model of a heat engine. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, 37, 62–70. [Google Scholar] [CrossRef]
- Salamon, P.; Nulton, J.D.; Siragusa, G.; Andersen, B.; Limon, A. Principles of control thermodynamics. Energy 2001, 26, 307–319. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. A quantum mechanical heat engine operating in finite time. A model consisting of spin-1/2 systems as the working fluid. J. Chem. Phys. 1992, 96, 3054–3067. [Google Scholar]
- Lloyd, S. Quantum-mechanical Maxwells demon. Phys. Rev. A 1997, 56, 3374–3382. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Meister, B.K. Entropy and temperature of a quantum Carnot engine. Proc. Roy. Soc. Lond. A 2002, 458, 1519–1526. [Google Scholar] [CrossRef]
- He, J.; Chen, J.; Hua, B. Quantum refrigeration cycles using spin-1/2 systems as working substance. Phys. Rev. E 2002, 65, 036145. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Liu, Y.X.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhang, X.; Su, G.; Chen, J. The performance analysis of a micro-/nanoscaled quantum heat engine. Phys. Stat. Mech. Appl. 2012, 391, 6432–6439. [Google Scholar] [CrossRef]
- Feldmann, T.; Geva, E.; Kosloff, R.; Salamon, P. Heat engines in finite time governed by master equations. Am. J. Phys. 1996, 64, 485–492. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 2000, 61, 4774–4790. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.Q.; He, J.Z. Thermal entanglement in two-atom cavity QED and the entangled quantum Otto engine. Phys. Rev. E 2009, 79, 041113. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Xian, H.; Wei, T. The performance characteristics of an irreversible quantum Otto harmonic refrigeration cycle. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1317–1323. [Google Scholar] [CrossRef]
- Henrich, M. J.; Rempp, F.; Mahler, G. Quantum thermodynamic Otto machines: A spin-system approach. Eur. Phys. J. 2005, 151, 157–165. [Google Scholar] [CrossRef]
- Jahnke, T.; Birkov, J.; Mahler, G. On the nature of thermodynamic extremum principles: The case of maximum efficiency and maximum work. Ann. Phys. 2008, 17, 88–100. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Johal, R.S.; Mahler, G. Work extremum principle: Structure and function of quantum heat engines. Phys. Rev. E 2008, 77, 041118. [Google Scholar] [CrossRef] [PubMed]
- Gemmer, J.; Mechel, M.; Mahler, G. Quantum Thermodynamics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Feldmann, T.; Kosloff, R. Characteristics of the limit cycle of a reciprocating quantum heat engine. Phys. Rev. E 2004, 70, 046110. [Google Scholar] [CrossRef] [PubMed]
- Rezek, Y.; Kosloff, R. Irreversible performance of a quantum harmonic heat engine. New J. Phys. 2006, 8, 83. [Google Scholar] [CrossRef]
- Abah, O.; Rossnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-ion heat engine at maximum power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef] [PubMed]
- Thomas, G.; Johal, R. Coupled quantum Otto cycle. Phys. Rev. E 2011, 83, 031135. [Google Scholar] [CrossRef] [PubMed]
- He, X.; He, J. Thermal entangled four-level quantum Otto heat engine. Sci. China Phys. Mech. Astron. 2012, 55, 1751–1756. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; He, J.; Ma, Y. Efficiency at maximum power of a heat engine working with a two-level atomic system. Phys. Rev. E 2013, 87, 042119. [Google Scholar] [CrossRef] [PubMed]
- Rezek, R.; Salamon, P.; Hoffmann, K.H.; Kosloff, R. The quantum refrigerator: The quest for the absolute zero. Euro. Phys. Lett. 2009, 85, 30008. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Minimal temperature of quantum refrigerators. Euro. Phys. Lett. 2010, 89, 20004. [Google Scholar] [CrossRef]
- Rempp, F.; Michel, M.; Mahler, G. Cyclic cooling algorithm. Phys. Rev. A 2007, 76, 032325. [Google Scholar] [CrossRef]
- Kaufman, A.M.; Lester, B.J.; Regal, C.A. Cooling a single atom in an optical tweezer to its quantum ground state. Phys. Rev. X 2012, 2, 041014. [Google Scholar] [CrossRef]
- Kosloff, R.; Feldmann, T. A discrete four stroke quantum heat engine exploring the origin of friction. Phys. Rev. E 2002, 65, 055102. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, T.; Kosloff, R. The quantum four stroke heat engine: Thermodynamic observables in a model with intrinsic friction. Phys. Rev. E 2003, 68, 016101. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, T.; Kosloff, R. Quantum lubrication: Suppression of friction in a first-principles four-stroke heat engine. Phys. Rev. E 2006, 73, 025107(R). [Google Scholar] [CrossRef] [PubMed]
- Diósi, L.; Feldmann, T.; Kosloff, R. On exact identity between thermodynamic and informatic entropies in a unitary model of friction. Int. J. Quantum Inf. 2006, 4, 99–104. [Google Scholar] [CrossRef]
- Chen, X.; Ruschhaupt, A.; Schmidt, S.; del Campo, A.; Guery-Odelin, D.; Muga, J.G. Fast optimal frictionless atom cooling in harmonic traps. Phys. Rev. Lett. 2010, 104, 063002. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lizuain, I.; Ruschhaupt, A.; Guery-Odelin, D.; Muga, J.G. Shortcut to adiabatic passage in two- and three-level atoms. Phys. Rev. Lett. 2010, 105, 123003. [Google Scholar] [CrossRef] [PubMed]
- Ibez, S.; Chen, X.; Torrontegui, E.; Muga, J.G.; Ruschhaupt, A. Multiple schrdinger pictures and dynamics in shortcuts to adiabaticity. Phys. Rev. Lett. 2012, 109, 100403. [Google Scholar]
- Salamon, P.; Hoffmann, K.H.; Rezek, Y.; Kosloff, R. Maximum work in minimum time from a conservative quantum system. Phys. Chem. Chem. Phys. 2009, 11, 1027–1032. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, K.H.; Salamon, P.; Rezek, Y.; Kosloff, R. Time-optimal controls for frictionless cooling in harmonic traps. Euro. Phys. Lett. 2011, 96, 60015. [Google Scholar] [CrossRef]
- Salamon, P.; Nitzan, A.; Andresen, B.; Berry, R.S. Minimum entropy production and the optimization of heat engines. Phys. Rev. A 1980, 21, 2115–2129. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; Chemical Rubber Corp: Cleaveland, OH, USA, 1996. [Google Scholar]
- Esposito, M.; Kawai, R.; Lindenberg, K.; van den Brook, C. Efciency at maximum power of low-dissipation carnot engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef] [PubMed]
- Van den Brook, C. Efficiency at maximum power in the low-dissipation limit. Eur. Phys. Lett. 2013, 101, 10006. [Google Scholar] [CrossRef]
- Wang, H. Quantum-mechanical Brayton engine working with a particle in a one-dimensional harmonic trap. Phys. Scripta 2013, 87, 055009. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. On the classical limit of quantum thermodynamics in finite time. J. Chem. Phys. 1992, 97, 4398–4412. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. The quantum heat engine and heat pump: An irreversible thermodynamic analysis of the three-level amplifier. J. Chem. Phys. 1996, 104, 7681–7698. [Google Scholar] [CrossRef]
- Kosloff, R.; Geva, E.; Gordon, J.M. The quantum refrigerator in quest of the absolute zero. J. Appl. Phys. 2000, 87, 8093–8097. [Google Scholar] [CrossRef]
- Palao, P.J.; Kosloff, R.; Gordon, J.M. Quantum thermodynamic cooling cycle. Phys. Rev. E 2001, 64, 056130. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Kieu, T.D. The second law, Maxwell’s demon, and work derivable from quantum heat engines. Phys. Rev. Lett. 2004, 93, 140403. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.; Nitzan, A. Molecular heat pump. Phys. Rev. E 2006, 73, 026109. [Google Scholar] [CrossRef] [PubMed]
- Bushev, P.; Rotter, D.; Wilson, A.; Dubin, F.; Becher, C.; Eschner, J.; Blatt, R.; Steixner, V.; Rabl, P.; Zoller, P. Feedback cooling of a single trapped ion. Phys. Rev. Lett. 2006, 96, 60010. [Google Scholar] [CrossRef] [PubMed]
- Boukobza, E.; Tannor, D.J. Thermodynamic analysis of quantum light purification. Phys. Rev. A 2008, 78, 013825. [Google Scholar] [CrossRef]
- Birjukov, J.; Jahnke, T.; Mahler, G. Quantum thermodynamic processes: a control theory for machine cycles. Eur. Phys. J. B 2008, 64, 105–108. [Google Scholar] [CrossRef]
- Segal, D. Vibrational relaxation in the Kubo oscillator: Stochastic pumping of heat. J. Chem. Phys. 2009, 130, 134510. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Lindberg, K.; van den Brook, C. Thermoelectric efficiency at maximum power in a quantum dot. Eur. Phys. Lett. 2009, 85, 043003. [Google Scholar] [CrossRef]
- Linden, N.; Popescu, S.; Skrzypczyk, P. How small can thermal machines be? Towards the smallest possible refrigerator. Phys. Rev. Lett. 2010, 105, 130401. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O. Quantum photocell: Using quantum coherence to reduce radiative recombination and increase efficiency. Phys. Rev. Lett. 2010, 104, 207701. [Google Scholar] [CrossRef] [PubMed]
- Svidzinsky, A.A.; Dorfman, K.E.; Scully, M.O. Enhancing photovoltaic power by Fano-induced coherence. Phys. Rev. A 2011, 84, 053818. [Google Scholar] [CrossRef]
- Sothmann, B.; Büttiker, M. Magnon-driven quantum-dot heat engine. Eur. Phys. Lett. 2012, 99, 27001. [Google Scholar] [CrossRef]
- Geusic, J.E.O.; Schulz-du Bois, R.D.G.; Scovil, H.E. Three Level Spin Refrigeration and Maser Action at 1500mc/sec. J. App. Phys. 1959, 30, 1113–1114. [Google Scholar] [CrossRef]
- Tsujikawa, I.; Murao, T. Possibility of optical cooling of ruby. J. Phys. Soc. Jpn. 1963, 18, 503–510. [Google Scholar] [CrossRef]
- Hnsch, T.W.; Schawlow, A.L. Cooling of gases by laser radiation. Opt. Commun. 1975, 13, 68–69. [Google Scholar] [CrossRef]
- Wineland, D.J.; Dehmelt, H. Proposed 1024 upsilon less that upsilon laser fluorescence spectroscopy on T1-Mono-Ion oscillator III. Bull. Am. Phys. Soc. 1975, 20, 637. [Google Scholar]
- Levy, A.; Kosloff, R. Quantum absorption refrigerator. Phys. Rev. Lett. 2012, 108, 070604. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Alicki, R.; Kosloff, R. Quantum refrigerators and the third law of thermodynamics. Phys. Rev. E 2012, 85, 061126. [Google Scholar] [CrossRef] [PubMed]
- Sandner, K.; Ritsch, H. Temperature gradient driven lasing and stimulated cooling. Phys. Rev. Lett. 2012, 109, 93601. [Google Scholar] [CrossRef] [PubMed]
- Gieseler, J.; Deutsch, B.; Quidant, R.; Novotny, L. Subkelvin parametric feedback cooling of a laser-trapped nanoparticle. Phys. Rev. Lett. 2012, 109, 103603. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Su, G.; Chen, J. The performance evaluation of a micro/nano-scaled cooler working with an ideal Bose gas. Phys. Lett. A 2012, 376, 270–274. [Google Scholar] [CrossRef]
- Yi, Z.; Gu, W.-J.; Li, G.-X. Sideband cooling of atoms with the help of an auxiliary transition. Phys. Rev. Lett. 2012, 109, 055401. [Google Scholar] [CrossRef]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Verhagen, E.; Deléglise, S.; Weis, S.; Schliesser, A.T.J.; Kippenberg, T.J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 2012, 482, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, A.; Kitagawa, T.; Demler, E.; Chamon, C. Cooling through optimal control of quantum evolution. Phys. Rev. A 2013, 87, 043607. [Google Scholar] [CrossRef]
- Pekola, J.P.; Hekking, F.W.J. Normal-Metal-Superconductor tunnel junction as a brownian refrigerator. Phys. Rev. Lett. 2007, 98, 210604. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Alicki, R.; Kosloff, R. Comment on Cooling by Heating: Refrigeration Powered by Photons. Phys. Rev. Lett. 2012, 109, 248901. [Google Scholar] [CrossRef] [PubMed]
- Cleuren, B.R.; van den Broeck, C. Cooling by heating: Refrigeration powered by photons. Phys. Rev. Lett. 2012, 108, 120603. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Minimal universal quantum heat machine. Phys. Rev. E 2013, 87, 012140. [Google Scholar] [CrossRef] [PubMed]
- Feingold, M.; Peres, A. Distribution of matrix elements of chaotic systems. Phys. Rev. A 1986, 34, 591–595. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef]
- Rigol, M.; Dunjko, V.; Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 2008, 452, 854–858. [Google Scholar] [CrossRef] [PubMed]
- Khasin, M.; Kosloff, R. Efficient simulation of quantum evolution using dynamical coarse graining. Phys. Rev. A 2008, 78, 012321. [Google Scholar] [CrossRef]
- Khasin, M.; Kosloff, R. Algorithm for simulation of quantum many-body dynamics using dynamical coarse-graining. Phys. Rev. A 2010, 81, 043635. [Google Scholar] [CrossRef]
- Partovi, M. Quantum Thermodynamics. Physics Letters A 1989, 137, 440–444. [Google Scholar] [CrossRef]
- Calderbank, A.R.; Shor, P.W. Good quantum error-correcting codes exist. Phys. Rev. A 1996, 54, 1098–1105. [Google Scholar] [CrossRef] [PubMed]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Breuer, H.P.; Petruccione, F. Open Quantum Systems; Oxford university press: Oxford, UK, 2002. [Google Scholar]
- Davis, E.B. Markovian master equations. Comm. Math. Phys. 1974, 39, 91–110. [Google Scholar] [CrossRef]
- Davis, E.B. Model of atomic radiation. Ann. Inst. H. Poincaré Phys. Théor. 1978, 28, 91–110. [Google Scholar]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications; Springer-Verlag: Berlin, Germany, 1987. [Google Scholar]
- Kraus, K. General State Change in Quantum Theory. Ann. Phys. 1971, 64, 311–335. [Google Scholar] [CrossRef]
- Lindblad, G. On the existence of quantum subdynamics. J. Phys A: Math. Gen. 1996, 29, 4197–4207. [Google Scholar] [CrossRef]
- Kubo, R.B. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Japan 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Martin, P.C.; Schwinger, J. Theory of many-particle systems. I. Phys. Rev. 1959, 115, 1342–1373. [Google Scholar] [CrossRef]
- Spohn, H.; Lebowitz, J. Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 1979, 38, 109. [Google Scholar]
- Kosloff, R.; Ratner, M.A. Beyond linear response: Lineshapes for coupled spins or oscillators via direct calculation of dissipated power. J. Chem. Phys. 1984, 80, 2352–2362. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R.; Skinner, J. On the relaxation of a two-level system driven by a strong electromagnetic field. J. Chem. Phys. 1995, 102, 8541–8561. [Google Scholar] [CrossRef]
- Lieb, E.H.; Yngvason, J. The physics and mathematics of the second law of thermodynamics. Phys. Rep. 1999, 310, 1–96. [Google Scholar] [CrossRef]
- Kosloff, R. Thermodynamic aspects of the quantum measurement process. Adv. Chem. Phys. 1980, 46, 153–193. [Google Scholar]
- Szilard, L. On the minimization of entropy in a thermodynamic system with interferences of intelligent beings. Z. Phys. 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Brilluin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Maruyama, K.; Nori, F.; Verdal, V. Colloquium: The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1–23. [Google Scholar] [CrossRef]
- Travis Bannerman, S.; Price, G.N.; Viering, K.; Raizen, M.G. Single-photon cooling at the limit of trap dynamics: Maxwell’s demon near maximum efficiency. New J. Phys. 2009, 11, 063044. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Polkovnikov, A. Microscopic diagonal entropy and its connection to basic thermodynamic relations. Ann. Phys. 2011, 326, 486–499. [Google Scholar] [CrossRef]
- Boukobza, E.; Tannor, D.J. Entropy exchange and entanglement in the Jaynes-Cummings model. Phys. Rev. A 2005, 78, 063821. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2007, 81, 865–942. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum discord and Maxwells demons. Phys. Rev. A 2003, 67, 012320. [Google Scholar] [CrossRef]
- Khasin, M.; Kosloff, R. Rise and fall of quantum and classical correlations in open-system dynamics. Phys. Rev. A 2007, 76, 012304. [Google Scholar] [CrossRef]
- Martinez, E.A.; Paz, J.P. Dynamics and thermodynamics of linear quantum open systems. Phys. Rev. Lett. 2013, 110, 130406. [Google Scholar] [CrossRef] [PubMed]
- Clausius, R. Ueber Die Bewegende Kraft Der Wrme Und Die Gesetze, Welche Sich Daraus Fr Die Wrmelehre Selbst Ableiten Lassen. Annalen der Physik 1850, 79, 368. [Google Scholar] [CrossRef]
- Spohn, H.; Lebowitz, J. Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 1978, 109, 38. [Google Scholar]
- Diosi, L. Continuous quantum measurement and ito formalism. Phys. Lett. A 1988, 129, 419–423. [Google Scholar] [CrossRef]
- Diosi, L. A Short Course in Quantum Information Theory-An Approach From Theoretical Physics, 2nd ed.; Lecture Notes in Physics; Springer: Berlin, Germany, 2011; Volume 827, pp. 31–37. [Google Scholar]
- Bloch, F.; Hansen, W.W. Packard M. Nuclear induction. Phys. Rev. 1946, 70, 460–474. [Google Scholar] [CrossRef]
- Allen, L.C.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Wiley, Courier Dover Publications: New York, NY, USA, 1975. [Google Scholar]
- Wangsness, R.K.; Bloch, F. The dynamical theory of nuclear induction. Phys. Rev. 1953, 89, 729–739. [Google Scholar] [CrossRef]
- Szczygielski, K.; Gelbwaser-Klimovsky, D.; Alicki, R. Markovian master equation and thermodynamics of a two-level system in a strong laser field. Phys. Rev. E 2013, 87, 012120. [Google Scholar] [CrossRef] [PubMed]
- Lamb, W. Theory of an optical maser. Phys. Rev. 1964, 134, A1429–A1450. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Nieuwenhuizen, T.M. Extraction of work from a single thermal bath in the quantum regime. Phys. Rev. Lett. 2000, 85, 1799–1802. [Google Scholar] [CrossRef] [PubMed]
- Lindblad, G. Expectation and entropy inequalities for finite quantum systems. Comm. Math. Phys. 1974, 39, 111–119. [Google Scholar] [CrossRef]
- Frigerio, A. Quantum dynamical semigroups and approach to equilibrium. Lett. Math. Phys. 1977, 2, 79–87. [Google Scholar] [CrossRef]
- Frigerio, A. Stationary states of quantum dynamical semigroups. Comm. Math. Phys. 1978, 63, 269–276. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Short time cycles of purely quantum refrigerators. Phys. Rev. E 2012, 85, 051114. [Google Scholar] [CrossRef] [PubMed]
- Comparat, D. General conditions for quantum adiabatic evolution. Phys. Rev. A 2009, 80, 012106. [Google Scholar] [CrossRef]
- Kosloff, R.; Feldmann, T. Optimal performance of reciprocating demagnetization quantum refrigerators. Phys. Rev. E 2010, 82, 011134. [Google Scholar] [CrossRef] [PubMed]
- Boldt, F.; Hoffmann, K.H.; Salamon, P.; Kosloff, R. Time-optimal processes for interacting spin systems. Euro. Phys. Lett. 2012, 99, 40002. [Google Scholar] [CrossRef]
- Nernst, W. Ueber die Berechnung chemischer Gleichgewichte aus thermischen Messungen. Nachr. Kgl. Ges. Wiss. Gött. 1906, 1, 1–40. [Google Scholar]
- Nernst, W. Ub̎er die Beziehung zwischen War̎meentwicklung und maximaler Arbeit bei kondensierten Systemen. Ber. Kgl. Pr. Akad. Wiss. 1906, 52, 933–940. [Google Scholar]
- Nernst, W. The Theoretical and Experimental Bases of the New Heat Theorem. [in German, Die Theoretischen und Experimentellen Grundlagen des Neuen War̎mesatzes.]; W. Knapp: Halle, 1918. [Google Scholar]
- Fowler, R.H.; Guggenheim, E.A. Statistical Thermodynamics; University Press: Cambridge, UK, 1939. [Google Scholar]
- Landsberg, P.T. Foundations of thermodynamics. Rev. Mod. Phys. 1956, 28, 363–392. [Google Scholar] [CrossRef]
- Landsberg, P.T. A comment on Nernst’s theorem. J. Phys A: Math. Gen. 1989, 22, 139–141. [Google Scholar] [CrossRef]
- Belgiorno, F. Notes on the third law of thermodynamics I. J. Phys A: Math. Gen. 2003, 36, 8165. [Google Scholar] [CrossRef]
- Belgiorno, F. Notes on the third law of thermodynamics II. J. Phys A: Math. Gen. 2003, 36, 8195. [Google Scholar] [CrossRef]
- Emch, G.G. Algebraic Methods in Statistical Mechanics and Quantum Field Theory; Wiley Interscience: New York, NY, USA, 1972. [Google Scholar]
- Bogoliubov, N.N. On the theory of superfluidity. J. Phys. (USSR) 1947, 11, 23. [Google Scholar]
- Dumcke, R. The low density limit for an N-level system interacting with a free Bose or Fermi gas. Commun. Math. Phys. 1985, 97, 331–359. [Google Scholar] [CrossRef]
- Whitney, R.S. Thermodynamic and quantum bounds on nonlinear dc thermoelectric transport. Phys. Rev. B 2013, 87, 115404. [Google Scholar] [CrossRef]
- Bruneau, L.; Jakšić, V.; Pillet, C.-A. Landauer-Büttiker formula and Schrödinger conjecture. 2013. [Google Scholar]
- Kolar, M.; Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Quantum bath refrigeration towards absolute zero: Unattainability principle challenged. Phys. Rev. Lett. 2012, 108, 090601. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100-2128. https://doi.org/10.3390/e15062100
Kosloff R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy. 2013; 15(6):2100-2128. https://doi.org/10.3390/e15062100
Chicago/Turabian StyleKosloff, Ronnie. 2013. "Quantum Thermodynamics: A Dynamical Viewpoint" Entropy 15, no. 6: 2100-2128. https://doi.org/10.3390/e15062100



