Localization of Discrete Time Quantum Walks on the Glued Trees
Abstract
: In this paper, we consider the time averaged distribution of discrete time quantum walks on the glued trees. In order to analyze the walks on the glued trees, we consider a reduction to the walks on path graphs. Using a spectral analysis of the Jacobi matrices defined by the corresponding random walks on the path graphs, we have a spectral decomposition of the time evolution operator of the quantum walks. We find significant contributions of the eigenvalues, ±1, of the Jacobi matrices to the time averaged limit distribution of the quantum walks. As a consequence, we obtain the lower bounds of the time averaged distribution.1. Introduction
The discrete time quantum walks (DTQWs) as quantum counterparts of the random walks, which play important roles in various fields, have been attractive research objects in the last decade [1–8]. In the theory of quantum algorithms, quantum walks on various graphs also play important roles, for example, graph isomorphism testing and network characterization [9–12], search algorithms on the hypercube [13] or the glued binary tree [14] and an algorithm for element distinctness on the Johnson graph [15]. In these studies, the algorithms are often reduced to DTQWs on the path graphs. Therefore, investigations of DTQWs on the path graph corresponding to the original graphs are important. Rohde et al. [16] studied the periodic properties of entanglement for DTQW on the path determined by biased Hadamard coins numerically. Godsil [17] studied the time averaged distributions of continuous-time quantum walks on the path using the average mixing matrix. Ide et al. [18] studied the time averaged distribution of DTQWs on the path graph, which can be viewed as a quantization of random walks on the path. In this paper, we consider DTQWs on the path graphs corresponding to the random walks on the glued trees. We obtain lower bounds of the time averaged distribution of the DTQWs by using spectral analysis of the corresponding Jacobi matrices.
The rest of this paper is organized as follows. The definition of our DTQW is given in Section 2, and the main result of this paper is stated in Section 3. The remaining section (Section 4) is devoted to the proof of our result.
2. Definition of the DTQW
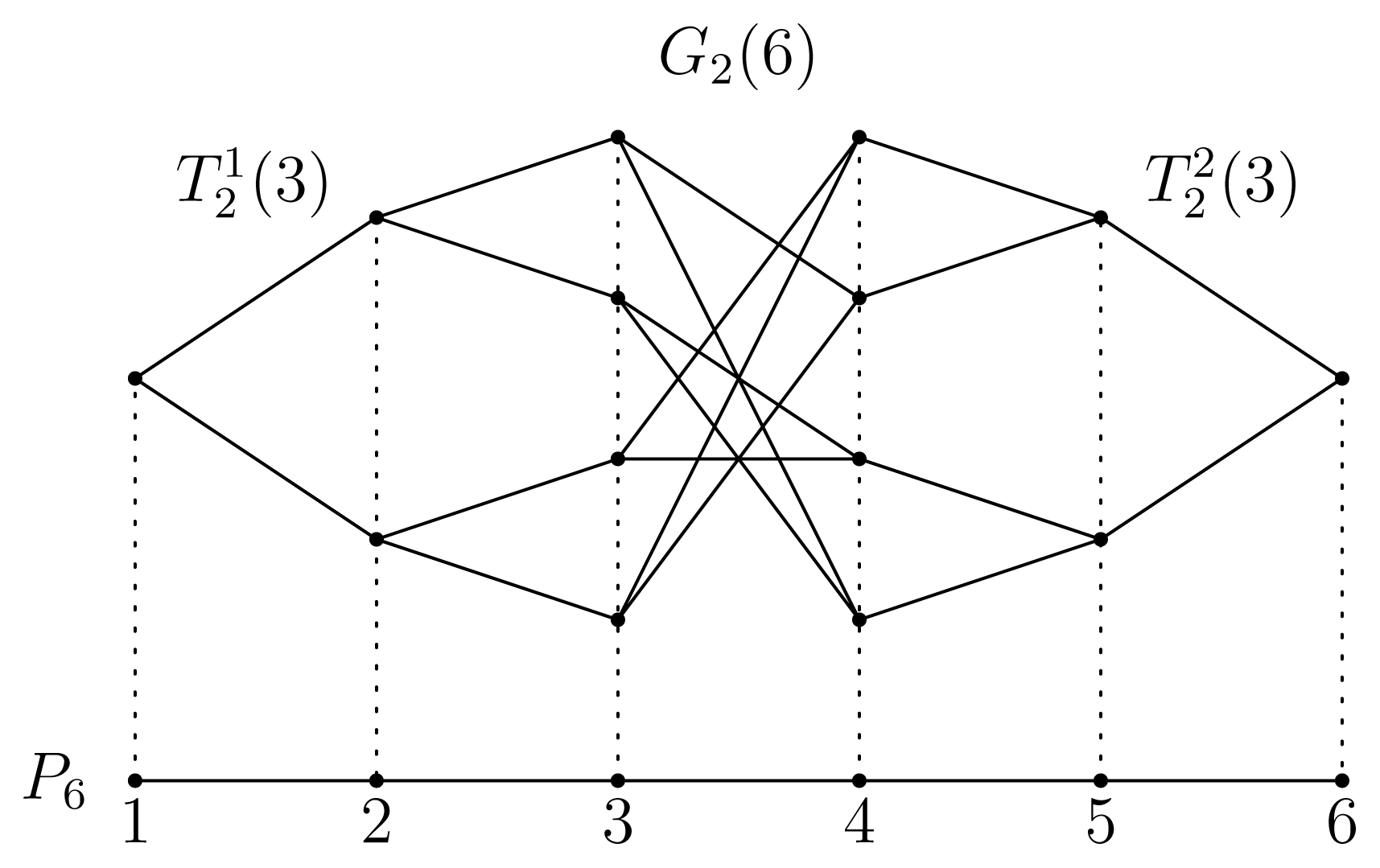
Let Tk(n) be the k-ary tree on vertices (height = n), i.e., the graph which is constructed inductively as follows: We start with a vertex called the “root” of Tk(n) and set the height of the root = 1. We add k numbers of vertices and set the height of these vertices = 2. Then, we connect the root and all the vertices with its height = 2. Similarly, for every vertex with its height = h, we add k numbers of new vertices and set the height of these vertices = h + 1. Then, we connect the vertex with its height = h and all the new k vertices with their height = h + 1. Note that there are kh−1 numbers of vertices with their height = h. We repeat this procedure, until all the vertices with its height = n − 1 connect with k numbers of new vertices with their height = n. We call each vertex with its height = n a “leaf”, because the degree of these vertices equals one. Note that the degree of the root equals k; the degree of the leaves is one, and the degree of all other vertices is k + 1.
In this paper, we consider the glued trees, Gk(2n), consisting of two k-ary trees, and . The glued tree, Gk(2n), is constructed as follows: Each leaf in and has k numbers of “potential edges”. We select a pair of potential edges (ei, ej) at random, where ei is a potential edge of a vertex, i, in and ej is that of j in . After that, we connect a pair of vertices, i and j, with an edge and erase the pair of potential edges, ei and ej. We continue this procedure until all the potential edges disappear. Note that the degree of the vertices in Gk(2n) except for the two roots of and are k + 1, and the degree of the roots are equal to k.
In a quantum search algorithm [14], it is known that the algorithms on the glued trees work on the path graphs. For the Grover walks on the spidernets, it can be shown that there is a subspace that is isomorphic to a DTQW on the path graph. On this subspace, the Grover walk behaves as the DTQW, which is called the Szegedy walk on the path graph (see [19] for more details). Using a similar argument, we can construct the Szegedy walks on the path graph corresponding to the Grover walks on the glued tree. Following these observations, we consider a reduction of Gk(2n) on the path graph, P2n, on 2n numbers of vertices with the vertex set V (P2n) = {1, 2, · · · 2n} and the edge set E(P2n) = {(i, i+1) : i = 1, 2, . . . 2n − 1}. The results shown in this paper are restricted to the Szegedy walks on the path graph. However, the results describe the behaviors of the corresponding Grover walks on the glued tree. Therefore, it is useful to consider the Szegedy walks on the path graph.
First of all, we identify all the vertices with their height = h in and as the vertex, h, in P2n and all the vertices with their height = h in as the vertex 2n − h + 1 in P2n. Figure 1 shows an example of the glued tree with the k = 2 and n = 3 case. The figure also exhibits the corresponding path graph.
Recall that the simple random walk on and has the transition probabilities from a vertex, i, to a neighboring vertex, j, as:
for the vertices, i, except for the roots and:
if the vertex, i, is the root. Based on this fact, we consider the following random walk on P2n corresponding to Gk(2n): let p = 1/(k + 1) and q = k/(k + 1). The transition probabilities of the random walk is:
Now, we define corresponding DTQWs, which we call the Szegedy walk [18,20,21] on P2n with the general settings of transition probabilities p and q with p+q = 1. This is the reduced DTQW on the path graph from the original Grover walk on the glued tree. Let 2n = span{|0,R〉, |1, L〉, |1,R〉, . . . , |2n − 1, L〉, |2n − 1,R〉, |2n, L〉} be a Hilbert space with |i, J〉 = |i〉 ⊗ |J〉 (i ∈ V (P2n), J ∈ {L,R}) the tensor product of elements of two orthonormal bases {|i〉 : i ∈ V (P2n)} for the position of the walker and {|L〉 = T [1, 0], |R〉 = T [0, 1]} for the chirality, which means the direction of the motion of the walker, where TA denotes the transpose of a matrix, A. Then, we consider the time evolution operator, U(2n), on 2n defined by U(2n) = S(2n)C(2n) with the following coin operator, C(2n), and shift operator, S(2n):
where and In are the n × n identity matrix.
Let be the position of our quantum walker at time t. The probability that the walker with initial state |ψ〉 is found at time t and the position, x, is defined by:
In this paper, we consider the DTQW starting from a vertex, i ∈ V (P2n), and choose the initial chirality state with equal probability, i.e., we choose the initial state as |ψ〉1 = |1〉⊗|R〉 for i = 1, |ψ〉i = |i〉⊗|L〉 or |ψ〉i = |i〉 ⊗ |R〉 with probability 1/2 for 2 ≤ i ≤ 2n − 1 or |ψ〉2n = |2n〉 ⊗ |L〉 for i = 2n. For the sake of simplicity, we write for . Let the time averaged distribution:
where the expectation takes the choice of the initial chirality state. For the sake of simplicity, we only consider the i, x ∈ {1, . . . , n} case from now on.
3. Results
In this section, we show our main result on the time averaged distribution, . We allow i, x ∈ {1, . . . , n} to be fixed and diverging in n cases. We have the following properties for :
Theorem 3.1
The time averaged distribution, , is symmetric, i.e., and for i, x ∈ {1, . . . , n}. The time averaged distribution has the following lower bounds:
This leads to the following result:
- (1)
If p > q, then,
- (2)
If p < q, then,
Note that the p = q = 1/2 case is included in the path graph case [18]. Theorem 3.1 shows that if the random walker is likely to go to the two roots, then the corresponding quantum walker localizes in vertices that are finitely close to the two roots. On the other hand, if the random walker is likely to go to the center of the glued tree, then the quantum walker localizes in vertices that are finitely close to the leaves in T1(n) and T2(n). The proof of Theorem 3.1 is based on [18,21]. In this proof, the eigenvalues and eigenvectors of the following 2n × 2n finite Jacobi matrix, J2n(p), induced by the random walk on P2n, the (i, j) component of which is determined by plays an important role:
Indeed, as is shown in Lemma 4.3, the eigenvalues and the eigenvectors of the time evolution operator, U(2n), are given by that of J2n(p). On the other hand, the time averaged distribution is completely described by all the eigenvectors of U(2n). Unfortunately, as is shown in Lemma 4.2, we cannot obtain all of the eigenvalues of J2n(p) explicitly. The lower bounds in Theorem 3.1 are calculated by the eigenvectors corresponding to ±1 eigenvalues of U(2n).
4. Proof of Theorem 3.1
In order to prove Theorem 3.1, we have the following result for the eigenspace of the Jacobi matrices at first:
Lemma 4.1
(The determinantal formula for a symmetric Jacobi matrix). Let J2n be the following 2n×2n finite Jacobi matrix:
where αi ∈ ℝ for i = 1, . . . n and wi ∈ (0, ∞) for i = 0, . . . n − 1. Then, the characteristic equation of J2n, i.e., det(λI2n − J2n) = 0, is:
where Ek is the following (n − k + 1) × (n − k + 1) matrix:
In addition:
- (1)
The eigenvector corresponding to the eigenvalue, λ, with
is:
- (2)
The eigenvector corresponding to the eigenvalue, λ, with is:
We should remark that every eigenvalue of J2n is simple (see, e.g., [22]). Therefore, the eigenvectors are mutually orthogonal.
Proof of Lemma 4.1
Let:
Note that by exchanging rows and columns, we have det(Ek) = det(Ēk).
By expanding det(λI2n − J2n) in the n-th row, we have:
On the other hand, repeating the expansion of the determinants, we obtain:
and:
Therefore, we have:
For the second equality, we use the following relation:
This completes the first half of the proof.
We can easily check that:
and:
for k = 2, . . . , n − 1.
From the condition , we have:
Similarly, from the condition , we have:
These conditions imply that the vectors described in the lemma are the corresponding eigenvectors.
Now, we apply Lemma 4.1 with parameters α1 = · · · = αn = 0, w0 = q2, w2 = · · · = wn−2 = pq and wn−1 = p to the Jacobi matrix, J2n(p). We obtain the following characteristic equation of J2n(p):
where is the following k × k matrix:
Remark that for k ≥ 2,
where Fk is the following k × k matrix:
Using these facts, we can calculate:
Therefore, the eigenvalues of J2n(p) are λ = ±1 and λ, satisfying det(Fn−1) ± p det(Fn−2) = 0.
For the λ = ±1 case, we have:
with det(F1) = ±1 and det(F0) = 1. This implies:
On the other hand, for the λ ≠ = ±1 case, we identify det(Fk) as , where Ũk(x) is the (monic) Chebyshev polynomial of the second kind, i.e., the series of polynomials satisfying the following recurrence relation:
In this case, we obtain:
with Ũ−1(x) = 0. Combining these results with Lemma 4.1, we have the following lemma for the eigen space of J2n(p):
Lemma 4.2
Let λ be the eigenvalue of J2n(p) and vλ be the corresponding eigenvector. Then, we have λ = ±1, and the remaining eigenvalues, λ, satisfy. The i-th component, vλ(i), of the eigenvectors, vλ, is the following:
- (1)
For λ = ±1
- (2)
For λ ≠ = ±1
The last part of Lemma 4.2, i.e., ||vλ||2, is calculated as follows:
Here, we us , obtained from the recurrence relation of the Chebyshev polynomial in the second equality. Using the recurrence relation of the Chebyshev polynomial, U−1(x) = 0 and the eigenvalue condition, we finally obtain:
The eigen space of the time evolution operator, U(2n), is described by that of J2n(p) (Lemma 2 of [18]) as follows:
Lemma 4.3
Let λk (k = 1, . . . , 2n) be the eigenvalues of J2n(p) and vλk (k = 1, . . . , 2n) be the corresponding eigenvectors. We set λ1 = 1 and λ2n = −1. Then, the eigenvalues μk (k = 1,±2, . . . ,±(2n − 1), 2n) and corresponding eigenvectors uk (k = 1,±2, . . . ,±(2n − 1), 2n) of U(2n) are obtained as follows:
Let Ṽλ = vλ/||vλ|| and for k = 1, . . . 2n,
Then, we have:
Now, we estimate the distribution . By the assumption of the choice of the initial state, we have:
Using the spectral decomposition and , we obtain:
with , because all eigenvalues of U(2n) are nondegenerate (this comes from nondegenerateness of J2n(p); see, e.g., [22]). Using this fact and Lemmas 4.2 and 4.3, we have the symmetric property of the time averaged distribution. Moreover, we also obtain:
for i = 1, . . . n. On the other hand, it is obvious that:
As a consequence, we have the desired lower bound.
Taking suitable limits, the remaining parts of Theorem 3.1 are obtained by this lower bound.
The eigenvectors, u±k, with k = 2, . . . , 2n − 1 are not obtained explicitly in the present stage. It is expected that the remaining part of the time averaged distribution converges to the uniform distribution after suitable normalization, because the remaining eigenvectors are similar to that of the time evolution operator of DTQW on the path graphs [18]. It is interesting future work to make clear whether this conjecture is true or not.
Acknowledgments
Yusuke Ide was supported by the Grant-in-Aid for Young Scientists (B) of the Japan Society for the Promotion of Science (grant no. 23740093). Norio Konno was supported by the Grant-in-Aid for Scientific Research (C) of the Japan Society for the Promotion of Science (grant no. 24540116). Etsuo Segawa was supported by the Grant-in-Aid for Young Scientists (B) of the Japan Society for the Promotion of Science (grant no. 25800088). Xin-Ping Xu was supported by the National Natural Science Foundation of China under project 11205110.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aharonov, D.; Ambainis, A.; Kempe, J.; Vazirani, U. Quantum Walks on Graphs. Proceedings of the 33rd Annual ACM Symposium on Theory of Computing, Heraklion, Greece, 6–8 July 2001; ACM Press: New York, NY, USA, 2001; pp. 50–59. [Google Scholar]
- Ahlbrecht, A.; Vogts, H.; Werner, A.H.; Werner, R.F. Asymptotic evolution of quantum walks with random coin. J. Math. Phys 2011, 52, 042201. [Google Scholar]
- Ambainis, A.; Bach, E.; Nayak, A.; Vishwanath, A.; Watrous, J. One-Dimensional Quantum Walks. Proceedings of the 33rd Annual ACMSymposium on Theory of Computing, Heraklion, Crete, Greece, 6–8 July 2001; ACM Press: New York, NY, USA, 2001; pp. 37–49. [Google Scholar]
- Kempe, J. Quantum random walks—an introductory overview. Contemp. Phys 2003, 44, 307–327. [Google Scholar]
- Kendon, V. Decoherence in quantum walks - a review. Math. Struct. Comp. Sci 2007, 17, 1169–1220. [Google Scholar]
- Konno, N. Quantum Walks. In Quantum Potential Theory, Lecture Notes in Mathematics; Franz, U., Schürmann, M., Eds.; Springer-Verlag: Heidelberg, Germany, 2008; Volume 1954, pp. 309–452. [Google Scholar]
- Manouchehri, K.; Wang, J.B. Physical Implementation of Quantum Walks; Springer-Verlag: Heidelberg, Germany, 2013. [Google Scholar]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quant. Inform. Process 2012, 11, 1015–1106. [Google Scholar]
- Berry, S.D.; Wang, J.B. Quantum-walk-based search and centrality. Phys. Rev. A 2010, 82, 042333. [Google Scholar]
- Berry, S.D.; Wang, J.B. Two-particle quantum walks: Entanglement and graph isomorphism testing. Phys. Rev. A 2011, 83, 042317. [Google Scholar]
- Douglas, B.L.; Wang, J.B. Classical approach to the graph isomorphism problem using quantum walks. J. Phys. Math. Gen 2008, 41, 075303. [Google Scholar]
- Rudinger, K.; Gamble, J.K.; Wellons, M.; Bach, E.; Friesen, M.; Joynt, R.; Coppersmith, S.N. Noninteracting multiparticle quantum random walks applied to the graph isomorphism problem for strongly regular graphs. Phys. Rev. A 2012, 86, 022334. [Google Scholar]
- Shenvi, N.; Kempe, J.; Whaley, K.B. Quantum random-walk search algorithm. Phys. Rev. A 2003, 67, 052307. [Google Scholar]
- Childs, A.M.; Cleve, R.; Deotto, E.; Farhi, E.; Gutmann, S.; Spielman, D.A. Exponential Algorithmic Speedup by Quantum Walk. Proceedings of the 35th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 9–11 June 2003; ACM Press: New York, NY, USA, 2003; pp. 59–68. [Google Scholar]
- Ambainis, A. Quantum Walk Algorithm for Element Distinctness. Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science (FOCS’04), Rome, Italy, 17–19 October 2004; IEEE Computer Society: Washington, DC, USA, 2004; pp. 22–31. [Google Scholar]
- Rohde, P.P.; Fedrizzi, A.; Ralph, T.C. Entanglement dynamics and quasi-periodicity in discrete quantum walks. J. Mod. Optic 2012, 59, 710–720. [Google Scholar]
- Godsil, C. Average mixing of continuous quantum walks. J. Comb. Theory A 2013, 120, 1649–1662. [Google Scholar]
- Ide, Y.; Konno, N.; Segawa, E. Time averaged distribution of a discrete-time quantum walk on the path. Quant. Inform. Process 2012, 11, 1207–1218. [Google Scholar]
- Konno, N.; Obata, N.; Segawa, E. Localization of the Grover walks on spidernets and free Meixner laws. Commum. Math. Phys 2013, 322, 667–695. [Google Scholar]
- Segawa, E. Localization of quantum walks induced by recurrence properties of random walks. J. Comput. Theor. Nanos 2013, 10, 1583–1590. [Google Scholar]
- Szegedy, M. Quantum speed-up of Markov Chain Based Algorithms. Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science (FOCS’04), Rome, Italy, 17–19 October 2004; IEEE Computer Society: Washington, DC, USA, 2004; pp. 32–41. [Google Scholar]
- Hora, A.; Obata, N. Quantum Probability and Spectral Analysis of Graphs; Springer-Verlag: Heidelberg, Germany, 2007. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ide, Y.; Konno, N.; Segawa, E.; Xu, X.-P. Localization of Discrete Time Quantum Walks on the Glued Trees. Entropy 2014, 16, 1501-1514. https://doi.org/10.3390/e16031501
Ide Y, Konno N, Segawa E, Xu X-P. Localization of Discrete Time Quantum Walks on the Glued Trees. Entropy. 2014; 16(3):1501-1514. https://doi.org/10.3390/e16031501
Chicago/Turabian StyleIde, Yusuke, Norio Konno, Etsuo Segawa, and Xin-Ping Xu. 2014. "Localization of Discrete Time Quantum Walks on the Glued Trees" Entropy 16, no. 3: 1501-1514. https://doi.org/10.3390/e16031501



