Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance
Abstract
:1. Introduction
2. Problem formulation and preliminaries
3. Description of the Fuzzy Logic System
4. Adaptive Fuzzy Controller Design
5. Numerical Simulations


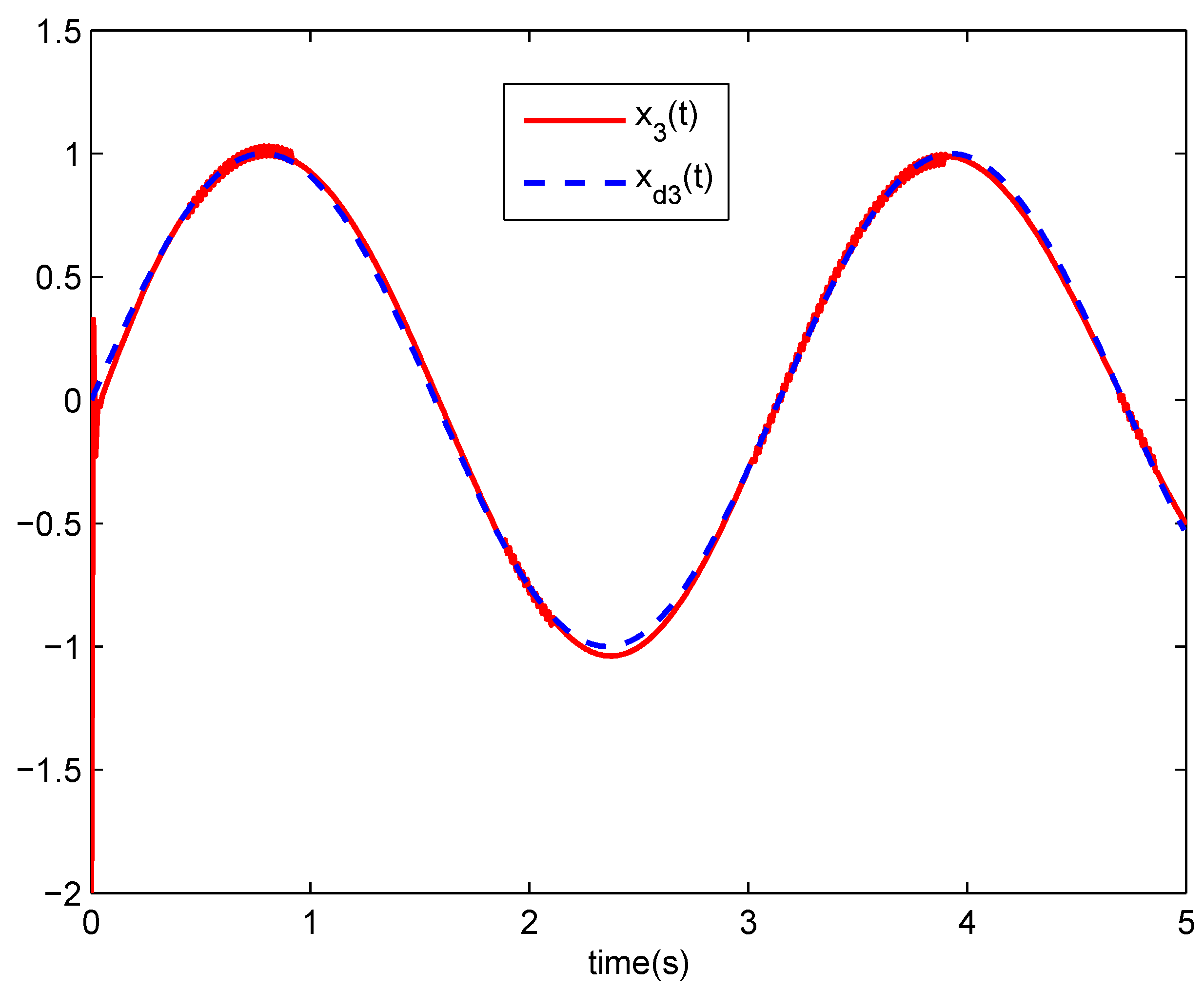


6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lu, J.G.; Chen, Y.Q. A note on the fractional-order Chen system. Chaos Solitons Fractals 2006, 27, 685–688. [Google Scholar] [CrossRef]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust Stability and of Fractional-Order Interval Systems with the Fractional Order α: The 0 < α < 1 Case. IEEE Trans. Autom. Control 2010, 55, 152–158. [Google Scholar]
- Qian, D.; Li, C.; Agarwal, R.P. Stability analysis of fractional differential system with Riemann-Liouville derivative. Math. Comp. Model. 2010, 52, 862–874. [Google Scholar] [CrossRef]
- Zhang, F.; Li, F. Stability analysis of fractional differential system with order lying in (1, 2). Adv. Differ. Equ. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability analysis of a class of nonlinear fractional-order systems. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Wen, X.J.; Wu, Z.M.; Lu, J.G. Stability analysis of a class of nonlinear fractional-order systems. IEEE Trans. Circuits Syst. II 2008, 55, 1178–1182. [Google Scholar] [CrossRef]
- Deng, W.H. Smoothness and stability of the solutions for nonlinear fractional differential equations. Nonlinear Anal. 2010, 72, 1768–1777. [Google Scholar] [CrossRef]
- Chen, L.; Chai, Y.; Wu, R.; Yang, R. Stability and Stabilization of a Class of Nonlinear Fractional-Order Systems With Caputo Derivative. IEEE Trans. Circuits Syst. II 2012, 59, 602–606. [Google Scholar] [CrossRef]
- Aghababa, M.P. Finite-time chaos control and synchronization of fractionalorder nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dyn. 2012, 69, 247–261. [Google Scholar] [CrossRef]
- Aghababa, M.P. Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. Int. J. Control 2013, 86, 1744–1756. [Google Scholar] [CrossRef]
- Shen, J.; Lam, J. Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 2014, 50, 547–551. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 3690–3694. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Castro-Linares, R.; Gallegos, J.A. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Ge, Z.M.; Jhuang, W.R. Chaos, control and synchronization of a fractional order rataional mechanical system with a centrifugal governor. Chaos Solitions Fractals 2007, 33, 270–289. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Sun, Y. Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance. Entropy 2015, 17, 5580-5592. https://doi.org/10.3390/e17085580
Li L, Sun Y. Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance. Entropy. 2015; 17(8):5580-5592. https://doi.org/10.3390/e17085580
Chicago/Turabian StyleLi, Ling, and Yeguo Sun. 2015. "Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance" Entropy 17, no. 8: 5580-5592. https://doi.org/10.3390/e17085580
APA StyleLi, L., & Sun, Y. (2015). Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance. Entropy, 17(8), 5580-5592. https://doi.org/10.3390/e17085580





