Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy
Abstract
:1. Introduction
2. Methods
2.1. Permutation Entropy
2.2. Multi-Scale Permutation Entropy
2.3. Empirical Mode Decomposition
3. The Analysis of the Permutation Entropy of Each Intrinsic Mode Function
3.1. The Choice of Permutation Entropy Parameters
3.2. The Empirical Mode Decomposition of the Ship-Radiated Noise
3.3. The PE of Each IMF
4. Feature Extraction of SRN Signal
4.1. Feature Extraction Based on the PE of the IMF with the Highest Energy
4.2. Feature Extraction Based on MPE
4.3. Feature Extraction Based on Energy Difference
4.4. Comparison of Feature Extraction Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, S.; Zeng, X. Robust underwater noise targets classification using auditory inspired time-frequency analysis. Appl. Acoust. 2014, 78, 68–76. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Liu, S.; Zhang, X.; Niu, Y.; Wang, P. Feature extraction and classification experiment of underwater acoustic signals based on energy spectrum of IMF’s. CEA 2014, 3, 203–206. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Hsieh, N.K.; Lin, W.Y.; Young, H.T. High-Speed Spindle Fault Diagnosis with the Empirical Mode Decomposition and Multiscale Entropy Method. Entropy 2015, 17, 2170–2183. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, X.; Chen, Z.; Tang, B. Fault Feature Extraction of Rolling Element Bearing Based on Improved EMD and Sliding Kurtosis Algorithm. J. Vib. Shock 2012, 31, 80–83. [Google Scholar]
- Wei, Q.; Liu, Q.; Fan, S.-Z.; Lu, C.-W.; Lin, T.-Y.; Abbod, M.F.; Shieh, J.-S. Analysis of EEG via Multivariate Empirical Mode Decomposition for Depth of Anesthesia Based on Sample Entropy. Entropy 2013, 15, 3458–3470. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Shih, M.-T.; Doctor, F.; Fan, S.-Z.; Jen, K.-K.; Shieh, J.-S. Instantaneous 3D EEG Signal Analysis Based on Empirical Mode Decomposition and the Hilbert–Huang Transform Applied to Depth of Anaesthesia. Entropy 2015, 17, 928–949. [Google Scholar] [CrossRef]
- Hou, W.; Feng, G.-L.; Dong, W.-J. A technique for distinguishing dynamical species in the temperature time series of North China. Acta Phys. Sin. 2006, 55, 2663–2668. [Google Scholar]
- Xue, C.; Hou, W.; Zhao, J.; Wang, S. The application of ensemble empirical mode decomposition method in multiscale analysis of region precipitation and its response to the climate change. Acta Phys. Sin. 2013, 62, 109203. [Google Scholar]
- Zhang, Z.; Liu, C.; Liu, B. Ship noise spectrum analysis based on HHT. In Proceedings of the 2010 IEEE 10th International Conference on Signal Processing (ICSP), Beijing, China, 24–28 October 2010; pp. 2411–2414.
- Yang, L. A empirical mode decomposition approach to feature extraction of ship-radiated noise. In Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 3682–3686.
- Yang, H.; Li, Y.; Li, G. Energy analysis of ship-radiated noise based on ensemble empirical mode decomposition. J. Vib. Shock 2015, 34, 55–59. [Google Scholar]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Ravelo-García, A.G.; Navarro-Mesa, J.L.; Casanova-Blancas, U.; Martin-Gonzalez, S.; Quintana-Morales, P.; Guerra-Moreno, I.; Canino-Rodríguez, J.M.; Hernández-Pérez, E. Application of the Permutation Entropy over the Heart Rate Variability for the Improvement of Electrocardiogram-based Sleep Breathing Pause Detection. Entropy 2015, 17, 914–927. [Google Scholar] [CrossRef]
- Shi, Z.; Song, W.; Taheri, S. Improved LMD, Permutation Entropy and Optimized K-Means to Fault Diagnosis for Roller Bearings. Entropy 2016, 18, 70. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Zhao, L.-Y.; Wang, L.; Yan, R.-Q. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Decomposition and Multi-Scale Permutation Entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef]
- Qin, N.; Jiang, P.; Sun, Y.; Jin, W. Fault Diagnosis of High Speed Train Bogie Based on EEMD and Permutation Entropy. J. Vib. Meas. Diagn. 2015, 35, 885–891. [Google Scholar]
- Wu, T.-Y.; Yu, C.-L.; Liu, D.-C. On Multi-Scale Entropy Analysis of Order-Tracking Measurement for Bearing Fault Diagnosis under Variable Speed. Entropy 2016, 18, 292. [Google Scholar] [CrossRef]
- Aziz, W.; Arif, M. Multiscale Permutation Entropy of Physiological Time Series. In Proceedings of the Pakistan Section Multitopic Conference INMIC, Karachi, Pakistan, 23–25 December 2005.
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]

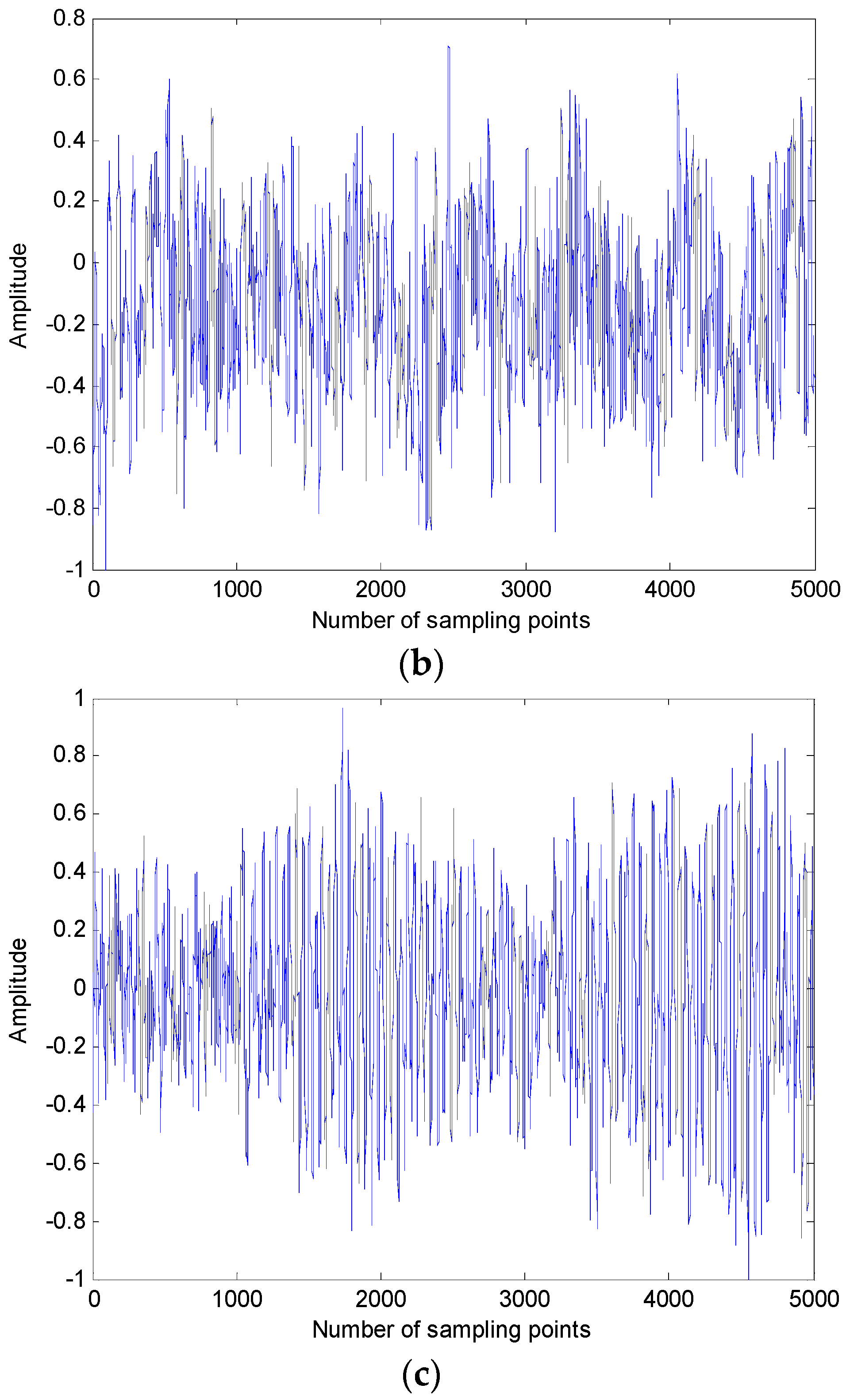






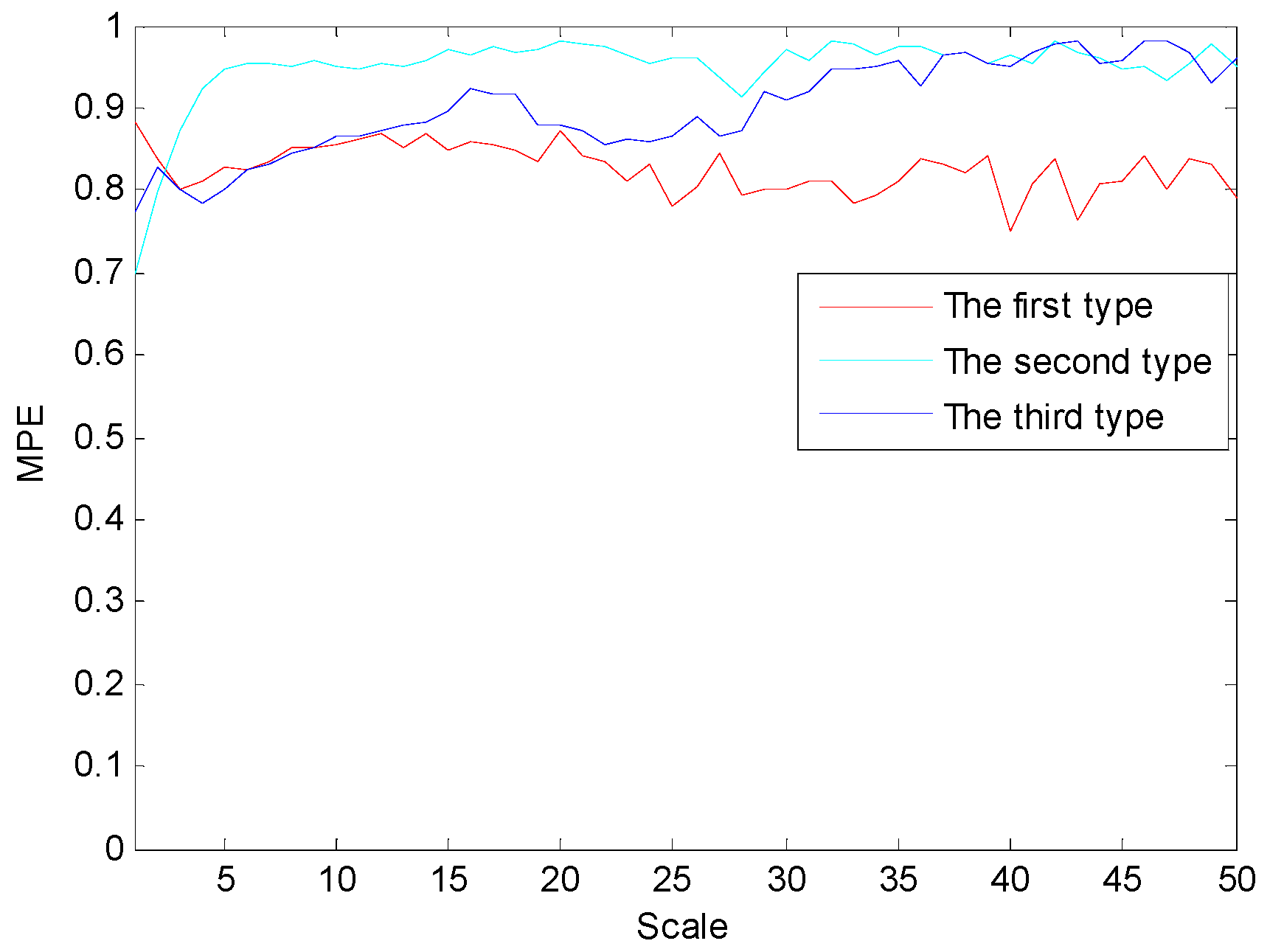




| First Type | Second Type | Third Type | |
|---|---|---|---|
| EIMF (level) | 6 | 4 | 3 |
| PE of EIMF | 0.2528 | 0.3310 | 0.4054 |
| First Type | Second Type | Third Type | |
|---|---|---|---|
| MPE (scale = 1) | 0.8837 | 0.7105 | 0.7852 |
| MPE (scale = 17) | 0.8562 | 0.9717 | 0.9123 |
| First Type | Second Type | Third Type | |
|---|---|---|---|
| Energy difference (db) | −12.013 | −2.4347 | −1.5990 |
| First Type | Second Type | Third Type | |
|---|---|---|---|
| The average value of PE of EIMF | 0.2524 | 0.3458 | 0.4287 |
| The range of PE of EIMF | 0.2473~0.2612 | 0.3325~0.3641 | 0.3825~0.4526 |
| The average value of PE | 0.8825 | 0.7164 | 0.7482 |
| The range of PE | 0.8673~0.8934 | 0.6926~0.7458 | 0.7129~0.7912 |
| The average value of MPE (scale = 17) | 0.8452 | 0.9758 | 0.9137 |
| The range of MPE (scale = 17) | 0.7912~0.9034 | 0.9553~0.9876 | 0.8457~0.9625 |
| The average value of energy difference (db) | −13.9462~−11.6412 | −4.3344~−1.7516 | −1.9847~−0.8835 |
| The range of energy difference (db) | −12.6240 | −2.9339 | −1.4713 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-X.; Li, Y.-A.; Chen, Z.; Chen, X. Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy. Entropy 2016, 18, 393. https://doi.org/10.3390/e18110393
Li Y-X, Li Y-A, Chen Z, Chen X. Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy. Entropy. 2016; 18(11):393. https://doi.org/10.3390/e18110393
Chicago/Turabian StyleLi, Yu-Xing, Ya-An Li, Zhe Chen, and Xiao Chen. 2016. "Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy" Entropy 18, no. 11: 393. https://doi.org/10.3390/e18110393
APA StyleLi, Y.-X., Li, Y.-A., Chen, Z., & Chen, X. (2016). Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy. Entropy, 18(11), 393. https://doi.org/10.3390/e18110393







