Multiphoton Controllable Transport between Remote Resonators
Abstract
:1. Introduction
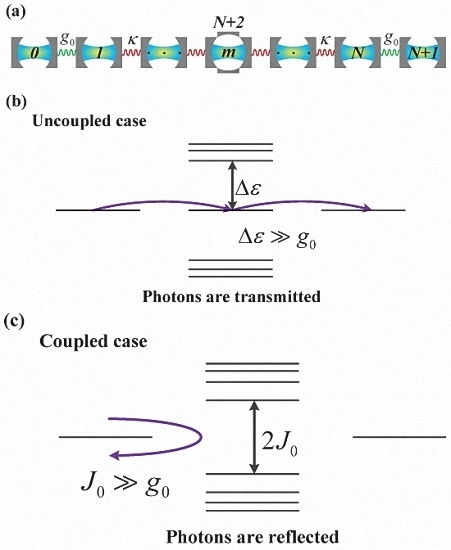
2. Physical Model and Effective Hamiltonian
3. Multiphoton Controllable Transport and Fidelities
4. Quantum Information Leakage
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix



References and Notes
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Naik, D.S.; Peterson, C.G.; White, A.G.; Berglund, A.J.; Kwiat, P.G. Entangled state quantum cryptography: Eavesdropping on the ekert protocol. Phys. Rev. Lett. 2000, 84, 4733–4736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Quantum cryptography using entangled photons in energy-time bell states. Phys. Rev. Lett. 2000, 84, 4737–4740. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68. [Google Scholar] [CrossRef]
- Salemian, S.; Mohammadnejad, S. An error-free protocol for quantum entanglement distribution in long-distance quantum communication. Chin. Sci. Bull. 2011, 56, 618–625. [Google Scholar] [CrossRef]
- Zheng, C.; Long, G.F. Quantum secure direct dialogue using Einstein-Podolsky-Rosen pairs. Sci. China Phys. Mech. Astron. 2014, 57, 1238–1243. [Google Scholar] [CrossRef]
- Zhang, J.F.; Long, G.L.; Zhang, W.; Deng, Z.W.; Liu, W.Z.; Lu, Z.H. Simulation of Heisenberg XY interactions and realization of a perfect state transfer in spin chains using liquid nuclear magnetic resonance. Phys. Rev. A 2005, 72. [Google Scholar] [CrossRef]
- Feng, G.R.; Xu, G.F.; Long, G.L. Experimental realization of nonadiabatic holonomic quantum computation. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef] [PubMed]
- Childress, L.; Dutt, M.V.G.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F.; Wrachtrup, J.; Hemmer, P.R.; Lukin, M.D. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 2006, 314, 281–285. [Google Scholar] [CrossRef] [PubMed]
- Zagoskin, A.M.; Johansson, J.R.; Ashhab, S.; Nori, F. Quantum information processing using frequency control of impurity spins in diamond. Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- Bermudez, A.; Jelezko, F.; Plenio, M.B.; Retzker, A. Electron-mediated nuclear-spin interactions between distant nitrogen-vacancy centers. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
- Yao, N.Y.; Jiang, L.; Gorshkov, A.V.; Maurer, P.C.; Giedke, G.; Cirac, J.I.; Lukin, M.D. Scalable architecture for a room temperature solid-state quantum information processor. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.F.; Ju, C.Y.; Shi, F.Z.; Du, J.F. Optimizing ultrasensitive single electron magnetometer based on nitrogen-vacancy center in diamond. Chin. Sci. Bull. 2013, 58, 2920–2923. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C.L. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wei, L.F.; Tsai, J.S.; Nori, F. Controllable coupling between flux qubits. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Niskanen, A.O.; Harrabi, K.; Yoshihara, F.; Nakamura, Y.; Lloyd, S.; Tsai, J.S. Quantum coherent tunable coupling of superconducting qubits. Science 2007, 316, 723–726. [Google Scholar] [CrossRef] [PubMed]
- Ashhab, S.; Niskanen, A.O.; Harrabi, K.; Nakamura, Y.; Picot, T.; De Groot, P.C.; Harmans, C.J.P.M.; Mooij, J.E.; Nori, F. Interqubit coupling mediated by a high-excitation-energy quantum object. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Xiong, W.; Jin, D.Y.; Jing, J.; Lam, C.H.; You, J.Q. Controllable coupling between a nanomechanical resonator and a coplanar-waveguide resonator via a superconducting flux qubit. Phys. Rev. A 2015, 92. [Google Scholar] [CrossRef]
- Sillanpää, M.A.; Park, J.I.; Simmonds, R.W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 2007, 449, 438–442. [Google Scholar] [CrossRef] [PubMed]
- Majer, J.; Chow, J.M.; Gambetta, J.M.; Koch, J.; Johnson, B.R.; Schreier, J.A.; Frunzio, L.; Schuster, D.I.; Houck, A.A.; Wallraff, A.; et al. Coupling superconducting qubits via a cavity bus. Nature 2007, 449, 443–447. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Gong, Z.R.; Liu, Y.X.; Sun, C.P.; Nori, F. Controllable scattering of a single photon inside a one-dimensional resonator waveguide. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef] [PubMed]
- Nataf, P.; Ciuti, C. Protected quantum computation with multiple resonators in ultrastrong coupling circuit QED. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.P.; Su, Q.P.; Nori, F. Entanglement generation and quantum information transfer between spatially-separated qubits in different cavities. New J. Phys. 2013, 15. [Google Scholar] [CrossRef]
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-high-Q toroid microcavity on a chip. Natrue 2003, 421, 925–928. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Rotter, S.; Yilmaz, H.; Liertzer, M.; Monifi, F.; Bender, C.M.; Nori, F.; Yang, L. Loss-induced suppression and revival of lasing. Science 2014, 346, 328–332. [Google Scholar] [CrossRef] [PubMed]
- Jing, H.; Özdemir, Ş.K.; Lu, X.Y.; Zhang, J.; Yang, L.; Nori, F. PT-Symmetric phonon laser. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Tame, M.; Noh, C.; Lim, J.; Maier, S.A.; Lee, J.; Angelakis, D.G. Robust-to-loss entanglement generation using a quantum plasmonic nanoparticle array. New J. Phys. 2013, 15, 083017. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P.; Kimble, H.J.; Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 1997, 78, 3221–3224. [Google Scholar] [CrossRef]
- Serafini, A.; Mancini, S.; Bose, S. Distributed quantum computation via optical fibers. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, M.J.; Brandão, F.G.S.L.; Plenio, M.B. Quantum many-body phenomena in coupled cavity arrays. Laser Photonics Rev. 2008, 2, 527–556. [Google Scholar] [CrossRef]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Douglas, J.S.; Habibian, H.; Hung, C.-L.; Gorshkov, A.V.; Kimble, H.J.; Chang, D.E. Quantum many-body models with cold atoms coupled to photonic crystals. Nat. Photonics 2015, 9, 326–331. [Google Scholar] [CrossRef]
- Wang, Z.H.; Li, Y.; Zhou, D.L.; Sun, C.P.; Zhang, P. Single-photon scattering on a strongly dressed atom. Phys. Rev. A 2012, 86. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, L.P.; Li, Y.; Sun, C.P. Quantum routing of single photons with a cyclic three-level system. Phys. Rev. Lett. 2013, 111. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, F.; Ciccarello, F.; Palma, G.M. Photon localization versus population trapping in a coupled-cavity array. Phys. Rev. A 2014, 89. [Google Scholar] [CrossRef] [Green Version]
- Hai, L.; Tan, L.; Feng, J.S.; Xu, W.B.; Wang, B. Single photon transport properties in coupled cavity arrays nonlocally coupled to a two-level atom in the presence of dissipation. Chin. Phys. B 2014, 23, 024202. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Z.H.; Zhou, L. T-shaped single-photon router. Opt. Express 2015, 23, 22955–22962. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.Z.; Ian, H.; Shi, T.; Dong, H.; Sun, C.P. Photonic Feshbach resonance. Sci. China Phys. Mech. Astron. 2010, 53, 1234–1238. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, Z.H.; Zhou, D.L. Multimode effects in cavity QED based on a one-dimensional cavity array. Phys. Rev. A 2014, 90. [Google Scholar] [CrossRef]
- Qin, W.; Nori, F. Controllable single-photon transport between remote coupled-cavity arrays. Phys. Rev. A 2016, 93. [Google Scholar] [CrossRef]
- Longo, P.; Schmitteckert, P.; Busch, K. Few-photon transport in low-dimensional systems: interaction-induced radiation trapping. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Longo, P.; Schmitteckert, P.; Busch, K. Few-photon transport in low-dimensional systems. Phys. Rev. A 2011, 83. [Google Scholar] [CrossRef]
- Roy, D. Few-photon optical diode. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Roy, D. Two-Photon scattering by a driven three-level emitter in a one-dimensional waveguide and electromagnetically induced transparency. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Chang, D.E.; Cirac, J.I. Multiphoton-scattering theory and generalized master equations. Phys. Rev. A 2015, 92. [Google Scholar] [CrossRef]
- Luo, M.X.; Wang, X.J. Universal quantum computation with qudits. Sci. China Phys. Mech. Astron. 2014, 57, 1712–1717. [Google Scholar] [CrossRef]
- Qin, W.; Wang, C.; Cao, Y.; Long, G.L. Multiphoton quantum communication in quantum networks. Phys. Rev. A 2014, 89. [Google Scholar] [CrossRef]
- Hua, M.; Tao, M.J.; Deng, F.G. Efficient generation of NOON states on two microwave-photon resonators. Chin. Sci. Bull. 2014, 59, 2829–2834. [Google Scholar] [CrossRef]
- Lieb, E.; Schultz, T.; Mattis, D. Two soluble models of an antiferromagnetic chain. Ann. Phys. 1961, 16, 407–466. [Google Scholar] [CrossRef]
- Christandl, M.; Datta, N.; Ekert, A.; Landahl, A.J. Perfect state transfer in quantum spin networks. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef] [PubMed]
- Yao, N.Y.; Jiang, L.; Gorshkov, A.V.; Gong, Z.-X.; Zhai, A.; Duan, L.-M.; Lukin, M.D. Robust quantum state transfer in random unpolarized spin chains. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Hofheinz, M.; Weig, E.M.; Ansmann, M.; Bialczak, R.C.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Wang, H.; Martinis, J.M.; Cleland, A.N. Generation of Fock states in a superconducting quantum circuit. Nature 2008, 454, 310–314. [Google Scholar] [CrossRef] [PubMed]
- In order to plot the transmission and reflection infidelities, we numerically perform the exact diagonalization of the coupling matrix A, and then calculate these infidelities according to Equations (26) and (27), and the definitions of such infidelities. The upper bounds, however, are straightforwardly plotted according to Equations (47) and (54). In addition, we plot these quantities at a specific evolution time, , to make the quantum state of either the transmitted or reflected photons remain unchanged
- Bose, S. Quantum communication through an unmodulated spin chain. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhou, D.L. Optimized quantum state transfer through an XY spin chain. Phys. Rev. A 2014, 89. [Google Scholar] [CrossRef]
- Qin, W.; Li, J.L.; Long, G.L. High-dimensional quantum state transfer in a noisy network environment. Chin. Phys. B 2015, 24, 040305. [Google Scholar] [CrossRef]
- Qin, W.; Wang, C.; Zhang, X.D. Protected quantum-state transfer in decoherence-free subspaces. Phys. Rev. A 2015, 91. [Google Scholar] [CrossRef]
- Fukuhara, T.; Hild, S.; Zeiher, J.; Schauß, P.; Bloch, I.; Endres, M.; Gross, C. Spatially resolved detection of a spin-entanglement wave in a bose-hubbard chain. Phys. Rev. Lett. 2015, 115. [Google Scholar] [CrossRef] [PubMed]
- Życzkowski, K.; Sommers, H. Induced measures in the space of mixed quantum states. J. Phys. A Math. Gen. 2001, 34, 7111–7125. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, M.; Qin, W. Transfer of high-dimensional quantum state through an XXZ-Heisenberg quantum spin chain. Int. J. Mod. Phys. B 2015, 29. [Google Scholar] [CrossRef]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, W.; Long, G. Multiphoton Controllable Transport between Remote Resonators. Entropy 2016, 18, 179. https://doi.org/10.3390/e18060179
Qin W, Long G. Multiphoton Controllable Transport between Remote Resonators. Entropy. 2016; 18(6):179. https://doi.org/10.3390/e18060179
Chicago/Turabian StyleQin, Wei, and Guilu Long. 2016. "Multiphoton Controllable Transport between Remote Resonators" Entropy 18, no. 6: 179. https://doi.org/10.3390/e18060179