Abstract
Automatically extracting quantities and generating final answers for numerical attributes is very useful in many occasions, including question answering, image processing, human-computer interaction, etc. A common approach is to learn linguistics templates or wrappers and employ some algorithm or model to generate a final answer. However, building linguistics templates or wrappers is a tough task for builders. In addition, linguistics templates or wrappers are domain-dependent. To make the builder escape from building linguistics templates or wrappers, we propose a new approach to final answer generation based on Predicates-Units Table (PUT), a mini domain-independent knowledge base. It is deserved to point out that, in the following cases, quantities are not represented well. Quantities are absent of units. Quantities are perhaps wrong for a given question. Even if all of them are represented well, their units are perhaps inconsistent. These cases have a strong impact on final answer solving. One thousand nine hundred twenty-six real queries are employed to test the proposed method, and the experimental results show that the average correctness ratio of our approach is 87.1%.
1. Introduction
Quantity extraction for numerical attribute is very useful in many occasions including question answering [1], image processing [2], human-computer interaction [3], etc. For example, quantity extraction is necessary to final answer solving for a numerical question in question answering. Extracted quantity (e.g., size of a physical object) is helpful to distinguish physical objects in image processing. In addition, extracted quantity is helpful to find incorrect input in human-computer interaction. However, it is a hard and intensive work to extract a quantity manually. Hence, automatically extracting quantities and generating final answers for numerical attributes is emphasized.
For general entity extraction, a common approach to final answer generation is to extract the candidate entities from information sources. Consequently, candidate entities are classified by semantic similarity. At last, the most frequent candidate entity is selected as the final answer. For numerical attributes, the process of final answer generation is a little different. If there is not the most frequent quantity, an alternative approach is to calculate the average value of all quantities as the final answer. However, they are not sometimes represented well. Some are absent of units. Some are perhaps wrong for a given question. Even if all of them are represented well, their units are perhaps inconsistent. These exceptions have a strong impact on final answer generation. An example is “What is the length of an automobile?” The quantity set is {4420, 166.25, 114, 106, 114, 5.0165, 4.19608, 3.9116, 4.93014}. Each quantity is absent of units. One hundred fourteen is selected as the final answer because it is the most frequent quantity. Obviously, the final answer is unmeaning because the unit is absent. Another example is “What is the weight of a dog?” The quantity set is {(2.0, kg), (2.5, kg), (10.0, kg), (50.0, cm), …}. Obviously, (50, cm) is a wrong quantity and should be dropped. Since the quality of the final answer depends on quantities, the keynote of our strategy is to drop all wrong quantities, keep all correct quantities, and infer units of the quantities which are absent of units. In addition, compared to a general entity, the quantity of numerical attributes is likely used as an operand for a complex numerical question. For instance, the answer (105.4, km2) is used as an operand to solve the question “How many times the area of Beijing is larger than Paris?” Obviously, accuracy of the answer of the question depends on accuracies of the operands. The more accurate are the operands, the more accurate is the answer of question. This shows that answer solving for numerical questions is worth exploring.
2. Preliminaries
Definition 1.
A query q is 2-tuple q = (subj, pred), where subj is the subject of q and pred is the predicate of q.
For example, q = (earth, radius) is a query that means “What is the radius of the Earth?”, and earth is the subject of q. radius is the predicate of q.
Definition 2.
For a query q, quantity set CASq is defined as CASq = {cai = (valuei, uniti)|1 <= I <= |CASq|}. CASq is returned when q is submitted to Sindice [4], a semantic searing engine. For any cai ∈ CASq, cai is said to be a quantity, valuei is said to be a value of cai, and uniti is said to be a unit of cai.
For example, one of the quantities is (6371 km) when query q = (earth, radius) is submitted to Sindice. This means that the radius of the earth is 6371 kilometres. Note that quantities are sometimes absent of units for some queries. For example, one of the quantities is 1,321,851,888 when a query q = (China, population) is submitted to Sindice. To apply the same format to represent these quantities which are absent of units, we use “count” as the unit of the quantity which is absent of unit. For example, the quantity 1,321,851,888 is represented as (1,321,851,888, count).
Definition 3.
Predicates-Units Table PUT is defined as {PUi = (ti, Pi, Ui, si, URi, Eqi)|1 < = I <= |PUT|}. For any PUi = (ti, Pi, Ui, si, URi, Eqi) ∈ PUT, PUi is called a predicates-units. ti is a semantic type of PUi and is also the identification of PUi. The first letter of ti is capitalised. Pi is a set of predicates that have the common semantic type ti. For any p ∈ Pi, ti is a semantic type of p. Ui is a set of units that have common semantic type ti. For any u ∈ Ui, ti is a semantic type of u. si ∈ Ui is an SI unit of PUi. URi is defined as {(unitj, ratioj)|unitj ∈ Ui, 1 <= j <= |Ui| and ratioj is a digital}. Mathematics equations between units are given in tuple Eq. Let T be {t1, t2, …, t|PUT|}.
A segment of PUT is shown in Table 1. For example, (Distance, {length, height, width, radius, diameter}, {metre, millimetre, inch, foot, yard, centimetre, kilometre}, metre, {(metre, 1), (millimetre, 1000), (inch, 39.37), (foot, 3.28), (yard, 1.09), (centimetre, 100), (kilometre, 0.001)}) is a predicates-units.

Table 1.
A segment of the Predicates-Units Table.
Definition 4.
For a quantity ca = (value, unit), t is a semantic type of ca if (t, P, U, s, UR, Eq) ∈ PUT ∧ unit ∈ U holds. Otherwise, count is said to be a semantic type of ca.
Definition 5.
For a set of quantities CA = {ca1, ca2, …, can}, t is semantic type of CA if for any two ai, aj ∈ CA, the semantic types of both ai and aj are t.
3. Our Approach
The framework for final answer solving is displayed in Figure 1.
- Step 1: According to the predicate pred of a query q(subj, pred) and PUT, compute the semantic type tq of CASq. Proceed to step 2.
- Step 2: If tq is included in T, proceed to step 3. Otherwise, delete quantities with units from CASq and proceed to step 4.
- Step 3: Delete quantities for which the semantic types are different than both tq and count. Try to infer the units of quantities which are absent of units. Unify units of quantities to the SI unit.
- Step 4: Solve the final answer. If the most common quantities occurs at least twice as often as the second most common quantity, the most common quantity is chosen as the final answer. Otherwise, if there is no obvious single quantity for a correct answer, the average value is chosen.
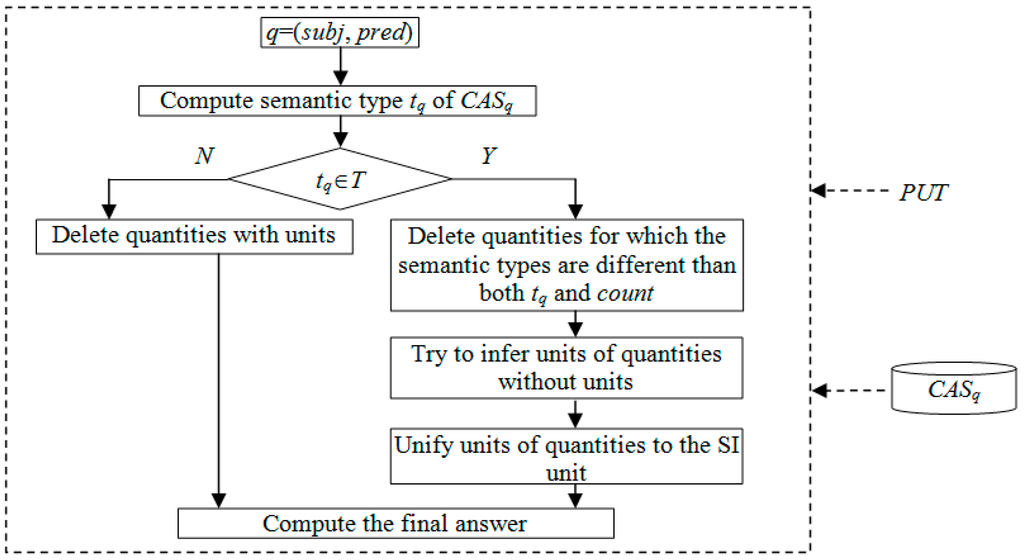
Figure 1.
The framework for final answer solving.
To make the proposed approach more comprehensible, three typical queries are introduced. The set of quantities is stated as follow.
- query 1: q1 = (boeing747, capacity).
- query 2: q2 = (automobile, length).
- query 3: q3 = (wind turbine, capacity).
(1) Algorithm 1 is employed to obtain the semantic type of a quantity set. If predicate pred of a query q is found in tuple P of some predicates-units, the corresponding tuple t is returned. If predicate pred of q is not found in tuple P of any predicates-units, we aggregate answers in the quantity set according to their semantic type. Then, we count the quantities for every division. If the semantic type of these quantities that are in the division with the most quantities is count, count is returned. If the semantic type of these quantities that are in the division with the most quantities is not count, the semantic type of these quantities that are in the division with the most quantities is returned.
Semantic type Distance is returned because the predicate length of q2 is found in PUT. For queries q1 and q3, we divide the quantity set and count the quantities for every division because the predicate capacity for queries q1 and q3 is not found in PUT. For query q1, the number of quantities which are absent of units can be taken as 7 7. For query q3, the number of quantities with semantic type Force is 6. The number of quantities without units is 1. Thus, for query q1, count is returned. For query q3, semantic type Force is returned.
| Algorithm 1. computeSemanticTypeOfCAS(q, PUT) |
|
Input: A query q = (subj, pred) and PUT. Output: tq, semantic type of q.
|
(2) Algorithm 2 is employed to refine the quantity set. Noisy answers are deleted from the quantity set. If the semantic type returned by Algorithm 1 is count, delete the quantities for which the semantic types are not count. Otherwise, delete the quantities for which the semantic type is not count or the semantic type returned by Algorithm 1. For queries q1, q2, and q3, the refined quantity set is displayed in Table 2.

Table 2.
The optimized quantities CASq1, CASq2, CASq3.
| Algorithm 2. optimizeQuantities(CASq, PUT) |
|
Input: CASq and PUT Output: CASq, refined quantity set.
|
Although all of CASq1, CASq2, CASq3 remain unchanged, the reasons for this are different. For query q1, the returned semantic type is count. Since there are no quantities for which the semantic types are not count, CASq1 remains unchanged. For query q2, the returned semantic type is Distance. Since the semantic types of all quantities are count, CASq2 remains unchanged. For query q3, the returned semantic type is Force. Since the semantic types of all quantities are count or Force, CASq3 remains unchanged.
(3) Algorithms 3 and 4 are employed to infer the units of quantities which are absent of units. If the semantic types of all quantities are count, Algorithm 3 is employed to infer the units of quantities which are absent of units. First, we obtain tuple UR, which meets (qt, P, U, s, UR, Eq) ∈ PUT. Second, we use the k-means algorithm to obtain cluster set Cs. Initially, the parameter “k” is set between 2 to sqrt(n), where n is the count of quantities. Consequently, we chose the optimal “k” according to DB (Davies–Bouldin) index which was proposed by Davies et al. [5]. Euclidean distance is exploited to calculate similarity. Third, we obtain all subsets of UR, each of which has |Cs| elements. According to Equation (1), compute the fit degree between every subset of UR and Cs. The subset of UR that has a maximum fit degree is used to assign the units of quantities.
| Algorithm 3. inferUnits1(CASq, PUT) |
|
Input: CASq and PUT Output: CASq, optimized quantity set.
|
- V is the number of values in the selected clusters. For instance of CASq2, V can be taken as 9.
- C is the total number of clusters. For instance of CASq2, C can be taken as 3.
- M is the number of values in the selected model. For instance of CASq2, M can be taken as 8 if the selected model is Distance.
- vi is the value of the ith element.
- wi is the identifier of the cluster to which the ith element belongs.
- cj is the value of jth cluster.
- mj is the value of the jth model’s variable.
If there exists some quantities whose semantic types are count, Algorithm 4 is employed to infer the units of quantities which are absent of units. First, we obtain tuples UR, s and rs, which meet (qt, P, U, s, UR) ∈ PUT and (s, rs) ∈ UR. Second, we unify the unit of every quantity with a unit to s. Calculate the average value of the quantities with the unit s. Third, according to Equation (2), we can compute the fit degree between every quantity which is absent of a unit and the average value of quantities with unit s and then decide the unit of the quantities without units. Finally, unify the unit of every quantity with a unit to s again.
- (v, count) ∈ CASq
- m is the average value of quantities with unit st
- (u, r), (s, rs) ∈ URt
| Algorithm 4. inferUnits2(CASq, PUT) |
|
Input: CASq and PUT Output: CASq, optimized quantity set.
|
For quantity set CASq2, the clusters are cluster1 = {4420}, cluster2 = {166.25, 114, 106, 114}, and cluster3 = {5.0165, 4.19608, 3.9116, 4.93014}. The subset of UR, which has a maximum fit degree with the cluster set, is {(millimetre, 1000), (inch, 39.37), (metre, 1)}. Hence, the units of the quantities of every cluster are “millimetre”, “inch” and “metre”, respectively. Unify the units of quantities to “metre”. For details, please refer to Table 3.

Table 3.
Quantities of CASq2 after unit inference and standardization.
For quantity set CASq3, the average value of the quantities with units is (3,600,000 × 4 + 2,300,000)/5 = 3,340,000 watt. The fit degree between the quantities without units and the average value is displayed in Table 5. The UR with a maximum degree with the quantity (306,000, count) is (watt, 1). Hence, the unit of quantity 3,060,000 is inferred as “watt”. Similarly, the unit of quantity 5.5 is inferred as “megawatt”. The units of the quantities of CASq3 are unified to “watt”. For details, one can refer to Table 4 and Table 5.

Table 5.
Quantities of CASq3 after unit inference and standardization.

Table 4.
Fit degrees of quantities of CASq3 without units.
(4) Algorithm 5 illustrates how to solve the final answer. For quantities, if the most common value of quantities occurs at least twice as often as the second most common value of quantities, the most common value is selected as the final answer. Otherwise, if there is no obvious single quantity for a correct answer, the average value is chosen.
| Algorithm 5. getFinalAnswer (CASq) |
|
Input: CASq Output: answerq, final answer of q
|
4. Experiments and Evaluation
4.1. Dataset Collection
We employ the Sindice search engine to collect quantities. Sindice is a lookup index over resources crawled on the Semantic Web. It allows applications to automatically locate documents containing information about a given resource. In addition, it allows resource retrieval through uniquely identifying inverse-functional properties, and offers a full-text search and index SPARQL end-points. The resources that support this particular semantic search engine include DBLP, Wikipedia article links, infoboxes, UniProt, and Geonames, etc. Around 26.6 million RDF documents have been indexed.
4.2. Dataset Statistics
We report on experiments with eight semantic types, which are “Length”, “Weight”, “Speed”, “Time”, “Volume”, “Area”, “Power”, “Count”, respectively. Based on the eight semantic types, we exploit Sindice, a semantic searching engine, to get quantities. For each query, the top 20 records returned by Sindice are retained. We extract quantities from each record to build a quantity set.
Finally, we collect 1926 real queries. The distribution is shown in Table 6. UinP is the set of queries whose predicates are found in the unit tuple of PUT. !UinP is the set of queries whose predicates are not found in the unit tuple of PUT. NU is the set of queries each of whose quantities is absent of units. !NU is the set of queries whose quantities are not absent of units.

Table 6.
Distribution of queries.
4.3. Dataset Validation
For any of semantic types, the number in set UinP∩!NU is far more than UinP∩NU, !UinP∩NU, or !UinP∩!NU. Hence, the whole effect of experiments heavily depends on the effect of experiments on UinP∩!NU. According to Table 6, the proportion of UinP∩!NU is far higher than UinP∩NU, !UinP∩NU and !UinP∩!NU for any of Distance, Weight, Speed, Time, Volume, Area, and Power. The proportion of !UinP∩NU is far higher than UinP∩NU, UinP∩!NU and !UinP∩!NU for Count.
The correctness ratio of queries is used to evaluate our approach. The correctness ratio of queries is calculated according to Equation (3). Correct answers are defined according to our knowledge. A correct answer is a 3-tuples (lb, ub, SU), where, lb and ub are values, SU is a SI unit. A final answer (v, u) is said to be correct if v is between lb and ub and u is same to SU. Otherwise, it is said to be incorrect. For instance, the correct answer of query (dog, weight) is (1.36, 81.81, kg). If a quantity is (30.0, kg), the quantity is said to be correct. The correctness ratio of queries is shown in Table 7.
- N is the number of queries.
- Nc is the number of the queries for which correct final answers are returned.

Table 7.
Correctness ratio of queries.
Figure 2 illustrates the direct-viewing chart of correctness ratio of queries. For Count, the correctness ratios of !UinP∩NU and !UinP∩!NU are high. Some queries fail because incorrect quantities are not dropped.
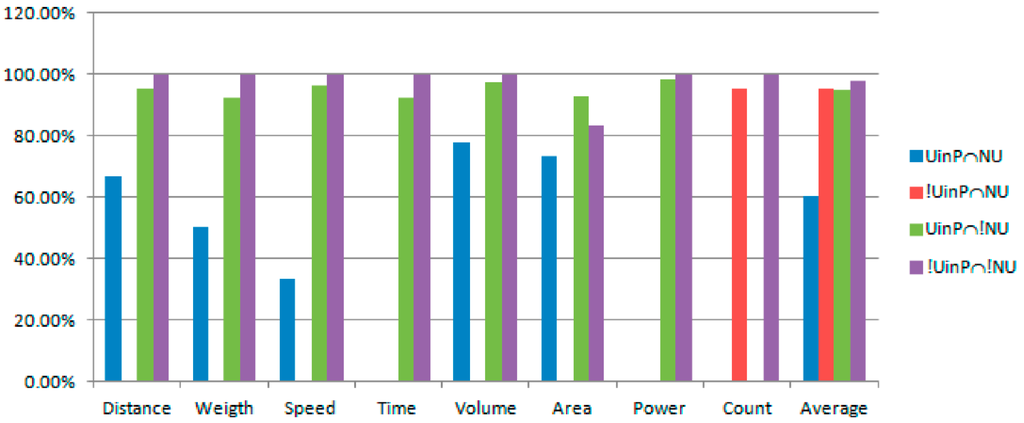
Figure 2.
The direct-viewing chart of correctness ratio of queries.
For any of Distance, Weight, Speed, Time, Volume, Area, and Power, the correctness ratio of UinP∩!NU and !UinP∩!NU are far higher than UinP∩NU. It shows that it gets better results than all of the candidate answers that are not absent of units. The correctness ratio of UinP∩!NU is higher than the correctness ratio of !UinP∩!NU because the number of UinP∩!NU is far more than !UinP∩!NU. For UinP∩!NU and !UinP∩!NU, some queries fail because incorrect quantities are not dropped. For UinP∩NU, there are two exceptions that do harm to the correctness ratio. The first exception is that the ratio records with a maximum fit degree are possibly more than one.
For example, quantity is {521,000, 521}. By calculating the fit degree, two ratio records with a maximum fit degree are obtained from the ratio model. The first ratio record is “millimetre:metre = 1000:1”. The second ratio record is “litre:cubic metre = 1000:1”. Obviously, only one of the two ratio records is correct. However, the proposed approach could not distinguish between them. Another exception is that the relationship between quantities is not discerned. For query (Russia, Area), seven quantities 79,400, 16,995,800, 17,075,200, 79400, 16,995,800, 17,075,200, 560 are returned. According to our approach, the final answer is (12.049779, m2). The correct answer is (17.035500 × 1012, m2). After looking up the sources of the quantities, we know that the quantity 17,075,200 is the total area of Russia. Quantity 16,995,800 is the land area of Russia. Quantity 79,400 is the water area of Russia. These data are clustered to three clusters, Cluster1 = {16,995,800, 17,075,200, 16,995,800, 17,075,200}, Cluster2 = {79,400, 79,400}, and Cluster3 = {506}. According to our approach, the units of the quantities of Cluster1 are inferred as “square millimetre”. The units of the quantities of Cluster2 are inferred as “square centimetre”. The units of the quantities of Cluster3 are inferred as “square inch”. The final answer based on the proposed approach is incorrect because the semantic relationship of quantities such as “total area”, “land area”, and “water area” is not considered in our approach. The equation model “landarea + waterarea = totalarea” should be introduced. Quantities 1,699,580, 79,400, and 17,075,200 are fitting for the equation model “landarea + waterarea = totalarea” rather than the ratio model. It is shown that besides the ratio model, more models should be considered in our approach.
5. Related Work
There are many previous studies concerned with automatically extracting values for numerical attributes. Davidov and Rappoport presented a strategy to extract and approximate numerical attributes from the web [6]. Attribute values (range) of the given object are inferred based on attribute values of similar objects. Likewise, our approach is based on a set of quantities. However, the set of quantities in our approach has less noise because quantities are obtained only based on the given object. For similar objects, the attribute values probably have a great difference. For example, the area of Russia is far larger than that of the Netherlands. Russia is not appropriate as a similar object of Netherlands. Moriceau presented an approach to numerical answers generation which serves a Q and A system [7]. The results are that candidate answers are only displayed to users. Some comments, which are generated by a set of logical rules, are attached to candidate answers. Compared to Moriceau’s work, we devote ourselves to processing candidate answers and generating a final answer. Maiya et al. employed a rule-based approach to extract measured information from a text document, e.g., scientific and technical documents [8]. The converted error, e.g., from PDF format to Word format, is also distinguished by their approach. Chakrabarti et al. aggregated snippet quantity and snippet text information from multiple information sources and proposed a statistical approach to learn to score and rank quantity intervals [9]. In addition, Chakrabarti et al. applied the approach to web tables [10]. Some extraction templates based on linguistics or wrappers need to be learned. Compared to extraction templates and wrappers, it takes minimal effort to build a PUT. Additionally, extraction templates and wrappers are domain-dependent and PUT is domain-independent. It is a critical task to recognize various formats of quantities in Chakrabarti’ approach. Accordingly, it is the key to standardize quantities, e.g., inferring the units of quantities in our approach. Takamura and Tsujii employed a combined regression and ranking model with two types of fragmentary clues, including absolute clues and relative clues, to extract numerical attributes of physical objects [3]. The numerical attributes are extracted from absolute clues directly. Relative clues are used to infer and verify numerical attributes of physical objects. Absolute clues and relative clues are obtained from thesaurus WordNet based on linguistic patterns. Compared to Takamura and Tsujii’s approach, quantities are obtained from a semantic web resource and a final answer is generated by analysing the returned quantity set. Numerical attributes are usually richer than absolute clues. Hence, our approach is suitable for a rich dataset.
A number of efforts have been made to solve the final answer in question-answering [11]. To the best of our knowledge, the process of answer solving is often divided into three phases [12]. The first phase is to retrieve quantities from information sources, such as databases and the web. Quantity retrieval is supported by some general tools such as ODBC and search engines. The second phase is to recognize the relations between two quantities. These relations are equivalence, inclusion, aggregation, and alternative [13,14]. The third phase is to decide the final answer. The common approach is to select the most frequent answers as the final answer. The result of the second phase has a significant impact on the final answer. Hence, we compare our strategy with the previous work on relation recognition.
- Equivalence. Generally, quantities are divided into a LOCATION category, DATE category, NUMBERIC category and text category. For the LOCATION category, DATE category, and NUMBER category, a normal format is defined [13,15]. For example, the format of DATE is defined as mm/dd/yyyy. The format of LOCATION is defined as the short form specified in the CIA World Factbook. The format of NUMBERIC is defined as a value-unit pair. Two quantities are equivalent if their values are the same after they are normalized. For the text category, the techniques for equivalence recognition include measuring the string similarity [16,17,18] or semantic similarity [19] between quantities. In our work, the categories of answers are limited to NUMBERIC. The format of answers is the value-unit pair. Two quantities are also the same after their values are the same.
- Inclusion. Quantities in the text category are perhaps connected through a hypernym or hyponymy relation in WordNet [20,21]. For example, “western Pacific” is included in “Pacific”. Dalmas and Webber recognized the inclusion relation between quantities [22]. Quantities with an inclusion relation are viewed as the same answer. In our work, the inclusion relation is not recognized because the quantities are limited to the NUMBERIC category.
- Contradiction. For quantities in the text category, contradictory quantities are antonymous, negative or in contrast. Harabagiu et al. applied a maximum entropy model to detect contradictory quantities [23]. Based on linguistic features, such as factual or modal words, structural and lexical contrasts, and world knowledge, De Marneffe et al. used logistic regression to detect contradictory quantities [24]. In our work, contradictory quantities are not detected. However, we introduce the definition of semantic type. If the semantic type of a quantity is different from the semantic type of a query, the quantity is dropped from the quantity set.
Old approaches to questions classification are based on linguistics. Some patterns are built in advance according to a semantic dictionary, such as Wordnet, Hownet, etc. Similarity is computed between object questions and patterns. The most similar pattern is selected as the class of the object question. After all, natural language is extremely flexible so that patterns are difficult to meet all kinds of object questions. Recent approaches are based on machine learning. Classes, such as UIUC (University of Illinois at Urbana-Champaign) data set are usually provided in advance. Consequently, a classifier is built according to feature words which are extracted from questions. Feature words of object questions are inputted into a classifier and the classifier outputs the classes of object questions. Approaches of questions classification are displayed in Table 8. The features are divided into lexical feature [25,26,27] (word bags, word format, sentence length), syntax feature [25,26,27,28,29] (the part of speech, the question word, head word, dependency structure), and semantic features [27] (hypernym, synonyms). Syntax feature is the primary feature. Bayesian classifer [25,29], SVM (Support Vector Machine) [25,26,27,29], KNN (k-NearestNeighbor) [25], and neural net [27,28,29] are employed to class questions. SVM is more popular than other classifers. The classification effect based on multiple features is better than that based on a single feature. The classification effect of integrated classifiers is superior to a single classifier.

Table 8.
Approaches of Questions Classification.
6. Conclusions and Future Work
In this paper we built the Predicates-Units Table as a prior knowledge base. Based on the Predicates-Units Table, we propose a set of algorithms for the semantic type of quantity set computation, quantity optimizing, units of quantity inference, and final answer solving. The results of the experiments show a high correctness ratio, although there are some limitations on semantic knowledge.
Our approach is very useful for information processing area, particularly the combination of machine learning, domain ontologies, and a human-in-the-loop [30,31]. In future research, we will apply our approach to biomedical area. Additionally, we will extend the Predicates-Units Table to an ontology so that more semantic knowledge, such as is-a relation and part-of relation between units could be included. For instance, we will define is-a relation between units “area” and “totalarea”, between units “area” and “landarea”, and between units “area” and “waterarea”. Furthermore, we will define part-of relation between units “totalarea” and “landarea”, and between units “totalarea” and “waterarea”. According to these relations, we are able to define equation “landarea + waterland = totalarea”. The equation is very helpful to infer units of quantities. For query (Russia, area), quantities 1,699,580, 79,400, and 17,075,200 are fitting for the equation “landarea + waterarea = totalarea” rather than the ratio model. A useful conclusion is that units of quantities 1,699,580, 79,400, and 17,075,200 are the same. The conclusion can avoid inferring the unit quantities incorrectly. We anticipate that better experimental results will be obtained.
Acknowledgments
We thank all reviewers for their useful comments to improve the paper. This work was supported by the Fundamental Research Funds for the Central Universities (3132015043, 3132014036, 3132016348), National Natural Science Foundation of China (61203283), Liaoning Provincial Natural Science Foundation of China (2014025004), The Open Project Program of Artificial Intelligence Key Laboratory of Sichuan Province (2013RZJ02, 2012RYJ02).
Author Contributions
Yaqing Liu conceived the research subject and contributed to the critical suggestions of the paper, Lidong Wang carried out the experiments, Rong Chen drafted the paper, Yingjie Song and Yalin Cai contributed to the conception and critical suggestions of the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, K.; Zhao, J.; He, S.; Zhang, Y. Question Answering over Knowledge Bases. IEEE Intell. Syst. 2015, 30, 26–35. [Google Scholar] [CrossRef]
- Zheng, Y.; Jeon, B.; Xu, D.; Wu, Q.M.J.; Zhang, H. Image segmentation by generalized hierarchical fuzzy C-means algorithm. J. Intell. Fuzzy Syst. 2015, 28, 961–973. [Google Scholar]
- Takamura, H.; Tsujii, J. Estimating Numerical Attributes by Bringing Together Fragmentary Clues. In Proceedings of the Human Language Technologies: The 2015 Annual Conference of the North American Chapter of the ACL, Denver, CO, USA, 31 May–5 June 2015; pp. 1305–1310.
- Oren, E.; Delbru, R.; Catasta, M.; Cyganiak, R.; Stenzhorn, H.; Tummarello, G. Sindice.com: A document-oriented lookup index for open linked data. Int. J. Metadata Semant. Ontol. 2008, 3, 37–52. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 2, 224–227. [Google Scholar] [CrossRef]
- Davidov, D.; Rappoport, A. Extraction and approximation of numerical attributes from the Web. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, Uppsala, Sweden, 11–16 July 2010; pp. 1308–1317.
- Moriceau, V. Generating Intelligent Numerical Answers in a Question-Answering System. In Proceedings of the Fourth International Natural Language Generation Conference, Sydney, Australia, 15–16 July 2006; pp. 103–110.
- Maiya, A.S.; Visser, D.; Wan, A. Mining Measured Information from Text. In Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, Santiago, Chile, 9–13 August 2015; pp. 899–902.
- Banerjee, S.; Chakrabarti, S.; Ramakrishnan, G. Learning to rank for quantity consensus queries. In Proceedings of the 32nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Boston, MA, USA, 19–23 July 2009; pp. 243–250.
- Sarawagi, S.; Chakrabarti, S. Open-domain quantity queries on web tables: Annotation, response, and consensus models. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 711–720.
- Mendes, A.C.; Coheur, L. When the answer comes into questions in question-answering: Survey and open issues. Nat. Lang. Eng. 2013, 19, 1–32. [Google Scholar] [CrossRef]
- Heie, M.H.; Whittaker, E.W.D.; Furui, S. Question answering using statistical language modeling. Comput. Speech Lang. 2012, 26, 193–209. [Google Scholar] [CrossRef]
- Moriceau, V. Numerical data integration for cooperative question-answering. In Proceedings of the Workshop KRAQ’06 on Knowledge and Reasoning for Language Processing, Trento, Italy, 3 April 2006; pp. 43–50.
- Webber, B.; Gardent, C.; Bos, J. Position statement: Inference in question answering. In Proceedings of the LREC Workshop on Question Answering: Strategy and Resources, Las Palmas, Spain, 27 May–2 June 2002; pp. 19–25.
- Nyberg, E.; Mitamura, T.; Carbonell, J.G.; Callan, J.P.; Collins-Thompson, K.; Czuba, K.; Duggan, M.; Hiyakumoto, L.; Hu, L.; Huang, Y.; et al. The JAVELIN question-answering system at TREC 2002. In Proceedings of the TREC’02, Gaithersburg, MD, USA, 19–22 November 2002.
- Tellez-Valero, A.; Montes-ntes-Gomez, M.; Villasenor-Pineda, L.; Penas, A. Towards multi-stream question answering using answer validation. Informatica 2010, 34, 45–54. [Google Scholar]
- Kwok, C.; Etzioni, O.; Weld, D.S. Scaling question answering to the web. ACM Trans. Inf. Syst. 2001, 19, 242–262. [Google Scholar] [CrossRef]
- Brill, E.; Dumais, S.; Banko, M. An analysis of the AskMSR question-answering system. In Proceedings of the ACL-02 Conference on Empirical Methods in Natural Language Processing, Philadelphia, PA, USA, 7–12 July 2002; pp. 257–264.
- Bos, J.; Curran, J.R.; Guzzetti, E. The pronto QA system at TREC-2007: Harvesting hyponyms, using nominalisation patterns, and computing answer cardinality. In Proceedings of the 16th Text RETrieval Conference, Gaithersburg, MD, USA, 5–9 November 2007; pp. 726–732.
- Nii, Y.; Kawata, K.; Yoshida, T.; Sakai, H.; Masuyama, S. Question answering system QUARK. In Proceedings of the NTCIR-4, Tokyo, Japan, 2–4 June 2004.
- Pasca, M.; Harabagiu, S. The informative role of WordNet in open-domain question answering. In Proceedings of the 2nd Meeting of the North American Chapter of the Association for Computational Linguistics, Pittsburgh, PA, USA, 2–7 June 2001; pp. 905–912.
- Dalmas, T.; Webber, B. Answer comparison in automated question answering. J. Appl. Log. 2007, 5, 104–120. [Google Scholar] [CrossRef]
- Harabagiu, S.; Hickl, A.; Lacatusu, F. Negation, contrast and contradiction in text processing. In Proceedings of the 21st National Conference on Artificial Intelligence (AAAI’06), Boston, MA, USA, 16–20 July 2006; pp. 755–762.
- Marneffe, M.D.; Rafferty, A.; Manning, C.D. Finding contradictions in text. In Proceedings of the ACL-08: HLT, Columbus, OH, USA, 15–20 June 2008; pp. 1039–1047.
- Gu, B.; Sheng, V.S.; Tay, K.Y.; Romano, W.; Li, S. Incremental Support Vector Learning for Ordinal Regression. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1403–1416. [Google Scholar] [PubMed]
- Gu, B.; Sheng, V.S.; Wang, Z.; Ho, D.; Osman, S.; Li, S. Incremental learning for ν-Support Vector Regression. Neural Netw. 2015, 67, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Huang, X.; Wu, L. Combined Multiple Classifiers Based on TBL Algorithm and Their Application in Question Classification. J. Comput. Res. Dev. 2008, 45, 535–541. [Google Scholar]
- Sagara, T.; Hagiwara, M. Natural language neural network and its application to question-answering system. Neurocomputing 2014, 142, 201–208. [Google Scholar] [CrossRef]
- Hu, B.S.; Wang, D.L.; Yu, G.; Ma, T. An Answer Extraction Algorithm Based on Syntax Structure Feature Parsing and Classification. Chin. J. Comput. 2008, 31, 662–676. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, J.; Tang, M.; Tian, Y.; Al-Dhelaan, A.; Al-Rodhaan, M.; Lee, S. Social network and tag sources based augmenting collaborative recommender system. IEICE Trans. Inf. Syst. 2015, E98-D, 902–910. [Google Scholar] [CrossRef]
- Girardi, D.; Küng, J.; Kleiser, R.; Sonnberger, M.; Csillag, D.; Trenkler, J.; Holzinger, A. Interactive knowledge discovery with the doctor-in-the-loop: A practical example of cerebral aneurysms research. Brain Inform. 2016, 1–11. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).